Abstract
We propose a deformable image registration algorithm that uses anisotropic smoothing for regularization to find correspondences between images of sliding organs. In particular, we apply the method for respiratory motion estimation in longitudinal thoracic and abdominal computed tomography scans. The algorithm uses locally adaptive diffusion tensors to determine the direction and magnitude with which to smooth the components of the displacement field that are normal and tangential to an expected sliding boundary. Validation was performed using synthetic, phantom, and 14 clinical datasets, including the publicly available DIR-Lab dataset. We show that motion discontinuities caused by sliding can be effectively recovered, unlike conventional regularizations that enforce globally smooth motion. In the clinical datasets, target registration error showed improved accuracy for lung landmarks compared to the diffusive regularization. We also present a generalization of our algorithm to other sliding geometries, including sliding tubes (e.g., needles sliding through tissue, or contrast agent flowing through a vessel). Potential clinical applications of this method include longitudinal change detection and radiotherapy for lung or abdominal tumours, especially those near the chest or abdominal wall.
Keywords: Abdominal computed tomography (CT), deformable image registration, locally adaptive regularization, respiratory motion, sliding motion, thoracic CT
I. Introduction
THE GOAL of deformable image registration [1] is to establish correspondence, i.e., to find the spatial mapping from anatomical locations in one image to their matching coordinates in the other image. Accurate correspondence detection is relied upon for nearly every clinical application of image registration. These include: 1) change detection in longitudinal patient datasets, to quantify disease progression or treatment effectiveness [2]; 2) image-based mapping of preoperative surgical plans onto the intraoperative patient in image-guided surgery and radiotherapy [3]; and 3) transfer of population atlas information such as expected functional site locations onto patient images [4]. In this paper, we focus on estimating respiratory motion between computed tomography (CT) images of the lungs and abdomen acquired at inhale and exhale, which is important for building respiratory motion models [5] and for eliminating the confounding effects of respiratory motion when accomplishing the three tasks listed above.
Medical images often contain large regions of nearly homogeneous intensity. In noncontrast CT, these include large organs such as the liver, and lung patches between visible vessels and airways (which are often 1–2 cm apart). In these regions, local deformations are unobservable, and correspondence detection is difficult because of the aperture problem [6]. Since deformable image registration based on image match alone is ill-posed, a regularization term is added to the registration cost function to encourage plausible displacement fields based on some prior knowledge [7]. Therefore, the resulting transformation is a compromise between image similarity and spatial regularity, the regularization completely dictates motion estimation within homogeneous regions, and the regularization forms a very strong prior on the final mapping.
Conventional regularizers enforce smooth transformations, and therefore are inaccurate near the discontinuous motion that occurs when multiple organs move independently. In particular, during respiration both the lungs and abdominal organs exhibit discontinuous sliding motion, which is facilitated by serous fluid-filled spaces between their enclosing membranes. In the lungs, sliding occurs between the visceral and parietal pleural membranes that form the pleural sacs surrounding each lung [8]–[10]. In the abdomen, a prominent sliding interface is at the peritoneal cavity between the abdominal cavity and the abdominal wall [11]. Globally smoothing regularizations will underestimate motion near such sliding boundaries by averaging discontinuous motions, and/or incorrectly smooth motion onto static structures. In general, without introducing additional degrees of freedom at sliding borders, unnecessary compromises in image match will be made for the sake of a motion regularity that does not exist.
The problem of recovering sliding motion using deformable registration, and of handling motion discontinuities in general, is receiving increasing attention in medical image analysis. The first approaches involved segmenting the images into regions that move together, registering each independently, and compositing the results [12]–[14]. Wu et al. [14] used masks to force the region boundaries to match when merging the resulting displacement fields. Risholm et al. [15] allowed the deformation field to “tear” during the registration iterations in regions of high strain, to register preoperative and intraoperative MR images in neurosurgical cases involving retraction. Sparse free-form deformations [16] or nonquadratic norms for the regularization penalty [17], [18] also allow motion discontinuities to develop. Kiriyanthan et al. [19], [20] used joint motion segmentation and registration, related to the Mumford–Shaw functional, to find foreground and background regions which are regularized separately. Freiman et al. [21] also investigated automatic identification of deformation field discontinuities, by evaluating gradients within local affine transformations that had been fit to neighborhoods in the dense deformation field.
Locally adaptive regularization has proven useful for sliding organ registration. Locally adaptive regularization varies across the image domain, and can therefore formulate complex deformation models (e.g., [22]–[25]). Locally adaptive regularization has been used to model spatially varying tissue elasticity or stiffness [26], [27], enforce rigid motion of rigid structures like bones [28], and apply volume preserving constraints to tumours to aid longitudinal change detection [29]. Examples in sliding organ registration include work by Yin et al. [30], who used inhomogeneous, but still isotropic, diffusive regularization to handle motion discontinuities at lung lobar fissures, and Ruan et al. [31], who developed a regularization allowing the shear discontinuities caused by sliding while preventing local volume changes.
The notion of direction-dependent, locally adaptive regularization for sliding motion was first introduced by Schmidt-Richberg et al. in [32]–[34]. Here, organs are not treated as completely independent structures. Instead, this approach allows sliding discontinuities while maintaining the coupling between them (along the direction normal to the sliding interface), and of course encouraging smooth motion within individual organs. Originally formulated for dense deformation fields, the general strategy has been applied to B-spline [35] and thin-plate spline [36] transformation models, and used primarily to register CT images of the lungs. Risser et al. [37] presented piecewise diffeomorphic sliding organ registration within the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, and also added direction-dependent sliding to the LogDemons algorithm. A prior segmentation of the sliding boundaries is required for the majority of the above methods, for which interactive tools [38] and fully-automatic methods (e.g., a workflow of standard image processing methods followed by level set segmentation [39]) have been very recently presented.
In this paper, we develop a locally adaptive regularization method for deformable image registration of sliding organs that is based on anisotropic diffusion smoothing. The work by Schmidt-Richberg et al. [32], [33] served as a starting point. Given a border where sliding is expected to occur, they propose to regularize the motion by explicitly defining separate foreground and background regularization domains, relying on this partitioning to ensure that tangential displacement components are not smoothed across the boundary. In contrast, our regularization is defined over the entire image domain, and achieves sliding by appropriate local weighting and direction-dependent anisotropic diffusion smoothing. This has many advantages. It simplifies gradient computations and implementation, especially when there are many sliding organs (and hence many potential separate domains). It allows open surfaces to be defined for the sliding boundary, allowing for an organ to have both adhesions and free sliding patches, more simply without the need to define boundary conditions for each edge voxel. Furthermore, our approach is more general, and permits the specification of alternative diffusion tensors, allowing, for example, the formulation of a sliding registration for tubular objects such as needles and catheters (as we describe in Appendix A).
We use the registration algorithm to accomplish respiratory motion estimation in longitudinal thoracic and abdominal CT datasets. This paper extends our previous work [40], [41] by providing a detailed description of the registration algorithm and implementation, a more effective optimization scheme, and more comprehensive evaluation with improved results.
A major challenge when comparing deformable image registration methods is that image similarity is a necessary, but not sufficient, condition for registration accuracy [42]. In particular, performance evaluation must include areas where correspondences are uncertain, i.e., homogeneous regions. These are often the most critical regions that motivate registration and data fusion in the first place. However, image match metrics do not measure the quality of the mapping in these areas (hence the original need for regularization), and evaluation of the estimated motion field itself must be used to compare algorithm performance.
The remainder of the paper is organized as follows. Section II describes the principles of sliding motion that underlie our registration algorithm, the novel sliding organ regularization formulation, and the numerical optimization and implementation. In Section III, the method is applied to synthetic, phantom and patient image datasets for validation. Finally, Section IV ends with a discussion of the results and our conclusions.
II. Methods
A. Deformable Nonparametric Image Registration
Let and be the target and moving images to be registered, respectively, on the domains and . The aim of deformable nonparametric image registration is to find a displacement field that warps the moving image to align it with the target image [7]. In this paper, we focus on monomodal images, and so after registration the intensities within the target and transformed moving images should ideally match. In Euler coordinates, this is expressed for each coordinate x ∈ ΩT as
| (1) |
Deformable image registration can be solved by minimizing a cost function, C(u), composed of an intensity (dis)similarity distance measure D(T, M, u) and a regularization S(u), whose relative importance is defined by a parameter α
| (2) |
D(T, M, u) is an image match term that quantifies the intensity differences between the target image and the transformed moving image. For monomodal image registration, the sum of squared differences (SSD) distance measure is appropriate
| (3) |
The regularization S(u) penalizes displacement fields deemed to be unrealistic, and is formulated based on domain knowledge. For example, the diffusive regularization favours smooth transformations by penalizing any gradients in the x,y or z components of the displacement field, and is related to linear, isotropic diffusion, i.e., Gaussian smoothing
| (4) |
where ▽ul(x) is the gradient of the lth scalar component of the displacement field evaluated at x.
B. Sliding Geometries
A regularization for deformable registration of images depicting sliding organs should allow sliding motion discontinuities at expected sliding interfaces, while enforcing smooth motion within individual structures.
Several principles of sliding motion can be uncovered after decomposing the displacement field u into components that are normal (u⊥) and tangential (u∥) to the sliding boundary surface [32], [33]. These principles are visualized in Fig. 1.
1) Sliding motion [Fig. 1(a)]: Sliding motion causes discontinuities in tangential displacements along the normal direction. Such discontinuities should not be penalized close to organ boundaries, but they should be penalized within organs to enforce smooth motion of the entire organ.
2) Intra-organ smoothing (IOS) [Fig. 1(b) and (c)]: Individual organs should deform smoothly, and so both the normal and tangential components of the displacement field (i.e., the displacement vectors themselves) should be smooth in the tangential plane.
3) Inter-organ coupling (IOC) [Fig. 1(d)]: We ensure that organs do not pull apart (a valid assumption for most medical images) and prevent tearing/folding in the displacement field by penalizing discontinuities in the normal displacements along the normal direction.
In summary, we require the equivalent of a globally smoothing regularization (e.g., the diffusive regularization), except that discontinuities from sliding motion are not penalized near organ boundaries. Also, note that registering each region separately using a mask, e.g., [12]–[14], is not guaranteed to satisfy the normal component smoothness required by the inter-organ coupling constraint.
Fig. 1.
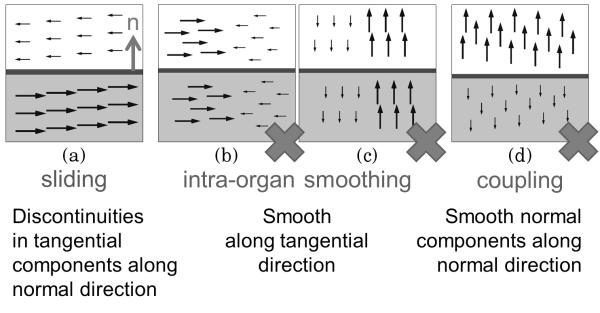
Principles of sliding motion. This example shows the four types of displacement field discontinuities that can occur in a 2-D domain. Vertical arrows are u⊥ (normal components); horizontal arrows are u∥ (tangential components). The motion discontinuities visualized in (b)–(d) should be penalized, but discontinuities that correspond to sliding motion that occur near specified sliding boundaries (a) are allowed.
C. Sliding Organ Deformable Image Registration
The following describes our “sliding organ” (SO) locally adaptive regularization based on inhomogeneous anisotropic diffusion.
1) Anisotropic Diffusion Smoothing
Inhomogeneous anisotropic diffusion implements smoothing with directionality and magnitude dictated by spatially varying diffusion tensors . Smoothing is modeled as the diffusion of particles with concentration against their concentration gradient ▽c(x). The flux (i.e., flow per unit area per unit time) is defined by j(x) = –D(x)▽c(x). j(x) and ▽c(x) are not parallel in general, because an anisotropic diffusion tensor D(x) will further direct the flow along certain preferred directions. The particle concentration evolves over time to reach equilibrium according to
| (5) |
where div is the divergence operator. Additional details and derivations for anisotropic diffusion can be found in [43].
When the diffusion tensor equals the identity matrix, Gaussian smoothing results. From linear algebra, the matrix
| (6) |
is the orthogonal projector onto a given unit normal vector , and the matrix
| (7) |
is the complementary orthogonal projector, which projects onto the plane normal to n(x) (where I is the 3 × 3 identity matrix). Therefore, DN_SO(x) allows diffusion (i.e., smooths) only in the normal direction, and I – DN_SO(x) smooths in the tangential plane. Here, “smooths in the tangential plane” is more accurate than “smooths in the tangential direction,” because for a 3-D image I – DN_SO is a projection onto a 2-D plane, not a 1-D line.
2) Sliding Organ Regularization
We use two locally adaptive diffusion tensors and to formulate the ideas described in Section II-B. In the following sliding organ regularization definition, the first term will penalize gradients in u(x) that violate the intra-organ smoothness constraint, and the second term will penalize gradients in the normal components of u(x) that violate the inter-organ coupling constraint
| (8) |
Near previously-specified sliding boundaries, sliding motion discontinuities will not invoke a cost, and thus are allowed to develop as the registration progresses.
Let be the sliding boundary surface normals based on a prior segmentation. Close to sliding boundaries, we define the diffusion tensor DIOS(x) to smooth all gradients of u(x) in the tangential plane [Fig. 1(b) and (c)], and the diffusion tensor DIOC(x) to smooth all gradients in the normal displacements u⊥(x) along the normal direction [Fig. 1(d)]. Note that the diffusion tensors dictate the smoothing direction, while the gradients ▽ul(x) and are the components of the displacement field that are being smoothed. We use ▽ul(x) in the intra-organ smoothing constraint because we want to penalize gradients in both the normal (u⊥) and tangential (u∥) components if they occur in the tangential plane. We use in the inter-organ coupling constraint because we do not want to penalize gradients in u∥ that occur along the normal direction, since that is sliding motion.
| (9) |
| (10) |
The locally adaptive parameter weights the degree to which sliding is allowed at a particular voxel. It enables a transition from allowing sliding near organ boundaries to using the diffusive regularization within organs. We set w(x) to decay exponentially as a function of the distance d(x) from x to the sliding boundary
| (11) |
where λ is a small constant user-defined parameter.
Near the sliding surface, w(x) ≈ 1 and motion discontinuities related to sliding motion are allowed, while enforcing the intra-organ smoothing and inter-organ coupling constraints. Within organs, w(x) ≈ 0, so DIOS(x) ≈ I DIOC(x) ≈ 0, and (8) collapses to the diffusive regularization defined in (4). The requirement for smooth transformations within individual organs is therefore maintained. Also, the ambiguous choice of n(x) at interior voxels, where w(x) ≈ 0, becomes unimportant. Since the displacement field is defined on the space of the target image, so are the sliding boundaries and the boundary normals. Therefore, n(x), w(x), DIOS(x) and DIOC(x) are all constant throughout the registration optimization, and can be precomputed only once. This is true even if the organ surface deforms between the two images to be registered.
Finally, u⊥(x) is the component of u(x) that is parallel to the surface normal, and is its displacement along the lth axis. is therefore the projection of u(x) onto the lth scalar component of n(x)
| (12) |
Throughout, we assume that the sliding boundary surface is smooth, and can be locally approximated by a plane. However, our formulation is general and (8) through (10) can be extended to consider sliding tubular geometries, as described in Appendix A. Additional subtle differences in the formulation compared to Schmidt–Richberg et al. [32], [33] are described in Appendix B.
D. Numerical Solution
1) Euler–Lagrange Equations
The following Euler–Lagrange equation will hold for the displacement field u that minimizes C(u) [defined in (2)] for all x ∈ ΩT
| (13) |
The gradient of the SSD intensity distance metric (3) at voxel x with respect to an infinitesimal perturbation in u is
| (14) |
The gradient of the sliding organ regularization term at voxel x with respect to u is derived in Appendix C, and equals
| (15) |
| (16) |
| (17) |
with el the lth canonical unit vector (e.g., ex = [1, 0, 0]T).
2) Optimization
Equation (13) is solved using an explicit finite difference scheme, and iteratively optimized using gradient descent with a line search method [44]. Let tk be the time step and uk the displacement field at iteration k. Using a forward difference in time and the initial conditions u0(x) = [0, 0, 0]T
| (18) |
On each iteration, ▽uC(uk–1, x) is computed using (13)–(17). First- and second-order central differences in space are used to calculate discrete gradient and divergence operations in a 3 × 3 × 3 neighborhood around each voxel. ▽uDSSD(T, M, u, x) is calculated by deforming the moving image using linear interpolation. To determine the time step tk in the line search, we found that for a precomputed descent direction ▽uC(uk–1, x), the plot of C(uk) with respect to tk is well approximated by a concave-up quadratic. We, therefore, perform the 1-D line search using second-order polynomial interpolation, based on function values at three sample points, and choose tk at the vertex. If the polynomial interpolation does not give satisfactory results [e.g., tk outside specified minimum/maximum bounds, or leads to an increase in C(uk)], we use golden section search to find tk optimizing C(uk). This setup gives good results while keeping evaluations of C(u) to a minimum, which are relatively expensive.
Registration is performed in a multiresolution framework, with resampling by a factor of two between each level. Before registration, image intensities are rescaled to [0, 1]. The stopping criterion at each level is determined by the convergence of C(u), by defining a minimum slope in C(u) versus t below which the registration is halted and a large number of maximum iterations. The values for α (weighting between the intensity distance measure and the regularization) and λ [the exponential decay constant used to compute w(x)] were determined empirically for each of the validation studies described below. To prioritize image match, for all experiments α was chosen to be roughly the smallest possible value that did not cause tearing or folding.
E. Implementation
The sliding organ registration algorithm is freely distributed as open-source software within the TubeTK Toolkit (www.tubetk.org). The algorithm is implemented in C++ as an Insight Toolkit (ITK) [45] deformable image registration filter, and uses multithreading to speed computations. The registration tool can be used either via the command line, or using a graphical user interface within 3D Slicer (www.slicer.org), an open-source software application for medical image computing and visualization [46].
F. Segmentation of Sliding Boundaries
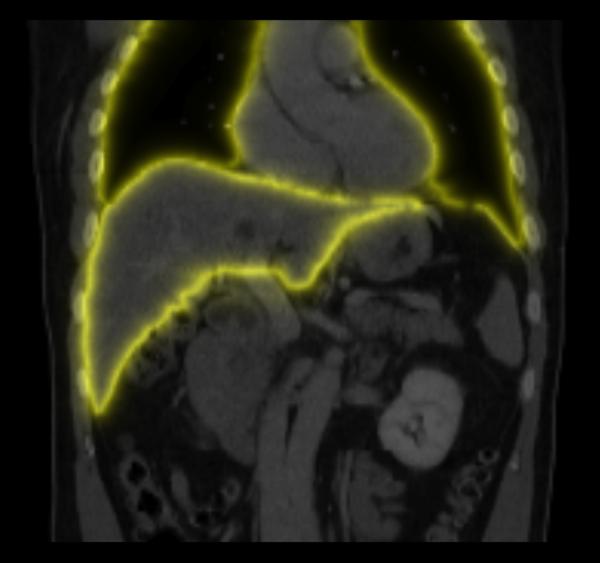
We segment the target image to define the sliding boundary surface(s), which is required to compute the images n(x) and w(x) (Fig. 2). Image segmentation is described separately for each validation study presented in Section III. A surface model is constructed using the Marching Cubes [47] implementation provided by 3D Slicer, and is stored as Visualization Toolkit (VTK) polydata [48]. We found that some surface model smoothing and decimation was beneficial, to remove any sharp corners caused by noise in the label map and reduce the computation time, respectively. The model may represent more than one organ. The normal vector n(x) is set to that of the nearest vertex on the surface model. At each voxel, the minimum distance d(x) to the polygonal mesh triangles is calculated. Especially when several multiresolution levels are used in the registration, it is useful to add the stipulation that any voxels that intersect the surface model have d(x). These distances are used to calculate the weight image w(x) using (11).
Fig. 2.
Sliding boundary normals n(x) and weights w(x). (a) Example surface models and associated normals extracted using image segmentation, which are subsequently discretized onto the image grid using nearest neighbors interpolation; (b) Example slice through the weight image w(x). At sliding boundaries, w(x) ≈ 1 and sliding motion may occur, while inside organs w(x) ≈ 0 and all motion discontinuities should be penalized.
III. Validation
Several datasets were used to validate the accuracy of the sliding organ registration method, and to compare its results to those from registration with the diffusive regularization, a globally smoothing regularizer [(4)].
1) A synthetic dataset of sliding geometrical shapes, which demonstrates better recovery of known applied displacements.
2) Simulated full-inhale/systole and full-exhale/diastole chest CT images created using the XCAT software phantom. This characterized the different displacement fields from the two regularizations in anatomically realistic images with especially large homogeneous regions, in which case the regularizer is especially influential.
3) Ten inhale and exhale thoracic CT image pairs, from the DIR-Lab open dataset [49], plus four inhale and exhale abdomial CT image pairs from Children’s National Medical Center/Stanford. We demonstate reduced target registration error (TRE) in the thoracic images and in the lungs of the abdominal images, and recovery of sliding motion in both.
We use landmarks to evaluate TRE wherever possible. Some abdominal organs, e.g., the liver, lack internal structure that is visible on CT that can be used to evaluate accuracy. In these cases, we also report Dice coefficients for the segmented organ, augmented with surface-to-surface distance measures to add another physically meaningful metric in millimeters. Finally, we examine the displacement field itself for the plausibility of the resulting correspondences.
Note that experiments (1) and (2) are extensions of our previous work [40], showing improved results with updated software and optimization process.
A. Synthetic Dataset
1) Registration Task
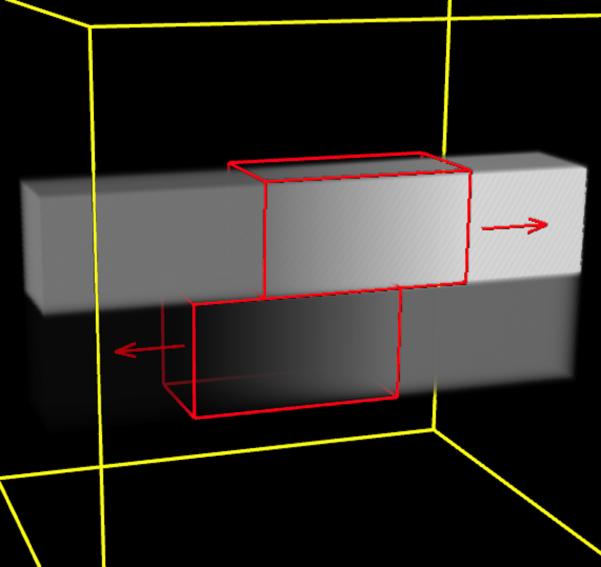
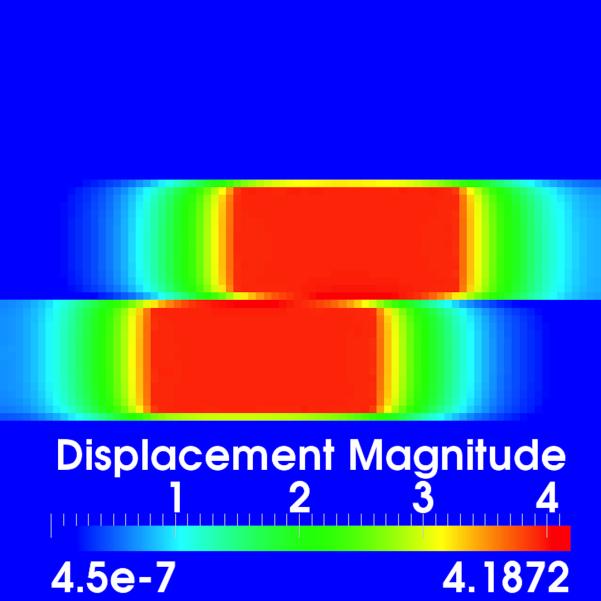
The sliding organ registration method was first evaluated using 3-D images of simple geometrical objects, which slide against each other and against their background. The two images to be registered [Fig. 1(a)–(c)] each contain two blocks suspended within a dark background. From left to right, each block has uniform intensity, followed by a ramp of increasing intensity, followed again by a uniform (higher) intensity. To mimic sliding motion in the moving image, the intensity ramp section in the upper block was translated four voxels to the right, and the intensity ramp section in the lower block was translated four voxels to the left. Fig. 3(c) shows a volume rendering of the target image with superimposed annotations of the applied motion. Each image has dimensions 80 × 80 × 80 with isotropic 1 mm3 spacing.
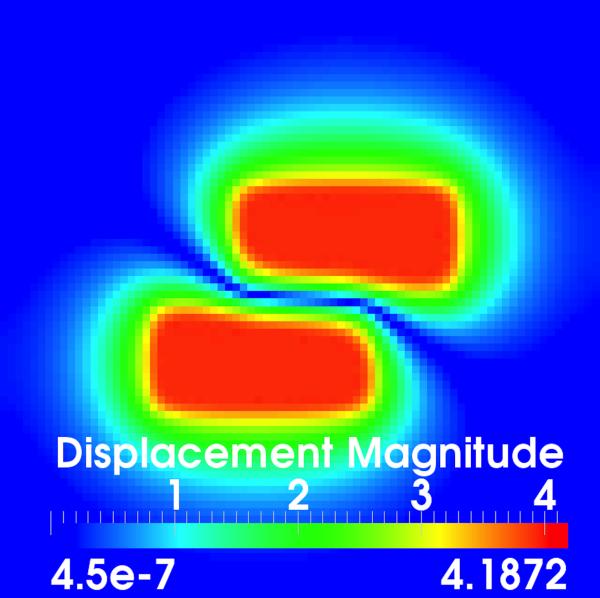
Fig. 3.
Evaluation using synthetic data. (a)–(b) Corresponding slices through the target and moving images, respectively; (c) Volume rendered target image with annotations of the applied translations; (d)–(e) Displacement field magnitudes (mm) for the diffusive and sliding organ regularizations, respectively. The sliding registration better captures the left and right block translations.
For this demonstration, we used SSD with normalized gradients1. This version gives a unit update vector ▽uDSSD(T, M, u, x) for all voxels with an intensity mismatch between the two images. The target and moving images were registered with one resolution level, using λ = 0.1 and α = 3, with uniform time step tk = 0.03 for 1000 iterations. Segmentation of the sliding boundaries is given by construction in this synthetic example.
2) Image Match and Displacement Fields
This example illustrates how using a globally smoothing regularization produces incorrect motion estimates when sliding motion is present, which can lead to a reduced image match after registration.
Fig. 3(d) shows a slice through the displacement field after registration with the diffusive regularization. It is clear that the estimated displacements do not match the applied translations, both at the interface between the two sliding boxes and in the dark background regions, which should be stationary. In contrast, the sliding organ registration [Fig. 3(e)] effectively isolates the motion within the translated blocks and preserves the motion discontinuities at the object interfaces.
Table I summarizes the displacement error magnitudes ∥uapplied(x) – u(x)∥ evaluated within the translated intensity ramp sections of the two blocks. The sliding organ registration more accurately estimates the known applied motion. Table I also shows that the diffusive regularization leads to a worse SSD by forcing smooth motion, while image match is better using the sliding organ registration.
TABLE I.
Accuracy Results for Registration in the Synthetic Dataset. SSD Is Reported for an Intensity Range of 0–1. Displacement Vector Error Magnitudes Are in the Intensity Ramp Sections of the Translated Blocks Only, Given as Mean ± Standard Deviation. The Sliding Organ Registration Is More Accurate Than the Diffusive Registration
| SSD | Displacement vector error magnitudes |
|
|---|---|---|
| Before | 15.28 | 4.00 ± 0.00 mm |
| Diffusive | 1.07 | 0.77 ± 0.88 mm |
| Sliding | 0.17 | 0.28 ± 0.35 mm |
B. XCAT Software Phantom Dataset
1) Registration Task
The second evaluation involved registering simulated chest CT images of the lungs, heart and superior liver generated using the 4-D extended cardio-torso (XCAT) software phantom [50]. The XCAT images are anatomically realistic but have a very simplified intensity profile, with only a few gray levels (Fig. 4). Thus, the large homogeneous regions present a challenging case with which to compare regularization strategies. In this way, we can evaluate how different regularizations would do “on their own” without a dense field of forces from the image match term.
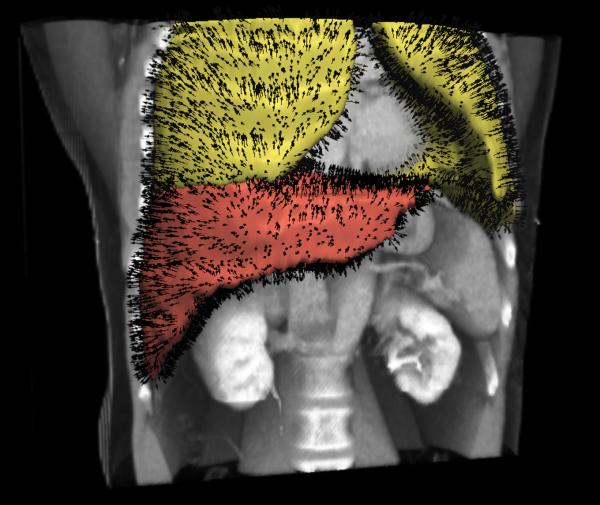
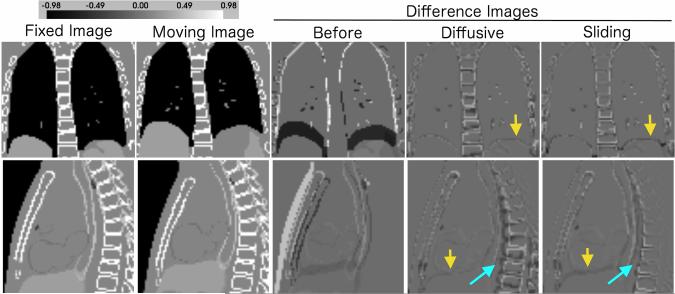
Fig. 4.
Image registration of XCAT phantom images. An ideal difference image is all gray. The sliding organ regularization gives a much better spine alignment (light blue arrows), while maintaining good registration of the heart, lungs and liver. The diffusive registration does have a better alignment at the lung-liver interface (yellow arrows) in the XCAT phantom images.
The XCAT phantom models human anatomy using images from the Visible Human Project, and creates images corresponding to user-defined respiratory rate, heart rate, and other parameters by applying motion models to organ surfaces represented by nonuniform rational B-splines (NURBS). Note that although the phantom can output the displacement field generated by the motion models, these have undergone significant smoothing [50]. This does not impact the realism of the organ shapes in the output images, but does preclude us from using the output displacement fields as a gold standard when characterizing discontinuous motion estimation.
The XCAT phantom was used to generate a target image at full inhale and systole, and a moving image at full exhale and diastole. Parameters corresponding to a typical healthy person were used (respiratory period 5 s, cardiac cycle 1 s), and the resulting six gray levels were adjusted to match those of a typical CT scan. The motion to be estimated includes the chest and lung expansion, the liver’s downward motion, the heart’s contraction, and the heart’s anterior and inferior motion.
The parameters used for registration were λ = 0.1 and α = 0.05, using two resolution levels and the line search strategy and stopping criteria described in Section II-D. Each image has dimensions 80 × 75 × 74 with isotropic 3.125 mm spacing. The sliding boundary was defined by segmenting the lungs, and thus incorporated both the lung/chest wall interface and the lung/liver interface (diaphragm). Segmentation involved thresholding, manual removal of the smaller bronchi, label map smoothing, surface model generation using Marching Cubes, and surface smoothing and decimation.
2) Image Match
Image registration results are shown in Fig. 4. In Table II, we report Dice coefficients and surface to surface distances calculated before and after registration. To calculate these, the lungs, liver and bones (ribs and spine) can be easily segmented in the original and transformed moving images via thresholding. For each pair of segmentations to be compared, the Dice coefficient is
| (19) |
The distances between organ surfaces were computed on generated surface models of the lungs, liver, and bones. The lower diaphragm surface and points within 1 cm of the lower boundary were eliminated from the lung surfaces, as this is replicated on the liver surface. The unsigned minimum surface vertex distances were computed using MeshValmet (www.nitrc.org/projects/meshvalmet), combining both the forward and backward distances.
TABLE II.
Accuracy Results for XCAT Phantom Image Registration. The Bone Class Includes Both the Spine and Ribs. The Sliding Registration Could Achieve a Smaller SSD Than the Diffusive Registration, and Is Better at Simultaneously Aligning the Bones. SSD Is Reported for an Intensity Range of 0–1. Surface Distances Are Unsigned Vertex Distances, Given as Mean ± Standard Deviation, in Millimeters
| Dice Coefficients | ||||
|---|---|---|---|---|
| SSD | Bone | Lungs | Liver | |
| Before | 3117.83 | 0.58 | 0.79 | 0.77 |
| Diffusive | 1553.77 | 0.54 | 0.99 | 0.97 |
| Sliding | 1528.95 | 0.66 | 0.98 | 0.94 |
| Surface Distances | |||
|---|---|---|---|
| Bone | Lungs | Liver | |
| Before | 2.21±3.32 | 5.66±4.25 | 8.26±6.38 |
| Diffusive | 2.04±2.66 | 0.17±0.47 | 1.21 ±1.33 |
| Sliding | 1.41±2.16 | 0.23±0.62 | 2.09±2.51 |
As shown in Table II and Fig. 4, the sliding organ registration could achieve better SSD image match after registration than the diffusive registration, and the Dice and surface distance metrics show that it was also much better at registering the spine. This is a good illustration of how modeling sliding in the motion prior can improve global registration results, allowing to simultaneously align multiple independent objects. In contrast, the diffusive registration actually reduces the bone Dice score compared to the value before registration. However, the diffusive registration does give a better alignment at the lung-liver interface. Including sliding at the boundary between the liver and the spine would completely decouple their inferior-superior (I-S) motion, and may remove any associated inhibition of the liver’s upward motion.
3) Displacement Fields
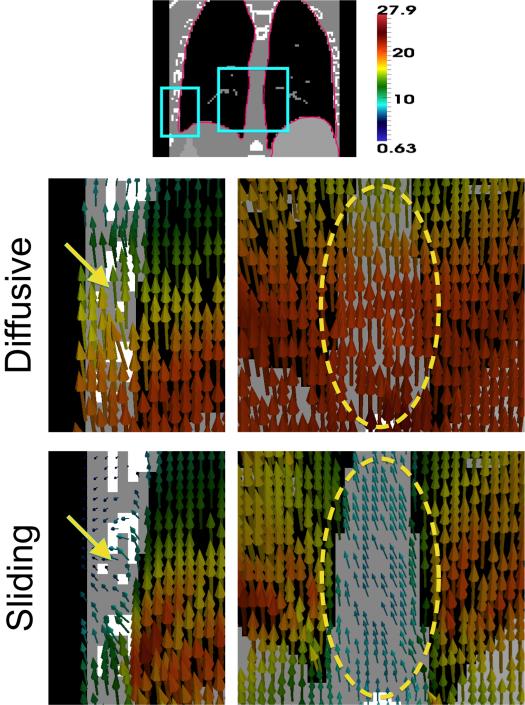
Fig. 5 illustrates the sliding motion recovered at the lung boundaries, both at the lateral sides and near the spine/mediastinum. This is compared to the smooth motion estimated by the diffusive regularization, which overestimates motion in the chest wall and spine. There is a significant difference in the estimated displacement fields ∥udiffusive(x) – usliding(x)∥ has mean 3.89 mm and standard deviation 3.07 mm. Difference vector magnitudes in the lungs are relatively small; instead, the biggest differences are in the spine, with magnitudes up to 2 cm inferiorly. There are also differences in the displacements measuring up to 1 cm in the chest wall, heart and liver. We note that in this example, the sliding organ regularization estimates less liver motion than the diffusive regularization, which gives smoother motion.
Fig. 5.
Representative displacement field patches from registering the XCAT images. The pink border in the top image shows the input sliding boundary. The diffusive regularization overestimates motion at the chest wall (yellow arrow) and mediastinum (yellow circle), while the displacement field from the sliding organ regularization shows sliding at these interfaces. Displacement vectors are from the target image (inhale) to the moving image (exhale), colored by displacement magnitude (mm).
C. Patient CT Image Pairs
1) Registration Task
We evaluated the sliding organ registration using fourteen paired inhale-exhale CT images from freely available datasets. This included ten thoracic CT patient images from the DIR-Lab dataset [49], plus four abdominal CT images hosted on ITK’s medical development database2 provided by researchers at Children’s National Medical Center and Stanford. Of the abdominal cases, Patient 3 showed substantial gating artifacts and was excluded from the study. In all cases, we selected the end-inhale image (0%) as the target image and the end-exhale image (50%) as the moving image.
The DIR-Lab images are cropped on the lungs, and show clear sliding motion at the chest wall interface. The four abdominal images depict the abdominal organs (liver, colon, intestines, etc.), the heart, and either the whole lungs or their lower half. The abdominal images show sliding between the abdominal wall and the abdominal organs (including the liver) in addition to the sliding at the lung boundary.
The lungs were segmented in all 14 images using 3D Slicer’s thresholding, island removal, label map smoothing, morphological and manual editing operators. The abdominal dataset includes expert manual segmentations of the liver. Before registration, the images were cropped, thresholded and intensity normalized. The abdominal images were linearly resampled to isotropic 2 mm3 spacing. The DIR-Lab images were registered at their original resolution, approximately 1 × 1 × 2.5 mm. The registration parameters were λ = 0.1, α = 0.02 (DIR-Lab) and λ = 0.2, α = 0.02 (abdominal), with three resolution levels, a line search to find the time step for each iteration, and stopping criterion based on convergence evaluated within body voxels only.
2) Image Match
Image match was evaluated using TRE. Each DIR-Lab dataset has 300 landmarks for registration accuracy evaluation. For the abdominal datasets, we computed TRE using approximately 75 manually identified landmarks: ≈55 on vessel/airway bifurcations in the lungs, and ≈20 on uniquely identifiable points inside the abdomen or heart. For the abdominal datasets, we also report Dice coefficients and surface to surface distances for the segmented liver. Features (landmarks or segmentations) were identified in both the target and moving images, and the moving image features were warped by the registration displacement field for subsequent comparison.
The DIR-Lab results are shown in Table III, and the abdominal CT results are shown in Tables IV and V. In all cases, both the diffusive and sliding registrations gave a statistically significant improvement in TRE compared to the values before registration (p = 0.05). The sliding organ regularization showed improved accuracy for lung registration in both datasets. For the DIR-Lab data, the average TRE was reduced from 3.71 ± 4.11 mm (diffusive) to 2.78 ± 2.96 mm (sliding). For reference, the results reported by Schmidt–Richberg et al. [33] were 3.02 ± 2.79 mm for the diffusive regularization and 2.13 ± 1.81 mm for their sliding implementation. The differences between these results are likely due to parameter selection and optimization strategy, especially for the diffusive registration as the same energy was implemented. In the abdominal CT dataset, the average TRE in the lungs was reduced from 2.39 ± 1.77 mm (diffusive) to 2.15 ± 1.42 mm (sliding). However, in the abdominal dataset there was some compromise in alignment of the abdominal landmarks. The TRE for the diffusive registration was 2.30 ± 1.45 mm, versus 2.53 ± 1.62 mm for the sliding registration. The Dice scores and surface distances for global liver alignment show a very slight improvement for the diffusive regularization: approximately 0.003 in Dice and <0.1 mm for surface distance. From these results, we conclude that the sliding organ registration is superior for lung registration, but that the application for abdominal registration is less certain.
TABLE III.
TRE Evaluating Registration Accuracy in the DIR-Lab Thoracic CT Cases. All Values in Millimeters. A (+) Indicates a Statistically Significant (p < 0.05) Improvement When Comparing the Diffusive and Sliding Registrations. The Sliding Organ Registration Shows a Reduced TRE, Indicating Better Registration Accuracy for Lung Registration
| DIR-Lab Thoracic CT Target Registration Error | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | All | ||
| Samples | N | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 3000 |
| Before | Mean | 3.89 | 4.34 | 6.94 | 9.83 | 7.48 | 10.89 | 11.03 | 14.99 | 7.92 | 7.30 | 8.46 |
| Stdev | 2.78 | 3.90 | 4.05 | 4.86 | 5.51 | 6.97 | 7.43 | 9.01 | 3.98 | 6.35 | 6.58 | |
| RMS | 4.78 | 5.83 | 8.04 | 10.96 | 9.28 | 12.92 | 13.29 | 17.49 | 8.86 | 9.67 | 10.72 | |
|
| ||||||||||||
| Diffusive | Mean | 1.29 | 1.70 | 2.80 | 2.89 | 3.78 | 3.98 | 5.89 | 8.22 | 3.30 | 3.29 | 3.71 |
| Stdev | 0.80 | 1.50 | 2.38 | 2.33 | 3.14 | 3.41 | 4.57 | 7.51 | 2.43 | 3.76 | 4.11 | |
| RMS | 1.52 | 2.27 | 3.67 | 3.71 | 4.91 | 5.24 | 7.45 | 11.12 | 4.09 | 4.99 | 5.54 | |
|
| ||||||||||||
| Sliding | Mean | 1.06 (+) | 1.45 (+) | 1.88 (+) | 2.04 (+) | 2.73 (+) | 2.72 (+) | 4.59 (+) | 6.22 (+) | 2.32 (+) | 2.82 (+) | 2.78 (+) |
| Stdev | 0.57 | 1.00 | 1.35 | 1.40 | 2.13 | 2.04 | 3.41 | 5.69 | 1.42 | 2.50 | 2.96 | |
| RMS | 1.21 | 1.76 | 2.31 | 2.48 | 3.46 | 3.40 | 5.72 | 8.42 | 2.72 | 3.76 | 4.06 | |
TABLE IV.
TRE Evaluating Registration Accuracy in the Abdominal CT Cases. All Values in Millimeters. A (+) Indicates a Statistically Significant (p < 0.05) Improvement When Comparing the Diffusive and Sliding Registrations. The Sliding Organ Registration Shows a Reduced TRE in the Lung Landmarks, Indicating Better Registration Accuracy There
| Abdominal CT Target Registration Error | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lung Landmarks | Abdominal Landmarks | ||||||||||
| P0 | P1 | P2 | P4 | All | P0 | P1 | P2 | P4 | All | ||
| Samples | N | 52 | 55 | 56 | 56 | 219 | 21 | 22 | 21 | 20 | 84 |
| Before | Mean | 10.89 | 6.83 | 5.11 | 5.61 | 7.04 | 9.08 | 5.89 | 6.30 | 4.42 | 6.44 |
| Stdev | 3.81 | 2.57 | 3.01 | 4.82 | 4.27 | 2.89 | 3.15 | 2.76 | 3.30 | 3.42 | |
| RMS | 11.52 | 7.29 | 5.92 | 7.37 | 8.23 | 9.51 | 6.65 | 6.85 | 5.47 | 7.28 | |
|
| |||||||||||
| Diffusive | Mean | 3.46 | 1.77 | 2.13 | 2.28 | 2.39 | 2.06 | 2.10 | 2.25 (+) | 2.82 | 2.30 (+) |
| Stdev | 2.39 | 0.76 | 1.10 | 1.94 | 1.77 | 1.10 | 1.23 | 1.41 | 1.92 | 1.45 | |
| RMS | 4.19 | 1.93 | 2.39 | 2.98 | 2.97 | 2.32 | 2.42 | 2.64 | 3.39 | 2.71 | |
|
| |||||||||||
| Sliding | Mean | 2.89 (+) | 1.64 (+) | 2.12 | 1.99 (+) | 2.15 (+) | 2.27 | 2.38 | 2.79 | 2.80 | 2.56 |
| Stdev | 2.03 | 0.66 | 1.01 | 1.39 | 1.42 | 1.23 | 1.55 | 1.75 | 1.94 | 1.62 | |
| RMS | 3.52 | 1.77 | 2.34 | 2.42 | 2.58 | 2.57 | 2.82 | 3.27 | 3.38 | 3.02 | |
TABLE V.
Dice Coefficients and Surface Distances Evaluating Abdominal CT Registration Accuracy. Surface Distances Are Unsigned Vertex Distances in Millimeters (mm), Given as Mean ± Standard Deviation
| Dice Coefficients | Surface Distances | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P0 | P1 | P2 | P4 | All | P0 | P1 | P2 | P4 | All | |
| Before | 0.864 | 0.903 | 0.931 | 0.902 | 0.900 | 4.23±4.50 | 2.98±2.79 | 2.42±2.33 | 3.38±2.82 | 3.18±3.21 |
| Diffusive | 0.957 | 0.967 | 0.967 | 0.941 | 0.958 | 1.41± 1.54 | 1.08±0.97 | 1.15±1.13 | 2.12±2.33 | 1.42±1.61 |
| Sliding | 0.955 | 0.961 | 0.966 | 0.940 | 0.955 | 1.44±1.58 | 1.24±1.19 | 1.21±1.16 | 2.21±2.48 | 1.51±1.71 |
3) Displacement Fields
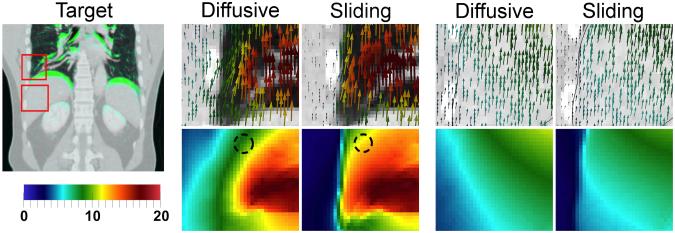
Example displacement field patches from the thoracic and abdominal registrations are shown in Figs. 6 and 7, respectively. The sliding organ registration effectively recovered sliding motion, giving more plausible displacement fields and correspondences, in the left and right lung surfaces near the chest wall, the posterior lung, and near the liver interface with the abdominal wall.
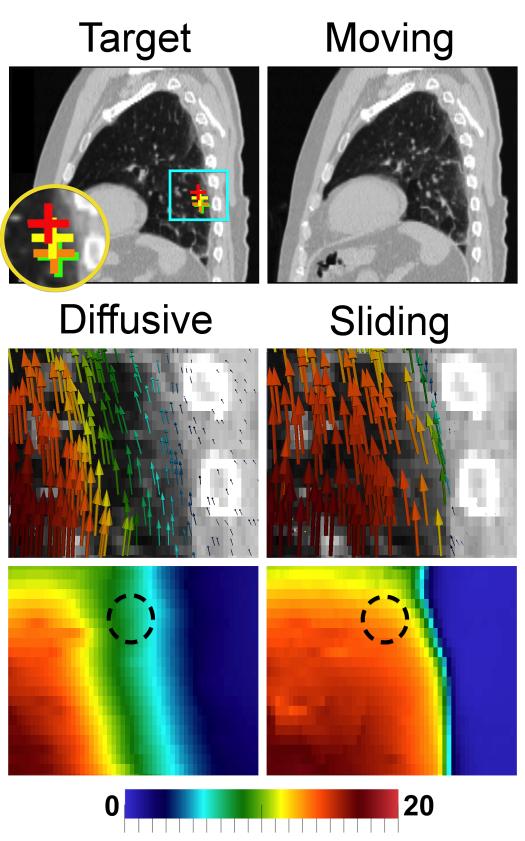
Fig. 6.
Thoracic CT registration (C4). Displacement fields are visualized with glyphs and displacement field magnitude (mm). The diffusive regularization underestimates motion inside the lung near the chest wall. The sliding registration recovers more uniform lung motion, with clear sliding. Crosses on the fixed image show the motion of an example landmark from its moving (red) to target (green) position. The sliding registration (orange) does better than the diffusive registration (yellow) in this region.
Fig. 7.
Abdominal CT registration (P0). At left, the target image (inhale) with superimposed differences in the moving image (exhale) in green. Displacement fields are visualized with glyphs and as displacement field magnitude (mm). In the lungs (middle), the sliding registration gives more uniform lung motion near the lung surface, and prevents incorrect motion overestimation in the chest wall. In the liver (right), the main difference is to fix the motion overestimation in the abdominal wall.
In the lungs, the diffusive regularization underestimates motion near the lung surface, where the “zero” motion in the background is blurred into the body (Figs. 6 and 7). This band of reduced motion was approximately 1.5–5.0 cm deep in the DIR-Lab datasets, and 1.5–3.0 cm deep in the abdominal datasets. The difference vector magnitudes ∥udiffusive(x) – usliding(x)∥ in this region were large: 5–10 mm in the thoracic cases, and 2–6 mm in the abdominal cases. Modeling sliding also removed the false motion that the diffusive regularization estimates in the chest/abdominal wall, compared to the true motion indicated by the ribs. Fig. 7 shows that this type of error was the primary difference near the liver, explaining why the sliding registration did not yield an improvement in accuracy inside the abdomen. Decomposing the displacement fields into left–right, anterior–posterior, and inferior–superior motion (well approximated by the x,y and z components) reveals that in all cases, the motion differences between the two regularizations are almost entirely in the I-S direction, which is the direction in which sliding occurs.
IV. Discussion and Conclusion
We have presented a locally adaptive regularization based on anisotropic diffusion that is designed for registering images of sliding organs. We have shown improved registration accuracy for lung registration in longitudinal thoracic and abdominal CT datasets. The proposed method also gives more realistic displacement fields than a globally smoothing regularization, given that respiration-induced sliding motion is known to occur within the chest and abdomen. This is important for accurate correspondence detection in regions thatlack distinguishing image features. Hence, the sliding organ registration should be useful for tasks such as longitudinal change detection of juxtapleural lung nodules, orradiotherapy for tumours located near a sliding interface.
Key advantages of our formulation are its generality and extensibility. As noted in Appendix C, there is an inherent assumption of a smooth sliding surface boundary so that the gradient can be computed. However, there are cases where organs have relatively sharp edges and the surface smoothness assumption is challenged. Examples include the shape of the lungs near the diaphragm, and the shapes of individual lung lobes (some additional areas where both the lung and liver surfaces have relatively sharp edges can also be seen in Fig. 2). The sliding organ regularization presented in Section II is not designed to directly handle this issue. However, in Appendix A we describe a “geometry conditional” extension that also models sliding of tubular structures, such as needles, catheters and contrast agent flowing through vessels. Although it is not the focus of this paper, the geometry conditional formulation could be extended in future to address the problem of surfaces that are not locally smooth. Specifically, one could modify the tube formulation to specify multiple normals locally at surface edges and corners, with one normal for each of the coincident planes. This would introduce additional degrees of freedom to allow sliding to occur along all of the planes simultaneously, which would address the problem of sharp surface edges.
Registering the clinical CT scans takes several hours. The proposed registration method uses two parameters, α and λ, the first of which is present in all registration methods involving regularization. We found that λ can be tuned fairly easily by picking an exponential decay factor that remains large within 1–2 voxel widths and subsequently decays. However, the method is sensitive to the accuracy of the prior segmentation, since this completely defines the borders along which motion discontinuities are allowed to develop.
An acknowledged limitation of this study is that we modeled sliding around the lungs and liver, but not along the entire abdominal wall. In actuality, the abdominal organs are enclosed in the peritoneal sac, and slide against the abdominal wall as a group. We suspect that enclosing all of the abdominal organs within one sliding surface at the abdominal wall would be a better model of how these organs slide, compared to segmenting the liver alone. Methods for abdominal wall segmentation have been very recently presented [38], [39], and should be taken advantage of in future to further improve the results in the abdomen.
Acknowledgment
The authors would like to thank Dr. A. Enquobahrie, G. Hart, Dr. R. Kwitt, B. Long, C. Mullins, Dr. R. Ortiz, N. Taylor, and Dr. H. Yang for technical assistance and discussions. The authors would also like to thank Dr. P. Segars for providing the XCAT phantom software, the members of the Deformable Image Registration Laboratory at the University of Texas MD Anderson Cancer Center for providing the DIR-Lab data, and Dr. Z. Yaniv and Prof. S. Dieterich for providing the additional four 4D abdominal CT patient datasets.
This work was supported in part by the National Institutes of Health/National Cancer Institute (NIH/NCI) under Grant 1R01CA138419, National Insitutes of Health/National Center for Biotechnology Information (NIH/NIBIB) under Grant 2U54EB005149, in part by NIH/NCI under Grant 1R41CA153488, in part by National Institutes of Health/National Institute of Mental Health (NIH/NIMH) under Grant 1R01MH091645, in part by NIH/NIBIB 5P41EB002025, in part by National Institutes of Health/National Institute of Neurological Disorders and Stroke (NIH/NINDS) under Grant R41NS081792, in part by NIH/NCI under Grant 1R43CA165621, and in part by the National Science Foundation under Grant NSF EECS-0925875 and Grant NSF ECCS-1148870.
Appendix A. Generalization to All Sliding Geometries
In Section II, we assumed that the surface along which sliding occurs is locally planar, i.e., smooth. However, the sliding organ regularization can be extended to handle sliding structures that have tubular geometries [41]. An example of a sliding tube is a needle sliding through tissue, or contrast agent flowing through a vessel.
We will use local structure classifications to form a “geometry conditional” sliding regularization. Image neighborhoods can be classified into four types: those representing homogeneous regions, roughly planar surfaces, tubes, and small point-like (spherical) structures. With respect to sliding motion:
1) Homogeneous regions do not contain a sliding boundary, and should undergo globally smoothing regularization.
2) As described above, for locally planar surfaces we allow sliding motion by not penalizing discontinuities in the tangential displacement components that occur along the plane’s normal direction.
3) For tubes, the tangential direction is along the tube’s axis, and there are two normal vectors. These lie in the tube’s cross-sectional plane, and can be any pair of orthogonal unit vectors that are perpendicular to the centerline. Then, tube sliding also manifests as discontinuities in the tangential displacements that occur in the normal plane. Allowing such discontinuities means that the tube can slide along its axis without influencing its surrounding structures.
4) Extending the above, point-like structures can be thought of as having three orthogonal normals. Spheres do not slide, and so they should also undergo a globally smoothing regularization.
A regularization implementing the rules for all four geometry types can be defined as follows. We begin with a segmentation of the expected sliding surfaces, sliding tubes, and any point-like structures (landmarks). In practice, this classification can come from combining the results of several segmentation algorithms, e.g., a multi-organ segmentation algorithm to define the locally planar surfaces, and a segmenter such as [51] to define tubular structures.
We add the geometry conditional variables a1, a2 : ΩT → {0, 1}. For planes, a1(x) = a2(x) = 0, for tubes a1(x) = 1 and a2(x) = 0, and for points a1(x) = a2(x) = 1. Up to three unit normals, n0(x), n1(x), and n2(x), are included at each coordinate, and are computed according to the given structure segmentations. Again, w(x) is defined based on the distance to the closest segmented geometry. Define as a diagonal matrix with diagonal elements (1, a1(x), a2(x)). Define as a matrix whose columns are given by n0(x), n1(x) and n2(x).
Then, the lth scalar component of the normal displacement is given by
| (20) |
and the diffusion tensor that smooths in the normal direction(s) is
| (21) |
Equations (8)–(10) can now be used to define the sliding regularization as before. The gradient in (15) and (16) is also the same, with the one exception being that (17) is substituted by rl(x) = N(x)A(x)Nl(x).
Appendix B. Comparison to Schmidt–Richberg et al. When w(x) = 1
For the sake of completeness, note that there are subtle differences between our formulation and that of [32], [33] in how motion is smoothed on the sliding boundary itself. Both methods use a function such that w(x) = 1 at the object boundary and w(x) = 0 inside the organ. In the limit case w(x) = 1, the tangential component is not smoothed across the boundary, but it should be smoothed in the tangential plane. When w(x) = 1 (and dropping the (x) notation for conciseness), the regularizer of Schmidt–Richberg et al. takes the form
| (21) |
where ΩT denotes the full target image domain, Γ denotes the domain of the object, Γ ⊂ ΩT, and ΩT \ Γ is the set difference. This can be rewritten as
| (23) |
where ∂ΩT is the boundary between the background and the object, and ΩT \ ∂ΩT is the full domain minus the boundary. When w(x) = 1, our proposed regularization is
| (24) |
Therefore, regularizer (22)/(23) penalizes only the gradient of the normal displacement component on the boundary. In contrast, regularizer (24) also smoothes the tangential components in the tangential plane, as desired.
Appendix C. Derivation of the Gradient of the Sliding Organ Regularization
The derivation of (15)–(17) is as follows. It includes taking the gradient of terms that include the surface normals, so there is an inherent assumption that these terms are sufficiently smooth so that one can differentiate. Relatively smooth surfaces are also required to accurately compute surface normals in the first place, and so that the direction-dependent smoothing using the DIOS and DIOC diffusion tensors is sensible. We drop the (x) notation for conciseness.
Proof
For a given l ∈ {x, y, z} and with P = nnT, we must find the gradient of
from (8). Define
The variation is then
Recalling the definition of the perpendicular component from (12) (with nl a scalar and defining rl := nln)
Hence, , and we can write the variation as
To get rid of the gradient, recall that the negative divergence is the adjoint to the gradient operator which can be seen through the divergence theorem. Assume a vector field F, then the divergence theorem states
where the integral on the right is over the boundary surface ∂Ω of Ω and n denotes the unit outward normal to this surface. Assume that the vector field F can be decomposed as F = Vu, where V is a scalar field and u a vector field. Substituting into the divergence theorem results in
which provides us with the multi-dimensional equivalent to integration by parts. The negative divergence is the adjoint of the gradient operator. Note that this adjoint also creates spatial boundary conditions. We obtain (picking appropriate boundary conditions)
Footnotes
itk::PDEDeformableRegistrationFunction:: SetNormalizeGradient(true)
Community “4D CT—Liver—with segmentations” http://midas.kitware.com/community/view/47
Contributor Information
Danielle F. Pace, Kitware Inc., Carrboro, NC 27510 USA
Stephen R. Aylward, Kitware Inc., Carrboro, NC 27510 USA.
Marc Niethammer, Department of Computer Science and the Biomedical Research Imaging Center, The University of North Carolina at Chapel Hill, Chapel Hill, NC 27514 USA.
References
- [1].Sotiras A, Davatazikos C, Paragios N. Deformable medical image registration: A survey. Inria Res. Centre Saclay, Ile-de-France, Tech. Rep. 2012 Sep.7919 [Google Scholar]
- [2].Li X, Dawant BM, Welch EB, Chakravarthy AB, Freehardt D, Mayer I, Kelley M, Meszoely I, Gore JC, Yankeelov TE. A nonrigid registration algorithm for longitudinal breast MR images and the analysis of breast tumor response. Magn. Reson. Imag. 2009;27(no. 9):1258–1270. doi: 10.1016/j.mri.2009.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Clatz O, Delingette H, Talos I-F, Golby AJ, Kikinis R, Jolesz FA, Ayache N, Warfield SK. Robust non-rigid registration to capture brain shift from intra-operative MRI. IEEE Trans. Med. Imag. 2005 Nov.24(no. 11):1417–1427. doi: 10.1109/TMI.2005.856734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Chakravarty MM, Sadikot AF, Germann J, Hellier P, Bertrand G, Collins DL. Comparison of piece-wise linear, linear, and nonlinear atlas-to-patient warping techniques: Analysis of the labeling of subcortical nuclei for functional neurosurgical applications. Human Brain Map. 2009;30(no. 11):3574–3595. doi: 10.1002/hbm.20780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].McClelland J, Hawkes D, Schaeffter T, King A. Respiratory motion models: A review. Med. Image Anal. 2013;17(no. 1):19–42. doi: 10.1016/j.media.2012.09.005. [DOI] [PubMed] [Google Scholar]
- [6].Beauchemin SS, Barron JL. The computation of optical flow. ACM Comput. Sur. 1995;27(no. 3):433–466. [Google Scholar]
- [7].Modersitzki J. Numerical Methods for Image Registration. Oxford Univ. Press; New York: 2004. [Google Scholar]
- [8].Vandemeulebroucke J, Bernard O, Rit S, Kybic J, Clarysse P, Sarrut D. Automated segmentation of a motion mask to preserve sliding motion in deformable registration of thoracic CT. Med. Phys. 2012;39(no. 2):1006–1016. doi: 10.1118/1.3679009. [DOI] [PubMed] [Google Scholar]
- [9].Wang N-S. Anatomy of the pleura. Clin. Chest Med. 1998;19(no. 2):229–240. doi: 10.1016/s0272-5231(05)70074-5. [DOI] [PubMed] [Google Scholar]
- [10].Agostoni E, Zocchi L. Mechanical coupling and liquid exchanges in the pleural space. Clin. Chest Med. 1998;19(no. 2):241–260. doi: 10.1016/s0272-5231(05)70075-7. [DOI] [PubMed] [Google Scholar]
- [11].Tortora GJ, Derrickson BH. Principles of Anatomy and Physiology. 12th ed Wiley; Hoboken, NJ: 2008. [Google Scholar]
- [12].Rietzel E, Chen GTY. Deformable registration of 4D computed tomography data. Med. Phys. 2006;33(no. 11):4423–4430. doi: 10.1118/1.2361077. [DOI] [PubMed] [Google Scholar]
- [13].Flampouri S, Jiang SB, Sharp GC, Wolfgang J, Patel AA, Choi NC. Estimation of the delivered patient dose in lung IMRT treatment based on deformable registration of 4D-CT data and Monte Carlo simulations. Phys. Med. Biol. 2006;51(no. 11):2763–2779. doi: 10.1088/0031-9155/51/11/006. [DOI] [PubMed] [Google Scholar]
- [14].Wu Z, Rietzel E, Boldea V, Sarrut D, Sharp GC. Evaluation of deformable registration of patient lung 4DCT with subanatomical region segmentations. Med. Phys. 2008;35(no. 2):775–781. doi: 10.1118/1.2828378. [DOI] [PubMed] [Google Scholar]
- [15].Risholm P, Samset E, Talos I, Wells W. A non-rigid registration framework that accommodates resection and retraction. In: Prince JL, Pham DL, Myers KJ, editors. Information Processing in Medical Imaging. Vol. 5636. Springer; New York: 2009. pp. 447–458. (ser. Lecture Notes Compu. Sci.). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Shi W, Zhuang X, Pizarro L, Bai W, Wang H, Tung K-P, Edwards P, Rueckert D. Registration using sparse free-form deformations. In: Ayache N, Delingette H, Golland P, Mori K, editors. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2012) Vol. 7511. Springer; New York: 2012. pp. 659–666. (ser. Lecture Notes Comput. Sci.). [DOI] [PubMed] [Google Scholar]
- [17].Heinrich M, Jenkinson M, Brady M, Schnabel J. Discontinuity preserving regularisation for variational optical-flow registration using the modified LP norm. In: van Ginneken B, Murphy K, Heimann T, Pekar V, Deng X, editors. MICCAI Workshop on Evaluation of Methods for Pulmonary Image Registration (EMPIRE), Medical Image Analysis for the Clinic: A Grand Challenge. Springer; New York: 2010. pp. 185–194. [Google Scholar]
- [18].Pock T, Urschler M, Zach C, Beichel R, Bischof H. A duality based algorithm for TV-L1-optical-flow image registration. In: Ayache N, Ourselin S, Maeder A, editors. Medical Image Computing and Computer Assisted Intervention (MICCAI 2007) Vol. 4792. Springer; New York: 2007. pp. 511–518. (ser. Lectures Notes Comput. Sci.). [DOI] [PubMed] [Google Scholar]
- [19].Kiriyanthan S, Fundana K, Cattin P. Discontinuity preserving registration of abdominal MR images with apparent sliding organ motion. In: Yoshida H, Sakas G, Linguraru M, editors. Abdominal Imaging. Computational and Clinical Applications. Vol. 7029. Springer; New York: 2012. pp. 231–239. (ser. Lecture Notes in Computer Science). [Google Scholar]
- [20].Kiriyanthan S, Fundana K, Majeed T, Cattin P. A landmark-based primal-dual approach for discontinuity preserving registration. In: Yoshida H, Hawkes D, Vannier M, editors. Abdominal Imaging. Computational and Clinical Applications. Vol. 7601. Springer; New York: 2012. pp. 137–146. (ser. Lecture Notes Comput. Sci.). [Google Scholar]
- [21].Freiman M, Voss S, Warfield S. Demons registration with local affine adaptive regularization: Application to registration of abdominal structures. Proc. IEEE Int. Symp. Biomed. Imag.: From Nano to Macro; 2011.pp. 1219–1222. [Google Scholar]
- [22].Cahill N, Noble J, Hawkes D. A Demons algorithm for image registration with locally adaptive regularization. In: Yang G-Z, Hawkes D, Rueckert D, Noble A, Taylor C, editors. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2009) Vol. 5761. Springer; New York: 2009. pp. 574–581. (ser. Lecture Notes Comput. Sci.). [DOI] [PubMed] [Google Scholar]
- [23].Stefanescu R, Pennec X, Ayache N. Grid powered nonlinear image registration with locally adaptive regularization. Med. Image Anal. 2004;8(no. 3):325–342. doi: 10.1016/j.media.2004.06.010. [DOI] [PubMed] [Google Scholar]
- [24].Tang L, Hamarneh G, Abugharbieh R. Reliability-driven, spatially-adaptive regularization for deformable registration. In: Fischer B, Dawant BM, Lorenz C, editors. Biomedical Image Registration. Vol. 6204. Springer; New York: 2010. pp. 173–185. (ser. Lecture Notes Comput. Sci.). [Google Scholar]
- [25].Forsberg D, Andersson M, Knutsson H. Adaptive anisotropic regularization of deformation fields for non-rigid registration using the morphon framework. Proc. 2010 IEEE Int. Conf. Acoust. Speech Signal Process.; 2010.pp. 473–476. [Google Scholar]
- [26].Kabus S, Franz A, Fischer B. Variational image registration with local properties. In: Pluim JP, Likar B, Gerritsen FA, editors. Biomedical Image Registration. Vol. 4057. Springer; New York: 2006. pp. 92–100. (ser. Lecture Notes in Computer Science). [Google Scholar]
- [27].Staring M, Klein S, Pluim JPW. Nonrigid registration with tissue-dependent filtering of the deformation field. Phys. Med. Biol. 2007;52(no. 23):6879–6892. doi: 10.1088/0031-9155/52/23/007. [DOI] [PubMed] [Google Scholar]
- [28].Modersitzki J. FLIRT with rigidity—Image registration with a local non-rigidity penalty. Int. J. Comput. Vis. 2008;76(no. 2):153–163. [Google Scholar]
- [29].Park S, Kim B, Lee J, Goo J, Shin Y. GGO nodule volume-preserving nonrigid lung registration using GLCM texture analysis. IEEE Trans. Biomed. Eng. 2011 Oct.58(no. 10):2885–2894. doi: 10.1109/TBME.2011.2162330. [DOI] [PubMed] [Google Scholar]
- [30].Yin A, Hoffman E, Lin C. Lung lobar slippage assessed with the aid of image registration. In: Jiang T, Navab N, Pluim JP, Viergever MA, editors. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2010) Vol. 6362. Springer; New York: 2010. pp. 578–585. (ser. Lecture Notes Comput. Sci.). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Ruan D, Esedoglu S, Fessler J. Discriminative sliding preserving regularization in medical imaging registration. Proc. IEEE Int. Symp. Biomed. Imag.: From Nano to Macro; 2009.pp. 430–433. [Google Scholar]
- [32].Schmidt-Richberg A, Ehrhardt J, Werner R, Handels H. Slipping objects in image registration: Improved motion field estimation with direction-dependent regularization. In: Yang G-Z, Hawkes D, Rueckert D, Noble A, Taylor C, editors. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2009) Vol. 5761. Springer; New York: 2009. pp. 755–762. (ser. Lecture Notes in Computer Science). [DOI] [PubMed] [Google Scholar]
- [33].Schmidt-Richberg A, Werner R, Handels H, Ehrhardt J. Estimation of slipping organ motion by registration with direction-dependent regularization. Med. Image Anal. 2011;16(no. 1):150–159. doi: 10.1016/j.media.2011.06.007. [DOI] [PubMed] [Google Scholar]
- [34].Schmidt-Richberg A, Ehrhardt J, Werner R, Handels H. Fast explicit diffusion for registration with direction-dependent regularization. In: Dawant B, Christensen G, Fitzpatrick J, Rueckert D, editors. Biomedical Image Registration. Vol. 7359. Springer; New York: 2012. pp. 220–228. (ser. Lecture Notes Comput. Sci.). [Google Scholar]
- [35].Delmon V, Rit S, Pinho R, Sarrut D. Registration of sliding objects using direction dependent B-splines decomposition. Phys. Med. Biol. 2013;58(no. 5):1303–1314. doi: 10.1088/0031-9155/58/5/1303. [DOI] [PubMed] [Google Scholar]
- [36].Xie Y, Chao M, Xiong G. Deformable image registration of liver with consideration of lung sliding motion. Med. Phys. 2011;38(no. 10):5351–5362. doi: 10.1118/1.3633902. [DOI] [PubMed] [Google Scholar]
- [37].Risser L, Vialard F-X, Baluwala HY, Schnabel JA. Piecewise-diffeomorphic image registration: Application to the motion estimation between 3-D CT lung images with sliding conditions. Med. Image Anal. 2013;17(no. 2):182–193. doi: 10.1016/j.media.2012.10.001. [DOI] [PubMed] [Google Scholar]
- [38].Zhu W, Nicolau S, Soler L, Hostettler A, Marescaux J, Remond Y. Fast segmentation of abdominal wall: Application to sliding effect removal for non-rigid registration. In: Yoshida H, Hawkes D, Vannier M, editors. Abdominal Imaging. Computational and Clinical Applications. Vol. 7601. Springer; New York: 2012. pp. 198–207. (ser. Lecture Notes in Computer Science). [Google Scholar]
- [39].Vandemeulebroucke J, Bernard O, Rit S, Kybic J, Clarysse P, Sarrut D. Automated segmentation of a motion mask to preserve sliding motion in deformable registration of thoracic CT. Med. Phys. 2012;39(no. 2):1006–1016. doi: 10.1118/1.3679009. [DOI] [PubMed] [Google Scholar]
- [40].Pace D, Enquobahrie A, Yang H, Aylward S, Niethammer M. Deformable image registration of sliding organs using anisotropic diffusive regularization. Proc. IEEE Int. Symp. Biomed. Imag.: From Nano to Macro; 2011; pp. 407–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Pace D, Neithammer M, Aylward S. Sliding geometries in deformable image registration. In: Yoshida H, Sakas G, Linguraru MG, editors. Abdominal Imaging. Computational and Clinical Applications. Vol. 7029. Springer; New York: 2011. pp. 141–148. (ser. Lecture Notes Comput. Sci.). [Google Scholar]
- [42].Rohlfing T. Image similarity and tissue overlaps as surrogates for image registration accuracy: Widely used but unreliable. IEEE Transactions on Medical Imaging. 2012;31(no. 2):153–163. doi: 10.1109/TMI.2011.2163944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Weickert J. A review of nonlinear diffusion filtering. In: ter Haar Romeny B, Florack L, Koenderink J, Viergever M, editors. Scale-Space Theory in Computer Vision. Vol. 1252. Springer; New York: 1997. pp. 3–28. (ser. Lecture Notes Comput. Sci.). [Google Scholar]
- [44].Nocedal J, Wright SJ. Numerical Optimization. 2nd ed Springer; New York: 1999. [Google Scholar]
- [45].Ibanez L, Schroeder W, Ng L, Cates J. The ITK Software Guide. 2nd ed Kitware, Inc., Insight Software Consortium; Clifton Park, NY: 2005. [Google Scholar]
- [46].Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin J-C, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J, Aylward S, Miller JV, Pieper S, Kikinis R. 3D Slicer as an image computing platform for the quantitative imaging network. Magn. Reson. Imag. 2012;30(no. 9):1323–1341. doi: 10.1016/j.mri.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Lorensen WE, Cline HE. Marching cubes: A high resolution 3-D surface construction algorithm. ACM SIGGRAPH Comput. Graph. 1987;21(no. 4):163–169. [Google Scholar]
- [48].Schroeder W, Martin K, Lorensen B. The Visualization Toolkit: An Object-Oriented Approach to 3-D Graphics. 4th ed Kitware; Clifton Park, NY: 2006. [Google Scholar]
- [49].Castillo R, Castillo E, Guerra R, Johnson V, McPhail T, Garg A, Guerrero T. A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets. Phys. Med. Biol. 2009;54(no. 7):1849–1870. doi: 10.1088/0031-9155/54/7/001. [DOI] [PubMed] [Google Scholar]
- [50].Segars W, Sturgeon G, Mendonca S, Grimes J, Tsui B. 4D XCAT phantom for multimodality imaging research. Med. Phys. 2010;37(no. 9):4902–4915. doi: 10.1118/1.3480985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Bullitt S. Aylward and E. Initialization, noise, singularities, and scale in height ridge traversal for tubular object centerline extraction. IEEE Trans. Med. Imag. 2002 Feb.21(no. 2):61–75. doi: 10.1109/42.993126. [DOI] [PubMed] [Google Scholar]