Bayesian approach to single-cell differential expression analysis

Abstract

Single-cell data provides means to dissect the composition of complex tissues and specialized cellular environments. However, the analysis of such measurements is complicated by high levels of technical noise and intrinsic biological variability. We describe a probabilistic model of expression magnitude distortions typical of single-cell RNA sequencing measurements, which enables detection of differential expression signatures and identification of subpopulations of cells in a way that is more tolerant of noise.

Advances in DNA sequencing and increased sensitivity of RNA analysis methods (RNA-seq) are making it practical to examine transcriptional states of individual cells on a large scale^1-4, facilitating unbiased analysis of cellular states in healthy and diseased tissues^5-8. Profiling the low amounts of mRNA contained within individual cell typically requires more than a million-fold amplification, which leads to severe non-linear distortions of relative transcript abundance and accumulation of nonspecific byproducts. Low starting amount also makes it more likely that a transcript will be “missed” during the initial reverse transcription step, and consequently not detected during sequencing. This can lead to so-called “drop-out” events, where a gene is observed at moderate or even high expression level in one cell but is not detected in another cell (Figure 1a). More fundamentally, gene expression is inherently stochastic, and some cell-to-cell variability will be an unavoidable consequence of transcriptional bursting of individual genes or coordinated fluctuations of multi-gene networks⁹. Such biological variability is of significant interest, and several methods have been proposed for detecting it from RNA-seq and other single-cell measurements^10-12. Collectively, this multi-factorial variability in single-cell measurements substantially increases the apparent level of noise, posing challenges for differential expression and other downstream computational analyses. Noting that standard RNA-seq analysis approaches may be thrown off by the patterns of cell-to-cell variability, we modeled single-cell measurements as a probabilistic mixture of successful amplification and detection failure events. We find that such a representation is effective at identifying differential expression signatures between cell groups, and improves the ability to discern distinct subpopulations in the context of larger single-cell datasets, such as the 92-cell mouse embryonic fibroblast (MEF) embryonic stem cell (ES) study by Islam et al², or cells from different stages of early mouse embryos analyzed by Deng et al¹².

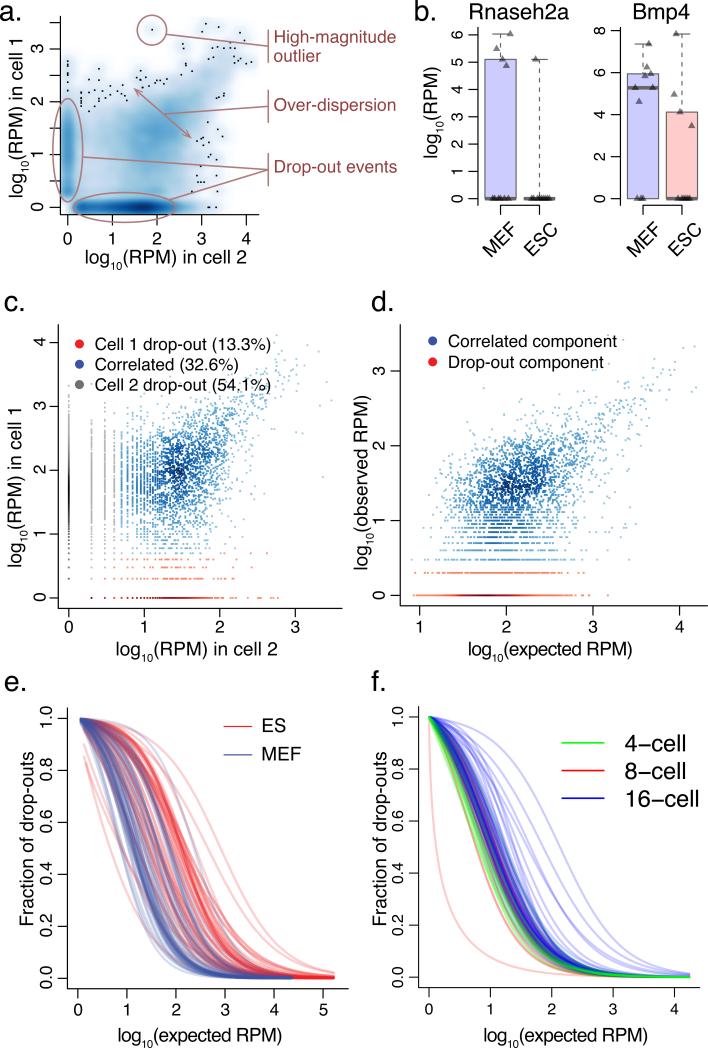
Figure 1. Modeling single-cell RNA-seq measurement as a mixture of two processes.

a. Types of cell-to-cell variability observed in single-cell RNA-seq measurements. A smoothed scatter plot compares gene expression estimates from two cells of the same type (MEF cells), illustrating prevalence of drop-out events, over-dispersion, and high-magnitude outliers.

b. Single-cell variability throws off standard RNA-seq analysis methods, with top differentially expressed genes influenced by difference in drop-out (Rnaseh2a) or outlier (Bmp4) events. The examples are taken from CuffDiff2¹⁴ comparison of 10 ESC and 10 MEF cells, with triangles showing expression magnitudes observed in different cells, and whiskers spanning the range of observed expression magnitudes.

c. To identify a reliable set of genes for fitting model parameters, our approach initially uses cross-comparison of single-cell measurements (using cells of the same type, e.g. MEF), determining whether the transcript is likely to have been successfully amplified in both experiments (correlated component). The true expression magnitude of such genes is estimated as a median expression level across cells in which the gene appears in a correlated component.

d. Each single-cell measurement is modeled as a mixture of drop-out and successful amplification processes. The parameters of the distributions and the magnitude-dependent mixing of the two processes are determined based on the expected population expression averages of genes appearing in many correlated components (c.).

e. Drop-out rates vary between different cell types. The rate of transcript detection failures (drop-out events) depends on the average expression magnitude of a gene in the cell population, and varies among the cells. In Islam et al. dataset², higher drop-out frequencies are observed for mouse ES cells compared to MEF cells.

f. Drop-out rates for 4, 8 and 16-cell embryo samples examined by Deng et al.¹² using a recently-developed protocol also show systematic differences.

Comparisons of RNA-seq data obtained from individual cells tend to show higher variability than typically observed in biological replicates of bulk RNA-seq measurements. In addition to strong over-dispersion, there are notable occurrences of high-magnitude outliers, as well as “drop-out” events (Figure 1a). Such types of variability are poorly accommodated by the standard RNA-seq analysis methods^13,14, and the reported sets of top differentially expressed genes can include genes driven by high-magnitude outliers or drop-out events, showing poor consistency within each cell population (Figure 1b). The abundance of the “drop-out” events has been previously noted in single-cell qPCR data and accommodated using zero-inflated distributions, such as the discrete/continuous model proposed by McDavid et al¹⁵.

Two prominent characteristics of the drop-out events make them informative in further analysis of expression state. First, the overall drop-out rates are consistently higher in some single cell samples than others (Supplementary Figures 1,2), indicating that the contribution of an individual sample to the downstream cumulative analysis should be weighted accordingly. Second, the drop-out rate for a given cell depends on the average expression magnitude of a gene in a population, with drop-outs being more frequent for lower expression magnitude genes. This trend is a consequence of both amplification biases and inherent biological variability. Importantly, quantification of such dependency provides additional evidence about the true expression magnitude. For instance, drop-out of a gene that is observed at very high expression magnitude in other cells is more likely to be indicative of true expression differences between the cells than stochastic variability.

To accommodate high variability of single-cell data we model the measurement of each cell as a mixture of two probabilistic processes – one in which the transcript is amplified and detected at a level correlating with its abundance, and the other where a gene fails to amplify or is not detected for other reasons. The first, “correlated” component is modeled using a negative binomial distribution commonly used to describe overdispersed RNA-seq data^13,16. The RNA-seq signal associated with the second, “drop-out” component could in principle be modeled as a constant zero (i.e. zero-inflated negative binomial process), however we use a low-magnitude Poisson process to account for some background signal that is typically detected for the drop-out and transcriptionally silent genes. Importantly, the mixing ratio between the correlated and drop-out processes depends on the magnitude of gene expression in a given cell population.

To fit the parameters of an error model for a particular single-cell measurement, we use a subset of genes for which an expected expression magnitude within the cell population can be reliably estimated (Figure 1c). Briefly, pairs of all other single-cell samples from the same subpopulation (e.g. MEF cells) are analyzed using a similarly-structured three-component mixture containing one correlated component, and drop-out components for each cell (Figure 1d, Supplementary Figures 1,2). A subset of genes that appears in correlated components in a sufficiently large fraction of pair-wise cell comparisons is deemed reliable, and their expected expression magnitude is estimated as a median magnitude observed across such correlated components. These expected magnitudes are used to fit the parameters of the negative binomial distribution as well as the dependency of the drop-out rate on the expression magnitude for a given single-cell measurement. We find that the drop-out rate dependency on the expected expression magnitude can be reliably approximated using logistic regression (Supplementary Figure 3). Notably, the drop-out rates vary among the cells, depending on the quality of a particular library, cell type, or RNA-seq protocol (Figure 1e,f).

The error models of individual cells provide a basis for further statistical analysis of expression levels. A common task is the analysis of expression differences between pre-determined groups of single cells. We have implemented a Bayesian method for such differential expression analysis (single cell differential expression - SCDE) that incorporates evidence provided by the measurements of individual cells in order to estimate the likelihood of a gene being expressed at any given average level in each of the single-cell subpopulations, as well as the likelihood of expression fold change between them (Figure 2a,b). The Bayesian approach provides a natural way of integrating uncertain information gained from individual measurements. For example, while an observation of a drop-out event in a particular cell does not provide a direct estimate of expression magnitude, it constrains the likelihood that a gene is expressed at high magnitude in accordance with the overall error characteristics of that cell measurement. To moderate the impact of high-magnitude outlier events, the joint posterior probability of expression in a cell group was calculated using bootstrap resampling. The resulting sets of top differentially expressed genes (can be browsed at http://pklab.med.harvard.edu/scde/) show high consistency and relevance to the examined cell types. To quantify the ability of the proposed approach to detect differentially expressed genes in single-cell RNA-seq, we evaluated false positive/false negative relationship bases on the expression differences observed in traditional bulk measurements of mouse ES and MEF cells¹⁷ (Figure 2c). We find that the proposed SCDE method shows higher sensitivity than the common RNA-seq differential expression methods (DESeq and CuffDiff) and the zero-inflated approach developed by McDavid et al. for qPCR data¹⁵. Higher SCDE sensitivity is particularly pronounced for genes that are expressed at higher magnitude in ES cells (Supplementary Figure 4), likely due to a lower total RNA abundance and higher noise levels observed in these cells.

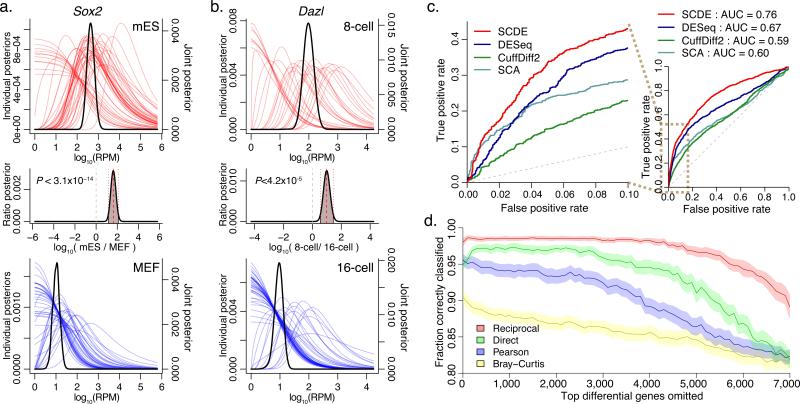
Figure 2. Applying single-cell models for differential expression and subpopulation analyses.

a. The model fitted for each single cell is used to estimate the likelihood that a gene is expressed at any particular level (i.e. posterior distribution) given the observed data (colored curves). The approach estimates joint posterior distribution for the overall level with each cell type (black curves), and the expression fold difference between the cell types (middle plot). The example demonstrates expression differences of Sox2 between all ES and MEF cells measured by Islam et al². The plots show posterior probability of expression magnitudes in proximal (top) and distal (bottom) cells. The posterior probability of the fold-expression difference magnitude is shown in the middle plot with the associated raw P-value of differential expression.

b. Differential expression of Dazl between cells of 8-cell and 16-cell mouse embryo stages, as determined by SCDE method. A regulator factor expressed in mammalian embryos^19,20 , Dazl is expressed at earlier stages, and shows a drop-off between 8- and 16-cell stages.

c. The ability of different analysis methods to detect differentially expressed genes is shown using the false/true positive rate relationship (ROC curve), using traditional bulk expression measurements as a benchmark. The SCDE method shows higher sensitivity at low false-positive range, as well as higher overall performance, as measured by area under the curve (AUC) scores.

d. Performance of error-model-based transcriptional similarity measures in distinguishing ES and MEF cell types. The plot shows the fraction of correctly classified cells, assessed for increasingly difficult classification problem by iteratively excluding up to 7000 most informative genes (i.e. genes differentially expressed between ES and MEF, x-axis). The 95% confidence bands are shown in light shading. Transcriptional similarity measures that take into account direct or reciprocal drop-out event probability show consistently better classification performance than Pearson linear correlation or Bray-Curtis similarity measure.

A key promise of the single-cell approach is the ability to discern novel subpopulations of cells within complex mixtures in an unbiased manner, without a priori knowledge of which cells are which. While a variety of existing multivariate analysis techniques can be used to group single cells by transcriptional signatures^2,5, drop-out and outlier events pose substantial problems for standard similarity and variability measures. The error models of individual cells can be used to derive more robust measures. For instance, Pearson linear correlation of gene expression magnitudes (on log scale) provides a good genome-wide similarity measure, and can be used in combination with hierarchical clustering methods to identify transcriptionally distinct subpopulations of cells. We compared the classification performance of the Pearson linear correlation measure with two modified correlation measures that take into account the likelihood of drop-out events. The first measure (“direct drop-out”) evaluates correlation over a simulated dataset where likely drop-out events are designated as missing data. The second (“reciprocal drop-out”) weights the contribution of each gene based on the probability that the gene will fail (drop-out) in the second cell given its expression level in the first cell (see Methods). Evaluating the performance of different correlation measures over increasingly difficult cell classification, we find that measures adjusted on the basis of the derived error models perform consistently better in resolving cell populations (Figure 2d, Supplementary Figure 5).

Recent progress in single-cell assays and microfluidic manipulation techniques is enabling genome-wide transcriptional examination of cellular heterogeneity within complex tissues. Such studies will likely redefine the boundaries separating cell types or key cellular states in statistical terms¹⁸. Here we have used a simple mixture model, to capture the uncertainty in expression magnitude observed in a given cell, propagating this uncertainty into subsequent analyses. As single-cell studies gain in scope, such probabilistic views of the transcriptional state will become increasingly important.

Online Methods

Datasets and initial abundance estimates

ES and MEF single-cell measurements (96 cells) from Islam et al² were used. The initial RPM estimates were obtained using TopHat²¹ and HTSeq. The mouse embryo data was taken from Deng et al, using the read alignments described in the manuscript¹².

Fitting individual error models

To identify a subset of genes that can be used to fit error models for a particular single-cell measurements, all pairs of individual cells belonging to a given subpopulation (e.g. all MEF cells) were analyzed using three-component mixture model. To do so, the observed abundance a given transcript in each cell was modeled as a mixture of the “drop-out” (Poisson) and “amplification” (negative binomial -NB) components. This way, the expression of a gene with observed RPM levels of r₁ and r₂ in cells c₁ and c₂ respectively was modeled as:

$$\{\begin{array}{c}{r}_1\sim Poisson\left({\lambda }_0\right)dropoutin{c}_1\hfill \\ \{\begin{array}{c}{r}_1\sim NB\left(r_2\right)\hfill \\ r_2\sim NB\left(r_1\right)amplified\hfill \end{array}\phantom{\}}\hfill \\ r_2\sim Poisson\left({\lambda }_0\right)dropoutin{c}_2\hfill \end{array}\phantom{\}}$$

The background read frequency for the dropout components was set at λ₀0.1. The mixing between the three components was determined by a multinomial logistic regression on a mixing parameter m = log(r₁) + log(r₂). Pseudo-counts of 1 were added to r₁ and r₂ for log transformations. The mixture was fit using EM algorithm, implemented under the FlexMix framework²². Alternatively, the initial three-component segmentation can be determined based on a user-defined background threshold, which is a lot less computationally intensive. The genes that were assigned to the “amplified” components were noted, and a set of genes appearing in the “amplified” components in at least 20% of all pair-wise comparisons of cells of the same subpopulation (excluding the cell for which the model is being fit) was used to fit the individual error models, as described below. The expected expression magnitude of these genes was estimated as a median observed magnitude between all the cell measurements in which a gene was classified to be in the “amplified” component. The aim of the 20% threshold is to have a sufficiently large number of measurements for a given gene so that the median expression magnitude estimate would be reliable, and the model parameters resulting from the fitting procedure correlate well for a range of values corresponding to 6-12 cells (Supplementary Figure 3d).

To fit an individual error model Ω_c for a measurement of a single cell c, the observed RPM values were modeled as a function of an expected expression magnitude, using the set of estimates for a subset of genes described in the previous paragraph. The RPM level r_c observed for a gene in cell c was modeled as a mixture of a “drop-out” and “amplified” components, as a function of an expected expression magnitude e:

$$\{\begin{array}{c}{r}_c\sim NB\left(e\right)amplified\hfill \\ r_c\sim Poisson\left({\lambda }_0\right)dropout\hfill \end{array}\phantom{\}}$$

with the mixing parameter m = log(e), λ₀ = 0.1. For each cell the model Ω_c was fit using EM algorithm based on the set of genes for which expected expression magnitudes have been obtained. The resulting estimates of parameters for the negative binomial and concomitant (mixing) regression were used as a description of an error model Ω_c in the subsequent analysis.

Differential expression analysis

Following Bayesian approach, the posterior probability of a gene being expressed at an average level x in a subpopulation of cells S, was determined as an expected value (E):

$$p_S\left(x\right)=E\left[\prod _{c\in B}p(x\mid r_c,{\Omega }_c)\right]$$

where B is a bootstrap sample of S, and p(x|r_c, Ω_c)is the posterior probability for a given cell c: p(x|r_c, Ω_c) = p_d(x)p_poisson (x + (1 − p_d (x)p_NB(x|r_c), where p_d is the probability of observing a drop-out event in a cell c for a gene expressed at an average level x in S, p_poisson x and p_NB(x|r_c) are the probabilities of observing expression magnitude of r_c in case of a drop-out (Poisson) or successful amplification (NB) of a gene expressed at a level x in a cell c, with the parameters of the distributions determined by the Ω_c fit. For the differential expression analysis, the posterior probability that the gene shows a fold expression difference of f between subpopulations S and G was evaluated as $p\left(f\right)={\sum }_{x\in X}{p}_s\left(x\right)p_G\left(fx\right)$, where X is the valid range of expression levels. The posterior distributions were renormalized to unity, and an empirical P value was determined to test for significance of expression difference.

Comparison of differential expression performance

The results if SCDE, DESeq, CuffDiff2 and SingleCellAssay (SCA) were benchmarked against an expression dataset by Moliner et al.¹⁷ that measured bulk MEF and ES cells grown using the same suspension growth protocol²³ as used by Islam et al.². The ability to recover top 1000 genes showing highest expression difference in Moliner et al. was assessed using ROC/AUC (Figure 2c, Supplementary Figure 4) ranking genes by significance of differential expression as determined by different methods.

Similarity measures and subpopulation analysis

Standard measure of the genome-wide similarity between two single-cell measurements was determined as a Pearson linear coefficient on log-transformed RPM values. Genes that did not show expression signals in any of the cells were excluded from the analysis. The Bray-Curtis similarity measure was also calculated on log-transformed values (linear-based values showed lower performance).

The “direct drop-out” similarity measure aims to estimate Pearson linear correlation excluding likely “drop-out” events in any given cell. To achieve that we evaluate average correlation across 1000 sampling rounds, in each round probabilistically excluding likely drop-out observations. Specifically, in each round, an observation of a given gene at an expression level x in a particular cell was substituted with a missing value with probability p_d(x)k, where p_d(x) is the probability of a drop-out event in the current cell at an expression magnitude level x, and k=0.9 is additional factor (to stabilize similarity measure in cases when drop out rates are very high in a given cell). The overall similarity between any two cells was then calculated as an average (across 1000 sampling rounds) Pearson linear correlation between log-transformed values of observations that are valid (not missing) in both cells.

The “reciprocal drop-out” similarity measure aims to reduce the impact of drop-out events on the Pearson linear correlation measure by weighting down the contribution of genes that are not likely to be reliably measured in both cells. For instance, if a gene was observed at a level x₁ in the first cell, we will weigh its contribution by the likelihood that such level of expression can be reliably detected (i.e. without drop-out) in the second cell. This kind of reciprocal weighting minimizes the contribution of discrepant (i.e. amplified vs. drop-out) measurements to the overall similarity. Specifically, the “reciprocal drop-out” similarity was calculated as a weighted Pearson linear correlation on log-transformed RPM values, weighting the contribution of each gene by $k\sqrt{(1-p_d^1\left(x_2\right))(1-p_d^2\left(x_2\right))}+(1-k)$, where $p_d^1\left(x_2\right)$ is a probability of observing a dropout event in cell 1 for an expression magnitude x₂ at which the gene was observed in the cell 2. k=0.95 was used in calculating reciprocal drop-out similarity. We find that both direct and reciprocal similarity measures show robust improvements in classification performance for a range of k values between above 0.85 (see Supplementary Figure 3e).

All similarity measures do well when all 90+ cells and a complete gene set are considered. To provide a meaningful comparison we measured performance on more challenging classification problems based on partial data. Specifically, a subset of 20 random ES and 20 MEF single-cell measurements was sampled in each iteration. Furthermore, increasing fraction of top differentially-expressed genes was excluded from the analysis (Figure 2d, x-axis) to pose a more challenging classification problem. The cells were clustered using Ward method. The fraction of correctly classified cells was determined based on the top-level split of the resulting clustering. The performance was evaluated based on 200 such random sampling iterations.