Efficient Generalized Least Squares Method for Mixed Population and Family-based Samples in Genome-wide Association Studies

Abstract

Genome-wide association studies (GWAS) that draw samples from multiple studies with a mixture of relationship structures are becoming more common. Analytical methods exist for using mixed-sample data, but few methods have been proposed for the analysis of genotype-by-environment (G×E) interactions. Using GWAS data from a study of sarcoidosis susceptibility genes in related and unrelated African Americans, we explored the current analytic options for genotype association testing in studies using both unrelated and family-based designs. We propose a novel method—generalized least squares (GLX)—to estimate both SNP and G×E interaction effects for categorical environmental covariates and compared this method to generalized estimating equations (GEE), logistic regression, the Cochran–Armitage trend test, and the W_QLS and M_QLS methods. We used simulation to demonstrate that the GLX method reduces type I error under a variety of pedigree structures. We also demonstrate its superior power to detect SNP effects while offering computational advantages and comparable power to detect G×E interactions versus GEE. Using this method, we found two novel SNPs that demonstrate a significant genome-wide interaction with insecticide exposure—rs10499003 and rs7745248, located in the intronic and 3′ UTR regions of the FUT9 gene on chromosome 6q16.1.

Introduction

Most genome-wide association studies (GWAS) of chronic diseases have used case-control samples of unrelated individuals—however, family-based designs can also be useful to test for both linkage and association. “Mixed” samples result from combining data from both case-control and family-based sampling methods, or where family sampling is incomplete. Such samples present analytic challenges due to correlation between individuals. There are three commonly used approaches that model the association between genotypes and disease status for mixed samples: the Efficient Mixed-Model Association eXpedited (EMMAX) [Kang et al., 2010] method; W_QLS [Bourgain et al., 2003] and M_QLS [Thornton et al., 2007]; and generalized estimating equations (GEE), recommended by Gray-McGuire et al. [2009] as well as Chen and Yang [2010] in their GWAF R package.

The EMMAX approach models phenotypes using a linear-mixed model with fixed and random effects; fixed effects include the candidate single nucleotide polymorphism (SNP) and covariates such as gender and age, while random effects are based on a phenotypic covariance matrix. Linear-mixed models assume the phenotype is a continuous variable. Although Kang et al. [2010] suggest that the same model can be used for dichotomized variables, the resulting estimates of the linear coefficients may not provide meaningful interpretation, as the estimated proportion difference is used less commonly than odds ratios or relative risks for the effect size estimation. The same problem exists for W_QLS and M_QLS, in which the test statistics are constructed by quadratic forms with the genotype data treated as a linear outcome. In these methods, different choices of symmetric weight matrices in the quadratic form are used to accommodate different population and pedigree structures; in particular, the W_QLS statistic [Bourgain et al., 2003]—which uses the Kinship matrix calculated from pedigree data—was proposed for related individuals without additional population structure. Neither EMMAX or W_QLS/M_QLS can be easily extended to genotype-by-environment (G×E) analyses; specifically, the multiplicative interaction term cannot be directly estimated because both methods treat the categorical data (case-control status or genotype data) as a continuous outcome. Conversely, the GEE model in the GWAF package uses an independent working correlation structure, with each family being a cluster in the robust variance estimate to test association between the phenotype of interest and each SNP. This method offers flexibility by modeling binary outcome with different link functions (e.g., identity or logit link) and the G×E effect can be tested by including an interaction term. However, the use of the independent working correlation and the computation burden for GWAS data makes the GEE approach less efficient.

We propose an extension of the GSK method originally developed by Grizzle et al. [1969], which has been used for categorical data analysis in traditional observational studies. It assumes that the hypotheses of interest can be expressed in terms of an underlying (S × R) contingency table, with S representing the cross-classification of a limited number of discrete covariates (e.g., case/control status), and R identifying the number of multinomial response profiles (e.g., genotypes). This approach retains flexibility to model marginal proportions, marginal logits, mean scores, and cumulative logits with increased power and computation efficiency versus competing methods.

For the analysis of GWAS data in mixed samples, our approach—the extended generalized least squares (GLX)—extends the GSK approach by incorporating kinship into the covariance matrix, as well as proposed different response functions to estimate additive, dominant, and recessive effects and G×E interaction effects. We outline the proposed approach and detail methods for genotype and G×E testing. We also present simulation results comparing the GLX method with the Cochran–Armitage trend test, ordinary logistic regression, EMMAX, W_QLS, M_QLS, and GEE (as implemented in GWAF). Finally, the proposed method is applied to GWAS data from a study of sarcoidosis susceptibility genes in African Americans.

Methods

Extended Generalized Least-Squares (GLX)

We start with the notation of GLX under the setting for individual SNP analysis. Let N subjects be categorized into three possible genotype categories (R = 3) for a SNP (i.e., AA, Aa, aa). Individuals with similar covariate values are grouped into stratum s, s = 1, …, S. Let n_sr, r = 1, 2, 3 represents number of subjects within stratum s and genotype r, and n_s stands for total count of subjects within strata s.

Following the definitions of Grizzle et al. [1969], let the expected cell probabilities be π_sr and the observed cell probabilities be p_sr = n_sr /n_s., r = 1, 2, 3. Define $P_s^t=[\begin{array}{ccc}{p}_{s1}& p_{s2}& p_{s3}\end{array}]$ as a vector of observed probabilities within stratum s, and $P^t=\left[\begin{array}{ccc}{P}_1^{\prime }& \dots & P_s^{\prime }\end{array}\right]$ as the long vector across strata; similarly, define ${\pi }_s^t=\left[\begin{array}{ccc}{\pi }_{s1}& {\pi }_{s2}& {\pi }_{s3}\end{array}\right]$ as a vector of expected probabilities in stratum s, and ${\pi }^t=\left[\begin{array}{ccc}{\pi }_1^{\prime }& \dots & {\pi }_s^{\prime }\end{array}\right]$ as the vector across strata. Without loss of generality, assume that a response function (e.g., F (π)) of the marginal probabilities is linearly related to the covariates X and parameter β (i.e., F (π)_u×1 = X _u×v β_v×1), where X is a design matrix of rank v(≤u) and u is associated with the choice of response function as illustrated in the following sections. The covariance matrix of response function F can be estimated using the delta method: V̂(F) = Ĥ [V̂(P)]Ĥ′, where Ĥ is dF^t/dP, and V̂(P) is the estimated covariance matrix of observed probabilities. The estimation of V̂(P) is discussed in detail in the following section. Therefore β is consistently estimated by β̂ = (X′ [V̂(F)]⁻¹X)⁻¹ X′ [V̂(F)]⁻¹ F̂, using the inverse of V̂(F) as the weight matrix and F̂ as the response vector. The covariance matrix of β̂ is V(β̂) = (X′[V̂(F)]⁻¹X)⁻¹.

F (π) includes a wide range of possible functions; the most commonly used can often be expressed in two families: (i) linear functions F (π) = A × π; and (ii) log-linear functions F(π) = K × log(A × π), where A and K are matrices of arbitrary constants that formulate a specific response function. For details, refer to Grizzle et al. [1969]. Examples for GWAS are illustrated in the following sections.

Estimating the Covariance-V̂(P)

In the above model, in order to estimate the weight matrix V̂(F), we must estimate V̂(P). In the case of SNP data, P^t can be expressed as C × Y where C is a block diagonal matrix having C_s = 1/n_s. × 1_ns. ⊗ I₃ on the diagonal, I_n is the identity matrix of size n, 1_n denotes a vector of size n with all entries one and ⊗ is the Kronecker product. Y = 1_ns. ⊗ Y_i, in which Y_i = [Y_i1 Y_i2 Y_i3] is the 3 × 1 vector of indicator variables for genotypes for each subject i. Y_ig = 1 if Y_i = g, and Y_ig = 0 otherwise, g = 1, 2, 3. Note that the covariance of Y between a pair of individuals is

$$\begin{array}{l}\mathrm{\sum }=cov(Y_i,Y_j)\\ =\left[\begin{array}{ccc}{f}^4{k}_{0ij}+f^3{k}_{1ij}+f^2{k}_{2ij}-f^4& 2f^{3}q{k}_{0ij}+f^{2}q{k}_{1ij}-2f^{3}q& f^2{q}^2{k}_{0ij}-f^2{q}^2\\ ·& 4f^2{q}^2{\pi }_{0ij}+fq{k}_{1ij}+2fq{k}_{2ij}-4f^2{q}^2& 2f{q}^3{k}_{0ij}+f{q}^2{k}_{1ij}-2f{q}^3\\ ·& ·& q^4{k}_{0ij}+q^3{k}_{1ij}+q^2{k}_{2ij}-q^4\end{array}\right],\end{array}$$ (1)

where f is the minor allele frequency, q = 1 − f and k_mij is the probability that two individuals i and j share m alleles identity by descent (IBD) under a given relationship, m = 0, 1, 2. Thus, V̂(P) can be estimated by CΣ̂C′. The “theoretical relationship IBD” statistics k_mij can be inferred using known pedigree structures. When errors of pedigrees exist, the degree of relationship can still be robustly estimated using the genome-wide genotype data, which is known as the “empirical relationship IBD.”

In this paper, we adopted the Kinship-based inference for genome-wide association studies (KING) method proposed by Manichaikul et al. [2010] to estimate kinship coefficient and IBD statistics in the real data analysis. The allele frequency f can be estimated by: (1) the sample frequency Ȳ/2; or (2) the best linear unbiased estimator (BLUE), given by $\widehat{f}={(1_n^t{\mathrm{\Phi }}^{-1}{1}_n)}^{-1}{1}_n^t{\mathrm{\Phi }}^{-1}(\overline{Y}/2)$, where Φ is the kinship matrix and as suggested by McPeek et al. [2004]. However, we have not found significant differences between the two estimates in the simulations.

Association Testing Between SNP and a Binary Outcome

To test for association between a single SNP and a binary outcome (e.g., case-control), we developed a general framework of the GLX method with several options for response function F(π) that provides estimates based on proportions. One is the linear response function F(π_s) =0 × π_s1 + 1 × π_s2 + 2 × π_s3, s = 1 (case) or 2 (control). We can use the following design matrix such that F(π) = Xβ: $X=[\begin{array}{cc}1& -1\\ 1& 1\end{array}]$, β = [β₁, β₂]^t. V̂(F) is estimated from CΣ̂C^t and Σ̂ is estimated from equation (1). This parameterized model allows for the estimation of genotypic means while accounting for the dependence between subjects. After estimation, the value of β̂₁ typically represents average effect of risk allele of two groups, and β̂₂ represents the differentially effect of risk allele between two groups. The association test can be constructed by the Wald test for β̂₂. The Wald statistic is computed as a ratio of β̂₂ over its standard error $\sqrt{V(\widehat{\beta })}$. We can assess the level of statistical significance using the normal approximation of the Wald statistic. Note that under this model, V̂(F) is reduced to JΦJ^t, where J is a block diagonal matrix having 1/n_s. × 1_ns on the diagonal and Φ is the kinship matrix.

Another option is the log-linear response function. Specifically, one can choose the adjacent logit link function for log-additive model, $F{({\pi }_s)}^t=[\begin{array}{cc}log\frac{{\pi }_{s2}}{{\pi }_{s1}}& log\frac{{\pi }_{s3}}{{\pi }_{s2}}\end{array}]$, s = 1 or 2, if the effect was expected to be additive on the log odds scale. In matrix form, F(π) is constructed as F(π) = K × log(A × π) with $K=[\begin{array}{ccc}-1& 1& 0\\ 0& -1& 1\end{array}]\otimes I_2$ and A is an identity matrix with dimension of 6. We note that dominant or recessive effects can similarly be tested for by modifying K appropriately. Recall that F(π) = Xβ, β = [β₁, β₂, β₃]^t. In this situation, the design matrix X is chosen as:

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 1& 0& 1\\ 0& 1& 1\end{array}\right].$$

β₁ and β₂ are the intercepts for each response function across groups. The effect of each copy of the second allele is β̂₃ on the log odds scale, corresponding to an odds ratio of exp(β̂₃). Similarly a Wald statistic $z={\widehat{\beta }}_3/\sqrt{var({\widehat{\beta }}_3)}$ can be constructed for testing the null hypothesis of β₃ = 0 as described above.

More generally, a test of the hypothesis H₀: Lβ = 0 is produced by conventional methods of weighted multiple regression, where L is a matrix of full rank d. Given the model, the test is produced by β̂^tL^t[L (X^t[V̂(F)]⁻¹X)⁻¹L^t]⁻¹ Lβ̂ that is asymptotically a χ² distribution with d degrees of freedom under H₀[Grizzle et al., 1969].

The choice between linear and log-linear response functions depends on data assumptions underlying the statistical analysis. Linear response functions using simple proportions assume that the theoretical distance between proportions is equal. Log-linear response functions, on the other hand, stretch out the distance between proportions. Therefore, the results obtained based on log-linear functions interpret differently from the results obtained from the linear model.

Interaction Between SNP and Environmental Factor on a Binary Outcome

The proposed approach can be extended to test the interaction for categorical outcome and environmental factors (G×E). Consider, an environmental risk factor (E), a “high-risk genotype” (G), and a disease of interest (D). In general, statistical gene–environmental interaction is defined as departure from additive or greater-than-multiplicative joint effects of gene/environmental effects. Statistical interactions are scale dependent; choice of measurement scale will affect the assessment of G×E interaction. Ottman [1996] presents a variety of definitions for gene–environment interactions using relative risks and odds ratios under additive and multiplicative scales; for illustrative purposes, we focus on the interaction based on odds ratios.

In order to apply the GLX test for the G×E multiplicative effect, we first conduct the SNP association test within each environmental factor stratum. Let β̂_t and var(β̂_t) represent the coefficient estimates and corresponding variance for the association test between G and D within stratum t. The adjacent logit link function, as described above, is used here. The G×E effect then can be tested using Cochran’s Q test [Cochran, 1954]. The test statistic consists of a weighted sum of squared deviations around the mean of the effect. Specifically for our G×E interaction testing, Q is defined as Σw_t(β̂_t − β̄)², where β̄= Σw_tβ̂_t/Σw_t is the weighted mean of the log odds ratio. Here we choose the weight w_t = 1/var(β̂_t), that is, the inverse of the estimated variance of log odds ratio in each strata. Under the null hypothesis of no interaction, Q follows a χ² distribution with T − 1 degrees of freedom, where T is the number of strata in E.

Simulation Studies

We examined the type I error and power of the proposed estimators in a variety of simulated pedigrees based on three real datasets: the Ancestry Mapping of African genes of Sarcoidosis Susceptibility study (AMASS) [Rybicki et al., 2011]; the multi-ethnic study of atherosclerosis (MESA) [Bild et al., 2002]; and the Framingham Heart Study [Govindaraju et al., 2008].

AMASS study data were compiled from three previously conducted studies: (1) a multisite case-control study; (2) a multisite affected sib-pair study; and (3) a single institution family-based study. Of 2,494 genotyped specimens, 1,877 had both genotype and environmental data. A total of 1,283 specimens were collected from 475 pedigrees with 277 sibships ranging in size from 2 to 6. The remaining 594 specimens were from the case-control study.

MESA was a study of characteristics of subclinical cardiovascular disease. One of its ancillary studies—the MESA Family Study—applied genetic analysis and genotyping methodologies to delineate the genetic determinants of early atherosclerosis. MESA pedigrees were more complex than those in AMASS. Among 3,735 specimens, there were approximately 702 families with family size varying from 3 to 16; however, a majority of the MESA families consisted of only parents and offspring.

The Framingham Heart Study included 6,870 individuals in families of up to three generations, including over 900 pedigrees and 230 singletons. The pedigree sizes varied from 2 to 296, more complex than the AMASS and MESA studies. Summary information for each study sample is provided in Table 1 and ordered by complexity of pedigree structures. We randomly selected 500 mixed families and singletons from the MESA and Framingham studies for the simulation.

Table 1.

Simulation configurations for each data type

Type	Total N	N families	N unrelated
AMASS	1,877	475	594
MESA	3,735	702	0
Framingham	6,870	765	435

Using Merlin [Abecasis et al., 2002] and pedigree structures from the real examples, we simulated 10,000 datasets of genotype “G” data through gene dropping, with a minor allele frequency of 0.2. The binary environmental factor “E” was generated assuming that individuals within the same family have the same environmental exposure—that is, it is more correlated than exposure for individuals in different families. The quantitative traits of all individuals in the pedigrees were generated according to the linear-mixed model described below. The phenotype of individual j in family i was generated by:

$$Y_{ij}={\beta }_0+{\beta }_{1}G+{\beta }_{2}E+{\beta }_{3}G\times E+r_i+e_{ij},$$

where β₀ is the population mean, β₁ is the additive effect for a SNP, β₂ is the environmental main effect and β₃ is the interaction effect between G and E. To allow for correlation between phenotypes within each family, we assumed a random family effect r_i that follows a multivariate normal distribution $N(0,{\sigma }_f^{2}2{\mathrm{\Phi }}_i)$, where the elements of 2Φ_i denote the kinship coefficient between individuals in family i. The residual e_ij is normally distributed with mean 0 and variance ${\sigma }_e^2$ . We considered ${\sigma }_f^2=3$ and ${\sigma }_e^2=1$, which corresponds to a heritability value of 0.75. Dichotomous traits were then generated from the Bernoulli distribution with probability p_ij, where p_ij is calculated from the inverse logit function, logit⁻¹(Y_ij).

We set β₀ to −3, representing a baseline disease risk of approximately 5%, independently of G and E. Type I error was estimated for testing H₀: β₁ = 0 and H₀ : β₃ = 0, corresponding to no genetic effect and no G×E interaction, respectively. For power analysis, we considered three types of values for β₁, β₂, and β₃. First, we set them to 0.405, 0, and 0, respectively, yielding an OR of approximately 1.5 for the gene main effect. Second, we set β₁, β₂, and β₃ to be 0.405, 0.405, and 0.69, respectively, yielding ORs of approximately 1.5 for the main effect of gene G, approximately 1.5 for the main effect of the environmental factor, and approximately 2 for the G×E interaction effect. This model represents the synergistic effect between G and E. Third, we set β₁, β₂, and β₃ to be 0, 0, and 0.69, respectively, yielding G×E interaction effect without marginal effects.

GLX was compared to the Cochran Armitage trend test, GEE with identity link, EMMAX, W_QLS, and M_QLS (for the linear mean score model), ordinary logistic regression, and GEE (for the log-additive effect model). The kinship coefficient and IBD estimates were calculated from the known pedigree structures. In the simulation, the allele frequency p was estimated by the sample frequency Ȳ/2, as we did not see a significant difference in the results using the sample frequency or BLUE for allele frequency estimation.

An Example From a Study of Sarcoidosis

To examine the performance of our proposed method in a real dataset, we applied GLX to the AMASS GWAS samples, consisting of 1073 African-American sarcoidosis cases and 804 controls drawn from unrelated case-control and family samples. Genotyping was performed on the Illumina Human Omi1-Quad at the Oklahoma Medical Research Foundation (Oklahoma City, OK) for 1.1 M SNPs across the genome. The details of genotyping and quality control process have been described in Adrianto et al. [2012].

After quality control processes, the final set comprised 887,296 autosomal SNPs. The SNP-based pairwise kinship coefficients and identity-by-descent coefficients were estimated using KING [Manichaikul et al., 2010]. Before applying the kinship estimates to the GLX method, a pair of individuals with kinship coefficient (ϕ) less than 1/2^9/2 was considered to be unrelated; the corresponding probability of zero IBD-sharing (k₀) was set at 1, and probability of one IBD-sharing (k₁) was set at 0. To test if the individual SNPs had significant effect on the risk of sarcoidosis, we applied the GLX method with both linear response function and adjacent logit response function.

Rossman et al. [2008] found that carrying HLA-DRB1^*1101 and exposure to workplace insecticides was associated with increased risk of developing sarcoidosis (P < 0.10), suggesting a potential G×E interaction. To illustrate the proposed G×E test from the GLX method, we focus here on evaluating the G×E interaction effects of SNP and insecticide exposure on sarcoidosis risk.

Simulation Results

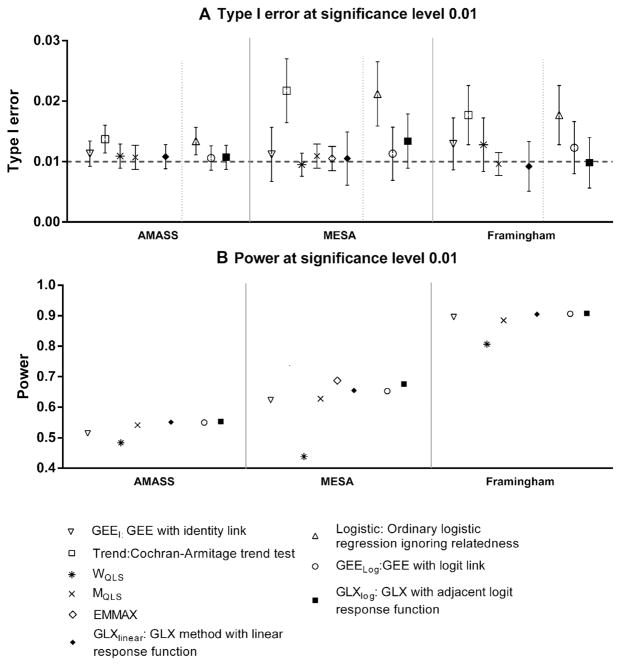
Figure 1A and B present the estimated type I error rates and power for a variety of SNP association tests. The GLX method with either linear response or log-additive response functions controls for Type I error rates when the nominal rate of statistical significance is P = 0.01. Ordinary logistic regression performs similarly to the trend test, and both are anticonservative under certain scenarios. This inflation of type I error is expected from a method that ignores relatedness within the mixed sample, consistent with the simulation results for the trend test reported by Manichaikul et al. [2012] and Feng et al. [2011]. When the related portion of the total samples is small (as with AMASS), the type I error of a simple logistic regression or trend test may not be greatly affected. But Type I error is more severely inflated when the sample consists of more complex pedigrees—for instance, using the MESA study sample, the type I error rates under logistic regression or the trend test are double those of the nominal level. Due to above observations, power is not reported for ordinary logistic regression and the trend test in Figure 1B. GEE models that use robust variance estimation with an independent working covariance control type I error for all three scenarios. The same conclusion is made for the W_QLS and M_QLS tests.

Figure 1.

Comparison of different methods for testing SNP association with risk of disease when minor allele frequency is 0.2. Nominal type I error rate was set at 0.01. Point estimates and 95% confidence intervals of type I error and power were presented.

However, GLX outperforms them in terms of power. The power of GLX with an adjacent logit response function is 68% ± 1% (MESA) and 91% ± 0.3% (Framingham) for each study sample configuration. The power of M_QLS with logit link is 63% ± 1% (MESA) and 88% ± 0.3% (Framingham) sample configurations. We observe larger differences in power between GLX, GEE, and W_QLS when using the linear function: GLX has 65% ± 1% power compared to 62% ± 1% (GEE with identity link), 44% ± 1% (W_QLS), and 63% ± 1% (M_QLS) in the MESA study; similar trends are seen using the AMASS and Framingham study sample configurations. Although GLX methods did not systematically show greater power than EMMAX, both methods are comparable in most of the scenarios.

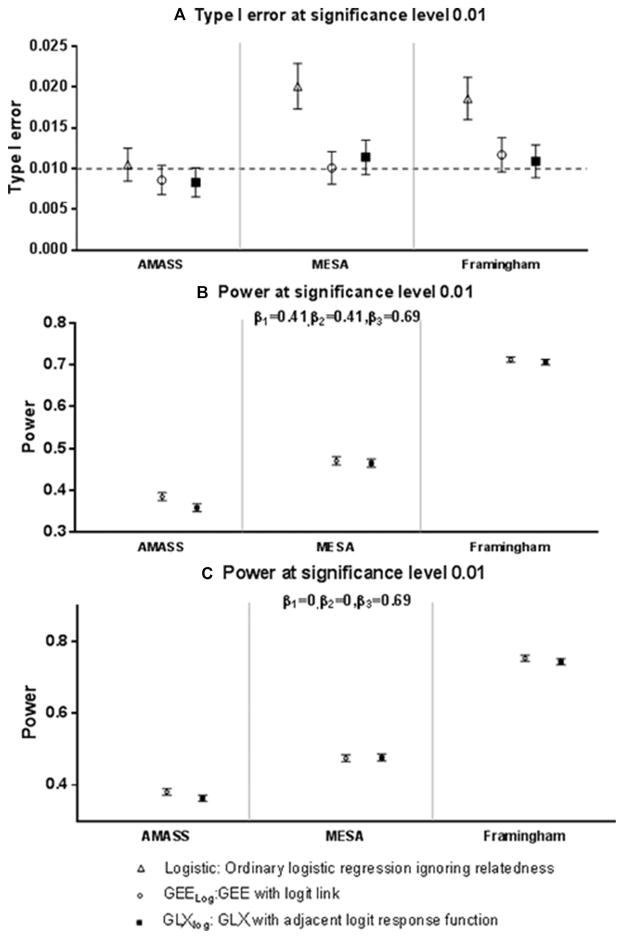
Figure 2A, B, and C present the results of estimated type I error rates and power for SNP-by-environment (SNP×E) interaction tests for different methods. As we observe for the SNP association testing, type I error is reasonably controlled by both GEE and GLX for all sample configurations (Fig. 2A). Logistic regression again demonstrates inflated type I error. Type I errors rates are around 2% for both MESA and Framingham pedigrees when the nominal significance was set at 1%. For these two sample configurations, GEE and GLX achieve nearly equivalent power (Fig. 2B). Both methods have power of 47% ± 1% (MESA) and 71% ± 0.6% (Framingham) in these study sample configurations. The performance of these three tests under the interaction-only model leads to the same conclusions (Fig. 2C).

Figure 2.

Comparison of different methods for testing SNP-by-environment multiplicative interaction with risk of disease when minor allele frequency is 0.2. Nominal type I error rate was set at 0.01. Point estimates and 95% confidence intervals of type I error and power were presented.

Exemplar Data Set

As a complement to the simulation studies, we analyzed GWAS data from the AMASS study. The single-marker association analysis using the GLX method with linear and logit response function showed modest genomic inflation factors (1.10 and 1.05). We further corrected the P-values based on the genomic inflation factors for each method. The six most significant SNPs are in the Major Histocompatibility Complex (chromosome 6p21); method-specific results are displayed in Table 2. The EMMAX analysis identified one SNP (rs2239803) approaching the genome-wide significance level (P < 5 × 10⁻⁸, using Bonferroni correction). As expected, M_QLS failed to control for population stratification. Odds ratios and 95% confidence intervals for the six SNPs were estimated using the GLX method with log-additive response function. The P-values for testing the odd ratios are slightly higher than the P-values using the linear response function. Table 3 lists the six SNPs that reach a suggestive significance level (P-values <1 × 10⁻⁵) for a SNP-by-insecticide-exposure interaction. Two of these passed the genome-wide significance level: rs10499003 and rs7745248, both located in the FUT9 gene on chromosome 6. The other two SNPs from chromosome 6 are neighboring SNPs in high linkage disequilibrium (LD) with rs10499003 (r² > 0.6). The estimated odds ratio of sarcoidosis risk for each additional copy of allele C at rs10499003 is 2.06 (95% confidence interval (CI): 1.88–2.25) if exposed to insecticide. The risk decreases (OR = 0.40 (95% CI: 0.37–0.43) for those who were not exposed to insecticide.

Table 2.

AMASS data results: SNPs associated with risk of Sarcoidosis with P-values passed genome-wide significance level

CHR	SNP	GLXlinear (GI = 1.10)	GLXlog (GI = 1.05)	OR	95% CI	EMMAX (GI = 1.01)	MQLS (GI = 1.15)
6	rs6931646	2.1 × 10−7	2.1 × 10−7	0.70	(0.61, 0.80)	1.1 × 10−7	1.1 × 10−6
6	rs2239804	1.7 × 10−7	1.8 × 10−7	0.69	(0.61, 0.79)	9.1 × 10−8	9.7 × 10−7
6	rs2239803	1.1 × 10−7	1.2 × 10−7	0.69	(0.60, 0.79)	5.4 × 10−8	6.0 × 10−7
6	rs6911419	1.3 × 10−7	1.4 × 10−7	0.69	(0.61, 0.79)	6.7 × 10−8	6.7 × 10−7
6	rs9268658	1.6 × 10−7	1.7 × 10−7	0.69	(0.61, 0.79)	8.2 × 10−8	4.5 × 10−7

GLX_linear, P-value for GLX method with linear response function; GLX_log, P-value for GLX method with log-additive response function; OR, odds ratio; 95% CI, 95% confidence interval for OR; GI, genomic inflation factor.

Table 3.

AMASS data results: SNP by insecticide exposure interaction with P-values < 1E-5

SNP	CHR	Position	Alleles	MAF	Gene	Insecticide exposure OR (95% CI)	No insecticide exposure OR (95% CI)	P-value (GI = 0.94)
rs6720972	2	98039926	G/A	0.07		0.46 (0.43, 0.50)	1.60 (1.48, 1.73)	5.35 × 10−6
rs13417566	2	111309077	A/C	0.35	ACOXL	0.76 (0.75, 0.78)	1.45 (1.42, 1.47)	7.85 × 10−6
rs10499003*	6	96611940	C/A	0.07	FUT9	2.06 (1.88, 2.25)	0.40 (0.37, 0.43)	1.47 × 10−8
rs7745248	6	96766835	A/G	0.08	FUT9	1.92 (1.76, 2.09)	0.38 (0.35, 0.41)	1.82 × 10−8
rs11156352	6	96794243	G/A	0.09		1.66 (1.55, 1.78)	0.50 (0.47, 0.53)	2.69 × 10−6
rs2341786	6	159848314	A/G	0.10		1.75 (1.65, 1.86)	0.55 (0.52, 0.58)	1.56 × 10−6

P-value: P-values for gene-by-insecticide-exposure interaction were obtained from GLX method with log-additive response function; OR, odds ratio; 95% CI, 95% confidence interval for OR; GI, genomic inflation factor.

Discussion

Large association studies that collect both unrelated case-control and family data have been conducted in several diseases [Bild et al., 2002; Edenberg et al., 2005; Govindaraju et al., 2008; Rybicki et al., 2011]. Motivated by a GWAS of sarcoidosis susceptibility genes in African Americans, we proposed an extended Generalized Least Squares approach to test for the association between disease and genes, as well as gene-by-environment interactions, when data comes from mixed samples of family-based and population studies. This method allows us to account for correlations among family members by using kinship estimated from GWAS data or known pedigrees. This approach is flexible in the sense that many response functions under varying model assumptions can be used, and corresponding effect size and confidence intervals can be estimated.

Insecticide exposure has been previously shown to be associated with sarcoidosis on both marginal and G×E interaction levels [Newman et al., 2004; Rossman et al., 2008]. Using the GLX method, we found significant interactions between insecticide exposure and the FUT9 SNPs rs10499003 (intronic) and rs7745248 (3′UTR). The protein encoded by this gene belongs to the glycosyltransferase family [Brito et al., 2008]; recent human cell-line work suggests that the FUT9 protein has an important role in the biosynthesis of human E-selectin ligands [Buffone et al., 2013]. Sarcoidosis patients are known to have elevated levels of circulating E-selectin in peripheral blood [Berlin et al., 1998; Hamblin et al., 1994]. Furthermore, recent work in mice has shown that E-selectin knockouts have a more severe grade of granuloma formation in lungs upon exposure to P. acnes versus wild-type mice [Kamata et al., 2013]; in humans, a common E-selectin polymorphism is associated with significantly reduced risk of developing sarcoidosis in patients with erythema nodosum [Amoli et al., 2004]. Although it is too preliminary to implicate FUT9 in sarcoidosis pathogenesis, this finding demonstrates the potential utility of the GLX method to uncover provocative G×E interactions worthy of further study.

GLX has also shown advantages over other methods in simulations. Traditional methods that assume independent sampling are anticonservative if applied to mixed sample data that is dominated by complex family structures, such as those found in the MESA and Framingham studies. Another option for mixed sample data is GEE, which provides robust inferences for most of the scenarios in our simulation; however, its computation time is relatively long. As a result, some researchers run the association test using EMMAX or M_QLS first, then use a GEE model with logit link function on the regions highlighted by EMMAX or M_QLS to obtain the estimates of odds ratios and corresponding standard errors. In contrast, the GLX method is computationally appealing for its simpler, noniterative procedure. To scan 10,000 SNPs for a study of sample size 4,000 using a 2.67 GHz Intel^® Xeon^® CPU running Linux, it took 15.4 min for GEE and just 1.3 min for GLX versus. In this case, GLX is 12 times faster than GEE.

The current version of GLX was written in the R programming language; GEE in the GWAF package was written in C language and called by R. We are currently developing a version of GLX implemented in C—we expect this to be even more computationally efficient. More importantly, our simulations show that GLX has superior power to GEE under linear and log-additive models for SNP association tests for a number of scenarios. The final advantage to using GLX rather than EMMAX or W_QLS/M_QLS is that GLX offers many different forms of response functions that can be specified by the user. Unlike EMMAX and W_QLS/M_QLS, which use linear models on categorical data, the interpretation of the model coefficient of the GLX method may be more meaningful than these two methods and may be easily extended to test for G×E interactions.

There are some limitations to this method. First, the behavior of tests in small samples is unknown. Occasional small cell counts may require adjustment of the data so that the weight matrix is not singular. However, this problem is not unique to our GLX test; in actual practice, SNP genotypes can be collapsed into dominant or recessive coding. Second, the GLX method is primarily developed for categorical data analysis. Continuous covariates may be used by considering them as categorical variables based on their unique values. However, computational difficulties may arise if a continuous covariate has a large number of unique values; in this case, we can still use this method by discretizing the variables. Third, while the proposed GLX method is an efficient method for accurately estimating both main and marginal effects from family-based data, effect estimates may not be generalizable to the general population if ascertainment bias exists. Correcting for ascertainment bias was beyond the scope of this study, but this issue has been extensively addressed by others [Epstein et al., 2002; Noh et al., 2005; Schaid et al., 2010]. And finally, population stratification was not observed in the exemplar dataset, nor was the GLX method assessed in the presence of population heterogeneity with simulated data. However, our method can be extended to account for population stratification by modifying the covariance matrix, similar to the approach used in ROADTRIPS [Thornton and McPeek, 2010].

In summary, we propose a novel generalized least squares (GLX) method to estimate both SNP and G×E interaction effects in mixed samples. Our simulation results demonstrate that this method improves upon existing methods used to analyze these types of data, both in terms of type I error and power under a variety of pedigree structures. Given the computational efficiency of the GLX method and its ability to be easily extended to test for G×E interactions, it should be very attractive for analysis of genome-wide marker datasets of mixed samples.