Tensegrity, cellular biophysics, and the mechanics of living systems

Abstract

The recent convergence between physics and biology has led many physicists to enter the fields of cell and developmental biology. One of the most exciting areas of interest has been the emerging field of mechanobiology that centers on how cells control their mechanical properties, and how physical forces regulate cellular biochemical responses, a process that is known as mechanotransduction. In this article, we review the central role that tensegrity (tensional integrity) architecture, which depends on tensile prestress for its mechanical stability, plays in biology. We describe how tensional prestress is a critical governor of cell mechanics and function, and how use of tensegrity by cells contributes to mechanotransduction. Theoretical tensegrity models are also described that predict both quantitative and qualitative behaviors of living cells, and these theoretical descriptions are placed in context of other physical models of the cell. In addition, we describe how tensegrity is used at multiple size scales in the hierarchy of life — from individual molecules to whole living organisms — to both stabilize three-dimensional form and to channel forces from the macroscale to the nanoscale, thereby facilitating mechanochemical conversion at the molecular level.

1. Introduction

Although modern biology and medicine have been dominated by genetics and biochemistry for the past century, recent work from a variety of fields has revealed that physical forces and mechanics play as important a role in control of cell and tissue development as chemicals and genes (Ingber 2006, Mammoto et al. 2013). The emergence of this new field of ‘Mechanobiology’ has garnered the interest of physicists and engineers. In fact, many have begun to develop models of cell and tissue behavior, and to venture even further by learning the tools and experimental methods of cell and developmental biology to test their new ideas. One of the most fundamental questions in the field of mechanobiology is how living cells physically organize themselves at the molecular level so as to exhibit their characteristics shapes and mechanical properties. A closely related question is how cells sense physical forces and transduce these mechanical cues into changes in intracellular biochemistry and gene expression—a process known as cellular mechanotransduction. In this article, we review work carried out by our laboratories over the past three decades that has led to the discovery that cells use tensegrity architecture to structure themselves at the molecular level, and that use of this structural system that depends on tensile prestress for its mechanical stability enables cells to sense and respond to mechanical signals. We review the central role that tensional prestress plays in biology, and describe theoretical tensegrity models that have been developed which predict both quantitative and qualitative behaviors of many different types of living cells. These models are also placed in context of other physical models of cell structure. Finally, we show how tensegrity is used at multiple size scales in the hierarchy of life — from individual molecules to whole organisms — and that this provides a mechanism to channel forces from the macroscale to the nanoscale, and to facilitate mechanochemical conversion in living organisms. The theoretical descriptions of tensegrity structures are explored because they may be used to depict, explain and predict behaviors of living cells and molecules, and because they potentially might be applied to help design man-made bioinspired materials and devices, as well as robots and even buildings, in the future.

2. Tensegrity Architecture

The term “Tensegrity” was first coined by the iconoclastic architect, R. Buckminster Fuller, to describe structures that gained their stability or integrity through a pervasive tensional force, rather than through continuous compression as used in most man-made (e.g., brick upon brick) type constructions (cf Fuller 1961). Fuller discovered that tensegrity is responsible for establishment of the force balance that stabilizes geodesic domes, even though they are constructed with all stiff elements (i.e., which can bear either tension or compression). However, his student - the sculptor Kenneth Snelson - created the first self-stabilizing tensegrity structure in which compression elements (struts) do not touch, and instead are suspended by connections to a continuous series of tension elements (cables). These cable-and-strut structures clearly visualize how structural stability in tensegrities depends entirely on tensional integrity or ‘continuous tension, discontinuous compression’ (Fig. 1A–D). The stability of tensegrity structures is due to the way in which their compressive and tensile load-bearing components interact: the cables pull in on both ends of the struts and place them under compression, while the struts push out and tense the cables. The result is that each cable element in a tensegrity structure is pre-tensed, and hence experiences a tensile ‘prestress’. Importantly, use of tension cables and struts is not core to the tensegrity definition as similar structures can be made of all springs, for example, as long as they are arranged to generate a stabilizing prestress in the entire network (Fig. 1B).

Fig. 1. Physical Tensegrity Models.

A) A 3-strut tensegrity model composed of wood sticks and nylon strjngs. Note that the struts do not come in direct contact, but rather are suspended open and stabilized through connection with the continuous series of tension elements. B) A 6-strut tensegrity composed entirely of metal springs. C) A large 6-strut tensegrity model composed of metal struts and elastic cables assembled in the same form as the spring structure shown in B, but also connected to a smaller stick and string spherical tensegrity at its center by black elastic strings that are not visible due to the black background. This hierarchical tensegrity model has been used to model shape alterations in nuclear cells as when a subset of the elements of the model are attached to a rigid substrate to model cell adhesion, the cell flattens, and the cell and nucleus spread in a coordinated manner, as shown in D. Living cells display the same behavior when the attach and spread on ECM or culture substrates.

Although this prestress endows tensegrities with shape stability, they are also extremely responsive to outside perturbation. The individual elements that comprise the structure immediately reorient when the structure is deformed or force is applied to one element, and they do so reversibly and without breaking. Moreover, because the structural members are connected by elements that transmit tensional forces throughout the whole tensegrity structure, application of a local force can result in an integrated structural response. Some have noted that disruption of a single element in a minimal Snelson-like tensegrity (e.g., as shown in Fig. 1A) can result in destabilization of the entire structure. However, multiple self-stabilizing tensegrity modules can be combined using similar rules (establishment of tensional integrity) to form larger tensegrity systems. In these multimodular tensegrities, individual tensegrity components can be disrupted without compromising overall system integrity. Fuller also noted that hierarchical tensegrities may be created in which smaller tensegrity structures function as compressive or tensile components in a larger tensegrity system, which in turn may perform a similar function in still larger systems (Fig. 1C). Furthermore, in tensegrity structures (single, multi-modular, hierarchical), force application to a single element results in a redistribution of forces and rearrangement of elements that can span across long distances and size scales throughout the tensionally-integrated system (Fig. 1D versus 1C).

It is common to think of tensegrities exclusively in terms of Snelson’s cable-and-strut structures. However, there is no requirement for the cable-and-strut systems or any specific topology, and structures as diverse as bicycle wheels, inflated balloons, soap foams and lung parenchyma have been described as tensegrities. Prestressed cable nets (e.g., spider webs) also have been described as tensegrities because prestress carried by tensile elements are balanced by forces at the anchoring points to the external world that resist this tension (Connelly and Back, 1988; Ingber, 1993), as we discuss in Sec. 4.1. Furthermore, in this review, we explain that while cable-and-strut systems models were initially used to model tensegrities, other groups have developed stochastic or purely mathematical tensegrity models; in fact, the mathematical models have no elements, only points in space that can resist getting to closer to each other or moving farther apart. It is noteworthy that having distinct tensile and compressive elements in a structure does not itself indicate that the structure is a tensegrity structure, unless there is synergy between tension-compression in the sense that compression elements oppose and balance forces in the tension elements to create a tensional prestress that stabilizes the entire structure in 3D space.

3. The Structure of Living Cells

3.1 Cytoskeletal Biopolymers

Before addressing the relevance of tensegrity for biology, it is important to understand the molecular and biophysical basis of cell organization. The shape and mechanical stability of living cells are governed by an internal molecular framework known as the cytoskeleton. The mechanical properties of the cytoskeleton arise from the complex network of biopolymers that comprise the cytoskeletal lattice. All of these biopolymers undergo continuous remodeling in that individual monomers can be added and removed. Some cytoskeletal polymers, such as contractile actomyosin filaments, also can actively generate tension, which are driven by molecular motors that convert chemical energy of adenosine triphosphate (ATP) into mechanical forces. Actin microfilaments, microtubules, and intermediate filaments comprise the three major filamentous components of the cytoskeleton, and they are linked to themselves (to form larger fibrils) and to each other (to form structurally coupled networks) by various cross-linking proteins. In general, these filamentous biopolymers are much less flexible than synthetic polymers, yet they can still exhibit significant conformational changes driven by thermal fluctuations.

Filamentous actin (F-actin) is composed of actin monomers, and it can organize within pure actin filaments or bundles, as well as associate with myosin motors to form larger contractile microfilaments that actively generate tension. Persistence length (L_p) of F-actin filaments (5–10 nm diameter) is on the order of 10¹ µm and its Young’s modulus of elasticity is E ~ 10³ MPa (Gittes et al 1993). In response to stretch, isolated actin filaments whose contour length is on the same order as their L_p exhibit initial strain-hardening at low tensions (0–50 pN) and low strains (0.4–0.6%), which is indicative of the filament’s internal conformational changes. The curve becomes linear at intermediate to high tensions (50–230 pN), which is indicative of the enthalpic elasticity (Liu and Pollack 2002). Since physiological contour length of cytoskeletal F-actin is ≤ 1 µm, much smaller than its L_p, this suggests that in living cells the passive contribution of actin filaments to the mechanical stresses of the cytoskeleton may be primarily through enthalpic elasticity.

When cytoskeletal actin filaments physically associate with myosin motor proteins within contractile microfilaments, active tension is generated through the ATP-driven process of cross-bridge cycling. As a result of this action, the cytoskeleton becomes prestressed. Multiple contractile filaments also can join together form larger bundles known as ‘stress fibers’, which contain multiple actomyosin filaments oriented in parallel and linked by actin-binding proteins such as α-actinin. Actin stress fibers have much a larger diameter (0.2–1 µm) and much lower elastic modulus (E ~ 10³ kPa) than individual actin filaments. In response to stretch, isolated stress fibers exhibit a non-linear stress-strain behavior characterized by strain-hardening (Deguchi et al. 2006).

Microtubules are polymers comprised of α- and β-tubulin dimers organized as hollow tubes (~25-µm outer diameter and ~12-µm inner diameter) whose elastic modulus E is ~ 10³ MPa and its L_p is ~ 10³ µm (Gittes et al 1993). Because their physiological contour length is smaller than their L_p, one would expect microtubules to appear straight on the whole cell level. Immunofluorescent images of cytoskeletal microtubules show, however, that they appear bent and wavy (cf Ingber 2003a), suggesting that some internal mechanical force must act on microtubules. This curved shape of cytoskeletal microtubules implied that they might buckle and bend as they oppose forces exerted by the contractile actin network, which in part led to the suggestion that microtubules may act as compression-bearing elements in the cellular tensegrity model (Ingber et al 1981, Ingber 1993).

While compressive elements appear as columnar struts that are fully isolated from each other in Snelson's sculptures, Fuller (Fuller, 1961) and others (Connelly and Whiteley, 1997; Hanaor, 1998) have shown that tensegrities can contain compression-bearing elements that are connected in a joint, or are in direct contact. Cytoskeletal microtubules generally form from a common microtubule organizing center. But as microtubules grow, they encounter resistance by the actin network, which causes them to buckle and break into many smaller isolated elements; however, each of these microtubules still resist local compression because they remain connected to the surrounding contractile actomyosin filament network (Waterman-Storer and Salmon 1997). Thus, the observation that cytoskeletal microtubules are interconnected is not at odds with the tensegrity idea as long as there is a tension-compression synergy between the actin cytoskeleton and microtubules that establishes a stabilizing mechanical force balance.

Intermediate filaments, which are long polymers composed of vimentin, desmin, keratin, lamin, or related proteins, are much more flexible (L_p ~10⁰ µm, diameter ~10 nm) and extensible (E ~10⁰–10¹ MPa) than either actin filaments or microtubules (Fudge et al 2003). Their physiological contour length (10–20 µm) is much greater than their L_p, which explains their wavy appearance in cells (Ingber 2003a). This suggests that the contribution of intermediate filaments to mechanical stresses of the cytoskeleton is primarily through the conformational entropy changes. The entropic nature of intermediate filament elasticity is also reflected in their strain-hardening behavior (Janmey et al 1991). However, in living cells, the contribution of intermediate filaments to the whole cell elasticity becomes prominent only when cells are highly strained (Wang and Stamenović 2000) and intermediate filaments presumably become fully extended. This, in turn, suggests that the contribution of intermediate filaments to cell elasticity arises primarily through enthalpic mechanisms.

There is a large numbers of cytoskeletal proteins that bind and crosslink actin filaments, microtubules and intermediate filaments, and thereby control filament lengths, generate mechanical forces, and provide elasticity and mechanical connectivity to the cytoskeletal lattice and other cellular structures. One of the most important is myosin, whose cross-bridges link myosin and actin, in addition to generating contractile forces. Filamin A crosslinks F-actin and anchors the cytoskeletal actin network to the cell membrane. Spectrin links F-actin to intermediate filaments and also provides mechanical stability of the cell membrane and the underlying supporting cortical cytoskeleton in erythrocytes. Titin is a large elastic protein that plays an important role in muscle contraction. Talin, vinculin, paxilin, α-actinin, and zyxin are backbone proteins of focal adhesion plaques that form a molecular bridge which links actin stress fibers to transmembrane integrin receptors that, in turn, bind and mechanically couple cells to the extracellular matrix (ECM).

3.2 Cell-Matrix and Cell-Cell Interactions

Most cells in our bodies normally live as components of larger tissue structures that are composed of distinct types of cells that are physically connected to each other by junctional complexes, and to a common ECM anchoring scaffold. Cells attach to ECM and to other cells through binding of specific cell surface receptor proteins. Cells primarily adhere to ECM using integrin receptors, which are heterodimeric glycoprotein composed of α and β subunits (Hynes 2002). Twenty four types of integrins are formed from different α and β subunit combinations, and this provides the specificity required to mediate anchorage to various types of ECM proteins (e.g., various collagen types, as well as glycoproteins such as fibronectin, laminin, vitronectin and fibrinogen). Integrins span the lipid bilayer of the plasma membrane and their cytoplasmic tails bind to various intracellular actin-binding proteins, such as talin, vinculin, and paxillin, that physically link the integrins to internal actin cytoskeleton. Cells are also not evenly glued to the ECM, but instead these complexes organize as spot weld-like ‘focal adhesions’ where multiple integrins and their intracellular binding partners cluster together to form multivalent ‘velcro-like’ anchoring complexes. Importantly, the terminal ends of contractile actomyosin filaments of the cytoskeleleton insert on the same sites and thus, the anchorage complex and linked integrins always experience a pre-existing tension or prestress. Moreover, these integrins can aggregate or cluster to form different sizes or shapes of aggregations, which have different names (focal adhesions, fibrillar adhesions, focal complexes, podosomes) depending on their morphology and the cell type that forms them. The degree of clustering or aggregation depends in part on the availability and density of the ECM proteins and the distance between the binding sites on the ECM proteins (Cavalcanti-Adam et al 2007). However, focal adhesion assembly is also exquisitely sensitive to mechanical forces, either applied externally to integrins or transmitted from the internal contractile cytoskeleton. This change in molecular assembly in response to changes in mechanical forces applied to integrins appears to be mediated by stress-induced influx of calcium through stress-sensitive ion channels in the focal adhesion (Matthews et al 2010) and resulting activation of previously inactive cell surface integrins (Friedland et al 2009), which promotes their ability to engage ECM proteins outside the cell and bind to talin in the focal adhesion (Calderwood 2004, Shattil et al 2010).

Cadherins are calcium-sensitive transmembrane surface proteins that link cells of the same kind together at lateral cell-cell junctions to form tissue monolayers or multilayers, and their action is fundamental to the maintenance of tissue integrity in multicellular organisms (Gumbiner 2005). The cytoplasmic tail of the cadherin is connected to the actin microfilaments via α-catenin and β -catenin and a number of other linker proteins, including vinculin and P120 (Gumbiner 2005, Leckband et al 2011). Recent evidence indicates that cadherins and -catenin play important mechanosensing roles at cell-cell junctions (le Duc et al 2010; Liu et al 2010, Yonemura et al 2010).

Cell-cell interactions are also important for maintaining cytoskeletal tension (Nelson et al 2005, Tambe et al 2011, Jasaitis et al 2012). For example, crosstalk between cell-cell adhesion molecules and cell-ECM adhesions molecules influences the global tensional and functional state of cells (Nelson et al 2005, Liu et al 2007). This crosstalk takes place through the actin cytoskeleton and requires the presence of active cytoskeletal tension generation. The two adhesion systems exert negative feedback on each other (Burute and Thery 2012), resulting in relocalization of cell-ECM adhesions to the periphery of a cell cluster in the presence of strong cell-cell adhesions (Maruthamutu et al 2012, Mertz et al 2013). In fact, in a cluster of confluent cells, the traction forces transmitted through cell-cell junctions are of greater magnitude than the traction forces at the cell-ECM adhesions (Maruthamutu et al 2012, Mertz et al 2013), suggesting that within a cluster of confluent cells, the major pathway of force transmission is via cell-cell rather than via cell-ECM adhesions.

3.3 Cytoskeletal Prestress

Because all of the different cytoskeletal filaments systems are interconnected with each other, and with focal adhesions and cell-cell adhesion complexes, a tensile prestress is generated in the cytoskeleton through a balance between opposing forces distributed throughout this network. Specifically, tensile forces that are actively generated within contractile actomyosin filaments are resisted internally by microtubules that can bear compression imposed on them by the surrounding contractile network, and externally by the ECM scaffolding that is generally larger and stiffer than the cell (Wang et al 2001, 2002, Stamenović et al 2002b, Hu et al 2004, Brangwynne et al 2006), and by adhesions to neighboring cells. The resulting tensile stress helps to stabilize the entire cytoskeleton.

The prestress in the cell can be elevated internally by stimulating actomyosin-based contraction or by disrupting microtubule compression struts, or externally increasing the ability of the ECM or other cells to resist cell contractile forces (e.g., by increasing ECM rigidity). When this occurs, the cytoskeleton spontaneously stiffens. The most familiar example of this is when we increase the ‘tone’ in our muscles, and they stiffen. Experiments with airway smooth muscle cells and endothelial cells have confirmed that the prestress is closely associated with cell stiffness for any given cell size, suggesting that prestress dictates cell rigidity and governs shape stability (Hubmayr et al 1996, Pourati et al 1998, Cai et al 1998, Fabry et al 2001, Wang et al 2001, 2002, Stamenović et al 2002a, Smith et al 2005). These findings are also supported by results in other cell types under different physiologic conditions (Engler et al 2004, 2006, Fernandez et al 2006, Solon et al 2007, Kim et al 2009, Krishnan et al 2009, von Dassow et al 2010, Lam et al 2012, Canović et al 2013).

3.4 Cellular Tensegrity

Thus, the pivotal idea of the cellular tensegrity model (as initially depicted in Figs. 1C,D) is that the living cytoskeleton is stabilized by a tensile prestress that is generated and maintained through a complementary force balance between contractile actomyosin filaments that actively generate tensional forces, which are resisted by both intracellular compression-supporting structures, such as microtubules, and extracellular tethering sites to the ECM and to other cells (Ingber et al 1981; Ingber and Jamieson 1985, Ingber 1993, 1997, 2003a, 2006). The cell is also viewed as a hierarchical and multimodular tensegrity structure. It is hierarchical because smaller elements such as the nucleus (which is stabilized by its own molecular skeleton or nuclear scaffold), submembranous cytoskeleton (which lies beneath the surface membrane) and actomyosin filament bundles (which generate tension) are independent self-stabilizing tensegrities on smaller size scales. These are, in turn, composed of smaller molecules and groups of molecules that similarly maintain their shape stability through establishment of tensional integrity. This concept may seem obvious now to those familiar with modern day cell biology, but it was heretical when it was first proposed because most scientists viewed the living cell as a membrane surrounding a viscous cytoplasm with a nucleus floating at the center. Below we discuss experimental observations in support of the cellular tensegrity model before describing theoretical formulations of the model.

In 1980, fibroblasts cultured on a flexible silicon rubber substrate were shown to cause the substrate to actively wrinkle (Harris et al 1980) and similar results were later obtained and quantitated in fibroblasts adherent to polyacrylamide gel substrates (Pelham and Wang 1997). These observations led to development of a technique known as traction microscopy to quantitatively measure traction forces that cells exert at its anchoring points to the ECM substrate (Dembo and Wang 1999, Butler et al 2002). Severing focal adhesion attachments of endothelial cells to the substrate by trypsin results in a quick retraction of these cells (Sims et al 1992), and more recent studies using green fluorescent protein (GFP)-labeled actin in living cells confirmed that individual actin stress fibers experience a basal tensile prestress (Kumar et al 2006) (Fig. 2). Taken together, these findings confirmed that the actin cytoskeleton carries prestress and that this prestress is transmitted to and balanced by traction forces that act at the cell-anchoring points to the substrate.

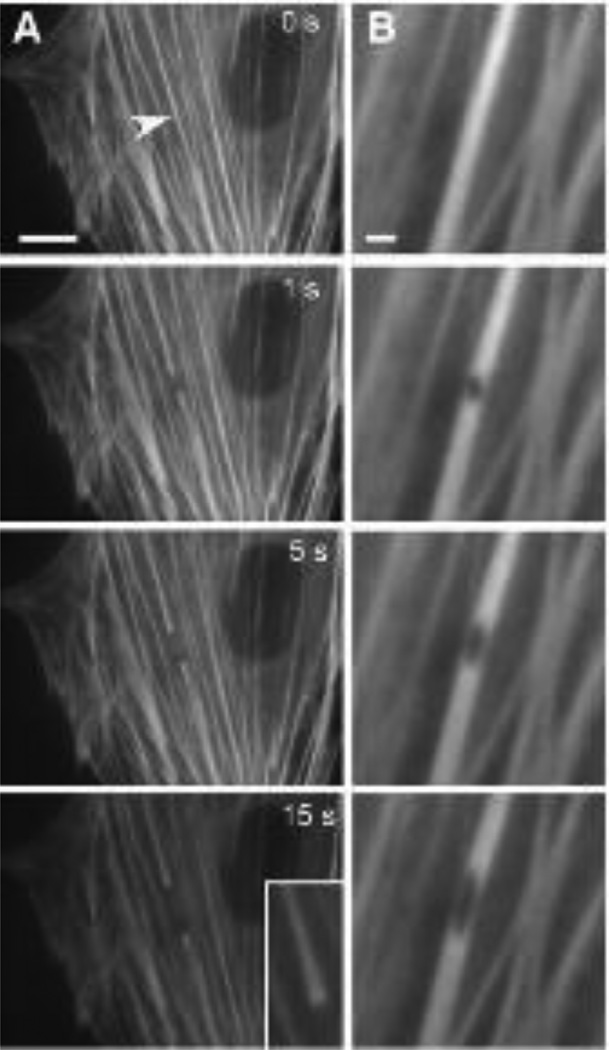
Fig. 2. Incision of actin stress fibers in living cells using a laser nanoscissor.

A) Severing of a single stress fiber bundle in an endothelial cell expressing EYFP-actin. Note that the severed ends splay apart (inset) as the stress fiber retracts over a period of 15 s (arrowhead indicates the position of the laser spot; bar, 10 µm). B) Strain relaxation of a single stress fiber bundle after a 300-nm hole was punched in the fiber using the laser nanoscissor. Note the hole becomes elliptical as it distended along the tension field line, indicating the presence of a prestress. Bar, 2 µm. (Reprinted with permission from Kumar et al 2006).

Several experimental studies have provided evidence that microtubules oppose contraction of the actin network in living cells. For example, as migrating cultured epithelial cells contract, microtubules in their lamellipodia region buckle as they resist the contractile force exerted on them by the surrounding actin network (Waterman-Storer and Salmon 1997). Extension of an elongated nerve cell process that is filled with parallel bundles of microtubules is also opposed by pulling forces of the actin microfilaments that surround those microtubules (Heidemann and Buxbaum 1990). Microtubules of endothelial cells, which appear straight in relaxed cells, similarly buckle immediately following contraction of the actin network (Wang et al 2001). Moreover, in cultured heart cells, microtubules buckle with each beat (contraction) of the cell (Brangwynne et al 2006) (Fig. 3). Together, those observations demonstrate that there is a coupling between the cytoskeletal contractile actin network and microtubules analogous to the tension-compression coupling in tensegrity structures. This has been confirmed by experimental studies that show cells shift compressive forces back and forth between their microtubules and ECM adhesions, such that microtubules bear most of the prestress in rounded cells, like those adherent to compliant ECMs in living tissues, whereas the ECM bears most of the load in highly spread cells on rigid substrates (Hu et al 2004). Experimental studies have confirmed that cytoskeletal microtubules do bear large-scale compressive loads that cause them to buckle in living cells, and their buckling wavelength is reduced significantly because of mechanical coupling to the surrounding elastic cytoskeleton, as demonstrated with a constrained buckling theory (Brodland and Gordon 1990, Stamenović et al 2002b, Brangwynne et al 2006). Those studies revealed that coupling of microtubules to the surrounding cytoskeletal lattice dramatically increases the compressive forces that they can sustain; this explains how they can make a more significant structural contribution to the mechanical behavior of the cell than previously thought possible.

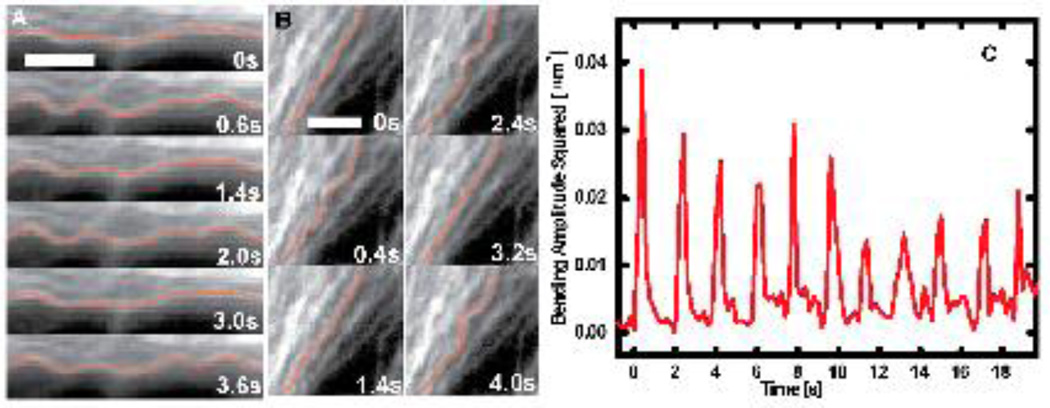
Fig. 3. Periodic microtubule buckling induced by contractile beating in cultured heart cells.

A) A time sequence showing a microtubule buckling and unbuckling successively three times in a beating cardiac myocyte. B) A similar time sequence showing one microtubule buckling and unbuckling at a single location, while neighboring microtubules remain straight. C) A Fourier mode analysis of the microtubule shown in B demonstrating that the amplitude of the bending on wavelengths of 3 µm shows periodic spikes induced by periodic buckling of the microtubule under successive contractile beats. There is some decrease in amplitude of the periodic buckling over time as the intensity of the contractile force decreases due to partial photodamage. Bar, 3 µm. (Reprinted with permission from Brangwynne et al 2006).

A more rigorous test of the tensegrity model came with the advancement of experimental techniques in which cell prestress and cell stiffness could be measured independently. One of the a priori predictions of the tensegrity model is that its structural stiffness increases in a direct proportion with the level of its prestress (see Section 4 for mathematical justification). Measurements of stiffness and prestress in living airway smooth muscle cells provided the first evidence for this relationship (Wang et al 2001, 2002), and this was confirmed using different techniques and cell types in later studies (Fernandez et al 2006, Lam et al 2012, Canović et al 2013) (Fig. 4).

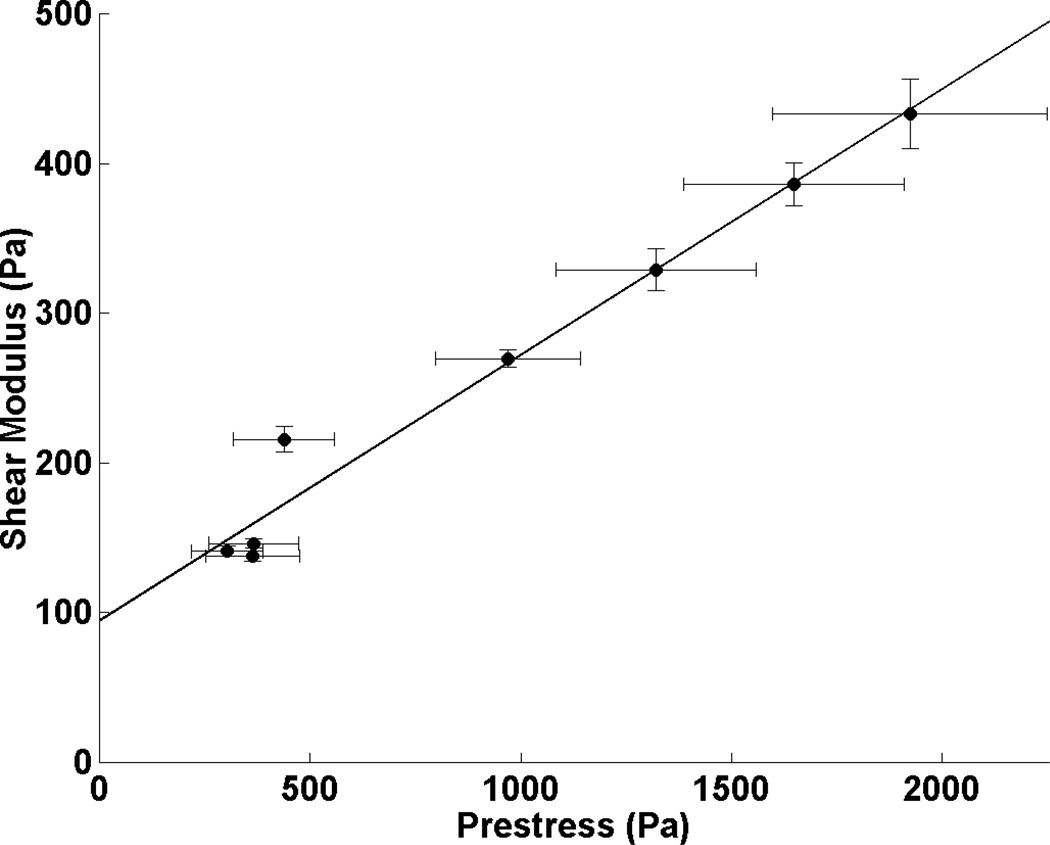
Fig. 4. Prestress dictates cell shear modulus.

Cell prestress was increased or decreased from baseline (normal cells at resting state, ~1000 Pa) by treatment with contractile agonist histamine (0.1–10 µM for 1 min) or relaxation reagent isoproterenol (0.01–10 µM for 10 min) in living human airway smooth muscle cells. Cell prestress was calculated by measuring cell tractions and estimating cell cross-sectional areas. Cell shear modulus was measured with magnetic twisting cytometry. Cell spreading areas were constant before, during, and after drug treatments. Data are presented as means ± S.E.M. (Reprinted with permission from Wang et al 2002)

4. Tensegrity Models

4.1 Structural Mechanics Modeling Approaches

From a structural mechanics perspective, tensegrity structures represent a special class of discrete structures that require initial tension (or prestress) in their structural members in order to maintain their structural integrity. In the absence of this initial tension, a single tensegrity module loses its structural integrity and collapses under an applied external load. In the structural mechanics literature, such structures are often referred to as underconstrained structures. When prestressed, these types of underconstrained structures resist external loads primarily through reorientation and changes in the spacing of their initially tensed structural members, and to a lesser extent through lengthening and shortening of those members. The greater the initial tension is, the greater resistance to external load and hence, the greater the rigidity (or stiffness) of the entire structure. Thus, it follows that changes of orientation and spacing of tensed discrete elements represent the central mechanism by which restoring forces arise in tensegrity structures

In underconstrained systems, the number (n) of forces carried by each structural member is always smaller than the number (m) of equilibrium equations. Consequently, these systems cannot maintain equilibrium under external loads and thus collapse. To be able to support external loads, an underconstrained structure must satisfy two basic requirements: a) it must be “prestressable”, i.e., must possess an initial prestressed equilibrium state, and b) the initial equilibrium state must be stable (cf Volokh and Vilnay 1997a, b). Mathematically, these two requirements can be written as follows

$$\mathrm{a}){\mathbf{A}}_0{\mathbf{p}}_0=\mathbf{0}\text{and}\mathrm{b}){\mathrm{\delta }}^{2}U>0,$$ (1)

where A₀ is a m×n initial “geometry” matrix consisted of direction cosines of structural members; p₀ is n×1 vector of initial member forces (i.e., prestressing forces); U is the elastic energy stored in the system, defined as U = ½ u^TKu and K is m×m the tangent stiffness matrix which relates an m×1 vector of externally applied forces f with an m×1 vector of nodal displacements u, i.e., f = Ku; δ symbolizes small variations.

It follows from (1a) that in order that p₀ ≠ 0 (i.e., in order to have a finite prestressing force), rank[A₀] < n. It follows from (1b) that δ²U = δu^TKδu > 0. Since displacement perturbations δu are arbitrary, then δu^TKδu > 0 implies that K is positive definite. One can show that for small deformation K admits a decomposition into an elastic stiffness matrix K^e (m×m) and prestress stiffness matrix K^p (m×m), i.e.,

$$\mathbf{K}={\mathbf{K}}^{\mathrm{e}}+{\mathbf{K}}^{\mathrm{p}}={\mathbf{A}}_0\mathbf{C}{{\mathbf{A}}_0}^{\mathrm{T}}+{\mathbf{K}}^{\mathrm{p}}({\mathbf{p}}_0),$$ (2)

where C the uncoupled stiffness matrix which is an n×n diagonal matrix whose diagonal terms represent elastic stiffness of individual structural members and therefore C is always positive definite. On the other hand, K^p depends on prestressing force p₀ carried by those members (Volokh and Vilnay 1997a, b, Murakami 2001a, b, Volokh 2011).

Since stability (1b) requires K to be positive definite, the it follows from to (2) that K^e and/or K^p must be positive definite. In conventional constrained structures (e.g., Eiffel tower), K^e is always positive definite and no initial prestress is required for stability. In underconstrained structures, however, K^e may become singular because of the restriction that rank[A₀] < n and hence the initial prestress is required for K^p to be positive definite to uphold stability. In other words, stability of unconstrained structures cannot be provided by elasticity of their structural members and thus they need prestress to maintain their shape and solidity.

It has been shown that K^p has the following general form (Murakami 2001a, b) ${\mathbf{K}}^{\mathrm{p}}=\sum _{i=1}^n{\mathbf{L}}_i^{\mathrm{T}}{\mathbf{K}}_i^p{\mathbf{L}}_i$, where L_i is 6×m matrix which links nodal displacements (m×1) to a member displacement (6×1) and

$${\mathbf{K}}_i^{\mathrm{p}}=\frac{{\mathrm{\sigma }}_i^0{S}_i^0}{l_i^0}\left(\begin{array}{cc}\hfill \mathbf{I}\hfill & \hfill -\mathbf{I}\hfill \\ \hfill -\mathbf{I}\hfill & \hfill \mathbf{I}\hfill \end{array}\right),$$ (3)

is the member prestress stiffness, ${\mathrm{\sigma }}_i^0$ is the initial prestress, $S_i^0$ is the initial cross-sectional area, and $l_i^0$ is the initial length of the i-th member, and I is a 3×3 identity matrix. Note that for K^p to be positive definite, ${\mathrm{\sigma }}_i^0>0$ must be satisfied in every member.

It follows from (3) that the stiffness of prestressed unconstrained structures changes proportionally to the level of prestress carried by the structural members. A similar behavior has been observed in a diverse type of soft materials, both living and inert, including living cells (Wang et al 2001, 2002, Stamenović et al 2002a, Fernandez et al 2006, Krishnan et al 2009, Lam et al 2012), reconstituted actin gels (Gardel et al 2006), liquid foams (Derjaguin 1933) and emulsions (Princen and Kisss 1986), cartilage (Khalsa and Eisenberg 1997) and lung parenchyma (cf Stamenović 1990). In all these materials stiffness increases approximately linearly with the increasing level of prestress. This, in turn, suggests that the observed behavior must not be determined by specific molecular mechanisms and organization or by specific material properties. Rather, it may reflect a generic structural-relationship principle of underconstrained structures.

It is noteworthy that the above analysis applies to both tensegrity cable-and-strut structures and to prestressed cable nets which have no internal compression-supporting members (e.g., spider web). From the analysis point of view, both classes of structures are similar and because cable nets must have external tension-resisting anchors to ensure their structural stability, we (Ingber 1993, 2003a, Fredberg et al 1998, Stamenović and Wang 2000, Wang et al 2002) and others (Calladine 1978, Connelly 1982, Connelly and Back 1998) have used the term ‘tensegrity’ for both. However, from an engineering point of view, possible geometrical configurations and force transmission through the network, these two classes of structures are different, as emphasized by Vilnay (1984). Importantly, in the case of cable nets the structure is always stable because K is positive-definite (Volokh and Vilnay, 2000). If, however, the structure is comprised of both tension- and compression-supporting members, its stability cannot be taken for granted even if det[K] ≠ 0 (Li et al 2010).

4.2 Cable-and-Strut Models of Cellular Tensegrity

First attempts to mathematically model the cytoskeleton as a tensegrity structure were centered around simple cable-and-strut modules composed of a limited number of structural members (Stamenović et al 1996, Coughlin and Stamenović 1997, 1998, Wendling et al 1999, Stamenović and Coughlin 1999, 2000, Volokh et al 2000; Wang and Stamenović 2000, Stamenović and Ingber 2002, Cañadas et al 2002, 2006, McGarry and Prendergast 2004, Sultan et al. 2004, Lazopoulos 2005, Pirentis and Lazopoulos 2010). Despite their simplicity, those models could account for a number of phenomena that were observed in living cells, as we describe below.

Strain hardening

It has been shown that stiffness progressively increases with increasing applied force in living cells (Wang et al 1993, Wang and Ingber 1994). This is known as strain hardening (or stiffening) and is indicative of a nonlinear stress-strain relationship of the cell. This nonlinearity may reflect intrinsic material nonlinearity of cytoskeletal polymers (Gardel et al 2006), or nonlinearities associated with bending/buckling of those polymers (Coughlin and Stamenović 1997, 1998, Fernandez et al 2006). On the other hand, tensegrity models have demonstrated that the observed stiffening response may also reflect geometrical realignment of structural members in the direction of applied force (“kinematic stiffening”), even if those members are linearly elastic (Stamenović et al 1996; Coughlin and Stamenović 1998). Some of the major force-bearing components of the cytoskeletal lattice, such as actin filaments, do exhibit a linearly elastic behavior (Storm et al 2005), whereas the others such as intermediate filaments (Janmey et al 1991, Fudge et al 2003, Storm et al 2005) and actin stress fibers (Deguchi et al 2006) can exhibit non-linear behaviors, if sufficiently strained. However, in the normal physiological range of strains, these nonlinearities have a minor contribution to overall cell behavior. On the other hand, cytoskeletal microtubules buckle when they oppose overwhelming tensile forces generated and carried by the contractile actin network (Wang et al 2001, Brangwynne et al 2006). Therefore, the stiffening observed in living cells may arise primarily from geometrical rearrangements of the cytoskeletal lattice and bending or buckling of cytoskeletal filaments. The latter is not inconsistent with the tensegrity model where buckling of individual compression-supporting struts may occur without compromising stability of the overall network (Coughlin and Stamenović 1997, 1998, Volokh et al 2000). Nevertheless, we should point out that strain-hardening behavior is not an intrinsic property of tensegrity structures. Tensegrities can also exhibit softening (i.e., stiffness decreases with increasing applied load) (Coughlin and Stamenović 1998, Volokh et al 2000), or they may, under certain conditions, have constant stiffness, independent of the applied load (Stamenović et al 1996).

Prestress-dependent stiffness

Micromechanical measurements have shown that in cultured airway (Wang et al 2001, 2002, Stamenović et al 2002a) and vascular smooth muscle cells (Lam et al 2012), stiffness increases with prestress in a nearly direct proportion (Fig. 4). This linear dependence suggests that cells use prestress to tune their mechanical properties as tensegrity structures do. Inhibition of the cell’s contractile force generation using pharmacological interventions (i.e., which lowers prestress) also leads to a reduction of cell stiffness (Hubmayr et al. 1996, Fabry et al 2001, Wang et al 2001, 2002, Stamenović et al, 2002a, Smith et al 2005). Thus, in the absence of prestress, cells lose their rigidity and hence, their ability to maintain shape stability in face of externally applied loads, which is consistent with the behavior of tensegrity structures. Importantly, this ability of cells to adjust their mechanical properties by tuning their contractile prestress is essential for regulation of vital cell functions, including mechanotransduction, crawling, spreading and invasion, (Ingber 2003a). Thus, the cellular tensegrity model can help to explain how cell shape, movement and cytoskeletal mechanics are controlled, as well as how cells sense and respond to mechanical forces.

The effect of cell shape on cell mechanics

When cells spread from round to flat, there are concomitant increases in cell stiffness and alterations in cell stiffening behavior (Wang and Ingber 1994). These increases have been linked to upregulation of cell contractility during spreading (Polte et al 2004), as well as to cell shape-dependent changes in cytoskeletal prestress (Hu et al 2004). The importance for structural shape-dependent changes in prestress for this response is supported by studies using simple cable-and strut tensegrity models in which their nodes are pinned down to a rigid substrate to mimic cell spreading (Coughlin and Stamenović 1998) (Fig. 5). These studies showed that anchoring the tensegrity in this manner results in increased stiffness and enhanced stiffening, the average prestress in the cable elements increases in parallel. Furthermore, studies with living cells held in spread versus round forms also confirmed that while external ECM tethers that resist cell contractile forces are responsible for the majority of cellular prestress when cells are in an extended form, internal microtubule struts are the dominant source of prestress in rounded cells with less ECM adhesions (Hu et al 2004).

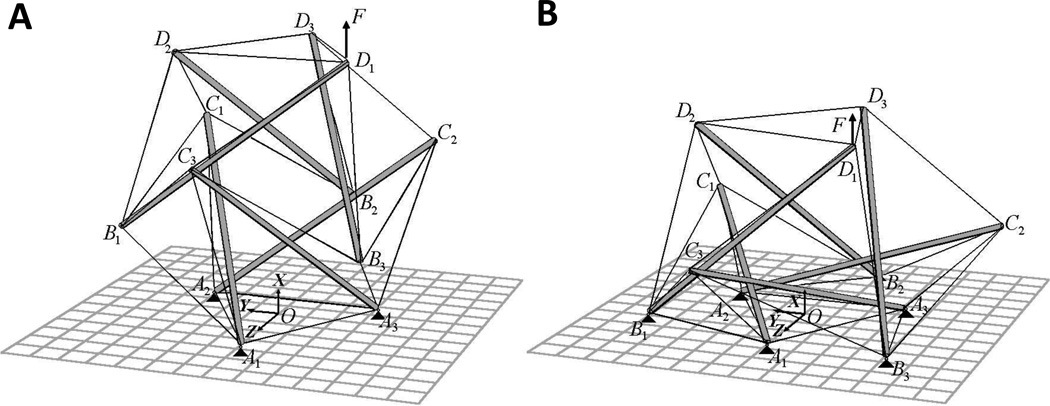
Fig. 5. Six-strut tensegrity model in the round (A) and spread (B) configurations.

The model is anchored to the substrate (gray grid) via nodes A₁, A₂ and A₃ (round) and A₁, A₂, A₃, B₁, B₂ and B₃ (spread) indicated by black triangles. The black arrow at node D₁ indicates the vector of applied force F. Increasing the number of anchored nodes results in a greater distension of the structure causing an increase in the structural stiffness, enhanced stiffening, and an increase in the average prestress in the cable elements. This behavior is consistent with the mechanical behavior observed in spread vs round cells (Ingber and Wang 1994). (Reprinted with permission from Coughlin and Stamenović 1998.).

Quantitation of cell elasticity

Using a tensegrity model comprised of 6 rigid struts and 24 linearly elastic cables subjected to uniaxial extension, an expression for the elastic modulus (E) of an “equivalent continuum” was derived using a coarse-grain procedure (Stamenović and Coughlin 1999). The key premise in this derivation is that the work done by external forces on uniaxial extension of the tensegrity model is equal to the strain energy stored in the equivalent continuum. The following relationships were obtained

$$E\approx \frac{{\mathrm{\sigma }}_{\mathrm{c}}^0{\mathbf{\varphi }}_{\mathrm{c}}}{3}\approx \frac{{\mathrm{\sigma }}_{\mathrm{s}}^0{\mathbf{\varphi }}_{\mathrm{s}}}{3},$$ (4)

where ${\mathrm{\sigma }}_{\mathrm{c}}^0$ is the initial tensile stress in the cable elements and ϕ_c is the volumetric fraction (relative density) of cables and ${\mathrm{\sigma }}_{\mathrm{s}}^0$ is the initial compression stress in the struts and ϕ_s is the volumetric fraction (relative density) of the struts. By identifying the cables with cytoskeletal actin filaments and the struts with cytoskeletal microtubules, it was possible to estimate the upper and lower bounds of the cell elastic modulus based on experimental data for ${\mathrm{\sigma }}_{\mathrm{c}}^0$, ϕ_c, ${\mathrm{\sigma }}_{\mathrm{s}}^0$ and ϕ_s (Stamenović and Coughlin 1999, 2000).

To estimate an upper bound (E_sup) of the elastic modulus using (4), it was assumed that ${\mathrm{\sigma }}_{\mathrm{c}}^0$ corresponds to a maximum stress that actin filaments can withstand before breaking, which is ~10¹ MPa (Tsuda et al 1996). The volumetric fraction of filamentous F-actin in living cells has been estimated to be ~0.21% (Satcher et al 1997, Stamenović and Coughlin 1999), which led to an estimated E_sup of ~10¹ kPa. To estimate a lower bound (E_inf) of the elastic modulus using (4), it was assumed that ${\mathrm{\sigma }}_{\mathrm{s}}^0$ represents a critical buckling stress of microtubules, which is ~142 kPa (Stamenović et al 2002b). ${\mathrm{\sigma }}_{\mathrm{s}}^0$ was calculated based on the experimentally measured bending rigidity of microtubules of 21.5 pN•µm² (Gittes et al 1993), the cross-sectional area of microtubules of 190 nm², the estimated critical buckling length of 2.8 µm (Stamenović et al 2002b), an estimation of the volumetric fraction of cytoskeletal microtubules of ~0.19% (Stamenović and Coughlin 1999). Thus, it was obtained that E_inf ~ 10⁻¹ kPa. Experimental values of material moduli of different cell types measured with different techniques fall within the range of 10⁻¹–10¹ kPa (Wang et al 2001, 2002, Fabry et al 2001, 2003, Smith et al 2005, Fernandez et al 2006, Lam et al 2012, Canović et al. 2013).

Dynamic rheological behavior

Tensegrity structures are generally defined as static systems and hence, they cannot describe time-dependent viscoelastic phenomena observed in living matter. Nevertheless, there have been several attempts to model cellular viscoelasticity using tensegrity structures (Cañadas et al 2002, 2006; Sultan et al 2004). In those models, linearly elastic cables were replaced with linearly viscoelastic Voigt elements (springs and dashpots in parallel). One of those models predicted that the elastic (storage) and viscous (loss) moduli will increase with increasing level of prestress in response to sinusoidal loading (Sultan et al 2004), which is consistent with the oscillatory response of living cells (Fabry et al 2001, 2003, Stamenović et al 2002a, Smith et al 2005). Because linear Voigt members do not change their viscoelasticity with increasing level of prestress, it follows that the observed prestress-dependent response of the viscoelastic tensegrity model is an emergent phenomenon. As structural members of the tensegrity model undergo periodic geometrical rearrangements in response to oscillatory loading (Cañadas et al 2002, 2006, Sultan et al 2004), those rearrangements may not be in phase with the applied load or with each other because of viscous damping in the Voigt members. As structural rearrangements are prestress-dependent in tensegrities, the corresponding phase-lag and hence, the elastic and viscous moduli, depend on the prestress (Sultan et al 2004).

These viscoelastic tensegrity models were less successful in explaining the observed power-law frequency-dependence of the material moduli of living cells (cf Fabry et al 2001, 2003, Smith et al 2005, Hoffman et al 2006). The reason that the models could not predict the power-law behavior is their discrete nature, which implies a discrete time constant distribution, whereas power-law rheology implies continuous time spectrum and time-scale invariance. It is possible, however, that a more complex tensegrity structure, with a much larger number of structural members than the six-strut model, and more modules of different size, may have a broader viscoelastic time spectrum that could eventually produce a power-law like response.

Reconciling tensegrity and soft glass rheology models of the cell

In the context of cell rheological behaviors, we should briefly discuss the soft glass rheology (SGR) model of the cell, which has gained a considerable interest in the cell biophysics community during the past decade, and how it relates to the tensegrity model. Since the discovery of a weak power-law rheology of living cells (Fabry et al 2001), several groups have tried to provide a theoretical basis for this phenomenon. The prevailing model (Fabry et al 2001, 2003) has been derived from the SGR theory of Sollich (Sollich et al 1997, Sollich 1998). According to this theory, individual elements (whatever they may be) of matter exist within an energy landscape containing many wells formed by neighboring elements. The energy wells are so deep that the elements are not able to escape the wells by thermal fluctuations. Instead, the elements are agitated and rearranged through interactions with their neighbors which enable them to escape from their energy wells. These agitations can be represented by an index referred to as an “effective temperature” and it is directly related to the power-law exponent. In living cells, it appears that the effective noise temperature may be ATP-related (Lau et al 2003, An et al 2004, Trepat et al 2007).

It is clear from the above description that soft glasses are metastable, non-equilibrium materials, quite opposite from static, self-equilibrated, stable tensegrities. Thus, the question is can tensegrity and SGR be brought together in the context of cellular mechanics? It is well known that some types of inert soft glassy materials, such as liquid foams and emulsions, exhibit prestress-dependent stiffening responses (Derjaguin 1933, Princen and Kiss 1986). While a relatively simple micromechanics of foams and emulsions makes it easy to understand how these materials exhibit both tensegrity-like (Reinelt and Kraynik 1993, Stamenović 1991) and SGR-like behaviors (Kraynik and Hansen 1986, Koehler et al 1999, Jiang et al 1999), it is much less obvious in the case of living cells. A cue that may link these two types of behaviors in cells comes from the observation that the prestress stabilizes the cytoskeletal lattice via tensegrity mechanisms and, at the same time, it reduces the effective temperature of the cytoskeleton (Fabry et al 2001) and therefore modulates the power-law behavior of cells (Stamenović et al 2004, Stamenović 2008). Thus, rather than viewing the tensegrity and SGR models as two mutually exclusive concepts of cytoskeletal mechanics, it is more appropriate to regard them as two complementary models that within their own rights can describe a broad class of phenomena observed in living cells, and that they are linked to one another through prestress (Stamenović 2008).

4.3 Subcellular Tensegrity Models

The cellular tensegrity model assumes that living cells are hierarchical and multimodular structures (Ingber 2003a, Ingber 2006). In fact, multiple groups have begun to describe how subcellular structures use tensegrity for their shape stability, and some have developed theoretical models to describe this behavior. For example, the cell’s surface membrane and supporting cortical cytoskeleton, which are most easily studied in the red blood cell, form a prestressed geodesic (triangulated) structure that gains its mechanical stability by incorporating rigid actin protofilaments that are held in place by surrounding spectrin molecules that act like tensed springs or cables suspended from the overlying lipid bilayer (Vera et al 2005). Nuclear lamins and interconnected nuclear pore complexes form another type of tensed geodesic lattice that withstands the expansion force of condensed chromatin at the center of the cell (Maniotis et al 1997, Ingber 2003a). A mechanical force balance between compressed microtubules and a tensed network of chromosomes and nuclear scaffolds also appears to stabilize the mitotic spindle (Pickett-Heaps et al 1997), and this also may potentially explain the ‘coherence’ or mechanical coupling of chromatin structures that has been recently observed over large distances in the living interphase nucleus (Zidovska et al 2013).

Tensegrity is also utilized at the molecular level. For example, actin microfilaments self-assemble into geodesic domes (actin geodomes) in the cytoskeleton of certain cells both in vitro (Lazarides 1976) and in vivo (Rafferty and Scholtz 1985). Geodesic tensegrity structures also can be seen in polyhedral enzyme complexes (Wagenknecht et al 1991), clathrin-coated transport vesicles (Vigers et al 1986), hexagonal arrangements of basement membrane proteins (Yurchenco and Schittny 1990), and all viral capsids (Caspar 1980). Biological polymers, such as microfilaments (Schutt et al 1997) and complex actin stress fibers composed of multiple actomyosin filaments connected by linker proteins have been described as tensegrities as well, and a multimodular tensegrity model predicts mechanical behaviors of living stress fibers (Luo et al 2008). Most importantly, individual protein, RNA and DNA molecules also all have been depicted as prestressed tensegrity structures (Ingber 1998, 2000, Farell et al 2002, Zanotti and Guerra 2003, Edwards et al 2012). This is because in individual molecules, stiffened regions (e.g. -helices and β -strands in proteins) act locally to resist inwardly directed forces generated by attractive (tensile) intramolecular binding forces. In fact, studies with optical tweezers reveal that individual DNA molecules exhibit stiffening behavior (Smith et al 1992) similar to that of living cells, tissues and tensegrity models. Most recently, molecular dynamic simulations of the globular proteins, ubiquitin and immunoglobulin, have confirmed that these molecules are tensegrity structures that require a dynamic prestress for their stability (Edwards et al 2012).

The ability of these prestressed hierarchical networks to channel mechanical forces over discrete molecular paths to sites deep inside the cytoplasm and nucleus, explains how cell distortion or mechanical stress application to cell surface integrins produces in structural changes in nuclei, nucleoli, and individual molecules at progressively smaller size scales (Ingber 2006). Mechanical coupling between integrins and the nucleus is mediated by primarily by intermediate filaments, and to a lesser degree by actin microfilaments and microtubules, which extend from cell surface adhesion sites to specific binding receptors on the nuclear surface that connect to internal nuclear scaffolds (Wang et al 2009). Forces that are transferred to individual molecules can then drive mechanochemical conversion by inducing molecular unfolding or producing changes in their thermodynamic and kinetic properties (Ingber 2006). And once again, because this is a hierarchical tensegrity structure, force transfer through this structural network and across size scales can be modulated by altering cytoskeletal prestress (Hu et al 2005).

4.4 Limitations of Cable-and-Strut Tensegrity Models

Despite their success in describing a broad range of cellular behaviors, cable-and-strut tensegrity models have a number of limitations. One is the absence of the effect of density of cross-linking from the models. The models can handle only two limit cases: one where the cables and struts are pinned at joints which represents cross-linking, and the other where cables are allowed to freely slide through nodal frictionless loops which represents the absence of cross-linking (Stamenović et al 1996). Although the “looped” models have lower stiffness than the “pinned” ones, stiffnesses of both models scale with ϕ_c. On the other hand, models of actin polymer networks show that the degree of cross-linking affects the elastic modulus of the network via the volumetric fraction ϕ of actin in the network; for low crosslink density, the elastic modulus of the network scales with ϕ, whereas for high crosslink density it scales with ϕ^5/2 (MacKintosh et al 1995). Another limitation of the discrete tensegrity models is that the prestress results from passive tension generated by initial elongation of elastic cable elements. In living cells, actin filaments carry isometric tension generated by molecular motors through ATP-dependent processes. Finally, tensegrity models are deterministic, stable, self-equilibrated, static systems, whereas the cytoskeleton of living cells is a stochastic, dynamic away-from-equilibrium system which undergoes continuous turnover driven by thermally and non-thermally driven processes (Fabry et al 2001, 2003, Bursac et al 2005, Trepat et al 2007).

One question about the simple six-strut model is whether it captures the essence of the complex cytoskeleton that consists of many more actin filaments, microtubules and intermediate filaments in a living cell. We and others have modeled the cytoskeleton using more complex tensegrity models than the minimal six-strut models, as well as hierarchical and multimodular tensegrities. For example, in two studies, 12 additional cables were added to the six-strut model that linked the geometrical center of the model with its vertices to account for the contribution of intermediate filaments, and this model led to predictions that were confirmed in experiments with living cells (Wang and Stamenović, 2000; Sultan et al., 2004). Both 6- and 12-strut tensegrity models were considered in a study of cell spreading on the substrate, and no qualitative difference could be demonstrated between the two models (Coughlin and Stamenović, 1998). The 12-strut model was also used in a study of cell mechanosensing of substrate stiffness (De Santis et al., 2011). A complex, multimodular tensegrity model of non-spherical shape and with a large number of elements was developed to describe the mechanical behavior of an actomyosin stress fiber bundle at the molecular level (Luo et al., 2008). The important point, however, is that while tensegrity models of different shape and different number of structural elements have been used to describe different aspects of cell mechanobiology, their mechanical responses reflect a common underlying mechanism that is displayed by even the simplest model: their structural stiffness and shape stability are conferred and tuned by the prestressing force of their tension-bearing components that are resisted by other elements which are in compression. Interestingly, a coarse-grained finite element model of the cytoskeleton has been proposed (Kim et al., 2009) that independently confirms that prestress is the key factor determining structural stability, again supporting the generality of the simplified tensegrity model. Finally, it also should be noted that we have built prestressed geodesic tensegrity models (made of soda straws held together by a tensed elastic thread) that undergo structural transformations that precisely mimic molecular scale structural changes observed when regions of the actin cytoskeleton transform from bundles to actin ‘geodomes’ in living cells; these models exhibited strut-for-strut and vertex-for-vertex identity on the nanometer scale as visualized in electron microscopic images of the actin cytoskeleton (Ingber, 1993).

The specific role of the red blood cell’s spectrin-rich cortical cytoskeleton and lipid bilayer in cell shape stability also deserves discussion. As described above, the non-compressible lipid bilayer serves as a key compressive element in the tensegrity model of the RBC model of Vera et al (2005), which is required to balance tensile forces in the spectrin network and establish a stabilizing force balance. This is supported by the experimental finding that a tensional prestress is required for cytoskeletal shape stability in the red blood cell (Discher et al., 1998), and by the work of Svoboda et al. (1992), which clearly shows that removal of surface membrane destabilizes the red blood cell shape. In contrast, we have shown that opening or partial removal of membranes from nucleated mammalian cells immediately rigidifies the cell. In this case where cell shape is largely stabilized by the internal cytoskeleton, stability is maintained without membrane bilayer integrity, but interestingly, flexibility and resiliency normally provided by prestressed tensegrities are lost. This is due to loss of actomyosindependent tension generation in the cytoskeleton because the flexibility and resiliency can be restored in membrane-permeabilized cells by adding back factors that permit active myosinbased tension generation, and this can be inhibited by including actin peptides that prevent rigor complex formation (Wang and Ingber, 1994). Thus, again, tensional prestress is required for shape stability here too, but now it acts throughout the complex cytoskeletal lattice that fills the cytoplasm, rather than just in the submembranous cytoskeleton that is more dependent on the surface membrane.

4.5 Statistical Mechanical Tensegrity Models

These apparently irreconcilable differences between the static tensegrity models and the dynamic cytoskeletal network have been a reason that the cellular tensegrity idea has not been fully accepted in the field of cellular biomechanics (Ingber et al 2000). However, Wolynes’s group (Shen and Wolynes 2005, Wang and Wolynes 2012) has shown that the cellular tensegrity concept can be generalized to a non-equilibrium, stochastic model of the cytoskeleton. For example, they proposed a generic statistical mechanical model of motorized particles as a theoretical tool to investigating non-equilibrium behavior of the cytoskeleton. Three type of forces act on those particles: 1) adhesion forces due to mechanical interactions (e.g., due to cross-linking), 2) thermally-driven forces and viscous forces, and 3) motor-generated propelling forces. Molecular motors contained within the particles generate power strokes through ATP consumption and produce kicking forces that are stochastic in nature. In the case of cytoskeletal filaments, kinetics of particle motors describes growing and shrinking of the filaments.

In the case where the motor propelling forces are not activated, adhesive forces dominate thermal fluctuations and the system is in equilibrium. When the motor propelling forces are activated, they tend to drive the system away from equilibrium. These models predict that the non-equilibrium effect of motorization may have as strong effect as adhesiveness due to cross-linking. Thus, the synergy between non-equilibrium kicking forces and equilibrium adhesion forces together provide tension and compression to maintain cell shape stability on one hand, and to facilitate fast remodeling on the other. Thus, the model of Shen and Wolynes (2005) represents a statistical mechanical underpinning for the cytoskeletal tensegrity model.

In a more recent development, the basic concepts of the statistical tensegrity model were expanded to actomyosin networks (Wang and Wolynes 2012). They modeled the actomyosin system as a cross-linked network of nonlinear elastic filaments subjected to spatially anti-correlated motor kicks acting on motorized cross-links. Simulation studies showed that a non-equilibrium, many-body system driven by correlated motor kicks can behave as if it were at an effective equilibrium, but with modified interactions that account for the correlation of motor-driven motions of the actively bonded nodes. This statistical mechanical approach therefore offers a new approach to study and model tensegrity in cells.

4.6 Insights from Other Models of Cell Mechanics

Cortical Membrane Models

In this model, it is assumed that the main stress-bearing elements of the cytoskeleton are confined either within a thin (~100 nm) cortical layer (Zhelev et al 1994) or several distinct layers (Heidemann et al 1999). The cortical membrane is under sustained tension that is either entirely balanced by the pressurized cytoplasm (in suspended cells), or balanced partly by the cytoplasmic pressure and partly by traction at the extracellular adhesions (in adherent cells). This model has been successful in describing mechanical behaviors of various suspended cells (Evans and Yeung 1989, Zhelev et al 1994, Discher et al 1998), but has enjoyed limited success with adherent cells (Fung and Liu 1993, Schmid-Schönbein et al 1995, Coughlin and Stamenović 2003). To illustrate shortcomings of this model, we simulated stiffness measurements obtained by twisting of a rigid microsphere embedded in the elastic cortical membrane. By applying a twisting torque to the bead in the vertical plane, we obtained that the shear stiffness (G) as follows (Stamenović and Ingber 2000)

$$G=\frac{Th\text{sin}\mathrm{\theta }}{\mathrm{\pi }D\mathrm{\theta }},$$ (5)

where T is tensile stress (prestress) in the membrane, h is the membrane thickness, D is the diameter of the microbead and θ is the twisting angle. While (5) predicts that G increases in proportion with T, consistent with experimental observations, it also predicts that G decreases with increasing θ, i.e., exhibits softening rather than the observed stiffening behavior, and that G decreases with increasing D, whereas experimental data show the opposite (Wang and Ingber 1994).

One reason for these discrepancies could be the assumption that the cortical layer is a membrane that carries only tensile force. In reality, the cortical layer can support bending, for example in red-blood cells (Evans 1983, Fung 1993), and hence a more appropriate model may be a shell-like rather than a membrane-like structure. Regardless, the assumption that the cytoskeleton is confined within the cortical layer is inconsistent with observations indicating that in adherent cells the cytoskeletal lattice is a three-dimensional network that spans the entire cytoplasmic domain of the cell and facilitates force transmission from the cell surface to the nucleus (Maniotis et al 1997, Wang et al 2001, Hu et al 2003). Some still view the cortical membrane model as a reasonable mechanical model for suspended cells where the cytoskeleton appears to be organized within a thin cortical membrane (Bray et al 1986). However, studies with living suspended cells clearly show that their stiffness still depends on actomyosin-dependent prestress in their internal cytoskeleton (Cai et al 1998), which is more consistent with a cellular tensegrity model containing a tensegrity-stabilized cortical cytoskeleton (Vera et al 2005) on a smaller scale.

Tensed Cable Net Model

These are cytoskeletal models where all structural members carry tensile forces. Because cables do not support compression, they need to carry initial tension to prevent their buckling and subsequent collapse in the presence of externally applied load. This initial tension defines prestress that is balanced externally (e.g., by attachment to the ECM or neighboring cells), and/or internally (e.g., by cytoplasmic swelling). Three-dimensional cable nets models of the cytoskeleton have often been described using an affine approximation (see next section) and two-dimensional cable nets have been used to model the cortical cytoskeleton. In those models, the cortical membrane is depicted as a two-dimensional network of triangles (Boey et al 1998) and hexagons (Coughlin and Stamenović 2003). The two-dimensional networks provide a good description of mechanical behaviors of suspended cells. For example, a two-dimensional model of the spectrin lattice successfully describes the behavior of red blood cells during micropipette aspiration measurements (Discher et al 1998). However, in the case of adherent cells, two-dimensional cable net models have enjoyed only moderate success (Coughlin and Stamenović 2003). It is also important to note that although these tensed nets are commonly modeled in isolation, establishment of a stabilizing prestress by balancing inward-directed tension with outward-direct resisting forces essentially represents tensegrity force balance.

Affine Models

A simplified approach used to describe how macroscopic behaviors of networks depend on their microstructural determinants is based on the so called “affine assumption”. The key premise of this approach is that deformation of microstructural elements (local deformation) can be directly linked to the global deformation of the network using methods of continuum mechanics. Because of this assumption, a detailed description of complex microstructural geometry (like the geometry of the cytoskeletal lattice) is not required. However, the assumed affine deformation field does not necessarily satisfy the local equilibrium. Because only a deformation field that satisfies both local kinematics and the local equilibrium minimizes the total deformation energy, affine models yield overestimates of network stiffness. Nevertheless, the mathematical simplicity and transparency of affine models have justified their practical usefulness, especially in cellular mechanics applications where the margin of experimental error often exceeds the degree of quantitative inaccuracy inherent to those models.

The cytoskeletal actin network has been depicted as an assembly of randomly oriented and initially prestressed elastic line elements whose main mode of deformation is stretching. By applying a small shear strain to the system and assuming an affine strain field for each line element, one can derive expressions for network prestress (P) and shear modulus (μ) as follows (Stamenović and Coughlin 1999, Stamenović et al 2002a):

$$\mathrm{a})P=\frac{1}{3}{\mathrm{\sigma }}^0\mathrm{\varphi }\text{and}\mathrm{b})\mathrm{\mu }=\frac{4}{5}P+\frac{1}{15}\mathrm{\varphi }{E}^{\mathrm{m}},$$ (6)

where σ⁰ is the initial member prestress, ϕ is the relative density of actin filaments in the network and E^m is the elastic modulus of individual members. Here, like in (2), we have that the network stiffness (i.e., the shear modulus) is decomposed into a prestress-dependent part and an elasticity-dependent part (6b). The model predicts a linear dependence of the shear modulus on the prestress [first term on the right-hand side of (6b)], which is consistent with experimental observations in living cells. Note, however, that in the absence of prestress the shear modulus does not vanish but has a finite value given by the second term on the right-hand side of (6b). This residual shear modulus is determined by elastic and structural properties of the network and thus, represents the intrinsic stiffness of the network.

Quantitative estimates of P and μ based on experimental data for σ⁰, ϕ and E^m of cytoskeletal actin revealed, however, a huge discrepancy with experimental data for the shear modulus of living cells. Considering that the elastic modulus of actin filaments E^m is ~ 10⁹ Pa (Gittes et al 1993) and ϕ~10⁻³, it follows from (6b) that μ should be ~ 10² kPa, which is at least an order of magnitude greater than values measured in living cells. This, in turn suggests that the assumption of stretching as a primary mode of actin filament deformation may not be tenable. An alternative assumption is that bending is the principal mode of deformation of actin filaments. This is reasonable considering that the length of F-actin segments in the cytoskeletal network (~10⁰ µm) is much smaller than actin’s persistence length (~10¹ µm) and hence filament bending can provide appreciable resistance to distortion.

Satcher and Dewey (1996) used an affine cellular solid model to estimate the material moduli of the cell. They showed that for the filament bending mode, the shear modulus scales with ϕ² E^m, which produced estimates of the shear modulus on the order of 10⁰ kPa which falls in the range of measured values. Thus, by replacing the second term on the right-hand side of (6b) with the result obtained by Satcher and Dewey, we obtain that

$$\mathrm{\mu }=\frac{4}{5}P+\frac{3}{8}{\mathrm{\varphi }}^2{E}^{\mathrm{m}}$$ (7)

Equation (7) can provide reasonably good quantitative predictions of the cell stiffness.

The above model considers only the contribution of cytoskeletal F-actin. It is likely that both cytoskeletal actin filaments and microtubules act simultaneously to resist deformation. In that case, the cytoskeleton would behave as a composite cellular solid (Stamenović 2005). Considering that the elastic moduli and the volumetric fractions of cytoskeletal F-actin and microtubules are of very similar values (cf Stamenović and Coughlin 1999), it follows that for the composite solid the second term in (7) would increase by a factor of four. Limitations that apply to the cable-and-strut tensegrity models also apply to the affine models. Furthermore, the affine approach precludes any interaction between the cell and the substrate, which is an important determinant of cell mechanics and function.

Isostatic Model

A fundamental property of the cytoskeleton is that it can transmit mechanical disturbances over long distances. This property is essential for efficient transduction of mechanical signals into biochemical responses during mechanotransduction. In actin networks, the prestress enhances long-distance propagation of mechanical signals in the transverse direction (Forgacs 1995, Hwang and Barakat 2009). However, for longitudinal longdistance transmission, the cytoskeletal network must satisfy certain requirements.

In this context, Blumenfeld’s isostatic model of the cytoskeleton is extremely relevant (Blumenfeld 2006). Isostatic (statically determinate) structures are structures where the number of equations of equilibrium equals the number of unknown forces in the structural members. Therefore, one can determine forces in structural members only from equilibrium equations and geometrical properties of the network, without invoking constitutive equations of structural members. Consequently, the stress field determined in such a way is described by a hyperbolic partial differential equation that predicts long-distance stress propagation over specified directions.

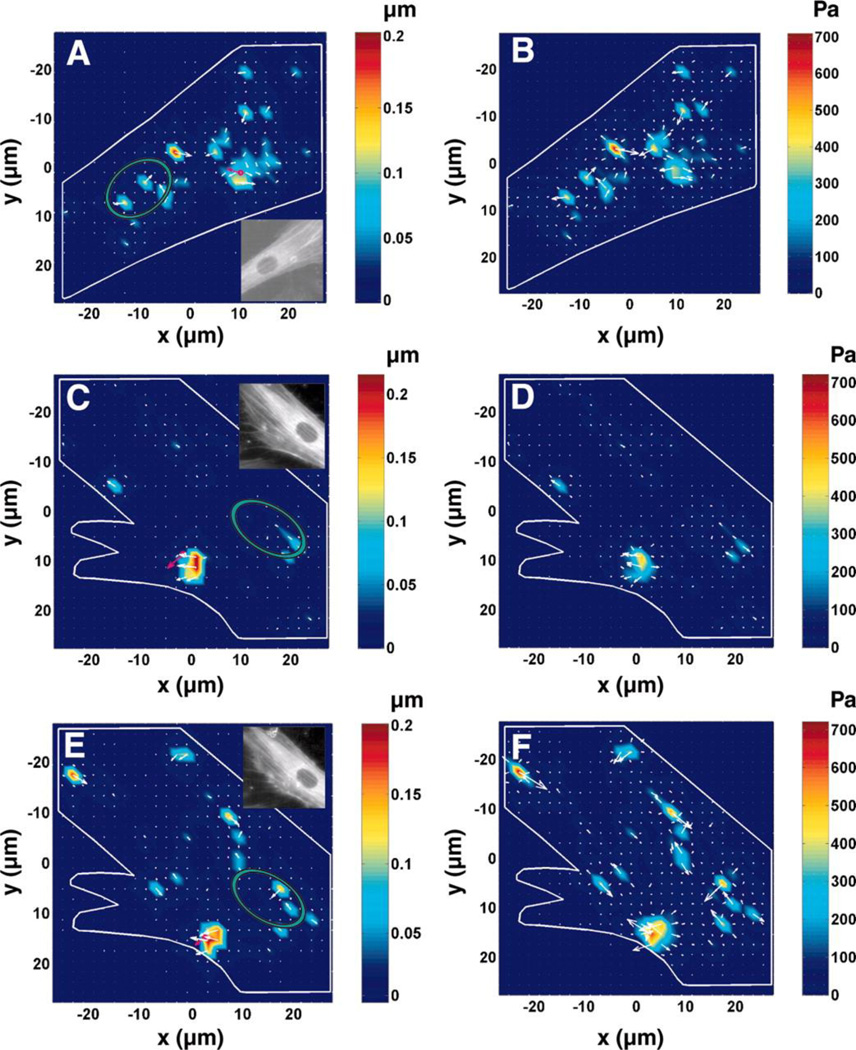
Blumenfeld (2006) described several scenarios for isostaticity of the cytoskeleton. One scenario is when all nodes of the cytoskeletal lattice can support torques, like for example in the cellular solid model of Satcher and Dewey (1996). This situation may occur when forces applied to the cell are too small such that filaments do not buckle. Another scenario is when only some nodes can support torques. For nodes that can support torque, all filaments at the node must carry tensile forces (e.g., actin filaments and intermediate filaments) except one filament that may carry compressive forces (e.g., microtubules). In the limit where none of the nodes can support torques, the structure becomes a tensegrity. Blumenfeld also argued that the cytoskeletal network could be partly isostatic and that through cytoskeletal remodeling, cells may favor partial isostaticity as an efficient strategy to selectively propagate mechanical signals through some parts of the cytoplasm and to block propagation through other parts. In addition, the isostatic model was used to explain the observed dependence of long-distance force transfer on the level of cytoskeletal prestress. For example, in airway smooth muscle cells over-expressing caldesmon that inhibits actomyosin-based tension generation, long distance force transmission becomes disrupted presumably due to reduction of cytoskeletal prestress (Hu et al 2003) (Fig. 6). Consequently, some of the cytoskeletal filaments “slacken” and thus lose their force-bearing ability, which, in turn, causes the cytoskeleton become unstable and lose its isostatic properties.

Fig. 6. Prestress dictates force propagation in the living cell.

A) and B): A normal smooth muscle cell displacement (A) and stress (B) maps, exhibiting long-distance force propagation behavior (inset in (A), YFP (yellow fluorescent protein)-actin image of the cell). C) and D): Long-distance force propagation disappears (loss of displacements and stress concentration spots away from the loading site, the magnetic bead) after inhibition of prestress by overexpressing caldesmon. Displacement and stress fields of a cell whose prestress was inhibited by being infected with a low level of green fluorescent protein (GFP)-caldesmon. E) and F): Long-distance force propagation resumes after caldesmon is inhibited. Displacement and stress maps of the same cell in (C) and (D) after treatment with calcium ionophore A-23187 (5 µg/ml for 10 min), an inhibitor of caldesmon. The pink arrow, bead direction and displacement magnitude. Note that when prestress is downregulated (inset in C) or is resumed (inset in E), there are no apparent changes in patterns of stress fibers compared with those in a normal cell (inset in A). Insets in C, and E are fluorescent images of the corresponding cell. Green ellipses represent the position of the nuclei. (Reprinted with permission from Hu et al 2003).

5. Implications of the Tensegrity Model

5.1 Prestress as a Key Control Element in Biology and Physiology

At a fundamental level, the dependence of stiffness on prestress appears to be universal in living matter and is independent of length scales. While it has been well documented on the organ, tissue and cell levels, more recent findings have shown that it exists at the subcellular (Park et al 2010) and even lower levels. For example, the stiffness of a single integrin molecule depends on its prestress (Kong et al 2009). Furthermore, subcellular structures, such as stress fibers and the submembranous cytoskeleton, also exhibit prestress-dependent stiffening behaviors, and they can be modeled as independent tensegrity modules, as described above (Vera et al 2005, Kumar et al 2006;). Taken together, these observations suggest that tensional prestress that is central to the tensegrity paradigm plays a key unifying role in regulating biological responses and physiological functions across a broad range of length scales. At the subcellular level, this implies that the cell can tune its local stiffness via local prestress, which is important for regulation of global functions of the cell, including directionality and speed of migration and signal transduction along preferential pathways (Ingber 2003c). This is also consistent with the concept of the cytoskeleton as a hierarchical and multimodular system, i.e., that the cytoskeleton is composed of multiple hierarchically organized tensegrity modules whose both local structural stiffness and long range harmonic coupling are determined by local prestress (Ingber 2003a).

At the tissue or organ level, it is known that mechanical distending forces are essential for regulation of physiological functions of many soft tissues including lung (Stamenović 1990, Fredberg et al 1998, Maina 2007), articular cartilage (Khalsa and Eisenberg 1997), and muscles (Fung 1993). For example, in mammalian lungs, the shear and bulk moduli increase with increasing transpulmonary pressure (i.e., prestress). However, while the bulk modulus increases nearly exponentially, indicative of elasticity of the parenchymal connective tissues and alveolar surface film, the rate of increase of the shear modulus is much smaller, nearly proportional with increasing transpulmonary pressure, which is indicative of the tensegrity-like organization of the parenchyma (cf Stamenović 1990). This difference in the elastic moduli dependencies on the prestress is physiologically important because it enables the lungs to maintain their inspired gas volume at an optimal level in face of shear deformation imposed by rib cage distortion.

5.2 Tensegrity and Mechanotransduction

The cellular tensegrity idea finds its most useful application in understanding cellular mechanotransduction. In fact, it was the tensegrity model that led to the concept that mechanical forces would be sensed by cells through discrete linkages between the cytoskeleton and the ECM (Ingber and Jamieson 1985), which led to the discovery that transmembrane integrin receptors function as mechanoreceptors (Wang et al. 1993). Much of the subsequent research in this area has focused on the role to tension applied on integrins at focal adhesions (Vogel and Sheetz 2006). However, this myosin-II dependent tension must be resisted and balanced by cytoplasmic structures; otherwise, the tension cannot be sustained and tensed structures will collapse. Importantly, the tension at focal adhesions is balanced inside the cell and throughout the cytoplasm based on the existing of the cellular tensegrity framework. It is now well documented that tensegrity-based, integrated cytoplasmic mechanotransduction and biological responses are critical for control of cell proliferation and apoptosis (Numaguchi et al 2002), gene expression (Chen et al 2001), differentiation (Engler et al 2004, 2006, Chowdhury et al 2010), and spreading of the cell (Zhang et al 2008, Chowdhury et al 2010) and endoplasmic reticulum (cytoplasmic coherence) (Cai et al 2010), as well as normal organ development (Moore et al 2005, Mammoto et al 2013), mechanotransduction in the endothelium (Chien 2007), and cancerous tissue growth (tensional homeostasis) (Paszek et al 2005).

Prestress and tensegrity also have been important for understanding how mechanical signals are transmitted inside living cells. The rapid, long distance force propagation across integrins that results in direct activation of cytoplasmic enzymes, such Src and Rac, inside the cytoplasm (Hu et al 2003, 2004) is fundamentally different from how growth factor-elicited signals propagate inside cells, and it only can be explained by elastic wave propagation along the tensed cytoskeleton (Na et al 2008, Poh et al 2009). Intracellular force propagation and transmission has been shown to result in rearrangements and displacements of actin filaments and microtubules (Wang 2010). Importantly, forces applied locally to integrins on the cell surface (but not to other transmembrane receptors) results in changes in nuclear and nucleolar shape deep inside the cell (Maniotis et al 1997, Hu et al 2005, Wang and Suo 2005), as well force-dependent dissociation of nuclear Cajal bodies (Poh et al 2012). It would be impossible to interpret all of these results obtained in living cells without invoking the cellular tensegrity model.

The ECM, a polymer network consisted of many different protein polymers, may be viewed as an extended cytoskeleton that connects cells within living tissues and organs (Ingber 1993, 2003a). In many soft tissues, the ECM is tensed by adherent living cells that exert traction forces on their adhesions, or by hydrostatic pressure; either way, this prestressed network essentially stabilizes itself like a tensegrity structure. Tension applied to ECM molecules, such as fibronectin, induces them to unfold and undergo a fibrillogenesis response that results in alignment of ECM fibrils along applied tension field lines (Smith et al 2007), which in turn realigns the cells that form these tissues. ECM tension may also regulate the timing and degree of release of growth factors that are trapped inside the ECM (Lee et al 2011). For example, rises in transpulmonary pressure increase distension and tension in the alveolar walls. This increasing tension stimulates adherent epithelial type II cells to secrete pulmonary surfactant, which lowers alveolar surface tension and lung recoil, thereby stabilizing alveolar airspaces (Nicholas and Barr 1981, Wirtz and Dobbs 1990). Transforming growth factor beta (TGF-β), which is the main cytokine that stimulates fibroblasts to produce and secrete ECM molecules, is also upregulated by mechanical tension (Gutierez and Perr 1990). As a result, material properties of lung parenchyma can significantly change both at the organ and the alveolar wall levels (Brewer et al 2003). Although the details and relative importance of the level of tensile prestress in the ECM is not well understood at this time, it is clear that it plays a critical role in both the physiology and pathology of living tissues and organs (Ingber 2003b, Ingber 2006).

5.3 Tensegrity and Control of Cytoskeletal Self-Assembly

Cells undergo continual turnover, and sustain their structure and function through continuous molecular self-assembly. However, this dynamic renewal process is commonly viewed from the ‘bottom-up’, by focusing on the properties and interaction functions of individual molecular components. In reality, all cells form from other cells using preexisting structures, such as the cytoskeleton, as orienting scaffolds that guide replication and formation of new cellular components. We previously used a ‘top-down’ approach to describe how living cells may use hierarchical tensegrity principles to stabilize the shape and structure of their internal subcomponents at multiple size scales (Stamenović and Ingber 2009). Use of tensegrity can provide a mechanism to focus mechanical forces on the molecular components that comprise these structures, and thereby control their biochemical activities and self-assembly behavior in living cells. In this manner, self-assembly of load-bearing structures in cells proceeds in particular patterns that precisely match the forces they need to bear. This also explains how cells seamlessly integrate structure and function at all size scales, a process that is fundamental to all living materials. An example how tensegrity regulates self-assembly of cytoskeletal structures is given below.

When tensile forces are applied to filamentous biopolymers of the cytoskeleton or to the molecular clusters that form focal adhesions, the chemical potential of those molecular aggregates decreases relative to the molecular reservoir of free, non-assembled monomers (Buxbaum and Heidemann 1988, Hill 1981, Ingber 1997, Shemesh et al 2005). Because a decrease in potential is favored physically, lowering the chemical potential through this mechanical means will drive biopolymer assembly. In contrast, when tensile forces are relaxed or compression forces are applied, polymer self-assembly is disfavored, and depolymerization is promoted. By combining this with the complementary force balance between tension-supporting contractile actin filaments, compression-supporting microtubules and traction-supporting adhesions as described by the cellular tensegrity model, it is possible to predict changes in molecular assembly in response to changes in cell contractility (Stamenović and Ingber 2009). For example, if tension in actin filaments increases because of contractile motor activity, then compression in microtubules and tractions at adhesions would also increase. Consequently, the chemical potential of actin filaments and adhesions should decrease as well driving their assembly (Balaban et al 2001, Burridge et al 1988, Geiger et al 2009, Lele et al 2006), whereas the chemical potential of microtubules would increase and they would disassemble, as observed in living cells (Putnam et al 2001, Riveline et al 2001). If, on the other hand, tractions are increased by straining the ECM, tension in the actin filaments would increase while compression in microtubules would decrease. Consequently, adhesions and microtubules should grow, and this is again what is seen in cells (Bray 1984, Balaban et al 2001, Kaverina et al 2002). Interestingly, catch-slip bond mediated actin polymerization and depolymerization have also shown to depend on the history of forcing and thus, prestress (Lee et al 2013).

5.4 Tensegrity and Design of Man-Made Structures

We cannot discuss tensegrity structures and physics without noting that the relevance of tensegrity models extend far beyond their implications for biology and medicine. Researchers and practitioners from many fields ranging from molecular self-assembly to robots and large-scale architecture have been inspired by the tensegrity paradigm. Because tensegrity provides shape stability at the molecular scale, leaders in DNA-based self-assembly have used tensegrity design principles to build stable structures (Liu et al 2004, Constantinou et al. 2006), including some that can assemble progressively to form 3D structures more than 250 µm along each edge from nanometer-sized tensegrity building blocks (Zheng et al 2009). The DNA origami building method was used to create a tensionally prestressed three-strut tensegrity structure with architecture identical to that shown in Fig. 1A, but built on the 100 nm scale (Liedl et al 2010). Others have used tensegrity to design robots (Paul et al 2006, Haller et al 2008) because the same structure simultaneously serves as sensor, actuator and controller (Skelton and Oliveira 2009). Moreover, advances in model tensegrity for these applications, such as development of computational methods for automated discovery and optimization of irregular tensegrity structures (Rieffel et al 2009), could have great value for those studying tensegrity in biology. Similarly, architects who have applied tensegrity design principles to construct large-scale buildings and enclosures (Motro 2003) can both gain from new insights into biological tensegrity, and produce physical embodiments of tensegrity that can inform biologist in tangible ways that are not possible by looking under the microscope alone.

6. Conclusion

At its core, tensegrity is a system that provides structural stability by imposing a tensile prestress in its compressive and tensile members. But nature has leveraged this fundamental building principle in many ways and at all size scales to create increasingly complex multimodular and hierarchical molecular structures, which has led to the emergence and evolution of living cells and organisms (Ingber 2000). Different materials are used to bear tension and compression at different scales and within different organic structures (e.g., polypeptides in proteins; microfilaments, microtubules, and intermediate filaments in the cytoskeleton; cells and ECM in tissues; bones and muscles in our bodies, etc.). However, the shape stability and immediate mechanical responsiveness of all these structures depends on the prestress that is transmitted across their structural elements. Because cells use tensegrity to structure themselves, mechanical forces and physical cues applied at the macroscale can be channeled over stiffened structural elements, and concentrated on individual structures (e.g., focal adhesions) and molecules at the micrometer and nanometer scales. Specifically, the use of structural hierarchies (systems within systems) that span several size scales and are composed of a tensed network of muscles, bones, ECMs, cells, and cytoskeletal filaments that focus stresses on specific mechanotransducer molecules is key to how living cells carry out mechanochemical transduction, which is critical for their growth and function. Thus, while the existing mathematical formulations of the tensegrity model have proved useful to validate this theory, and to gain better insight into how tensegrity has been leveraged for molecular regulation and cellular mechanotransduction, the simplicity of existing theoretical tensegrity formulations limits their use for analysis of complex living systems that are both hierarchical and multimodular. Hence, the challenge for the future is to develop more robust models that can effectively describe behaviors of more complex tensegrities, and that can enable development of multi-scale mathematical formulations that potentially could couple models of whole cell and tissues to molecular dynamics simulations of individual molecules. Only then will the true importance of tensegrity for biology be fully appreciated.