How Relevant Is Malthus for Economic Development Today?

The Malthusian model of population and economic growth has two key components. First, there is a positive effect of the standard of living on the growth rate of population, resulting either from a purely biological effect of consumption on birth and death rates, or a behavioral response on the part of potential parents to their economic circumstances. Second, because of the existence of some fixed resource such as land, there is a negative feedback from the size of population to the standard of living. These two components generate a number of predictions. Specifically, in the absence of technological change or expansion in the stock of the fixed resource, population will be stable around a constant level. Second, without changes in the function generating population growth, technological improvements or increases in the stock of resources will eventually result in more people but not a higher standard of living.

As a description of population-income interactions, the Malthusian model had a long period of success, covering most of human history in most of the world until the beginning of the industrial revolution. In this paper we ask whether the model has any relevance to the world today.

For the first part of the model—the positive causality running from income to population growth—the answer is clearly no. For reasons that have not fully been determined, countries that get richer now see falling rather than rising rates of population growth. Regarding the second part of the model—whether higher population lowers the standard of living—some further clarification is required before we can even pursue this issue.

First, it important to differentiate among the different channels through which population affects economic outcomes. We will characterize as non-Malthusian those channels that work through the growth rate or demographic structure of the population. These include the effect of population growth in diluting capital per worker; the effect of the population age structure (itself a function of fertility) on the ratio of working age adults to dependents; the association of lower fertility with higher human capital investment via a quality-quantity mechanism; and the effect of lower fertility in freeing up female labor for output production. We reserve the term Malthusian for channels having to do with the size of the population, such as the congestion of fixed resources. This channel was the one Malthus thought about, and it is also the only one that pins down the level of population in steady state, which matches historical experience. Thus, in our typology, it is perfectly possible for reductions in population growth to raise income per capita even though the Malthusian channel is irrelevant.

A second issue to be clarified is at what geographic scale we are looking. It is possible that in a world with trade, a high level of population in a single country will not lower that country’s income relative to others, but that a world with more people will be worse off because of congestion of productive resources or the environment. We do not pursue that possibility here. Instead, we ask whether there are countries or subnational regions in the world where the local version of Malthusianism hold true.

The likeliest place to look for Malthusian effects is among poor countries, for several reasons. First, poor countries have had (and are continuing to have) the largest increases in population. The population of Africa is expected to multiply by a factor of 9.8 between 1950 and 2050. In India, during the century of most rapid population growth (1920–2020) population is expected to multiply by a factor of 5.5. By contrast, in Europe over the period 1800–1900 (roughly the century of fastest population growth), population increased by a factor of 2.2. If the initial population in these regions represented some equilibrium in the relation between population and resources (given available technology), the more rapid population growth is more likely to result in a disequilibrium in this relationship. Second, poor countries are least able to use trade as a means of avoiding resource constraints. Finally, as discussed further below, poor countries empirically have much higher shares of natural resource rents in national income than do rich countries.

The idea that poor countries might suffer negative economic effects from overpopulation has a long pedigree. However, in recent decades, the Malthusian perspective has fallen out of favor among development economists, who have stressed the substitutability of technology, capital, and labor for fixed factors, as well as the productive benefits of density per se or of the technological and institutional changes induced by population pressure (see Allen C. Kelley 2001). We take as an operative test of the Malthusian channel the answer to the question: if a country had fewer people but was otherwise unchanged in terms institutions, human and physical capital per capita, productivity, terms of trade, etc., would it be significantly better off in per capita terms?

I. Theory

The effect of resource dilution on income per capita depends on how the resource enters an aggregate production function. We set up the production function as simply as possible, with only the fixed factor and labor as inputs. The interpretation is that all accumulable factors (human capital, physical capital) will be accumulated proportionally with labor. A_L is productivity that augments nonfixed resources, which can include institutions, higher accumulation rates for physical or human capital, and similar factors. The CES function serves as an approximation to multiple productive sectors with different factor intensities and elasticities of substitution. In per-worker terms:

$$y={\left((1-a)A_L^{(\sigma -1)/\sigma }+a{(A_{x}x)}^{(\sigma -1)/\sigma }\right)}^{\sigma /(\sigma -1)},$$ (1)

where x is land per capita. If factors of production are paid their marginal products, the share of the fixed factor in national income will be

$${\varphi }_x=\frac{a{(A_{x}x)}^{(\sigma -1)/\sigma }}{(1-a)A_L^{(\sigma -1)/\sigma }+a{(A_{x}x)}^{(\sigma -1)/\sigma }}.$$ (2)

In many cases, of course, factors of production are not paid their marginal products or, in the case of environmental services, not paid at all. For convenience, however, we continue to refer to ϕ_x as the resource share. Knowing ϕ_x and σ, the elasticity of substitution between labor (along with other accumulable factors) and the fixed factor, we can do a calculation of how population level affects income. For two levels of population, L_i and L_j, holding constant the level of the fixed factor as well as the two technology parameters, the ratio of output per capita is given by the equation

$$\frac{y_i}{y_j}={\left((1-{\varphi }_{x,j})+{\varphi }_{x,j}{\left(\frac{L_j}{L_i}\right)}^{(\sigma -1)/\sigma }\right)}^{\sigma /(\sigma -1)}.$$ (3)

For concreteness, we take as our benchmark that population is half of its current level. Table 1 shows how such a difference in population would affect income per capita.

Table 1.

Percentage Increase in Income Per Capita if Population Were 50 Percent Lower

Current natural resource share in income (ϕx)	Elasticity of substitution (σ)
	0.5	1	2	3	5
0.1	5.3	7.2	8.5	8.9	9.3
0.2	11.1	14.9	17.3	18.1	18.9
0.3	17.6	23.1	26.4	27.6	28.5
0.4	25.0	32.0	35.9	37.2	38.3
0.5	33.3	41.4	45.7	47.1	48.3

II. Resource Shares

Fixed factors are most obviously important in agriculture. Three out of four people in the developing world live in rural areas, and the majority of them rely on agriculture for their livelihoods (World Bank 2008). The World Bank (2006 Appendix 1) reports the results from a series of studies that calculate implicit land rents as the difference between the market value of crops and crop-specific input costs, including proprietors’ labor. Values from these benchmark studies are then averaged by crop and extrapolated on a crop-by-crop basis to the rest of the world. The average rental rates (unweighted across countries, but weighting by crop value within each country) are 57 percent for sub-Saharan Africa, 37 percent for South Asia, 37 percent for Latin America and the Caribbean, and 57 percent for East Asia and the Pacific.

These estimates for land’s share of agricultural output are appreciably higher than values that have appeared in long-run historical analyses in the growth literature. In the model of Gary D. Hansen and Edward C. Prescott (2002), the “Malthus sector,” which is the only part of the economy producing output prior to the industrial revolution, has a land share of 0.3. Michael Kremer (1993) uses one-third as an upper-end estimate of land’s share, based on evidence from share-cropping contracts. Nancy L. Stokey (2001) applies a Cobb-Douglas production function to the agricultural sector for Britain in 1850, with an exponent on land of 0.45. Francesco Caselli and Wilbur Coleman III (2001) derive a value of 0.19 as land’s share in agriculture in the United States in the twentieth century. In the calculation reported below, we use a conservative value of one-third as the land share in agriculture.

A second major natural resource input is in-ground energy or mineral resources. Since our goal is to measure the impact of population on conventionally measured national income, we follow convention in treating the difference between the value of output in mineral extraction and the cost of inputs as value added in mining or energy production, thus ignoring the loss of natural capital involved in removing a nonrenewable resource. The World Bank (2006 Appendix 3) reports this value as “resource depletion” as a fraction of national income.

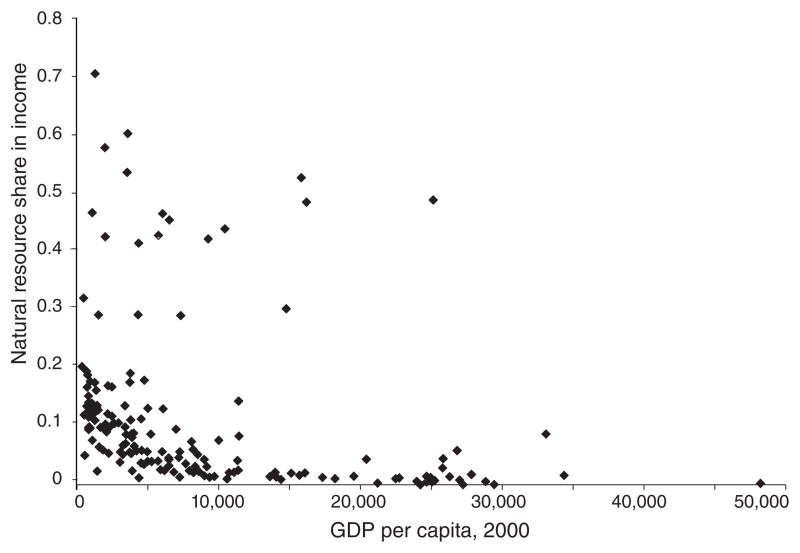
Putting the data together, we construct a crude measure of resource rents as a fraction of GDP. We add together resource depletion for minerals and energy plus one-third times agricultural value added as a fraction of GDP (from the World Development Indicators database). Figure 1 shows the relationship between this measure of rents and the level of GDP per capita.

Figure 1.

Resource Share and Income Per Capita

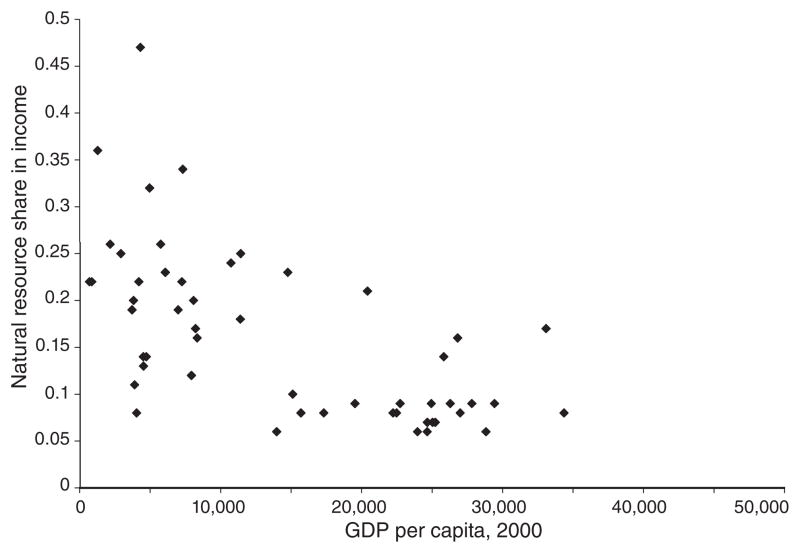
An alternative measure of the income share of nonreproducible factors of production comes from Caselli and James Feyrer (2007), and is in turn built on data from the World Bank (2006) on the values of physical capital, crop land, pasture land, and subsoil resources, along with estimates from Ben S. Bernanke and Refet S. Gurkaynak (2001) on the share of national income going to factors other than labor. Figure 2 shows the relationship between this measure of rents and income per capita. The two measures of rents/GDP constructed here have a correlation of 0.69. The measures are not completely independent because the World Bank (2006) measures of the value of crop and pasture land are capitalized versions of the rent measures discussed above. According to either measure, in poor countries, resource shares of 30 percent are not unusual. Both measures presented here also understate the role of nonpriced environmental factors.

Figure 2.

Resource Share, Alternative Measure

III. Elasticities of Substitution

As shown above, the second piece of information we need in order to assess the quantitative importance of the pure Malthusian effect is the elasticity of substitution between fixed and accumulable factors. The historical growth studies cited above all assume unit elasticity of substitution between land and other factors within the agricultural sector. William Nordhaus and James Tobin (1972), using time-series data for the United States over the period 1909–1958 on capital and labor stocks and the income share of natural resources, estimate the elasticity of substitution between land and a labor-capital aggregate in the overall economy as 2.02. Sometimes the elasticity of substitution can be observed directly. In the case of some developing country resource exporters, it seems clear that the quantity of the natural resource produced is unrelated to domestic accumulation of labor, physical, or human capital. For example, it is hard to imagine that Nigeria’s oil production would be substantially different if the country had half (or twice) its current population. In this case, the elasticity of substitution is infinite.

We can also learn about the elasticity of substitution from observing the natural resource shares discussed above. Figures 1 and 2 show a strong negative relationship between income per capita and the share of natural resource rents in national income. If variation in income comes primarily from differences in accumulation of nonfixed factors of production (A_L in the simple setup above), then this implies an elasticity of substitution greater than one. Here we pursue this idea, extending the methodology of Quamrul Ashraf, Ashley Lester, and Weil (forthcoming). Substituting equation (1) into equation (2) and taking logs,

$$ln({\varphi }_x)=ln(a)+\frac{\sigma -1}{\sigma }ln(A_{x}x)+\frac{1-\sigma }{\sigma }ln(y).$$ (4)

In Table 2, we estimate this equation using the values of ϕ_x from Caselli and Feyrer (2007).

Table 2.

Resource Share Regressions

	1	2	3	4	5	6
ln(y)	−0.368 (0.059)	−0.607 (0.094)	−0.484 (0.082)	−0.875 (0.163)	−0.433 (0.063)	−0.781 (0.161)
Control for natural resources	No	Yes	No	Yes	No	Yes
R2	0.422	0.674
Instruments	None	None	Set A	Set A	Set B	Set B
Instrument f-statistic			39.3	8.36	105.3	13.24
p-value of OID test			0.149	0.264	0.579	0.936
Implied value of s	1.58 (0.15)	2.54 (0.61)	1.94 (0.31)	8.00 (10.4)	1.76 (0.20)	4.57 (3.37)
Observations	52	51	49	48	50	49

Column 1 has only the log of GDP per capita on the right-hand side. Column 2 adds three variables to the right-hand side to control for variations in natural resource availability: the logs of arable land, the value of exports for a set of commodities, and agricultural value added (all per capita). Columns 3 through 6 use two different sets of instruments for y. “Set A” is a set of instruments that change the levels of factors besides land: investment as a fraction of GDP, average years of schooling, and the growth rate of the population over the period 1960–2000. “Set B” measures institutional determinants of productivity: Risk of Expropriation from the International Country Risk Guide and Constraints on Executive from Polity IV data-set. The estimates in the table point to an elasticity of substitution greater than unity, perhaps in the neighborhood of two, as being appropriate.

IV. Conclusion

The Malthusian channel by which a high level of population reduces income per capita is still relevant in poor developing countries that have large rural populations dependent on agriculture, as well as in countries that are heavily reliant on mineral or energy exports. Whether these Malthusian effects are large or small is in the eye of the beholder. Many developing countries have resource shares in income of 30 percent. Using an estimated elasticity of substitution of 2, such a country would be 26 percent richer in per capita terms if it had half as many people. This increment is significant, but it is pretty small in comparison to the differences in income between rich and poor countries, which exceed a factor of 20.

We have analyzed the Malthusian channel in a ceteris paribus context. Thus, Malthus being relevant does not mean that high population dooms countries with large populations or rapid population growth to poverty, since many other things could counteract the negative effect of population. Similarly, a country getting richer despite rapid population growth does not mean that the Malthusian model is wrong. Nor does our analysis imply that policies aimed at reducing fertility are the most efficient means to achieve economic growth.