Abstract
Reference point indentation (RPI) is a microindentation technique involving 20 cycles of loading in “force-control” that can directly assess a patient’s bone tissue properties. Even though preliminary clinical studies indicate a capability for fracture discrimination, little is known about what mechanical behavior the various RPI properties characterize and how these properties relate to traditional mechanical properties of bone. To address this, the present study investigated the sensitivity of RPI properties to anatomical location and tissue organization as well as examined to what extent RPI measurements explain the intrinsic mechanical properties of human cortical bone. Multiple indents with a target force of 10 N were done in 2 orthogonal directions (longitudinal and transverse) per quadrant (anterior, medial, posterior, and lateral) of the femoral mid-shaft acquired from 26 donors (25–101 years old). Additional RPI measurements were acquired for 3 orthogonal directions (medial only). Independent of age, most RPI properties did not vary among these locations, but they did exhibit transverse isotropy such that resistance to indentation is greater in the longitudinal (axial) direction than in the transverse direction (radial or circumferential). Next, beam specimens (~ 2 mm × 5 mm × 40 mm) were extracted from the medial cortex of femoral mid-shafts, acquired from 34 donors (21–99 years old). After monotonically loading the specimens in three-point bending to failure, RPI properties were acquired from an adjacent region outside the span. Indent direction was orthogonal to the bending axis. A significant inverse relationship was found between resistance to indentation and the apparent-level mechanical properties. Indentation distance increase (IDI) and a linear combination of IDI and the loading slope, averaged over cycles 3 through 20, provided the best explanation of the variance in ultimate stress (r2=0.25, p=0.003) and toughness (r2=0.35, p=0.004), respectively. With a transverse isotropic behavior akin to tissue hardness and modulus as determined by micro- and nano-indentation and a significant association with toughness, RPI properties are likely influenced by both elastic and plastic behavior of bone tissue.
Keywords: reference point indentation, human cortical bone, anisotropy, mechanical behavior, toughness
1 Introduction
Standard bone densitometry measurements by dual energy x-ray absorptiometry (DXA) do not fully explain the increase in fracture risk with age (Johnell et al., 2005; Kanis et al., 2001) or diseases such as diabetes (Oei et al., 2013; Saito and Marumo, 2013; Vestergaard, 2007). While these measurements are sensitive to bone loss, they do not necessarily assess the various ways aging and diseases can lower fracture resistance as DXA is insensitive to certain tissue-level properties that contribute to bone’s resistance to fracture (e.g., damage accumulation, mineral and collagen quality, collagen cross-linking pattern, and mineralization heterogeneity) (Friedman, 2006; Ruppel et al., 2008). A striking example is the association of long-term use of bisphosphonates – a drug that inhibits osteoclast activity – and atypical femoral fractures (Shane et al., 2014), even though bisphosphonates increase bone mineral density (Boivin et al., 2000). There are likely deleterious changes in the material properties of the bone tissue with suppression of bone resorption (Donnelly et al., 2012; Gourion-Arsiquaud et al., 2010) that make bone less resistant to fracture (Allen and Burr, 2007; Ettinger et al., 2013).
This calls for the development of diagnostic tools that would provide, not just a surrogate of fracture resistance, but also a direct measure of bone properties at the material level (i.e., independent of mass or structure). In this sense, promising technologies for in vivo fracture risk assessment include reference point indentation (RPI), a new microindentation method that can probe bone material properties of a patient’s tibia on a length scale of 100 μm. Two clinical studies involving relatively small patient cohorts (N=35 to 70) (Diez-Perez et al., 2010; Guerri-Fernandez et al., 2013) have reported that a measure of indentation depth using RPI can discriminate fractured patients from age-matched, non-fracture controls. However, the mechanisms that sustain the association between the RPI parameters and overall fracture resistance are not well identified. Hence, despite encouraging preliminary clinical observations, further basic investigations are needed to identify the determinants of RPI parameters and clarify what mechanical behavior they assess. For example, it is unclear whether RPI provides a measure of hardness (i.e. the resistance to plastic deformation) or brittleness (i.e. a higher propensity to propagate cracks), or a combination thereof. Moreover, RPI can involve successive indentation cycles, and, as such, potentially provides a wealth of information other than indentation depth that remains underexploited.
Therefore, we aimed to assess to what extent RPI measurements explain the mechanical behavior of human cortical bone at the apparent level. We hypothesized that (i) similar to properties from nanoindentation (Fan et al., 2002; Franzoso and Zysset, 2009; Rho et al., 1999) and fracture mechanisms of micron-scale cracks (Akkus et al., 2000; Koester et al., 2008; Nalla et al., 2005; Ural and Vashishth, 2007), RPI measurements are sensitive to bone anisotropy; and (ii) RPI parameters are related to conventional mechanical parameters acquired at the millimeter length scale. Our hypotheses were evaluated via two independent ex vivo experiments. Such knowledge should provide insight into interpreting differences or changes in RPI properties and guide the application of RPI to bone in future studies.
2 Material and methods
2.1 Reference Point Indentation (RPI)
The tissue-level mechanical properties of excised human bone samples (see section 2.2) were assessed using a BioDent™ instrument (Active Life Scientific, Inc., Santa Barbara, CA). The general principle of RPI has been described in detail by others (Aref et al., 2013; Diez-Perez et al., 2010; Guerri-Fernandez et al., 2013; Hansma et al., 2008; Rasoulian et al., 2013). Briefly, the instrument measures the displacement (relative to the bone surface) of a stainless steel test probe (375 μm diameter, 90° cono-spherical, 2.5 μm radius tip) that indents into the bone to a given load, dwells for a short period of time (typically <200 ms), and unloads to ~0 N. In our experiments, each load-controlled indentation consisted of 20 cycles at 2 Hz with a maximum force of 10 N per cycle. Throughout RPI testing, the samples were kept hydrated with phosphate buffered saline (PBS) at room temperature.
2.1.1 Data processing
At the time that indentation data was collected, the manufacturer software primarily provided averaged values for each parameter, instead of cycle-by-cycle analysis (Aref et al., 2013), with a set number of significant digits. In order to take full advantage of the raw load vs. displacement data as well as to control for round-off error and to adjust the significant digits of each properties, we used custom MATLAB® code (The MathWorks, Natick, MA) to determine a number of indentation resistance properties as follows.
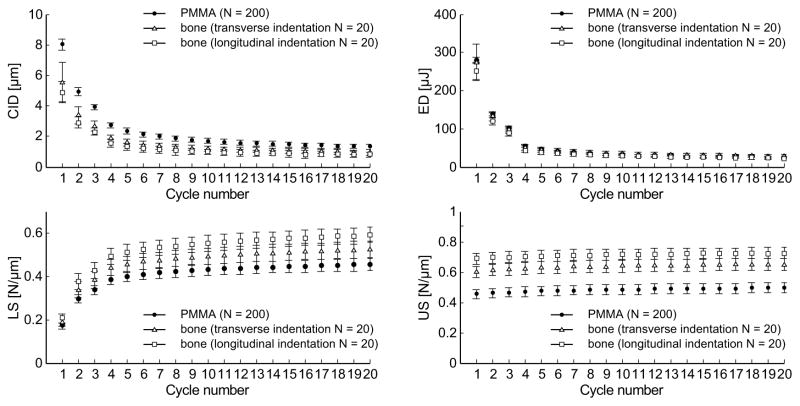
Two parameters quantified the depth of indentation, namely the total indentation increase (TID) and the indentation distance increase (IDI) (Fig. 1). The following parameters were calculated for each cycle: creep indentation distance (CID), energy dissipation (ED) (i.e., the area under the load-displacement curve for a given cycle), loading slope (LS) and unloading (US) slope (Fig. 1). Similar to the tissue behavior subjected to nanoindentation, the unloading slope is likely a surrogate for the matrix modulus, while the loading slope is related to matrix hardness, that is, the ability of bone to resist to plastic deformation (Zysset et al., 1999). For human cortical bone and an acrylic standard, these parameters (except for US) typically exhibit a significantly different value for the first cycle (about five-fold higher indentation distance and energy compared to following cycles) and rapidly reach a steady state from the third cycle to the last cycle (Fig. 2). Hence, subsequent to Fig 2, only values at the first cycle (CID1, ED1, LS1, US1) and the average value from cycles 3 to 20 (avgCID, avgED, avgLS, avgUS) are presented. Since indentation distance (ID), the penetration depth at 10 N, is a function of LS and CID, this parameter is not reported in the present study. Nonetheless, the evolution of ID with cycle number can be found in Supplemental Figure 1, together with IDI.
Figure 1.
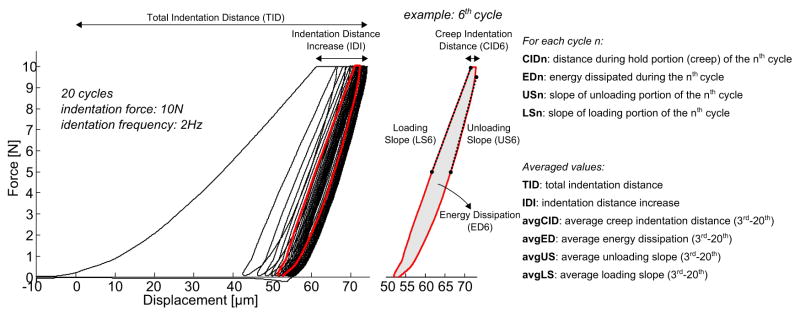
Representative load-displacement curve from a RPI measurement on human bone. A cycle-by-cycle analysis provides outcome parameters that relate to bone tissue properties.
Figure 2.
Evolution of the RPI parameters per cycle (creep indentation, energy dissipation, loading and unloading slope). Results are plotted as mean and standard deviations from measurements on PMMA (N=200), and one human bone sample in the transverse (N=20) and longitudinal (N=20) directions.
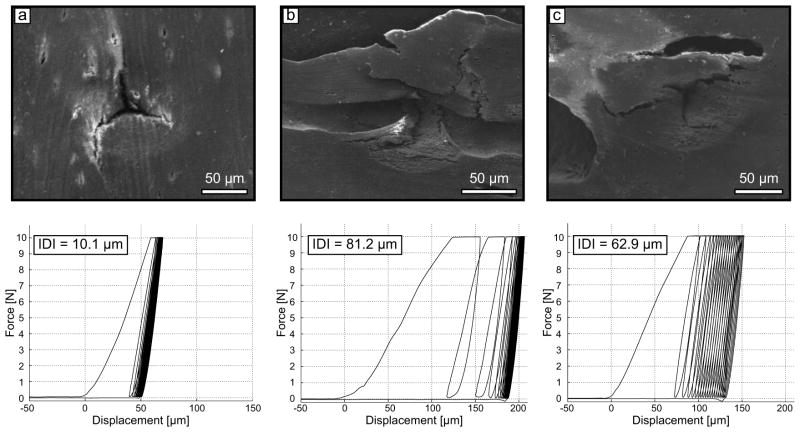
Since no single RPI measurement can precisely reflect the material properties of bone tissue as a whole, each measurement was repeated six times per tested bone surface. A 2 mm space was maintained between two indentation sites or between an indentation site and the sample edge. This mitigated the possibility of testing a site with deformed tissue or damage. Certain indentation sites gave rather excessive values related to indentation depth, as compared to adjacent measurements. Scanning electron microscopy imaging confirmed that these high values do not necessarily reflect a property of bone tissue but were influenced by the presence of a microscopic pore (i.e., Haversian canal, resorption cavity) in the indentation area (Fig. 3). Because there is no microscope with our indentation system, inadvertently selecting a site with pore could not be avoided. Therefore, outliers among the indentations per tested surface for any given RPI property were identified using the Thompson Tau method (Thompson, 1935) and discarded from further analysis. Less than 5% of the measurements were found to be outliers, and after removing the outliers, a minimum of 4 indents was always available to compute the average value per tested surface.
Figure 3.
Scanning electron microscopy images of three RPI indents and the corresponding load-displacement curve. The significant difference in RPI parameters between indent a and indent b (or c) cannot be interpreted as a change in the sample material properties. Instead, it essentially reflects the presence of pores in the indentation area. As such, the measurements b and c cannot be considered when assessing the ability of bone tissue to resist indentation.
2.1.2 RPI precision error
To evaluate changes arising from the technique’s precision only (and not from the material heterogeneity), we used a dataset of 85 measurements on a calibration material (polymethylmetacrylate, PMMA), each measurement being computed as the average of 3 repeated acquisitions at different sites on the PMMA block. This block is indented before each session of bone testing to ensure consistency in the relative position of the probe tip to the surface of each sample. Thus, measurements were made at different time points over the course of 8 months and involved 24 probe tips. Although they were obtained from two operators, the measurements were pooled since one-way analysis of variance (ANOVA) showed no differences between operators. The precision error, often referred to as reproducibility of the technique, was calculated as the root-mean-square standard deviation in absolute terms (RMSSD) and root-mean-square coefficient of variation (RMSCV %) of the aforementioned dataset, as described by Glüer et al. (Glüer et al., 1995), following these formulas:
| (1) |
| (2) |
where N = 85 and (x̄l) and (SDi) are the mean and standard deviation of the measurement i, respectively.
2.2 Experimental protocol
All cadaveric tissues used in this work were stored fresh-frozen and obtained from the Musculoskeletal Transplant Foundation (Edison, NJ) and the Vanderbilt Donor Program (Nashville, TN).
2.2.1 Experiment 1: sensitivity to tissue anisotropy
Bone sample preparation
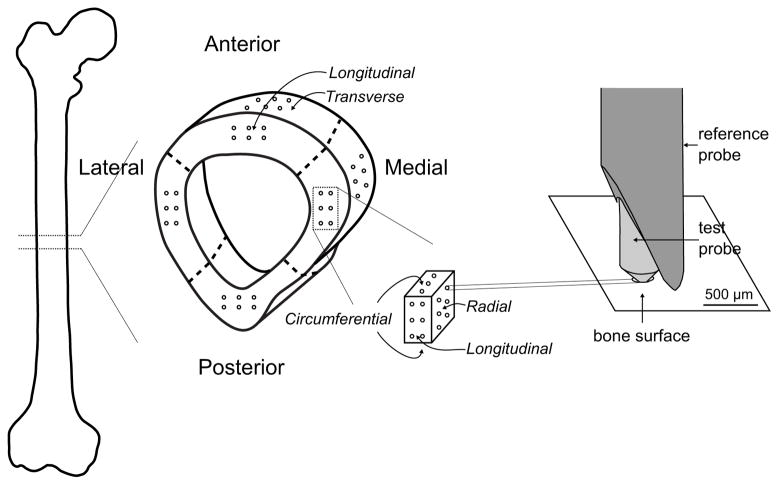
Bone specimens were prepared from a collection of 26 human cadaveric femurs (13 male donors, aged 25 – 91 years old, mean ± standard deviation: 61.8 ± 20.7 years; and 13 female donors, aged 29–101 years old, 64.8 ± 23.3 years). A 5 mm thick cross-section was cut from the mid-diaphysis of each femur and subsequently divided into four specimens following the anatomical quadrants (lateral, anterior, medial, and posterior) using a low speed diamond saw (660, South Bay Technologies, Inc., Torrance, CA). The curvature of the periosteal surface was flattened (no more than 500 μm of material was removed) (Fig. 4). After cutting, the samples were stored in phosphate-buffered saline (PBS) soaked gauze at −20°C until testing. All samples were thawed at room temperature 2 hours prior to RPI measurements.
Figure 4.
Schematic of experiment 1 design. A 5 mm thick cross-section was cut from the mid-diaphysis of each femur and subsequently divided into four specimens following the anatomical quadrants (lateral, anterior, medial, and posterior). Six RPI measurements were collected from each quadrant in the radial and longitudinal directions. In addition, a cube of bone was generated from the medial quadrant, and RPI measurements were acquired from 3 orthogonal surfaces.
RPI measurements
To examine the sensitivity of RPI to human cortical bone anisotropy and dependence on position within the cortex, RPI measurements were collected from the 4 quadrants of each cross-section in the radial (periosteal surface, 6 indents), and longitudinal (distal transverse surface, 6 indents) directions following the procedure detailed in section 2.1 (Fig. 4). In addition, for just the medial quadrant, a cube of bone was generated per donor, and another set of RPI measurements were acquired from 3 orthogonal surfaces (Fig. 4).
2.2.2 Experiment 2: association with standard mechanical properties
Bone sample preparation
Cortical bone samples were extracted from the medial quadrant of the femoral mid-shaft of thirty-four human donors (22 male, age = 59.6 ± 25.3 years, range 21–98, and 12 female, 73.8 ± 21.1 years, range 32–99). The samples (one per donor) were machined using an end mill to nominal dimensions of 2 mm × 5 mm × 70 mm. Care was taken to remove any cortical remnants stemming from the trabecularization of the endosteal cortex (Zebaze et al., 2010) such that the final specimens were pure cortical bone. Each beam specimen was subsequently divided into two samples for RPI and mechanical testing.
Mechanical testing
Hydrated bone specimens (2 × 5 × 40 mm3) were subjected to monotonic three-point bending (ASTM D790). The samples were positioned horizontally on two supports with a span of 35 mm (Instron miniature 3pt or 4pt bend fixture) and loaded at the mid-point using an axial servo-hydraulic testing system (DynaMight 8841, Instron, Norwood, MA). The force-displacement data was recorded at 50 Hz from a 100 N load cell and the linear variable displacement transformer, respectively, as the hydrated bone was loaded to failure at 5 mm/min.
The load-displacement data was converted into stress-strain curves using standard flexural equations (Turner and Burr, 1993) and intrinsic (material) properties relevant to fracture risk in bone were retrieved: flexural modulus, yield and ultimate stress, post-yield strain, and toughness to failure.
RPI measurements
RPI measurements were performed in the circumferential direction on an adjacent sample (2 × 5 × 5 mm3). After removing the outliers, the average of the remaining indents (4 ≤ indents ≤ 6) were retained for subsequent analysis.
2.3 Statistical analysis
Statistical analysis
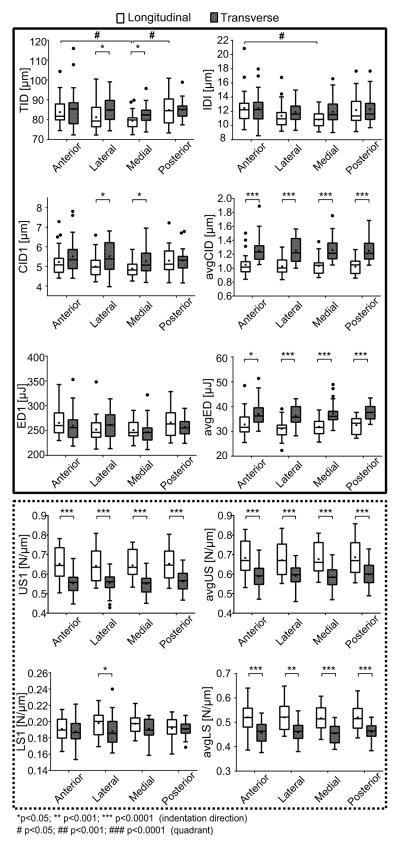
To determine which factor best explained the variance in a RPI parameter, linear mixed-effects models were developed using the data from experiment 1. Initially, each model included all main effects (age, direction, and quadrant) plus all interaction effects. Donor was treated as a random effect to account for repeated measures on the same femoral cross-section. As several RPI parameters did not follow a normal distribution, the models were applied on bootstrapped data (500 replicates). Then, the model was adjusted by successively removing non-significant interactions. P-values for each main effect are given in Table 1. Post hoc analysis was completed with a Holm-Sidak correction for multiple pairwise comparisons (Mann-Whitney) to investigate whether there were significant differences in RPI parameters i) between directions within quadrant and ii) between quadrants within direction (Fig. 5). The same analysis was applied to the medial specimen with indentation in 3 orthogonal faces with only age and orientation as fixed effects (Table 2). The corresponding mean and standard deviation of each RPI property, as well as the results of the post hoc analysis are provided in Table 3.
Table 1.
P-values obtained from general linear models investigating the RPI parameters as dependent variables, and age, direction and quadrant as independent variables
| TID | IDI | CID1 | ED1 | US1 | LS1 | avgCID | avgED | avgUS | avgLS | |
|---|---|---|---|---|---|---|---|---|---|---|
| Age | 0.002 | <0.0001 | 0.003 | <0.0001 | <0.0001 | 0.025 | 0.778 | 0.657 | <0.0001 | <0.0001 |
|
| ||||||||||
| Direction | 0.016 | 0.054 | <0.001 | 0.436 | 0.001 | 0.002 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
|
| ||||||||||
| Quadranta | ||||||||||
| _ medial | 0.031 | 0.026 | 0.197 | 0.230 | 0.530 | 0.135 | 0.708 | 0.068 | 0.628 | 0.960 |
| _ lateral | 0.056 | 0.002 | 0.143 | 0.208 | 0.457 | 0.026 | 0.800 | 0.637 | 0.545 | 0.460 |
| _ posterior | 0.059 | 0.567 | 0.292 | 0.557 | 0.449 | 0.433 | 0.515 | 0.734 | 0.366 | 0.845 |
|
| ||||||||||
| Direction*Age | NI | NI | NI | NI | 0.031 | NI | NI | NI | NI | 0.013 |
|
| ||||||||||
| Quadrant*Agea | ||||||||||
| _ medial | 0.017 | NI | 0.133 | 0.094 | NI | NI | NI | NI | NI | NI |
| _ lateral | 0.006 | 0.033 | 0.027 | |||||||
| _ posterior | 0.115 | 0.254 | 0.539 | |||||||
compared to the anterior quadrant
interaction terms were not included (NI) because their contribution was not significant.
Note that Quadrant*Direction*Age was never significant.
Figure 5.
Box plot graphs of RPI parameters per quadrant (anterior (A), medial (M), lateral (L), posterior (P)) and probing direction (transverse (t), longitudinal (l)). The solid and dotted frames gather the parameters related to the indentation depth and tissue stiffness, respectively. In post hoc analyses of RPI parameters, the family of null hypothesis tests only involved comparisons in which Quadrant or Direction was significant in the general linear model. Significant differences are indicated with a horizontal bar.
Table 2.
P-values obtained from general linear models investigating the RPI parameters as dependent variables, and age and direction as independent variables
| TID | IDI | CID1 | ED1 | US1 | LS1 | avgCID | avgED | avgUS | avgLS | |
|---|---|---|---|---|---|---|---|---|---|---|
| Age | <0.0001 | <0.0001 | 0.026 | 0.019 | 0.029 | 0.034 | 0.026 | 0.007 | 0.039 | <0.0001 |
|
| ||||||||||
| Directiona | ||||||||||
| _circumf. | 0.742 | 0.424 | 0.335 | 0.284 | 0.776 | 0.143 | 0.051 | 0.056 | 0.644 | 0.369 |
| _longitudinal | 0.183 | 0.026 | 0.036 | 0.617 | <0.0001 | 0.042 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
|
| ||||||||||
| Direction*Age | NIb | NI | NI | NI | NI | NI | NI | NI | NI | NI |
compared to the radial direction
Interaction terms were not included (NI) if removing them improved the model fit.
Table 3.
Mean (SD) values of RPI parameters from 3 orthogonal directions (data obtained on the bone cube from the medial quadrant). Superscript symbols indicate significant differences between indentation directions from the post hoc analysis.
| TID [μm] | IDI [μm] | CID1 [μm] | ED1 [μJ] | US1 [N/μm] | LS1 [N/μm] | avgCID [μm] | avgED [μJ] | avgUS [N/μm] | avgLS [N/μm] | |
|---|---|---|---|---|---|---|---|---|---|---|
| Radial | 78.0 (7.2) | 12.2 (2.3) | 5.1 (0.6) | 236 (25) | 0.57* (0.05) | 0.20 (0.02) | 1.19* (0.19) | 33.4* (3.8) | 0.60* (0.06) | 0.48* (0.04) |
| Circumferential | 77.5 (7.7) | 11.8 (2.0) | 5.0 (0.7) | 228 (32) | 0.57* (0.05) | 0.21 (0.02) | 1.12* (0.16) | 32.0* (3.5) | 0.61* (0.06) | 0.48* (0.04) |
| Longitudinal | 76.1 (8.2) | 11.3 (2.0) | 4.8 (0.7) | 239 (32) | 0.67†‡ (0.07) | 0.21 (0.02) | 1.02†‡ (0.16) | 30.2†‡ (4.7) | 0.70†‡ (0.07) | 0.54†‡ (0.06) |
Significantly different from radial
Significantly different from circumferential
Significantly different from longitudinal
In experiment 2, RPI properties followed a normal distribution (Shapiro-Wilk test). Hence, inter-correlations between RPI parameters were examined with Pearson’s correlation coefficient (Table 4). Uncorrelated RPI parameters were considered as independent predictors in a backward, stepwise, multiple regression with the mechanical parameters as dependent variables to determine which parameter best explains the variance in the apparent-level mechanical properties (i.e., highest unadjusted r2).
Table 4.
Inter-correlation matrix between the RPI parameters (Pearson correlation coefficients (r) are indicated when significant at p<0.05)
| r | TID | IDI | CID1 | ED1 | US1 | LS1 | avgCID | avgED | avgUS | avgLS |
|---|---|---|---|---|---|---|---|---|---|---|
| TID | 1 | 0.58 | 0.59 | 0.84 | n.s. | −0.74 | n.s. | n.s. | n.s. | n.s. |
| IDI | 1 | 0.83 | 0.63 | 0.40 | −0.35 | 0.63 | 0.66 | 0.37 | n.s. | |
| CID1 | 1 | 0.78 | n.s. | −0.65 | 0.68 | 0.60 | n.s. | n.s. | ||
| ED1 | 1 | n.s. | −0.87 | 0.40 | 0.37 | n.s. | n.s. | |||
| US1 | 1 | 0.43 | n.s. | n.s. | 0.98 | 0.86 | ||||
| LS1 | 1 | n.s. | n.s. | 0.40 | 0.46 | |||||
| avgCID | 1 | 0.83 | n.s. | −0.41 | ||||||
| avgED | 1 | n.s. | n.s. | |||||||
| avgUS | 1 | 0.87 | ||||||||
| avgLS | 1 |
Finally, using the dataset of experiment 2, the relative contribution of age to RPI parameters and mechanical properties was investigated using simple linear regressions and Pearson’s correlation coefficients. All statistical analyses were performed using the MatLab Statistics Toolbox (The Mathworks Inc., Natick, MA) and STATA 12 (StataCorp LP, College Station, TX). Statistical results were considered significant for p-values less than 0.05, unless otherwise stated.
3. Results
3.1 Precision error
The precision errors from indentation tests on a homogeneous, calibration standard with a smooth surface, as expressed in absolute terms (RMSSD) and coefficient of variation (RMSCV) as a percentage, were: TID = 0.66 μm (0.8%), ED1 = 3.33 μJ (1.2%), LS1 = 0.002 N/μm (1.3%), avgUS = 0.010 N/μm (2.1%), avgLS = 0.009 N/μm (2.1%), US1 = 0.012 N/μm (2.6%), IDI = 0.36 μm (2.9 %), CID1 = 0.30 μm (3.8%), avgED = 1.33 μJ (3.9%), avgCID = 0.08 μm (4.6%). With respect to instrument performance and consistency in tip geometry, TID had the lowest precision error and thus is potentially the most sensitive to detect small differences between groups. However, this assumes the surface of the material is smooth like the plastic block, which is not the case for bone.
3.2 Influence of quadrant and indentation direction (anisotropy) on RPI measurements
General linear regression conducted on data from the four quadrants showed that, independent of age, most of the RPI parameters were sensitive to indentation direction (Table 1), this effect being marked for parameters averaged over cycles (avgCID, avgED, avgUS, and avgLS in Fig. 5). Unloading slope of the first cycle (US1) and the averaged loading slope were the only properties in which anisotropy depended on age (i.e., significant interaction). Within each quadrant, avgCID and avgED, which are parameters related to the indentation depth, were higher when the indentation direction was transverse to the osteons. Conversely, RPI parameters representative of tissue stiffness (avgLS, avgUS) were higher when indentations were performed parallel to the direction of osteons (Fig. 5).
The anatomical position (quadrant) mostly did not account for the variance in RPI parameters (Table 1); and when quadrant was a significant explanatory variable (TID, IDI, and LS1), the differences between quadrants for a given direction, namely longitudinal, were marginal (Fig. 5).
Statistical analyses performed on additional indentation data from the 3 orthogonal surfaces confirmed these observations (Tables 2 and 3). Moreover, post hoc analyses revealed a behavior consistent with transverse isotropy, that is the RPI measures in the radial and circumferential directions are not different (plane of isotropy), but both are significantly different from the measurements in the longitudinal direction. This was the case for US1, avgCID, avgED, avgUS, and avgLS. There was no significant difference with indentation direction for the other parameters.
3.3 Association with standard, apparent-level mechanical properties
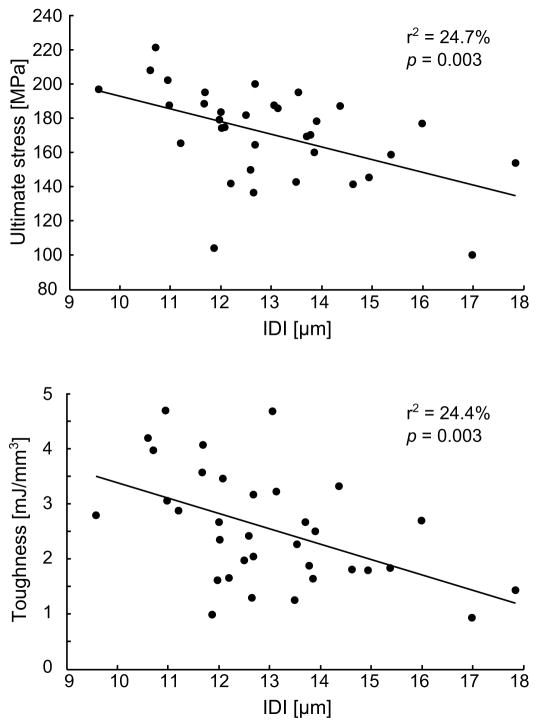
The RPI parameters were significantly inter-correlated (Table 4), suggesting a redundancy of the information when evaluating the link between RPI and mechanical testing. Upon running a multivariate analysis that included only uncorrelated RPI parameters as co-variables and an intercept term, IDI was found to best explain the variance in post-yield strain (r2= 0.16, p=0.019), yield stress (r2=0.16, p=0.019), and ultimate stress (r2=0.25, p=0.003). Variance in toughness was best explained by the linear combination of IDI and avgLS including a significant interaction (r2=0.35, p=0.004). Changes in flexural modulus were not explained by any of the RPI parameters. The correlations between IDI and mechanical properties are illustrated for ultimate stress and toughness on Fig. 6.
Figure 6.
Regression between mechanical properties and RPI illustrated for IDI.
3.4 Age-related changes in RPI and mechanical properties
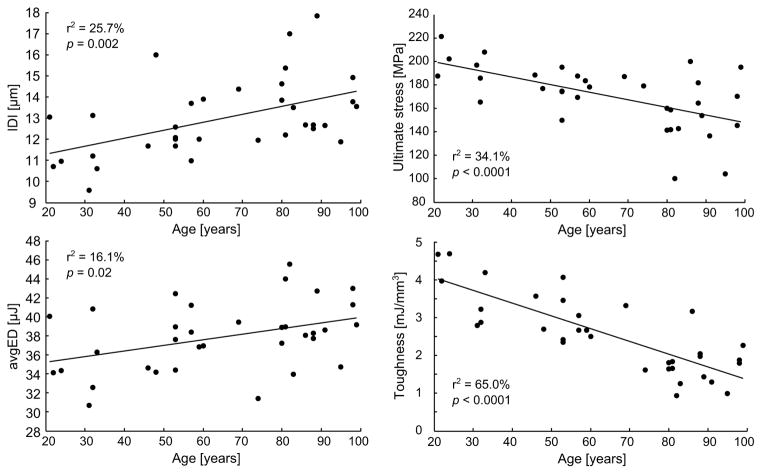
A moderate but significant correlation was found between age and IDI (r2 = 0.26, p = 0.002), CID1 (r2 = 0.13, p = 0.034), and avgED (r2 = 0.16, p = 0.019). Except for flexural modulus, the mechanical properties were significantly associated with aging: yield stress (r2 = 0.14, p = 0.028), ultimate stress (r2 = 0.34, p = 3.10−4), post-yield strain (r2 = 0.61, p<10−5), and toughness to failure (r2 = 0.65, p <10−5). The linear regressions are shown for IDI, avgED, ultimate stress and toughness on Fig. 6
4. Discussion
Unlike current clinical assessment tools of fracture resistance, reference point indentation can acquire a direct measurement of a patient’s bone tissue properties, namely resistance to microindentation. To understand how local RPI properties relate to fracture resistance at the apparent-level, we first investigated the sensitivity of RPI parameters to anatomical location and tissue organization (anisotropy); and then we examined to what extent RPI measurements explain the intrinsic mechanical properties of human cortical bone. Most RPI properties do not vary among the quadrants of the femur mid-shaft, but they do exhibit transverse isotropy such that resistance to indentation is greater in the longitudinal (axial) direction than in the transverse direction (radial or circumferential). RPI provided properties that partially explained the variance in the flexural properties of bone at the apparent-level, even though it probed tissue at the local level in a direction orthogonal to the mode of deformation in bending. This suggests that the ability of bone to resist micro-indentation at 10 N contributes to overall material properties of cortical bone along with other known determinants (e.g., intracortical porosity, degree of mineralization, microstructural organization of cement lines, heterogeneity).
Independent of age, the probe tip penetrates deeper into the tissue when traveling transverse to the axial direction of the osteons; whereas, the unloading slope (surrogate of tissue stiffness) is steeper when the tip is indenting in the axial direction. The former observation concurs with the findings of RPI tests on cortical bone from 48-month old pigs (Rasoulian et al., 2013). The latter observation is in agreement with published data from nanoindentation testing (Fan et al., 2002; Franzoso and Zysset, 2009; Hengsberger et al., 2003; Rho et al., 1999) on human bone in which tissue modulus is higher for axial than for transverse indentation. Moreover, human cortical bone matrix (i.e. excluding Haversian and Volkmann canals) at the mid-shaft of lower limbs typically exhibits transversely isotropic behavior (Fan et al., 2002; Granke et al., 2011). We found that this was also the case in the complementary experiment where RPI was performed on 3 orthogonal faces. We note that the effect of anisotropy was much less pronounced for IDI, TID, CID1, ED1, and LS1 (Fig. 5). All these parameters have in common the initial portion of the load-displacement curve, which typically has higher scattering (the first cycle is more prone to be perturbed by a tipping of the probe). Even though such properties as TID and ED1 have the lowest precision error, this observed perturbation of the 1st cycle could explain the smaller sensitivity to tissue anisotropy for the aforementioned RPI properties.
As observed for swine femurs (Rasoulian et al., 2013), most RPI parameters for human femurs did not depend on the quadrant of the cortex being indented, irrespective of indenting direction (Table 1 and Fig. 5). Microhardness of human bone also do not vary among quadrants (Yoon and Katz, 1976). This could be due to a lack of strong regional preference in both tissue mineralization and collagen fiber orientation with high variability throughout the cortex in human mid-shaft femurs as demonstrated by Goldman et al. (Goldman et al., 2003a; Goldman et al., 2003b) in studies that included 37 and 67 donors, respectively. A lack of dependency of RPI properties on anatomical location with the femur mid-shaft suggests RPI measurements on one quadrant of the bone could be indicative of mechanical behavior of bone at another quadrant, though this has not been investigated to date.
With traditional microindentation (e.g., Vickers), the pyramidal diamond tip indents ~10 lamellae within osteonal and interstitial tissue sites (about 70 μm wide, 10 μm deep (Zwierzak et al., 2009)), and with nanoindentation, the Berkovich diamond tip indents individual lamellae or several lamellae (depth from 0.1 μm to 1 μm). Age-related changes in tissue hardness and tissue modulus of human bone do not generally occur at these length-scales when considering mean values of multiple indents within a sample (Boivin et al., 2008; Hoffler et al., 2000; Houde et al., 1995; Rho et al., 2002; Zioupos et al., 2008). These elastic properties at the micron length scale are sensitive to tissue age (e.g., higher values for interstitial than for osteonal tissue) (Hoffler et al., 2005; Rho et al., 1999) but not donor age. Interestingly, several RPI parameters did vary with donor age. Unlike the other rather precise indentation techniques, RPI performs cycles of loading in force control in which the stainless steel, spherical tip penetrates (60 μm to 110 μm depth) the bone tissue to a greater extent than traditional indentation tests. Engaging more of the tissue matrix in this manner perhaps makes RPI sensitive to age-related decreases in fracture resistance, although correlations with donor age are not as strong as the correlations between age and apparent-level properties (Fig. 7).
Figure 7.
Age-related changes in tissue properties (RPI) compared to age-related changes in apparent material properties of human cortical bone.
As observed in our study, significantly higher indentation depth (IDI) was found in old donors (>70 years old) compared to young donors (age < 45 years old) (Diez-Perez et al., 2010; Hansma et al., 2008). Unlike the present study, the aforementioned RPI study involving swine bone (Rasoulian et al., 2013) found an inverse relationship, that is the indentation distance decreased with age. However, this data was obtained on developing bone (1 to 48 months old), and thus reflects bone maturation more than the effect of aging on mature bone. Taken together, our results suggest that RPI differs from traditional indentation techniques as it measures tissue properties that can change with advancing age. It is possibly sensitive to some of the known age-dependent changes in the bone matrix (e.g. non-enzymatic collagen crosslinks (Wang et al., 2002), microdamage (Schaffler et al., 1995)).
The mean values of nanoindentation modulus and hardness of bone tissue do not typically correlate with the apparent-level elastic modulus and strength of human (Rho et al., 2002) or mouse cortical bone (Silva et al., 2004). Similarly in our study, avgUS and avgLS did not correlate with the apparent-level modulus. This is not too surprising since the overall mechanical properties at the apparent level (2 mm × 4 mm) depend on the multiple levels of bone’s hierarchical organization (from collagen fibril organization to lamellar patterning to porosity). As an example, nanoindentation-derived modulus corresponded well to macroscopic modulus of bovine cortical bone when anisotropy of the matrix modulus and porosity was included in its calculation (Hengsberger et al., 2003). Without accounting for the contribution of porosity to mechanical behavior, we still found that some RPI properties partially explained the material properties of bone as determined by bending millimeter-sized specimens (with numerous osteons, pores, cement lines, and interstitial lamellae) to failure. The present correlations (Fig. 6) are similar to previously reported correlations between IDI and bone toughness for rat (bending of femur mid-shaft and compression of lumbar vertebrae) and dog (bending of rib) (Gallant et al., 2013). The higher correlation coefficient between IDI and toughness (r = −70 in (Gallant et al., 2013) vs r = −0.51 in our study) is likely explained by the fact that our study includes human bones with no known disease while the previous study used bones from animal models of disease or treatment, thereby increasing the range in mechanical properties and consequently the RPI properties. Correlations between RPI properties and apparent level mechanical properties will likely remain moderate as RPI does not assess all the different hierarchical levels of organization that contribute to fracture resistance. In addition, RPI is a local measurement with a practical limit to how much of the bone can be tested. Thus, correlations with mechanical properties do not exceed those reported for bulk measurements of bone specimens such as apparent bone density (Keller et al., 1990), porosity (Granke et al., 2011; McCalden et al., 1993) and bound water volume fraction as measured by 1H NMR (Horch et al., 2011).
Since there is similarity between micro-hardness (Amprino, 1958) and resistance to indentation with respect to tissue anisotropy and since there is a significant correlation between indentation depth and yield strength (e.g., r = −0.40 for IDI vs. yield stress), certain RPI properties could be indicative of tissue hardness, i.e. the resistance to plastic deformation. However, the inverse relationship between IDI and bone toughness indicates that RPI measurement is not simply hardness but also reflects bone brittleness, i.e. its propensity to absorb energy before fracture. The sensitivity of RPI to toughness may explain why RPI could discriminate between fracture patients and controls (Diez-Perez et al., 2010; Guerri-Fernandez et al., 2013) while hardness measurements do not (Fratzl-Zelman et al., 2009). Loading in RPI is a dynamic process (loading rate 60 N/s for RPI relative to <10 mN/s for nanoindentation (Ferguson and Olesiak, 2010)) involving a greater peak load (10 N) than those used in nanoindentation (<0.6 mN) or microindentation (<2N) (Zysset, 2009). This presumably generates larger microdamage ahead of the probe tip that further propagate over a few microns than other indentation techniques, and thereby it is possible that RPI captures some of bone intrinsic toughening mechanisms (Koester et al., 2008). Additional measurements are necessary to closely examine to what extent RPI evaluates tissue fracture toughness, e.g. by measuring the resistance to crack initiation and propagation via R-curves.
Finally, the present work stresses the importance of taking advantage of all the information contained within a RPI measurement, and not only the indentation depth as it is the case in the current clinical research. For example, one would expect that RPI measurements on highly (e.g. osteopetrosis) or poorly (e.g. osteomalacia) mineralized bone would both lead to high indentation depth, the former due its brittleness and the latter due to a lower hardness. However, the unloading slope (stiffness) should be different in these two cases. In the same line of thinking, in clinical settings, avgUS may be better suited than IDI to discriminate between osteomalacia and control because this property is likely more prone to detect changes of matrix stiffness than IDI or avgED, which may be more useful for diseases affecting bone toughness (e.g., diabetes).
Conclusions
Reference point indentation is sensitive to tissue organization in that indentation depth is greater in the transverse direction (perpendicular to osteonal axis) while stiffness is greater in the longitudinal direction (parallel to osteonal axis). Resistance to indentation at the tissue-level partially explains the strength and brittleness of human cortical bone at the material-level with IDI providing the strongest correlation. RPI properties change with age, although not to the same extent as bone toughness.
Supplementary Material
Supplemental Figure. Evolution of the indentation distance (ID) and indentation distance increase (IDI) per cycle. Results are plotted as mean and standard deviations from measurements on PMMA (N=200), and one human bone sample in the transverse (N=20) and longitudinal (N=20) directions.
Highlights.
Reference point indentation properties of human cortical bone are transversely isotropic.
Resistance to micro indentation of human cortical bone decreases with age.
Penetration depth inversely correlates with material strength and toughness of bone.
Acknowledgments
This purchase of the BioDent instrument was supported in part by the Vanderbilt CTSA grant UL1 RR024975 from NCRR/NIH. Additional funding to perform the work was received from NIAMS/NIH (AR063157), NSF (1068988), VA BLR&D (1I01BX001018).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akkus O, Jepsen KJ, Rimnac CM. Microstructural aspects of the fracture process in human cortical bone. J Mater Sci. 2000;35:6065–6074. [Google Scholar]
- Allen MR, Burr DB. Mineralization, microdamage, and matrix: How bisphosphonates influence material properties of bone. BoneKEy-Osteovision. 2007;4:49–60. [Google Scholar]
- Amprino R. Investigations on some physical properties of bone tissue. Cells Tissues Organs. 1958;34:161–186. doi: 10.1159/000141381. [DOI] [PubMed] [Google Scholar]
- Aref M, Gallant MA, Organ JM, Wallace JM, Newman CL, Burr DB, Brown DM, Allen MR. In vivo reference point indentation reveals positive effects of raloxifene on mechanical properties following 6 months of treatment in skeletally mature beagle dogs. Bone. 2013;56:449–453. doi: 10.1016/j.bone.2013.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boivin G, Bala Y, Doublier A, Farlay D, Ste-Marie LG, Meunier PJ, Delmas PD. The role of mineralization and organic matrix in the microhardness of bone tissue from controls and osteoporotic patients. Bone. 2008;43:532–538. doi: 10.1016/j.bone.2008.05.024. [DOI] [PubMed] [Google Scholar]
- Boivin GY, Chavassieux PM, Santora AC, Yates J, Meunier PJ. Alendronate increases bone strength by increasing the mean degree of mineralization of bone tissue in osteoporotic women. Bone. 2000;27:687–694. doi: 10.1016/s8756-3282(00)00376-8. [DOI] [PubMed] [Google Scholar]
- Diez-Perez A, Guerri R, Nogues X, Caceres E, Pena MJ, Mellibovsky L, Randall C, Bridges D, Weaver JC, Proctor A, Brimer D, Koester KJ, Ritchie RO, Hansma PK. Microindentation for in vivo measurement of bone tissue mechanical properties in humans. J Bone Miner Res. 2010;25:1877–1885. doi: 10.1002/jbmr.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnelly E, Meredith DS, Nguyen JT, Gladnick BP, Rebolledo BJ, Shaffer AD, Lorich DG, Lane JM, Boskey AL. Reduced cortical bone compositional heterogeneity with bisphosphonate treatment in postmenopausal women with intertrochanteric and subtrochanteric fractures. J Bone Miner Res. 2012;27:672–678. doi: 10.1002/jbmr.560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ettinger B, Burr DB, Ritchie RO. Proposed pathogenesis for atypical femoral fractures: lessons from materials research. Bone. 2013;55:495–500. doi: 10.1016/j.bone.2013.02.004. [DOI] [PubMed] [Google Scholar]
- Fan Z, Swadener JG, Rho JY, Roy ME, Pharr GM. Anisotropic properties of human tibiae cortical bone as measured by nanoindentation. Journal of Orthopaedic Research. 2002;20:806–810. doi: 10.1016/S0736-0266(01)00186-3. [DOI] [PubMed] [Google Scholar]
- Ferguson VL, Olesiak SE. Nanoindentation of Bone. In: Oyen ML, editor. Handbook of nanoindentation with biological applications. World Scientific Press; 2010. [Google Scholar]
- Franzoso G, Zysset PK. Elastic anisotropy of human cortical bone secondary osteons measured by nanoindentation. J Biomech Eng. 2009;131:021001. doi: 10.1115/1.3005162. [DOI] [PubMed] [Google Scholar]
- Fratzl-Zelman N, Roschger P, Gourrier A, Weber M, Misof BM, Loveridge N, Reeve J, Klaushofer K, Fratzl P. Combination of nanoindentation and quantitative backscattered electron imaging revealed altered bone material properties associated with femoral neck fragility. Calcif Tissue Int. 2009;85:335–343. doi: 10.1007/s00223-009-9289-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman AW. Important determinants of bone strength: beyond bone mineral density. J Clin Rheumatol. 2006;12:70–77. doi: 10.1097/01.rhu.0000208612.33819.8c. [DOI] [PubMed] [Google Scholar]
- Gallant MA, Brown DM, Organ JM, Allen MR, Burr DB. Reference-point indentation correlates with bone toughness assessed using whole-bone traditional mechanical testing. Bone. 2013;53:301–305. doi: 10.1016/j.bone.2012.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glüer CC, Blake G, Lu Y, Blunt BA, Jergas M, Genant HK. Accurate assessment of precision errors: How to measure the reproducibility of bone densitometry techniques. Osteoporosis Int. 1995;5:262–270. doi: 10.1007/BF01774016. [DOI] [PubMed] [Google Scholar]
- Goldman HM, Bromage TG, Boyde A, Thomas CDL, Clement JG. Intrapopulation variability in mineralization density at the human femoral mid-shaft. Journal of Anatomy. 2003a;203:243–255. doi: 10.1046/j.1469-7580.2003.00212.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman HM, Bromage TG, Thomas CD, Clement JG. Preferred collagen fiber orientation in the human mid-shaft femur. Anat Rec A Discov Mol Cell Evol Biol. 2003b;272:434–445. doi: 10.1002/ar.a.10055. [DOI] [PubMed] [Google Scholar]
- Gourion-Arsiquaud S, Allen MR, Burr DB, Vashishth D, Tang SY, Boskey AL. Bisphosphonate treatment modifies canine bone mineral and matrix properties and their heterogeneity. Bone. 2010;46:666–672. doi: 10.1016/j.bone.2009.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granke M, Grimal Q, Saied A, Nauleau P, Peyrin F, Laugier P. Change in porosity is the major determinant of the variation of cortical bone elasticity at the millimeter scale in aged women. Bone. 2011;49:1020–1026. doi: 10.1016/j.bone.2011.08.002. [DOI] [PubMed] [Google Scholar]
- Guerri-Fernandez RC, Nogues X, Quesada Gomez JM, Torres Del Pliego E, Puig L, Garcia-Giralt N, Yoskovitz G, Mellibovsky L, Hansma PK, Diez-Perez A. Microindentation for in vivo measurement of bone tissue material properties in atypical femoral fracture patients and controls. J Bone Miner Res. 2013;28:162–168. doi: 10.1002/jbmr.1731. [DOI] [PubMed] [Google Scholar]
- Hansma P, Turner P, Drake B, Yurtsev E, Proctor A, Mathews P, Lulejian J, Randall C, Adams J, Jungmann R, Garza-de-Leon F, Fantner G, Mkrtchyan H, Pontin M, Weaver A, Brown MB, Sahar N, Rossello R, Kohn D. The bone diagnostic instrument II: indentation distance increase. Rev Sci Instrum. 2008;79:064303. doi: 10.1063/1.2937199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hengsberger S, Enstroem J, Peyrin F, Zysset P. How is the indentation modulus of bone tissue related to its macroscopic elastic response? A validation study. J Biomech. 2003;36:1503–1509. doi: 10.1016/s0021-9290(03)00131-3. [DOI] [PubMed] [Google Scholar]
- Hoffler CE, Guo XE, Zysset PK, Goldstein SA. An application of nanoindentation technique to measure bone tissue Lamellae properties. J Biomech Eng. 2005;127:1046–1053. doi: 10.1115/1.2073671. [DOI] [PubMed] [Google Scholar]
- Hoffler CE, Moore KE, Kozloff K, Zysset PK, Goldstein SA. Age, gender, and bone lamellae elastic moduli. J Orthop Res. 2000;18:432–437. doi: 10.1002/jor.1100180315. [DOI] [PubMed] [Google Scholar]
- Horch RA, Gochberg DF, Nyman JS, Does MD. Non-invasive predictors of human cortical bone mechanical properties: T2-discriminated 1H NMR compared with high resolution X-ray. PLoS One. 2011;6:e16359. doi: 10.1371/journal.pone.0016359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houde J, Marchetti M, Duquette J, Hoffman A, Steinberg G, Crane GK, Baran D. Correlation of bone mineral density and femoral neck hardness in bovine and human samples. Calcif Tissue Int. 1995;57:201–205. doi: 10.1007/BF00310259. [DOI] [PubMed] [Google Scholar]
- Johnell O, Kanis JA, Oden A, Johansson H, De Laet C, Delmas P, Eisman JA, Fujiwara S, Kroger H, Mellstrom D, Meunier PJ, Melton LJ, 3rd, O’Neill T, Pols H, Reeve J, Silman A, Tenenhouse A. Predictive value of BMD for hip and other fractures. J Bone Miner Res. 2005;20:1185–1194. doi: 10.1359/JBMR.050304. [DOI] [PubMed] [Google Scholar]
- Kanis JA, Johnell O, Oden A, Dawson A, De Laet C, Jonsson B. Ten year probabilities of osteoporotic fractures according to BMD and diagnostic thresholds. Osteoporos Int. 2001;12:989–995. doi: 10.1007/s001980170006. [DOI] [PubMed] [Google Scholar]
- Keller TS, Mao Z, Spengler DM. Young’s modulus, bending strength, and tissue physical properties of human compact bone. J Orthop Res. 1990;8:592–603. doi: 10.1002/jor.1100080416. [DOI] [PubMed] [Google Scholar]
- Koester KJ, Ager JW, Ritchie RO. The true toughness of human cortical bone measured with realistically short cracks. Nat Mater. 2008;7:672–677. doi: 10.1038/nmat2221. [DOI] [PubMed] [Google Scholar]
- McCalden RW, McGeough JA, Barker MB, Court-Brown CM. Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization, and microstructure. J Bone Joint Surg Am. 1993;75:1193–1205. doi: 10.2106/00004623-199308000-00009. [DOI] [PubMed] [Google Scholar]
- Nalla RK, Stolken JS, Kinney JH, Ritchie RO. Fracture in human cortical bone: local fracture criteria and toughening mechanisms. J Biomech. 2005;38:1517–1525. doi: 10.1016/j.jbiomech.2004.07.010. [DOI] [PubMed] [Google Scholar]
- Oei L, Zillikens MC, Dehghan A, Buitendijk GH, Castano-Betancourt MC, Estrada K, Stolk L, Oei EH, van Meurs JB, Janssen JA, Hofman A, van Leeuwen JP, Witteman JC, Pols HA, Uitterlinden AG, Klaver CC, Franco OH, Rivadeneira F. High bone mineral density and fracture risk in type 2 diabetes as skeletal complications of inadequate glucose control: the Rotterdam Study. Diabetes Care. 2013;36:1619–1628. doi: 10.2337/dc12-1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasoulian R, Raeisi Najafi A, Chittenden M, Jasiuk I. Reference point indentation study of age-related changes in porcine femoral cortical bone. J Biomech. 2013;46:1689–1696. doi: 10.1016/j.jbiomech.2013.04.003. [DOI] [PubMed] [Google Scholar]
- Rho JY, Roy ME, Tsui TY, Pharr GM. Elastic properties of microstructural components of human bone tissue as measured by nanoindentation. Journal of Biomedical Materials Research. 1999;45:48–54. doi: 10.1002/(sici)1097-4636(199904)45:1<48::aid-jbm7>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Rho JY, Zioupos P, Currey JD, Pharr GM. Microstructural elasticity and regional heterogeneity in human femoral bone of various ages examined by nano-indentation. J Biomech. 2002;35:189–198. doi: 10.1016/s0021-9290(01)00199-3. [DOI] [PubMed] [Google Scholar]
- Ruppel ME, Miller LM, Burr DB. The effect of the microscopic and nanoscale structure on bone fragility. Osteoporos Int. 2008;19:1251–1265. doi: 10.1007/s00198-008-0579-1. [DOI] [PubMed] [Google Scholar]
- Saito M, Marumo K. Bone quality in diabetes. Front Endocrinol (Lausanne) 2013;4:72. doi: 10.3389/fendo.2013.00072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaffler MB, Choi K, Milgrom C. Aging and matrix microdamage accumulation in human compact bone. Bone. 1995;17:521–525. doi: 10.1016/8756-3282(95)00370-3. [DOI] [PubMed] [Google Scholar]
- Shane E, Burr D, Abrahamsen B, Adler RA, Brown TD, Cheung AM, Cosman F, Curtis JR, Dell R, Dempster DW, Ebeling PR, Einhorn TA, Genant HK, Geusens P, Klaushofer K, Lane JM, McKiernan F, McKinney R, Ng A, Nieves J, O’Keefe R, Papapoulos S, Howe TS, van der Meulen MC, Weinstein RS, Whyte MP. Atypical subtrochanteric and diaphyseal femoral fractures: second report of a task force of the american society for bone and mineral research. J Bone Miner Res. 2014;29:1–23. doi: 10.1002/jbmr.1998. [DOI] [PubMed] [Google Scholar]
- Silva MJ, Brodt MD, Fan Z, Rho JY. Nanoindentation and whole-bone bending estimates of material properties in bones from the senescence accelerated mouse SAMP6. J Biomech. 2004;37:1639–1646. doi: 10.1016/j.jbiomech.2004.02.018. [DOI] [PubMed] [Google Scholar]
- Thompson WR. On a criterion for the rejection of observations and the distribution of the ratio of deviation to sample standard deviation. Ann Math Stat. 1935;6:214–219. [Google Scholar]
- Turner CH, Burr DB. Basic biomechanical measurements of bone: a tutorial. Bone. 1993;14:595–608. doi: 10.1016/8756-3282(93)90081-k. [DOI] [PubMed] [Google Scholar]
- Ural A, Vashishth D. Anisotropy of age-related toughness loss in human cortical bone: a finite element study. J Biomech. 2007;40:1606–1614. doi: 10.1016/j.jbiomech.2006.07.023. [DOI] [PubMed] [Google Scholar]
- Vestergaard P. Discrepancies in bone mineral density and fracture risk in patients with type 1 and type 2 diabetes--a meta-analysis. Osteoporos Int. 2007;18:427–444. doi: 10.1007/s00198-006-0253-4. [DOI] [PubMed] [Google Scholar]
- Wang X, Shen X, Li X, Agrawal CM. Age-related changes in the collagen network and toughness of bone. Bone. 2002;31:1–7. doi: 10.1016/s8756-3282(01)00697-4. [DOI] [PubMed] [Google Scholar]
- Yoon HS, Katz JL. Ultrasonic wave propagation in human cortical bone--II. Measurements of elastic properties and microhardness. J Biomech. 1976;9:459–464. doi: 10.1016/0021-9290(76)90089-0. [DOI] [PubMed] [Google Scholar]
- Zebaze RM, Ghasem-Zadeh A, Bohte A, Iuliano-Burns S, Mirams M, Price RI, Mackie EJ, Seeman E. Intracortical remodelling and porosity in the distal radius and post-mortem femurs of women: a cross-sectional study. Lancet. 2010;375:1729–1736. doi: 10.1016/S0140-6736(10)60320-0. [DOI] [PubMed] [Google Scholar]
- Zioupos P, Gresle M, Winwood K. Fatigue strength of human cortical bone: age, physical, and material heterogeneity effects. J Biomed Mater Res A. 2008;86:627–636. doi: 10.1002/jbm.a.31576. [DOI] [PubMed] [Google Scholar]
- Zwierzak I, Baleani M, Viceconti M. Microindentation on cortical human bone: effects of tissue condition and indentation location on hardness values. Proc Inst Mech Eng H. 2009;223:913–918. doi: 10.1243/09544119JEIM634. [DOI] [PubMed] [Google Scholar]
- Zysset PK, Guo XE, Hoffler CE, Moore KE, Goldstein SA. Elastic modulus and hardness of cortical and trabecular bone lamellae measured by nanoindentation in the human femur. J Biomech. 1999;32:1005–1012. doi: 10.1016/s0021-9290(99)00111-6. [DOI] [PubMed] [Google Scholar]
- Zysset PK. Indentation of bone tissue: a short review. Osteoporos Int. 2009;20:1049–1055. doi: 10.1007/s00198-009-0854-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Figure. Evolution of the indentation distance (ID) and indentation distance increase (IDI) per cycle. Results are plotted as mean and standard deviations from measurements on PMMA (N=200), and one human bone sample in the transverse (N=20) and longitudinal (N=20) directions.