Compound cueing in free recall

Abstract

According to the retrieved context theory of episodic memory, the cue for recall of an item is a weighted sum of recently activated cognitive states, including previously recalled and studied items as well as their associations. We show that this theory predicts there should be compound cueing in free recall. Specifically, the temporal contiguity effect should be greater when the two most recently recalled items were studied in contiguous list positions. A meta-analysis of published free recall experiments demonstrates evidence for compound cueing in both conditional response probabilities and inter-response times. To help rule out a rehearsal-based account of these compound cueing effects, we conducted an experiment with immediate, delayed and continual-distractor free recall conditions. Consistent with retrieved context theory but not with a rehearsal-based account, compound cueing was present in all conditions, and was not significantly influenced by the presence of interitem distractors.

Introduction

Freely recalling a list of items is a path dependent process. If I've just recalled a list item, r₁, it is likely to remind me of another item, r₂, which reminds me of r₃ and so forth. Thus, an earlier response r₁ should influence a later response r₃ through its effect on the intermediate response r₂. When considering the responses made within a given recall period (in contrast to responses across lists), a model is said to be stochastic, or have the first-order Markov property, if r₁ influences r₃ only through its effect on r₂. Such models have a simplicity and elegance that makes them very appealing. As such it is perhaps not surprising that they have been around for a long time, and have been used to explain a variety of intralist recall phenomena (Anderson, 1972; Feigenbaum & Simon, 1962; Laming, 2010; Lewandowsky & Murdock, 1989; Raaijmakers & Shiffrin, 1981).

The assumption of a stochastic retrieval process is also implicit in many empirical analyses of the free recall paradigm. For instance, perhaps one of the most prominent forms of organization in free recall is the temporal contiguity effect, quantified by the tendency to follow recall of the item from serial position i with one of the available items i + lag for smaller values of |lag|. The temporal contiguity effect appears robustly across manipulations of list length, presentation rate, and presentation modality (Kahana, 1996). The temporal contiguity effect appears to be relatively insensitive to the time-scale of item presentation, as it is unaffected by a demanding interitem arithmetic distractor task (Howard & Kahana, 1999), and it appears at very long time scales in both list memory tasks (Howard, Youker, & Venkatadass, 2008; Unsworth, 2008) and autobiographical memory tasks (Moreton & Ward, 2010). Another major form of organization in free recall of random word lists is semantic proximity, wherein participants tend to successively recall words with similar meanings (Howard & Kahana, 2002b).

Although temporal contiguity, semantic proximity, and other forms of organization in free recall assume that the retrieval cue is the just-recalled item, an alternative possibility is that multiple prior items combine to form a compound cue for the next response. As discussed below, this idea has parallels in empirical studies of other memory tasks, and in theories of the temporal contiguity effect itself. According to retrieved context theory, recalling an item retrieves its previously associated contextual states which combine with the current state of context to form the retrieval cue for the next response (e.g., Howard & Kahana, 2002a). Because context is a recency-weighted sum of previously activated cognitive states, retrieved context models embody a compound cue assumption, and predict that the temporal contiguity effect should be enhanced when a sequence of previously recalled items were studied at neighboring list positions.

Here we aim to test the predicted compound cue effect in both a meta-analysis of previously published free recall studies and in a new experiment that allows us to examine the degree to which compound cueing reflects inter-item rehearsal. We also compare the empirical compound cue results to predictions to three sets of model simulations. Whereas most of the organizational analyses in free recall suggest that recall is stochastic inasmuch as the just-recalled item substantially informs recall of the next item, the compound cue analyses would allow us to detect violations of this property, both qualitatively from the empirical results as well as quantitatively based on model predictions. First, we present simulations of a retrieved context model of free recall (the context maintenance and retrieval model; Polyn, Norman, & Kahana, 2009) which uses the recency-weighted sum of recalled items to cue retrieval. To contrast, we also compare the compound cue results to predictions of a model that relies primarily on the just-recalled item as a cue (the episodic search of associative memory model, eSAM; Sirotin, Kimball, & Kahana, 2005). Such a model may help to determine whether seemingly second-order Markovian processes could be predicted by a first-order Markovian model. To confirm that the eSAM predictions reflect its retrieval cue assumption, we also present simultions of a SAM variant that relies on compound cues for recall (fSAM; Kimball, Smith, & Kahana, 2007).

In the literature on priming and item recognition tasks, compound cueing has frequently been used to refer to the joint influence of the current cue item and the preceding cue item or prime on task performance (Clark & Shiffrin, 1987; Dosher & Rosedale, 1989; Ratcliff & McKoon, 1988; Schwartz, Howard, Jing, & Kahana, 2005). In recall tasks, however, compound cueing usually refers to the influence of multiple prior items on recall performance; specifically, whether the response before the last combines with the last response to form a compound retrieval cue.

Studies of probed recall and serial learning suggest that participants can use compound cueing to facilitate retrieval (Chance & Kahana, 1997; Cohen & Sekuler, 2010; Kahana & Caplan, 2002; Posnansky, 1972). Posnansky (1972) examined the advantage of three previous items over one previous item to cue recall of the next item. On a small but significant number of trials, participants failed to recall the correct item using one previous item as a cue, but could recall the item when additionally provided with the two items presented before the one-item cue. If participants relied exclusively on associations between adjacent items, we would not expect that providing additional items would aid recall. However, because the compound cue was given only when the single-item cue failed, this study leaves open the possibility that participants simply benefited from having a second recall attempt. In a more direct investigation of compound cueing, Kahana and Caplan (2002) had participants study lists of word triples or entire serial lists and then probed them for recall with either single item or double item cues. Although they found that participants exhibited superior recall accuracy in the double item cue condition irrespective of whether the cue was in the forward or backward direction, they found that participants exhibited greater recall accuracy and faster response times when probed in the forward direction than the backward direction.

Chance and Kahana (1997) examined a more endogenous form of compound cueing in a study of inter-response times (IRTs) in serial list learning. They instructed participants to learn two sequences of 15 common nouns that contained an overlapping subsequence of 1, 2, 4 or 8 items. According to classic chaining theories, which assume item i serves as the cue for item i + 1 (Lewandowsky & Murdock, 1989; Wickelgren, 1966), one would expect to find slower IRTs when exiting the overlapping subsequence due to associative interference from the other list. Chance and Kahana (1997) did find slower exit IRTs, but only when the overlapping segment had more than two elements. We would expect this result if participants were using a compound cue comprised of more than two items: Because the compound cue contains more items than the overlapping subsequence, this helps to eliminate the ambiguity in the repeated subsequence, thus attenuating the associative interference seen in the exit IRTs. Cohen and Sekuler (2010) extended these findings to a motor sequence task. Participants learned a series of motor movements as either one complete sequence (control group) or as a set of subsequences (experimental group). Consistent with a compound cue account, they found that the control group outperformed the experimental group.

A common feature of these previous studies is that the retrieval cue is largely determined by the experimenter. Even in serial recall, where there is no explicit cue, the requirement of ordered recall makes the sequence of prior responses a reliable cue for the next response. If, however, compound cueing is a general feature of the memory system then one would expect to observe a compound cueing advantage even in free recall. Here we examine compound cueing in free recall: As an extension of traditional analyses of temporal contiguity, which examine how the just-recalled item influences the next transition, we investigate how the previous two items serve as a compound cue for the next transition. In the analyses reported here, we examine the conditional response probability as a function of serial position lag in the study list (lag-CRP). Given that a participant has just recalled the item from serial position i, the lag-CRP indicates the probability that the next recalled item comes from serial position i + lag.

Meta-analysis

To examine compound cueing in free recall we considered a set of free recall studies in which each participant contributed a large enough number of recall transitions such that we could estimate the lag-CRP conditional on the previous response.

Methods

Studies

Murdock (1962)

Ninety participants performed immediate free recall of 80 lists. Lists were composed of words chosen randomly and without replacement from the Thorndike and Lorge (1944) word pool with G count > 20. Using group testing, 15 participants contributed to each of 6 condition as follows, where the first number indicates list-length and the second number indicates presentation rate in seconds: 10–2, 15–2, 20–1, 20–2, 30–1, 40–1. Immediately following presentation of the last list item, participants had 90 s to write down as many words as possible from the just-presented list.

Sederberg et al. (2006)

Forty-eight participants performed delayed free recall of 48 lists. Lists were composed of 15 high-frequency nouns each presented visually for 1600 ms with a 800–1200 ms blank ISI. After the presentation of the last item, participants performed math problems of the form A + B + C =?, where A, B, and C are positive, single-digit integers, for 20 s. Immediately following the distraction period, participants had 45 s to vocally recall as many words as possible from the just-presented list. Participants' responses were digitally recorded and processed offline to specify exact response onset times. The Sederberg et al. (2006) article reports analyses of the first 35 of the 48 participants included here.

Sederberg et al. (2010)

Twenty-seven participants performed delayed free recall of 48 lists. Lists were composed of 16 high-frequency nouns each presented visually for 1000 ms with a 300-700 ms blank ISI. After the presentation of the last item, participants performed math problems of the form A + B + C =?, where A, B, and C are positive, single-digit integers, for 20 s. Immediately following the distraction period, participants had 45 s to vocally recall as many words as possible from the just-presented list. Participants' responses were digitally recorded and processed offline to specify exact response onset times. In each list, noun pairs were divided into four groups of increasing semantic relatedness (Steyvers, Shiffrin, & Nelson, 2004) such that two pairs of items from each of four groups were selected without replacement and arranged such that one pair occurred at adjacent serial positions and the other pair was separated by at least two other items.

Polyn et al. (2009) and Lohnas et al. (2011)

One hundred and six participants performed immediate free recall of 24-72 lists. Lists were composed of 24 words each presented visually for 3000 ms with an 800-1200 ms blank ISI. Immediately following presentation of the last list item, participants had 90 s to vocally recall as many words as possible from the just-presented list. Participants' responses were digitally recorded and processed offline to specify exact response onset times. For each item, participants made either a size or animacy judgment, indicating their response during item presentation via a keypress. On single-task lists, every word was judged with the same task. On task-shift lists, participants shifted back and forth between the two judgment tasks. We restricted our analyses to the single-task lists.

Measures

Conditional response probability as a function of lag (lag-CRP)

For each participant, we initialized a set of numerators and denominators to 0, one for each possible transition lag, (Figure 1A). For a list-length of l, there are 2(l − 1) − 1 possible lags: l − 1, l − 2, l − 3, …, 2, 1, −1, −2, …, −(l − 2), −(l − 1). We excluded transitions to and from items repeated within a recall period, e.g. transitions of with lag = 0. We also excluded transitions to and from intrusions, as the lag is not defined for those items. For each list, we stepped through each recall transition, incrementing the numerator value matching the actual serial position lag of that transition and incrementing the denominators matching the set of all possible recall transitions. Specifically, possible transitions excluded lags that would be to an item outside of the list, as well as to items already recalled during the current trial. After incrementing the numerators and denominators for all of a participant's lists, the lag-CRP for that participant was simply the numerator divided by the denominator for each possible lag.

Figure 1. Calculation of conditional response functions.

A. Sample list presentation and recall sequence. B. Lag calculation used for the conditional response probability as a function of lag (lag-CRP) based on the recall sequence provided in A. The boxes around each lag indicate that all lags contribute to the lag-CRP shown in Figure 2A. C. Calcuation of lag₁ and lag₂ as used in the compound lag-CRP. Each box uses the same line scheme as the plots provided in Figures 2,4 and 5, i.e. conditional on a particular value of lag₁. The light gray box for the final pair of lag₁, lag₂ values indicates that this transition does not contribute to the compound lag analyses, as lag₁ = −2 does not fit any considered lag₁ criteria. D. Calculation of lag and conditional response latency (CRL) used for the lag-CRL analysis. E. Calcuation of lag₁ and lag₂ as used in the compound lag-CRL. The line scheme is the same as panel C. IRT = inter-response time.

Compound lag-CRP

Most broadly, the compound lag-CRP can be considered as a lag-CRP that considers only a subset of transitions. Specifically, a compound lag-CRP considers transitions assuming that the previous transition lag₁ meets a particular criterion. That is, in addition to requiring that the transition lag₂ does not include a repetition or intrusion, we also require that it follows a transition of a particular value, e.g. lag₁ = +1. As with the lag-CRP, we initialized a set of numerators and denominators for each possible transitions lag. We stepped through each recall transition, and for those transitions that met the specified criterion, we incremented the numerators and denominators matching the set of possible transitions. The compound lag-CRP for a participant was the numerator divided by the denominator at each lag.

An example of the lags contributing to the compound lag-CRP calculation on a single trial is shown in Figure 1C. Whereas in the standard lag-CRP analysis, each of the first two output transitions contribute separately to the conditional probabilities (e.g. lag = 1, lag = 4), in the compound lag-CRP, these two transitions are considered together as lag₁ = 1 and lag₂ = +4. Based on the value of lag₁ = +1, the value of lag₂ = +4 increases the numerator of the actual transition made in the +1 compound lag-CRP. This is indicated by the solid box online, corresponding to the function of the same linestyle in Figure 2. For the next considered transition, now the transition from item 2 to 6 becomes the lag₁ value of interest, and based on the subsequent transition we get lag₂ = −1. Here, |lag₁| > 3, and so this transition contributes to the corresponding compound lag-CRP and compound lag-CRL with dotted lines in Figure 2.

Figure 2. Single and compound cues in a meta-analysis of free recall studies.

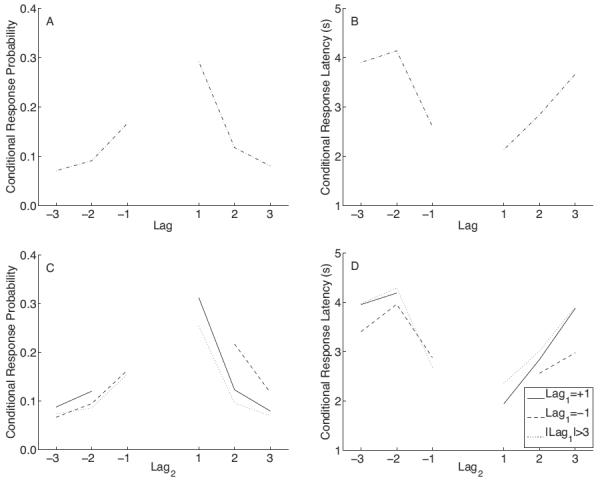
A. The contiguity effect, or tendency to successively recall neighboring items, is reflected in the conditional response probability as a function of lag (lag-CRP). B. Neighoboring items recalled successively also exhibit faster inter-response times (IRTs), as exhibited in the conditional response latency as a function of lag (lag-CRL). C. Compound cueing and the contiguity effect. The conditional response probability as a function of the current lag (lag₂) illustrates the tendency to transition between neighboring items in recall. Here we show the lag-CRP separately for three cases of the lag of the previous transition, lag₁: lag₁ = +1 (solid); lag₁ = −1 (dashed); |lag₁| > 3 (dotted). Included studies are Lohnas et al. (2011), Murdock (1962), Polyn et al. (2009), Sederberg et al. (2006) + replication, Sederberg et al. (2010). D. Compound cueing influences recall timing. The conditional response latency as a function of the current lag (lag₂) illustrates the tendency to transition between neighboring items in recall with faster IRTs. Here we show the lag-CRL separately for three cases of the lag of the previous transition, lag₁: lag₁ = +1 (solid); lag₁ = −1 (dashed); |lag₁| > 3 (dotted). Data are from Lohnas et al. (2011), Polyn et al. (2009), Sederberg et al. (2006, 2010).

For the immediate free recall studies, we excluded the first two output transitions, as temporal contiguity is artifactually enhanced due to the pronounced recency effect (Davelaar, Goshen-Gottstein, Ashkenazi, Haarmann, & Usher, 2005; Sederberg, Howard, & Kahana, 2008). We excluded 11 participants because they did not contribute at least one observation to each of the lags considered in the t-tests reported below. In total, 260 participants were included in this analysis.

Conditional response latency as a function of lag (lag-CRL)

For each participant, we initialized a set of elements to 0, one for each possible transition lag (Figure 1D). For a list-length of l, there are 2(l − 1) − 1 possible lags: l − 1, l − 2, l − 3, …, 2, 1,−1,−2, …, −(l − 2), −(l − 1). We excluded transitions to and from items repeated within a recall period, which includes transitions of lag = 0. We also excluded transitions to and from intrusions, as the lag is not defined for those items. For each list, we stepped through each recall transition, keeping track of the inter-response times (IRTs) for the value matching the lag of each transition. The lag-CRL for a participant was the mean value of all IRTs made at a particular lag. For instance, as shown in the sample calculation in Figure 1D, both the first and last output transitions would contribute CRLs to lag = 1.

Compound lag-CRL

For the compound lag-CRL, the mean IRT is calculated conditional on the previous transition being of a particular lag value, termed lag₁ (Figure 1E). In addition to requiring that participants had at least one observation for each of the t-tests reported below, we also required that they actually made each of those transitions at least once (i.e., it needed to be a possible transition and an actual transition). Whereas in the compound lag-CRP, if a participant never makes an actual transition for a possible lag this corresponds to a CRP of zero, in the compound lag-CRL this corresponds to an undefined CRL. As a result, we excluded an additional 48 participants. This analysis also excluded participants from Murdock (1962), as response times were not recorded in that experiment. In total, 122 participants were included in this analysis.

Results

Given that a participant has successively recalled items from serial positions r₁ and r₂, we sought to characterize the probability that the next recalled item was from serial position r₃ = r₂ + lag₂, conditional on the availability of the appropriate lags (i.e. that r₃ falls within the list boundaries and has not been recalled on the current trial). We refer to this as the conditional response probability as a function of lag, or lag-CRP (Figure 2A). Because we further examined the dependence of the lag-CRP on the lag between two previously recalled items (lag₁ = r₂ − r₁) we refer to it as the compound lag-CRP to distinguish it from the traditional lag-CRP that only considers items r₂ and r₃.

Figure 2B shows the compound lag-CRPs averaged across the included studies. The solid line shows the compound lag-CRP of each transition conditional on the previous transition satisfying lag₁ = +1. For this function, which we term the +1 compound lag-CRP, transitions to an item of lag₂ = +1 are more likely than any other transition. Similarly, the dashed line shows the compound lag-CRP conditional on the previous transition satisfying lag₁ = −1. For the −1 compound lag-CRP, the highest conditional probabilities of lag₂ are also in the forward direction, and even exceed those of the +1 compound lag-CRP.

For these compound lag-CRPs, not all values of lag₂ are possible. For the +1 compound lag-CRP, the transition to the item of lag₂ = −1 is a repetition: Because the participant just transitioned from item of serial position r₁ to r₂ + 1, then lag₂ = −1 defines a transition from r₂ − 1 back to r₁. Following the same logic, the transition of lag₂ = +1 in the −1 compound lag-CRP corresponds to a repetition as well.

The compound lag-CRP for |lag₁| > 3 (dotted line) closely approximates a standard lag-CRP, and can be considered a control for the |lag₁| = 1 compound lag-CRPs. Although it is tempting to compare the +1 and −1 compound lag-CRPs to a standard lag-CRP function, the latter includes all possible compound lags, including the two conditions we wish to compare. As mentioned in the introduction, transitions at larger absolute lags are much rarer, and thus the control (compound) lag-CRP reflects compound transitions from items that are less influential on the current transition.

To quantify the compound cue advantage, we defined a compound cue score separately for the forward and backward recall transitions. For forward transitions, the compound cue score is the difference between the lag₂ = +1 point of the +1 compound lag-CRP and the lag₂ = +1 point of the control lag-CRP. For backward transitions, the compound cue score is the difference between the lag₂ = −1 point of the −1 compound lag-CRP and the lag₂ = −1 point of the control lag-CRP. Positive compound cue scores indicate a compound cue advantage, whereas negative scores indicate a disadvantage.

Analysis of the forward compound cue score across all experiments revealed a strong compound cue advantage (mean compound cue score = 0.06; t(259) = 6.48, p < 0.001). Thus, a participant is more likely to recall the next item presented in the list if the previous two recalled items were presented successively.

In the studies analyzed here we did not find reliable differences in the compound lag-CRPs for negative values of lag₂ (mean compound cue score = 0.01; t(259) = 0.94, p > 0.3). This suggests that participants benefit most from compound cueing when the next recall is in the forward direction. These results are consistent with the benefits of compound cueing in serial learning because in that task participants benefit from compound cues when recalling in forward order (Chance & Kahana, 1997; Cohen & Sekuler, 2010; Kahana & Caplan, 2002; Posnansky, 1972).

To further characterize the contribution of compound cues in free recall, we examined the inter-response times (IRTs) of transitions. Analogous to the standard and compound lag-CRPs, Figure 2D,E plot the standard and compound lag-CRLs, respectively. The IRTs are faster for lag₂ = +1 in the +1 compound lag-CRL than the control lag-CRL, which we can again quantify as compound cue scores reliably greater than zero (t(121) = 2.76, p < 0.01). Thus, following a transition of lag₁ = +1, not only is the lag₂ = +1 item more likely to be recalled, but it will also be recalled with a faster inter-response time. Similar to response probabilities, this benefit in faster IRTs is only seen in the forward direction, as the backward compound cue score is not reliably greater than zero (t(121) = 0.44, p > 0.5).

Experiment

One possible explanation for the compound cueing effect observed in our meta-analysis is that participants use rehearsal to group items into “chunks” such that a sequence of three (or more) items may become bound together as a group (Laming, 2010). Overt rehearsal studies provide some support for this view, as participants often rehearse sequences of neighboring list items together (Rundus, 1971; Tan & Ward, 2000). Thus, one could argue that compound cueing arises because participants are recalling the sequences that they have rehearsed. To help rule out this possibility, we conducted a free recall experiment that included a continual-distractor condition designed to attenuate rehearsal.

Methods

These data were collected as part the Penn Electrophysiology of Encoding and Retrieval Study, involving three multi-session experiments that were sequentially administered. The data reported here come from 108 young adults who took part in Experiment 2. These data exclude 4 additional participants who performed poorly in the distractor tasks (taking on average more than 4 s per arithmetic problem, as described below), suggesting that they might have used the distraction intervals for rehearsal. One session from one participant was excluded due to a fire alarm sounding in the middle of the session.

Each session consisted of 12 lists of 16 words presented one at a time on a computer screen. Each study list was followed by a free recall test and each session ended with a recognition test. Half of the six sessions were randomly chosen to include a final free recall test before recognition, but only the initial free recall test phase is considered here.

Words were either presented concurrently with a task cue, indicating the judgment that the participant should make for that word. Each word was presented with one of two encoding tasks: a size judgment (“Will this item fit into a shoebox?”) or an animacy judgment (“Does this word refer to something living or not living?”), and the current task was indicated by the color and typeface of the presented item. The task manipulation was not considered here.

Each word was drawn from a pool of 1638 words. Lists were constructed such that varying degrees of semantic relatedness occurred at both adjacent and distant serial positions, although the manipulation of semantic relatedness is not considered here. Each item was on the screen for 3000 ms, followed by jittered 800 – 1200 ms inter-stimulus interval. If the word was associated with a task, participants indicated their response via a keypress. After the last item in the list, there was a 1200 – 1400 ms jittered delay, after which a tone sounded, a row of asterisks appeared, and the participant was given 75 s to attempt to recall any of the just-presented items.

In each distractor interval, participants solved math problems of the form A + B + C =?, where A, B, and C were positive, single-digit integers, though the answer could be one or two digits. When a math problem was presented on the screen, the participant typed the sum as quickly as possible. The task was self-paced, such that a participant may have been presented with but not responded to a problem at the end of the distraction interval. Participants were given a monetary bonus based on the speed and accuracy of their responses. In the first two trials, participants performed free recall with one trial having a distractor period following the last word presentation for 8 s. For the other of the first two trials, participants performed an 8 s distractor period prior to and following each word presentation. In the remaining 10 trials, participants performed free recall with 5 possible time durations for the between-item and end-of-list distractor tasks. As listed here, the first number indicates the between-list distractor duration and the second number indicates the end-of-list distractor, both in seconds: 0-0, 0–8, 0–16, 8-8, 16-16. A 0 s distractor refers to the typical, non-filled duration intervals as described in the previous paragraph.

Participants who did not have valid recalls for all possible values of lag₁ in a particular condition were excluded only from that condition. To control for multiple comparisons, here we consider the Bonferroni-corrected p = 0.01 threshold to indicate significance.

Results

Figure 3A shows the serial position curves for all five conditions: the two continual-distractor conditions (8 s or 16 s), the two delayed conditions (8 s or 16 s), and the immediate recall condition. Comparing the immediate and delayed conditions, the introduction of a distractor greatly reduces recall of recency but not primacy or mid-list items. To quantify the recency effect, in each condition we calculated the correlation between the last three serial positions and the corresponding recall probabilities at those serial positions. Each of the recency correlations for the delayed conditions were reliably reduced from the immediate condition (both p < 0.01). However, participants do exhibit striking long-term recency in the continual-distractor conditions (Bjork & Whitten, 1974; Howard & Kahana, 1999), as the recency correlations was not reliably different between each of the continual-distractor conditions and the immediate condition (both p > 0.05). Nonetheless, primacy remained relatively constant across conditions. Analogous to our measure of the recency effect, we quantified the primacy effect as the correlation between the first three serial positions and the corresponding recall probabilities at those serial positions. Pairwise comparisons between each of the distractor conditions and the immediate condition revealed comparable levels of primacy (all p > 0.2). Consistent with Howard and Kahana (1999), participants exhibited strong long-range temporal contiguity, as seen in the lag-CRPs in both the delayed and continual-distractor conditions (Figure 3B).

Figure 3. Recall probabilities in the experiment.

In each panel, the five free recall conditions are plotted: continual-distractor 8 s (squares), continual-distractor 16 s (upward triangles), delayed 8 s (downward triangles), delayed 16 s (circles), immediate (stars). A. Serial position curves. B. Conditional response probabilities as a function of lag.

In the continual-distractor conditions participants performed arithmetic distractor tasks between each word presentation. A size or animacy encoding task helped to direct participants attention to the word during its presentation. These manipulations would be expected to reduce rehearsal of prior items during and between presentations, thus providing a measure of compound cueing that is less susceptible to the influence of rehearsal processes. As shown in the top two panels of Figure 4, participants exhibit strong forward compound cueing in the continual distractor conditions (8 s: t(107) = 2.75, p < 0.01; 16 s: t(100) = 3.09, p < 0.005). Replicating the major finding of our meta-analysis, the forward compound cue score is also reliable in the delayed conditions (middle panels of Figure 4; 8 s: t(106) = 4.81, p < 0.0001; 16 s: t(105) = 4.67, p < 0.0001) and in the immediate recall condition (t(107) = 3.10, p < 0.005). In addition, a t-test between the 16 s conditions of delayed and continual-distractor free recall (presumably, the two conditions most strongly attenuating rehearsal) revealed that the compound cue scores are not reliably different (t(100) = .08, p > 0.5), suggesting that the same underlying mechanism motivates compound cueing in the two conditions. For the backward compound cue score, the value was significant only in the continual-distractor 16 s condition (t(100) = 2.78, p < .01), although this distribution of values did not differ reliably from the distribution of backward compound cue scores in the delayed 16 s condition (t(100) = 0.42, p > 0.5).

Figure 4. Compound cueing in the experiment.

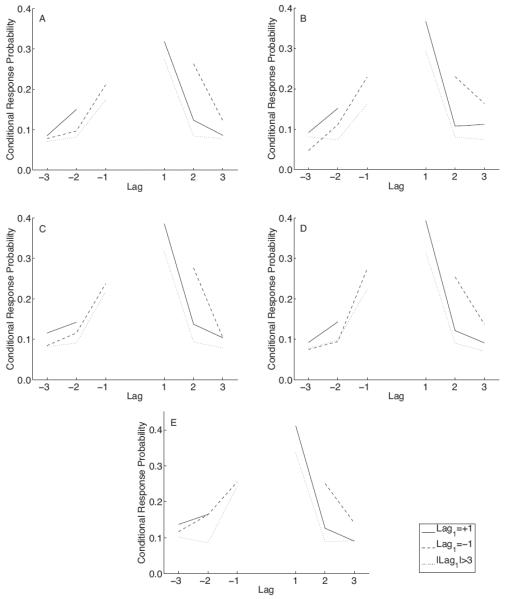
Within-subject comparisons revealed significant compound cueing across all five conditions of distraction intervals. In each panel, the lag-CRP is plotted separately for three cases of the lag of the previous transition, lag₁: lag₁ = +1 (solid); lag₁ = −1 (dashed); |lag₁| > 3 (dotted). Top row: Continual-distractor free recall. A. Interstimulus and end-of-list distractor interval = 8 s. B. Interstimulus and end-of-list distractor interval = 16 s. Middle row: Delayed free recall. C. End-of-list distractor interval = 8 s. D. End-of-list distractor interval = 16 s. E. Immediate free recall.

Simulation 1: Context Maintenance and Retrieval Model

The compound cueing results we have observed in immediate, delayed and continual-distractor free recall are exactly what one would expect if the cue for recall included information not only from the just-recalled item but also from the sequence of prior recalls. This idea is embodied in retrieved context models of episodic memory such as the temporal context model of Howard and Kahana (2002a) and its more recent variants (e.g., Sederberg et al., 2008; Polyn et al., 2009; Sederberg, Gershman, Polyn, & Norman, 2011; Howard, Kahana, & Wingfield, 2006; Gershman, Moore, Todd, Norman, & Sederberg, 2012). According to these models, the context cue used for recall of items contains a recency-weighted sum of previously activated cognitive states, and as such predict that the temporal contiguity effect should be enhanced when a sequence of previously recalled items were studied at neighboring list positions. Here we examine whether a specific version of retrieved context theory—the context maintenance and retrieval model (CMR)—can predict our observed results at a quantitative level. After presenting simulations of the CMR model we also consider two recent variants of the Search of Associative Memory model that have been successful in explaining a wide range of free recall phenomena (Sirotin et al., 2005; Kimball et al., 2007).

CMR model

According to CMR, the vector representation of the item presented at serial position i (denoted f_i) and its corresponding context representation (denoted c_i) interact through associative matrices (M^FCand M^CF) that are updated according to a standard Hebbian learning rule, such that $\Delta M^{\mathit{FC}}={\mathbf{c}}_i{\mathbf{f}}_i^{⊺}$ and $\Delta M^{\mathit{CF}}={\mathbf{f}}_i{\mathbf{c}}_i^{⊺}$. The context-to-item associative matrix, M^CF, is initialized to represent the semantic relations between items as determined using Latent Semantic Analysis (LSA, Landauer & Dumais, 1997, see Polyn et al. 2009 for details). The item-to-context matrix, M^FC, is initialized to the identity matrix.

Context evolves according to the equation:

$${\mathbf{c}}_i={\rho }_i{\mathbf{c}}_{i-1}+\beta M^{\mathit{FC}}{\mathbf{f}}_i,$$ (1)

where ρ_i is defined such that ∥c_i∥ = 1. Context is a weighted sum of the past several contextual states, and recent states dominate the representation. β is a model parameter that determines how much c_i changes with each studied item.

To simulate delayed free recall, we assume that c further evolves according to Equation 1 as participants engage in a distracting mental activity. In this case, we consider the distractor to be a single orthogonal item f_D with the value of β_D determining the change in c.

As a simplified implementation of the primacy effect, a primacy gradient ϕ_i scales the strengths of the item-to-context associations of early list items according to:

$${\varphi }_i={\varphi }_s{e}^{-{\varphi }_d(i-1)}+1,$$ (2)

where ϕ_s and ϕ_d are model parameters.

At the time of recall, cueing with c_i retrieves a vector f^IN = M^CF c_i. To determine which item the model recalls, f^IN serves as the input to a leaky, competitive accumulation process (Usher & McClelland, 2001) whose value at time step t is determined by

$$\begin{array}{cc}\hfill {\mathrm{x}}_t& =(1-\tau \kappa -\tau \lambda \mathbf{N})+{\mathrm{x}}_{t-1}+\tau {\mathbf{f}}^{\mathbf{IN}}+∊,\hfill \\ \hfill ∊& ~\mathcal{N}(0,\eta ),\hfill \\ \hfill {\mathrm{x}}_t& \to \mathit{max}({\mathrm{x}}_t,0).\hfill \end{array}$$ (3)

This process runs iteratively until one of the accumulating elements crosses a threshold or until the recall period is over. Each element of x_t corresponds to an element in f^IN. τ is a time constant, κ is a leak parameter, η is a noise parameter, and λ is a parameter that controls lateral inhibition, by scaling the strength of an inhibitory matrix N which connects each accumulator to all of the others except itself.

The recall period is modeled as a series of competitions; each competition either produces a winning item, or runs out of time, at which point the recall period is over and the next trial begins. When an item wins the recall competition, it is re-presented to the model, updating context according to Equation 1. The rate of context updating can differ between encoding and recall events (β_enc and β_rec, respectively). The updated state of context activates a different set of features on f^IN and the recall competition begins again. Thus, the contextual cue for recall of the next item is a blend of the previous state of context and the input from the most recently presented item.

The foregoing description omits several model details that are not critical to explain our current findings, such as the parameters that govern the relative influence of pre-experimental and experimental associations (for a full description see Polyn et al., 2009).

Results

We fit the CMR model to the mean data from the 16 s delayed free recall condition of our experiment (Figure 4). Specifically, we were interested in whether CMR could produce the three compound lag-CRPs of Figure 4D, while maintaing accurate predictions of the standard lag-CRP that is not conditionalized on prior responses (Figure 3B, open circles), and the serial position curve (Figure 3A, open circles).

To find the best-fitting model parameters, we first performed a grid search 10,000 parameter sets. Each parameter value was randomly selected on a uniform distribution of a pre-determined range. Twenty generations of a genetic algorithm search were run from this initial grid search, where each successive generation took the most fit 20% of the previous generation, and used these parent parameter sets to form 1,000 new parameter sets to simulate, by randomly repairing the parameters and adding random mutation to all values, using a normal distribution with mean zero and standard deviation 10% of the parameter range. The goodness-of-fit for a particular simulated data set was quantified using the root-mean squared deviation between the model and the analyses described above.

CMR predicts compound lag-CRPs that are quite similar to those observed in all conditions of our experiment and in our meta-analysis. As shown in Figure 5A, transitions of lag₂ = 1 are more likely for the +1 compound lag-CRP than the control compound lag-CRP. In the case of the +1 compound lag-CRP, the two previously recalled items (r₁ and r₂) are associated with similar context representations. Because the context retrieval cue is most strongly influenced by the contexts associated with these two items, this more strongly encourages recall of items with contexts similar to r₂, including its closest neighbor lag₂ = +1. The model parameters used in fitting these data are reported in Table 1.

Figure 5. Model predictions of compound lag-CRPs, standard lag-CRPs, and serial position curves.

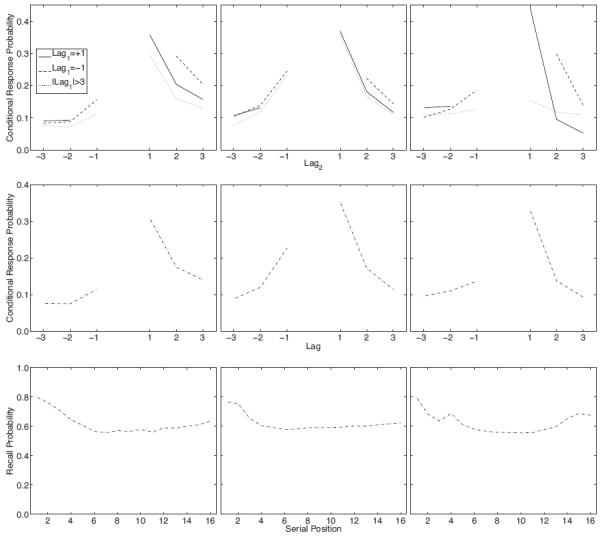
The left column shows predictions of the context maintenance and retrieval model (CMR); the middle column shows predictions of the episodic search of associative memory model (eSAM); the right column shows predictions of a version of the search of associative memory model that assume a multiplicative rule for associations between items at encoding and retrieval (fSAM). A,B,C. The conditional response probability as a function of lag (lag-CRP) is plotted separately for three cases of the lag of the previous transition, lag₁: lag₁ = +1 (solid); lag₁ = −1 (dashed); |lag₁| > 3 (dotted). D,E,F. Standard lag-CRP. G,H,I. Serial position curves.

TABLE 1.

CMR refers to the Context Maintenance and Retrieval model.

Best-Fit Parameters of CMR
Parameter	Description	Value
β enc	context drift rate during encoding	.313
β D	context drift rate during distractor interval	.960
β rec	context drift rate during recall	.674
γ FC	forward asymmetry during encoding	.571
ϕ s	weight of primacy factor during encoding	.698
ϕ d	decay of primacy factor during encoding	.544
s	retrieval weight for inter-item semantic strength	2.98
κ	decay weight in decision process	.100
λ	lateral inhibition weight in decision process	.500
η	standard deviation of noise in decision process	.218

Because our primary interest concerns each model's ability to fit the compound cue effect, here we report each model's goodness-of-fit based on the Akaike information criterion (AIC; Akaike, 1974) applied to the forward compound cue score. In comparison to the two models reported below, CMR's fit yields the lowest AIC value, indicating the closest performance to the experimental data (AIC = 12).

Simulation 2: Search of Associative Memory

Although we have suggested that the context-integration mechanism in CMR is necessary to reproduce the compound cueing effect, the central role of this mechanism in the model makes it difficult to uniquely identify its role in generating the effect. As a comparison to the CMR model, we examine the compound cueing predictions of the eSAM model (Sirotin et al., 2005). The eSAM model builds on the class of Search of Associative Memory models, which can account for a variety of memory findings in recall tasks (e.g., Gillund & Shiffrin, 1984; Raaijmakers & Shiffrin, 1980, 1981; Raaijmakers, 2003; Shiffrin, Ratcliff, & Clark, 1990). The eSAM model was introduced to account for numerous effects concerning the role of semantic associations in episodic recall tasks. As with previous versions of SAM, the strengths of associations in long-term episodic memory are governed by the operation of a short-term memory buffer and its control processes, as described below. Relevant to our current interests, the just-recalled item (along with a list-context representation) serve as the cue for the next response. Thus, if eSAM predicts the compound cue effects, this would imply that the context-integration mechanism of CMR is sufficient but not pivotal in explaining the compound cueing results.

eSAM

In eSAM there are two memory stores that contain item-to-item associations: a short-term memory (STM) buffer and long-term memory (LTM). LTM is comprised of a semantic component (S_s) which represents the semantic assocations between items (these values are set identically to those used for CMR, as specified in the previous section). LTM is also comprised of two episodic components that store item-to-item associations (S_e) and item-to-context associations (S).

When item i is presented to the model, it enters a limited capacity STM, which contains four recently presented items except during presentation of the first three items (Raaijmakers & Shiffrin, 1980; Sirotin et al., 2005). If the buffer is full, the newly presented item displaces the n^th buffer item with probability $\frac{q{(1-q)}^{n-1}}{1-{(1-q)}^{r_{\mathit{cur}}}}$ where r_cur refers to the number of items currently in the buffer and q is a free parameter that determines the degree of bias to displace older items versus displacing all items uniformly (Phillips, Shiffrin, & Atkinson, 1967).

Episodic interitem associations are initialized to 0.001. Forward and backward associations between any pair of items (i and j) that co-occupy the STM buffer are incremented, respectively, according to

$$\begin{array}{cc}\hfill S_e(i,j)& =S_e(i,j)+\frac{b_{\mathit{for}}}{r_{\mathit{cur}}}\hfill \\ \hfill S_e(j,i)& =S_e(j,i)+\frac{b_{\mathit{bac}}}{r_{\mathit{cur}}}\hfill \end{array}$$ (4)

The association between items in STM and list context are similarly incremented as

$$S(i,c)=S(i,c)+\frac{a}{r_{\mathit{cur}}}.$$ (5)

The weights of these associations are controlled by the free parameters a, b_for, b_bac.

In delayed free recall, recall begins with recalling items from long-term memory. An item i is recalled only if it is successfully sampled and recovered, which occur with probabilities P_s, P_r, respectively:

$$\begin{array}{c}\hfill P_s(i\mid j,c)=\frac{S_s{(i,j)}^{W_s}{S}_e{(i,j)}^{W_e}S{(i,c)}^{W_c}}{\sum _{k=1}^{\mathit{LL}}{S}_s{(k,j)}^{W_s}{S}_e{(k,j)}^{W_e}S{(k,c)}^{W_c}}\hfill \\ \hfill P_r(i\mid j,c)=1-e^{-W_s{S}_s(i,j)-W_e{S}_e(i,j)-W_{c}S(i,c)}\hfill \end{array}$$ (6)

where LL refers to list-length, c refers to the current list context and j refers to the previously recalled item. At the beginning of the recall period, only list context contributes to recall; specifically W_e = W_s = 0, and W_c = 1. For subsequent recalls that incorporate item information, then W_e, W_s, W_c are free parameters.

A recalled item's associative strengths to list context is incremented with the scalar parameters e_c, and item-to-item associations are also updated according to

$$\begin{array}{c}\hfill S_e(j,i)=S_e(j,i)+f_{\mathit{for}}\hfill \\ \hfill S_e(i,j)=S_e(i,j)+f_{\mathit{bac}}{\forall }_j,\hfill \end{array}$$ (7)

where f_for, f_bac are model parameters.

If an item-context cue is used L_max times but still fails to recover an item, then eSAM reverts to using only context as a cue. The recall process ends for a trial when K_max recovery failures have accumulated across all retrieval cues. K_max is a model parameter, and L_max is set such that L_max = 0.1K_max.

Results

Model parameters used to fit these data were determined with the same algorithm described in the CMR section, and are reported in Table 2. As implemented here, the eSAM model does not predict any reliable differences in the compound lag-CRPs. That is, in eSAM recall of an item r₃ is minimally influenced by the recall r₁ (Figure 5B). This is most apparent in eSAM's inability to predict the forward compound cue effect: the transition of lag₂ = +1 is not markedly different conditional on lag₁ = +1 or |lag₁| > 3. Although the eSAM predicts the difference between these two transition probabilities, termed the forward compound cue score, to be 0.01, in the experimental data the forward compound cue score is 0.08. Moreover, the goodness-of-fit of the eSAM model is less than that of the CMR model (AIC = 17).

TABLE 2.

eSAM refers to the Search of Associative Memory model using classic item-item associations at encoding and retrieval. fSAM refers to the SAM model that assumes a multiplicative compound cue rule defines item-item associations formed during encoding and used during retrieval.

Best-Fit Parameters of SAM
Parameter	Description	eSAM	fSAM
bfor	forward inter-item strength during encoding	.687	.946
bbac	backward inter-item strength during encoding	.527	.466
a	item-context increment during encoding	.361	.300
ffor	forward inter-item strength during recall	.058	.731
fbac	backward inter-item strength during recall	.528	0
ec	item-context increment during recall	.719	.035
We	retrieval weight for inter-item episodic strength	2.17	5.00
Wc	retrieval weight for item-context strength	.010	4.12
Ws	retrieval weight for inter-item semantic strength	3.69	.350
Kmax	number of attempts after which recall stops	25	188
q	bias for displacing old items from buffer	.165	.308
as	semantic item-context increment during encoding	-	.410

This result is not meant to imply that the SAM framework cannot account for these effects, but rather that the most basic version of eSAM which relies heavily on interitem associations does not predict influences of compound cues. Whereas the CMR model, which embodies retrieved context theory, can explain the compound cue effects, the eSAM model which lacks explicit context representations cannot explain these effects. Thus, this simulation suggests that some non-stochastic process, which incorporates more than the just-recalled item into the retrieval cue, influences recall organization. In the next simulation we consider the fSAM model, a variant of the eSAM model which uses compound cues to guide retrieval.

fSAM

Kimball et al. (2007) introduced the fSAM model to generalize the SAM framework to explain the false memory paradigm. The major distinction of the fSAM model concerns item encoding and retrieval: whether each item is stored and retrieved individually, or whether all items in STM serve as a multiple-item cue. Kimball et al. (2007) compared performance of the fSAM model based on encoding and retrieval using single items, an additive combinatorial rule, or a multiplicative combinatorial rule. Here we only consider the version of the model that used the multiplicative mutiple-item encoding and retrieval rules, as this was the only version that could account for behavioral performance in the false memory paradigm. Thus, our assumptions of the fSAM model are identical to the eSAM model except:

• (a)
  In addition to updating the item-context association of the just-presented item i, the item-context association for each list item k (including i) is updated according to

  $$S(k,c)=S(k,c)+a_s\prod _j^{j\in M}{S}_s(k,j)$$ (8)

  where a_s is a model parameter and M refers to the set of items currently in STM;
• (b)
  When an item-context cue is used during recall, item i is sampled with probability

  $$P_s(i\mid j\in M,c)=\frac{{\left(\prod _j^{j\in M}{S}_s\right(i,j\left)\right)}^{W_s}{\left(\prod _j^{j\in M}{S}_e\right(i,j\left)\right)}^{W_e}S{(i,c)}^{W_c}}{\sum _{k=1}^{\mathit{LL}}{\left(\prod _j^{j\in M}{S}_s\right(k,j\left)\right)}^{W_s}{\left(\prod _j^{j\in M}{S}_e\right(k,j\left)\right)}^{W_e}S{(k,c)}^{W_c}},$$ (9)

  and recovered with probability

  $$P_r(i\mid j\in M,c)=1-e^{-W_s\prod _j^{j\in M}{S}_s(i,j)-W_e\prod _j^{j\in M}{S}_e(i,j)-W_{c}S(i,c)}.$$ (10)

Results

The predictions of the fSAM concerning compound cueing are shown in Figure 5C. The fSAM model captures the compound cueing effect, in that a transition of lag₂ = 1 is much more likely following a transition of lag₁ = +1 than |lag| > 3. This suggests that the ability of the SAM framework to predict a forward compound cueing effect relies on the model's use of compound cues during encoding and retrieval. Consistent with the predictions of the CMR model, using a recency-weighted sum of recalled items to cue recall benefits successive recalls of items with lag₁ = +1. Although fSAM's goodness-of-fit is poorer than eSAM (AIC = 21), this reflects the fact that fSAM predicts a forward compound cue effect greater than the experimental data (fSAM = 0.21; data = 0.08), and thus captures qualitatively the main effect of interest.

Discussion

A model with a stochastic retrieval process assumes that recall of an item r₃ is only directly influenced by the prior recall r₂. Our analysis of the dynamics of responses in free recall shows that people exhibit striking violations of the stochastic assumption. In a meta-analysis of five free recall studies, we found that participants were more likely to make a transition of lag₂ = +1 when the previous transition, lag₁, was also +1, in comparison to when the previous transition was more remote, i.e. |lag₁| > 3 (Figure 2B). Participants were not only more likely to make such transitions, but additionally made such transitions more quickly, as exhibited in their inter-response times (Figure 2D). We also reported this benefit in probability of recall in the forward compound cue in a new experiment that included a continual-distractor free recall condition (Figure 4). The presence of compound cueing in continual-distractor free recall (as well as in immediate and delayed free recall) suggests that compound cueing is not simply a product of recalling sequences of rehearsed items.

We also assessed the predictions of compound cueing in the context maintenance and retrieval model (CMR; Polyn et al., 2009). The CMR model assumes that context is a recency-weighted sum of presented and recalled items, and uses this context to cue recall of the next item. The nature of this retrieval cue leads CMR to predict the patterns of compound cueing found in a delayed recall condition of the new experiment. A context-based framework such as CMR would also predict compound cueing in continual-distractor free recall for the same reason it predicts compound cueing in delayed free recall: The relative strengths of item representations in context will be highest for successively presented items.

In contrast, a variant of the search of associative memory model (eSAM; Sirotin et al., 2005) does not predict strong differences in lag₂ as a direct function of lag₁. In eSAM, the retrieval cue is based on the relatedness between r₂ and not-yet-recalled items; as such, recall of r₃ is only directly influenced by the prior recall r₂. That eSAM cannot account for the compound cue advantage suggests that the retrieved context assumption, as embodied in CMR, may be necessary, if not also sufficient, to explain the compound cue result. In general, the retrieval process SAM framework is not restricted to be stochastic. Compound cues can be implemented in SAM by assuming that a set of recently recovered items contribute to the cue (e.g., Kimball et al., 2007; Ratcliff & McKoon, 1988, 1995). Here we considered a version of the fSAM model (Kimball et al., 2007) which shares most assumptions of the eSAM model except that items are associated via a multiplicative rule at encoding and retrieval, rather than only being directly associated with one another. This version of the SAM model did predict the advantage of the forward compound cue.

The critical distinction between CMR and fSAM, which predict compound cueing, and eSAM, which does not, is the retrieval cue. Even if context associations are formed at encoding, our results suggest that such context representations must be incorporated into the retrieval cue in order to a produce compound cue effects. Consistent with this idea, Kimball et al. (2007) found that fSAM could only account for false-memory paradigm effects when fSAM assumes that compound associations were used both at encoding and retrieval. An open question concerns whether models that assume chunking or grouping processes at encoding but not at recall (e.g., Farrell, 2012) can produce the forward compound cue effect.

Nonetheless, we do not wish to make strong arguments defining the set of models that can or cannot capture the compound cue effect; our primary focus to provide a set of novel findings as predicted by retrieved context models such as CMR. This model assumes that context is a recency-weighted sum of recalled items, and thus assumes that r₃ is more strongly influenced by r₂ than r₁. We found this to be the case in our experimental data as well: Although r₁ and r₂ form a compound cue for retrieval of r₃, the influence of r₂ is clearly stronger than that of r₁. In the extreme case where r₁ and r₂ equally informed the next recall r₃, we would not expect a meaningful interpretation of r₃ when only considering r₂. Yet previous analyses have shown that a large proportion of the variance in transitions can be explained when considering only the previous transition (Kahana, 1996). The stronger influence of r₂ can be intuited from the retrieved context account, as in the simulations of CMR. Because context is a recency-weighted sum of recalled items, r₂ is more strongly represented in the context used to cue recall than r₁.

The reported compound cue advantage in free recall can be used to understand the part list cueing effect. In the part list cueing paradigm, participants are provided with a subset of presented items as cues immediately preceding the recall period. In initial studies, performance was worse than standard free recall (Slamecka, 1968). If participants benefit from a double or triple item cue over a single item cue in serial recall, it may seem counterintuitive that presentation of a subset of the list hinders recall. However, in part list cueing, the cues may not be the most beneficial to the participant. Indeed, studies in which the items comprised a randomly selected subset of items hindered recall (Roediger, 1973; Slamecka, 1968), but when cued stimuli are re-presented in their original presentation order, this can attenuate or eliminate the inhibitory effect (Allen, 1969; Basden, 1973; Sloman, Bower, & Rohrer, 1991). Whereas in free recall the units of organization imposed by the participant can be unclear, in serial recall the optimal units are implicit in the instruction to recall items in order. Thus, the fact that participants benefit from being presented with compound rather than single cues in serial recall is also consistent with these ideas (Kahana & Caplan, 2002; Posnansky, 1972).

Our reported free recall results seem relatively consistent with the results in serial recall. In serial learning the benefit of compound cues is greater in the forward than in the backward direction (Kahana & Caplan, 2002). In our free recall meta-analysis and experiment, we always found a benefit of forward compound cues, and in only one condition of our experiment did we find a benefit of a backward compound cue. Although in free recall participants may recall list items in any order, they nonetheless exhibit striking asymmetry in their transitions in free recall (Kahana, Howard, & Polyn, 2008), and thus it is not surprising that the compound cue advantage is more reliable in the forward direction.

Our finding of compound cueing demonstrates that intraitem transitions in free recall are not stochastic. These results are consistent with retrieved context theory, which assumes that the retrieval cue is a recency-weighted sum of prior recalls.