A joint test for progression and survival with interval-censored data from a cancer clinical trial

Abstract

Clinical trials often assess efficacy by comparing treatments on the basis of two or more event-time outcomes. In the case of cancer clinical trials, progression-free survival (PFS), which is the minimum of the time from randomization to progression or to death, summarizes the comparison of treatments on the hazards for disease progression and mortality. However, the analysis of PFS does not utilize all the information we have on patients in the trial. First, if both progression and death times are recorded, then information on death time is ignored in the PFS analysis. Second, disease progression is monitored at regular clinic visits, and progression time is recorded as the first visit at which evidence of progression is detected. However, many patients miss or have irregular visits (resulting in interval-censored data) and sometimes die of the cancer before progression was recorded. In this case, the previous progression-free time could provide additional information on the treatment efficacy. The aim of this paper is to propose a method for comparing treatments that could more fully utilize the data on progression and death. We develop a test for treatment effect based on of the joint distribution of progression and survival. The issue of interval censoring is handled using the very simple and intuitive approach of the Conditional Expected Score Test (CEST). We focus on the application of these methods in cancer research.

1. Introduction

The primary outcome of clinical trials in cancer is often progression-free survival (PFS), which is the time from randomization to the first of progression or death. This outcome is chosen because it is clear that the delay of progression confers a benefit to the cancer patient. Also, although survival is arguably the most important outcome for a life-threatening disease such as cancer, using PFS can shorten the time it takes to report results of a trial and is sensitive to both rapid progression as well as lethal treatment toxicity. Finally, because therapy is usually ended or changed at progression, the use of PFS does not require any untestable assumptions about the impact of a treatment after it is discontinued at progression. However, the analysis of PFS does not utilize all the information we have on patients in the trial. First, if both progression and death times are recorded, then the information on death time is ignored in the PFS analysis. Second, progression is monitored at pre-determined clinic visits by clinic, lab and radiologic tests, and progression time is recorded at the first visit at which it was detected. However, many patients miss or have irregular visits, and sometimes patients die (of cancer) before the progression was recorded with variable gaps in time between the visit at which there was no evidence of progression and the visit at which progression was first detected. In this case, the data on when a patient was last seen in stable condition could provide additional information on the analysis of treatment benefit. In fact, progression time is actually interval-censored data, as the data set will consist of overlapping intervals when progression occurred. In light of these issues, both US Food and Drug Administration and European Medicines Agency have issued guidelines for industry on clinical endpoints for the approval of cancer drugs and biologics [1, 2]. In the guidelines, different recommendations have been made for the PFS analysis, covering various issues such as event and censoring rules, event and censoring timing for progression documented between scheduled visits, treatment discontinuation, start of new anticancer treatment, death before the first progressive disease assessment or between adequate assessment visits, death or progression after more than one missed visits, and so on. In general, these guidelines urge consideration of the interval-censored nature of progression data.

The analysis of interval-censored data is challenging as one cannot directly apply standard methods such as the proportional hazards model because when a failure is censored into an interval of time, one knows neither when the failure happened nor when the subject was at risk and event free during that interval. Rather, it is necessary to parameterize the underlying distribution as well as the treatment effect. Often, this likelihood is not in closed form. We have proposed methodology for the estimation and regression analysis of the effect of baseline predictors on interval-censored failure time data [3, 4]. Goggins et al. [5] developed a method for handling multivariate interval-censored data but not the specific case we handle here, where the failures are known to be ordered. We will jointly model progression and death. We assume that progression occurs before a death from cancer even if it is not recorded.

The aim of this paper is to propose a test for comparing treatments that could more fully utilize the data on both survival and progression by considering the joint outcomes rather than the minimum of the two. The method will handle the fact that the data are interval-censored data and that patients who die before progression is recorded should be treated differently in the analysis than those whose progression is detected prior to their death. In the next section, we will first introduce notation and the models and likelihood we will use for the data on survival and death for the case when all progressions are exactly observed. We then apply the principle of Conditional Expected Score Test (CEST) [6] to derive the score test to handle the case where some visits are missed, resulting in interval-censored event data. We apply our methods to analyze a breast cancer study and suggest extensions to this work.

2. Methods

2.1. Notation, model, and likelihood for complete data

Suppose that we completely observe the data on progression time for all subjects i, for i = 1, …, N, and have recorded death (or most recent follow-up) times. We assume that progression occurs before (or at) death, because we are in the context of a cancer clinical trial where deaths that are observed during follow-up are almost always related to the cancer. We will let Y_ij be an indicator for whether patient i was in follow-up at time j. Thus Y_ij = 1 until the patient dies or leaves follow-up, after which time Y_ij = 0. Let ρ_ij be an indicator of whether or not patient i had first evidence of progression at time j. We assume ρ_i0 = 0. We let W_ij be an indicator for whether patient i is at risk for progression at time j and note that $W_{ij}=Y_{ij}·\left[1-{\sum }_{k=1}^{j-1}{\rho }_{ik}\right]$. Let δ_ij be an indicator for whether patient i has died at time j. All indices are measured from the time of the start of study. Let the set of times j = 1, …, M represent all the times at which a progression was assessed, a death was recorded, or a patient was censored. Deaths will be coarsely grouped and recorded into these intervals. Finally, let X_i be the covariate (treatment indicator) for patient i.

To model the relationship between the covariate (treatment) and failure, we will utilize a generalized person-exam risk model described in [7], by which observations over multiple time intervals are pooled into a single sample, and logistic regression is used to relate the risk factors to the occurrence of the event. When grouping intervals between exams are short, this Pooling Repeated Observations method (PRO) is asymptotically equivalent to grouped proportional hazards model for a time-dependent covariate [8]. In our application, the response variable of the logistic model will indicate progression as a function of the covariate x. Thus, the logistic model for hazard of progression at time j given treatment x is

$$\text{logit}{p}_j(x)=log\frac{p_j(x)}{1-p_j(x)}={\alpha }_j+{\beta }^{\prime }x$$ (1)

where p_j is the conditional probability of observing the progression at the j^th time given the individual was free of progression through time j − 1 and x is the value of the covariate for treatment. We treat progression as non-reversable, and patients are only under observation for death after they progress. Finally, we assume that the patient who dies of cancer progressed prior to death.

Similarly the model for hazard of death at k^th time given progression at time j is

$$\text{logit}{q}_{jk}(x)=log\frac{q_{jk}(x)}{1-q_{jk}(x)}={\theta }_{jk}+{\gamma }^{\prime }x$$ (2)

where q_jk is the conditional probability of observing the death at time k after progression at the j^th time and x is the value of the covariate for treatment.

For the test of treatment benefit on progression and mortality, we let the coefficient of x be the same in both models: β = γ using a single parameter for treatment effect, β (under the null). If we were in the simple case where p_j = p for all j and q_jk = q for all j, k, the contribution to likelihood for someone who progresses at j and dies at k > j would be (1 − p)^j−1p(1 − q)^k−jq.

More generally, the contribution of the i^th subject to the log likelihood under the PRO logistic models for data (1) and (2) is

$${\mathcal{L}}_i=\sum _{j=1}^M\left[-W_{ij}log\left(1+e^{{\alpha }_j+{\beta }^{\prime }{x}_i}\right)+{\rho }_{ij}({\alpha }_i+{\beta }^{\prime }{x}_i)\right]+\sum _{j=1}^M\left[\sum _{k=j}^M-Y_{ik}log\left(1+e^{{\theta }_{jk}+{\beta }^{\prime }{x}_i}\right)+{\delta }_{ik}({\theta }_{jk}+{\beta }^{\prime }{x}_i)\right]·{\rho }_{ij}$$ (3)

where j = 1, …, M indexes all times of clinic visits, deaths, or censoring, measured from randomization.

The numerator of the score test for the hypothesis H₀ : β = 0 is found by taking the derivative of the log-likelihood with respect to β, evaluated at β = 0, which gives

$$U=\sum _{i=1}^N\left[\sum _{j=1}^M\left[{\rho }_{ij}-W_{ij}{\widehat{p}}_j\right]x_i+\sum _{j=1}^M\left(\sum _{k=j}^M[{\delta }_{ik}-Y_{ik}{\widehat{q}}_{jk}]x_i\right){\rho }_{ij}\right]$$ (4)

where $W_{ij}=Y_{ij}·\left[1-{\sum }_{k=0}^{j-1}{\rho }_{ik}\right]$, p̂_j (progression) at j is estimated by $\frac{{\sum }_i{\rho }_{ij}}{{\sum }_i{W}_{ij}}$ and q̂_jk (death) at k ≥ j is estimated by $\frac{{\sum }_i{\rho }_{ij}{\delta }_{ik}}{{\sum }_i{Y}_{ik}{\rho }_{ij}}$ .

2.2. Derivation of score with interval-censored data using Conditional Expected Score Test

We now consider the problem that the progression can be censored into intervals bracketed by the missed visits. Suppose that the i^th subject missed visits after time L_i, came back at time R_i, and that ρ_iL_i = 0 and ρ_ij = 1 for some L_i < j ≤ R_i. In this case, ρ_ij is missing for L_i +1 ≤ j ≤ R_i. Also because progression is an absorbing state, if any subject misses a visit but returns at time k still progression free, then we assume ρ_ij = 0 for all j ≤ k. Let M_i be the index of the last time subject i was observed. Finally, we assume that if the patient dies (of cancer) at time k and no progression time was recorded, then they had to have progressed at some time after the last observed time at which they were progression free (prior to time k) and the exact time of progression is unknown.

In our earlier paper [6], we discussed how it is possible to derive a score test in the context of missing data in a simple way using a technique we have called the CEST. For this, we reference a principle noted by Efron as a discussant in Dempster, Laird and Rubin (1977) JRSS-B [9]: “The score based on incomplete data is the expected value of the complete data score conditional on the observed data.” Efron [10] actually acknowledged a result of Fisher from 1926, stating this earlier. This method simplifies an otherwise complex derivation for the score as we need only to obtain the expectations for data that are missing. We used this approach in other recent papers [6, 11]. The four steps to obtain the score test from incomplete data using CEST are to select a model, find the score test for complete data, determine the expected value of the score given the incomplete data (under the null), and use this as a score test statistic. For example, suppose that we only had progression data, where ρ_ij be indicator subject i has progression at time j and W_ij is an indicator that they are under observation at time j (for progression). Thus $W_{ij}=Y_{ij}·\left[1-{\sum }_{k=0}^{j-1}{\rho }_{ik}\right]$. It is simple to see that the numerator of the score test for complete data is

$$U=\sum _i\sum _j({\rho }_{ij}-W_{ij}{\widehat{p}}_j)x_i$$

where ${\widehat{p}}_j=\frac{{\sum }_i{\rho }_{ij}}{{\sum }_i{W}_{ij}}$ is the probability of progressing at time j. Using the CEST, we can see that the numerator of the score test for incomplete data can be derived by calculating the expected value of score (under H₀), which is

$$U=\sum _i\sum _j\left({\widehat{\rho }}_{ij}-{\widehat{W}}_{ij}{\widehat{p}}_j\right)x_i$$

where ρ̂_ij = E(ρ_ij |(L_i, R_i], β = 0), Ŵ_ij = Y_ij ·[1 − Σ_k<j ρ̂_ik], and ${\widehat{p}}_j=\frac{{\sum }_i{\widehat{\rho }}_{ij}}{{\sum }_i{\widehat{W}}_{ij}}$.

We note that the notation of hat above observed data (such as ρ̂) is referring to an expectation of the quantity, while the hat notation over a parameter (such as p̂) refers to an estimated value. Also note that these quantities are found by iteration as they depend on each other. The result of this approach is the same as the test derived in [3].

For the case of the joint model for progression and death, we will apply the likelihood based on the PRO logistic models in (4) applied earlier. For our data, progression is censored into (L_i, R_i] for each subject, and death is exact or right censored at a time after R_ij. In this case, the likelihood (with interval-censored data) is complex. However it simplifies under the null hypothesis.

To apply the CEST, we note that the score based on incomplete data is the expected value of the complete data score conditional on the observed data. Using the numerator of the score test from the complete data derived earlier (4), we need only to obtain the expectations of the score for observations with missing data. For this, we note that because under H₀: β = 0, both (ρ_ij, W_ij) and (δ_ik, Y_ik) are independent of x_i, the score contribution for each subject i is

$$\sum _{j=1}^{M}E[({\rho }_{ij}-p_j{W}_{ij})\mid (L_i,R_i]]x_i+\sum _{j=1}^{M}E\left[\sum _{k=j}^M({\delta }_{ik}-q_{jk}{Y}_{ik})x_i{\rho }_{ij}\mid (L_i,R_i]\right]$$

We will need to obtain expectation of ρ and W conditional on the observed data evaluated at β = 0. Now the expected value of ρ is

$$E({\rho }_{ij}\mid \mathit{\rho },\mathbf{Y},\mathbf{W},{\delta }_{\mathbf{ik}}=\mathbf{1},\mathit{\delta },\beta =0)=\{\begin{array}{ll}\frac{p_j{\prod }_{r=1}^{j-1}(1-p_r)·q_{jk}{\prod }_{s=j}^{k-1}(1-q_{js})}{{\sum }_{m=L_i+1}^{R_i}{p}_m{\prod }_{r=1}^{m-1}(1-p_r)·q_{mk}{\prod }_{s=m}^{k-1}(1-q_{ms})}\hfill & \text{if}j\in (L_i,R_i]\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

We note E(ρ) is informed by the death as well as progression times (by p as well as q).

For the expected value of the indicators of being at risk and of dying following progression, we note that the expected indicator for death after progression is

$$E({\rho }_{ij}{\delta }_{ik}\mid \text{data})=E({\rho }_{ij}\mid \text{data})·{\delta }_{ik}={\widehat{\rho }}_{ij}{\delta }_{ik}$$

where ρ̂_ij = E(ρ_ij |data).

It can now be shown from (4) that for data with interval-censored progression times, the score is

$$U=\sum _{i=1}^N\sum _{j=1}^M\left[\left({\widehat{\rho }}_{ij}-{\widehat{W}}_{ij}{\widehat{p}}_j\right)x_i+\sum _{k=j}^M({\delta }_{ik}-Y_{ik}{\widehat{q}}_{jk})x_i{\widehat{\rho }}_{ij}\right]$$ (5)

where ${\widehat{p}}_j=\frac{{\sum }_i{\widehat{\rho }}_{ij}}{{\sum }_i{\widehat{W}}_{ij}},{\widehat{W}}_{ij}=Y_{ij}·\left[1-{\sum }_{k<j}{\widehat{\rho }}_{ik}\right]$, Ŵ_ij = Y_ij ·[1 − Σ_k<j ρ̂_ik], and ${\widehat{q}}_{jk}=\frac{{\sum }_i{\widehat{\rho }}_{ij}{\delta }_{ik}}{{\sum }_i{Y}_{ik}·{\widehat{\rho }}_{ij}}$. This can be estimated iteratively by an application of the EM algorithm.

3. Calculation of the variance for the Conditional Expected Score Test

To simplify the calculation of the variance of the test, we begin by noting that the log likelihood in (3) can be written as a general linear function in the data that are missing (in our case ρ_ij). For this, we note that the contribution of the i^th subject to the log likelihood under the PRO logistic models for data (1) and (2) is

$${\mathcal{L}}_i=\sum _{j=1}^M\left[-Y_{ij}·\left(1-\sum _{k=0}^{j-1}{\rho }_{ik}\right)log\left(1+e^{{\alpha }_j+{\beta }^{\prime }{x}_i}\right)+{\rho }_{ij}({\alpha }_j+{\beta }^{\prime }{x}_i)\right]+\sum _{j=1}^M\left[\sum _{k=j}^M-Y_{ik}log\left(1+e^{{\theta }_{jk}+{\beta }^{\prime }{x}_i}\right)+{\delta }_{ik}({\theta }_{jk}+{\beta }^{\prime }{x}_i)\right]·{\rho }_{ij}$$ (6)

where ρ_i0 = 0. This likelihood can be expanded out to

$$\begin{array}{l}{\mathcal{L}}_i=\sum _{j=1}^M-Y_{ij}log\left(1+e^{{\alpha }_j+{\beta }^{\prime }{x}_i}\right)+\sum _{j=1}^M\left(\sum _{k=0}^{j-1}{\rho }_{ik}\right)Y_{ij}log\left(1+e^{{\alpha }_j+{\beta }^{\prime }{x}_i}\right)+\sum _{j=1}^M({\alpha }_j+{\beta }^{\prime }{x}_i)·{\rho }_{ij}\\ +\sum _{j=1}^M\left[\sum _{k=j}^M-Y_{ik}log\left(1+e^{{\theta }_{jk}+{\beta }^{\prime }{x}_i}\right)+{\delta }_{ik}({\theta }_{jk}+{\beta }^{\prime }{x}_i)\right]·{\rho }_{ij}\end{array}$$

If we assign Y_{i(M +1)} = 0 and add over all subjects, then the likelihood can be rewritten as a linear function of ρ as $\mathcal{L}={\sum }_{i=1}^N{\sum }_{j=1}^M{\mathcal{L}}_{ij}$ where

$${\mathcal{L}}_{ij}=-Y_{ij}log\left(1+e^{{\alpha }_j+{\beta }^{\prime }{x}_i}\right)+\left[\sum _{k=j+1}^{M+1}(Y_{ik}log\left(1+e^{{\alpha }_k+{\beta }^{\prime }{x}_i}\right)+({\alpha }_j+{\beta }^{\prime }{x}_i)\right]·{\rho }_{ij}+\left[\sum _{k=j}^M-Y_{ik}log\left(1+e^{{\theta }_{jk}+{\beta }^{\prime }{x}_i}\right)+{\delta }_{ik}({\theta }_{jk}+{\beta }^{\prime }{x}_i)\right]·{\rho }_{ij}$$

Thus the likelihood is linear in the incomplete data, which is the indicator for the time of progression, ρ_ij. Let ${\mathcal{L}}_{ij}^{\ast }=E({\mathcal{L}}_{ij}\mid X_C)$ and E(ρ_ij |X_C) = ρ̂_ij, with ρ̂_i0 = 0, where X_C is the observed data (the set of (L_i, R_i]). This representation makes it easier to use the formula of Louis [12] to calculate the information matirix of ϕ = (p_j, q_jk, β) because the expectation of any derivative of 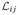is just the derivative of 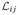with ρ̂_ij replacing ρ_ij. Thus, applying the formula 3.2′ on page 228 of [12], the Fisher information for the incomplete data is the matrix I with rs entry:

$$I_{rs}=\sum _i\sum _j-\frac{{\partial }^2{\mathcal{L}}_{ij}^{\ast }}{\partial {\varphi }_r\partial {\varphi }_s}-\sum _{i}E\left[\sum _j\frac{\partial {\mathcal{L}}_{ij}}{\partial {\varphi }_r}·\sum _{j^{\prime }}\frac{\partial {\mathcal{L}}_{i{j}^{\prime }}}{\partial {\varphi }_s}\mid X_C\right]-2\sum _{i<l}\left[\sum _j\frac{\partial {\mathcal{L}}_{ij}^{\ast }}{\partial {\varphi }_r}\right]\left[\sum _l\frac{\partial {\mathcal{L}}_{ij}^{\ast }}{\partial {\varphi }_s}\right]+\left[\sum _i\sum _j\frac{\partial {\mathcal{L}}_{ij}^{\ast }}{\partial {\varphi }_r}\right]\left[\sum _i\sum _j\frac{\partial {\mathcal{L}}_{ij}^{\ast }}{\partial {\varphi }_s}\right]$$

Note that because ρ_ij ρ_ik = ρ_ij whenever j = k and is zero otherwise, the quantity under the expectation (in the second term) can be simplified to be linear in ρ_ij as well so that its expectation given the complete data is also found by replacing ρ_ij by ρ̂_ij. Also note that the last term $\left[{\sum }_i{\sum }_j\frac{\partial {\mathcal{L}}_{ij}^{\ast }}{\partial {\varphi }_r}\right]\left[{\sum }_i{\sum }_j\frac{\partial {\mathcal{L}}_{ij}^{\ast }}{\partial {\varphi }_s}\right]$ is 0 except at ϕ = β and thus becomes a matrix with the square of the score given in (5) in the lower right corner and zeros elsewhere. Finally, the variance of the statistic is the inverse of the lower right element of I⁻¹, which follows from [13], page 417 (6e.2.4). Thus the inverse of I simplifies (as shown in [13], page 33) because it is a symmetric partitioned matrix. Alternatively, we could calculate the bootstrap estimate of the variance. The program for this can be found on our website http://hedwig.mgh.harvard.edu/biostatistics/tools/software.

4. Simulations

We performed simulations, comparing the proposed joint test on progression and survival following progression, to the logrank test on PFS that is usually used. For simplification, we considered the case where the probability of progression (p) in each interval was the same at each time and the probability of death after progression (q) was the same regardless of when progression occurred. We considered various combinations of these two hazards and associated hazard ratios for two treatment groups. We varied the probability of missing visits, which drove the degree of interval censoring (Int Censor). Each run is based on N = 100 and 1000 simulations unless an alternate sample size is noted. We considered the impact of increasing N. We used underlying hazard of progression of about 0.1 to 0.2, and hazard ratios of about 1.5 to 2 to assess power. We assumed that the subjects had a maximum of 12 visits. From simulations, the size of both tests was right. This is shown in the lines (j) and (k) of Table I.

Table I.

Results of simulations: power of proposed versus logrank on PFS.

Sim	p (prog)	q (death)	HR for p	HR for q	Int Censor	N	Proposed	Logrank
a)	0.2	0.1	2	2	0.2	100	0.91	0.84
b)	0.2	0.1	2	2	0.5	100	0.88	0.77
c)	0.2	0.1	2	1.5	0.2	100	0.87	0.86
d)	0.1	0.2	2	1.5	0.2	100	0.62	0.59
e)	0.1	0.2	2	2	0.2	100	0.75	0.56
f)	0.1	0.2	1.5	2	0.2	100	0.56	0.29
g)	0.2	0.1	2	1	0.2	100	0.63	0.77
h)	0.03	0.2	2	1.5	0.2	300	0.76	0.75
i)	0.2	0.1	2	1	0	100	0.73	0.84
j)	0.1	0.2	1	1	0.5	100	0.05	0.04
k)	0.1	0.2	1	1	0.2	100	0.04	0.03

HR, hazard ratio; PFS, progression free survival.

We found that if the hazard is higher for progression than for death after progression, and the hazard ratios both reflect treatment benefit, the proposed test has more power (see (a)). If the chance of making a visit drops, the power drops more for the logrank test than the proposed test (b). If the hazard ratio for death drops, the power of the two tests are close (c). If the hazard is higher for death (with a lower hazard ratio) but lower for progression, the power again drops and is similar for both (d). If the hazard for death is higher and the two hazard ratios are about the same, the proposed test outperforms the logrank substantially (e). When the hazard ratio is reversed (higher for death after progression than for progression), the two methods decline dramatically in power, but the logrank does worse (f). However, if the hazard for death after progression is low, the hazard ratio for death after progression is 1, but the hazard and hazard ratio for progression is as before, then the logrank does better (g). If the study has lower progression hazard rate, but more patients (300), then the tests do about the same on power (h). Finally, without interval censoring, the logrank does better (i). As shown in rows j and k, both tests have the right size.

5. Analysis of efficacy of treatment on progression-free survival from an early breast cancer trial

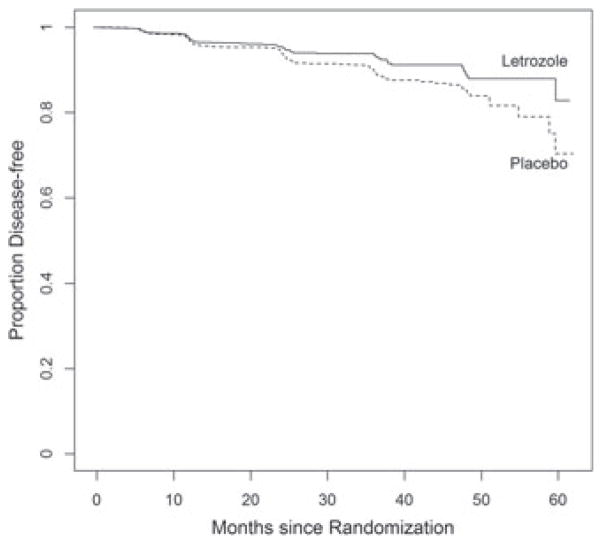
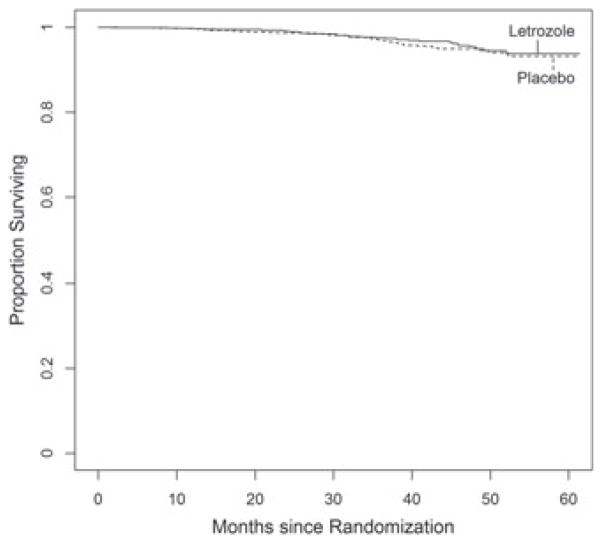
The clinical trial MA17 was conducted by the National Cancer Institute of Canada to compare the efficacy of letrozole versus placebo in early breast cancer post-menopausal women with hormone receptor positive tumors who had been treated with 5 years of tomoxifen. The 5187-patient trial was published in NEJM I in 2003 [14]. The study was stopped at an interim analysis (after a median of 2.5 years of follow-up) on the basis of the primary outcome of PFS, with 207 local or metastatic recurrences of breast cancer or new primary cancers in the contralateral breast (75 in letrozole group and 132 in placebo) and estimated 4-year disease-free survival rates of 93% and 87%, respectively, in the two groups (p < 0.0001). A total of 42 women in the placebo group and 31 in the letrozole group had died. All deaths were included as events regardless of the cause of death. At the early termination of the trail, patients were unblinded, and those who had been assigned placebo were offered letrozole. While the treatment advantage on PFS was clear, an analysis of mortality from the trial found no significant difference. After additional data were collected (up until the crossover), the study was re-analyzed and published in JNCI [15]. This analysis is made using the updated data, which included 113 deaths and 247 breast cancer events. The medical community were puzzled by this result, wondering why the benefit of letrozole on PFS did not translate to a benefit on overall survival. In addition, there was curiosity about whether the analysis would be impacted by considering the interval-censored nature of the data and by treating the outcome of death in the absence of earlier progression in a more thoughtful way. The analysis of PFS made by treating the first of progression detected or survival as the outcome (ignoring interval censoring) was significant at p < 0.0001 (Figure 1). The treatment comparison of survival shows no significant treatment difference (Figure 2). If we analyzed the data on progression alone, taking into account the interval-censored nature, the treatment comparison (using [3]) resulted in p = 0.0003. When we analyze survival after progression (including all deaths regardless of cause), we obtain p = 0.6502. Finally, using our proposed test for the joint impact of treatment on delay of progression as well as death after progression, we obtain a significance of p = 0.0016. Thus, letrozole is associated with a delay of progression, a delay of death, or both. We note that an alternative analysis would be to censor subjects whose first event of death was from a non-cancer cause. This would be reasonable in the case of an early breast cancer trial with long follow-up after treatment ended. However, because of lingering concerns on late treatment complications, the all-cause mortality is the more common endpoint in cancer clinical trials, so we have reported only these results.

Figure 1.

Progression free survival.

Figure 2.

Overall survival.

6. Discussion

We have proposed a test for the joint effect of treatment on progression and death after progression. The development of the test using CEST is intuitive and straightforward. Simulations show that the test has more power than the standard logrank on PFS except for the cases where the hazard for death after progression (q) is low, and the hazard ratio on the q is 1, and for the case where there was no interval censoring on progression.

We note that there are several generalizations to these methods. We could generalize to multiple dependent (monotone) events. Also, we simplified the expressions by assuming all slopes (β and γ) equal, but it is straightforward to generalize this. Finally, we coarsely grouped the death times to simplify the programming and avoid issues of sparse data, but with large data sets, it might be possible to allow death times to be treated as continuous.

We simplified the development of our test by the use of the CEST. We hope that others will use this approach for their applications, as we have in recent work [3, 6, 16, 17]. There are several potential extensions of our methods. For example, we made the assumption in this analysis that the censoring was independent. We believe it may be useful to extend this approach to handle dependent censoring [16,18].

In addition, we note that one could develop a two-degree (rather than one-degree) of freedom test of whether the two parameters are simultaneously zero, but it would lose power for the primary comparison of the treatment effect, which is the main focus of a clinical trial. Alternatively, we note that if the proposed overall test is significant, one could divide the test statistic into the requisite parts to determine the direction of the treatment effect on each outcome, and the overall type I error would be preserved.

Finally, the focus of this paper is on testing for treatment differences, and the approach would not easily provide estimates. The issue is that E(ρ_ij) becomes complex except under the null. However, it would be straightforward to do estimation under maximum likelihood, and we are currently working on another paper that does this directly.