Universal area distributions in the monolayers of confluent mammalian cells

Abstract

When mammalian cells form confluent monolayers completely filling a plane, these apparently random “tilings” show regularity in the statistics of cell areas for various types of epithelial and endothelial cells. The observed distributions are reproduced by a model which accounts for cell growth and division, with the latter treated stochastically both in terms of the sizes of the dividing cells as well as the sizes of the “newborn” ones – remarkably, the modeled and experimental distributions fit well when all free parameters are estimated directly from experiments.

Monolayers of cells – commonly epithelial and endothelial – are the simplest tissues in multicellular organisms [1]. In development, more complex tissues are formed as a result of movement, rearrangement and deformation of cell monolayers [2]. In the human body, cell monolayers line body cavities and serve as a physical and selective barrier between the exterior and the interior. These cellular structures have several unique and important characteristics. Because they have to withstand externally applied forces, their elastic modulus – owing to the existence of specialized cell-cell junctions – is much higher than that characterizing individual cells [3]. Under special circumstances (wound healing, cancer metastasis, embryogenesis) cell monolayers may display collective cell migration [4], during which intercellular forces are propagated cooperatively through cell-cell junctions across large distances spanning several cell diameters, and each cell in the monolayer migrates such as to minimize local intercellular shear stress [5]. Given all these properties, it is not surprising that considerable effort has been devoted to understand and quantify organization of cells within monolayers, though the accuracy of mathematical models proposed has been limited [6–8]. Here, we combine experiments with theory to model distributions of cell areas of confluent monolayers of both epithelial (rat kangaroo kidney cells, PtK1; Madin-Darby canine kidney cells, MDCK; human breast epithelial cells, MCF10A; Chinese hamster ovary, CHO, epithelial-like cells) as well as endothelial (cow pulmonary aortic cells, CPAE; porcine pulmonary artery endothelial cells, PPAEC) cells. As we show, monolayers of all cell types fit well the same monomodal and skewed cell-area distribution. The master equation describing the emergence of this distribution accounts for the cell growth and division, where the latter – based on experimental observations – is treated stochastically both in terms of the sizes of the dividing cells as well as the sizes of the “newborn” ones. With other parameters also derived directly from experiments, this model reproduces faithfully the area-distributions, both for cell monolayers that are unconstrained as well as for those forming within bounded regions (here, micropatterned islands).

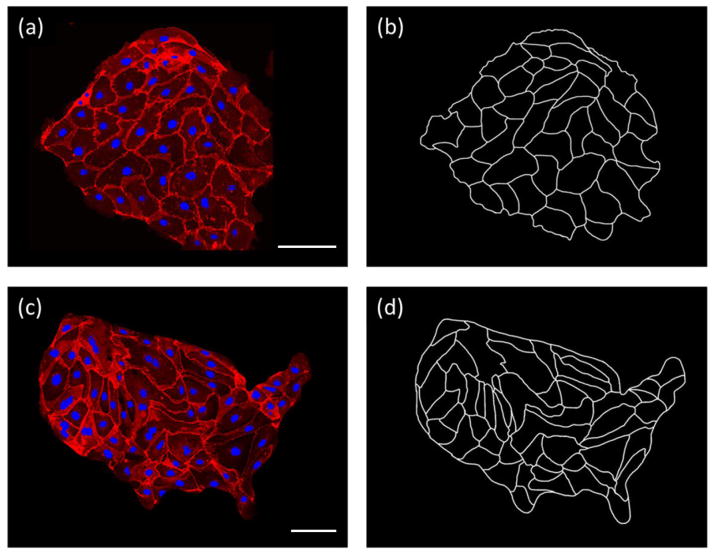
In a representative experiment, epithelial PtK1 cells, widely studied in mitosis investigations [1], were plated on a glass slide covered with a cell-adhesive substrate of extracellular matrix glycoproteins, either fibronectin or laminin (for all technical details, see SI). After plating at intermediate density and after three days from plating (roughly the time for reaching confluence), the cell layers were fixed and, to facilitate detection of their contours, were stained using an antibody to E-cadherin, a protein found at the periphery of cells and responsible for forming adherens junctions. Nuclei were also dyed (with Hoechst 33342) for easy visualization and dual-wavelength fluorescent (confocal) microscopy (on Nikon A1 system) was used to image the two-dimensional cell layers. Figure 1(a) shows an example of such a layer; Figure 1(b) has the corresponding black-and-white contours. These contour images were digitally traced and analyzed by a house-written Processing Java script (available from the authors upon request) to extract the areas of individual cells from which probability distribution functions were then constructed.

FIG. 1.

Unpatterned and “USA” patterned cells and their traced contours. (a) Unpatterned glass slides plated with PtK1 cells. Cell nuclei were dyed blue and cell borders were visualized using a fluorescent antibody to E-Cadherin (red). Scale bar is 100 μm. (b) Cell borders were traced to obtain a binary image for image processing. (c) A PtK1 confluent layer grown on a micropatterned island whose shape corresponds to the continental U.S.A. Scale bar is 100 μm. (d) The corresponding digitized image.

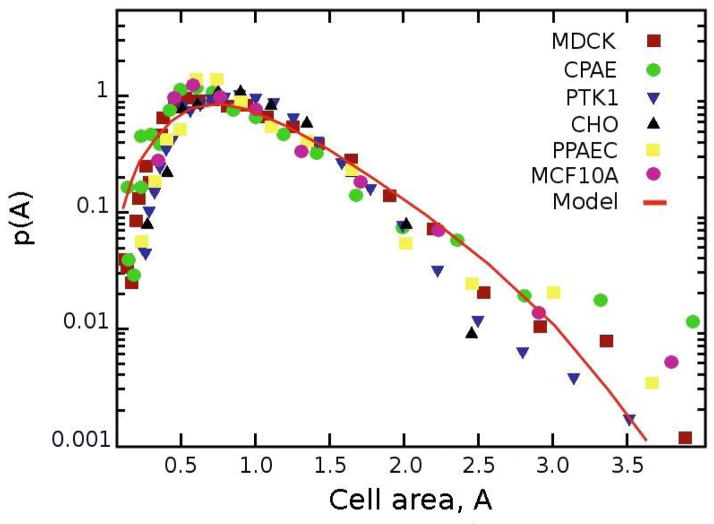
We collected statistics comprising N_PtK1 = 1484 PtK1 cells from 25 independent experiments and plotted normalized distributions of cell areas (blue triangle markers in Fig 2) on glass substrates. In addition, we conducted analogous experiments with CPAE endothelial cells (N_CPAE = 1187 cells analyzed) and with MDCK epithelial cells (N_MDCK = 1634). The statistics from these experiments correspond to, respectively, green-circle and brown-square markers in Fig. 2. Furthermore, publicly available images for three additional epithelial/endothelial cell types were analyzed for comparison: CHO (N_CHO = 226) taken from reference [9], MCF10A (N_{MCF 10A} = 190) from [10], and PPAEC (N_PPAEC = 403) from [11].

FIG. 2.

Distributions of cell areas from unpatterned monolayers on glass substrates. Markers give the probability distributions based on the experimental data (numbers of cells: N_PtK1 = 1484, N_CPAE = 1187, N_MDCK = 1634) and images of cell monolayers found in the literature (N_CHO = 226, N_{MCF 10A} = 190, N_PPAEC = 403). Cell areas are non-dimensionalized with respect to the average area of a cell in a monolayer, A_ave. The line is based on the steady state model described in the main text with parameters derived directly from experiments (with μ = 0.7, σ = 0.5, non-dimensionalized cell areas A_max = 7.0, A_min = 0.4, and g = 0.5 hr⁻¹).

Also, given recent interest in studying behavior of groups of cells on micropatterns [12–14] we also investigated whether confinement of the cell layers influenced the distributions of cell areas. To this end, PtK1 (N_PtK1 = 713) cells were plated on relatively large (~500 μm across) islands etched in thin gold-on-glass layers by the Wet Etching technique (see SI and [15–18]). Figure 1(c) shows an example of cells on an island having a shape of the mainland U.S. (chosen as an example of a shape with irregular boundary conditions); the corresponding contour plot is shown in Fig. 1(d). As illustrated by the quantification in Fig. S2, confinement of the monolayer had no measurable effect on its cell area distribution.

Taken together, the above data indicate that the area distributions for all cells types are similar – with heavy tails clearly visible on the semi-log plot – suggesting that the same process determines the evolution and morphology of the cellular patterns.

To understand the process mathematically, we developed a model accounting for the growth and division of cells within the monolayer. Specifically, we considered the evolution of a collection of cells which 1) grow at a rate, g, approximated as constant (this is a simplifying assumption) since the cells grew in size during early stages of monolayer formation such as studied here (see also [21]), and 2) divide with a certain probability, B(A), which depends on the cell size, A, and is discussed in more detail below. In addition, when a cell divides into two, the sizes of these progeny cells are determined according to a certain probability, R(A). With these assumptions, the dynamics of the number of cells in a monolayer having size A at time t, n(A,t), is given by the following differential equation:

$$\frac{\partial n(A,t)}{\partial t}=-g\frac{\partial n(A,t)}{\partial A}-B(A)n(A,t)+2R(A){\int }_0^{\infty }B(A^{\prime })n(A^{\prime },t){dA}^{\prime }.$$ (1)

The meaning of terms on the right-hand side of this equations is as follows: The first term describes the growth of cells with constant growth rate, g = dA / dt. The second term gives the number of cells that “disappeared” due to cell division at time t. The third term gives the number of cells “produced” by cell division. In this term, the integral has the total number of cells which divided, the factor of two denotes that each of these cells divided into two progenies, and function R(A) (see later in the text) quantifies the probabilities that the newly divided cells have a certain area A. The framework of this model is mean-field in the sense that it does not explicitly take into account the sizes/divisions of neighboring cells – this assumption simplifies the equations and is justified by the agreement of the model with experimental data. The steady-state solution n_st (A) – that is, a solution for dn / dt = 0 – satisfies the following first-order ordinary linear differential equation:

$$\frac{{dn}_{st}(A)}{dA}=\frac{B(A)}{g}{n}_{st}(A)-\frac{2R(A)}{g}\underset{0}{\overset{\infty }{\int }}B(A^{\prime })n_{st}(A^{\prime }){dA}^{\prime }.$$ (2)

Noting that the integration, $\underset{0}{\overset{\infty }{\int }}B(A^{\prime })n_{st}(A^{\prime }){dA}^{\prime }$, yields a constant, we can solve for the steady state distribution to obtain:

$$n_{st}(A)\propto \underset{0}{\overset{A}{\int }}{dA}^{\prime }R(A^{\prime })exp\left[\frac{-1}{g}\underset{A^{\prime }}{\overset{A}{\int }}d{A}^{″}B(A^{″})\right].$$ (3)

This analytical expression holds for arbitrary functional forms of B(A) and R(A). Unlike some previous models [7,8], it does not propose the steady state distribution ad hoc and describes an entire distribution (and not only division-size distribution). In our calculations, we chose R(A) as Gaussian,

$$R(A)=\frac{1}{\sigma \sqrt{2\pi }}exp\left[-\frac{{(A-\mu )}^2}{2{\sigma }^2}\right],$$ (4)

where μ and σ denote, respectively, the average size and variance of the newly-born cells – these parameters were determined from experiments (data not shown) and supported by the work of Sung et al. [22]. Next, our function B(A) does not prescribe cell division as always occurring at the same critical cell size. In experiments, cells divide over a range of sizes but with only a small fraction growing significantly larger than others before division takes place – this means that the probability of division increases rapidly with increasing cell size [22,23]. To account for this, we prescribe the likelihood of cell division as monotonically increasing with cell area. One convenient way, but not crucial to the ultimate predictions of the model, is to take

$$B(A)=exp\left[\frac{A-A_{\mathit{max}}}{A_{\mathit{max}}-A_{\mathit{min}}}\right],$$ (5)

where A_max is the maximal cell area below which the cells always divide, and A_min is the minimal cell area the cells need to have before we observe their division. These parameters come directly from experiments and give A_max = 7.0 and A_min = 0.4, where the specific values are non-dimensionalized by the average area of a cell in the monolayer, A_ave. With these preliminaries, the probability distribution, p(t,A), can be calculated as

$$p(t,A)=\frac{n(t,A)}{\underset{0}{\overset{\infty }{\int }}n(t,A)dA}.$$ (6)

The red line in Fig. 2 shows the numerical solution after the cells reached a steady state starting at time t = 0 from the normal distribution, R(A). Importantly, the solution uses experimental, not fitted, values of μ = 0.7 and σ = 0.5 (from the analysis of seven independent samples; values non-dimensionalized by A_ave, see also [22]). Furthermore, the average growth rate, g = 0.5 hr⁻¹ was derived from imaging the dynamics of PtK1 cells over the period of 48 hrs. As seen in Fig. 2, the predictions of the model agree with the experimental distributions well for all cell types we studied.

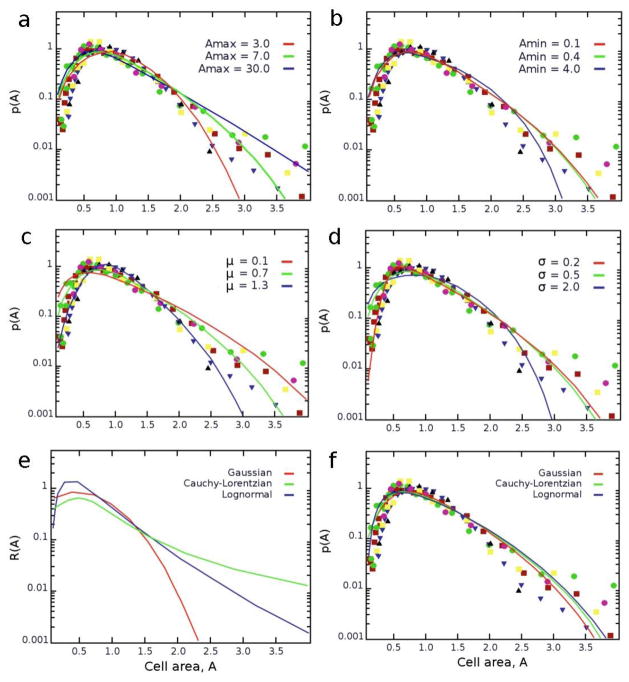
Although the model uses strictly defined biological parameters and no fitting, it is instructive to consider how the steady-state solutions would vary if these parameters were changed. For instance, when the probability of cell division, B(A), is changed by increasing A_max, the maximum of p(A) shifts to lower cell areas, while the overall probability distribution becomes more positively skewed, exhibiting a heavier tail (Fig. 3(a)). On the other hand, changing A_min has relatively small effect on p(A), slightly reducing the distribution’s breadth at its tail (Fig. 3(b)). For the parameters in the Gaussian R(A) controlling the areas of dividing cells, increasing μ reduces the positive skewness of p(A) while shifting its maximum to higher values (Fig. 3(c)); similar effects are observed for increasing values of σ albeit in this case the distribution also broadens slightly (Fig. 3(d)). Finally, regarding the choice of the functional form of R(A), we also considered two other popular distributions as plausible alternatives: lognormal (with the mean μ and standard deviation σ of the variable’s natural logarithm set equal to the values of the Gaussian distribution) and Cauchy-Lorentzian (with the median equal to that of the Gaussian, and half-width at half-height equal to the standard deviation of the Gaussian; since the mean and standard deviation for the Cauchy-Lorentzian cannot be finite). Although these distributions differ significantly from the Gaussian in equation (4) (Fig. 3(e)), they lead to very similar distributions p(A) (Fig. 3(f)). In other words, the distribution of cell areas is largely insensitive to the specific choice of the function R(A) prescribing the sizes of newly divided cells.

FIG. 3.

Dependence of the steady state distributions on various parameter values (a) A_max (b) A_min defining function B(A); (c) μ and (d) σ defining function R(A). The plot in (e) has three continuous probability distributions tested for the robustness of R(A). (f) All three distributions lead to very similar distributions of cell areas, p(A).

Two other comments about the model are due. First, we note that there is no simple relationship between the shapes of cell boundaries and the locations of the nuclei within these cells. This is relevant given that several prior works [24–26] suggested that for confluent cells, their boundaries correspond to the so-called Voronoi tessellations [27] with the centers of Voronoi polygons at the geometric centers of the cells’ nuclei. Although such a result would be appealing (see SI), our results summarized in the supplementary Fig. S1 in the SI evidence that it generally does not hold. The second point to make is that the distributions p(A) we derive are similar in shape to lognormal (which, incidentally, rationalizes why the distributions for all cells can be rescaled by A_ave). In fact, in an upcoming paper [28] we show that these lognormal shapes are not a coincidence but that under certain conditions, processes of birth, growth and division tend to the steady-state approximating lognormals faithfully. However, the equations we derive here link p(A) to the experimental, biologically relevant parameters determining the process (e.g., growth rate, division probability), whereas fitting the lognormal does not tell us (i) how and why the steady-state distribution emerges and (ii) its parameters μ and σ cannot be directly linked to the underlying cell behaviors.

The general conclusion of this work is therefore that the morphology of epithelial or endothelial cell layers is determined by a process of cell growth and division, with the latter being a stochastic process allowing for the variability in the sizes of the dividing cells. A mean field approach neglecting details of cell-cell interactions is sufficient to explain the emergence of a heavy-tailed distribution that is robust to the model’s parameters (notably, different functions describing stochastic cell divisions) and is conserved across multiple epithelial and endothelial mammalian cell lines.