Magnetic Resonance Based Electrical Properties Tomography: A Review

Abstract

Frequency-dependent electrical properties (EPs; conductivity and permittivity) of biological tissues provide important diagnostic information (e.g. tumor characterization), and also play an important role in quantifying radiofrequency (RF) coil induced Specific Absorption Rate (SAR) which is a major safety concern in high- and ultrahigh-field Magnetic Resonance Imaging (MRI) applications. Cross-sectional imaging of EPs has been pursued for decades. Recently introduced Electrical Properties Tomography (EPT) approaches utilize the measurable RF magnetic field induced by the RF coil in an MRI system to quantitatively reconstruct the EP distribution in vivo and non-invasively with a spatial resolution of a few millimeters or less. This paper reviews the Electrical Properties Tomography approach from its basic theory in electromagnetism to the state of the art research outcomes. Emphasizing on the imaging reconstruction methods rather than experimentation techniques, we review the developed imaging algorithms, validation results in physical phantoms and biological tissues, as well as their applications in in vivo tumor detection and subject-specific SAR prediction. Challenges for future research are also discussed.

I. INTRODUCTION

The electrical properties (EPs), which consist of the conductivity and the permittivity, largely vary as a function of the relative intracellular and extracellular fluid volumes and ionic concentrations, and the cellular membrane extent in the tissue, respectively [1]–[3]. EPs values also vary as a function of the frequency of applied electromagnetic (EM) wave. It was reported that malignant tissues differ from normal tissues (brain, breast, skin, prostate, liver, bladder etc.) in EPs, generally attributing to the different water content in neoplastic tissue due to the variation of protein hydration and vascularization, as well as to the membrane permeability, amount of extracellular fluid, packing density and orientation of the malignant cells [4]–[7]. Experimental results have shown that cancerous tissues have significantly higher EPs values than normal tissues over a wide electromagnetic frequency spectrum, e.g., >200% for breast cancer and >100% for bladder cancer via ex vivo measurement at radio and microwave frequencies [8]–[17]. At the same time, while in some cases it is impossible to discriminate the malignance from tumors with conventional Magnetic Resonance (MR) techniques, statistically significant EPs differences between cancerous and benign tissues were reported in ex vivo measurements, e.g. basal cell carcinoma vs. benign nevi, and prostate cancer vs. benign prostatic hyperplasia at radio frequencies [18]–[21]. These data suggest that development of an imaging modality for mapping electrical properties with a high spatial resolution and high specificity will have a significant impact on detection and diagnosis of cancer, and may thus improve substantially survival rate of cancer patients.

In the meantime, high- and ultrahigh-field (HF and UHF: 3 Tesla and above) MRI has been pursued with increasing interest and potentially wide clinical applications. The advantages of using HF or UHF MRI include the promise of improved signal-to-noise ratio (SNR), higher spatial resolution and increased sensitivity for contrast mechanisms such as the blood-oxygenation-level-dependent (BOLD) contrast [22]. However, elevated thermal effects due to tissue heating accompany with increased main magnetic field strength, posing a safety concern in HF-MRI applications [23]. Specific Absorption Rate (SAR) is directly related to RF-induced heating [24]; absence of quantification of local SAR values on a subject-specific basis yields a worst-case safety limit in current MRI RF power transmission, and, as a consequence, may compromise the underlying improved SNR and image contrast associated with high field MRI [25]. EPs distributions play a fundamental and important role in SAR calculation in HF-MRI – a reliable calculation of local SAR hot spots necessitates the knowledge of local tissue EPs values at the operating radiofrequency (RF) [24]. Therefore, real-time and subject-specific EPs imaging is highly desirable for SAR quantification and for the purpose of constraining tissue heating in pulse sequence design in HF-MRI applications.

There have been a number of research efforts attempting to non-invasively image EPs of biological tissues in the past decades. 1) Electrical Impedance Tomography (EIT) inversely reconstructs impedance images from electric potential measurement induced by current injection through surface electrodes [13], [26], [27]. Its merits include low cost, simplicity of application and high speed of data collection, while the major limitation lies in its poor spatial resolution due to a limited amount of measured data and the ill-posedness of the corresponding inverse problem involved in image reconstruction. 2) Magnetic Induction Tomography (MIT) uses the interaction of an oscillating magnetic field with conductive media, and the EPs can be reconstructed from the measurements of perturbed magnetic field outside the object [28], [29]. However, similar to EIT, the surface measurements and ill-posedness of the inverse problem result in low spatial resolution. 3) Magnetic Resonance Electrical Impedance Tomography (MREIT), which originates from Magnetic Resonance Current Density Imaging (MRCDI) [30], [31], measures the local magnetic field induced by surface current injection, and reconstructs static cross-sectional conductivity images [32]–[35]. While MREIT provides high spatial resolution, what remains to be demonstrated includes the safety issues due to the usage of high level of current injection in order to achieve sufficient SNR, and the shielding effect due to the use of surface electrodes for current injection. 4) In Hall Effect Imaging (HEI), the sample is located in a static magnetic field with current injection through surface electrodes. The sample will emit acoustic waves which are collected around the object and processed to reconstruct images related with the conductivity of the tissues [36]. While HEI has the potential to obtain high resolution images, it remains to be demonstrated of its ability to quantitatively reconstruct conductivity distribution and to overcome the shielding effect. 5) Magneto-acoustic Tomography with Magnetic Induction (MAT-MI) exploits the Lorentz force effect due to the interaction of a magnetic field and eddy current induced by a time varying magnetic field, and emitted acoustic waves are collected by ultrasound transducers in proximity to the object surface for conductivity image reconstruction [37]–[39]. Current MAT-MI experimental studies focus on gel phantoms and tissue samples, and there have been no in vivo experiments reported so far.

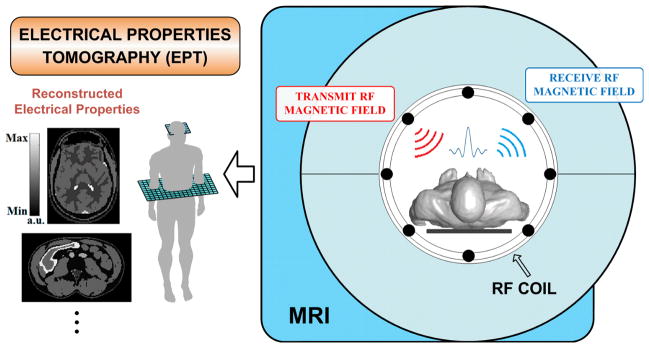
By employing Maxwell’s Equations that govern electromagnetic fields, MR based Electrical Properties Tomography (EPT) utilizes measurable RF-coil-induced magnetic fields (B₁ fields) in an MRI system to quantitatively reconstruct the local EPs of biological tissues. The concept of imaging EPs from MR signals was firstly suggested by Haacke et al. [40]: the wavelength of the RF radiation was of the order of the body size, leading to a distortion of the B₁ field inside the irradiated object; by using certain imaging algorithm, the EPs can be estimated using MRI images which reflect the disrupted RF profile. Wen [41] later pointed out that the perturbation of the RF field in high-field MRI directly related to the conductivity and permittivity distribution, which can be explained by electromagnetic wave equation. In recent years, EPT has drawn considerable attention by various research groups. Based upon B₁-mapping techniques in MRI measuring induced B₁ field distributions, various MR-EPT methods have been proposed using different coil designs (e.g. birdcage quadrature, multi-channel transceiver) and at different radio frequencies (64MHz~300MHz) of the operating static main field (1.5T~7T) [42]–[53].

Figure 1 shows the conceptual diagram of EPT approach. Differing from other noninvasive EPs imaging techniques, e.g. EIT or MREIT, EPT requires no electrode mounting, and no additional external energy is introduced into the body during an MRI scanning other than the inherent B₁ fields. Meanwhile, unlike EPs imaging technologies involving acoustic coupling, e.g. HEI and MAT-MI, applied B₁ fields could easily penetrate into most biological tissues, making EPT suitable for whole body imaging. In addition, MR-EPT is performed using a standard MRI system with regular RF coils, and its spatial resolution is determined by MRI images and the quality of the employed B₁-mapping technique.

Figure 1.

Conceptual diagram of Electrical Properties Tomography.

The following sections review the recent cutting-edge development of EPT, from its basic theories in electromagnetism to the most recent research outcomes. We focus our discussions on the mathematical reconstruction methods and inverse imaging algorithms, the validation results, as well as applications in in vivo tumor detection and subject-specific SAR estimation.

II. MAPPING RF-COIL-INDUCED MAGNETIC FIELDS

In MRI, there are several types of magnetic fields applied to manipulate the magnetic moments of nuclei in tissues to generate MR signals. Besides the static magnetic field from the main MR magnet (B₀) which aligns nuclear spins along itself under the equilibrium state, the RF magnetic field (B₁) induced by the RF coil, which oscillates at the Larmor frequency of the target nuclei, reorients the net nuclear magnetization of the spins so that a MR signal can be induced and detected by the receive coil. In principle, the effective B₁ fields consist of two components: transmit B₁ (denoted as $H_1^{+}$ in this paper), the effective RF magnetic field to induce flip angle of nuclear spin procession, rotating in the same direction of spin procession; receive ${\mathrm{B}}_1(H_1^{-})$, rotating in the opposite direction, also perceived as the receive sensitivity of a receive coil to pick up MR signal. Figure 2 shows vector plots of both B₁ components on an axial plane when, a quadrature volume coil is used (upper row), or a multi-channel transceiver array is used with a single channel for RF power transmission and signal reception (lower row). Note that in RF electromagnetism regime, both magnetic and electric fields generated by the RF coil are complex quantities with magnitude and phase oscillating at the Larmor frequency [54]–[56].

Figure 2.

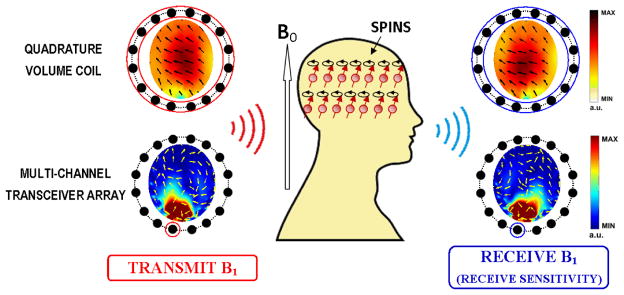
B1 field components on a transverse plane, when using a quadrature volume coil (3T; upper row) and a multi-channel transceiver array (7T; bottom row) for head imaging. In the transceiver array, a single coil element is used for RF power transmission and signal reception. Color maps indicate the magnitude of complex B1 fields, while arrows represent their phase variations in space (real part in horizontal direction vs. imaginary part in longitudinal direction).

The effect of the B₁ fields on the magnetization of spins and received MR signals can be traced separately to their magnitude and phase. For regular RF pulses at Larmor frequency on resonance, the flip angle of the magnetization from B₀ direction is proportional to the magnitude of the locally transmit B₁ field, while the received MR signal intensity is further weighted by the magnitude of receive B₁ sensitivity, and phase of the complex MR signal is the accumulative phases of both transmit and receive B₁ fields – which is also known as the transceiver phase – and other B₁-independent phase components such as imperfect gradient profile, B₀ variation, chemical shift, etc. Both the excitation of the nuclear magnetization and the reception of signal intensity rely on interactions between applied RF magnetic fields and local electrical properties that can be described by Maxwell’s Equations. Therefore, knowing B₁ fields can provide a tangible step towards EPs imaging; feasible and practical B₁-mapping methods have served as the groundwork in EPT studies. On one hand, various B₁-mapping methods have been proposed to measure the magnitude of B₁ components (especially for transmit B₁ component), such as using multiple acquisitions with different flip angles of spins [57], [58], applying identical RF pulses followed by two delays of different repetition times (TRs) [59], utilizing phase-sensitive means based on composite RF pulses [60] or on the Bloch-Siegert phase shift [61], and employing stimulated echoes acquisition mode (STEAM) in multi-pulse sequences [62], [63] or in a single sequence followed by a tailored gradient echo train [64]. On the other hand, there is no direct measurement to quantitatively obtain the absolute phase distribution of the transmit or receive B₁ field. Instead, the phase information carried in the MR signal phase can be used to infer the absolute phase as will be introduced later in this review.

III. RECONSTRUCTION METHODS

A. Fundamental Electromagnetism Equation

The fundamental theory of EPT is derived from the physical relationship between the distribution of the object’s electrical properties and wave propagation of the RF-coil-induced EM fields, as described in Maxwell’s Equations. We assume the main magnetic field of the MR scanner is oriented in the Z-direction, and consider the magnetic permeability inside biological tissues to be equal to that in vacuum. The RF fields excited in MRI coils at the Larmor frequency of protons can be treated as time-harmonic EM fields [65], [66]. It is also assumed, as in most existing EPT researches, that the electrical properties of the object of interest are isotropic; there have been a few studies investigating EPs anisotropy at Larmor frequency [67], [68], which are beyond the scope of this review. The core equation of EPT, which directly links EPs and RF-coil-induced magnetic fields, can be obtained by combining the Ampere’s Law and Faraday’s Law as

$$-{\nabla }^2\mathbf{H}={\omega }^2{\mu }_0{\epsilon }_c\mathbf{H}+(\nabla {\epsilon }_c/{\epsilon }_c)\times (\nabla \times \mathbf{H})$$ (1)

where H is the RF-coil-induced magnetic field strength vector in the Cartesian coordinate, ω the operating angular frequency (Larmor frequency), ε_c = ε_r ε₀ − iσ /ω the complex permittivity as a function of the electrical conductivity σ and the relative permittivity ε_r, ε₀ and μ₀ are the free space permittivity and permeability, respectively.

Eq. (1) provides a theoretical expression of electromagnetic wave equation by directly linking EPs and RF-coil-induced magnetic fields, and thus it serves as the fundamental equation in EPT. Eq. (1) can be simplified according to various assumptions in terms of 1) the spatial variation of EPs and/or 2) spatial RF magnetic field distributions. Although distribution of the Cartesian components of the RF magnetic fields cannot be measured straightforwardly in MRI, the principle of reciprocity [54] links transverse RF magnetic field components in Cartesian and rotating frames. Therefore, the classic EPT problem lies in the course that: simplified Eq. (1) is re-formalized into B₁ terms, i.e. $H_1^{+}$ and/or $H_1^{-}$, through which EPs can be computed from measurable information of $H_1^{+}$ and/or $H_1^{-}$ distributions, as discussed below.

1. By assuming the EPs distribution is locally homogeneous, Eq. (1) can be simplified and re-organized into the Helmholtz Equation as

   $$-{\nabla }^2{H}_1^{+}={\omega }^2{\mu }_0{\epsilon }_c·H_1^{+}$$ (2)

   in which absolute EP values can be directly computed via the fraction derived from measured B₁ fields [40]–[42].

2. The spatial variation of EPs distribution is considered. Other than EP values themselves, which are taken into account only as in Eq. (2), Eq. (1) is further expanded with terms of EPs’ gradients as below

   $$\begin{array}{l}-{\nabla }^2{H}_1^{+}={\omega }^2{\mu }_0{\epsilon }_c{H}_1^{+}-(\partial H_1^{+}/\partial z)[(\partial {\epsilon }_c/\partial z)/{\epsilon }_c]\\ -(\partial H_1^{+}/\partial x-i\partial H_1^{+}/\partial y)[(\partial {\epsilon }_c/\partial x+i\partial {\epsilon }_c/\partial y)/{\epsilon }_c]\end{array}$$ (3)

   in which the curvature of RF-coil-induced H_z is assumed negligible within coils, e.g. birdcage, transverse electromagnetic (TEM) and microstrip coils, and only the transverse components of RF magnetic fields are taken into account as in [43], [50]. The unknown EPs information, shown as terms associated with ε_c in Eq. (3), can be calculated through solving the linear equations formed by multiple $H_1^{+}$ measurements.

B. In Consideration of Measurable RF Magnetic Fields

I) Quadrature Coil Application with Transceiver Phase Assumption

Measurement of $H_1^{+}$ magnitude – $\left|H_1^{+}\right|$– has been well-established [59], [61], [62], [64], [69], while there has been so far no generic means for $\left|H_1^{-}\right|$ measurement. In the meantime, using a quadrature volume coil, absolute $H_1^{+}$ phase – arg( $H_1^{+}$) – can be roughly assumed as half of the transceiver phase [41], [42], that can be obtained from MRI phase image by using refocusing pulse, e.g. spin echo (SE) sequences [44], and by manually removing residual phase components resulted from, e.g., ΔB₀ and gradient-field-induced eddy currents [46]. As such, with retrieved $H_1^{+}$ complex information, EPs distribution can be directly reconstructed via Eq. (2). Note that Eq. (2) can be separated into real and imaginary parts, and the conductivity and permittivity can be expressed in the form of $\left|H_1^{+}\right|$ and arg( $H_1^{+}$); it has been found that, to the leading order, the conductivity mainly affects the phase distribution of B₁ fields, while the permittivity mainly affects the magnitude distribution of B₁ fields [41], [44], [49].

II) Multi-channel Transmit Coil Application with B₁ Phase Deduction

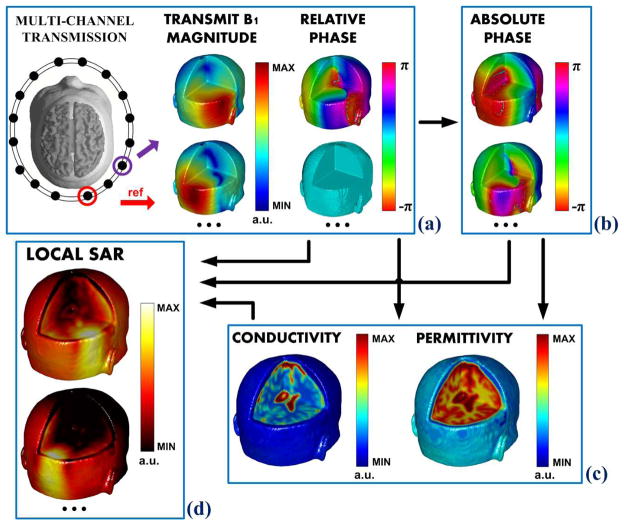
By using a multi-channel transceiver array, employing B₁- mapping methods, e.g. hybrid B₁-mapping technique (merging large and small flip angle data for B₁ mapping) [59], [70]– [73], absolute B₁ phase computation can be attained: abundant B₁ information, i.e. measurable magnitude of $H_1^{+}$ and $H_1^{-}$ for individual coil element, as well as their relative phase maps between each coil element, can effectively facilitate their absolute phase deduction, so to consolidate subsequent calculations of EPs and/or local SAR. This concept was firstly introduced in [47], [49]. By using simulation data on a realistic human head model, Figure 3 shows the generalized flowchart: using multi-channel transmission, the magnitude and relative phase distributions can be measured for each coil element as illustrated in Fig. 3(a), then their absolute phase can be computed as in Fig. 3(b), and finally the electrical properties can be reconstructed as in Fig. 3(c), while all measurable and retrieved information lead to the ultimate local SAR estimation for each coil element as in Fig. 3(d).

Figure 3.

A flowchart of EPT problem when using a multi-channel transceiver array. Taking a reference channel, (a) the magnitude and relative phase distributions can be measured for each coil element, then (b) their absolute phase can be computed, and (c) the electrical properties can be reconstructed. Ultimately, utilizing all measurable and retrieved information, (d) local SAR for each coil element can be estimated.

As reported in [47], [51], [74], Eq. (2) was the central equation in absolute B₁ phase retrieval and the subsequent EPs reconstruction. In [74], measurable proton-density-biased $\left|H_1^{-}\right|$ is taken into account, and the phase and EP values can be directly reconstructed altogether – this approach has been named as Local Maxwell Tomography (LMT).

Unlike above approaches which assume locally-homogeneous EPs distribution and may introduce artifacts in the vicinity of tissue boundaries in reconstructed EPs maps, in [49] Gauss’s Law has been employed, utilizing the continuously differentiable nature of the magnetic field vector in space, in order to retrieve the absolute phase of $H_1^{+}$ and $H_1^{-}$. The retrieved phases were applied consequently to reconstruct EPs via Eq. (3) [50], removing the piece-wise homogeneous assumption and thus providing a practical way to study complex anatomical structures. Note that to apply Gauss’s Law necessitates the knowledge of $\left|H_1^{-}\right|$; nevertheless, proton density can be estimated on fairly left-right symmetric anatomical structures, e.g. the human brain, about the sagittal plane through the object center [49], [72].

More recently, evolving from Eq. (3), a gradient-based EPT (gEPT) approach was introduced to reconstruct EPs from the estimated gradient of EPs [75]. The central equation of gEPT is

$$\{\begin{array}{l}{\nabla }^2{H}_1^{+}=-{\omega }^2{\mu }_0{H}_1^{+}{\epsilon }_c+{(\nabla H_1^{+})}^T\left[\begin{array}{ccc}1& i& 0\\ -i& 1& 0\\ 0& 0& 1\end{array}\right](\nabla ln{\epsilon }_c)\hfill \\ {\nabla }^2{H}_1^{-}=-{\omega }^2{\mu }_0{H}_1^{-}{\epsilon }_c+{(\nabla H_1^{-})}^T\left[\begin{array}{ccc}1& -i& 0\\ i& 1& 0\\ 0& 0& 1\end{array}\right](\nabla ln{\epsilon }_c)\hfill \end{array}$$ (4)

Eq. (4) can be further decomposed into variables including 1) aforementioned known (measurable) variables such as B₁ magnitude and relative phase, 2) unknown variables such as ε_c, ∇lnε_c, as well as absolute B₁ phase. Utilizing measured multiple B₁ data sets, a set of linear equations can be formed to derive the gradient ∇ lnε_c. Then using a priori information of the electrical properties, e.g. literature-reported ε_c value(s) at one (or several) specific location(s) with known tissue type(s), quantitative maps of ε_c can be determined through spatial integration across the imaging plane. Taking advantage of derived ∇ lnε_c, reduced boundary artifact and improved robustness against noise contamination are anticipated to improve the overall reconstruction performance.

From the perspective of RF coils per se, Eq. (2) based algorithms preserve a generality that they can be implemented on various kinds of coil design, as long as negligible spatial EPs variation pervades locally – dedicated image segmentations such as that in [76] can potentially reduce tissue boundary artifacts in EPT reconstruction. On the other hand, Eqs. (3) and (4) based approaches work well on coils with strip element design (e.g. birdcage, TEM and microstrip coils), in which the spatial variations of RF-coil-induced H_z have been much restrained and thus are reasonably assumed to be negligible compared to those of H_x and H_y.

C. Local SAR Estimation

Local SAR is defined by:

$$\text{SAR}=\sigma ({\left|E_x\right|}^2+{\left|E_y\right|}^2+{\left|E_z\right|}^2)/2\rho$$ (5)

where E_x, E_y and E_z are Cartesian components of the RF-coil-induced electric fields, and ρ is material mass density [24], [77], [78]. Note that, by far, the absence of a practical Bz-mapping method – measuring the z-component of RF-coil-induced magnetic fields that does not contribute to nuclear precession – limits the computation of the full components of RF-coil-induced electric fields, and only E_z component can be calculated theoretically from measured/estimated transverse components of RF magnetic fields (B₁) via Ampere’s Law. As a consequence, it constrains current SAR estimation methods due to incomplete information of the full components of RF electric fields. Nevertheless, for RF coils (e.g. birdcage, TEM and microstrip coils), E_z dominates the electric field due to the coil structure [42], [43], [47], [49], [50], [79], thus only E_z component is considered in local SAR estimation. Since local E_z can be derived as a function of $H_1^{+}$ and $H_1^{-}$ according to Ampere’s Law, measuring/estimating the complex B₁ distribution and reconstructing EPs values through the course of EPT calculation allow for efficient estimation of subject-specific and real-time local SAR [50].

IV. EXPERIMENT STUDIES: A HISTORIC REVIEW

A. Phantom Validations

The first phantom validation has been conducted on 1.5T and 4.7T MRI machines as reported in [41]. With the mapping of $\left|H_1^{+}\right|$ and transceiver phase, by utilizing the transceiver phase assumption, good agreement was reached between known and measured EP values of saline phantoms with different concentrations. The piecewise-homogeneous Helmholtz equation as in Eq. (2) was used as the reconstruction equation. In addition, it has also been shown that the increased wave propagation effects at 4.7T allowed improved spatial resolution and better measurement accuracy compared to 1.5T.

Originating from the Helmholtz equation, the phase-based conductivity imaging and magnitude-based permittivity imaging methods have been proposed, and its feasibility has been tested using a saline phantom on a 1.5T MRI machine equipped with a quadrature head coil [44]. Reasonable experimental results revealed that the phase-based approximation works well in the case of ωε ≪ σ, while magnitude-based approximation suits better when ωε ≫ σ. The simplified method, especially phase-based conductivity imaging, holds promise towards clinical applications due to its potential merits in shortened scan time as well as preserved reconstruction stability.

Built upon above work, fast phase-based conductivity imaging has been tested in a saline phantom to monitor the dynamic change in conductivity along the time course when salt was added during a 1.5T scan. An SSFP (steady-state free-precession) sequence was utilized, and the scan time was reduced from the order of minutes to several seconds. The real-time reconstruction results preserve good quality [80]. An extensive study has been conducted to further investigate the effect of B₀ strength for Helmholtz-based EPT at 1.5, 3 and 7T on a head-shaped phantom [52], and it was concluded that using Eq. (2) based approach: 1) the transceiver phase assumption is more reliable for lower-field MRI (i.e. 1.5T and 3T) and on object with lower permittivity and with symmetric structure (about the sagittal plane through the center), 2) the phase-based conductivity imaging mainly preserves its feasibility at 1.5T and 3T, and 3) the precision of EPT reconstruction (especially for permittivity) benefits from a higher B₀ strength, which is associated with increased B₁ SNR and more prominent curvature of B₁ distribution (in the consideration of spatial differential computation involved in EPT algorithms).

Using multi-channel transmit technique, Eq. (2) based methods have been tested on single-compartment saline phantoms, and reasonable EPs results [47], [74], [49]–[51] suggest that reliable B₁ phase calculation and EPs reconstruction can be achieved through mathematical deductions, instead of being limited to quadrature coil application which suffers from diminished accuracy of coil-dependent transceiver phase approximation, as well as intrinsic and prominent B₁ inhomogeneity at UHF MRI. Successful implementations with non-quadrature coils would substantially expand the applicability of EPT for future clinical applications.

B. In vivo Brain EPs Imaging

Most in vivo EPT studies have focused on brain imaging of healthy subjects. The first in vivo study was performed in six subjects at 1.5T [44]: average EP values inside regions of interest (ROI), i.e. grey matter (GM), white matter (WM) and cerebrospinal fluid (CSF), showed good agreement with literature values, while up to 15%~20% differences in reconstructed EP results were observed among subjects. The quadrature-dependent transceiver phase assumption was utilized in Helmholtz-based algorithm, and it has been further evaluated in [52] on a single human subject at 1.5T, 3T and 7T: 1) the transceiver phase error was found minimal at 3T and maximal at 7T in the head; 2) elevated reconstructed conductivity was produced at 7T compared with 1.5T and 3T when using phase-based method, while 1.5T and 3T showed inferior permittivity reconstruction results due to higher noise levels observed at lower B₀ field; 3) boundary artifacts were observed in all reconstructed EP maps due to piece-wise homogeneous assumption when employing the Helmholtz-based algorithm.

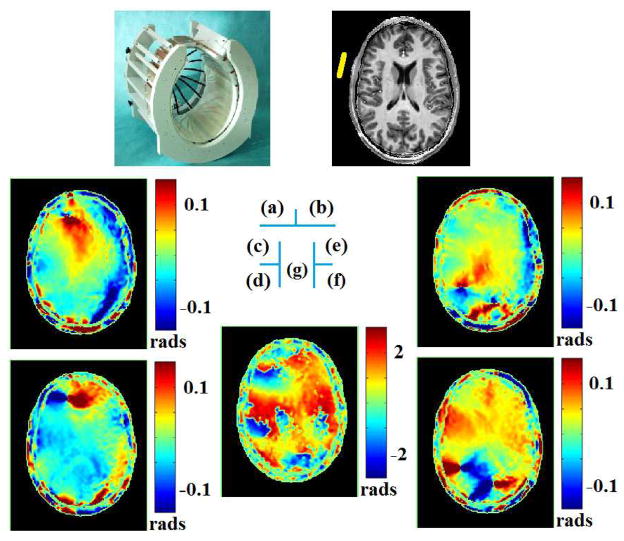
At 7T, the first in vivo human study using multi-channel transceiver technique has been reported in [49], in which aforementioned approximate symmetry nature of human brain and Gauss’s Law-based B₁ phase retrieval method were utilized to estimate the full complex information of B₁. As an example, Figure 4 depicts, on the transverse slice of interest, computed phase gradients of transmit and receive B₁ for a selected reference coil element, as well as their phase difference. Reconstructed EP maps for one subject are shown in [49], and the CSF in the lateral ventricle can be observed in shape, while the average bias and standard deviation for reconstructed conductivity in vivo were 28% and 67%, and 10% and 43% for relative permittivity, respectively. Most recently, employing the same B₁-mapping technique at 7T [70], [71], [81], [82], the gEPT approach based on Eq. (4) has been tested in a human subject, in which ∇lnε _c was derived and further integrated in space to produce in vivo EP maps [75]. Figure 5 [75] presents the reconstructed maps of conductivity as in Fig. 5(b) and permittivity in Fig. 5(c), both exhibiting clear anatomical boundaries and brain structures in comparison with the T1-weighted image shown in Fig. 5(a). Reconstructed EP values are close to literature reported values at 300MHz.

Figure 4.

When using a 16-channel transceiver array (a) for brain imaging, on a human subject, for a selected reference coil element and on the slice of interest (b), computed x- (c) and y- (d) gradients of transmit B1 phase, (e) x- and (f) y-gradients of receive B1 phase, and (g) phase difference between transmit and receive B₁ [49],[50].

Figure 5.

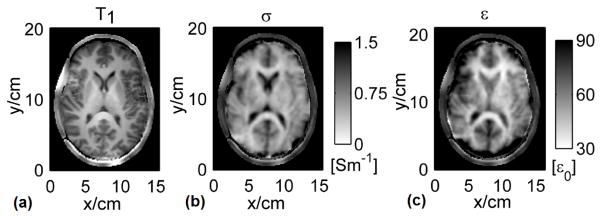
Human results on a transverse slice: (a) the normalized T1-weighted images, (b) reconstructed conductivity and (c) relative permittivity images [75].

By using Eq. (2) based method with quadrature B₁ measurement and transceiver phase assumption, several cases of brain tumors (i.e. brain glioma, grade II and IV astrocytoma) have been studied at 1.5T and 7T, and it was reported with a >150% higher electrical conductivity compared to the surrounding white matter [83], [84]. Twelve patients with primary brain tumor, metastases and resected primary brain tumor have been examined at 1.5T and 3T using SSFP, and several findings have been reported: supratentorial localized primary brain tumors consistently showed higher conductivity than healthy supratentorial white matter, while infratentorial tumors showed lower or equivalent conductivity values compared to healthy infratentorial white matter; phylogenetic older parts, e.g. basal ganglia and the cerebellum, showed higher conductivity compared to the cerebrum as a phylogenetic newer part [85]. A single patient with ischemic stroke has also been studied at 7T, and the reconstructed conductivity showed local increase in the region containing tissues affected by the infarction [86].

C. In vivo Body EPs Imaging

Liver conductivity imaging has been performed over ten healthy subjects during a single breath hold at 1.5T [87] by applying the similar method reported in [80]. Reconstructed results showed good agreement with literature values. Artifacts were presumably attributed to transferred cardiac motion, blood flow and perfusion effects, and may also result from the piece-wise homogeneous assumption applied in Eq. (2).

A single patient with breast cancer was studied at 3T [76]. Considering significant variations in conductivity values among breast tissues, e.g. gland and fat, image segmentation was implemented for shaping the kernel when applying Eq. (2), and parabola-fitting was used to restrain boundary artifacts. As shown in Figure 6 [76], much higher conductivity was found in cancerous tumor, while moderately higher values were found in cysts compared to the surrounding fat. A following study has been conducted over eight patients with breast-containing lesion, including four classified as malignant and four as benign, and significant maxima in suspicious areas were observed: the conductivity of all benign lesions are below ~2–3 S/m, one malignant lesion below ~2 S/m, and the other three malignant tumors exhibited elevated values of up to ~4–6 S/m [88], compared to typical thymus conductivity value of ~0.8 S/m at the operating frequency [1]–[3]. High EP values of breast cancer tissue has also been reported in [89], [90].

Figure 6.

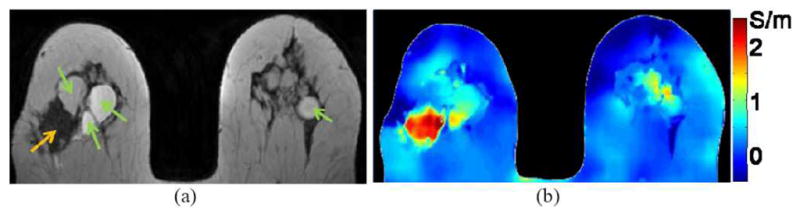
Breast cancer imaging example. (a) TSE image, showing several cysts (green arrows) and tumor (orange arrow). (b) Conductivity of breast shown in (a). Low/medium/high conductivity is found for fat/cysts/tumor, respectively. (From [76] with permission)

D. In vivo SAR Estimation

Using the Helmholtz-based algorithm and transceiver phase assumption, in vivo local SAR mapping using quadrature coil at 1.5T and 3T has been reported in human brain imaging [79]. Estimated local SAR revealed overall similar structure with simulated distribution. Maximum 10-gram average local SAR values showed lower value than those obtained from simulation, e.g. 25–55% lower at 1.5T.

However, elevated energy deposition is intrinsically associated with increased operating frequency, resulting in higher local heating and thus causing a more serious safety concern at UHF. While multiple-channel transmission has been widely recognized in its advantage in B₁ inhomogeneity compensation at UHF, real-time and subject-specific local SAR quantification and management under international safety guidelines are highly desirable to fully unfold its potentials in B₁ shimming or parallel transmission to attain superior MRI images at UHF. Towards this goal, built upon their recent work on complex B₁ imaging [49] and Eq. (3)- based EPT algorithm [43], in vivo single-coil-element local SAR mapping has been recently reported using a multi-channel transceiver array coil at 7T in human brain imaging [50]. Estimated voxel-wise local SAR distributions on two subjects exhibited patterns with reasonable similarity compared with simulation results, as shown in Figure 7 [91], and noticeable differences may result from certain factors in numerical modeling, such as coil coupling, head anatomical structure and assumption of dominant E_z. This approach holds promises for enabling subject-specific local SAR computation which in turn can be used as explicit constraint in B₁ shimming calculation and parallel transmission RF pulse design.

Figure 7.

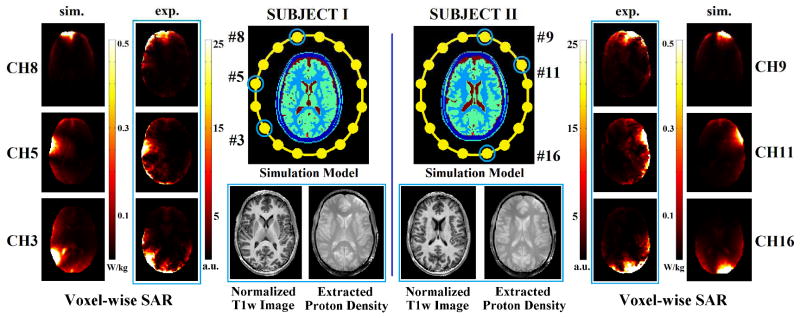
Using a 16-channel transceiver head coil, on two human subjects, normalized T1w images, extracted proton density, and estimated voxel-wise local SAR for selected channels. Simulation results on slices (with similar anatomical structures) shown as references. (Experiment results encircled by blue rectangles) (From [91] with permission)

V. FUTURE PROSPECT AND CONCLUSION

Electrical properties are passive tissue properties. When external electric fields are exerted, electric currents flow and magnetic fields are induced inside the object. Electrical Properties Tomography (EPT) exploits the highly nonlinear relationship between tissues’ electrical properties and resulted RF magnetic fields, reconstructing conductivity and permittivity images through investigating the underlying physical principles, i.e. Maxwell’s Equations and MR physics. Only B₁ maps – the curvature distributions inside the object that can be noninvasively measured in vivo by an MRI scanner – are required for subsequent computations, thus well-posed reconstruction problems can be formulated and hereby high-resolution EP images can be produced. Compared with other EPs imaging technique, EPT has certain advantages including its non-invasiveness, high spatial resolution and superior feasibility for in vivo study. In the past several years, there has been a blossom of EPT studies covering a broad spectrum of investigations over the MRI measurement techniques and correlated inverse algorithms.

Along the development of EPT, more accurate EPs reconstruction has been pursued. Although piece-wise homogeneous assumption can be locally applied after careful manual tissue segmentation, its complexity and performance, when extending EPT to whole body application and over tissues with complicated anatomical structures, deserve further investigation and evaluation [45]. Several studies have devoted efforts focusing on inhomogeneous EPs distribution. For example, methods reported in [49], [50], [75] originate from the Gauss’s Law for magnetism by utilizing the continuously differentiable nature of the magnetic field vector in space, and the spatial variation of EPs distribution is taken into account in the central inverse equation; the recently proposed gEPT approach [75] demonstrates superior performance in in vivo brain EPs imaging, suggesting the high quality of EPs imaging one can anticipate. In the meantime, through simulation evaluations and phantom validations, there have also been several pilot studies to deal with such boundary issues towards refined EP image reconstruction [92]–[95]; whether they can be successfully applied to in vivo studies is yet under investigation. Future works are needed to develop generic EPT algorithms, which should be independent of anatomy structure, RF coil design, and B₀ field strength.

Local SAR calculation requires frequency-dependent electrical properties of local tissues, as well as locally distorted electric fields – both of which are subject-specific. Differing from other EPs imaging modalities, EPT studies EP values at the operating Larmor frequency, with which the local electric fields can be directly deducted from measured B₁. In addition, unlike external model-based SAR simulation methods that are based on a few human models (i.e., not derived on a per subject basis) and are highly time-consuming, the EPT approach begins with B₁-mapping in vivo, and further calculate EPs and electric fields, overarching all associated quantities on a subject-specific basis, and may also allow for fast real-time SAR calculation. Furthermore, EPT-based SAR estimation can account for positions of subjects relative to the RF coil during an MRI scan, which, on the contrary, is unpredictable in SAR calculation based on computational EM simulation. As documented in [50] and in agreement with [96], significant SAR estimation discrepancies can be introduced with a trivial position offset. This suggests that the EPT based approach, which does not require or rely heavily on accurate 3-D modeling (in terms of model structure and position), preserves certain merits being subject-specific. As reported in [50], in vivo SAR estimation results for brain imaging are encouraging, suggesting real-time local SAR prediction for a specific human subject may be eventually feasible, relying only on measurable B₁ information (i.e., magnitude and relative phase). It is anticipated that future studies will provide generalized estimation of absolute B₁ phase and EPs map, independent of the current assumption of negligible Bz component; and ultimately, full components of RF-coil-induced EM fields can be fully measured/retrieved, furnishing EPT with complete electric fields information towards more accurate and reliable SAR estimation.

Lastly but importantly, B₁-mapping techniques play an important role on the overall performance of EPT in terms of, e.g. image resolution, the reliability and accuracy of reconstruction results. As illustrated above in the method section, a series of mathematical deduction involved in EPT reconstruction steps requires B₁ maps with desirable qualities such as high SNR in the region of interest, minimally biased by various tissue properties (e.g. T1, T2*, proton density, blood flow, etc.), largely robust against chemical shift (i.e. in fat tissue) and body motion. In general, precise B₁-mapping within a practically fast acquisition time deserves relentless pursuing for future promising clinical applications of EPT.

In summary, MR based Electrical Properties Tomography represents an important development in our efforts to map the electrical properties of biological tissues, which promises to have important clinical applications including cancer detection and diagnosis, as well as bettering management of MR safety through subject-specific real time SAR estimation. The establishment of Electrical Properties Tomography may also play a significant role in managing subject safety in high field or ultra-high field MRI, thus maximizing its clinical potential.

Biographies

Xiaotong Zhang received his B.S. and Ph.D. degrees in Electrical Engineering from Zhejiang University, China, in 2004 and 2009, respectively. He worked as a Postdoctoral Associate from 2009–2012 in Dr. Bin He’s lab in Department of Biomedical Engineering (BME) at University of Minnesota (UMN), USA, and then has been working as a Research Associate in UMN BME until now. His research interests cover numerical electromagnetic modeling and computation, electrical properties tomography (EPT) of biological tissues using MRI scanner, quantitative real-time local SAR estimation and management in ultra-high field MRI application, RF magnetic fields mapping (B1-mapping) in MRI, and RF safety in parallel transmission.

Jiaen Liu received his B.S. and M.S. degrees in Engineering from Tsinghua University, Beijing, China, in 2005 and 2007, respectively. He is now a Ph.D. candidate in the Department of Biomedical Engineering at University of Minnesota, Minneapolis, US. Currently, he is working on developing reconstruction algorithms and experiment techniques for MR-based electrical properties tomography and investigating its application in pathology diagnosis and MRI safety. His research interests include functional biomedical imaging, bioinstrumentation, applied mathematics, and computational approaches to understand biological systems.

Bin He (F’04) is Distinguished McKnight University Professor of Biomedical Engineering, Medtronic-Bakken Endowed Chair for Engineering in Medicine, Director of Institute for Engineering in Medicine, Founding Director of Center for Neuroengineering, and Director of NSF IGERT Training Program in Systems Neuroengineering at the University of Minnesota. Dr. He’s research interests cover a broad spectrum in biomedical engineering and neuroscience, including neuroengineering, biomedical imaging, and medical devices. He has made pioneering contributions to functional neuroimaging, brain-computer interface, cardiac electrophysiological tomography, and bioimpedance imaging. He has published over 200 peer reviewed articles in leading international journals and delivered over 300 plenary, keynote, and invited talks and seminars in international conferences and institutions worldwide. Dr. He was a recipient of the NSF CAREER Award, the AHA Established Investigator Award, and the Outstanding Research Award from the International Federation of Clinical Neurophysiology. He is a Fellow of IEEE, AIMBE, International Academy of Medical and Biological Engineering, and Institute of Physics.