Abstract
In randomized trials, investigators typically rely upon an unadjusted estimate of the mean outcome within each treatment arm to draw causal inferences. Statisticians have underscored the gain in efficiency that can be achieved from covariate adjustment in randomized trials with a focus on problems involving linear models. Despite recent theoretical advances, there has been a reluctance to adjust for covariates based on two primary reasons: (i) covariate-adjusted estimates based on conditional logistic regression models have been shown to be less precise and (ii) concern over the opportunity to manipulate the model selection process for covariate adjustments to obtain favorable results. In this paper, we address these two issues and summarize recent theoretical results on which is based a proposed general methodology for covariate adjustment under the framework of targeted maximum likelihood estimation in trials with two arms where the probability of treatment is 50%. The proposed methodology provides an estimate of the true causal parameter of interest representing the population-level treatment effect. It is compared with the estimates based on conditional logistic modeling, which only provide estimates of subgroup-level treatment effects rather than marginal (unconditional) treatment effects. We provide a clear criterion for determining whether a gain in efficiency can be achieved with covariate adjustment over the unadjusted method. We illustrate our strategy using a resampled clinical trial dataset from a placebo controlled phase 4 study. Results demonstrate that gains in efficiency can be achieved even with binary outcomes through covariate adjustment leading to increased statistical power.
Keywords: clinical trials, efficiency, covariate adjustment, variable selection
1. Introduction
In many randomized clinical trials (RCT), the investigator is interested in evaluating the causal effect of a binary treatment (e.g., new drug versus current standard of care) on a health outcome. In particular, for binary outcomes, one is often interested in estimating the difference in the probability of an event (e.g., death) between the treated and untreated arms, referred to as the risk difference. This is typically estimated as the observed difference in the proportion of subjects with the event in the treated and untreated arms. We refer to this estimator as the unadjusted estimator.
The unadjusted estimator is efficient when no other information is collected besides the data on the treatment, A, and outcome, Y, of interest. Indeed, from estimation theory [1], it is known that the non-parametric maximum likelihood estimator (MLE), that is, the MLE in the model with no constraints on the observed data distribution, is the efficient estimator of the effect of interest. Because the likelihood of the observed data is P (A)P (Y |A) when the data only contain information on the treatment and outcome, the unadjusted estimator does thus correspond to the nonparametric MLE when the treatment variable, A, is binary.
In most RCT however, data are also collected on baseline (pretreatment) covariates, W, in addition to the treatment and outcome of interest. In such cases, the unadjusted estimator of the risk difference is no longer equivalent to the MLE because the likelihood of the observed data is now P (W)P (A|W) P (Y |A, W), and the unadjusted estimator ignores the information from the covariates W. The unadjusted estimator can be viewed instead as a reduced data MLE. It follows that ignoring covariate information by using the unadjusted estimator can lead to a loss in estimation efficiency (precision) in practice.
With the MLE principle in mind, statisticians have thus proposed alternative estimators that (i) incorporate the information of covariates W to improve estimation efficiency [2–10] and (ii) do not require any additional parametric modeling assumptions to maintain their consistency property. Although it has been known that such a gain in precision can be theoretically achieved in RCT, it has rarely been implemented in practice.
One reason for the reluctance to apply newly proposed estimators that incorporate information about covariates W is due in part to the apparent contradiction in the literature between the efficiency performance of the typical adjusted estimator in the linear and logistic case (for a discussion of this issue, see [11]).
This article aims at clarifying the issue of efficiency gain with baseline covariates in RCT based on the recently developed framework of targeted MLE (TMLE) and at unifying the different analytical protocols for covariate adjustment that have been proposed. This approach to statistical learning provides a new window into studying covariate adjustment in RCT. This problem has previously been studied from different perspectives, including the estimating function approach [5, 6] and many others [2, 12–14].
Under this new framework, we demonstrate the complete generality of the potential gain in efficiency that can be achieved from covariate adjustment in both the linear and logistic case and reconcile this result with the apparent contradictions in the literature. In short, reconciliation can be attained by noting that the typical adjusted estimator described previously is not the MLE of the marginal effect of interest in general but instead the MLE of the conditional effect (given all covariates W). There is correspondence between the estimands of the adjusted and unadjusted estimators only in the linear case. In other words, the previously mentioned adjusted estimator does not correspond to the MLE estimator in general and in particular, not in the binary case. This explains the apparent loss in efficiency in comparison with the unadjusted estimator because one cannot in fact compare the efficiency performance of both approaches because they do not aim at evaluating the same effect in the logistic case (for further discussion of this issue, see [15]). We hope that such clarifications will allow the broad application of these new techniques in RCT.
In addition, we explore the origin of the gain in efficiency and criteria that can be used to anticipate whether the study design and the covariates collected can actually lead to increased estimation precision in practice. It is important to note that the criteria presented in this paper rely on the assumption that the probability of receiving treatment is 0.5. Our recommendations for adjustment rely on this assumption and therefore do not deviate from the work of Freedman [12] where it is found that if the probability of receiving treatment is 0.5, that adjustment at worst simply does not result in a gain in efficiency. We illustrate how empirical confounding explains the gain in efficiency that can be achieved from an adjusted analysis. In short, empirical confounding is defined as an imbalance between the treated and untreated arms in the distribution of a covariate that also affects the outcome. Empirical confounding can occur because of bad luck in the randomization process, for example, a higher percentage of older patients are assigned to the placebo arm, and age has an effect on the outcome. Some RCT designs ensure perfect covariate balance for some of the baseline covariates; however, there are typically many other covariates collected that do not have a perfect balance. Empirical confounding can introduce a large estimation error (sample bias) for which the unadjusted estimator cannot correct because it ignores covariate information. We note that this error occurs by chance for a given dataset. If the experiment was repeated many times, one would not expect this imbalance to occur in each sample, and this estimation phenomenon can thus not be qualified as bias (for an analogous discussion, see [16]). We refer to it as sample bias or sample imbalance. The method for covariate adjustment presented in this paper can account for such a covariate imbalance and thus improve over the poor finite sample performance of the unadjusted estimator because of empirical confounding.
Another issue that has obstructed the broad application of methodologies for covariate adjustment, in both the linear and logistic settings, is concern about the selection of the parametric covariate adjustment. Incorrect covariate adjustment can indeed typically lead to estimation bias. However, in RCT, the MLE estimator has been shown to be doubly robust ([11]). We establish this property based on the TMLE framework and further describe its practical implication. Despite this double robust (DR) property that ensures MLE consistency independent of the covariate adjustment, unease arises over the fact that investigators could still select the covariate adjustment that provides the most favorable inference without accounting for multiple testing. However, this is not an issue if one uses an a priori specified algorithm for model selection. When the model selection procedure is specified in the analysis protocol, the analysis is protected from investigators guiding causal inferences based on selection of favorable covariates and their functional forms in a parametric model.
Throughout this article, we illustrate the proposed general methodology for covariate adjustment using a sampled dataset from an actual RCT. The goals of this paper are to outline and review all the aforementioned issues involved in covariate adjustment and suggest a concrete analytical protocol for covariate adjustment to improve estimation efficiency by accounting for empirical confounding using TMLE.
In Section 2, we introduce the study and the data that are analyzed for illustration purposes throughout the paper. We also outline the hypothesis tests of interest and their concrete implementation. In Section 3, we provide an example of the apparent failure of logistic regression models, conditional on treatment and baseline covariates, to improve estimation efficiency for the treatment effect of interest. In Section 4, we formally introduce the causal parameter of interest in RCT based on the counterfactual framework borrowing from causal inference literature. In Section 5, we describe the MLE and link it to the typical adjusted estimator based on conditional models to explain the apparent loss in efficiency illustrated in Section 3. We also illustrate its implementation with the study described in Section 2. In Section 6, we introduce the TMLE, outline its properties, and link it to the MLE estimator in RCT from Section 5 to demonstrate the complete generality of the potential gain in efficiency that can be achieved from covariate adjustment in RCT with the TMLE even when the model used is logistic or misspecified. In that section, we also discuss the origin of the gain in estimation precision based on the formula originally provided in [11] that relates the prediction power of the baseline covariate W to the efficiency gain from the TMLE as compared with the unadjusted estimator. We also discuss model selection for TMLE implementation in RCT based on this formula. In Section 7, we illustrate how the performance and resulting inferences from the unadjusted and TMLE estimators compare based on the study and data presented in Section 2. We provide a recommended strategy for analyzing randomized trial data using covariates with the TMLE in Section 8. Finally, we conclude with a discussion in Section 9.
2. Study and data example
The study of interest in this paper is an international, multicenter, double-blind, parallel, placebo controlled RCT, which aims to evaluate safety based on mortality because of drug-to-drug interaction. We randomized the patients to receive either Drug1 or a placebo. All patients received Drug2 concomitantly as a background therapy. The primary objective was to determine whether the mortality rates between patients receiving Drug1 and placebo remained within a 1% margin or less. We note that this is an exploratory safety analysis and an example to illustrate the methodology to evaluate whether there exists a drug-to-drug interaction that could result in higher mortality in the treated patients as compared with those that received the placebo.
The data consist of n independent and identically distributed observations of O = (W, A, Y) ~ p0, where W is a vector of 40 baseline covariates, A is the treatment variable, where A = 1 for the treated group and A=0 for the placebo group, and the outcome Y is all-cause mortality (0=Survived, 1 = Died) at 28 days. We obtained the data available for this article from the original data by random sampling with replacement such that the distribution of the patient characteristics in the original study were maintained. We gave the new subjects sampled a unique but different patient ID to protect the confidentiality of the original data. Therefore, the number of subjects, mortality, and other crude rates may not be similar to that of the original clinical study. We treat each of the 2135 observations in the available data as independent realizations of O. Nine observations had missing outcomes, and we deleted them from the dataset leaving n = 2126 observations. Five of the 40 variables had proportions of missing values over 90%. The remaining 35 variables had proportions of missing values less than 1.3%. For the continuous variables, we imputed the missing values at the median for the given variable and the categorical variables at the category with the highest proportion of observed values. We created corresponding indicator variables of whether or not the value was imputed, resulting in 80 baseline covariates. This was a simple, crude approach to imputing the missing values, and we can apply other more sophisticated approaches in general. Regardless of the approach, the indicator values for imputation must be created to ensure that the original information collected is preserved in the imputed data. Additionally, we created dummy variables for each of the categorical variables, resulting in 162 variables. Of the 1054 subjects in the placebo group, 337 died, and of the 1072 subjects in the test drug group, 306 died.
The hypothesis test for the research question is expressed as follows:
If the upper limit of the 100(1–2α)% confidence interval (CI) for P (Y =1 | A=1)−P (Y 0=1| A=0) is less than 0.01, then the null is rejected, and the conclusion is that the mortality rate of the test group is similar (i.e., not much inferior) to that of placebo using a 1% equivalence margin. This is equivalent to testing the previously mentioned hypothesis test at a level of α. The International Conference on Harmonisation guidelines state ‘The approach of setting Type I errors for one-sided tests at half the conventional Type I error used in two-sided tests is preferable in regulatory settings’ [17]. Because the generally accepted level for a two-sided hypothesis test is 0.05, we set the type I error level for this one-sided test to 0.025.
We note that a second test for superiority is expressed as,
This test can be similarly performed at the 0.025 level as the aforementioned formula by observing whether 95% upper confidence limit is less than 0 (i.e., test drug is superior to placebo).
To illustrate the proposed general methodology for extraction of covariate information to improve estimation efficiency over the standard unadjusted estimation approach used in clinical trials, we compare results from both approaches for this latter test in addition to the results from the noninferiority test described previously.
3. Covariate adjustment with logistic models
To illustrate the decrease in estimation efficiency from logistic models, conditional on treatment and baseline covariates, relative to unadjusted logistic models, we fit such a conditional logistic model to the dataset and compare the corresponding estimate of the odds ratio with the unadjusted odds ratio. An estimate of the conditional odds ratio is easily obtained from a logistic model by simply exponentiating the coefficient for A. Note that this applies when there are no interaction terms between the treatment A and covariates W in the parametric model used. In this section, we place focus on the odds ratio representation of the effect of interest versus the aforementioned risk difference measure because it is not clear how one typically derives a marginal risk difference from a model conditioning on W. We do provide a method in later sections based on averaging over the covariates W to obtain a marginal risk difference estimate from a logistic model, conditional on treatment and baseline covariates; however, here we focus on the comparison of odds ratios to replicate and further illustrate published results [3, 18].
For clarity, we base covariate adjustment on a single covariate BULTRA, the indicator variable that a bilateral compression ultrasound was performed. We chose this covariate because it is most correlated with the outcome. We later explain this selection criterion in Section 6.2. The following logistic model was thus fit,
where W = BULTRA.
We provide the estimate β̂1 and the corresponding standard error (SE) for β̂1, in addition to the unadjusted estimates, in Table I. Note that the odds ratio estimate is given by exp(β̂1) and that the SE for β̂1 is indeed larger for the conditional estimate from the logistic model with BULTRA than the unadjusted SE. However, the upper confidence limit of the conditional estimate is lower than the unadjusted because of the face that the point estimate is further from the null as compared with the unadjusted, −0.217 and −0.163, respectively. Thus, one would reject the following test based on the conditional but not unadjusted method,
Table I.
Conditional (BULTRA) and unadjusted log odds ratio estimates.
| log (OR) | SE | 95%CI | |
|---|---|---|---|
| Unadjusted | −0.163 | 0.095 | (−0.348, 0.023) |
| Conditional | −0.217 | 0.108 | (−0.428, −0.006) |
OR, odds ratio; SE, standard error; CI, confidence interval.
These results are consistent with those previously demonstrated [3, 18].
Furthermore, note that these results are based on models conditional on treatment and baseline covariates with no interaction terms between the treatment variable and covariates. With the presence of an interaction term, the logistic model becomes
and similar to the risk difference, it is not clear what one should report as the estimate of the causal odds ratio of interest. We note that this issue also applies in the linear model setting, and thus no interaction terms are typically included in linear models. This observation will be helpful in understanding the apparent loss in estimation efficiency from logistic models for covariate adjustment and will be revisited in Section 5 when we reconcile the empirical results from this section with the theoretical results from MLE estimation from which one expects a gain in estimation efficiency through covariate adjustment even with logistic models.
4. Counterfactual framework
Despite the example in the previous section, it is nevertheless expected from theory that proper covariate adjustment can improve estimation efficiency even with logistic models. We present such an estimation approach in the next section and illustrate its ease of implementation. This method is based on the causal inference framework for observational studies that we present now with the counterfactual notation required to clearly outline our covariate adjustment method as well as its properties.
Causal effects of A on Y are defined based on a hypothetical full data structure X = (W, (Ya : a ∈
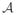 )) ~ FX containing the entire collection of counterfactual or potential outcomes Ya under treatment regimen a for a ranging over the set of all possible treatments
)) ~ FX containing the entire collection of counterfactual or potential outcomes Ya under treatment regimen a for a ranging over the set of all possible treatments
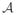 . In our study example,
. In our study example,
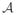 = {0, 1}. The observed data structure O only contains a single counterfactual outcome Y = YA corresponding to the treatment that the subject actually received. The observed data O = (W, A, Y ≡ YA) is thus a missing data structure on X with missingness variable A. We denote the conditional probability distribution of treatment A given the full data X with g(a|X) ≡ P (A = a|X) and refer to it as the treatment mechanism. The no unobserved confounders (NUC) assumption, also referred to as the randomization assumption or coarsening at random assumption, states that A is conditionally independent of the full data X, given W, g(A|X) = g(A|W). In words, the NUC assumption requires that the treatment mechanism be a function of observed covariate(s) W only. In most RCTs, the treatment is assigned completely at random, and by design the NUC assumption holds (g(A|X) = g(A)). In our application,
and ĝ(0) = 1 δ̂ = 0.496.
= {0, 1}. The observed data structure O only contains a single counterfactual outcome Y = YA corresponding to the treatment that the subject actually received. The observed data O = (W, A, Y ≡ YA) is thus a missing data structure on X with missingness variable A. We denote the conditional probability distribution of treatment A given the full data X with g(a|X) ≡ P (A = a|X) and refer to it as the treatment mechanism. The no unobserved confounders (NUC) assumption, also referred to as the randomization assumption or coarsening at random assumption, states that A is conditionally independent of the full data X, given W, g(A|X) = g(A|W). In words, the NUC assumption requires that the treatment mechanism be a function of observed covariate(s) W only. In most RCTs, the treatment is assigned completely at random, and by design the NUC assumption holds (g(A|X) = g(A)). In our application,
and ĝ(0) = 1 δ̂ = 0.496.
The primary causal parameter of interest in this article (i.e., the causal risk difference) is defined as E(Y1) − E(Y0). In words, it is the average difference over all subjects between the counterfactual outcomes corresponding with treatment (A = 1) and no treatment (A = 0). In an RCT, when no confounding is present, this parameter is equal to Ep0 (Y |A = 1) − Ep0 (Y |A = 0), which explains why causal effects can be estimated based on observed differences in the outcome between treatment groups. As stated in the introduction, an estimator based on the latter representation (i.e., the unadjusted estimator) is not a nonparametric MLE, rather a reduced data nonparametric MLE, because it ignores covariates W. We can easily derive the nonparametric MLE approach to the estimation of the effect of interest by rewriting the parameter of interest as follows:
| (1) |
In the next section, we show how this representation of the causal effect can be used to derive the non-parametric MLE that properly incorporates covariate information to increase estimation efficiency over the unadjusted estimator. We first explain why covariate adjustment through simple fitting of a logistic model, conditional on treatment and baseline covariates, as described in Section 3, does not permit increased estimation precision and revisit the issue of covariate adjustment with models, conditional on treatment and baseline covariates, that include interaction terms between treatment and covariates.
5. Covariate adjustment through maximum likelihood estimation
From the representation of the estimator in the previous section, we can now clearly distinguish the effect estimands from logistic models, conditional on treatment and baseline covariates, versus the effect estimands from unadjusted logistic models. From Equation (1), it is indeed clear that the adjusted estimate obtained by simple fitting of a model for Q(A, W) ≡ E(Y | A, W) is not a consistent estimate of the parameter of interest, E(Y1) − E(Y0), in general. The estimand based on a model, conditional on treatment and baseline covariates, represents in fact a conditional (subgroup specific) causal effect under the NUC and thus not actually the population-level effect of interest, that is, the marginal effect of A on Y represented by E(Y1) − E(Y0). An additional step of integration (averaging) over the covariates W is required to obtain a marginal effect estimate from the fit of a model, conditional on treatment and baseline covariates, as it is made explicit by Equation (1).
One possible explanation for the lack of explicitly noting this previously in the applied literature is due to the fact that the estimand from an adjusted analysis is equivalent to that of an unadjusted analysis when the model for E(Y |A, W) and E(Y |A) are linear and have no interaction terms between the treatment and covariates. We explain this result in the following text.
Suppose the observed data are again given by O = (W, A, Y) where the outcome Y is now continuous. Let the parameter of interest be the marginal effect of A on Y represented by E(Y1) − E(Y0) and equal to the parameter ψ1 in the model ψ0 + ψ1 A for E(Y | A) in an RCT. For a continuous outcome Y, Q(A, W) = E(Y |A, W) is typically estimated using a linear regression model. In the case that this regression model does not contain any interaction terms between A and W, the coefficient for treatment coincides with ψ1 and is estimated at least as precisely as ψ1. When this regression model contains one or more interaction terms between A and W, one must integrate out the covariate(s) W from Q(A, W) (Equation (1)). The corresponding estimator is the MLE, and it has also been referred to as the G-computation estimator in the causal inference literature introduced in [19, 20]. Concretely, the MLE estimate of the marginal effect of interest is as follows:
Note that the MLE implementation described previously is not limited to problems involving a linear model for Q(A, W). For example, when the outcome is binary, one could use a logistic regression model to estimate Q(A, W) and average over the covariates W in the same way as the aforementioned formula to obtain the MLE of the causal risk difference. Unlike with the linear model case, however, the coefficient for treatment defined from the logistic regression model with no interaction terms between A and W is not typically equivalent to the effect estimand of interest, ψ1, and thus when the outcome is binary, the additional integration step over W is always necessary for proper MLE estimation whether or not the model for Q contains interaction terms between treatment and covariates. It has been shown that integrating over the covariates even in the logistic setting does indeed improve efficiency in comparison with the unadjusted method [11]. However, if this additional integration step is not performed, then the effect estimates are less precise as illustrated in Section 3 and represent estimates of conditional effects instead of estimates of the marginal effect of interest [3, 18]. Finally, note that the MLE of the relative risk and odds ratios can be similarly obtained [11].
We now illustrate the implementation of the MLE estimator for the effect of interest in the data analysis based on the saturated logistic model (i.e., the model that includes all interaction effects between the A and W) involving the covariate BULTRA, that is, Q(A, W) = (1+exp(−(β0+β1A+β2W +β3AW)))−1 and W = BULTRA. For each of the n subjects, we use the logistic model to predict the probability of death when the subject receives the drug (A = 1) and when the subject receives the placebo (A = 0). Thus, for each subject, we compute two predicted probabilities and the difference in these probabilities. The average of these n differences is the MLE estimate of the causal risk difference of interest.
Table II provides this MLE estimate (MLE (BULTRA)) and the corresponding SE based on the bootstrap procedure. We provide the unadjusted estimate for comparison. A clear increase in precision is achieved including only this single covariate as observed by the relative efficiency (RE) (1.196), estimated as the unadjusted SE divided by the adjusted estimate SE.
Table II.
Maximum likelihood estimation and unadjusted risk difference estimates.
| Estimate | SE | RE | |
|---|---|---|---|
| Unadjusted | −0.034 | 0.020 | 1.0 |
| MLE (BULTRA) | −0.035 | 0.017 | 1.2 |
| MLE (AGE75) | −0.039 | 0.020 | 1.0 |
SE, standard error; RE, relative efficiency; MLE, maximum likelihood estimation.
RE = SE(unadjusted)/SE(adjusted).
We now consider a second model, where W is now AGE75, which is the indicator that the subjects are older than 75 years. We provide the results corresponding to this model in Table II, ‘MLE (AGE75)’. There is now no decrease in the width of the CIs; however, the point estimate shows a marked difference as compared with the unadjusted. This is a result of an imbalance in treatment between the older and younger patients in addition to the fact that age is associated with the outcome. The probability of being treated among those patients older than 75 years is 0.55 as compared with 0.49 for those younger than 75 years. Thus, the MLE has accounted for the empirical confounding by age in the data, which results in an increase in precision through a shift in the point estimate.
These two simple examples demonstrate how covariate adjustment in an RCT with a binary outcome can result in a gain in estimation efficiency (precision) of a marginal effect through either a decrease in the SE or/and a shift in the point estimate.
In both examples, W was binary, and the models chosen for Q(A, W) were saturated models and thus correctly specified. Therefore, the gain in precision could not be attributed to model misspecification. However, if W were continuous and such a saturated (nonparametric) model were not possible, one may question whether consistency of the MLE is based on the model for Q(A, W). In observational settings where treatment is not assigned completely at random and thus confounding is present, this is indeed true. In RCT settings, consistency of the MLE estimator does however not rely on the model for Q(A, W), and the MLE estimator remains consistent even when the model is misspecified. To establish this fortunate property of the previously mentioned MLE estimator in RCT, we introduce TMLE developed in [21] and link it to MLE estimation discussed in this section.
6. Targeted maximum likelihood estimation
Maximum likelihood estimation aims for a trade-off between bias and variance for the whole density of the observed data. Investigators however are typically not interested in the whole density of the data O but rather a specific parameter of it (in our case, the risk difference). Procedures that aim at optimizing the trade-off between variance and bias for that specific parameter result in more desirable estimators of the parameter of interest compared with the MLE estimator. TMLE is such a procedure that carries out a bias reduction specifically tailored for any parameter of interest. This estimation procedure is based on altering an initial model for the density of the observed data such that the resulting substitution estimator of ψ1 derived from this updated density model solves the efficient influence curve estimating equation for the parameter of interest. The model fluctuation is chosen such that bias associated with the estimation of ψ1 decreases at the cost of a small increase in the likelihood compared with the likelihood associated with the initial model for the density of the observed data. The estimator from this approach is referred to as the TMLE. For technical details about this general estimation approach, we refer the reader to [21]. Here, we underscore two important results from TMLE estimation that can be applied to improve estimation efficiency through covariate adjustment in RCT: (i) the TMLE equivalence with the MLE in RCT and (ii) the double robustness property of the TMLE.
Moore and van der Laan [11] provided the TMLE for the risk difference in an RCT. The authors showed that in RCT, the TMLE estimator is equivalent to the MLE estimator. Properties from the TMLE estimator thus transfer to the MLE estimator in RCT. Note that the MLE does not typically coincide with the TMLE. One important such property of the TMLE is its equivalence to the DR estimator from the causal inference literature. Note that this equivalence is not restricted to the RCT setting but is instead a general result.
Many authors have studied extensively double robust estimators [1, 22–24]. They rely on estimation of two nuisance parameters: the treatment mechanism, g, and another parameter, Q, which in our RCT setting is defined as Q(A, W) = E(Y | A, W). Their name (DR) relies on their consistency property. DR estimators are consistent if they rely on either a consistent estimator of the treatment mechanism g or a consistent estimator of Q. When the treatment is assigned completely at random, like in RCT, the treatment mechanism P (A|W) = P (A) is always known, and thus the DR estimator is always consistent whatever the estimator for Q on which it relies. That is, even when the estimator Q̂(A, W) of Q(A, W) is inconsistent (e.g., if it relies on a misspecified model), the TMLE remains consistent, and one should hence not be concerned with estimation bias with this method in RCT. More specifically, if Q̂ (A, W) converges to Q*(A, W) ≠ Q(A, W), then DR estimators remain asymptotically linear and consistent in RCT. In practice, this means that the investigator is protected against bias at large sample sizes even when the a priori specified model selection algorithm selects a misspecified model for Q(A, W). Note that if Q̂ (A, W) is a consistent estimator of Q(A, W), then the DR estimator is consistent but also efficient. These results transfer to the TMLE estimator in RCT because as discussed previously, the TMLE is equivalent to the DR estimator in RCT. Note that Tsiatis et al. and Zhang et al. [5, 6] had previously proposed DR estimators for applications in RCT; however, they did not explicitly noted the fact that the MLE coincided with the DR estimator.
Based on these properties, using an a priori specified method for the model selection for Q(A, W), bias is not a concern in RCT with large sample sizes when applying the MLE/TMLE method. We note that the estimation method outlined in Section 3 is based on logistic regression, conditional on treatment and baseline covariates. Estimation consistency is hence entirely dependent on the correctness of the logistic regression model used.
We note that with the TMLE method, the model for Q(A, W) is not selected for the purpose of describing or estimating subgroup specific or conditional effects. Rather, its purpose is for improving the precision of the marginal effect estimate.
We proceed with presenting our results under the TMLE framework because the MLE and TMLE are equivalent in RCT. In particular, we now provide a formula to estimate the variance of the TMLE estimator and discuss the relation between the cross-validated coefficient of determination (R2) of the regression of Y on W (implied by the regression Q(A, W) of Y on A and W) and efficiency gain from the TMLE.
6.1. Inference with the targeted maximum likelihood estimation
For the results presented thus far, the bootstrap procedure has been implemented to estimate the SEs of the estimators described. Although this general approach may also be applied to obtain accurate estimates of the SE of the TMLE estimator, the computation time associated with the bootstrap can be a barrier to the practical application of the TMLE procedure, particularly in settings involving a large number of covariates.
A closed-form formula for the asymptotic SE of the TMLE can be used instead for inference purposes:
where IC denotes the TMLE influence curve
It can be shown that the variance of the TMLE (i.e., IC) is minimized at the true value for Q(A, W), that is, when Q̂ (A, W) = Q(A, W). It is important to note here that the IC in the aforementioned formula provides a fast, analytical mean to estimate the variance of the TMLE in practice. The correctness of inference based on the IC relies on the assumption that the model for Q, used to derive Q̂ (A, W), is not an overfit of the true nuisance parameter Q(A, W). In such a situation, the asymptotic results on which the correctness of the IC-based inference rely do break down and one may run the risk of underestimating the variance with the IC, that is, artificially attributing the gain in precision to covariate adjustments. This is due to the fact that IC-based inference is based on first-order asymptotics, whereas in finite samples, second-order terms can affect the inference [25, Chapter 3]. We can avoid this problem by fitting Q(A, W) with an appropriate criterion that will be discussed in the following sections.
We note that we have not studied finite sample behavior of the IC-based inference for very small sample sizes. The simulation studies provided in [11] showed that the IC-based SE resulted in appropriate 95% coverage probabilities for a sample size of n = 500.
6.2. Relation between R2 and efficiency gain with targeted maximum likelihood estimation
In [11], a formula was given that describes the relationship between the R2 of the regression of Y on W and the RE of the TMLE to the unadjusted estimator. Let Q(W) = E(Q(A, W) | W) = E(Y |W). The formula demonstrated that as increases, so does the gain in RE of the TMLE over the unadjusted estimator. This formula (see Appendix B for the proof) is based on the assumption that P (A = 1) = P (A = 0) = 0.5 and thus is consistent with the result in [12], which states that ‘adjustment is either neutral or helps’ when P (A = 1) = P (A = 0) = 0.5:
| (2) |
where Q(A)=E(Y |A), σ2(TMLE(Q(A, W))) is the variance of the TMLE influence curve at Q(A, W) (see previous section) and σ2(TMLE(Q(A))) is the variance of the influence curve at Q(A) (i.e., the variance associated with the unadjusted estimator). In short, the outcome prediction with W implied by the model for Q(A, W) (Q(W) = 0.5Q(0, W) + 0.5Q(1, W)) must outperform outcome prediction through the simplest intercept model (E(Y)) to achieve a gain in efficiency with the TMLE approach.
This relation was derived based on the ratio of variances of the influence curves. These variances are based on first-order asymptotics, and thus the relation in the aforementioned formula only holds in first order. In the case that the model for Q used to derive Q̂(A, W) is an extreme overfit of the true nuisance parameter Q(A, W), the relation may not hold as second-order terms may influence the behavior. However, as we discuss in Section 6.4, it is our experience that the use of cross-validation will prevent one from selecting an overfit model for Q(A, W).
The RE formula is valid only in the model that only assumes A is randomized and P (A = 1) = 0.5, that is, if the data collection protocol relies on not only treatment randomization but also matching (balancing) on some covariates, then this formula may not apply. In the latter scenario, one could condition on the matched covariates to make use of this formula because it would then hold within each stratum. Ongoing research includes the formal development of this stratum-specific approach as well as results that establish the link between covariate adjustments and gains in efficiency with the TMLE when matching on baseline covariates.
6.3. Empirical confounding and the origin of efficiency gain with the targeted maximum likelihood estimation
In this section, we conjecture that, for a given sample, the gain in efficiency from the TMLE is not only a function of the correlation between the covariates and the outcome ( as described previously) but also a function of imbalances in these covariates with respect to treatment. More specifically, we conjecture that the origin of efficiency gain through covariate adjustment is empirical confounding, that is, if one had perfect balance in all covariates affecting the outcome, the adjusted estimate should not be more precise than the unadjusted estimate even though the covariates used for adjustment could be predictive of the outcome, that is, .
To support our conjecture and illustrate the efficiency gains with the TMLE in the presence and absence of empirical confounding, 10,000 datasets of size n = 1000 were simulated with a binary treatment A, such that P (A = 1) = P (A = 0) = 0.5, two binary covariates, W = (W1, W2), such that P (W1 = 1) = 0.4 and P (W2 = 1) = 0.6 and an outcome Y with logit (P (Y = 1|A, W)) = 5A−3W1−3W2. The true risk difference is 0.616 with E(Y1) = 0.761 and E(Y0) = 0.145. In the first setting, the treatment arms were balanced (matched) perfectly on W1 and W2, in the second setting, the treatment arms were balanced on W1 only, and in the third setting, the treatment arms were not balanced perfectly on either covariate. We computed the unadjusted estimate and three adjusted estimates (TMLE) under each of these three settings, where the three adjusted estimates correspond to adjusting for W1 and W2 (Q̂(A, W) = Q̂ (A, W1, W2)), W1 only (Q̂ (A, W) = Q̂ (A, W1)), and W2 only (Q̂ (A, W) = Q̂ (A, W2)).
We provide the mean squared error (MSE) results for each simulation setting and TMLE estimate in Table III. In the first setting where there is perfect balance of treatment on both covariates, no gain in MSE is achieved through covariate adjustment with any of the three TMLE estimates, even though both covariates have an effect on the outcome Y. In the second setting where treatment is perfectly balanced on W1 only, a small amount of empirical confounding by W2 is present, and a precision gain is achieved by adjusting for W2. Note that even though no gain is achieved by adjusting for W1 only, adjusting for W1 and W2 results in a slightly lower MSE than adjusting for W2 only. This may at first seem counterintuitive; however, although W1 and W2 are independent, for any given sample, a small amount of correlation exists between the two variables. Because W1 is not perfectly balanced on W2, adjusting for it as well as W2 is akin to adjusting for empirical confounding. Therefore, even if there is a perfect balance of treatment on a covariate, adjusting for it when there exists another covariate on which there is not a perfect balance will provide a further gain in efficiency.
Table III.
Mean squared errors for simulation results.
| Balanced on | Adjusted for | MSE |
|---|---|---|
| W1 and W2 | None | 4.31e –04 |
| W1 and W2 | W1 and W2 | 4.31e –04 |
| W1 only | None | 5.19e –04 |
| W1 only | W1 and W2 | 4.34e –04 |
| W1 only | W1 only | 5.19e –04 |
| W1 only | W2 only | 4.35e –04 |
| None | None | 6.12e –04 |
| None | W1 and W2 | 4.36e –04 |
MSE, mean squared error.
These results supports the conjecture that in the extreme scenario of a perfectly balanced trial in all covariates, one could not obtain an increase in precision through covariate adjustment, even if the covariates are strongly predictive of the outcome. The TMLE method of adjustment can then be viewed as an attempt to mimic this ideal setting in which perfect balance is present in all covariates. This is evidenced by comparing the MSE of the adjusted estimate in the third setting where treatment was not perfectly balanced on either covariate and the MSE of the unadjusted estimate with perfect balancing on W in the first setting. The MSE are almost equivalent, indicating possibly an efficiency bound for the adjusted estimate.
We note that empirical confounding results in covariate imbalances that are typically quite small. In our dataset, only four covariates had significant associations with treatment (p-values < 0.05). For example, the probability of receiving treatment among those patients older than 75 years is 0.55 as compared with 0.49 for those younger than 75 years, and adjusting for age results in a change in the point estimate. Note however that adjustment for variables not significantly associated with treatment but affecting the outcome, that is, whose imbalances are very small with respect to the treatment, can still result in a gain in precision. Thus, testing for a significant imbalance is not a valid strategy because one could miss a covariate that is strongly associated with the outcome with only a small imbalance. Furthermore, it has been pointed out that tests for covariate imbalance do not make sense in RCT because by definition, all imbalances are due to chance. Thus, such a test is a test of a null hypothesis that is by definition true [14,26,27]. Because a perfect balance is very unlikely, it is a better strategy to include those covariates in the adjustment that are predictive of the outcome, based on the relation in formula (2), as recommended in [2, 4, 14, 27]. The findings here agree with the discussion of random imbalances and blocking in [16].
6.4. Selection of the covariate adjustment for targeted maximum likelihood estimation
The implementation of the TMLE estimator relies on estimating the nuisance parameter Q(A, W), which will typically be based on a parametric model in practice (e.g., logistic model). Given Equation (2), the relation between and efficiency gain, one may be tempted to include as many covariates as possible in the model for Q(A, W) because the corresponding observed increases as one increases the set of covariates W to predict Y. As already noted in Section 6.2, we caution that such an approach may result in overfitting Q(A, W), which in turn can lead to incorrect (optimistic) inference from the influence curve associated with the TMLE and more seriously also result in loss of estimation efficiency because formula (2) does not apply in this context.
To demonstrate this issue with the data analysis, we fit a model for Q(A, W) including all 162 covariates as main terms. The SE computed based on the influence curve was 0.016, whereas the corresponding SE based on the bootstrap procedure was 0.0229, a 43.4% increase. We note that as a comparison, the unadjusted influence curve and bootstrap SEs were equivalent (within 0.3%). It thus appears that the bootstrap estimate of the TMLE variance is accounting for second-order terms contributing to the variability of the TMLE estimator that are ignored by the first-order asymptotic approximation of the TMLE variance with the influence curve. In fact, the bootstrap-based estimate of the TMLE SE associated with the overfit model for Q(A, W) is even higher than that of the unadjusted estimate and demonstrates that overfitting Q(A, W) results in a loss of efficiency.
The phenomenon illustrated previously does not invalidate formula (2) but instead can be explained by noting that the observed calculated on the same sample as the one on which Q(A, W) is fit, is not a good estimate of the true . To obtain an appropriate estimate of the , cross-validation is typically applied [28]. This cross-validated can subsequently be used as a model selection criterion for Q(A, W) to avoid overfitting the nuisance parameter, which results in incorrect inference from the influence curve and more importantly, in a loss in estimation efficiency. As noted previously, if the standard (non-cross-validated) was used in practice to select a model for Q(A, W), one would always use a model for Q(A, W) that includes the maximum number of covariates because the associated would be largest. This is not necessarily the case if the cross-validated is applied instead.
In V -fold cross-validation, the data are divided into V subsets of equal size. Of the V subsets, V − 1 are selected to be used as a training set, and the remaining subset is used as the validation set. The process is repeated V times such that each time a different subset acts as the validation set. To compute for Q(W) = 0.5Q(0, W) + 0.5Q(1, W) with a V -fold cross-validation splitting scheme, one fits the model for Q(A, W) on each of the V training sets and computes the associated with the observations from the corresponding validation sets. The mean of the V estimates for from each validation set is the associated with the model for Q(A, W) on which the TMLE is based.
Returning to our example with overfitting of Q(A, W), the corresponding observed was 0.35 as compared with the fivefold (V = 5) of 0.23. When the model for Q(A, W) only involves one single covariate, the observed is 0.23 and the is 0.22. These results clearly demonstrate that the model for Q(A, W) based on a single covariate does not overfit Q(A, W) and thus the near equivalence between the cross-validated and standard , whereas the very large model for Q(A, W) shows a large difference in the two estimates signaling an overfitting problem.
Applying a cross-validated model selection criterion, one can avoid such overfitting issues when the algorithm is not overly aggressive. There exist algorithms that use cross-validated criterion such as the deletion/substitution/addition algorithm, which searches through a large space of possible polynomial models using the cross-validated risk as the selection criterion [29]. This algorithm can be computationally intensive. Other model selection algorithms that are based on a likelihood criterion, such as stepwise based on AIC, do not ensure an increase in (decrease in risk) and thus do not guarantee a gain in efficiency.
A model selection procedure that uses the as a criterion would guarantee a gain in efficiency, given that P (A = 1) = P (A = 0) = 0.5. We have provided such a procedure in Appendix C. However, this procedure is quite involved and uses logistic regression only for the model for E(Y | W) and requires a linear model for Q(A, W). Because we focus only on logistic modeling in this paper, we present a simpler procedure for covariate adjustment that does not directly use this criterion. Instead, our proposal involves first building a logistic regression model for E(Y | W), which we denote with V (W), using as the selection criterion. We then obtain an estimate for Q(A, W) by adding to V̂(W) a main term for A. This method ensures that , rather than . Although it is unlikely that and , we can however check directly that using cross-validation using the relation Q(W) = 0.5Q(0, W) + 0.5Q(1, W).
We applied a practical, simple, and fast variant of the backward deletion algorithm for the selection of V(W) and thus Q(A, W) (obtained by adding a main term for A to V(W)) based on the maximum fivefold (see Appendix D for details).
We provide results from the application of the method described previously to select the model for Q(A, W) but also include results from the more simple approach of selecting the model for Q(A, W) based on the identification of the covariate most associated with the outcome. The single covariate selected and used to derive the model for Q(A, W) in this second approach was the BULTRA covariate discussed earlier. We based the CIs corresponding with the tests discussed in Section 2 on the bootstrap procedure. For each bootstrap sample, we ran the entire model selection process, including the ranking of the covariates by their false discovery rate (FDR)-adjusted p-values and the model selection procedure. Thus, the honest bootstrap procedure accounts for all sources of variability, including the second-order terms discussed earlier. For each of these two methods for estimating Q(A, W), the risk difference was estimated based on the TMLE method. SEs were computed using three methods: the influence curve (IC), the cross-validated IC (cv-IC), and the bootstrap procedure based on 20, 000 bootstrap samples. The cv-IC, as opposed to the standard IC was applied based on the same reasoning for using the as opposed to the . However, if the model selection algorithm is based on , the standard IC can be used for inference because the use of cross-validation avoids the issue of overfitting Q(A, W). We note that the cross-validated variance of the IC itself could also be used as a criterion for model selection; however, in this paper, we present results based on the criterion only.
7. Results
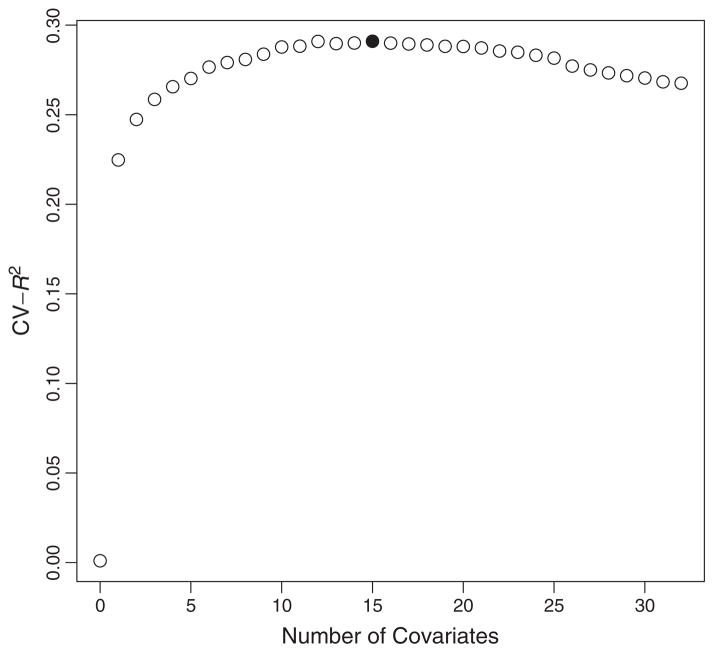
The single most associated covariate (BULTRA) had a strong univariate association with the outcome (p-value = 5.4e − 78). We used this covariate as a main term (with intercept) only model for the first method of selecting Q(A, W). The backwards deletion method selected a model with 15 covariates, not including the treatment variable A. We provide the plot of the cross-validated in Figure 1 with the solid circle highlighting the maximum cross-validated corresponding with a model with 15 covariates. This plot shows that there is little change in the cross-validated for models with 15 through 22 covariates. The largest gain results from adding a single covariate.
Figure 1.
Cross-validated by number of covariates in model.
Table IV provides all estimates including the unadjusted and TMLE methods. We first note that the upper confidence limit of the unadjusted test is greater than 0, and thus we would conclude that there is no evidence that the test drug is superior to the placebo at the 0.025 level. However, when we adjust for covariates using TMLE, using only the single most associated covariate, the upper confidence limit is reduced to 0 with an RE of 1.14. The RE is calculated as where is the unadjusted SE and is the adjusted SE. Applying the backwards deletion algorithm, the upper confidence limit is reduced even further and the RE increases to 1.211, and we now have evidence to reject the null hypothesis and conclude that the mortality is lower in the test group as compared with the placebo. We note that the research hypothesis was that the mortality for the test drug could be tolerated up to an increase of 1% in comparison with placebo. In this case, all of the upper confidence limits fall below 0.01 and the conclusion of noninferiority is the same using both the unadjusted or TMLE methods. It would still be of interest to the investigator that although the mortality falls within the prespecified margin, the observed reduction in mortality in the treated group is statistically significant.
Table IV.
Estimates based on unadjusted and targeted maximum likelihood estimation.
| Estimate | 95% CI | RE | |
|---|---|---|---|
| Unadjusted | −0.034 | (−0.073,0.005) | 1.000 |
| TMLE 1 Cov | −0.035 | (−0.07, −0.00) | 1.140 |
| TMLE BD | −0.041 | (−0.074, −0.009) | 1.210 |
1 Cov, single most associated covariate; BD, backward deletion; SE, standard error; RE, relative efficiency.
RE = SE(unadjusted)/SE(adjusted).
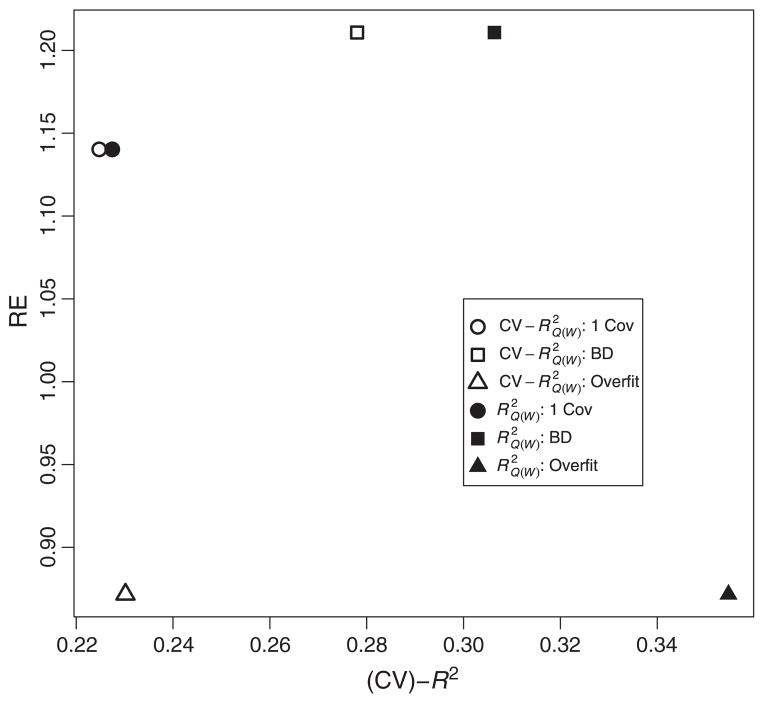
Figure 2 shows that as the fivefold increases, so does the RE. Because this dataset contains highly predictive covariates of the outcome and the study design did not balance treatment on covariates, the large gain in also translates into a gain in estimation efficiency.
Figure 2.
Relative efficiency (RE) against cross-validated and . BD, backward deletion.
The results outlined in the previous text are based on SEs computed based on the bootstrap procedure. Table V provides a comparison of the IC, cv-IC, and bootstrap SEs. The SEs for the unadjusted, single covariate, and backwards deletion estimates are almost identical using the bootstrap as compared with the IC and cv-IC. The bootstrap SE for the overfit method is 43.4% higher than the IC-based SE. However, the cv-IC method accounts for some of the overfit in that it is significantly higher than the IC method. We again note that the IC-based inference is valid in the first order. However, with serious overfits, second-order terms can play a role and the bootstrap procedure is indeed picking up these second-order effects. We include this example as an extreme case to demonstrate when the methodology breaks down. It is our experience that using a cross-validated criterion in the model selection algorithm would avoid such a scenario. In our example, based on the , the overfit model would not have been selected.
Table V.
Comparison of influence curve, cross-validated influence curve, and bootstrap-based (boot) standard errors.
| SE IC | SE cvIC | SE Boot | % Diff in SE | |
|---|---|---|---|---|
| Unadjusted | 0.0199 | 0.0199 | 0.02 | 0.3 |
| 1 Cov | 0.0175 | 0.0175 | 0.0175 | 0.1 |
| BD | 0.0166 | 0.0167 | 0.0165 | −0.4 |
| Overfit | 0.016 | 0.0175 | 0.0229 | 43.4 |
SE, standard error; IC, influence curve; cvIC, cross-validated IC; 1 Cov, single most associated covariate; BD, backward deletion; overfit, all covariates.
% Diff in SE = ((SE Boot − SE IC)/SE IC)*100.
It important to note that the error in the bootstrap based method is on the order of where 20, 000 is the number of bootstrap samples. The difference in the SEs are within this margin. Second, we note that the SEs for the IC and the other two methods differ quite significantly (although, still within this margin) for the overfit model. These results indicate that the cross-validated criterion is performing well with respect to not overfitting the data. They also indicate that when cross-validation is not used in the model fitting procedure, as in the overfit method, then the cv-IC and IC-based estimates differ. Thus, one should always rely on the cv-IC or bootstrap-based SEs in such situations.
The results also show that the point estimates for the TMLE and the unadjusted methods differ. This difference can be attributed largely to the empirical confounder AGE (Section 5), which is highly associated with the outcome (p-value=7.4e −13). The TMLE estimate using the backward deletion method for selecting Q(A, W) includes the covariate AGE. Thus, this estimate has adjusted for this small amount of empirical confounding and changes the point estimate from −0.034 to −0.042. The gains in efficiency are reflected in the SE estimate as well as the point estimate. When the covariate AGE is removed from the backward deletion selected model and the TMLE is computed, the estimate becomes −0.038. The RE however is 1.196, and thus a gain is still achieved. The remaining difference in the point estimate and precision from the unadjusted after removing AGE indicates that there remains some empirical confounding because of variables other than AGE.
8. Recommended strategy for analyzing randomized trial data
A clear strategy needs to be outlined in the study protocol detailing the analysis of RCT data. We provide an approach based on our theoretical and simulation results presented in this paper. The strategy is as follows:
As discussed throughout this paper, gains in efficiency are related to gains in . Thus, one should attempt to collect covariates known or speculated to be predictive of the outcome and outline them in the study protocol.
-
Estimate the model for Q(A, W).
Based on a model a priori specified in the study protocol (for example, include age only), or
Apply the model selection algorithm a priori specified in the study protocol and based on a cross-validated criterion (cv-R2 or cross-validated variance of the IC) such as the backwards deletion algorithm provided in this paper or the approach described in Appendix C.
If (or cross-validated variance of the IC) associated with the model for Q(A, W), is significantly different than 0 according to a test (work on such a test is in progress, see Section 9), then proceed to step 4. Otherwise, no gain in efficiency can be achieved by the covariate adjustment procedure a priori specified and the unadjusted estimate should be used (i.e., the next steps are skipped).
Apply TMLE based on the fitted model for Q(A, W) obtained from the previous step to derive an estimate of the parameter of interest.
Estimate the SE based on the IC or the bootstrap procedure. For honest bootstrap estimates, one must perform the entire model selection procedure (if used) on each bootstrap sample.
Note that steps 2 and 3 could involve a double layer of cross-validation. However, this can be replaced with a single layer of cross-validation if the algorithm is not overly aggressive, that is, the algorithm does not search over an overly large space of basis functions, involving many possible terms. This can be achieved by not allowing interaction or high-order terms and by specifying a maximum model size, such as 30 observations per main term.
9. Discussion
In this paper, we have shown that covariate adjustment for binary outcomes using logistic models can increase the estimation efficiency (precision) for the marginal effect of treatment when the probability of receiving treatment is 50%. The difference from conventional approaches for covariate adjustment using logistic models, conditional on treatment and baseline covariates, lies in the fact that the method presented in this paper averages over the covariates in the logistic model to obtain a marginal (unconditional) effect estimate that can be compared with the standard unadjusted effect estimate. The logistic models presented in this paper are not meant to describe subgroup effects but rather have the purpose of increasing efficiency in the estimation of the marginal effect.
The gain in efficiency can have real implications in phase III RCT as was demonstrated with the fact that the test for superiority would provide different conclusions using either the unadjusted or adjusted estimation approaches.
Using an a priori specified algorithm for covariate adjustment protects the investigators from guiding their analyses in the direction that provides the most desirable results. The comparison of the bootstrap and analytic-based (IC and cv-IC) SEs demonstrated the need for a cross-validated criterion for the selection of the covariate adjustment (Q(A, W)) to avoid the problem of overfitting, which results in incorrect inference with the influence curve and a loss in the possible precision gain from covariate adjustment. We provided a fast and easily implementable algorithm based on a cross-validated R2 criterion that resulted in an RE of 1.211 as compared with the unadjusted method. Even adjusting for the single most associated covariate resulted in a significant gain. These results indicate that predictive covariates of the outcome that do not have a perfect balance in treatment can significantly increase efficiency. This gain in efficiency is reflected in the reduction of the SE and also possibly a change in the point estimate because of sampling bias. We conjecture that this gain in efficiency is the sole result of adjustment for empirical confounding.
Ongoing work includes studying and formalizing the relation between efficiency gain and empirical confounding. Based on this relation, a model selection algorithm could be developed using this relation as a basis for the selection criterion. In addition, future work involves developing a formal test for the hypothesis , either a nonparametric permutation test of independence between W and Y or a model-based test for the fixed model approach similar to the likelihood ratio test comparing the model for Q(W) with the intercept model.
Acknowledgments
The authors of this paper thank the referees for their critical comments and helpful suggestions.
APPENDIX A. Extensions of the methodology
We note that the covariate adjustment methodology presented in this paper can be extended beyond the risk difference. In fact, investigators may be interested in the relative risk or odds ratio, given by,
Note that under the assumptions listed in Section 4 for the risk difference, this parameter can be interpreted as the causal odds ratio, . The TMLE estimator of this parameter is described in the following text (see [11] for details):
In Section 3, we discussed the issues involved in obtaining an estimate of the odds ratio based on the logistic model such as
We pointed out that exp(β1) is the conditional odds ratio, whereas our parameter of interest is the marginal odds ratio. Both parameters are different in general, and using the conditional logistic method to estimate the marginal odds ratio is thus entirely model-dependent as opposed to the TMLE. Thus, we can extend the TMLE to any number of other parameters. In particular, the TMLE has been extended to survival problems with right-censored data, and we intend to apply it to other datasets of this nature in future work.
Table VI includes the estimates of the odds ratio using the logistic model, conditional on treatment and baseline covariates, method as well as the unadjusted and TMLE methods. We use the 95% upper confidence limit to test the hypothesis that the OR was greater than 1 at the 0.025 level. Note that if we were interested in testing within a margin of equivalence, then the margin would need to be specified a priori according to this parameter of interest. In the study presented in this paper, the margin was determined a priori according to the risk difference. Because we do not have access to the data upon which this margin was determined, we could not translate this margin to a margin for the odds ratio. The results are similar to that of the risk difference, that is, one would reject the null based on the TMLE using either a single covariate or the backwards deletion. The conditional logistic method would also reject the null, however, the precision has actually decreased as compared with the unadjusted method, whereas the point estimates is much lower than the unadjusted. The latter fact is what actually drives the upper confidence limit below one for the conditional logistic method.
Table VI.
Unadjusted, targeted maximum likelihood estimation, and logistic model estimates of the odds ratio.
| Estimate | p-value | 95%CI | RE | |
|---|---|---|---|---|
| Unadjusted | 0.849 | 0.042 | (0.706, 1.022) | 1.000 |
| TMLE 1 Cov | 0.845 | 0.021 | (0.718, 0.995) | 1.137 |
| Logistic 1 Cov | 0.804 | 0.021 | (0.651, 0.994) | 0.878 |
| TMLE BD | 0.821 | 0.006 | (0.703, 0.958) | 1.200 |
| Logistic BD | 0.751 | 0.012 | (0.600, 0.940) | 0.826 |
TMLE, targeted maximum likelihood estimation; 1 Cov, single most associated covariate; BD, backward deletion; SE, standard error; CI, confidence interval; RE, relative efficiency.
RE = SE(unadjusted)/SE(adjusted).
APPENDIX B. Proof of relation between and relative efficiency
In this appendix, we prove that given P(A = 1) = P(A = 0) = 0.5,
| (3) |
Useful results for the proof:
| (4) |
| (5) |
| (6) |
| (7) |
The SE for the TMLE of β = E(Y1) − E(Y0) can be derived based on the influence curve, IC(O), given in Section 6.1:
Similarly, the SE for the MLE of β = E(Y1) − E(Y0) can be derived based on the influence curve, IC(O), given in Section 6.1 where W is nil:
We thus have
We also have
and thus
From this last result, we can rewrite
APPENDIX C. Model selection algorithm for Q(A, W) that ensures
We propose an algorithm for estimating Q(A, W) that guarantees . We first observe that formula (2) can be expressed as,
| (8) |
Therefore, to ensure a gain in efficiency, the following must hold:
| (9) |
Thus, to ensure that , the following relation must hold to ensure gain in efficiency with the TMLE:
| (10) |
To guarantee that the previously mentioned relation holds, we propose the following for estimating Q(A, W):
Regress Y on W using a logistic regression model, denoted by θ(W), selected with cross-validation such that it is ensured that E(Y − θ(W))2 < E(Y − E(Y))2 (e.g., using the deletion/substitution/addition algorithm approach).
-
Using a linear model, regress Y on θ(W) and γ(A − E(A)), with θ(W) set as an offset, that is,Note that setting θ(W) as an offset fixes its coefficients rather than refitting the whole regression. To justify that these two steps guarantee that relation (10) holds, we observe that because A ⊥ W,
Therefore, this means that we only need to guarantee that θ(W) has a higher R2 than the intercept model.
APPENDIX D. Backwards deletion model selection algorithm for selecting Q(A, W)
The algorithm is as follows:
Find all marginally associated covariates with FDR-adjusted p-values less than 0.01. Let there be M such covariates.
Fit multivariate logistic regression including all M covariates and compute .
Delete covariate with largest p-value based on multivariate fit from the previous step.
Fit new model with deleted covariate and compute new .
Repeat steps 3 and 4 until only one covariate remains in the model.
Select the model among the M models with the largest and add the treatment A to this model to obtain the model for Q(A, W).
Note that we applied the FDR procedure in the first step because of the multiple tests performed to assess the univariate association of each covariate with the outcome [30].
Footnotes
The views expressed in this article do not necessarily represent those of the US Food and Drug Administration
References
- 1.van der Laan MJ, Robins JM. Unified Methods for Censored Longitudinal Data and Causality. Springer; New York: 2003. [Google Scholar]
- 2.Pocock SJ, Assmann SE, Enos LE, Kasten LE. Subgroup analysis, covariate adjustment and baseline comparisons in clinical trial reporting: current practice and problems. Statistics in Medicine. 2002;21:2917–2930. doi: 10.1002/sim.1296. [DOI] [PubMed] [Google Scholar]
- 3.Hernández AV, Steyerberg EW, Habbema JD. Covariate adjustment in randomized controlled trials with dichotomous outcomes increases statistical power and reduces sample size requirements. Journal of Clinical Epidemiology. 2004 May;57(5):454–460. doi: 10.1016/j.jclinepi.2003.09.014. [DOI] [PubMed] [Google Scholar]
- 4.Assmann SF, Pocock SJ, Enos LE, Kasten LE. Subgroup analysis and other (mis)uses of baseline data in clinical trials. Lancet. 2000 Mar;355(9209):1064–1069. doi: 10.1016/S0140-6736(00)02039-0. [DOI] [PubMed] [Google Scholar]
- 5.Tsiatis AA, Davidian M, Zhang M, Lu X. Covariate adjustment for two-sample treatment comparisons in randomized clinical trials: a principled yet flexible approach. Statistics in Medicine. 2008;27(23):4658–4677. doi: 10.1002/sim.3113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang M, Tsiatis AAA, Davidian M. Improving efficiency of inferences in randomized clinical trials using auxiliary covariates. Biometrics. 2008;64(3):707–715. doi: 10.1111/j.1541-0420.2007.00976.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Braun TM, Feng Z. Misunderstandings between experimentalists and observationalists about causal inference. Journal of the American Statistical Association. 2001;96(456):1424–1432. [Google Scholar]
- 8.Gail MH, Mark SD, Carroll RJ, Green SB, David Pe E. On design considerations and randomization-based inference for community intervention trials. Statistics in Medicine. 1996 Jun;15(11):1069–1092. doi: 10.1002/(SICI)1097-0258(19960615)15:11%3C1069::AID-SIM220%3E3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- 9.Raz J. Testing for no effect when estimating a smooth function by nonparametric regression: a randomization approach. Journal of the American Statistical Association. 1990;85(409):132–138. [Google Scholar]
- 10.Rosenbaum PR. Covariance adjustment in randomized experiments and observational studies. Statistical Science. 2002;17(3):286–327. [Google Scholar]
- 11.Moore KL, van der Laan MJ. Covariate adjustment in randomized trials with binary outcomes: targeted maximum likelihood estimation. Statistics in Medicine. 2009;28(1):39–64. doi: 10.1002/sim.3445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Freedman DA. On regression adjustments to experimental data. Advances in Applied Mathematics. 2008;40(2):180–193. [Google Scholar]
- 13.Koch GG, Tangen CM, Jung JW, Amara IA. Issues for covariance analysis of dichotomous and ordered categorical data from randomized clinical trials and non-parametric strategies for addressing them. Statistics in Medicine. 1998;17(15–16):1863–1892. doi: 10.1002/(sici)1097-0258(19980815/30)17:15/16<1863::aid-sim989>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 14.Senn S. Testing for baseline balance in clinical trials. Statistics in Medicine. 1994;13(17):1715–1726. doi: 10.1002/sim.4780131703. [DOI] [PubMed] [Google Scholar]
- 15.Freedman DA. Randomization does not justify logistic regression. Statistical Science. 2008;23(2):237–249. [Google Scholar]
- 16.Imai K, King G, Stuart EA. Misunderstandings between experimentalists and observationalists about causal inference. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2008 Apr;171(2):481–502. doi: 10.1111/j.1467-985X.2007.00527.x. [DOI] [Google Scholar]
- 17.US FDA. International conference on harmonisation: guidance on statistical principles for clinical trials. 1998;63(179) [PubMed] [Google Scholar]
- 18.Robinson LD, Jewell NP. Some surprising results about covariate adjustment in logistic regression models. International Statistical Review/Revue Internationale de Statistique. 1991;59(2):227–240. [Google Scholar]
- 19.Robins JM. A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Mathematical Modelling. 1986;7(9–12):1393–1512. Mathematical models in medicine: diseases and epidemics, Part 2. [Google Scholar]
- 20.Robins JM. A graphical approach to the identification and estimation of causal parameters in mortality studies with sustained exposure periods. Journal of Chronic Diseases. 1987;40:139S–161S. doi: 10.1016/s0021-9681(87)80018-8. [DOI] [PubMed] [Google Scholar]
- 21.van der Laan MJ, Rubin D. Targeted maximum likelihood learning. The International Journal of Biostatistics. 2006;2(1):Article 11. doi: 10.2202/1557-4679.1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Robins JM. Robust estimation in sequentially ignorable missing data and causal inference models. Proceedings of the American Statistical Association; Alexandria, VA: American Statistical Association; 2000. [Google Scholar]
- 23.Robins JM, Rotnitzky A. Comment on the Bickel and Kwon article, “Inference for semiparametric models: Some questions and an answer”. Statistica Sinica. 2001;11(4):920–936. [Google Scholar]
- 24.Neugebauer R, van der Laan M. Why prefer double robust estimators in causal inference? Journal of Statistical Planning and Inference. 2005;129(1–2):405–426. [Google Scholar]
- 25.van der Vaart A, Wellner JA. Weak Convergence and Empirical Processes. Springer; New York: 1996. [Google Scholar]
- 26.Begg C. Significance tests of covariate imbalance in clinical trials. Controlled Clinical Trials. 1990;11(4):223–225. doi: 10.1016/0197-2456(90)90037-3. [DOI] [PubMed] [Google Scholar]
- 27.Permutt T. Testing for imbalance of covariates in controlled experiments. Statistics in Medicine. 1990;9(12):1455–1462. doi: 10.1002/sim.4780091209. [DOI] [PubMed] [Google Scholar]
- 28.van der Laan MJ, Dudoit S, Keles S. Asymptotic Optimality of Likelihood Based Cross-Validation. UC Berkeley Division of Biostatistics Working Paper Series. 2003 Feb; doi: 10.2202/1544-6115.1036. Working Paper 125. http://www.bepress.com/ucbbiostat/paper125. [DOI] [PubMed]
- 29.Sinisi S, van der Laan MJ. The deletion/substitution/addition algorithm in loss function based estimation: applications in genomics. Statistical Applications in Genetics and Molecular Biology. 2004;3(1) doi: 10.2202/1544-6115.1069. [DOI] [PubMed] [Google Scholar]
- 30.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B (Methodological) 1995;57(1):289–300. doi: 10.2307/2346101. [DOI] [Google Scholar]