Bargaining and fairness

Abstract

The idea that human morality might be the product of evolution is not popular. The reason is partly that the moral principles that actually govern our day-to-day behavior have been idealized in a way that makes a natural origin seem impossible. This paper puts the case for a more down-to-earth assessment of human morality by arguing that the evolution of our sense of fairness can be traced to the practicalities of food-sharing. When animals share food, they can be seen as enjoying the fruits of an implicit bargain to ensure each other against hunger. The implications of this observation are explored using the tools of game theory. The arguments lead to a structure for fair bargains that closely resembles the structure proposed by John Rawls, the leading moral philosopher of the last century.

Why do fairness considerations matter so much to us? The answer offered here depends on the observation that human social life can be seen largely as the play of a succession of coordination games. The Driving Game is perhaps the simplest example. We play this game each morning when we drive to work. It has three Nash equilibria. [A Nash equilibrium is a profile of strategies—one for each player—in which each strategy is a best reply to the other strategies (1). It is a Nash equilibrium if each player uses the same evolutionary stable strategy in a symmetric game, but evolutionary processes in some games can easily converge on Nash equilibria that do not correspond to an evolutionary stable strategy.] We can all drive on the left; we can all drive on the right; or we can randomize between left and right. Cultural evolution may eliminate the randomizing option, but there is nothing to distinguish between the two other alternatives. However, human societies are equipped with conventions or social norms for solving such equilibrium selection problems. In the Driving Game, France uses the social norm in which everybody drives on the right; Japan uses the social norm in which everybody drives on the left.

My contention is that fairness originated as such a social norm. Its function was to serve as an equilibrium selection device for certain coordination problems typified by the sharing of food. Such evolutionary explanations are unacceptable to most moral philosophers. Even the fact that the fairness norms of my theory resemble those proposed by John Rawls—widely regarded as the leading moral philosopher of the twentieth century (2)—carries no significance. Nor is my approach popular with behavioral economists, who commonly argue that evolution somehow has equipped us with altruistic preferences that make us care in a substantial way about the welfare of strangers (3). My own theory better fits an earlier approach to fairness pioneered by a school of social psychologists—Adams (4), Wagstaff (5), and many others—who call themselves “modern equity theorists.”

They argue that their laboratory experiments support Aristotle’s contention that “What is fair … is what is proportional.” They claim that fairness requires that gains for each person over the status quo should be proportional to what I shall call a “social index.” Psychologists are at pains to emphasize that the value of the social index depends both on the society under consideration and on the particular context in which the coordination problem arises. Relevant social parameters on which psychologists have focused are need, effort, ability, and social status. Everybody agrees, for example, that need should be paramount in distributing food in a famine but that need has no place in the award of Nobel Prizes.

The enterprise outlined in this article is to describe an evolutionary theory compatible with the principles of the neo-Darwinian orthodoxy that traces the origins of fairness norms from food-sharing arrangements that perhaps date from before language evolved in our species to the manifestations of fairness that have survived into modern times. This project is wildly ambitious—especially when squeezed into only a few pages—but I hope readers will understand that the aim is not to create a theory that will stand against all comers but only to demonstrate that a theory of this type is not beyond the bounds of possibility. More detail is provided in my various books and papers on fairness norms (6–9). For a biologist’s introduction to bargaining theory, see ref. 10.

Coordination in Repeated Games

From the perspective of game theory, human social life consists largely of the play of a succession of coordination games that we commonly solve without thought or discussion and usually so smoothly and effortlessly that we do not even notice that there is a coordination problem to be solved. Who goes through that door first? How long does Adam get to speak before it is Eve’s turn? Who should take how much of a popular dish of which there is not enough to go around? Who gives way to whom when cars are maneuvering in heavy traffic? Whose turn is it to wash the dishes tonight? These are picayune problems, but if conflict arose every time one of them needed to be solved, our societies would fall apart. Such coordination games commonly have a continuum of Nash equilibria. Repeated games will be used here to illustrate this phenomenon because of their special interest in modeling the possibility of food-sharing in prehuman times.

It is not easy to appreciate in the abstract the extent to which implicit agreements to coordinate on an equilibrium can generate high levels of cooperation among populations of egoists. That reciprocity is the secret seems to have been pointed out first by David Hume in 1739, but the idea has been repeatedly rediscovered, notably by a number of game theorists in the early 1950s (11).

The folk theorem of repeated game theory tells us that external enforcement is unnecessary to make a collection of Mr. Hydes cooperate like Dr. Jekylls. Trivers (12) aptly refers to this phenomenon as “reciprocal altruism.” It is necessary only that the players be sufficiently patient and that they know they are to interact together for the foreseeable future. The outcome can be left to their enlightened self interest, provided that they all can monitor each other’s behavior without too much effort—as, for example, must have been the case when we were all members of small hunter-gatherer communities.

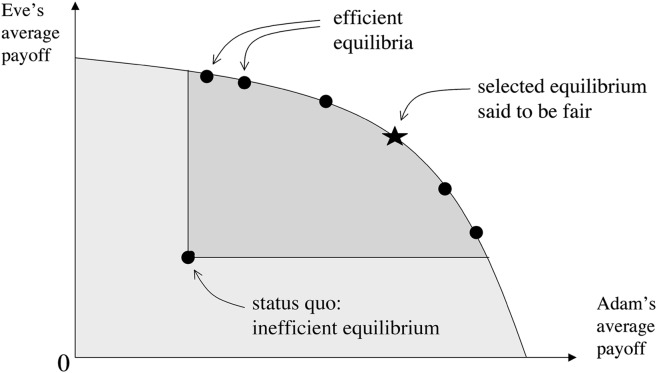
What outcomes can be sustained as Nash equilibria when a one-shot game—which need not be the Prisoners’ Dilemma—is repeated indefinitely often? The answer provided by the folk theorem is that any outcome whatever of the one-shot game can be sustained on average as a Nash equilibrium of the repeated game, provided that it awards each player a payoff that is not too small (i.e., a payoff that is at least as large as the minimax payoff in the one-shot game, which is the most one can receive if an opponent seeks to minimize the player’s payoff). In particular, as illustrated in Fig. 1, any outcome that assigns each player at least as much as some Nash equilibrium of the repeated game can itself be sustained as a Nash equilibrium outcome in the repeated game. This fact implies that indefinitely repeated games generically have a continuum of efficient Nash equilibria. (An outcome is efficient if no outcome that assigns each player a greater payoff is feasible.)

Fig. 1.

The folk theorem. The shaded region represents the set of payoff pairs available as outcomes in a one-shot game played between Adam and Eve. The more deeply shaded region shows the pairs of average payoffs available as Nash equilibrium outcomes in the indefinitely repeated game that assign each player at least as much as they get at an inefficient equilibrium serving as a status quo. For this result it is important that the players be very patient and that they cannot conceal their past play from each other.

Fig. 1 shows why the problem in equilibrium selection that fairness evolved to solve can be regarded as a bargaining problem. If a consensus cannot be reached, Adam and Eve will remain at the inefficient status quo. If they were to bargain face-to-face in a rational way, they would end up at one of the efficient outcomes in which both get more than they do at the status quo. The strongest contender for the rational outcome of such bargaining is the Nash bargaining solution, which is not to be confused with a Nash equilibrium (ref. 7, p. 25, and ref. 13).

Fairness norms presumably were operating before our species was capable of rational bargaining, and so the work of getting to a fair equilibrium needs to be attributed to evolution. The first step on the way is to explain why evolution should be expected to move a population from an inefficient equilibrium to an efficient equilibrium. Numerous computer simulations point in this direction, but I prefer the following retelling of a standard evolutionary story (ref. 7, p. 25, and ref. 13). (The story is not an example of Wynne-Edwards’ group selection fallacy because social norms are identified with equilibria of whatever game is being played, and selection among equilibria does not require that individuals sacrifice anything for the public good. What is unusual is only that a social norm of a parent society is transmitted to its colonies by cultural rather than genetic means.)

Suppose that many small societies are operating one of two social norms, a and b. If a is more efficient, and payoffs are interpreted as biological fitnesses, then the society operating norm a will grow faster. Assuming that societies cope with population growth by splitting off colonies that inherit the social norms of the parent society, we eventually will observe larger numbers of societies operating norm a than norm b.

The Golden Rule

The views expressed in this article so far largely share common ground with numerous scientifically minded authors, but I think we need to go much further if we are to make any progress in understanding how modern fairness norms work. However, I seem to be alone in arguing that all of the fairness norms that we actually use in daily life have a common deep structure captured in a stylized form by an idea that John Rawls (2) called “the original position” in his celebrated A Theory of Justice.

Rawls uses the original position as a hypothetical standpoint from which to make judgments about how to organize a just society. Citizens are asked to envisage the social contract to which they would agree if their current roles were concealed from them behind a “veil of ignorance” so that the distribution of advantage would seem determined as though by a lottery. “Devil take the hindmost” then seems unattractive, because you might end up at the bottom of the heap yourself.

The Golden Rule says that you should do unto others as you would have them do unto you. Rawls’ original position is a version that meets the objection: Do not do unto others as you would have than do unto you—they may not have the same tastes as you. Its basic structure is captured by our traditional personification of justice as a blindfolded matron bearing a pair of scales in one hand and a sword in the other. Her blindfold is Rawls’ veil of ignorance. She needs a sword to enforce her decisions. Her scales are necessary to weigh the relative well-being of different people in different situations.

The problem of comparing the utility of different people is vital for the question of fairness. In particular, if we were unable to say that we thought it preferable to be Adam in one situation as opposed to being Eve in another, we would be helpless to say anything at all behind Rawl’s veil of ignorance. Under mild conditions, John Harsanyi (14) showed that such empathetic preferences requiring us to see things from another’s point of view can be summarized by naming a rate at which Adam’s units of utility are to be traded off against Eve’s units (ref. 8, p. 293).

However, how do we acquire such standards of interpersonal comparison to which we implicitly appeal every time we make a fairness judgment? Further, why should it be thought that evolution would create fairness norms whose deep structure resembles the original position? Indeed, why should one suppose any deep structure in the first place?

Anthropology.

On the last question, the anthropological evidence is persuasive. There is no shortage of cultural differences between Kalahari bushmen, African pygmies, Andaman islanders, Greenland Eskimos, Australian aborigines, Paraguayan Indians, and Siberian nomads, but the consensus among modern anthropologists is strong that these and other pure hunter-gatherer societies that survived into the twentieth century all operated social contracts without bosses or social distinctions in which food, especially meat, was shared on a markedly egalitarian basis (15). Even Westermarck, a leading anthropologist who was famous for his moral relativism, agreed that the Golden Rule was universally endorsed in such societies (16).

How do we explain the strong parallels that anthropologists have uncovered between the social contracts of geographically distant groups? It sometimes is argued that the similarities are the result of parallel cultural evolution, but this notion seems unlikely to me because the groups live in such starkly different environments. It does not matter much to the theory being presented here, but I think the anthropological evidence suggests that we have a genetically determined disposition to use fairness norms that continues to exist uncomfortably underneath the layer upon layer of cultural imperatives that accompanied the agricultural revolution and the ensuing progression to a modern economy (17).

Implicit Insurance Contracts.

Why should evolution generate the original position? A possible answer requires looking at the economics of food-sharing. By sharing food, animals ensure each other against hunger. They cannot write insurance contracts in the human manner. Even if they could, they would have no legal system to which to appeal if one animal failed to honor its contractual obligation. However, the folk theorem tells us that evolution can get around the problem of external enforcement even for unrelated animals if they interact together repeatedly.

What would Adam and Eve need to take into account when bargaining over such a mutual insurance pact? Imagine a time before cooperative hunting had evolved in which Adam and Eve foraged separately for food. Each would be lucky sometimes and unlucky sometimes. An insurance pact between them would specify how to share the available food on days when one was lucky and the other unlucky.

If Adam and Eve were rational players negotiating an insurance contract, they would not know in advance who was going to be lucky and who unlucky on a given day. To keep things simple, suppose that both possibilities are equally likely. Adam and Eve then can be seen as bargaining behind a veil of uncertainty that conceals who is going to turn out to be Ms Lucky or Mr. Unlucky. Both players then bargain on the assumption that they are as likely to end up holding the share assigned to Mr. Unlucky as they are to end up holding the share assigned to Ms Lucky.

I think the parallel between bargaining over such mutual insurance pacts and bargaining in the original position is no accident. To establish the similarity, we only need to give Adam and Eve new names when they take their places behind Rawls’ veil of ignorance. To honor the founders of game theory, Adam and Eve will be called John and Oskar. Instead of Adam and Eve being uncertain about whether they will turn out to be Ms Lucky or Mr. Unlucky, the new paradigm requires that John and Oskar pretend to be ignorant about whether they will turn out to be Adam or Eve. It then becomes clear that a move to the device of the original position requires only that the players imagine themselves in the position of somebody else—either Adam or Eve—rather than in the position of one of their own possible future selves (ref. 9, p. 212 et seq.).

If Nature wired us to solve the simple insurance problems that arise in food-sharing in a rational way, she simultaneously provided much of the wiring necessary to operate the original position.

Empathetic Preferences

What will the outcome be if Adam and Eve bargain behind Rawls’ veil of ignorance? In my theory, the outcome is predicted by using the Nash bargaining solution on the assumption that players use their empathetic preferences to evaluate the possible outcomes from behind the veil of ignorance (ref. 9, p. 422 et seq.).

Someone expresses an empathetic preference when they say that they would prefer to be Adam drinking a cup of tea than Eve drinking a cup of coffee. [Expressing such an empathetic preference does not imply that one would make any sacrifice to help Adam get a cup of tea, but it is easy to see how empathetic preferences can be confused with altruistic (or sympathetic) preferences which imply a readiness to make such sacrifices.] Nobody denies the existence of empathetic preferences, but why has evolution provided us with the expensive mental equipment needed for making such hypothetical comparisons? I think they are necessary inputs to the device of the original position.

How could empathetic preferences evolve? John Harsanyi’s (13) theory of empathetic preferences reduces the problem to the evolution of the interpersonal comparison of utility, and here biology offers some solid ground.

Aristotle’s observation that the origins of moral behavior are to be found in the family is generally accepted. A game theorist will offer the explanation that the equilibrium selection problem is easier for evolution to solve in such games. The reason is found in Hamilton’s (18) rule, which explains that animals should be expected to care about a relative in proportion to their degree of relationship to the relative. Family relationships therefore provide a natural basis for making the kind of interpersonal comparison of utility that is necessary to operate the device of the original position. All that is required is that unrelated people be treated in the same way as sisters, cousins, or uncles for the purpose of making fairness judgments, much as newcomers to hunter-gatherer communities are treated as honorary kinfolk when adopted into the clan by marriage. If you interact only with kinfolk on a regular basis, what other template for behavior is available?

The social indices we use when discounting the fitnesses of our partners in a family game are somehow obtained by estimating our degree of relationship to our kinfolk from the general dynamics of the family. However, where do we get the social indices with which to discount Adam and Eve’s personal utilities when constructing an empathetic utility function? I think we develop the appropriate social indices by unconsciously imitating the behavior of fellow citizens whom we admire or respect. That is to say, the standard of interpersonal comparison of utility for dealing with folk outside our intimate circle of family and friends is attributed to the workings of cultural evolution.

Egalitarian Bargaining Solution

Noncooperative game theory has proved most useful in evolutionary biology, but rational bargaining solutions usually are studied using the axiomatic methods of cooperative game theory. It turns out that all sets of axioms that have been proposed for a bargaining solution in which full interpersonal comparison of utility is allowed (the axioms for the Nash bargaining solution mentioned earlier deny any comparison at all) lead to the egalitarian (or proportional) bargaining solution (ref. 7, p. 31). This solution yields the same bargaining outcome that modem equity theorists discovered empirically by asking laboratory subjects what they thought fair in various contexts. That is to say, it is fair that everybody’s share is proportional to whatever social index is appropriate to the context.

The final step in the theory is to show that the action of cultural evolution on culturally determined empathetic preferences eventually will result in the device of the original position implementing the egalitarian bargaining solution with social indices that are determined by the average shape of the feasible set from which fair selections have been made in the past. One then can vary this shape to examine how the social indices depend on such social parameters as need, effort, ability, and social status. For example, a person’s social index increases with need, provided that need is equated with the risks people are willing to take to satisfy their wants.

The details of these calculations are to be found in ref. 9, Chapter 4. We comment here only on the crucial criterion used to characterize evolutionary stability in the cultural context of the model.

Empathy Equilibrium

The empathetic preferences held by individuals in a particular society are seen as an artifact of their upbringing. As children mature, they are assimilated to the culture in which they grow up largely as a consequence of their natural disposition to imitate those around them. One of the social phenomena they will observe is the use of the device of the original position in achieving fair compromises. They, of course, are no more likely to recognize the device of the original position for what it is than we are when we use it in deciding such matters as who should wash how many dishes. Instead, they simply copy the behavior patterns of those they see using the device when they find themselves in a similar situation. They thereby come to behave as although they share the empathetic preferences of those whose fairness behavior they imitate.

The complexities of the actual transmission mechanism are short-circuited by regarding a set of empathetic preferences as being packaged in a social signal or meme. The imitative process is seen as a means of propagating such memes in much the same way that the common cold virus finds its way from one head to another. Only when the stability of the system in which everyone has been using a normal meme N is threatened by the appearance of a mutant meme M will anyone have reason to deviate from normal behavior.

Suppose that Adam is infected by a mutant meme M. What will happen when he interacts with Eve hosting a normal meme N in the circumstances of the original position? Both players will adjust their bargaining strategies according to the empathetic preferences they each find themselves holding until they reach a Nash equilibrium of their bargaining game. In realistic bargaining games with perfect information, such equilibrium play implements the Nash bargaining solution (which greatly simplifies the ensuing calculations) (ref. 7, Chapter 2). As a result, Adam and Eve each will receive some share of the available benefits and costs.

The imitation mechanism that determines when it is appropriate to copy the memes we observe others using will take into account who gets what share. Almost all onlookers currently will be subject to the normal meme N and so will evaluate the shares they see Adam and Eve receiving in terms of the empathetic preferences embedded in N. If Adam’s share exceeds Eve’s, then it is assumed that onlookers are more likely to be taken over by the meme M controlling Adam than by the meme N controlling Eve. However, M then will be a better reply to N than N is to itself, and so N will not be evolutionarily stable.

Therefore a necessary condition for the evolutionary stability of a normal population is that the empathetic preferences held by the players constitute what I call an “empathy equilibrium” (ref. 9, p. 224). To test whether a pair of empathetic preferences constitutes an empathy equilibrium, each player should be asked the following question:

Suppose that you could deceive everybody into believing that your empathetic preferences are whatever you find it expedient to claim them to be. Would such an act of deceit seem worthwhile to you in the original position relative to the empathetic preferences that you actually hold?

The right answer for an empathy equilibrium is no.

It is important that this criterion assumes that imitation is based on a person’s empathetic preferences rather than on their personal preferences or biological fitnesses. Onlookers are placed in the circumstances of the original position because, when we imitate the behavior of others, we do so in the circumstances in which we see the behavior being used. However, the neo-Darwinian paradigm is not threatened, because the function of a fairness norm in this theory is only to solve the equilibrium selection problem in coordination games whose payoffs are biological fitnesses. According to this account, fairness evolved as a quick way of balancing power rather than as the substitute for power that moral philosophers commonly think necessary.