Culture-dependent strategies in coordination games

Abstract

We examine different populations’ play in coordination games in online experiments with over 1,000 study participants. Study participants played a two-player coordination game that had multiple equilibria: two equilibria with highly asymmetric payoffs and another equilibrium with symmetric payoffs but a slightly lower total payoff. Study participants were predominantly from India and the United States. Study participants residing in India played the strategies leading to asymmetric payoffs significantly more frequently than study participants residing in the United States who showed a greater play of the strategy leading to the symmetric payoffs. In addition, when prompted to play asymmetrically, the population from India responded even more significantly than those from the United States. Overall, study participants’ predictions of how others would play were more accurate when the other player was from their own populations, and they coordinated significantly more frequently and earned significantly higher payoffs when matched with other study participants from their own population than when matched across populations.

Convention is a sense of common interests; which sense each man feels in his own breast, which he remarks in his fellows, and which carries him, in concurrence with others into a general plan or system of actions, which tends to public utility….

David Hume, 1748, Enquiry Concerning Human Understanding

There are strong evolutionary and selective pressures that push humans toward correctly coordinating their behaviors (see refs. 1–6). Indeed, when study participants repeatedly play games that involve coordination among multiple equilibria, they often eventually coordinate successfully (e.g., refs. 7–12). However, in many settings individuals interact with new people over time and thus must draw on other cues to guide their play and resolve strategic uncertainty over how others might play. To this end, societies can evolve culture or convention, operating through social norms that guide expected behaviors and help them coordinate in settings in which there are multiple possible stable (equilibrium) outcomes. These can help provide a sense of what play is “focal” (ref. 13, p. 57) and evidence of focal play has been found, for instance, by the authors of ref. 14 who ran pure coordination experiments in which two study participants simultaneously chose numbers from a list and coordinated on specific numbers more frequently than if they chose at random. Nonetheless, what is focal in the presence of multiple equilibria is not always obvious, and one can then expect that different conventions or expectations might arise in different cultures. There is some evidence that culture can affect play in games. In particular, the authors of ref. 15 conducted experiments on ultimatum games, dictator games, and public-goods games, with “study participants from 15 small-scale societies exhibiting a wide variety of economic and cultural conditions” (ref. 15, p. 73). They found study participants deviating from self-interested play and with some levels of cooperation dependent on their backgrounds, and that “substantial variability in experimental behaviors across groups is an expression of the large between-group differences in the structures of social interaction and modes of livelihood” (ref. 15, p. 77), with degree of market integration being positively correlated with cooperative behavior.

This issue of cultural determinants of what is focal can be important as it makes cross-cultural interaction challenging and could potentially be a driving force for homophily: the tendency of individuals to associate with others of similar characteristics or backgrounds with greater frequency than they appear in the population (e.g., refs. 16 and 17). The precise driving forces behind homophily are still not well understood, and evidence that people with similar backgrounds are better able to coordinate and anticipate each others’ play than people with differing backgrounds would provide some foundation for a preference to interact with others of similar backgrounds. Shared history and expectations allow people from a similar background to predict each others’ behaviors and what they might anticipate as focal, and that facilitates coordination; whereas interacting with people from different cultures can lead to costly miscoordinations in behavior (see ref. 18 for a related model of the evolution of homophily). This would be consistent with findings indicating that with (revealed) preference, in some settings people may prefer to associate with others who are similar to themselves (e.g., refs. 19 and 20).

Here we investigate the influences of study participants’ backgrounds on their behaviors in one-shot coordination games—and whether study participants of similar backgrounds are better able to coordinate. The game we consider is a variation of a battle-of-the-sexes game. Study participants have three possible strategies. If they both choose the same strategy they earn a positive payoff, but if they choose different strategies they earn nothing. One of the strategies leads to equal payoffs (30 units each), whereas the other two lead to asymmetric payoffs (50 for one player and 20 for the other player). Such asymmetries can complicate coordination (e.g., ref. 21) and offer a potential role for culture. For example, does a culture provide a sufficient convention for equalizing payoffs for study participants to find the symmetric strategy focal, or will study participants expect each other to opt for more asymmetric payoffs?

To access a study participant pool with diverse cultural backgrounds, we recruited study participants from Amazon Mechanical Turk (https://requester.mturk.com). As pointed out by ref. 22, study participants in many university-based experiments tend to be “WEIRD,” i.e., from Western, educated, industrialized, rich, and democratic backgrounds. Ref. 22 states that (as for 2008) WEIRD study participants comprise 96% of study participants in a sample of published articles, but 12% of the world population. In addition, they tend to be university students, which is then a small subset of the populations within WEIRD settings. Amazon Mechanical Turk gives us access to a much richer and larger study participant pool than from a standard university study participant pool. For most of our sessions we focused on comparisons of populations from India and the United States, with a variety of demographic backgrounds as discussed in The Experiments and Findings.

We find that there are significant differences in the play across study participants’ country of origin. Study participants from India play the asymmetric equilibrium significantly more than study participants from the United States, and they are also significantly more likely to react to a prompt to play it. Study participants’ predictions of their partner’s play are more accurate when their partner is from the same country, and they earn higher average payoffs when their partner is from their own country.

The Experiments and Findings

The Study participant Pool.

Our experiments* were run on Amazon Mechanical Turk between September and December of 2013 and involved more than 1,300 study participants, 1,290 of whom passed the understanding test and allowed to proceed to the rest of the experiment^† (precise population sizes for various treatments^‡ appear in SI Appendix, Table S19). The population was 43% from India and 54% from the United States.^§ In both locations the study participant pool was approximately 10% students, 63% employed, 11% unemployed, and 3% retired, with the rest in either informal employment or “other” categories. The Indian study participant pool had higher education levels whereas the US study participant pool had higher nominal income levels. The study participants’ ages ranged from 18 to 83, with the average equal to 31 in India and 34 in the United States, and the Indian population was 61% male whereas it was 53% in the United States. Detailed demographics appear in SI Appendix, Figs. S6 and S7.

A typical treatment took roughly 15 min and study participants earned on average about US$1 (on par with typical Amazon Mechanical Turk payments), consisting of a 50-cent fixed payment and earnings based on play in the games and answering of other questions (e.g., regarding beliefs and elicitation of certainty equivalence). We also ran some sessions with 10 times higher payments per token, and the results are analogous and still significant, but with many fewer observations and reported in SI Appendix, section 6.3.2.

The Structure.

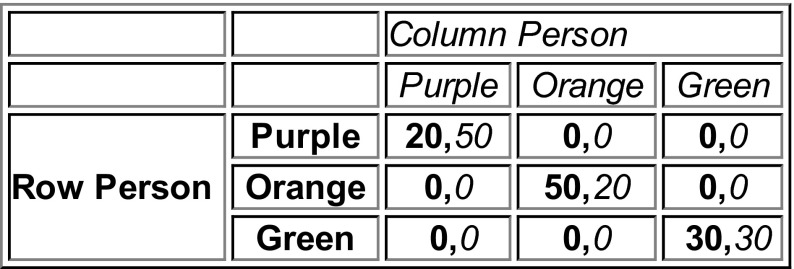
Our experiments were based on the coordination game in Fig. 1, which is a variation of the well-known battle-of-the-sexes game, with an additional symmetric option. If the two players chose the same color, they would earn positive payoffs, whereas if they miscoordinated on their choices of colors then they would earn zero (although they did earn a base payoff from participating in the experiment). The game had two asymmetric pure strategy equilibria, and one symmetric pure strategy equilibrium, as well as four mixed strategy equilibria.

Fig. 1.

The game. This figure displays the base game played by the study participants. A study participant was randomly assigned to be either the “column person” or “row person.” Each study participant chose one of the three colors: purple, orange, or green. A study participant did not know the other’s choice when making his/her own choice. The pair of numbers in each cell represented the study participants’ payoffs when the corresponding pair of colors were chosen, with the first number for the row person (boldface) and the second number for the column person (italics). This matrix as well as verbal interpretations were presented to all study participants.

Game theory, through refinements such as stochastic stability, suggests that a society should end up playing pure strategy equilibria over time in this game, but is agnostic on which one of the equilibria. Moving beyond formal analyses based on evolutionary forces or stochastic refinements, there is a suggestion that the (a)symmetries in the game provide some basis for coordination. For example, both players playing the color green could serve as a focal point of the game because it is the only symmetric positive payoff pair of pure strategies of the game.

Let us begin by examining how players play in the absence of any prompts, and then examine how they are influenced both by explicit prompts in the experiment, and based on their backgrounds.

Base Play.

When faced with a one-shot play of this game, the study participants played as listed in Table 1.^¶ As we see in Table 1, the study participants fail to coordinate on any particular equilibrium, including any of the mixed strategy equilibria. The play differs significantly from play in the fully mixed equilibrium at the 1% level ($P=0.000$ under Hotelling’s T-squared generalized means test). Nevertheless, although they fail to coordinate fully on any equilibrium, they are biased toward the pure strategy equilibrium of playing green, with 62% playing green and that being the unique best response to the population play. One argument for green being the focal equilibrium is that it is the only pure strategy equilibrium which offers equal payoffs to the players and thus might be seen as “fair,” which has been seen as an attractor in previous experiments (e.g., refs. 10 and 23).

Table 1.

Play of the base game

Item	Color with high payoff for self, %a	Color with low payoff for self, %	Green, %b	Sample size
Play	23	15	62	351
(Fully) mixed equilibrium	48	19	32	—

The first row presents the frequency of possible plays in the base game among the whole population. The second row presents the corresponding probabilities in the fully mixed equilibrium of the game, which is significantly different from what study participants did. As an overall population, study participants failed to coordinate on any particular equilibrium. Green (that leads to symmetric payoffs upon coordination) is the most played color, with a 30% higher frequency than predicted by the fully mixed equilibrium $\left(P=0.000\right)$.

^aRefers to the color of play with high payoff (50) for self when coordination is achieved: orange for the row person or purple for the column person. The column indicating color with low payoff for self is the reverse of these.

^bLeads to symmetric payoff (30,30) when coordination is achieved.

The Influence of Study participants’ Backgrounds.

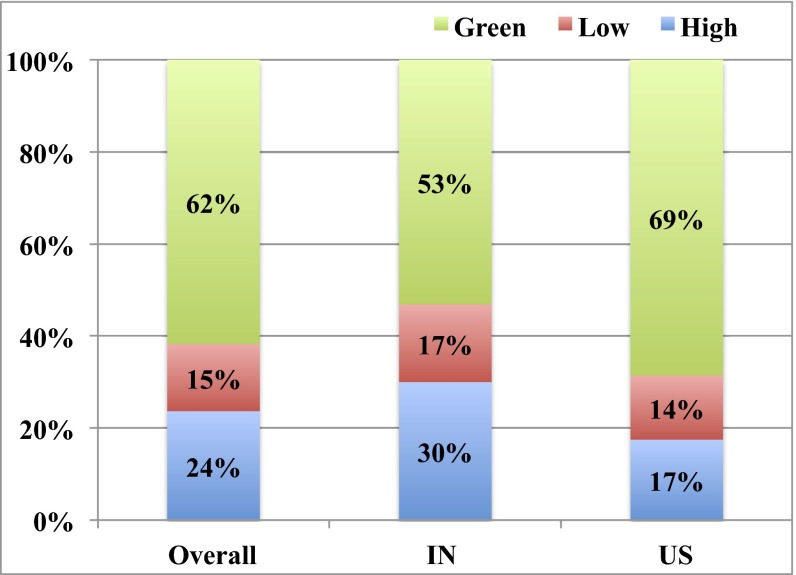
The backgrounds of the study participants also turn out to play a significant and substantial role in determining their play. In particular, the study participants’ country in which they reside affects how they play. We see this first in the base play. As seen in Fig. 2, the study participants located in India play the actions that lead to asymmetric payoffs (both high and low) with higher probabilities, and the green action that leads to symmetric payoffs with lower probability than study participants located in the United States. In particular, the study participants located in India play Green with a 16% lower probability than those in the United States $\left(P=0.001\right)$, and that percentage of play is mostly (13%, $P=0.003$) transferred to playing the color that leads to the high payoff, although there is also a small increase in the play of the low payoff action. (Unless otherwise noted, the P values are from direct regressions of play on study participants’ locations. Regressions controlling for additional demographics are provided in Location and Other Demographics.)

Fig. 2.

Play of the base game by study participant background. This figure presents the frequency of play by color in the aggregated population (left bar), the Indian population (center bar), and the US population (right bar). “IN” and “US” refer to the study participant’s location in either India or the United States, whereas “high” and “low” are as defined in Table 1. Sample sizes: 151 in India, 180 in the United States, and 351 overall (including 20 study participants from outside of India/United States in the base games). Green is the most frequently played color (by 62% of the population). Study participants from India played green with a 16% lower frequency than those from the United States $\left(P=0.001\right)$, and 13% of that frequency is transferred to playing high $\left(P=0.003\right)$.

The backgrounds also affect the reactions of the study participants to the prompts, as we examine next.

Play with a Prompt: An Artificial Culture.

Let us examine how the study participants reacted to a prompt.

The prompt was simply an observation of a color that corresponded to one of the labels of the three possible actions. In particular, study participants were told that they were in a room of a given color and that the person that they were matched with was also in the same room.^‖ We did not call attention to the color as a correlating device in any way: We just offered the information before asking the study participants how they would play the game. We intentionally chose to present the prompts in the above form instead of as an explicit recommendation (see refs. 23–25 for experiments examining the effects of explicit recommendations on coordinating behaviors), so that the study participants have a common signal that can be used as a cue, mimicking something which may be focal in the real world, but without feeling pressured to act by the experimenter.

Let us first examine the distribution of play when the prompt was for the players being in either a purple or orange room. These are similar in that one of the players is advantaged by the prompt, in that it could suggest that one of the players earns his or her highest payoff if the players play the equilibrium corresponding to the room’s color, while the other player is disadvantaged. (Game theory is largely silent on such issues, as it is an equilibrium for both players to see that they are in an orange room and then play the strategies of purple. Thus, for the prompt to have any impact, natural language has to have some connotation, so that study participants associate the color of the prompt with the same color action and believe that other study participants might also do so. For more on this, see refs. 26–29.) Given this symmetry, we pool these two different room color prompts together and report play based on which player was advantaged by the prompt and which was disadvantaged.

The partner's location does not affect study participants’ play significantly (SI Appendix, Table S13), so we pool together observations.

As we see in Table 2, the prompt to play an asymmetric equilibrium makes a significant difference in the play. Overall, the play of the symmetric (green) strategy drops by 16% $\left(P=0.000\right)$ when faced with the prompt, whereas the corresponding play of the asymmetric strategies increases by the same amount. The effect is present for both the advantaged and disadvantaged players. Despite having a similar drop in the amount of green play, the advantaged and disadvantaged players’ reaction differed in terms of following the prompt versus going against it and playing the reversed asymmetric equilibrium. The advantaged are more likely to follow the prompt, whereas the disadvantaged are relatively more likely to go against the prompt. Both, however, have a substantial increase in the amount of play that is coordinated on the prompted equilibrium. The effect is sufficiently large that for the advantaged players it becomes a unique best response to the population distribution of plays to follow the prompt although not so for the disadvantaged who are still best off playing green in response to the population distribution of plays.

Table 2.

Play of the game with a prompt for one of the asymmetric equilibria (purple or orange)

Population	Follow the prompt, %a	Opposite of the prompt, %b	Green, %	Sample size
Overall	39	16	46	994
Advantagedc	44	11	46	500
Disadvantaged	34	21	46	494

This table presents the frequency of play of each color in the game with a prompt for one of the asymmetric equilibria (purple or orange), in the overall population (first row), the advantaged study participants (second row), and the disadvantaged (third row). Compared with play in the base game (Table 1, first row), the play of green drops by 16% $\left(P=0.000\right)$. The advantaged and disadvantaged study participants’ reactions have a similar drop in green, but the advantaged are significantly more likely to follow the prompt.

^aRefers to playing the color of the prompt.

^bRefers to playing the color other than the prompt and other than green.

^cA study participant is advantaged if he or she is the one who earns the higher (50) payoff if both study participants in the game follow the color of the prompt; with disadvantaged having the other obvious definition.

We also included a prompt of green. Interestingly, as we see in Table 3, the prompt for green does not affect play significantly—as it matched the baseline case fairly closely.

Table 3.

Play of the game with a prompt for the symmetric equilibrium (green), compared with play of the base game

Item	Color with high payoff for self, %	Color with low payoff for self, %	Green, %	Sample size
Play, with the green prompt	26	15	59	153
Play, base game	23	15	62	351

The first row presents the frequency of play of each color in the game with a prompt for the symmetric equilibrium (green), in the overall population. The second row presents (for comparison) the corresponding frequencies from the base game (Table 1, first row). The frequencies with the prompt for green are similar to those from the base game (without any prompt).

The Influence of Study participants’ Backgrounds, with the Artificial Culture.

Let us consider how the study participants react to the prompt to play the asymmetric equilibrium as a function of their location.

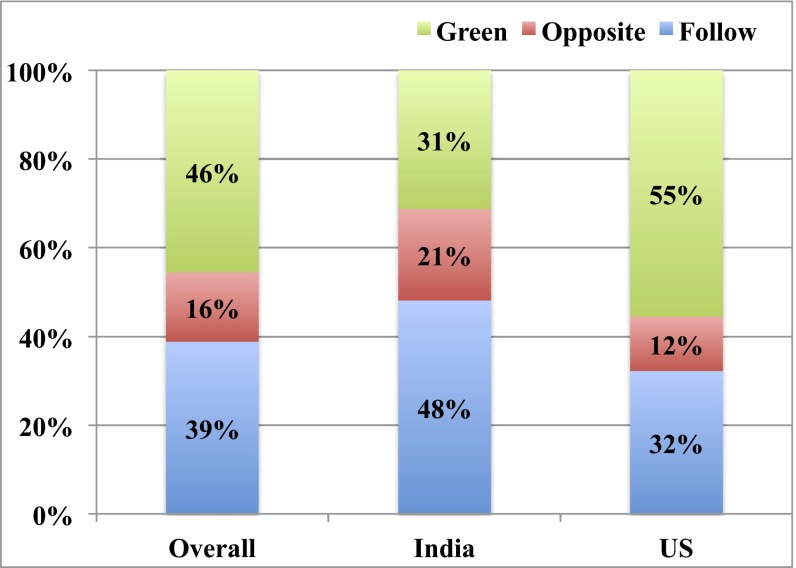
In Fig. 3 and Table 4, we see strong differences in how the two different populations react to the prompts. Again, the Indian study participants play the asymmetric equilibrium substantially more than the US population, and are more likely to follow the asymmetric prompt. When advantaged, study participants from India play the prompted color 58% of the time, compared with 34% for the US-based study participants; a difference of 24% $\left(P=0.000\right)$.

Fig. 3.

Play of the game with prompt for an asymmetric equilibrium by study participant background. This figure presents the frequency of play of each color in the game with a prompt for one of the asymmetric equilibria (purple or orange), in the aggregated population (left bar), the Indian population (center bar), and the US population (right bar). “Follow” and “Opposite” are defined in Table 2. Sample sizes: 994 overall with 408 in India and 586 in the United States.

Table 4.

Play of the game with prompt for an asymmetric equilibrium by study participant background

Population	Follow the prompt, %	Opposite of the prompt, %	Green, %	Sample size
Overall	39	16	46	994
Advantaged	44	11	46	500
Disadvantaged	34	21	46	494
India	48	21	31	408
Advantaged	58	14	28	202
Disadvantaged	38	27	34	206
United States	32	12	55	586
Advantaged	34	9	57	298
Disadvantaged	31	16	54	288

This table presents the frequency of play of each color in the game with a prompt for one of the asymmetric equilibria (purple or orange), in the aggregated population (rows 1–3), the Indian population (rows 4–6), and the US population (rows 7–9). The advantaged in both populations play high more often when prompted to do so than when not (Fig. 2). In particular, that increase is 27% $\left(P=0.000\right)$ for the India-based study participants, compared with 17% $\left(P=0.000\right)$ for the US-based study participants; and the former is significantly larger than the latter $\left(P=0.079\right)$. Thus, not only are the India-based study participants more likely to play the asymmetric equilibrium to begin with, they also react significantly more frequently to an asymmetric prompt to play it.

For the advantaged, playing the prompted color is choosing “the color with high payoff for self” (i.e., high). The advantaged in both populations play high more often when prompted to do so than when not (Fig. 2). In particular, that increase is 27% $\left(P=0.000\right)$ for the India-based study participants, compared with 17% $\left(P=0.000\right)$ for the US-based study participants; and the former is significantly larger than the latter ($P=0.079$; from a difference-in-difference regression). Thus, not only are the India-based study participants more likely to play the asymmetric equilibrium to begin with, they also react significantly more frequently to an asymmetric prompt to play it.

This holds to the point where it is a best response when matched with the Indian population to follow the prompt to play the asymmetric strategies (when either advantaged or disadvantaged); whereas it is best to play the symmetric green strategies when matched with the US population.

There are also interesting effects from the green prompt.

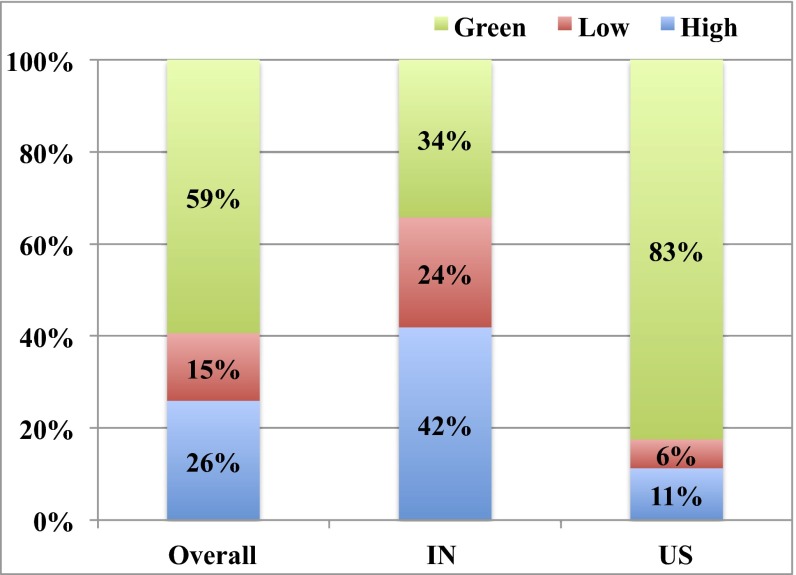
As we see from Fig. 4, although the prompt for symmetric play has little effect on the average play, it actually has quite different effects on the two populations. For the Indian population it leads to more asymmetric play—they play green 19% less frequently $\left(P=0.006\right)$ than in the base case, whereas for the US population it leads to 14% more $\left(P=0.017\right)$ play of green than in the base play (comparing with Fig. 2).

Fig. 4.

Play of the game with a prompt for the symmetric equilibrium (green) by study participant background. This figure presents the frequency of play of each color in the game with a prompt for the symmetric equilibrium (green), in the aggregated population (left bar), the Indian population (center bar), and the US population (right bar). Sample sizes: 153 overall with 73 in India and 80 in the United States. The US-based study participants are more likely to react to the symmetric prompt by playing green: they play green more than the India-based study participants by 49% (83–34%, $P=0.000$), larger $\left(P=0.000\right)$ than the 16% difference (69–53% in Table 1, $P=0.001$) in the base game (without any prompt).

One conjecture that would account for this reaction to the prompt is that it causes the study participants to think more about each other’s potential actions and forecasting of plays, which leads to different expectations for the two populations (see more in Beliefs, where we discuss belief elicitation).

Homophily, Best Responses, and Beliefs

Homophily and Best Responses.

Players from different locations are best matched with others from their own location. Given that none of the populations are fully coordinating on an equilibrium, this is not implied directly. It could be, for instance, that both populations would fare best when matched with one of the two and not the other. In fact, in the pure base play this is true: Both of the populations’ frequencies of play achieve their highest payoff against the US population. This comes from the fact that green is the best response to both populations, and played by a majority of both populations, but played with higher frequency in the US population. We see this in Table 5.

Table 5.

Coordination and payoffs of the base game by study participant background

	Probability of coordination		Expected payoff
Population/play	Against India	Against the United States	Against India	Against the United States
India	0.38	0.44	12.0	13.6
United States	0.44	0.52	13.2	15.8
High	0.17	0.14	8.4	7.0
Low	0.30	0.17	6.0	3.5
Green	0.53	0.69	15.9	20.6

This table presents the frequencies of coordination (left two columns) and the average payoffs (right two columns) in the base game (without any prompt). Rows 1 and 2 are respectively for representative study participants (who play according to the frequency in the own population) from India and the United States, and rows 3–5 are respectively for study participants who play high, low, and green. Columns 1 and 3 are calculated when the other player is a representative India study participant, and columns 2 and 4 are when the other player is a representative US study participant. All numbers are calculated based on the empirical frequencies of play in the base game (Fig. 2). Both populations achieve their highest expected payoff against the US population, given that green is the best response to baseline play in each country and the US plays it more.

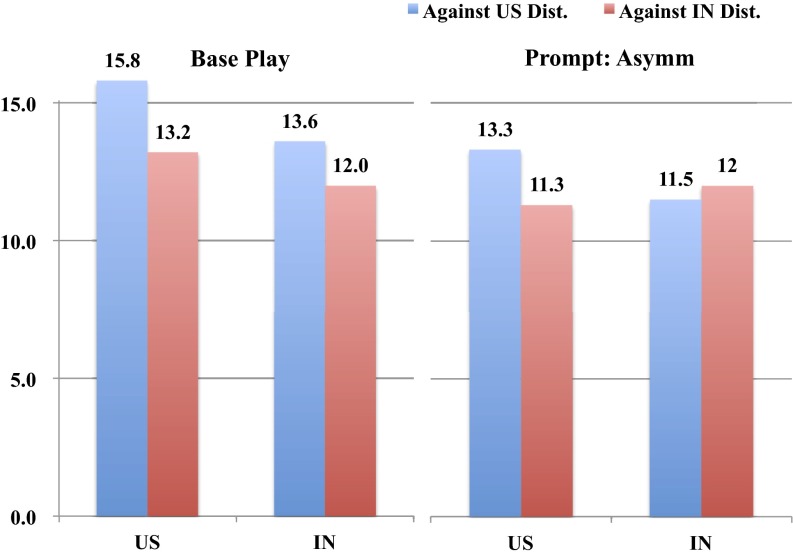
However, in the game with the prompts there are greater asymmetries entering, and each population fares better when matched with itself, as we see in Fig. 5, Right.

Fig. 5.

Expected payoffs by study participant background. This figure presents the expected payoff in the base play (without any prompt in Left), and in the game with a prompt for an asymmetric equilibrium (Right). US and IN refer to a representative study participant who follows the empirical frequency of play in the United States and Indian populations. “Against US Dist.” indicates that the other player follows the empirical frequency of play in the US population (blue bars) and “Against IN Dist.” is similarly defined (red bars). Unlike the base play, where both populations achieve a higher payoff against the US population, with a prompt for an asymmetric equilibrium (Right) each population earns a higher payoff when matched with itself.

Table 6 provides details on the payoffs from various strategies against the different populations. There we see that the best response of players in India when matched with others from India is to follow the prompt (when both advantaged and disadvantaged), whereas in the United States it is to ignore the prompt and play green.

Table 6.

Coordination and payoffs of the games with prompt for an asymmetric equilibrium by study participant background

	Probability of coordination		Expected payoff
Population/play	Against India	Against the United States	Against India	Against the United States
Advantaged
India	0.36	0.35	14.8	13.9
United States	0.35	0.42	12.8	14.7
Follow	0.38	0.31	19.2	15.4
Opposite	0.27	0.16	5.5	3.1
Green	0.34	0.54	10.3	16.1
Disadvantaged
India	0.36	0.35	9.2	9.2
United States	0.35	0.42	9.7	12.0
Follow	0.58	0.34	11.6	6.7
Opposite	0.14	0.09	6.8	4.5
Green	0.28	0.57	8.5	17.2
Overall
India	0.36	0.35	12.0	11.5
United States	0.35	0.42	11.3	13.3

This table reports the right half of Fig. 5 in more detail. It presents the frequencies of coordination and the average payoffs in games with a prompt for an asymmetric equilibrium (purple or orange). Rows 1–5 are for advantaged study participants and rows 6–10 are for disadvantaged study participants. Among both the advantaged and the disadvantaged, both the Indian and the US populations fare better when matched with themselves, both in terms of the frequencies of coordination and the payoffs.

Most importantly, we see from the bottom of Table 6 that each population earns a strictly higher payoff when matched against itself than when matched with the other population, and also coordinates more often. The pattern that a higher payoff is earned when matched with a player's own population can also be found in the game with the symmetric prompt (green), as reported in Table 7.

Table 7.

Coordination and payoffs of the game with a prompt for the symmetric equilibrium by study participant background

	Probability of coordination		Expected payoff
Population/play	Against India	Against the United States	Against India	Against the United States
India	0.32	0.34	10.5	10.3
United States	0.34	0.69	10.3	20.9
High	0.24	0.06	12.0	3.1
Low	0.42	0.11	8.4	2.3
Green	0.34	0.83	10.3	24.8

This table presents the frequencies of coordination and the average payoff in the game with a prompt for the asymmetric equilibrium (green). The labels of the rows and columns are similar to those defined in Table 5. Both populations achieve higher payoffs when matched with themselves. In particular the US population’s payoff is doubled when matched with itself (20.9) compared with when matched with the Indian population (10.3).

The background culture of the societies, through the way it affects their proclivity to play the symmetric equilibrium or the asymmetric ones, provides reasons for the population to interact with itself.

Beliefs.

Some of the study participants were asked to report how they expected their partners to play. Results are reported in Tables 8–10. Players’ beliefs differ across their backgrounds, just as their play does, and in directions that correspond to the biases in their play. There was a substantial variation in the beliefs reported by individual, but the group averages are roughly in line with the actual play of their own group’s play even when asked to predict the other group’s play.

Table 8.

Reported beliefs of the base game by study participant background

Population	Color with high payoff for selfa	Color with low payoff for self	Green	Sample size
Overall	23.4 [23.3]	35.0 [24.1]	41.6 [27.4]	101
India	25.4 [25.2]	35.1 [24.6]	39.5 [27.2]	66
United States	19.5 [18.9]	34.9 [23.4]	45.5 [27.9]	35

This table presents the reported beliefs (in percent) in the base game, for the aggregated population (row 1), the Indian population (row 2), and the US population (row 3). Beliefs are elicited in percentage points, and each number is the average of those reported in the corresponding population, across the two cases (one against another Indian study participant and the other against another US study participant). SDs appear in brackets.

^aRefers to the color of play with the high payoff (50) when coordination is achieved for the study participant whose belief is elicited: orange for the row person or purple for the column person (color with low payoff for self is the reverse of these).

Table 9.

Reported beliefs with prompt for an asymmetric equilibrium by study participant background

Population	Follow the prompta	Opposite of the prompt	Green	Sample size
Overall	38.5 [25.9]	30.4 [23.2]	31.1 [25.2]	117
Advantaged	33.5 [25.6]	39.1 [25.7]	27.3 [24.6]	54
Disadvantaged	42.7 [25.7]	23.0 [17.8]	34.3 [25.4]	63
India	37.7 [23.7]	34.7 [22.4]	27.6 [20.9]	78
Advantaged	34.9 [24.4]	41.0 [24.2]	24.1 [17.9]	40
Disadvantaged	40.7 [22.9]	28.0 [18.5]	31.3 [23.8]	38
United States	39.9 [30.3]	22.0 [22.6]	38.1 [31.2]	39
Advantaged	29.6 [29.4]	33.9 [30.2]	36.6 [37.2]	14
Disadvantaged	45.7 [29.8]	15.3 [13.8]	39.0 [28.0]	25

This table presents the reported beliefs in games with a prompt for an asymmetric equilibrium, for the aggregated population (rows 1–3), the Indian population (row 4–6), and the US population (row 7–9). Beliefs are elicited and reported as in Table 8. SDs appear in brackets.

^aDefined as in Table 2.

Table 10.

Reported beliefs with a prompt for the symmetric equilibrium by study participant background

Population	Color with high payoff for selfa	Color with low payoff for self	Follow prompt: Green	Sample size
Overall	22.2 [20.7]	35.8 [23.5]	42.0 [25.3]	149
India	27.6 [23.9]	35.2 [22.2]	37.3 [25.4]	69
United States	17.6 [16.2]	36.4 [24.8]	46.0 [24.8]	80

This table presents the reported beliefs in the game with a prompt for the symmetric equilibrium, for the aggregated population (first row), the Indian population (second row), and the US population (third row). Beliefs are elicited and reported in a manner as in Table 8. SDs appear in brackets.

^aDefined as in Table 8.

We also had treatments in which study participants were told they would be matched with players in certain locations—either the United States or India. When told the other player’s location, the players do not significantly adjust their strategies (SI Appendix, Table S13). This suggests that players’ beliefs about how others will behave is not changing with cultural background, even though the play and beliefs differ across study participants’ own backgrounds. Moreover, the study participants are not substantially more confident in the predictions about players from their own country compared with those from the other country. When study participants were asked to choose whether they would like to double the payoff of their play versus other players in the United States or India, they chose their own country only between 50% and 60% of the time (SI Appendix, Table S14).

Location and Other Demographics

Our analysis has focused on location as the distinguishing characteristic in play. There are other demographics that correlate with location and so we can examine their influences. An obvious one is religion. The Indian population is predominantly Hindu, with some Christian. The United States is predominantly Christian and nonreligious. (See SI Appendix, Fig. S6 for more details.) The only overlap that allows for some identification is the Christian population.

We examine whether Christians’ play differs based on location. Table 11 reports on study participants’ play in games with the prompts to play the asymmetric (purple or orange) equilibria, for Christians by location.

Table 11.

Play of the game with a prompt for the asymmetric equilibrium by Christians, by study participant background

Population	Follow the prompt, %a	Opposite of the prompt, %	Green, %	Sample size
Overall	39	16	46	994
India	48	21	31	408
United States	32	12	55	586
Christian	41	14	44	315
Christian India	55	23	22	65
Christian US	37	12	51	233

This table presents the frequency of play of each color in the game with a prompt for one of the asymmetric equilibria (purple or orange) in the aggregated population (rows 1–3) and the Christian population (rows 4–6). The differences in play based on locations remain in the Christian population, who play indistinguishably from the overall population and in both locations.

^aDefined as in Table 2.

In Table 11, we see that the Christian population plays quite differently based on location, and in fact Christians in India play statistically indistinguishably from the Indian population as a whole, and similarly for Christians within the United States. Thus, we do not see evidence that it is religion that drives behavior rather than the study participant’s country of residence; in fact we find that study participants of the same religion play quite differently based on their country of residence.

To examine study participants’ play in more detail, we control for other demographic variables such as employment, education, and gender. Even when controlling for these demographic characteristics, the country of residence is still a significant predictor of behavior as shown in the Table 12. (Income is not included in this table as we only have it for a subset of the study participants. We include regressions with income variables in SI Appendix, Table S15 and the country of residence remains a significant predictor of behavior.)

Table 12.

Regressions of play based on demographics

	Base play			With a prompt for the asymmetric equilibrium; purple/orange			With a prompt for the symmetric equilibrium; green
Variable	High	Low	Green	Followa	Oppositeb	Green	High	Low	Green
Dummy_Indian	0.150***	0.004	−0.154**	0.150***	0.075***	−0.225***	0.298***	0.170***	−0.467***
Dummy_advantagedc	—	—	—	0.099***	−0.101***	0.002	—	—	—
Certainty_equivalentd	−0.019**	0.001	0.018*	−0.008	−0.009*	0.017***	−0.012	0.002	0.011
Observations	331	331	331	994	994	994	152	152	152

The symbols ***, **, and * indicate significance at the 99%, 95%, and 90% levels respectively. The dummy for residence in India is still significant in showing less play of green and more asymmetric play after controlling for other demographics (including gender, education, employment, and whether reversals exhibited when answering the certainty_equivalent question).

^aRefers to playing the color of the prompt.

^bRefers to playing the color other than the prompt and other than green.

^cOnly applies to columns 4–6; dummy_advantaged, 1 if the study participant is the one who earns the higher (50) payoff if both study participants in the game follow the color of the prompt; with disadvantaged having the other obvious definition.

^dThe reported certainty equivalent of 10 tokens with 50% chance and 0 tokens with 50% chance.

One possible reason for country residence to still be a significant predictor, is that individuals in a common location have to coordinate with each other even across some other characteristics, and thus they develop some aspects of conventions or culture to help guide this coordination.

Discussion

The differences in play by study participant background are significant, suggesting that some aspect of those backgrounds might influence which play they find focal (and expect the other study participants to find focal) in these one-shot coordination games. Given that the main thing to focus on in these games is the symmetry or asymmetry of different equilibria, it might be that differences in symmetries of treatments within a population are more or less common and affect their views. For example, although both countries have reasonably high levels of income inequality, there is a striking difference in terms of the percentages of the two populations living below the poverty line. According to the World Development Indicators (The World Bank, http://databank.worldbank.org): India had 32.7% of its population lying below US$1.25 in purchase power parity in 2010, whereas that number in the United States was negligible (less than 1%). Are such background factors responsible for differences in propensities to choose strategies leading to asymmetric payoffs or are there other influences at work? Understanding the forces in peoples’ backgrounds that shape their expectations and behaviors in a variety of settings may help us to better understand homophily and why it is such a pervasive phenomenon. Given the differences found here, further examination of the factors that may influence peoples’ abilities to coordinate and anticipate others’ behaviors seems to be an important area for further research, including a closer look at cultural divisions within a country.