Abstract
In this work, the temperature effects due to Joule heating obtained by application of a DC electric potential were investigated for a microchannel with cylindrical insulating posts employed for insulator based dielectrophoresis (iDEP). The conductivity of the suspending medium, the local electric field, and the gradient of the squared electric field, which directly affect the magnitude of the dielectrophoretic force exerted on particles, were computationally simulated employing COMSOL Multiphysics. It was observed that a temperature gradient is formed along the microchannel which redistributes the conductivity of the suspending medium leading to an increase of the dielectrophoretic force towards the inlet of the channel while decreasing towards the outlet. Experimental results are in good agreement with simulations on the particle trapping zones anticipated. This study demonstrates the importance of considering Joule heating effects when designing iDEP systems.
Keywords: dielectrophoresis, Joule heating, electrokinetic, microchannel
1. Introduction
Microfluidics is a rapidly growing field that made significant contributions in many areas, including bioanalytical applications. Working with miniaturized devices offer attractive advantages such as shorter processing times, portability and enhanced resolution and sensitivity. There are important efforts devoted towards the development of separation and analytical techniques that can be used in microfluidic devices. Electrokinetic (EK) techniques have become one of the main pillars in microfluidics due to their great flexibility and simplicity. EK processes can be used with a wide array of bioparticles: DNA, proteins, bacteria, mammalian cells, parasites, etc. [1-3]
Proposed by Pohl in 1951, dielectrophoresis (DEP) is the EK motion of particles due to polarization effects when particles are subjected to alternating current (AC) or direct current (DC) non-uniform electric fields [4]. A great number of traditional microdevices which apply this technique rely on the use of arrays of electrodes to create regions of low and high electric field intensity, i.e. non-uniformity of the electric field, and therefore induce the polarization effect on particles [5]. There are some drawbacks on electrode-based DEP (eDEP) such as the cost and complexity related to microfabrication of electrodes and the loss of performance of electrodes due to fouling, which is common when handling bioparticles [6].
As an alternative to traditional eDEP, in insulator-based dielectrophoresis (iDEP) the non-uniformity of the electric field is achieved by straddling insulator structures or posts between two electrodes. In 2003, Cummings and Singh introduced a straight channel with an arrangement of cylindrical insulating posts to dielectrophoretically manipulate microparticles [7]. Since then, multiple applications have been reported using devices with diverse changes in their designs. Trapping and separation of live and dead cells, separation of bacteria and yeast, concentration of DNA and proteins, among others, have been published [6, 8-12]. Mathematical modeling for the dielectrophoretic force combined with electroosmotic pathlines has also been shown for similar channels [9, 12-15]. Other iDEP devices have been used to manipulate microparticles, which use AC or DC electric fields and change the shape of the channel to induce their non-uniformity [10, 16-18].
Such novel iDEP designs rely on the application of an electric potential and manipulate cells and other particles with a combination of electroosmotic flow (EOF), electrophoretic, and DEP forces, often using high potentials to achieve a desired response. The electric current coupled with these potentials can produce significant Joule heating through a microchannel, which may lead to considerable temperature increase of the sample fluid. The dielectric properties, such as conductivity and permittivity, of the suspending medium are temperature dependent. This means that a change in temperature will be reflected in those properties and will have a direct effect on the local electrokinetic (EK) and dielectrophoretic forces [8, 19, 20].
Temperature effects due to Joule heating have been reported for microfluidic systems. Xuan et al. [21] studied velocity perturbations in electroosmotic flow in a capillary employing fluorescence-based thermometry. In a more recent study [22] this group modeled the separation efficiency when Joule heating was considered employing a voltage ramp for capillary zone electrophoresis. By applying the initial voltage ramp, heating is lowered resulting in a higher number of theoretical plates and therefore, improved separation is achieved. Other important studies have been reported on the effect of Joule heating in CE [23, 24]. The temperature dependence of the zeta potential was experimentally proved by Venditti et al. [25] for straight microchannels. Although the temperature was controlled by a hot plate and Joule heating was neglected for the experimental conditions, electroosmotic flow was observed to be temperature dependent.
Joule heating effects have been extensively studied in dielectrophoresis-based microdevices. Temperature rise due to Joule heating was modeled by Yao [26] for a quadrupole electrode-based dielectrophoretic device. When 3 V of electric potential were applied to the electrodes an increase of around 1 K was detected. The effect is more significant when iDEP devices are used, since usually higher potentials are applied, as mentioned before. An increase of around 50 K was reported by Sabounchi et al. [27] downstream of a channel with circular insulators when 1500 V were applied for 20 seconds, and a gradient of temperature was observed along the channel. According to the authors, failure of dielectrophoretic trapping at highly conductive suspending mediums and high electric fields was attributed to Joule heating effects. The electrothermal effects on a channel with a single constriction were modeled by Hawkins and Kirby when a DC-offset, AC electric field was generated [28]. Joule heating creates vorticity near the channel reduction, especially when the channel is between 2 and 7 times wider than the constriction and the media has a high conductivity, which affect the EOF, particle deflection, and the dielectrophoretic trapping of particles. A similar iDEP device with a constriction was used by Sridharan et al. [29], where the focus was on the temperature effects on the electroosmotic flow. Mathematical and experimental results were presented, and the temperature was related to the local electric field intensity, which was more important at the channel constriction. More recent studies reported by this group [30, 31] also analyzed the effects of Joule heating on dielectrophoretic particle trapping. Another work presented by Lewpiriyawong et al. [32] demonstrated that a DC-AC offset reduces Joule heating by lowering the necessary trapping voltage for microspheres, but insight about the temperature role in the system is not provided. Zellner et al. [20] and Braff et al. [8] have also been proposed 3D-iDEP devices to lower significantly the voltage needed in order to achieve dielectrophoretic trapping of targeted particles and therefore minimize Joule heating effects. In these reports, 3D constrictions were molded on microchannels to induce large electric gradients with low potentials, and trapping of microspheres [20] and bacteria [8] was obtained with very low temperature increases.
Other important efforts have been devoted to study and control heating in iDEP devices [20, 28-31]. In a related study Davalos et al. [33] explored the use of surfactants to lower the voltage trapping threshold, which could be employed to mitigate Joule heating effects. Simmons et al. [34] showed that different materials can be used to make iDEP devices, which could alter these results and should be considered based on the investigators specific design. The present work was done assuming the devices were made from PDMS/glass. Other studies have explored a number of different materials to make iDEP devices including glass [35], polymers [33], PDMS, and silicon [20].
Although there are reports on the modeling of temperature profiles on iDEP devices, the effect of Joule heating on the dielectrophoretic force has not been fully explored. The present research is focused on the assessment of the temperature gradients generated within a microchannel with insulating structures due to an applied DC electric potential; its effect on the dielectrophoretic force and the particle trapping capacity of the device. Mathematical modeling was carried out to enable a comparison of a system that takes into account Joule heating effects to one without such consideration. These results have to potential to be used as a guideline for considering the effects on temperature gradients on the dielectrophoretic force and trapping efficiency on the design of future iDEP microdevices.
2. Theory
Dielectrophoresis relies on the polarization effects of a particle when it is subjected to non-uniform electric fields. Within this condition, the Coulombic forces at each end of the particle will be different and therefore an electrokinetic movement will be created by a net force imbalance. This dielectrophoretic force for a spherical particle can be expressed as [4]:
| (1) |
where εm is the permittivity of the suspending medium, rp is the particle radius, ∇E2 is the gradient of the squared electric field, and Re(fCM) is the real part of the Clausius-Mossotti (CM) factor. When low frequency AC or DC electric fields are used, the CM factor can approximated using the real conductivities of the particle (σp) and the suspending medium (σm) [36]:
| (2) |
Depending on the dielectric properties of the particle and the suspending medium, the sign of the dielectrophoretic force can be either positive or negative. If the CM factor is positive (positive DEP) the particle will move towards regions of higher electric field gradient since it is more polarizable than the suspending medium. On the other hand, if the particle is less polarizable than the medium, the CM factor is negative (negative DEP) and the particle will move away from those regions of high electric field gradient.
The dielectrophoretic mobility (μDEP) and velocity (v⃗DEP) for a spherical particle on a suspending medium with a viscosity η are defined as [37]:
| (3) |
| (4) |
Other electrokinetic forces present in a system when a DC electric field is generated are electrophoresis (EP) and electroosmotic flow (EOF). The electrokinetic force (EK) is the superposition of EP and EOF, and for a microchannel with a negative surface charge, such as glass or PDMS [38], the electrokinetic particle velocity (v⃗EK) can be defined as follows [39]:
| (5) |
| (6) |
| (7) |
where μEO and μEP are the electroosmotic and electrophoretic mobilities, and v⃗EO and v⃗EP are the electroosmotic and electrophoretic velocities, respectively, which can be estimated from the Helmholtz-Smoluchowski equation [40]:
| (8) |
| (9) |
where ζp and ζs are the zeta potential of the particle and substrate, respectively.
To achieve trapping of particles, v⃗DEP must overcome v⃗EK, if neglecting any other motion forces. It can be assumed that particle immobilization is achieved when the expression j⃗ · E⃗ = 0 is satisfied, where j⃗ is the flux of particles and can be expressed as [14, 41, 42]:
| (10) |
where C is the concentration of particles. Considering the dielectrophoretic and electrokinetic mobilities, the trapping expression can be deduced as:
| (11) |
where c is a correction factor that accounts for unconsidered phenomena and measurement errors. Hence, trapping of particles can be obtained at any region when the following condition is satisfied:
| (12) |
As shown, the magnitude of the local electric field is related to the overall particle mobility (μEO and μEP) and to the magnitude of the dielectrophoretic force exerted on the particle. The focus of this manuscript is to show that this field (E⃗) depends greatly on the conductivity of the suspending medium which is affected by changes in temperature; this relationship can be expressed as:
| (13) |
where σ0 is the conductivity at a reference temperature T0, and α is the temperature coefficient of the suspending medium electric conductivity (0.02 1/K) [43]. The temperature dependence on fluid viscosity and media permittivity were considered negligible in this study as they are not parameters in the trapping condition (Equation 12).
A mathematical model was built with COMSOL Multiphysics (Version 4.2, Comsol Inc., Burlington, MA, USA) to estimate the temperature rise and conductivity changes of the suspending medium within the microchannel. The model allowed predicting the distribution of the electric field, dielectrophoretic force, conductivity, and temperature gradients. Two dimensional geometries were created using AutoCAD (AutoCAD Mechanical 2012, Autodesk Inc., San Rafael, CA, USA) and imported into COMSOL. The device domain was defined as a 0.5 cm × 2.25 cm rectangle representative to typical device dimensions. The microfluidic device geometry was inserted into the center of this domain. The Joule Heating module was used to solve for the potential distribution, as described by the Laplace Equation, within the device:
| (14) |
where ϕ is the electric potential, this equation is solved with boundary conditions:
| (15) |
| (16) |
| (17) |
where n⃗ is the normal vector to the surface, J⃗ is the electrical current and Vin is the electrical potential applied between the posts. The boundaries considered are the surface of the microchannel walls and cylindrical insulating posts. To achieve dielectrophoretic trapping of the microparticles, DEP must overcome EK forces [14].
The heat generated by resistive losses (Qt) was calculated assuming Joule heating occurred strictly due to conduction currents:
| (18) |
Time domain heat transfer was solved using a combination of the Solid and Fluid Heat Transfer Modules. Heat transfer in fluid domains was calculated as:
| (19) |
where ρ is the density, Cp is the heat capacity, u is the local velocity field, and Qt is the total heat generated. Heat transfer in solid domains was calculated as:
| (20) |
Fluid domains were assigned a velocity based on electroosmotic flow due to the electric field distribution (Equation 5). The left most boundary of the sample channel was prescribed a constant temperature of 20°C to account for the inflow of room temperature media. The right most boundary of the sample channel was prescribed an outflow boundary to account for fluid flow out of the system:
| (21) |
where k is the thermal conductivity, n⃗ is a vector normal to the surface, and T is the element temperature. The thermal conductivity of the media (km) was modeled using a third order approximation of water:
| (22) |
The exterior boundaries of the geometry representing the edges of the device were prescribed a Surface-to-Ambient Radiation boundary condition:
| (23) |
with the ambient temperature (Tamb) fixed to 20 °C. The electrical and thermal parameters used in the model are shown in Table 1. All solutions were calculated using a Time Dependent solver for a minimum of 30 seconds. Additional simulations were run (results not shown) with constant temperature (T =20°C), thermal insulation (−n·(k∇T) = 0), and convection (−n·(k∇T) = h·(Tamb−T), h=300 W/m2s) exterior boundary conditions which resulted in a maximum deviation in temperature within the sample channel of 0.092%, 1×10-12%, and 0.035% in each case, respectively.
Table 1.
Parameter values used in the finite element model with COMSOL.
| Parameter | Value | Units |
|---|---|---|
| εm | 80ε0 | [m-3kg-1s4A2] |
| η | 8.90E-04 | [N1s1m-2] |
| ζ | 0.1 | [V] |
| σ0 | 0.01 - 0.001 | [S1m-1] |
| T0 | 293.15 | [K] |
| α | 0.02 | [K-1] |
| kPDMS | 0.2 | [W1m-1K-1] |
| εPDMS | 4ε0 | [m-3kg-1s4A2] |
| σPDMS | 8.33E-13 | [S1m-1] |
A triangular mesh was created and successively refined until the solution changed less than 0.2% between refinements. The final geometry contained 70,782 elements, 289,890 degrees of freedom, and solutions took 26 minutes and 50 seconds to solve on a quad core 3.0 GHz processor with 8GB of RAM.
3. Materials and methods
3.1 Microdevice
A schematic representation of the microchannel used in the experiments is presented in Figure 1. The design consisted on a 20 mm-long, 750 μm-wide, and 10 μm-deep channel with cylindrical insulating structures embedded at its center. The insulators were 100 μm in diameter, in a square array spaced 150 μm center-to-center, and arranged in 30 columns of 4 rows each, having a half cylindrical post row located along the channel sides.
Figure 1.
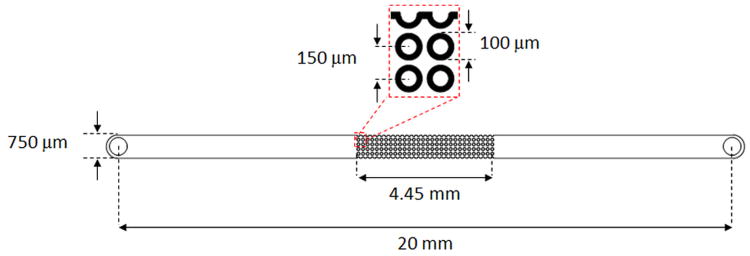
Schematic representation of the channel. It consists of a 20 mm-long, 750 μm-wide, and 10 μm-deep straight channel containing an array of insulating cylindrical structures of 100 μm in diameter arranged 150 μm center-to-center.
This device was fabricated in polydimethylsiloxane (PDMS) using standard photolithographic procedures. SU8 2007 photoresist (MicroChem Corp., Newton, MA, USA) was spun at 1500 rpm for 50 seconds into a clean glass slide, and then followed by a soft bake process at 95 °C for 10 minutes. The design of the microchannel was patterned on the photoresist by exposition through a mask to a longwave UV lamp (B100AP, UVP LLC, Upland, CA, USA) for 40 s. Post exposure bake was then achieved at 95 °C for 10 minutes, afterwards SU8 developer was used to remove unpolarized photoresist, and finally the mold was baked at 120 °C for 10 minutes. Previously degassed liquid PDMS on a 10:1 ratio of monomers to curing agent (Sylgard 184, Dow Corning, Midland, MI, USA) was poured into the mold and then cured at 120 °C for 20 minutes. Fluid connections were punched into the cured PDMS channel using a 1.5-mm core borer (Harris Uni-Core, Ted Pella Inc., Redding, CA, USA). Degassed liquid PDMS on a 10:2 ratio of monomers to curing agent (Sylgard 184, Dow Corning, Midland, MI, USA) was spun into a clean glass slide followed by a soft bake at 120 °C for 3 minutes for the bonding process with the PDMS containing the fluidic channel. Finally, after the bonding process, the device was post baked at 120 °C for 20 minutes.
3.2 Equipment
Dielectrophoretic effects on the microspheres were observed with the use of an Axiovert 200 inverted microscope (Carl Zeiss, Göttingen, Germany), which has an integrated color camera to record the behavior as pictures and videos processed with the software AxioVision LE (Carl Zeiss, Göttingen, Germany). A 10× objective was used for the experiments. The microscope has a fluorescent lamp used for excitation of fluorescent polystyrene beads. Direct current electric fields were generated with a 3000 V high voltage sequencer, model HVS448 (LabSmith, Livermore, CA, USA) by employing 0.3048 mm in diameter platinum wire electrodes (Electron Microscopy Sciences, Hatfield, PA, USA) placed at each reservoir. Both, the inverted microscope and the high voltage sequencer require the use of a personal computer for operation.
3.3 Sample preparation and dielectrophoretic experiments
For the dielectrophoretic experiments, yellow-green carboxylate-modified polystyrene microspheres with 1 μm in diameter (Invitrogen, Carlsbad, CA, USA), ex/em 505/515 nm, were resuspended in mediums to a concentration of 1×108 spheres/mL. Suspending mediums consisted on DI water with a conductivity of 0.0025 S/cm and DI water adjusted to a conductivity of 0.01 S/m by adding KH2PO4.
4. Results and discussion
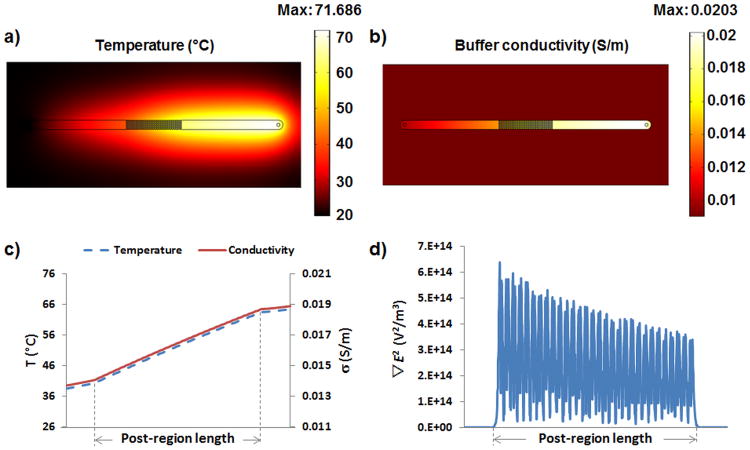
A set of experiments was carried out in order to assess the effect of Joule heating on the magnitude of the dielectrophoretic force required to achieve particle trapping. Figures 2a-2c illustrate the temperature and conductivity increase within the microdevice, due to Joule heating when 1,500 V are applied for 30 s across the microchannel. For these experiments the buffer employed had an initial conductivity of 0.01 S/m at a starting temperature of 20 °C. Simulations with COMSOL also show a significant rise in temperature (Fig. 2a) to about 71 °C and an increase in conductivity (Fig. 2b) of more than 100% from its initial value (from 0.01 to 0.0203 S/m). The electroosmotic flow induced by the applied DC potential drives cold water into the channel from the inlet, which is then heated by Joule heating at the post region and finally continues its flow to the outlet. This creates the gradient of temperature and buffer conductivity across the post region as seen in Figure 2c. The slope of the graphs suggests that the area acts as an electric resistor which produces the increase in the temperature. Figure 2d represents the effect that the change in temperature, and therefore in conductivity, has on the gradient of the electric field squared (∇E2). As shown in Figure 2d, this value decreases across the post region (from 6.36 ×1014 to 3.24 ×1014 V2/m3), directly decreasing the dielectrophoretic force exerted on the particles – thus, decreasing particle trapping.
Figure 2.
a) Temperature and b) conductivity gradient inside the iDEP microdevice when 1,500 V are applied for 30 s to a buffer with σ0= 0.01 S/m; c) temperature and conductivity gradient in the post-region of the device when 1,500 V are applied for 30 s with σ0= 0.01 S/m; d) gradient of the electric field squared (∇E2) in the post-region of the device, where a significant decrease in the magnitude can be observed longitudinally to the channel.
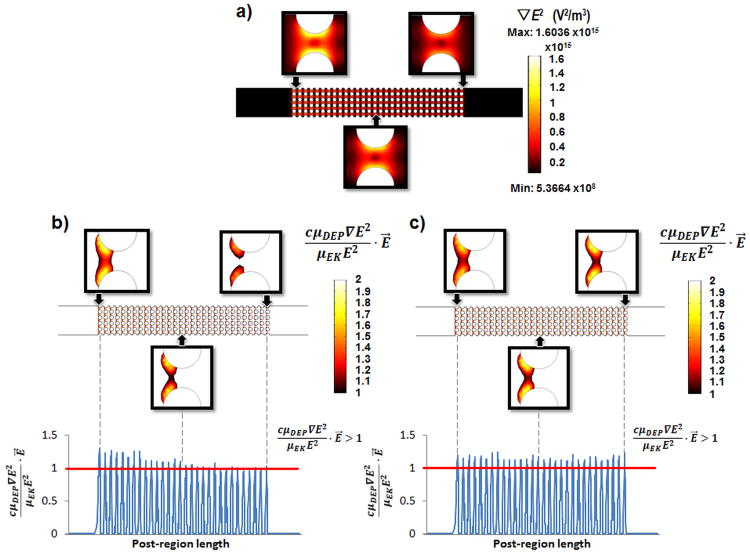
To further study the effect of temperature and conductivity gradients on the dielectrophoretic force, simulations were carried out to predict the effectiveness of particle trapping as a temperature dependent parameter. Figure 3a presents the distribution of ∇E2 within the device, and therefore the areas where the dielectrophoretic force will have maximums. The regions of ∇E2max are shown in orange-yellow; these are the specific regions where particles will be repelled due to negative dielectrophoretic forces when DC potentials are applied. It can be noticed that further along the device, these regions decrease in area and magnitude, which means lower dielectrophoretic trapping; increasing the possibility for targeted particles to continue their electroosmotic flow path instead of being trapped by DEP. Figure 3a demonstrates that particle trapping is stronger at the beginning of the post region and decreases along the post region.
Figure 3.
a) Gradient of the electric field squared (∇E2) when Joule heating is considered; b) particle trapping zones when Joule heating is considered; and c) particle trapping zones when Joule heating is neglected. Simulations with 1,500 V applied for 30 seconds in a channel filled with a buffer with σ0= 0.01 S/m, with a correction factor (c) of 200 for eqn. (12).
To assess the effect of Joule heating on particle immobilization, the regions of particle trapping as denoted by eqn. (12) were simulated with COMSOL [14]. Figures 3b and 3c represents the trapping zones obtained when 1,500 V are applied for 30 s (same conditions as Fig. 2). For these simulations the correction factor (c) for the trapping condition in eqn. (12) was set to 200. Figure 3b depicts the trapping regions considering Joule heating, while Figure 3c neglects these effects. It can be observed that, by considering Joule heating, the regions where particles can be immobilized decrease in size across the length of the post region and at the last column of posts effective traps are not obtained. By plotting the magnitude of the trapping condition (which has to be >1) along the center of the device it can be seen that particle immobilization will only be achieved in the first half of the post-region, since only these values are greater than 1. On the other hand, by neglecting Joule heating effects (Fig. 3c) the magnitude of the trapping condition is above 1 for the entire length of the post region, which would mean effective dielectrophoretic trapping across the entire post array.
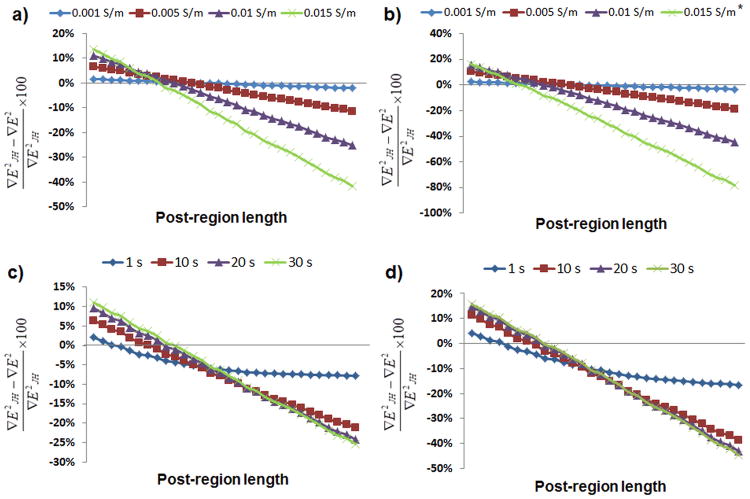
Buffers with different conductivities were evaluated through simulations in order to further analyze the effect of conductivity on ∇E2. Figure 4a-b shows the changes in ∇E2 obtained considering four buffer conductivities (σ0): 0.001, 0.005, 0.01, and 0.015 S/m. These values were obtained considering an applied potential of 1,000 V in Figure 4a and 1,500 V in Figure 4b for 30 s at an initial temperature of 20 °C. It should be noticed that the simulation of an applied voltage of 1,500 V with an initial conductivity of 0.015 S/m was terminated at 17 s because after that time the temperature achieved in the system exceeded the 100 °C which would create evaporation of water and therefore the end of an experiment. The computed values for these buffers were then compared to those simulated when Joule heating is not considered (constant conductivity of σ0). Figure 4a-b shows the % variation in ∇E2 when Joule heating is considered (∇E2JH) by comparing with values obtained neglecting Joule heating (∇E2). It can be observed that greater variations in ∇E2 are obtained when higher buffer conductivities (σ0) are employed. This is an important consideration when designing a device to be used with high conductive buffers, such as 0.015 S/m. In these cases, heating must be considered or errors up to 41.67% with 1,000 V or even up to 78.33% with 1,500 V at the last column of posts can be reached (half of the post section will have variation > 15%). At an applied potential of 1,000 V, buffers with a σ0 of 0.01 and 0.005 S/m will have maximum variations of 25.31% and 11.44%, respectively, which correspond to the end of the post region. On the other hand, when 1,500 V are applied in the system, these buffers will present differences up to 44.71% and 18.83%, for buffers with σ0 of 0.01 and 0.005, respectively, achieved also at the last column of posts. Buffers with low conductivities, such as 0.001 S/m, are not expected to produce significant heating, thus, leading to variations around 3% as shown by the simulations. Mathematical simulations were also performed considering non-steady state to evaluate the behavior of ∇E2 as function of time. It can be observed from Figure 4c-d that even after 1 s of applying either potential studied a difference of more than 5% is obtained, and that the value of ∇E2 remains stable after 30 s. These simulations were calculated for a buffer with σ0 = 0.01 S/m at 20 °C.
Figure 4.
Difference between the values for the gradient of the electric field squared (∇E2) when Joule heating is considered and when it is not. By applying a) 1,000 V and b) 1,500 V for 30 s to buffers with four different initial conductivities; by applying c) 1,000 V and d) 1,500 V to a buffer with σ0= 0.01 S/m and graphing the difference at 1, 10, 20, and 30 s. * The simulation with σ0= 0.015 S/m at an applied potential of 1,500 V was terminated at 17 s since the system reached 100 °C after this time.
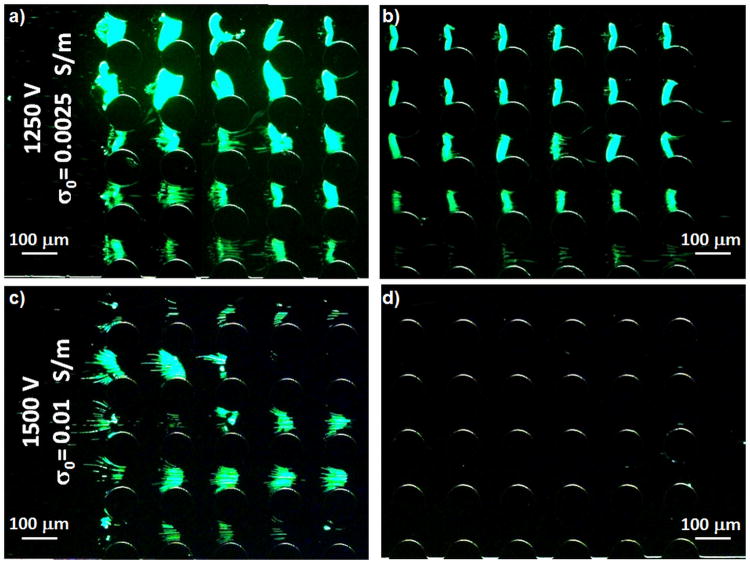
An experimental comparison of the results with two suspending buffer conductivities of σ0 of 0.0025 and 0.01 S/m was performed to evaluate the dependence of dielectrophoretic trapping capabilities on initial buffer conductivity (σ0). Figure 5 shows the results obtained when 1250 V and 1500 V were applied for 30 s; the images show the particle trapping obtained at the beginning and at the end of the post array for both buffer conductivities and both applied potentials. As anticipated with the simulations, a lower temperature increase and less significant effect on the negative dielectrophoretic trapping of the particles was obtained with the lower buffer conductivity (σ0 = 0.0025 S/m). DEP is strong enough to overcome EK and therefore immobilize particles throughout the entire microdevice, close the inlet (Fig. 5a) and close the end of the post array (Fig. 5b). One would expect stronger DEP effect at a higher applied voltage, however, when 1500 V are applied for 30 with a buffer with σ0 = 0.01 S/m, Joule heating generates a significant temperature rise, leading to a temperature gradient along the post region. This temperature difference rearranges the electric field distribution which in turn varies the gradient of the electric field squared (∇E2) in the post region; decreasing the magnitude of the dielectrophoretic force along the post array. Thus, the dielectrophoretic force is high enough to overcome EK at the beginning of the posts area and particles are trapped (Fig. 5c), but this is not the case closer to the microchannel outlet, as particles escape from their dielectrophoretic traps (Figure 5d).
Figure 5.
Experimental results on the dielectrophoretic behavior of 1 μm microspheres. a) DEP overcomes EK and trap particles by negative DEP when 1,250 V are applied with σ0 = 0.0025 S/m at the beginning of the insulating structures; b) 1,250 V are also enough to trap particles by negative DEP at the end of the post regions with σ0 = 0.0025 S/m; c) DEP overcomes EK and trap particles by negative DEP when 1,500 V are applied with σ0= 0.01 S/m at the beginning of the insulators; d) 1,500 V are not enough to overcome EK at the end of the insulating structures array when σ0= 0.01 S/m.
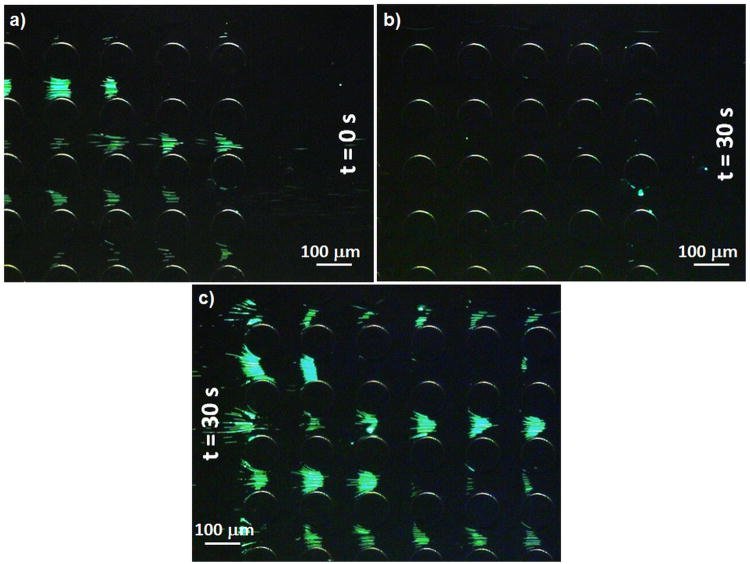
Figure 6 shows a second experiment performed to analyze the effect of time with Joule heating; a potential of 1500 V was applied in a device filled with buffer with σ0 = 0.001 S/cm. Figure 6a shows the end of the post area when the voltage was just applied (t = 0 s). Particles are getting trapped since heating has just started; and no significant temperature gradient has been generated yet. However, even during this initial stage, some particles have escaped from their dielectrophoretic traps, as shown by the empty traps. After 30 s, it can be seen that there are no particles left at the last columns of posts, as they have flown towards the outlet of the device. After 30 s of accumulated heating, DEP was no longer strong enough to overcome EK (Fig. 6b) and immobilize the particles. Fig. 6c shows that successful particle trapping can still be obtained at the beginning of the post array after 30 s clearly demonstrating that a significant temperature and conductivity gradient is generated along the post region. Joule heating significantly decreases the device capacity since dielectrophoretic trapping is no longer achievable in large portions of the post region.
Figure 6.
Experimental results on the dielectrophoretic behavior of 1 μm microspheres by applying 1,500 V to a channel with σ0= 0.01 S/m. a) Just when the electric field was generated particles are shown to be trapped in the last posts; b) after 30 s of applying 1,500 V most particles escaped from their dielectrophoretic traps at the end of the post region and flowed to the channel outlet; c) after 30 s of applying 1,500 V to the channel particles are still being trapped at the beginning of the insulators area.
No recirculation vortexes due to electrothermal flows, caused by temperature gradients, were observed during these experiments. Research published by Hawkins and Kirby [28] and Sridharan et al. [29] found that electrothermal flow effects decrease in high local electric fields, for EOF dominates electrothermal effects. Hawkins and Kirby [28] concluded that higher bulk-channel-depth/constriction-depth ratios create higher local electric fields which decrease electrothermal effects. Although the device used in this work has a low constriction ratio (value of 3), the high electric potential is enough to overcome the temperature effects on the flow, as stated by Sridharan et al. [29] who reported that recirculation vortexes were formed when potentials between 100 and 500 V were applied to a channel with one constriction, but were not present at applied potential of 600 V.
5. Concluding remarks
Insulator-based DEP (iDEP) is a leading technique in microfluidics due to its great flexibility and potential for handling a wider array of bioparticles. There is a growing interest on the development of novel and improved systems based on iDEP. Joule heating is a common phenomenon in many iDEP applications, in particular when buffers used have high conductivities. The present study demonstrated by both, simulations and experiments, that buffer conductivity variations should be considered in order to determine the magnitude of heating effects. A device containing a long insulating post-region was employed in order to observe the heating effect along the length of the entire channel.
Negative DEP behavior of inert particles was observed in the experiments under the conditions reported, and the particle trapping capacity of the device was observed to decrease due to heating of the buffer inside the microchannel by the application of a DC voltage. Buffer heating created temperature gradients along the microchannel that significantly decreased particle trapping closer to the end of the posts, i.e., important sections of the post region lost their trapping capability. These results demonstrate that Joule heating is important for iDEP devices that use buffers with high conductivities and their designs can be optimized by taking Joule heating into consideration.
Acknowledgments
The authors would like to acknowledge the financial support provided by Cátedra de Investigación CAT142 of Tecnológico de Monterrey, Virginia Tech – Wake Forest University, and CONACYT-Mexico in the form of a PhD fellowship that included a research stay at Virginia Tech for R. C. Gallo-Villanueva. The authors would also like to acknowledge the Institute of Critical Technologies and Applied Sciences at Virginia Tech for general support during this research, and Centro de Investigación y Estudios Avanzados del IPN Unidad Monterrey and Javier A. Hernández-Castro for their collaboration on the fabrication of the devices.
Abbreviations
- AC
alternating current
- CM
Clausius-Mossotti
- DC
direct current
- DEP
dielectrophoresis
- EK
electrokinetic
- EOF
electroosmotic flow
- EP
electrophoresis
- iDEP
insulator-based dielectrophoresis
References
- 1.Jesús-Pérez NM, Lapizco-Encinas BH. Electrophoresis. 2011;32:2331–2357. doi: 10.1002/elps.201100107. [DOI] [PubMed] [Google Scholar]
- 2.Martinez-Duarte R. Electrophoresis. 2012;33:3110–3132. doi: 10.1002/elps.201200242. [DOI] [PubMed] [Google Scholar]
- 3.Khoshmanesh K, Nahavandi S, Baratchi S, Mitchell A, Kalantar-zadeh K. Biosens Bioelectron. 2011;26:1800–1814. doi: 10.1016/j.bios.2010.09.022. [DOI] [PubMed] [Google Scholar]
- 4.Pohl HA. J Appl Phys. 1951;22:869–871. [Google Scholar]
- 5.Washizu M, Kurosawa O. IEEE Trans Ind Appl. 1990;26:1165–1172. [Google Scholar]
- 6.Moncada-Hernandez H, Baylon-Cardiel JL, Pérez-González VH, Lapizco-Encinas BH. Electrophoresis. 2011;32:2502–2511. doi: 10.1002/elps.201100168. [DOI] [PubMed] [Google Scholar]
- 7.Cummings EB, Singh AK. Anal Chem. 2003;75:4724–4731. doi: 10.1021/ac0340612. [DOI] [PubMed] [Google Scholar]
- 8.Braff WA, Pignier A, Buie CR. Lab Chip. 2012;12:1327–1331. doi: 10.1039/c2lc21212a. [DOI] [PubMed] [Google Scholar]
- 9.Gallo-Villanueva RC, Jesús-Pérez NM, Martínez-López JI, Pacheco A, Lapizco-Encinas BH. Microfluid Nanofluid. 2011;10:1305–1315. [Google Scholar]
- 10.Jen CP, Chen TW. Biomed Microdev. 2009;11:597–607. doi: 10.1007/s10544-008-9269-1. [DOI] [PubMed] [Google Scholar]
- 11.Camacho-Alanis F, Gan L, Ros A. Sens Actuator B-Chem. 2012;173:668–675. doi: 10.1016/j.snb.2012.07.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gallo-Villanueva RC, Rodríguez-López CE, Díaz-de-la-Garza RI, Reyes-Betanzo C, Lapizco-Encinas BH. Electrophoresis. 2009;30:4195–4205. doi: 10.1002/elps.200900355. [DOI] [PubMed] [Google Scholar]
- 13.Chávez-Santoscoy AV, Baylon-Cardiel JL, Moncada-Hernández H, Lapizco-Encinas BH. Sep Sci Technol. 2011;46:384–394. [Google Scholar]
- 14.Baylon-Cardiel JL, Lapizco-Encinas BH, Reyes-Betanzo C, Chávez-Santoscoy AV, Martínez Chapa SO. Lab Chip. 2009;9:2896–2901. doi: 10.1039/b906976c. [DOI] [PubMed] [Google Scholar]
- 15.Moncada-Hernández H, Lapizco-Encinas BH. Anal Bioanal Chem. 2010;396:1805–1816. doi: 10.1007/s00216-009-3422-4. [DOI] [PubMed] [Google Scholar]
- 16.Jones P, Staton S, Hayes M. Anal Bioanal Chem. 2011;401:2103–2111. doi: 10.1007/s00216-011-5284-9. [DOI] [PubMed] [Google Scholar]
- 17.Zhu J, Xuan X. Biomicrofluidics. 2011;5:024111. doi: 10.1063/1.3599883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Patel S, Showers D, Vedantam P, Tzeng TR, Qian S, Xuan X. Biomicrofluidics. 2012;6:034102–034112. doi: 10.1063/1.4732800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xuan X. Electrophoresis. 2008;29:33–43. doi: 10.1002/elps.200700302. [DOI] [PubMed] [Google Scholar]
- 20.Zellner P, Agah M. Electrophoresis. 2012;33:2498–2507. doi: 10.1002/elps.201100661. [DOI] [PubMed] [Google Scholar]
- 21.Xuan X, Xu B, Sinton D, Li D. Lab Chip. 2004;4:230–236. doi: 10.1039/b315036d. [DOI] [PubMed] [Google Scholar]
- 22.Xuan X, Hu G, Li D. Electrophoresis. 2006;27:3171–3180. doi: 10.1002/elps.200500871. [DOI] [PubMed] [Google Scholar]
- 23.Tang G, Yan D, Yang C, Gong H, Chai JC, Lam YC. Electrophoresis. 2006;27:628–639. doi: 10.1002/elps.200500681. [DOI] [PubMed] [Google Scholar]
- 24.Chein R, Yang YC, Lin Y. Electrophoresis. 2006;27:640–649. doi: 10.1002/elps.200500314. [DOI] [PubMed] [Google Scholar]
- 25.Venditti R, Xuan X, Li D. Microfluid Nanofluid. 2006;2:493–499. [Google Scholar]
- 26.Yao GF. 2004 NSTI Nanotechnology Conference and Trade Show; Boston, MA. 2004; pp. 201–204. [Google Scholar]
- 27.Sabounchi P, Huber DE, Kanouff MP, Harris AE, Simmons BA. The 12th International Conference on Miniaturized Systems for Chemistry and Life Sciences(MicroTAS 2008) Royal Society of Chemical Special Publications; London UK., San Diego CA: 2008. pp. 50–52. [Google Scholar]
- 28.Hawkins BG, Kirby BJ. Electrophoresis. 2010;31:3622–3633. doi: 10.1002/elps.201000429. [DOI] [PubMed] [Google Scholar]
- 29.Sridharan S, Zhu J, Hu G, Xuan X. Electrophoresis. 2011;32:2274–2281. doi: 10.1002/elps.201100011. [DOI] [PubMed] [Google Scholar]
- 30.Kale A, Patel S, Hu G, Xuan X. Electrophoresis. 2013;34:674–683. doi: 10.1002/elps.201200501. [DOI] [PubMed] [Google Scholar]
- 31.Zhu J, Sridharan S, Hu G, Xuan X. J Micromech Microeng. 2012;22:075011. [Google Scholar]
- 32.Lewpiriyawong N, Yang C, Lam Y. Microfluid Nanofluid. 2012;12:723–733. [Google Scholar]
- 33.Davalos RV, McGraw GJ, Wallow TI, Morales AM, Krafcik KL, Cummings EB, et al. Anal Bioanal Chem. 2008;390:847–855. doi: 10.1007/s00216-007-1426-5. [DOI] [PubMed] [Google Scholar]
- 34.Simmons BA, McGraw GJ, Davalos RV, Fiechtner GJ, Fintschenko Y, Cummings EB. MRS Bulletin. 2006;31:120–124. [Google Scholar]
- 35.Lapizco-Encinas BH, Davalos R, Simmons BA, Cummings EB, Fintschenko Y. J Microbiol Methods. 2005;62:317–326. doi: 10.1016/j.mimet.2005.04.027. [DOI] [PubMed] [Google Scholar]
- 36.Markx GH, Dyda PA, Pethig R. J Biotechnol. 1996;51:175–180. doi: 10.1016/0168-1656(96)01617-3. [DOI] [PubMed] [Google Scholar]
- 37.Kirby BJ. Micro- and Nanoscale Fluid Mechanics Transport in Microfluidic Devices. Cambridge University Press; New York: 2010. [Google Scholar]
- 38.Sze A, Erickson D, Ren L, Li D. J Colloid Interface Sci. 2003;261:402–410. doi: 10.1016/S0021-9797(03)00142-5. [DOI] [PubMed] [Google Scholar]
- 39.Martínez-López JI, Moncada-Hernández H, Baylon-Cardiel JL, Martínez-Chapa SO, Rito-Palomares M, Lapizco-Encinas BH. Anal Bioanal Chem. 2009;394:293–302. doi: 10.1007/s00216-009-2626-y. [DOI] [PubMed] [Google Scholar]
- 40.Ermolina I, Morgan H. J Colloid Interface Sci. 2005;285:419–428. doi: 10.1016/j.jcis.2004.11.003. [DOI] [PubMed] [Google Scholar]
- 41.Kwon JS, Maeng JS, Chun MS, Song S. Microfluid Nanofluid. 2008;5:23–31. [Google Scholar]
- 42.Cummings EB. IEEE Eng Med Biol Mag. 2003;22:75–84. doi: 10.1109/memb.2003.1266050. [DOI] [PubMed] [Google Scholar]
- 43.Mazzoleni AP, Sisken BF, Kahler RL. Bioelectromagnetics. 1986;7:95–99. doi: 10.1002/bem.2250070111. [DOI] [PubMed] [Google Scholar]