Performance tuning non-uniform sampling for sensitivity enhancement of signal-limited biological NMR

Abstract

Non-uniform sampling (NUS) has been established as a route to obtaining true sensitivity enhancements when recording indirect dimensions of decaying signals in the same total experimental time as traditional uniform incrementation of the indirect evolution period. Theory and experiments have shown that NUS can yield up to two-fold improvements in the intrinsic signal-to-noise ratio (SNR) of each dimension, while even conservative protocols can yield 20–40 % improvements in the intrinsic SNR of NMR data. Applications of biological NMR that can benefit from these improvements are emerging, and in this work we develop some practical aspects of applying NUS nD-NMR to studies that approach the traditional detection limit of nD-NMR spectroscopy. Conditions for obtaining high NUS sensitivity enhancements are considered here in the context of enabling ¹H,¹⁵N-HSQC experiments on natural abundance protein samples and ¹H,¹³C-HMBC experiments on a challenging natural product. Through systematic studies we arrive at more precise guidelines to contrast sensitivity enhancements with reduced line shape constraints, and report an alternative sampling density based on a quarter-wave sinusoidal distribution that returns the highest fidelity we have seen to date in line shapes obtained by maximum entropy processing of non-uniformly sampled data.

Introduction

Extending the detection limit of nuclear magnetic resonance spectroscopy (NMR) is yielding exciting returns. Dynamic nuclear polarization promises to transform studies of biological solids, while microcoil and cryogenic probe technologies permit challenging multi-dimensional spectroscopy on unprecedented mass-sensitivities on the order of 1–100 μg for important small molecules such as natural products and metabolites (Hilton and Martin 2010). Continued instrumentation innovations can be expected to yield more returns on improving signal detection, but recent work has shed light on extending the detection limit of multi-dimensional NMR spectroscopy by non-uniform sampling (NUS) (Rovnyak et al. 2011; Paramasivam et al. 2012; Waudby and Christodoulou 2012; Qiang 2011; Kumar et al. 1991; Hyberts et al. 2010, 2013). Specifically, for the case of NUS of selecting a subset of samples (termed a sampling schedule) from a uniform Nyquist grid, exact theory and experimental verifications show that NUS data of decaying signals experience an enhanced intrinsic signal-to-noise ratio (iSNR) on the order of up to two fold over uniformly sampled data in the same experimental time (Rovnyak et al. 2011; Paramasivam et al. 2012). The intrinsic SNR (iSNR) in the time domain of uniform data is defined here as the ratio of the area of the signal envelope to the square root of the evolution time prior to any post-acquisition signal processing. This definition is easily extended to NUS and is equivalent to the familiar ratio of the integrated peak area to the r.m.s. noise in the frequency domain. The NUS-based iSNR gains have been correlated with the ability to detect new signals (Rovnyak et al. 2011; Paramasivam et al. 2012; Hyberts et al. 2013) and early applications suggest that bio-solids NMR (Paramasivam et al. 2012) as well as solution NMR of natural products (Palmer et al. 2013) stand to reap some of the best gains from this approach, including by taking the best advantage of compounding the sensitivity enhancement in multiple indirect dimensions (Paramasivam et al. 2012; Hyberts et al. 2013).

Tailoring data acquisition to the regions of the signal envelope in which the signal intensity is highest is an established concept for improving sensitivity in a given time (Levitt et al. 1984) Obtaining sensitivity benefits in 2D-NMR using exponential NUS fulfills this criterion and was first noted over 20 years ago, including protein applications (Barna et al. 1986, 1987). Subsequently, enhanced SNR by NUS in indirect evolution periods was described for the practice of acquiring all indirect increments uniformly but with a non-uniform distribution of the number of transients (Kumar et al. 1991) a practice sometimes termed non-uniform weighted sampling (NUWS) which is seeing renewed interest (Waudby and Christodoulou 2012; Qiang 2011). Estimates of SNR enhancements were later refined by the exact solution (Rovnyak et al. 2011). Specifically, the NUS-based enhancement may be exactly calculated for a signal decaying with a time constant T₂ as (Paramasivam et al. 2012).

$$\eta =\frac{\chi {\int }_0^{t_{max}}h(t)e^{-t/T_2}dt}{T_2(1-e^{-t_{max}/T_2})}$$ (1)

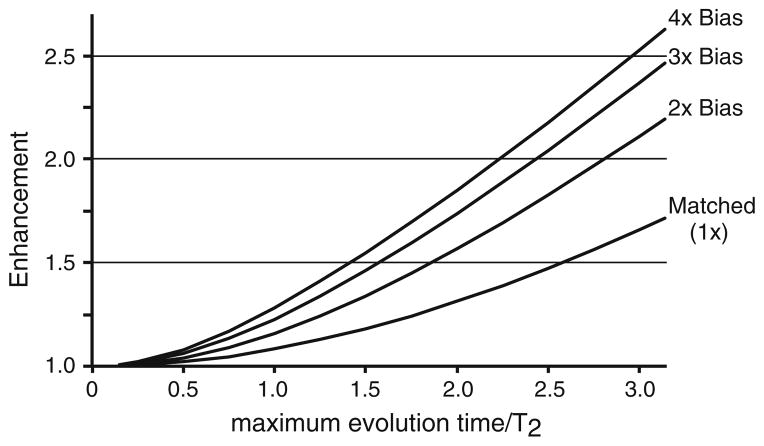
where χ is a scaling factor which enforces equal total experimental times for NUS and uniform sampling (US) experiments, h(t) is the density of nonuniform samples, T₂ is the decay constant of the signal, and t_max is the time corresponding to the last recorded sample. For an exponential sampling density, h(t) = e^−t/T_SMP where T_SMP is the decay constant of the sampling density. If the density of samples is matched to the decay of the signal (a.k.a. ‘matched NUS’) then h(t) = e^−t/T₂ and Eq. (1) shows that the NUS-based iSNR enhancement can be as high as about 1.7 versus uniform sampling (Fig. 1).

Fig. 1.

Exact intrinsic SNR enhancements computed with Eq. (1) of the time domain of an exponential signal acquired through nonuniform sampling with an exponentially weighted density that equals the signal decay (matched) or which is biased to even shorter times (exponential weighting two, three or of our times the decay rate of the signals, e.g. 2×, 3×, or 4×). The NUS-based improvements are most compelling at long times, while diminishing returns are encountered when the exponential weight is about three times the signal decay

If the density of samples is biased to decay more quickly than the T₂ signal decay, say twice as fast (labeled ‘2X’ in Fig. 1), then this has the effect of concentrating a greater number of samples at earlier times, for which the NUS-based iSNR enhancement versus uniform sampling can reach up to about two-fold. Biasing the exponential NUS schedule even more steeply, such as to three or four times the T₂ decay, delivers some incremental additional enhancements but approaches the effect of truncating the signal and sacrificing resolution in the process. For these reasons, biased exponential NUS of no more than about two fold is the recommended limit. However it is interesting to consider that there may be some exceptions to this rule of thumb when more steeply biased densities may still be desired.

In two indirect NUS dimensions, compounded NUS enhancements can be realized on the order of three- to fourfold and were recently tested and found to be consistent with predictions based on compounding Eq. (1) (Paramasivam et al. 2012). Since the key strategy is to concentrate data samples at regions where the signal is high, NUS-based sensitivity enhancement is only applicable to signals with a non-constant amplitude during evolution. Thus NUS cannot yield any enhancements of constant time (CT) evolution periods, although the time savings of using NUS in CT dimensions remains an important incentive for its use (Schmieder et al. 1994). And while NUS-based signal enhancements have so far been applied and developed for exponentially decaying signals, it is equally feasible to obtain an iSNR enhancement from signals that experience other non-constant amplitude profiles.

As NUS has matured into a robust sampling technique which can be paired with a variety of spectral reconstruction tools, a great deal of effort has been directed upon achieving significantly shorter overall experimental times for recording information-rich multi-dimensional NMR spectra. A long-standing rule of thumb for NUS practice is that it should be applied in situations where uniform sampling would also have enough sensitivity. With the realization now that NUS can have considerably higher intrinsic SNR over uniform sampling and thereby lead to the ability to detect new peaks, the opportunity arises to consider how to configure NUS to extend the sensitivity limit of multi-dimensional NMR and to try to better understand constraints upon realizing these enhancements. This work will investigate applications of NUS-based signal enhancements on a natural abundance protein sample (2D ¹H,¹⁵N-HSQC) and on a plant natural product (2D ¹H,¹³C-HMBC, ¹H-¹³C-HSQC). Biasing the exponential NUS density to shorter times to improve enhancements is contrasted with reduced constraints on the line shape, while an alternative quarter-wave sinusoidal density is shown to provide both favorable enhancements and exact line shapes in conjunction with maximum entropy reconstruction for processing the NUS data. Using NUS-based iSNR enhancements, screening natural abundance proteins for ¹H,¹⁵N-HSQC folding fingerprints becomes much more feasible, while challenging natural products become more accessible to nD-NMR.

Results

Strictly, the NUS-based enhancement is obtained relative to T₂*, which describes the measured signal envelope. For convenience, just T₂ will be denoted herein. Some notational conventions will be introduced to facilitate describing paths to achieving NUS-based time domain iSNR enhancements. First, Eq. (1) predicts that the time domain iSNR of NUS can be increased further if the NUS density is biased to shorter times by setting the time constant T_SMP < T₂, where T_SMP is the decay constant of the NUS exponential density. Matched exponential NUS corresponds to T_SMP = T₂, while setting T_SMP < T₂ is termed biased exponential NUS. It is also convenient to recast the choice of the NUS exponential density in terms of equivalent line widths (units of Hz). For example, for a signal decay yielding a line width of 4 Hz then matched NUS would correspond to choosing an NUS sampling density that also decays at the same rate of 4 Hz = 1/(πT_SMP). A biased exponential NUS density can then be described in convenient and more relatable line width units. To bias the NUS schedule to earlier times, a shorter T_SMP could be chosen to yield 8 Hz = 1/πT_SMP. We use the notation of referring to 8 Hz NUS schedules, or 4 Hz NUS schedules and so on. Finally, we also adopt the notation of referring to biased exponential NUS according to the ratio between the sampling decay line width and the signal linewidth. For example, 2X biased NUS means the sampling line width is two fold greater than the signal line width (e.g. if the NUS schedule follows an 8 Hz decay and the signal line width is 4 Hz). See Fig. 1 again for use of these terms. In this work, all NUS spectra are processed with maximum entropy reconstruction (MaxEnt) implemented in the Rowland NMR toolkit (http://rnmrtk.uchc.edu) (Hoch and Stern 1996). While many superb algorithms exist for obtaining spectral estimates from NUS data, MaxEnt has been used for at least two decades as a high fidelity algorithm for obtaining spectral estimates from NUS data (Hoch and Stern 1996; Stern et al. 2002; Hoch et al. 2014).

The potential to apply NUS for iSNR enhancement in liquid phase biomolecular NMR of proteins is considered first. It should be appreciated from Fig. 1 that the most compelling iSNR enhancements are obtained by NUS relative to uniform sampling when the evolution time is long compared to T₂. When performing three-dimensional experimentation, such as for ¹H,¹³C, and ¹⁵N backbone assignments, achieving evolution times even on the order of T₂ in certain biomolecular experimentation is nearly intractable, even with the aid of NUS (Rovnyak et al. 2004). Furthermore, NUS-based enhancements cannot be obtained in any constant-time dimension since the basis for NUS enhancements requires tailoring the density of samples to a non-constant signal envelope (Kumar et al. 1991; Levitt et al. 1984). Given the twin concerns of the prevalence of constant-time evolution periods in 3D bioNMR experiments, and the difficulty to achieve evolution times on the same order as T₂, other applications of NUS-based signal enhancements should be considered at this time.

Contrasting sensitivity and line shape in NUS

One opportunity for exploiting NUS-based enhancements lies in performing 2D ¹H-¹⁵N HSQC spectroscopy of protein samples prepared with natural abundance levels of all isotopes. In 2D NMR it is much more straightforward to reach long evolution times in order to obtain high resolution and thereby enter the regime where NUS significantly out-performs uniform sampling (Fig. 1). Eliminating enrichment by ¹⁵N provides cost savings and would make it more feasible to screen larger numbers of samples if spectra could be obtained in relatively short total times. A natural abundance sample of human ubiquitin was prepared to a concentration of about 6 mM and subjected to a systematic set of ¹H,¹⁵N-HSQC experiments at 600 MHz using a room-temperature probe. The high concentration (6 mM) mimics the use of a much lower concentration in a spectrometer equipped with a cryogenic probe. Further, given the increasing installed base of 700 MHz and higher fields, the results presented here are somewhat conservative, and users can expect improved results at higher fields.

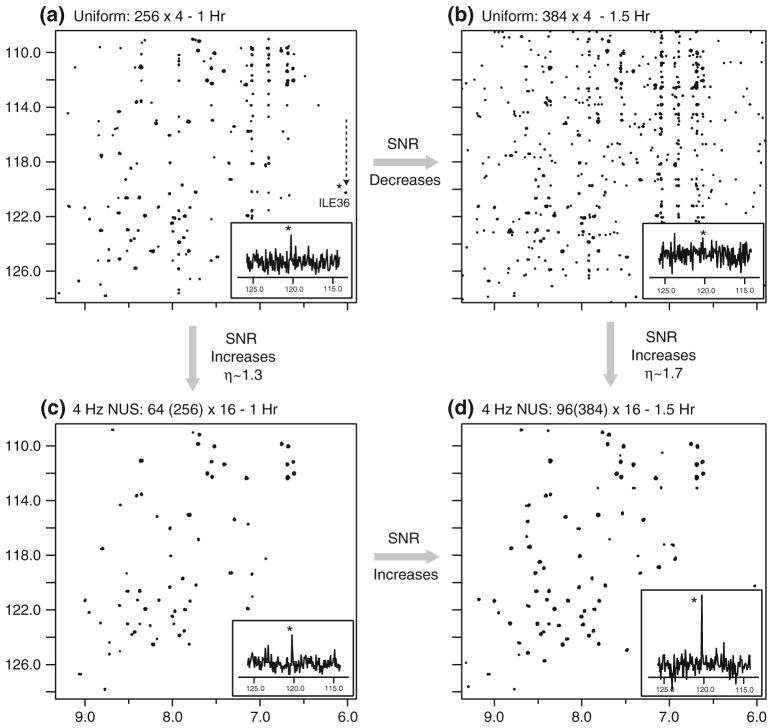
A systematic set of experiments was designed to contrast uniform and non-uniform sampling for long evolution times and for a range of different exponential NUS densities in ¹H,¹⁵N-HSQC NMR. Total evolution times of 0.128 and 0.191 s were chosen and corresponded to 256 uniform increments and 384 uniform increments, respectively. Non-uniform sampling retained 25 % of the samples according to exponential densities of 4, 6, 8 and 10 Hz. Given that a reasonable estimate of the total signal decay in this case (e.g. T₂*) would correspond to 3–4 Hz, the 4 Hz schedule is approximately a matched NUS schedule, whereas the 6 Hz schedule is approximately a 2× biased schedule, while the 8 and 10 Hz schedules explore more severe biasing of the NUS density to short times. It also follows from the line width considerations that a 0.128 s evolution lies between 1.5 and 2 T₂* and the 0.193 s evolution falls between 2.5 and 3T₂*.

It will be seen that NUS presents an improved route to obtaining sensitive HSQC spectra on natural abundance proteins. However first, contrasting FFT processing of uniform data to MaxEnt processing of matched exponential NUS data (Fig. 2) supports two key concepts in NUS-based sensitivity enhancement (Rovnyak et al. 2011; Paramasivam et al. 2012; Kumar et al. 1991; Hyberts et al. 2013; Palmer et al. 2013; Rovnyak et al. 2004). Simultaneously extending the evolution time of uniform sampling and the total experimental time (Fig. 2a, b) will only decrease the iSNR for all samples acquired beyond 1.26 T₂ (Rovnyak et al. 2004). Thus it is a serious limitation of uniform sampling that high resolution can only be obtained at the expense of iSNR. In contrast, Fig. 2b, c establishes, consistent with theory, that iSNR increases by exponential NUS if evolution time is simultaneously increased with experimental time. It is difficult to make any case for performing uniform sampling if the total evolution time will extend beyond 1.26 T₂. It should also be recognized from Fig. 2 that NUS-based enhancements are more significant for long evolution times (Fig. 2b, d) than for midrange evolution times (Fig. 2a, c), another key prediction of Eq. (1) and illustrated in Fig. 1. Some processing considerations should be noted in Fig. 2. Each spectrum was obtained with apodization (cosine squared) in the direct dimension and employing only zero-filling in the indirect dimension. Thus no apodization or deconvolution or any other treatment that would change the iSNR was employed in the indirect dimension prior to the use of the FFT or MaxEnt algorithms. Still, the SNR values of the frequency spectra would be misleading as they would have to be regarded as apparent SNR values not only because the directly acquired dimension was apodized, but also because MaxEnt has a nonlinear response that has been well documented previously (Hoch and Stern 1996; Schmieder et al. 1997; Donoho et al. 1990). Rather, improvements are evident through inspection of peak heights in a representative ¹⁵N cross-section as well as observing that contours for expected cross peaks become significantly more distinguishable from noise contours in Fig. 2d, which will be more amenable to visual and automated peak-picking routines. That is, these data establish that many expected peaks, which are ambiguous or undetectable relative to noise in US spectra such as in Fig. 2a, b, are unambiguously detectable above noise levels with NUS spectra (e.g. Fig. 2c, d). In contrasting panels (c) and (d) in Fig. 2, it is interesting to see where the additional 32 samples are distributed. In Fig. 2d, there are now 84 samples spanning up to sample 256, representing an increase of 20 versus Fig. 2c. Then twelve samples span the region 257–384. (Supporting Information section S.2).

Fig. 2.

Contrasting uniform sampling with matched exponential NUS (4 Hz) for ¹H,¹⁵N HSQCs of ubiquitin at natural abundance. a, b Extending uniform sampling to longer indirect evolution times by adding more experimental time incurs significant additional noise. a, c Mid-range evolution times, 4 Hz weighted exponential NUS delivers a moderate but useful enhancement, on the order of 20–30 % as noted in Fig. 1. b, d Much greater NUS-based enhancement is obtained for long evolution times, again consistent with theoretical predictions (Fig. 1) that indicate a ~70 % improvement. Notably, (c) and (d) show that extending the evolution time with NUS along with experimental time improves the SNR and resolution simultaneously

Detailed experimental confirmations of enhancements predicted by Eq. (1) have been established using linear transforms such as maximum entropy interpolation (Paramasivam et al. 2012). Also, since this work will only compare uniform to non-uniform experiments that consume equivalent experimental times, it is possible to use the terms SNR and sensitivity interchangeably, where sensitivity is conventionally defined as the ratio of SNR to the square root of experimental time (Ernst et al. 1987). Recognizing that sensitivity is increasingly viewed as a metric for peak detection (Hyberts et al. 2013) it is also useful to apply to the discussion of the final processed data shown here.

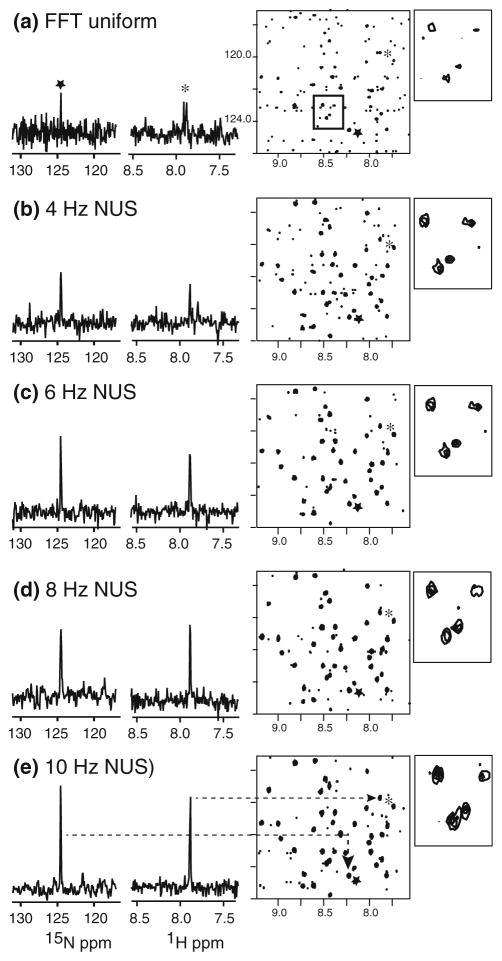
The ¹H,¹⁵N-HSQC is a sensitive test for the folded state of a protein as well as for externally induced perturbations of protein structure such as guest binding, self aggregation, pH, changes in dynamics, and macroscopic physical factors including temperature. Although Fig. 2 supports that non-uniform sampling enables the ability to obtain sensitive ¹H,¹⁵N-HSQC spectra on natural abundance proteins on a time frame of 60–90 min, further sensitivity would facilitate acquiring these data more efficiently. What would be the consequences of exploiting greater exponential biasing of the sampling to achieve higher enhancements? Figure 3 illustrates a progression of ¹H,¹⁵N-HSQC data from uniform sampling to steeply biased (10 Hz exponential) NUS to better characterize the consequences of obtaining higher enhancements at the expense of reduced constraints on the signal at long evolution times. Inspection of the detailed sampling schedules shows that even 3x biasing begins to closely approach the process of simply truncating the signal evolution (Palmer et al. 2013). Cross-sections through each dimension as well as a selected region of the 2D-spectrum strongly support that increased bias in the exponential NUS delivers continued improvements in the sensitivity. Many peaks are absent or ambiguous in the uniform data that are unambiguously realized in the spectra obtained by NUS. The cases of severe biasing (e.g. 8 or 10 Hz) introduce some broadening that can be seen with lower altitude contours in the insets, but also present much more sensitive spectra compared to 4 Hz exponential NUS.

Fig. 3.

Representative one- and two-dimensional views of ¹H,¹⁵N-HSQC spectra of a 6 mM human ubiquitin sample (Aldrich, Inc.) obtained by uniform sampling and exponential NUS. All NUS spectra are processed by maximum entropy reconstruction in the Rowland NMR Toolkit. http://rnmrtk.uchc.edu) (Hoch and Stern 1996) Each experiment consumed 1.5 Hr total time. Uniform acquisition employed 384 increments with 4 transients per increment, while NUS employed 96 exponentially distributed samples according to the indicated decays (expressed as line widths, see text) with 16 transients per increment

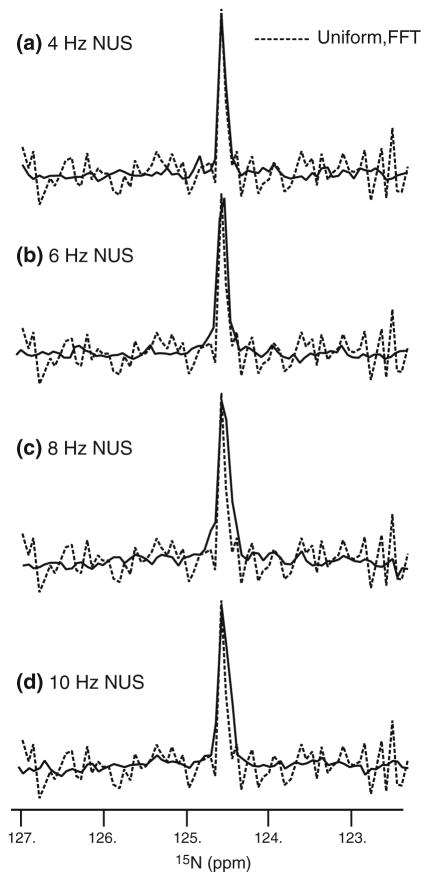
Again, while it is not advised to discuss numerical values of the apparent SNR in Fig. 3, it should be pointed out that Fig. 3b–e are all processed with identical maximum entropy parameters, and a more direct comparison between these five spectra can be made. Specifically, the improvements between Fig. 3b–e must be attributed to higher iSNR in the raw time domain data since these five spectra have been treated with equivalent processing. Since 96 samples are selected from a grid of 384 uniform samples to span the long evolution time of 0.191 s, even the steeply biased spectra (Fig. 3d, e) still show high resolution despite experiencing some broadening, where it should be added that the 384th sample is included in every NUS schedule in Fig. 3. A closer examination of line broadening that occurs when the exponential density is heavily biased is given in Fig. 4. When the NUS is matched or weakly biased, then the line width by MaxEnt processing of exponential NUS is closely approximates that for FFT processing of uniform data. It is evident from Fig. 4 that when NUS is applied conservatively (Fig. 4a,b), then there are sufficient constraints to define the line width correctly. As the exponential density becomes more concentrated upon early times, the loss of samples after about 1 T₂ is too severe and line widths do increase moderately, ca. 30 % in these data (Fig. 4a,c).

Fig. 4.

A comparison of ¹⁵N line shapes in the indirect dimension of the 2D-HSQC spectra in Fig. 3 from FFT processing of uniform data and MaxEnt processing of exponential NUS data. Line shapes are closely conserved when the NUS density is approximately matched or weakly biased (a, b), but begin to exhibit broadening to the significant reduction in samples at long times when the exponential density is strongly biased to early times (c, d)

Sinusoidal NUS preserves line shape for conservative NUS

The consequences of reduced constraints on the data relative to uniform sampling should be considered further. The data presented so far indicate that matched or weakly biased exponential NUS do not distort the line width measured at half height. However, when frequency spectra are reconstructed from NUS data there is no longer a Nyquist guarantee on the detected bandwidth, and there are also not at this time objective criteria for when the sparseness of samples are sufficient to report on line widths accurately. One area of concern is that the use of a non-uniform sampling schedule means that the data can be more or less sensitive to certain frequencies. For example, a particularly eccentric sampling schedule might only sample positions on the Nyquist grid that lie on or near to nodes of certain frequencies. More precisely, the task of presenting a frequency spectrum from NUS data can be described as deconvolving the Fourier transform of the sampling schedule from the Fourier transform of the uniformly sampled signal. The Fourier transform of the sampling schedule is known as the point spread function and is obtained as the FFT of the schedule in which omitted samples are replaced by zeros. To date, guidelines are being established around some key concepts of sampling. If the NUS schedule is not too sparse with respect to the number of samples on the uniform grid, if gaps are minimized, and if the NUS schedule has random character, then it is found that spectral estimation techniques deliver extremely high fidelity frequency spectra from NUS data and folding artifacts are negligible (Hyberts et al. 2010; Hoch et al. 2008; Mobli et al. 2012; Maciejewski et al. 2009).

As described in the previous data, when exponential NUS is applied to exponentially decaying signals, the resulting frequency spectra do not experience a decrease in the line width at half maximum, if the density of samples is approximately matched to the decay rate of the signals. When NUS densities are strongly biased to earlier times relative to the signal decay, then NUS begins to approximate signal truncation and line broadening due to severe biasing of NUS relative to the signal can be measured as in Fig. 4.

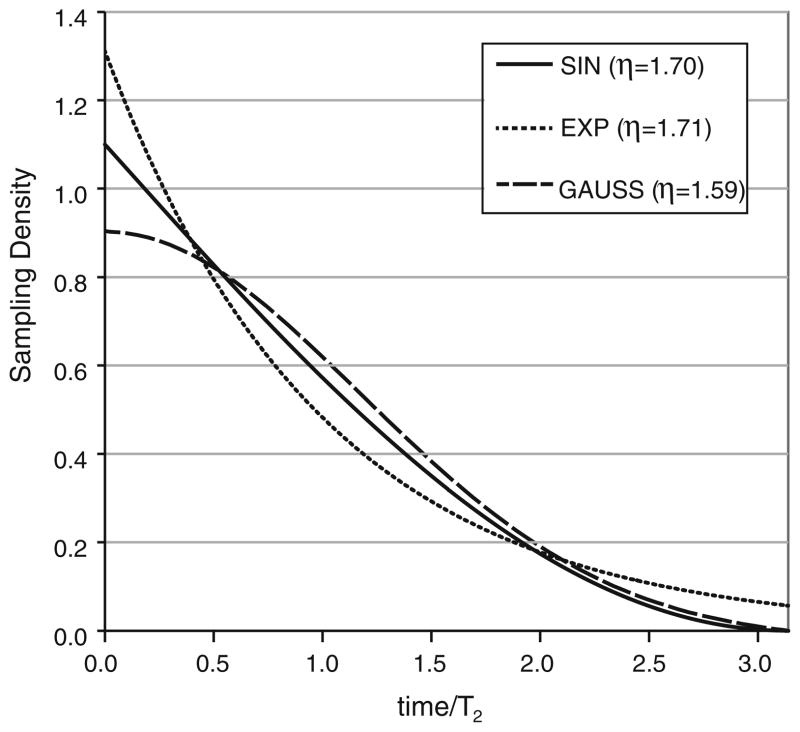
However, we began to investigate the question of whether there might be minor systematic line shape distortions even in traditionally conservative applications of exponential NUS. That is, could other areas of line shape quality be affected by reduced constraints even if line widths are correctly obtained? Broadly, it is of interest to identify alternative sampling densities that have intrinsic NUS-based enhancements similar to exponential NUS densities, but which do not decay as quickly as the exponential decay. Indeed some have reported favorable experiences with Gaussian-distributed NUS (Qiang 2011; Eddy et al. 2012) which does achieve a greater distribution of samples at longer evolution times compared to exponential NUS (Fig. 5). However, if the Gaussian density is matched to the line width of the decay, as is done with exponential densities, then the intrinsic SNR enhancement by Eq. (1) for a Gaussian is somewhat less than for exponential NUS (enhancements of about 1.6 and 1.7 respectively).

Fig. 5.

Comparison of sampling densities normalized such that the areas under the densities are equivalent, which means they each correspond to the same number of samples. Gaussian and exponential densities are adjusted to correspond to frequency domain line widths of πT₂. The sinusoidal density refers to the π–3π/2 segment of a sine function (i.e. the inverted 0–π/2 segment of sine)

We sought a monotonic function for a sampling density that could achieve a theoretical enhancement similar to an exponential density, while also distributing samples to longer times like the Gaussian. We report here on the use of a sampling density which is defined as the quarter-wave portion of a sine function which spans π to 3π/2. (Fig. 5) Following Eq. (1) the sinusoidal density will give an enhancement essentially identical to that for a matched exponential density for an acquisition which spans ~3T₂, but yet the sinusoidal sampling density localizes many more samples in the region of T₂–2T₂ closely following the Gaussian function in this region. Although in theory and in practice the sinusoidal density will have fewer samples at the very end of the evolution period ca. 3T₂, this region is so sparsely sampled in both densities that the sinusoidal and exponential densities are nearly equivalent in this regime.

We conducted an analysis of line shapes for synthetic signals injected into real acquired spectrometer noise that has been validated by us previously to be white and Gaussian. These data are essentially indistinguishable from measured data for this reason but allow us to carefully control line width, intensity and evolution parameters. Line shapes were analyzed for signals sampled to 3T₂ by uniform, matched exponential and sinusoidal sampling. Frequency spectra were obtained by processing the uniform data by FFT, and the exponential and quarter-wave sinusoidal NUS data by maximum entropy reconstruction (Fig. 6).

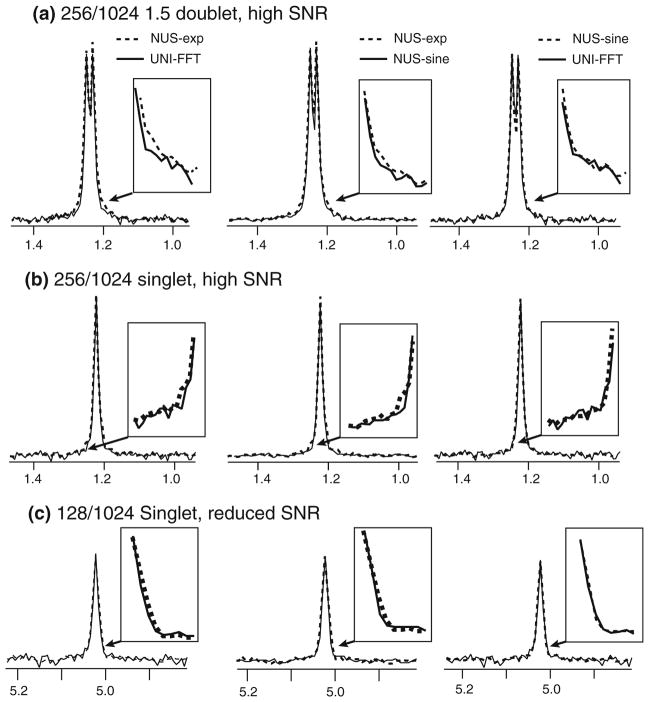
Fig. 6.

Peak broadening near the baseline is examined for synthetic signals injected into real spectrometer noise for sinusoidal and exponential NUS and for uniform sampling. Exponential NUS results in broadening of the beak base relative to uniform sampling. Sinusoidal NUS is always seen to give a narrower peak shape that agrees closely with the peaks produced from uniform data. (NUS spectra obtained by MaxEnt reconstruction and uniform spectra by FFT). Row (a) represents retaining 25 % of samples for the NUS spectra (256 out of a uniform grid of 1,024) and employed a doublet separated by just 1.5 times the line widths of the peaks. Row (b) examines a singlet also retaining 25 % of samples. Row (c) examines a singlet with lower SNR and retaining just 12.5 % of samples (128 out of a uniform grid of 1,024)

A grid of different NUS conditions and densities is considered in Fig. 6. Comparing the rows first, in Fig. 6a, a closely spaced doublet emulates crowded spectra (separation is 1.5 the line width), and exponential NUS results in noticeable broadening near the baseline of the peaks. Similar observations have been reported in the past for MaxEnt processing of closely spaced doublets (Kubat et al. 2007). In Fig. 6b, a singlet with strong SNR is examined and there is only negligible baseline broadening; yet when there is more noise and more data reduction (128 samples chosen from a grid of 1,024) as in Fig. 6c, then there is again visible a small degree of broadening by exponential NUS. To contrast the performance of sinusoidal NUS with exponential NUS, consider next the columns of Fig. 6. Again, the first column shows that exponential NUS can broaden particularly the regions near the bases of peaks, to different degrees depending on spectral crowding, SNR and sparsity of the NUS schedule. The middle column in Fig. 6 illustrates that sinusoidal NUS always results in a narrower base of the peaks in every case. The right-most column of Fig. 6 shows that sinusoidal sampling with MaxEnt reconstruction provides peak shapes that are essentially coincident with those obtained by FFT processing of uniform sampling in all cases considered here.

The results of the tests illustrated in Fig. 6 indicate that the reduced constraints of NUS can have small impacts on other aspects of the line shape besides the line width at half height. It is of interest that these minor effects are predicted to be more noticeable in crowded regions of spectra, and so we turned to 2D-NMR of a plant natural product to see if the predicted effects from simulations would manifest in a challenging application of NUS. Selected crowded regions in 2D-HMBC and 2D-HSQC spectra are shown in Fig. 7 for uniform, sinusoidal NUS and matched exponential NUS in the indirect dimension (details in figure caption). In all cases the directly acquired dimension is processed by FFT, while the indirect dimension was processed either by FFT for the uniform case or by MaxEnt reconstruction for the NUS cases.

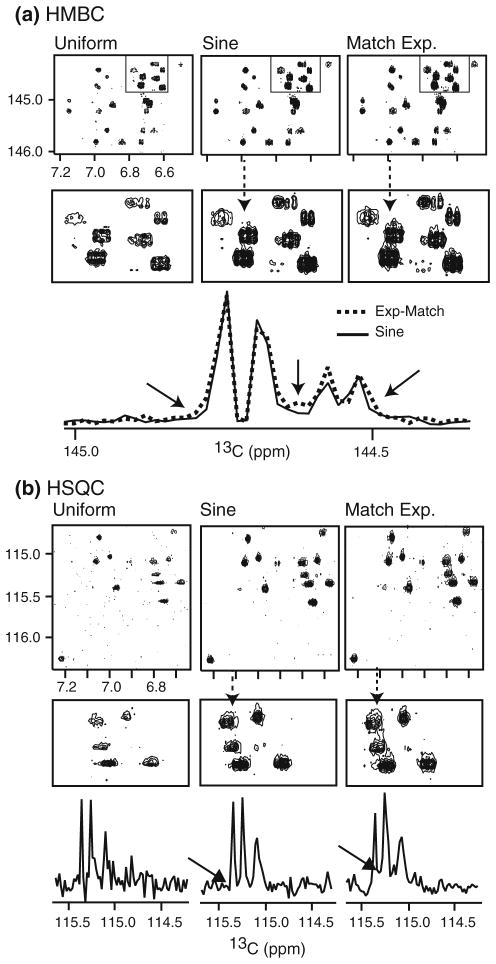
Fig. 7.

Representative 2D contour regions of a ¹H,¹³C-HMBC spectra and b ¹H,¹³C-HSQC spectra (14.1 Tesla, RT probe) of a plant natural product (Courtesy Prof. G. Henry, Susquehanna University, details in acknowledgements). The uniform, sinusoidal and matched exponential experiments used identical total times in each of a and b. Cross-sections through closely spaced peaks in both cases (note scale much less than 1 ppm) show a strong agreement with findings in Fig. 6, namely that sinusoidal sampling suppresses weak broadening near the bases of the peaks (arrows draw attention to these regions) IN a exponential and sinusoidal NUS each selected 351 samples from a Nyquist grid of 1,400, and in b exponential and sinusoidal NUS each selected 400 samples from a Nyquist grid of 1,600 (difference is due to different choices of spectral windows; see S.2 in Supplementary Information). The exponential schedules in (a) and (b) were both matched to 3.7 Hz

An inspection of the data in Fig. 7 shows that the NUS trials resulted in stronger peaks relative to uniform sampling in the same total experimental time, as expected. However, a closer view of the indicated inset regions in Fig. 7ab from crowded areas of the spectra reveals that low-altitude contours on neighboring peaks show much more broadening in the indirect dimension of the spectrum obtained by exponential NUS than in the spectrum obtained by sinusoidal NUS. Representative ¹³C one-dimensional cross-sections of the indirect frequency dimensions provide an even closer look at the effect of including more samples at longer times with sinusoidal NUS. The cross-sections, which include doublet features in Fig. 7a and crowding in Fig. 7b, show a striking agreement with the simulations in Fig. 6a, confirming that the tails of the peaks in sinusoidal NUS spectra are not as broad as with exponential NUS. Based on the line width of about 3.7 Hz, the sinusoidal schedule has 24 additional samples in the region 1T₂*–2T₂* compared to the matched exponential schedule in Fig. 7a, and 27 additional samples compared to exponential in this region for Fig. 7b, representing significantly greater restraints on the signal at these longer evolution times. While the improved peak shape is recognized in Fig. 7 for this challenging real-world application of NUS to a dilute small molecule, it is cautioned that the peak shape changes discussed here remain small.

Hyberts and Wagner have reported the use of half- and quarter-wavelength sinusoidal sampling densities gapped according to a Poisson distributions (Hyberts et al. 2010). The half-wavelength sinusoidal Poisson gap (PG) schedule is sparse between 1T₂–2T₂ in contrast to the quarter-wave sinusoid schedules. Enhancements with PG schedules that lead to detecting new peaks have been clearly demonstrated, and the acquisition of many samples at very long times does provide significant constraints on signals (Hyberts et al. 2013).

We devised an in-house strategy for generating sinusoidally distributed NUS samples on a uniform grid following the segment π to 3π/2 (this code is shared in the Supplementary Information). As noted previously, there are several interesting design challenges for generating such schedules. There must be a degree of randomness in the schedule to minimize artifacts introduced by the point spread function (Hoch et al. 2008). Yet, the series of discrete samples must be optimized in some fashion to ensure that it conforms as well as reasonably possible with the desired distribution function, since no coarse list of samples can perfectly follow a continuously defined distribution. Also the schedule must minimize gaps, another critical feature in optimizing NUS strategies (Hyberts et al. 2010, 2012). A python script was written for generating quarter-wave (e.g. π–3π/2) sinusoidally distributed sampling schedules, and includes several measures such as ensuring that no samples are double counted, and ensuring that the maximum evolution time is also sampled. In order to fulfill the important performance criteria described above, we decided upon a method of averaging a large number of randomly generated schedules together. The benefits of this simple but powerful approach are illustrated in Fig. 8, which examines characteristics of sinusoidal schedules obtained with no averaging (n = 1), with averaging 10, and with averaging 100 randomly generated schedules.

Fig. 8.

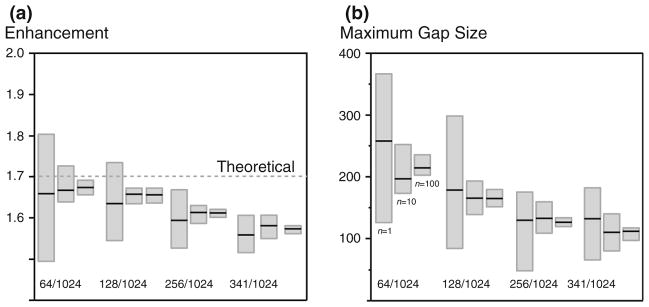
Randomly generated sinusoidal NUS sampling schedules were analyzed for their enhancement and gap characteristics as a function of averaging together 1, 10 or 100 schedules. The retention of samples is indicated on the figures and was based on a uniform grid of 1,024 samples. Each box summarizes results from analyzing 15 schedules: extrema are the minimum and maximum values, and the median is the solid black line. See text for discussion

When only single schedules are considered (n = 1), the enhancement of any individual schedule (which can also be exactly calculated using a discretized approach to Eq. (1)) is found to vary widely. For example, for selecting 64 samples from a uniform grid of 1,024, the individual schedules have iSNR enhancements from 1.5 to 1.8 due to random deviation from the intended distribution. Not surprisingly, there is more iSNR variation when contrasting individual schedules that are very sparse. When 341 samples are retained, then there are far fewer ways to arrange these samples and they all have enhancements between 1.5 and 1.6. Importantly, these tests show that sparser schedules are able to approach the theoretical enhancement far more closely since denser NUS schedules are forced to have uniform tracts at early times. Similar trends are noticed when considering the maximum gap of a given schedule. As noted, Hyberts and Wagner have analyzed the distribution of gaps and suggest forcing gaps to a Poisson distribution to minimize gaps; (Hyberts et al. 2010) here we choose as a reporter of gap distribution the analysis of the largest gap since all remaining gaps are then smaller. Any one schedule can result in sometimes very large maximum gap sizes. Averaging 10 or 100 individual schedules together forces the maximum gap to converge to a tight range and prohibits pathologically large gaps from occurring. In considering gaps, we now face an incentive to retain more samples (Hyberts et al. 2012). For example the maximum gap in a sinusoid schedule (n = 100) retaining 12.5 % of the samples (128/1,024) is guaranteed to be less than 200, while the maximum gap for retaining 6.25 % of the samples (64/1,024) is guaranteed to be over 200. It is satisfying to notice that even when 100 individual schedules are averaged together, the result is not deterministic. The enhancement and maximum gap both are observed to vary among 15 averaged schedules, each the result of averaging 100 individual schedules together. This observation that averaged schedules are not deterministic therefore is seen to be consistent with recommendations that schedules retain a random character to avoid complications with the point spread function (Hoch et al. 2008).

An additional interesting conclusion is reached from considering Fig. 8. Achieving progressively lower levels of sparseness has little to offer in improving performance criteria since the maximum theoretical enhancement is already closely reached by 12.5 or 25 % reduction, and since significant penalties in gap size are incurred when fewer samples are retained. Also, point spread functions become increasingly complex as sparsity increases (Maciejewski et al. 2012).

Discussion

Non-uniform sampling following an exponential density provides an enhancement of the intrinsic SNR (iSNR) of the raw time domain data of decaying NMR signals that is fully under user control if knowledge of the signal envelope is available (Eq. (1) and prior citations). Enhancements are significant and can approach two fold, even exceeding this if the user is willing to accept some loss of resolution.

However, there is limited potential at this time for NUS-based signal enhancements to improve many 3D biomolecular experimentation in liquids. The NUS-based enhancements are only significant for long evolution times exceeding 1T₂, and it is usually prohibitive to achieve these evolution times when pursing typical 3D-NMR backbone and sidechain assignment experiments (Rovnyak et al. 2004). It is also appreciated that NUS cannot enhance the raw time domain data of constant-time (non-decaying) signals and so can only be used for time savings or to reach the maximum available evolution in constant-time periods (Schmieder et al. 1994). In contrast, NUS-based sensitivity enhancements are ideally suited for achieving near-maximum iSNR improvements in many biosolids experiments where relaxation times are more favorable and for which CT dimensions are still not commonly employed; compounding the effect in multiple dimensions of biosolids NMR achieves dramatic enhancement that are on the same scale as cryogenic probes (Paramasivam et al. 2012). Compelling NUS-based sensitivity enhancements are achieved in 2D-NMR of dilute natural products, where it is necessary to reach new detection limits without compromising resolution (Palmer et al. 2013). Yet more work is needed to determine if useful NUS-based enhancements could be achieved in typical backbone and side chain 3D-NMR liquid phase experiments of proteins. For example, it is worth studying what the trade-offs would be in reverting constant-time dimensions to decaying dimensions in order to have access to NUS-based enhancements.

This work arrives at three general regimes in employing NUS-based enhancement in biological samples that are distinguished on the basis of constraints on the line shape in the NUS recorded dimension.

One case is to place more focus on optimizing sensitivity than on preserving high resolution. We identify one class of bioNMR experiments in liquids that is ideally suited to reap NUS-based signal enhancements: NUS enables recording sensitive and resolved ¹H,¹⁵N-HSQC’s on natural abundance protein samples on relatively short time frames (ca. 60–90 min in this work), that can be even shorter for many investigators depending on available instrumentation, and which are shown to be inaccessible by uniform sampling in the same time. Indeed, comparable spectra could only be obtained with uniform sampling if the total experimental time was about four fold longer (data not shown). Recording ¹H,¹⁵N-HSQC’s on natural abundance samples is recognized as a problem of optimizing sensitivity over resolution, and so is able to accept some moderate line broadening in order to take advantage of enhancements that exceed two-fold (Fig. 1). In this work, the line broadening was ca. 30 % in tests reported here (Fig. 4cd) in which the sampling decay was about three times faster than the signal decay. This degree of broadening does not strongly impact the final spectra since the use of NUS still allows for exploring long evolution times, so that resolution remains very favorable overall.

An intermediate criterion is also identified here. This work shows in two independent classes of carefully designed tests that when the density of samples is matched or is weakly biased relative to the decay of the signal, then the line width at half maximum is closely conserved relative to the line width measured from uniform sampling. At present this regime of NUS is probably of greatest interest to most spectroscopists, and it is reassuring to see that only approximate knowledge of the average sample T₂ value is needed to perform NUS and be confident that line widths are conserved (again, technically T₂* value since it is the net signal envelope that is the crucial basis for achieve NUS enhancements of iSNR). Yet a very weak peak distortion can be observed near the base of peaks in this case that is negligible in some cases but can be more observable in noisy or crowded spectra.

Therefore, in response to the weak line shape changes with matched exponential NUS, this work has also explored a third scenario of the application of NUS-based enhancements in which one wishes to still obtain a useful enhancement, but no degradation to peak shape can be tolerated. This work has shown through careful simulations and experiments that weak broadening of the base of peaks can result even from matched exponential NUS, even when the line width at half maximum is not changed. We report that an alternative density based on a quarter-wave segment of a sinusoid does not result in such peak distortions and yet still delivers the same iSNR enhancement as a matched exponential NUS schedule. Verification was obtained of the improved performance of this sinusoidal schedule over exponential sampling by analyzing the peak shapes from 2D-HSQC and 2D-HMBC experimentation on a natural product.

It follows from these results that for any experiment in which one would choose to record evolution times ca. 3T₂, and also to operate in the intermediate or the highly conservative regime of achieving sensitivity relative to resolution, then the quarter-wave sinusoidal density is always preferable to a matched exponential schedule. The sinsusoidal density does not generalize to steeper biasing towards earlier times, which raises an additional issue that needs more work. Specifically, it is worthwhile to discover alternatives to strongly biased exponential schedules that may not sacrifice as much peak shape to achieve higher enhancements. For the present, if sensitivity is the user’s only goal, then biasing the exponential density up to threefold is still the only choice.

A consideration of sinusoidal schedules supports the current understanding of best practices in NUS schedule design and leads to some additional generalizations. Sparser schedules improve agreement with the desired sampling density, but also incur greater gaps and incur more complex point spread functions that must be deconcolved from the frequency domain signals. Limiting returns in any one dimension are encountered for about four-fold sample reduction. This does mean also, when employing NUS in N multiple indirect dimensions, that data reduction by a factor of 4^N is a worthy goal. Individual circumstances still apply. The degree of reduction that can be tolerated is greater if signals are strong, but lower if samples must be selected from a very short uniform grid. For example, selecting 8 samples from a uniform grid of 32 achieves four-fold reduction, but detected signals may be under-constrained by having only 8 samples.

Finally, this work wishes to advocate for distinguishing the intrinsic SNR of the raw time domain data as the critical metric for gauging NUS-based sensitivity improvements. Analysis of spectra show that exponential NUS enhances the ability to detect new peaks and to enable new science, and the basis for user control over these gains is the intrinsic SNR of the raw data.