Statistical wiring of thalamic receptive fields optimizes spatial sampling of the retinal image

Summary

It is widely assumed that mosaics of retinal ganglion cells establish the optimal representation of visual space. However, relay cells in the visual thalamus often receive convergent input from several retinal afferents and, in cat, outnumber ganglion cells. To explore how the thalamus transforms the retinal image, we built a model of the retinothalamic circuit using experimental data and simple wiring rules. The model shows how the thalamus might form a resampled map of visual space with the potential to facilitate detection of stimulus position in the presence of sensor noise. Bayesian decoding conducted with the model provides support for this scenario. Despite its benefits, however, resampling introduces image blur, thus impairing edge perception. Whole-cell recordings obtained in vivo suggest that this problem is mitigated by arrangements of excitation and inhibition within the receptive field that effectively boost contrast borders, much like strategies used in digital image processing.

INTRODUCTION

The dendritic arbors and, consequently, the receptive fields (RFs) of retinal ganglion cells (RGCs) form spatial arrays that approach the theoretical limit for optimal packing of a hexagonal lattice (Wässle et al., 1981b; Eglen et al., 2005; Borghuis et al., 2008; Gauthier et al., 2009; Liu et al., 2009). Therefore, it has been widely assumed that retinal mosaics set the limit on visual resolution. Acuity in cat, however, is higher than the density of On or Off RGCs predict (Hall and Mitchell, 1991), suggesting that other factors improve image perception.

Indeed, visual space is rewired in the thalamus, transforming the retinal message sent to cortex. Retinal output reaches the primary visual cortex (V1) through relay cells in the dorsal lateral geniculate nucleus (LGN) of the thalamus. Even though retinal and thalamic neurons have similar RFs (Hubel and Wiesel, 1961; So and Shapley, 1981; Kaplan and Shapley, 1984; Usrey et al., 1999), relay cells often receive convergent retinal inputs (Cleland et al., 1971; Hamos et al., 1987; Mastronarde, 1992; Usrey et al., 1999; Yeh et al., 2009). Further, there are approximately twice as many thalamic relay cells as RGCs in cat (Madarász et al., 1978; Stone and Campion, 1978; LeVay and Ferster, 1979). Retinothalamic convergence, combined with the increase in cell number from stage to stage could, in principle, provide an interpolated map of visual space (Barlow, 1981) that might heighten the LGN's capacity to resolve stimulus position.

To explore these and associated consequences of the thalamic resampling, we constructed a statistical connectivity model of retinothalamic circuitry based on the synaptic structure of retinal and thalamic RFs that we mapped using whole-cell recording in vivo and on simple wiring rules (Chklovskii et al., 2002; Ringach, 2007). The model yielded a circuit in which patterns of retinothalamic convergence provided an interpolated map that improved coverage of visual space and thus allowed better signal localization than the retina alone achieved, assuming that noise in neural responses is independent, Gaussian and additive.

The benefits of interpolation come at a cost, however. Interpolation blurs the image, reducing local contrast to degrade edge perception. Our experimental evidence points to a solution to this problem. Our results suggest that the anatomical organization of relay cells and interneurons in the LGN produce physiological arrangements of excitation and inhibition within the RF centers that effectively boost contrast borders and increase the dynamic range of the visual message that the LGN relays. Thus, the retinothalamic circuit we describe operates like techniques manmade devices employ to improve the appearance of visual images.

RESULTS

We recorded extracellularly from 34 X-RGCs and intracellularly from 43 X-relay cells and 6 local interneurons in laminae A/A1 of the LGN. We used these experimental results to build a computational model for studying the functional consequences of divergence and convergence in connections from RGCs to relay cells and interneurons in the LGN as well as connections from interneurons to relay cells.

Receptive field transformations in retinothalamic networks

Spatial extent of excitation and inhibition in the receptive field center

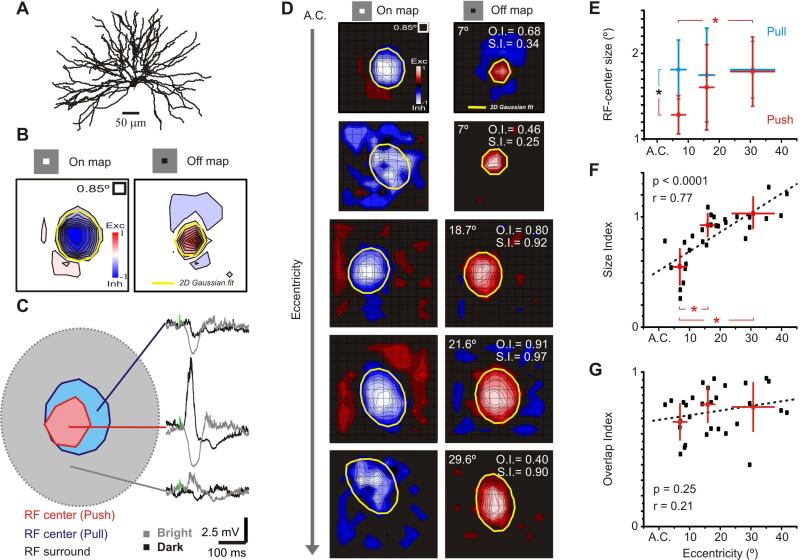
We used sparse noise, individual bright and dark squares, to map RFs of retinal input and inhibition in thalamic relay cells; see Supplementary Methods. The RF of a thalamic X-cell (Figure 1A), recorded at an eccentricity of 7°, is shown as two separate contour plots (Figure 1B). Since this was an Off-center cell, dark squares in the center evoked a depolarization followed by a hyperpolarization that corresponded to the withdrawal of the stimulus. White squares flashed in the same positions evoked responses of the opposite polarity (Figure 1C)—an arrangement called push-pull (Jones and Palmer, 1987; Ferster, 1988; Martinez et al., 2005).

Figure 1.

Asymmetric distribution of excitation and inhibition in the thalamic RF. (A) Anatomical reconstruction of an X Off-center relay cell recorded 7° away from the area centralis. (B) The RF is shown as two separate contour plots for responses to the bright (left) and dark (right) squares. Stimulus size was 1.7° and grid spacing was 0.85°. (C) Dark squares that fell in the center pixels evoked a depolarization followed by a hyperpolarization that corresponded to the withdrawal of the stimulus. White squares flashed in the same positions evoked the opposite response. The small vertical green dashes indicate the onset of the stimulus, which was flashed for 31 ms. The excitatory and inhibitory centers of the RF, however, differed in extent and relative eccentricity. (D) RFs of five geniculate cells recorded at increasing distances from the area centralis (top to bottom). RFs are shown as two different contour plots for responses to the bright (left) and dark (right) stimulus. Red and blue code for excitation and inhibition, respectively. Individual values of overlap (O.I.) and size (S.I.) indices and distance to area centralis (A.C.) are overlaid. (E) Average push and pull size for cells recorded at different eccentricities, within 10° of the area centralis, between 10° and 20° and, finally, at more than 20°. The intersection of the crosses at each point corresponds to the mean and the length to the standard deviation. *denote statistically significant differences (p<0.005. Student's t-test). (F) Scatter plot of size index versus eccentricity. The intersection of the crosses in each cluster of points corresponds to the mean and the length to the standard deviation. The three groups are the same as in (E). The dotted line represents the best linear fit. *denote statistically significant differences (p<0.008. Student's t-test). (G) Scatter plot comparing overlap index versus eccentricity. The intersection of the crosses in each cluster of points corresponds to the mean and the length to the standard deviation. The three groups are the same as in (E, F). The dotted line represents the best linear fit. See also Figures S1, S2 and S3.

The layout of push and pull at the center of the RF differed at different eccentricities in the visual field. For central locations in visual space, the push was restricted to the RF center (red contour in Figure 1C), while the pull (blue contour in Figure 1C) extended to the surround (approximated by gray contour in Figure 1C). A detailed view of this representative RF can be found in Supplementary Figure 1. We obtained RF maps from 30 relay cells in the A laminae of the LGN (Figure 1D), sampling central and peripheral regions of the visual field. These results show that even as the spatial extent of the push within the thalamic RF center grows with eccentricity, as is the case in retina (Supplementary Figure 2), the size of the pull remains constant, on average (Figure 1D,E).

We used a size index (S.I.) to quantify the relative area of excitation and inhibition (Figure 1F, Supplementary Figure 1B,C, and Experimental Procedures). The values of the index correlated linearly with eccentricity in the visual field. Further, we used an overlap index (O.I.) to evaluate the spatial displacement of push and pull (Martinez et al., 2005), which was similar at all eccentricities (Figure 1G and Supplementary Methods).

Implications for thalamic circuitry

The pull is dominated by inhibition rather than the withdrawal of excitation (Supplementary Figure 3; see also Wang et al., 2011). Since retinal afferents are excitatory, thalamic RFs apparently emerge through a simple circuit: excitation comes from RGCs of the same center sign (On or Off) whereas inhibition is routed through local interneurons driven by RGCs of the opposite center sign.

Statistical connectivity model of the early visual pathway

The wiring rules underlying the asymmetric, or nested, arrangement of push and pull in thalamic RF centers are not known. Our working hypothesis is that thalamic RFs reflect spatial statistics of the On and Off RGC mosaics (Wässle et al., 1981a; Eglen et al., 2005) and that a simple, probabilistic wiring rule instructs retinogeniculate connectivity during development (Soodak, 1987; Ringach, 2007; Paik and Ringach, 2011). We built a computational model of the LGN informed by our experimental results to test this hypothesis and investigate potential consequences for visual processing.

Retinal layer

The first layer of the model simulated two independent mosaics representing the centers of X-type On and Off RGCs (Figure 2A) at an eccentricity of 7°, the average location of thalamic RFs we recorded in the central visual field. The retinal mosaics were constructed using established means (Eglen et al., 2005; Ringach, 2007); see Experimental Procedures and Supplementary Methods. The spatial statistics of the mosaics were based on classic studies of retina (Wässle et al., 1981a; Stein et al., 1996) and fulfilled the conditions of quasi-regularity and positional independence (Eglen et al., 2005; Ringach, 2007). Thus, the conditional density of cells of the same class (On or Off) becomes a function of distance from the soma. The probability of finding a same-sign neighbor is initially low, increases to a peak value and then, at larger distances, settles to the mean probability (Figure 2B, left). By contrast, the probability of finding an opposite-sign neighbor is the same at all distances, provided that two cells cannot lie at the same site (Eglen et al., 2005; Ringach, 2007) (Figure 2B, right). Retinal RF centers (Figure 2A, right inset) were modeled as two-dimensional Gaussian functions, centered at the location of the soma in the home mosaic. The average size of the retinal RF centers was fitted to experimentally measured values we obtained using the same stimulus as for the LGN (Supplementary Figure 2) and the RF center shapes were determined by the cells’ Dirichlet domains; see Experimental Procedures.

Figure 2.

Statistical wiring model of the early visual pathway. (A) Mosaics of On and Off RGCs. Inset shows a typical RF. (B) Conditional density plots of same sign (left) and opposite sign (right) RGCs in the model retinal mosaic (δ in the scale marks average probability). (C) Mosaics of On and Off LGN interneurons (left) and relay cells (right). Insets show samples of typical RFs in each mosaic. (D) Each thalamic cell receives a unique complement of retinal inputs (insets in the middle) based on a Gaussian probability function of the distance between pre- and postsynaptic neurons. The strength of each individual connection is also modulated by the same probability function. The figure shows the case for an On-center relay cell. Similar operations were used to wire up the RGCs to the LGN inhibitory mosaic and the inhibitory neurons to the relay cells in the LGN. See also Figures S2, S4 and S7.

Thalamic layer

The second layer of the model represented the LGN, and included one array of relay cells (Figure 2C, right) and another of local interneurons (Figure 2C, left). Current estimates suggest that there are twice as many relay cells as RGCs but half as many interneurons (Madarász et al., 1978; Stone and Campion, 1978; LeVay and Ferster, 1979) throughout the LGN (Fitzpatrick et al., 1984). The spatial layout of the modeled network preserved homogeneous distributions of these two cell types. The polarity (On or Off) of each relay cell was inherited from its nearest retinal input. Conversely, the polarity of the local inhibitory neurons was the opposite of their nearest neighboring relay cell. Connection probability was an (isotropic) Gaussian function of the relative distance between the RF centers of the pre- and postsynaptic partners (Figure 2D); and see Experimental Procedures. Notably, the model used only a simple placement optimization protocol that minimized the cost of wiring (Ramon y Cajal, 1995; Chklovskii et al., 2002).

Construction of push-pull

The push at the RF center in both thalamic interneurons and relay cells was the linear sum of all retinal afferents weighted with the same Gaussian function used to calculate connection probability (Figure 2D, bottom insets). The pull at the RF center of relay cells was derived from the linear sum of their weighted inhibitory inputs. There was no spiking mechanism in the simulated retinothalamic network (see also Ringach, 2007; Paik and Ringach, 2011); thus, the modeled RFs represent the synaptic RFs obtained experimentally.

After computing the RF center of each relay cell, we calculated the distributions of four defining characteristics—push radius, pull radius, overlap index and size index (Table 1)—for increasing values of retinothalamic convergence (Experimental Procedures). The model was fitted to the data by minimizing the Kullback-Leibler distance between the empirical and theoretical distributions of these four RF properties (Figure 3A); see Experimental Procedures. This procedure allowed us to obtain the values for retinal convergence onto relay cells and onto interneurons as well as the values for the convergence of thalamic interneurons onto relay cells that best explained our experimental results (p=0.001); see Experimental Procedures. Thus, push-pull in the RF centers that this ideal retinothalamic circuit produced (Figure 3B and Table 1) were virtually identical those mapped in vivo (Figure 3C).

Table 1.

Measurements of model retino-thalamic connectivity patterns and geniculate RF structure.

OI	SI	Rpush	Rpull	RxT	IxT	RxI
0.7679	0.5510	1.2087	1.9303	3.1894	6.2938	4.3113
0.1100	0.1504	0.1633	0.4468	1.3985	2.3678	1.7986

OI = Overlap Index. SI = Size index. R_push= Radio Push (°). R_pull= Radio Pull (°). RxT= Number of different RGC inputs per LGN relay cell. IxT = Number of different interneuron inputs per relay cell. RxI = Number of different RGC inputs per interneuron. Top row: average. Bottom row: Standard deviation.

Figure 3.

Synaptic structure of thalamic RFs in experiments and model. (A) Distributions of the four defining characteristics of a thalamic RF—push radius, pull radius, overlap index and size index—in the experiments (black) and the probabilistic retinothalamic model (gray). (B) Schematic view of the “optimum” retinothalamic circuit. Numbers represent the average convergence on each branch of the network. (C) Comparison of experimental (top) and model (bottom) RFs shown as separate contour plots (push in red and pull in blue). Insets show values of push radius (R_push), pull radius (R_pull), overlap index (O.I.) and size index (S.I.). See also Figure S7.

Local architecture of the LGN

Our detailed knowledge about the stereotyped structure of retinal mosaics contrasts with our limited understanding of the thalamic functional architecture. To help fill this gap, we made the assumption that neural connections minimize total axon length (Supplementary Figure 4). This developmental wiring rule introduces a strong bias in the relative distribution of cells in the LGN. In addition, since relay cells outnumber RGCs and inherit their polarity from their nearest retinal input, they should form partially overlapped clusters of same-sign neighbors. Further, since relay cells greatly outnumber interneurons, within each same sign cluster of relay cells, there should be an interneuron of the opposite sign. Accordingly, in the conditional density plots of relay cells (Figure 4A, middle panels) and interneurons (Figure 4A, bottom panels) from the model LGN, the probability of finding a same-sign neighbor is initially very high for relay cells and almost zero for interneurons, whereas the opposite is true at larger distances. This is unlike retina (Figure 4A, top panels), where the likelihood of finding adjacent RGCs that share the same center sign is low. Therefore, the dipoles of On- and Off-center cells that characterize the retinal mosaic (Figure 4B, left panels) are transformed into small clusters of same-sign relay cells (Figure 4B, right panels). Cluster size depends on the relative local densities in the retina and thalamus and the degree of retinothalamic convergence.

Figure 4.

Local structure of the lateral geniculate nucleus. (A) Conditional density plots of same sign (left) and opposite sign (right) RGCs (top), relay cells (middle) and interneurons (bottom) in the model retina and LGN (δ in the scale marks average probability). While, unlike in the retina, relay cells form clusters of same sign (On or Off) cells, inhibitory neurons tend to be located within the clusters of the thalamocortical cells. (B) The dipoles of On- and Off-center RGCs that characterize the retinal mosaic (left) are transformed in clusters of On- and Off-center relay cells in the thalamus (right). See also Figure S4.

Experimental tests of the model predictions

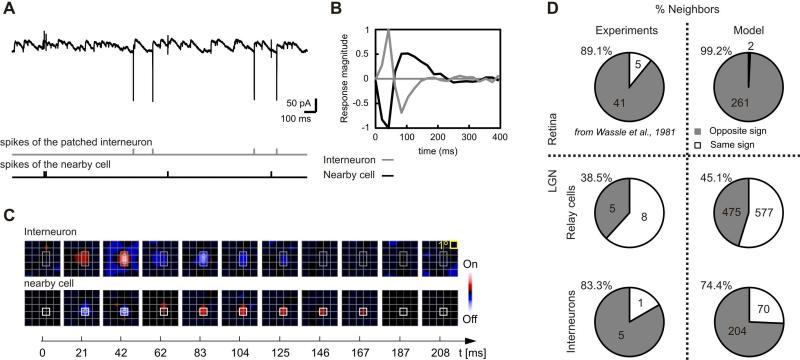
To test the biological plausibility of the model predictions, we obtained simultaneous intra- and extracellular recordings from relay cells and interneurons in the LGN. These experimental results were not used to fit the model or its parameters. A record from a local interneuron shows three different types of neural events (Figure 5A). The most common are excitatory and inhibitory postsynaptic currents (PSCs) and spikes; these are the cell's inputs and outputs respectively. In addition, we were able to resolve another type of event, called the “third potential”. These are small, usually biphasic, waveforms—spikes from a cell near the one recorded directly (Kaplan and Shapley, 1984). The third potentials that we recorded clearly came from a separate cell; they were not affected by polarization of the patched cell and their RFs often had a different sign and/or size. The nearby cell depicted here was likely a relay cell since it fired signature bursts of action potentials (e.g. Guido et al., 1992); local interneurons do not fire such bursts (Pape and McCormick, 1995).

Figure 5.

Local spatial correlation between opposite sign excitatory and inhibitory neurons in the lateral geniculate nucleus. (A) Intracellular recording from an interneuron including the simultaneously recorded spikes of a nearby putative relay cell. The spike times of the interneuron (gray) and the nearby cell (black) are represented at the bottom. (B) Impulse responses of the interneuron (gray) and the relay cell (black). (C) Snapshots of the RFs for each cell taken at the latencies indicated below each frame. (D) Distributions of first neighbor identities in the experiments (left) and model (right).

Both the patched and nearby neurons had similar response time-courses (Figure 5B) and largely overlapping RFs (Figure 5C). However, the interneuron's RF (Figure 5C, top) was larger, as expected from the greater retinothalamic convergence onto interneurons vs. relay cells that our model predicts (Figure 3B and Table 1). Furthermore, the two cells had the opposite preference for luminance contrast (On-center interneuron and Off-center relay cell), as anticipated from the minimum wiring algorithm (Figure 4A). We have recorded intracellularly from 13 relay cells and 6 local interneurons that had associated third potentials. Figure 5D shows that the distributions of first-neighbor identities derived from experiments (left) or the model (right) are remarkably similar, both in the retina (top panels) and the LGN (middle and bottom panels). The neighbor of each interneuron (n=6) we patched was a relay cell. For all but one of the interneuron/relay cell pairs, the RFs had the opposite center sign. Given the relative numbers of relay cells and interneurons (~80%/20%) and On- and Off-center cells (~50%/50%), we were able to calculate a p value for this finding: p=0.024. Thus, the LGN transforms the local spatial organization of the On and Off populations.

Functional consequences of retinothalamic rewiring

Receptive field diversity in the model LGN

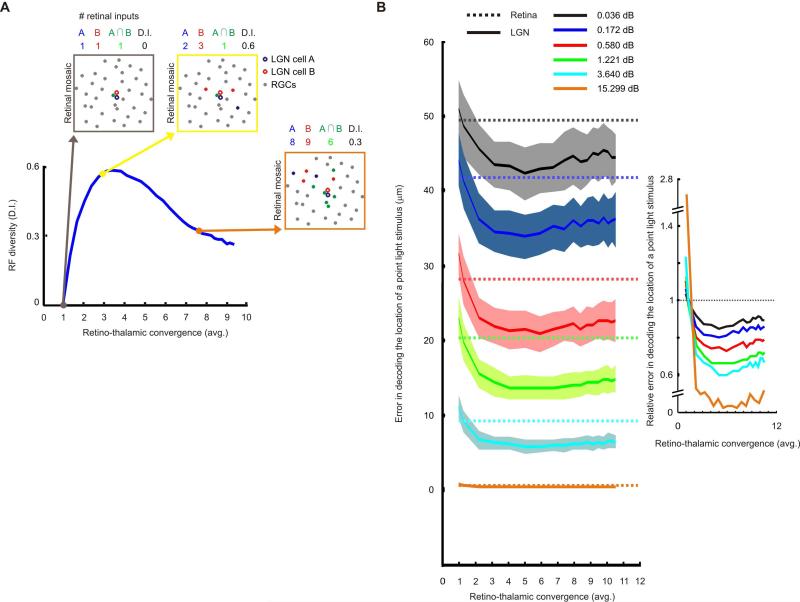
By increasing neuronal divergence within the retinogeniculate pathway, the pool of different retinal inputs available to contact each relay cell expands to permit greater diversity of RFs in the thalamic vs. retinal array. This is a fundamental requirement for an optimal information code (e.g. Barlow 1981; Atick and Redlich, 1990; Dan et al., 1996; Liu et al., 2009). To investigate how RF diversity might change as a function of mean retinothalamic convergence (i.e. the average number of retinal inputs each LGN neuron receives), we defined a diversity index (D.I.); see Experimental Procedures. This index is based on the differences between the identities of the various retinal inputs to first neighbor relay cells. The value of the D.I. is zero when thalamic cells receive input from just one retinal afferent (here, the set of synaptic partners coincide and thalamic RFs duplicate the retinal map). RF diversity reaches a peak value for convergence ratios between 2 and 6 and then approaches the minimum at larger values (Figure 6A). This drop reflects the local nature of the retinothalamic circuit and not the relative numbers of RGCs and thalamic relay cells (Supplementary Figure 5A). Since the probability of connection is a function of distance between the pre- and postsynaptic RFs, the number of retinal inputs that two relay cells share increases rapidly when the mean retinogeniculate convergence exceeds 4 (Figure 6A, inset, green dots). Remarkably, the maximum RF diversity is produced by the same circuit design that best fits the distributions of the experimental results (Figure 3B). Larger values of RF diversity indicate that neighboring relay cells receive complementary combinations of retinal inputs, potentially improving coverage and reducing redundancy in the thalamic array.

Figure 6.

Statistical wiring results in high diversity of thalamic RFs and small decoding errors. (A) Evolution of RF diversity (D.I. index) as a function of average retinothalamic convergence. Insets show how the complement of retinal inputs to a pair of thalamic cells that share their first retinal afferent change as retinothalamic convergence is increased. (B) Error in decoding the location of a point light stimulus under different finite levels of signal-to-noise (color coded). Dotted lines represent the mean retinal error. Solid lines show the evolution of the mean LGN error as a function of average retinothalamic convergence for the same levels of signal-to-noise; shadows indicate the standard deviation. (B inset) Mean thalamic error (solid lines) relative to the retinal error (dotted line). Other conventions as in (B). See also Figure S5 and Supplementary Video 1.

Optimal retinal coverage by thalamic receptive-fields

Our model and data both suggest that thalamic RFs of the same center sign are more likely to be direct neighbors than their retinal counterparts (Figures 4A and 5D). Thus, RF tiling in retina and thalamus seem topologically different. The most efficient distribution of thalamic RFs relative to the retinal mosaic maximizes the area of the retina covered by the peak of at least one thalamic RF (insets in Supplementary Figure 6B). To investigate how the coverage of the retinal mosaics changes as a function of retinothalamic convergence, we thresholded thalamic RFs at different levels relative to peak value (Supplementary Figure 6B). This step was necessary because Gaussian fits are boundless: without thresholding, each RF covers the entire visual field. Our model shows that the most effective coverage of the retinal mosaic by the thalamic RF array is achieved by retinothalamic convergence values between 2 and 6, and drops steadily at larger values, like the pattern for RF diversity (Figure 6A). Thus, the same wiring rules that optimize RF diversity in the thalamus also improve the coverage of visual space, indicating that retinal input is efficiently distributed in the LGN. These circuit properties have the potential to improve the accuracy of read out of spatial position, as below.

Decoding capability of thalamic arrays

We use the term spatial decoding capability to describe the accuracy of a given retinothalamic circuit's ability to resolve the spatial location of small visual targets. To quantify the spatial decoding capability of different circuit arrangements, we used the power of combinatorial coding available to the geniculate array and an analysis based on Bayesian decoding (Ruderman and Bialek, 1992). Specifically, we asked if the retinothalamic circuits our model generates (Figure 3B) can perform computations that improve estimates of signal location beyond those obtained directly from retina, given the presence of sensor noise. We built a decoder that estimated the position of point stimuli from neural responses in either retina or LGN. Here, the RFs in the retinal layer were modeled after a classical dataset (Peichl and Wässle, 1979) obtained with minimal stimulation protocols. The retinal response to the stimulus was computed by summing the signal, the point stimulus convolved with the RF, and independent Gaussian noise; see Experimental Procedures. The retinal output was supplied to the LGN and convergence ratios were varied from 1-10.5. Then, using prior information that the stimulus is localized, an estimate of the stimulus position was decoded from the responses of relay cells; the mean error of the decoded stimulus position was measured as a function of retinothalamic convergence. The results of this analysis show that, for a broad range of finite retinal noise levels, retinothalamic convergence reduces the mean LGN estimation error and improves decoding of stimulus position compared with retinal performance (Figure 6B and Supplementary Video 1). This improvement is particularly pronounced for the same range of convergence ratios (3-6) that optimize RF diversity and coverage of visual space in the LGN (Figure 6A; Supplementary Figure 6B).

Consequences of interpolation for image perception

Because RFs of relay cells are interpolated versions of the retinal map (Supplementary Figure 6C), the thalamic array samples visual space more densely than the retina. In addition, interpolation reduces high frequency noise in the input signal, an effect that is enhanced by the Gaussian shape of the RFs (Barlow, 1981). However, these benefits have the undesirable consequence of increasing local spatial correlations. Imagine a sharp contrast border (an edge) falling over the RFs of a group of thalamic cells (Figure 7A). The slope of the depolarization profile for the population, e.g. for On-center cells (Figure 7B, black solid line), becomes shallower than that in the image (Figure 7B, black dotted line), thus blurring perception of the edge. Observe how the depolarization profile in Figure 7B (black solid line) starts to rise well before the real edge in the stimulus. Note that the population responses shown in this figure are equivalent to changes in synaptic response at the single cell level in the model, when the same luminance edge is moved across the cell's RF.

Figure 7.

Local contrast enhancement by retinothalamic circuits. (A) Mosaic of On-center relay cells stimulated with a luminance border (overlaid). (B) Population response curves of the thalamic mosaic in (A) to the stimulus with (red) and without (black) feedforward inhibition (pull). (C) Population response curves of the same thalamic mosaic with feedforward inhibition to a set of three stimuli with different strengths showing contrast independent zero crossing. See also Figures S6 and S8.

Our model shows how the patterns of push-pull inhibition we recorded can counteract deleterious effects of image interpolation. Push-pull at the RF center increases the dynamic range of the thalamus, steepening the slope of the depolarization, hence compensating for the loss in local contrast around the luminance border (Figure 7B, red line; see Discussion). Further, this effect is independent of stimulus contrast; note that the red lines in Figure 7B,C enter the depolarizing range precisely where the sharp luminance border lies. This element of the thalamic relay is akin to image interpolation and local contrast enhancement (LCE) in photography (Supplementary Figure 6; see Discussion). Thus, the specific arrangement of push and pull in the thalamic RF may explain, at least in part, why image perception in the cat is better than the Nyquist limit based on the spatial sampling density of retinal receptors (Robson and Enroth-Cugell, 1978; Hall and Mitchell, 1991).

DISCUSSION

Each sheet of ganglion cells in the retina forms a complete representation of visual space that is transmitted to the thalamus (Wässle and Riemann, 1978). When individual retinal axons enter the LGN they branch profusely to synapse with multiple relay cells and interneurons (Hamos et al., 1987), at once rewiring the sensory map and engaging local inhibition. We asked how these key elements of the thalamic circuit might contribute to vision. Using existing statistics from retinal mosaics (Wässle et al., 1981a; Eglen et al., 2005), our own maps of synaptic excitation and inhibition within the relay cell's RF and simple statistical wiring rules, we constructed a model of the retina and LGN. The parameters for retinothalamic convergence that our model generated matched experimental data and yielded an interpolated map of visual space that optimized functional properties of the network. Interpolation, unfortunately, blurs the image. This deficit, however, was mitigated by thalamic push-pull inhibition. Specifically, the extent of the pull is larger than the push in receptive fields of relay cells that tile central visual space. This arrangement has the effect of heightening responses to local contrast borders, much like the strategies used to improve the appearance of digital images.

Local structure of the thalamic network

Our model and experimental results highlight differences between retinal vs. thalamic maps. In the model, the degree of overlap between adjacent thalamic RFs with the same center sign is greater than predicted if the RGC mosaics were simply reproduced; neighboring RGCs in a mosaic almost always have the opposite sign (Wässle et al., 1981a) (Figure 5D). In addition, relay cells frequently neighbor interneurons of the opposite center sign. Notably, the model predictions were confirmed by our own experiments (Figure 5D) and further corroborated by extracellular studies that report same-sign clusters of On or Off relay cells (Bowling and Wieniawa-Narkiewicz, 1986; Berman and Payne, 1989; Yeh et al., 2009; Jin et al., 2011).

This match between computational predictions and experimental results suggests that the model parameters approximate the natural situation. Thus, the development of retinal and thalamic circuits might follow different principles. The structure of RGC mosaics can be explained by simple minimal spacing rules in retina (Kay et al., 2012). By contrast, since there are spatial correlations within the thalamic arrays, different or additional cellular mechanisms must be employed, perhaps influenced by activity dependent interactions and physical tension between the neurites and cell bodies of synaptically connected neurons (Cook and Chalupa, 2000; Huckfeldt et al., 2009).

Diverse input patterns to receptive fields in the lateral geniculate nucleus

What is the significance of spatial remapping for vision? It has long been clear that relay cells receive convergent input from different retinal afferents. While cross-correlation analyses of retinal and thalamic spike trains (Cleland et al., 1971; Mastronarde, 1992; Usrey et al., 1999; Yeh et al., 2009) typically reveal the RF structure of single afferents to a given relay cell, this approach does not resolve the pooled retinal input that a single relay cell receives. Intracellular recording allowed us to measure the aggregate synaptic response of both excitatory and inhibitory inputs. Thus, we were able to make independent estimates of the number of retinal afferents converging on a single relay cell or single interneuron as well as the number of presynaptic interneurons that contact a given cell (Figure 3B).

Our model suggests that relay cells pool inputs from an average of 3-4 retinal afferents (Supplementary Figure 7), consistent with the number obtained from previous cross-correlation analyses (Cleland et al., 1971; Mastronarde, 1992; Usrey et al., 1999; Yeh et al., 2009) and ultrastructural studies (Hamos et al., 1987). This result is also compatible with a report showing that the average amount of synchronous firing recorded from pairs of thalamic neurons that are driven by common retinal input is far lower (≈ 10%) than would be expected (90-100%) if a single afferent dominated all its postsynaptic targets (Yeh et al., 2009).

Notably, the specific value of convergence that fits the data also optimizes RF diversity in the LGN (Figure 6A). Thus, by virtue of RF diversity, neighboring relay cells are able to process information independently, even if some of their input derives from a common retinal source. This independence reduces redundancy in the sampling of the retinal mosaics and supports the view that visual processing in the thalamus serves to recode information efficiently (Barlow, 1981; Atick and Redlich, 1990; Dan et al., 1996; Wang et al., 2010).

Enhanced decoding capability in the lateral geniculate nucleus

It is assumed that cellular sampling in the retina sets limits on visual acuity, optical aberrations aside (Rossi and Roorda, 2010). For instance, human visual resolution at the fovea, where RGCs receive input from a single cone, is limited by cone spacing (Rossi and Roorda, 2010). In the periphery, however, substantial cone-toganglion cell pooling leads to poorer resolution than the cone sampling limit predicts. Peripheral acuity is more consistent with the spacing of the mosaic of midget RGCs (Rossi and Roorda, 2010).

In cat, ganglion cells at all eccentricities pool inputs from several cones (Hughes, 1981). But visual acuity in cat, 9 cyc/deg (Hall and Mitchell, 1991), is neither predicted by the average spacing of X-RGCs, 6.5 cyc/deg (Hughes, 1981), as for the human periphery, nor by the minimum intercone distance, 16 cyc/deg (Steinberg et al., 1973), as at the human fovea. This discrepancy had suggested that the mosaics of On and Off X-RGCs might function as a single retinal sampling grid (Hughes, 1981); however subsequent studies do not support this scheme. For example, in macaque, resolution is limited by the density of On or Off midget ganglion cells (Merigan and Katz, 1990). In addition, the high degree of irregularity of the combined On and Off mosaic in the cat (Wässle et al., 1981a) and the functional independence of the On and Off pathways in many species (Schiller, 2010) including human (Westheimer, 2007), argue against the utility of considering On and Off X-RGCs as a single sampling grid.

Our results provide an alternative explanation for visual performance in cat that is consistent with functional segregation of the On and Off X-RGCs mosaics. We have shown that thalamic RFs have greater diversity (Figure 6A) than their retinal precursors. Assuming that the noise in retinal spike trains is independent, Gaussian and additive, this greater diversity allows the thalamic circuit to decode stimulus position more readily than the retinal mosaic is able to do (Figure 6B and Supplementary Video 1) and thus might improve behavioral performance on tasks that measure visual acuity.

Local contrast enhancement by retinothalamic circuits

So far, we have concentrated on retinothalamic divergence and convergence. Here we discuss how inhibitory input can sharpen vision. Our intracellular records show that, in the central 10° of the visual field, the pull signal in the RF center covers a larger region of space than does the push. Our model suggests that the greater expanse of the pull reflects highly convergent retinal input onto thalamic interneurons, an idea supported by ultrastructural studies (Montero, 1991; Van Horn et al., 2000). Further, relay cells in the model are supplied by several local inhibitory neurons, again consistent with past experimental work (Hamos et al., 1985; Crunelli et al., 1988; Blitz and Regehr, 2005).

From the standpoint of signal processing, the push-pull structure we have found allows for interaction, or extrapolation, between the On and Off channels, which acts to increase the dynamic range of the circuit (Barlow, 1981; Pouille et al., 2009). Moreover, even as the larger pull blurs the original image, it also changes the amplitude of the derivative of perceived brightness with respect to space, or acutance. This operation is equivalent to LCE by morphological filters in digital photography and related forms of signal processing (Supplementary Figure 6). Note that an LCE filter simply amplifies high-frequency components. Thus, by increasing acutance it is possible to sharpen an image without changing its actual resolution. Taken together, our results suggest that push-pull inhibition at the RF center can remove redundancy from the stimulus while increasing the salience of informative features.

Consequences for subsequent visual cortical processing

The transformation of the retinal image by the thalamic relay might affect the emergence of cortical orientation selectivity. As a result of the interpolation of the retinal output, the overlap between the active On- and Off-center relay cells in the LGN array (Supplementary Figure 8A) overlying the contour of a visual object is increased (Supplementary Figure 8B), particularly at high stimulus contrasts. In the absence of pull this would result in a larger overlap between the On and Off subregions of target simple cells and, hence, broader orientation tuning in cortical layer 4. In the presence of pull, however, the slope of the depolarization profile of the populations of active On- and Off-center cells is increased and the overlap around the edge largely reduced (Supplementary Figure 8C).

Conclusion

Decreasing the number of visual detectors from the level of the photoreceptors to the X-RGCs mosaics has the disadvantage of limiting visual resolution, but has the advantage of reducing the amount of cable needed to transmit information downstream. The structure of the retinothalamic circuit we described represents an efficient solution to the problem of maximizing spatial sampling of visual images at low metabolic cost. Our work also shows how the structure of local circuits in the LGN can improve visual performance, at least in part, with a strategy routinely used in manmade image processing devices.

Similar mechanisms might operate in other retinothalamic circuits, the thalamocortical stage and beyond. For example, retinal Y cells compose only 5-10% of the entire ganglion cell population (Illing and Wässle, 1981; Stein et al., 1996), yet these cells contact many more relay cells than their X-type counterparts in the LGN (Sur and Sherman, 1982; Yeh et al., 2009). Therefore, the functional principles we have described here might also aid stimulus detection in the highly divergent Y pathway. Our results are also relevant for primate V1, since the thalamorecipient layer, 4cβ, is dominated by cells with center-surround RFs that largely outnumber their thalamic afferents (Chow et al. 1950). Thus, the same strategy we describe could mediate linearization of afferent inputs, hyperacuity (Barlow, 1981) and even boundary completion of real and illusory contours (Gegenfurtner et al., 1997) in primates and humans.

EXPERIMENTAL PROCEDURES

Physiological preparation and RF mapping

Recordings from retina and LGN were performed in anesthetized cats. The surgery, anesthesia, visual stimulation, intracellular recordings and histological processing were as described (Martinez et al., 2005; Wang et al., 2011); and see Supplementary Methods. Extracellular recordings from RGCs were obtained by inserting a matrix of 7 electrodes in the optic chiasm. All procedures were in accordance with the guidelines of the US National Institutes of Health, the European Commission and the Institutional Animal Care and Use Committees of the University of Southern California and the Instituto de Neurociencias de Alicante.

Statistical wiring model of the early visual pathway

The model was based on previous experimental and theoretical work (Wässle et al., 1981a,b; Eglen et al., 2005; Ringach, 2007). Our retinal and thalamic mosaics each simulate a square patch of tissue of size 3.5 mm². To avoid boundary effects, only those relay cells and interneurons that were separated from the edges of the mosaic by at least 467.5 and 280.5 μm, respectively, were considered for further analysis.

The model retina

The first layer of the model simulated two independent mosaics representing the centers of the On and Off X-RGCs at an eccentricity of 7°. We chose this value because the spatial statistics of retinal arrays are best understood in paracentral retina (Wässle et al., 1981a; Stein et al., 1996). To construct the retinal mosaics we used two different approaches. First, a pairwise interaction point process (PIPP) model previously described by Eglen et al. (2005) and adopted by Ringach (2007). Second, a model based on two independent (noisy) hexagonal lattices as proposed by Ringach (2004). The implementation of the model retina and how the resulting retinal mosaics match the spatial statistics obtained from the anatomical work of Wässle et al., (1981a) and Stein et al., (1996) are described in detail in the Supplementary Methods. Our results did not depend on the method used; for simplicity, only those obtained with the PIPP model are illustrated in the Figures.

Arrangement of the LGN layer

Relay cells were randomly distributed with the sole restriction that two cells cannot occupy the same location in the mosaic. The polarity (On or Off) of each relay cell was inherited from its nearest neighbor in the antecedent RGC mosaic, following a minimum wiring paradigm (Ramon y Cajal, 1995; Chklovskii et al., 2002). RGCs, on the other hand, outnumber thalamic interneurons by at least a factor of two (Madarász et al., 1978; Stone and Campion, 1978; LeVay and Ferster, 1979). Like relay cells, interneurons were randomly positioned in the thalamic mosaic but with a more stringent neighborhood condition that imposed a minimum distance of 100 μm between interneurons of the same polarity, to achieve the uniform distribution that has been reported experimentally (Fitzpatrick et al., 1984). To comply with our minimum wiring paradigm, their polarity was determined as the opposite of that of their nearest relay cell.

Retinothalamic connectivity

Each relay cell in the thalamus was first connected to its nearest neighbor in the retinal mosaic, i.e. the one from which it inherited its polarity. We then modeled the probability that the thalamic cell, re-centered in retinal coordinates at the position of its first retinal input (x), was connected to another RGC centered at y as a Gaussian function of the x-y distance. The synaptic strength of the connections was also assumed to be a Gaussian function of the distance between the receptive-field centers. The function for both connection probability and strength was:

$$\mathrm{Pr}=\min \left\{q\cdot \exp \left(-\frac{{\Vert x-y\Vert }^2}{2^{\ast }{{\sigma }_{ret}}^2}\right),1\right\}$$

where σ_ret is the mean nearest neighbor distance within a cell class and it was chosen to describe the spatial spread, in visual space, of the ganglion cells axons in the thalamic mosaic. q is the free parameter that allowed our values of retinogeniculate convergence to change (independently onto relay cells and interneurons) in order to search for the circuit design that best explained the experimental data.

To simulate the connections from the inhibitory neurons to the excitatory cells in the thalamus we first computed the interneuron's RF as indicated in the next paragraph. We then assumed that the probability of connection between a geniculate interneuron with a RF centered at × with a geniculate relay cell centered at y was also given by a Gaussian function of the x-y distance

$$\mathrm{Pr}=\min \left\{q\cdot \exp \left(-\frac{{\Vert x-y\Vert }^2}{2^{\ast }{{\sigma }_{\mathrm{int}}}^2}\right),1\right\}$$

but in this case σ_int is the radius of the interneuron RF in order to simulate the spatial spread, in visual space, of the inhibitory neurons axons in the thalamic mosaic. q is, again, the only free parameter that allowed our values of LGN interneuron to relay cell convergence to change when searching for the circuit design that best explained the experimental results.

Thus, our model is consistent with a general Hebbian framework for circuit development in that the probability of finding a connection between two neurons in the network is a function of the distance between their receptive-field centers.

Model retinal and thalamic RFs

RGCs’ RFs were modeled as two-dimensional (elliptical) Gaussian functions with average σ = 90.7 μm, for a final RF radius of 210.4 μm (or 1.06° of visual angle). RF radius thus matched that obtained from RGCs recorded at an average eccentricity of 7° using our sparse-noise protocol (Supplementary Figure 2). To account for the anisotropies in RF spatial structure imposed by the profile of the RGC's dendritic trees, the shape of the RF was based on the neuron's Dirichlet Domain (Wässle et al., 1981b). The RFs of thalamic interneurons and the excitatory component of relay cells’ RFs were constructed by linearly combining all their pooled retinal inputs, weighted with the same Gaussian function we used to calculate connection probability

$$\mathrm{RF}=\sum _{i\in N}\mathrm{Pr}\cdot R{F}_i$$

where N is the group of the pooled retinal inputs, RF_i is the RF of the neuron i and Pr is the probability of connection between the target cell and neuron i.

The inhibitory component of each relay cell's RF was constructed by pooling input from all presynaptic interneurons. The contribution of each presynaptic receptive field was determined by the strength of the synaptic connection. Finally, the synaptic efficacy of each connection in the model was calculated by taking its strength and dividing by the sum of all the synaptic weights to the thalamic neuron.

To compare their area, radius, distance, overlap and size indexes with those of our experimental data, computational thalamic subfields were also cut at 5% of their peaks.

Optimization of the retinogeniculate model

To make a quantitative comparison with the empirical data, we first calculated the distributions of 4 RF properties in both the model and the experiments: push radius, pull radius, overlap index and size index. These 4 measures were selected because they are sufficient to describe the spatial layout of synaptic inputs at the center of thalamic receptive-fields.

The raw distributions were smoothed using a Laplacian function to prevent the distributions from having zeros.

$$distrSmoothed=\frac{distr+0.01}{length\left(distr\right)+length\left(binning\right)}$$

The range and the binning of the experimental and model distributions were fixed for each of the 4 parameters as follows: we calculated the maximum (M) and the minimum (m) of all configurations of the model and binned the segment [m M] in 10% increments. Similar results were obtained for other bin sizes (20% and 30%).

We then assessed how well the model fitted the experimental data using the Kullback-Leibler Distance (KLd):

$$D_{KL}(P\Vert Q)=-\sum _{x}p\left(x\right)\cdot \log q\left(x\right)+\sum _{x}p\left(x\right)\cdot \log p\left(x\right)$$

where P and Q are the experimental and theoretical distributions, respectively.

In order to correct for a possible undersampling bias, we also calculated the KLd between the model distribution and 1000 samples extracted from it (reference KLd). Then we evaluated how good the fit was using the corrected KLd (cKLd), which we obtained as follows:

$$cKLd=\frac{KLd-mKLd}{stdKLd}$$

Where mKLd is the mean KLd between the 1000 samples and the model distribution and stdKLd is its standard deviation.

We considered a total of 9092 different retinothalamic circuits, all preserving the same number of retinal and thalamic neurons, and with convergence values for retino-relay cell, retino-interneuron and interneuron-relay cell projections ranging from 1.3-9.5, 1.1-9.3 and 1.2-11, respectively. After computing the cKLd for all 9092 different circuit designs, we selected the 20 circuit configurations that rendered the lowest cKLd for the 4 RF properties. Then, to identify the best result from the entire set of possible circuits, we measured the KLd between the distributions of convergence values predicted by the 20 configurations with the lowest cKld, and those obtained from the entire sample of 9092 different circuit designs. Finally, we calculated the probability of obtaining similar average convergence values by simply extracting random series of 20 different configurations from the entire set of 9092 circuits. The results we obtained for retino-relay cell, retino-interneuron and interneuron-relay cell projections were highly significant (p=0.001 for the three convergence distributions; N=1000). Similar results were obtained when considered the best 10 and even 30 results.

Diversity index (D.I.)

We compared how the RFs of relay cells that share their first retinal input change as retinogeniculate convergence is increased using a novel diversity index (D.I.).

$$D.I.=1-\left(\frac{2•NEI}{NI\_C1+NI\_C2}\right)$$

Where NEI is the number of equal retinal inputs received by cells C1 and C2, and NI_C1 and NI_C2 are the number of total retinal inputs received by cells C1 and C2 respectively. RF diversity (D.I.) is set to zero when LGN cells (C1, C2) receive input from just one retinal afferent.

Spatial decoding capability

We analyze the retinothalamic circuit using Bayesian decoding of the position of a localized visual stimulus, inspired by Ruderman and Bialek, 1992. In short, we assume the response of each neuron follows a Gaussian distribution centered on a point of the space:

$$y_i=f_i\left(x\right)+\eta$$

where × is a small localized point stimulus, with η ∈ N(0,σ)being sensor noise and $f_i\left(x\right)=\max \cdot e^{\frac{-{(x-x_i)}^2}{2\cdot {\sigma }^2}}$ the ideal response of the i-th neuron. To fit the experimental data σ was set to 50 micrometers and connection strength (max) was, in a first step, equal to connection probability. After all connections were established, their strengths were normalized so that each LGN neuron received the same input strength regardless of the individual numbers of retinal afferents. We also assume that the sensor noise is additive and independent in each channel. Given a response pattern y, Bayesian decoding determines the estimate of the stimulus × by maximizing the posterior distribution:

$$\widehat{x}=\underset{x}{\max }\{\log \left(p(x\mid y)\right\}$$

With Gaussian sensor noise, the conditional probability of a neural response is:

$$p(y_i\mid x)\propto e^{\frac{-{(y_i-f_i\left(x\right))}^2}{2\cdot {\sigma }^2}}$$

Since the responses of individual neurons are conditionally independent we have:

$$p(y\mid x)=\prod p(y_i\mid x)$$

By virtue of Bayes theorem, we can now write the maximization of the posterior probability as:

$$\underset{x}{\max }\{\log (p(y\mid x)\cdot p\left(x\right)∕p\left(y\right)\}$$

Note, p(y) acts only as a normalization constant as it is independent on the stimulus. Thus, the previous equation simplifies to:

$$\underset{x}{\max }\{\log (p(y\mid x)\cdot p\left(x\right)\}$$

Which is equal to:

$$\underset{x}{\max }\{-\frac{1}{2\cdot {\sigma }^2}\sum _i{(y_i-f_i\left(x\right))}^2+\log \left(p\left(x\right)\right)\}$$

If we finally assume a uniform or flat prior distribution (i.e., make no prior assumptions about the location of the stimulus), the estimated location of the stimulus is given by:

$$\underset{x}{\max }\{-\sum _i{(y_i-f_i\left(x\right))}^2\}$$

To compute the decoding error (Figure 6B) we calculate the mean and the variance of the difference between the estimated and actual location.

Thalamic population response

We first calculated the activity of the thalamic neurons as:

$$A-\sum _{VF}B•R{F}_e-\sum _{VF}{B}_N•R{F}_i$$

Where RF_e and RF_i are the excitatory and the inhibitory centers of the thalamic RFs, respectively; B is the stimulus, which represents a vertical luminance border from 0 to 255; and B_N is its negative.

Individual values of RF activation were summed along the vertical dimension of the mosaic to obtain the relative population response curves shown in Figure 7 and Supplementary Figure 10. The magnitude of the luminance step (Figure 7C and Supplementary Figure 10B,C) was changed to study variations of the population response at different stimulus contrast.