Abstract
Comparing rates of growth, or rates of change, across covariate-defined subgroups is a primary objective for many longitudinal studies. In the special case of a linear trend over time, the interaction between a covariate and time will characterize differences in longitudinal rates of change. However, in the presence of a non-linear longitudinal trajectory, the standard mean regression approach does not permit parsimonious description or inference regarding differences in rates of change. Therefore, we propose regression methodology for longitudinal data that allows a direct, structured comparison of rates across subgroups even in the presence of a non-linear trend over time. Our basic longitudinal rate regression method assumes a proportional difference across covariate groups in the rate of change across time, but this assumption can be relaxed. Rates are compared relative to a generally specified time trend for which we discuss both parametric and non-parametric estimating approaches. We develop mixed model longitudinal methodology that explicitly characterizes subject-to-subject variation in rates, as well as a marginal estimating equation-based method. In addition, we detail a score test to detect violations of the proportionality assumption, and we allow time-varying rate effects as a natural generalization. Simulation results demonstrate potential gains in power for the longitudinal rate regression model relative to a linear mixed effects model in the presence of a non-linear trend in time. We apply our method to a study of growth among infants born to HIV infected mothers, and conclude with a discussion of possible extensions for our methods.
Keywords: longitudinal data, non-linear trajectory, rate of change
1. Introduction
With repeated measures data obtained in a longitudinal study the comparison of the response profiles over time for different groups of subjects is frequently a primary objective. In particular, longitudinal designs allow the direct linking of changes in exposure, such as medical treatments or environmental factors, and the corresponding changes in health indicators, such as measures of disease progression, symptom burden, or disease-specific functional status. Powerful regression approaches have been developed [1, 2] that directly allow inference regarding the mean outcome, and by incorporating time as a key covariate, these longitudinal models also permit inference regarding rates of change. However, the standard regression approach directly focuses on the mean response through the inclusion of mean level differences associated with each covariate. By allowing inclusion of time as a covariate, these regression models can then indirectly permit structuring of the differences in the rate of change over time by considering appropriate interaction terms in the mean model. The primary focus of this paper is to directly specify a regression relationship linking the longitudinal rate of change with covariates. We shift the applied focus from an emphasis on the mean response to a direct focus on the rate of change, and on how rates may differ across covariate-defined groups. We then indirectly obtain an induced mean model that characterizes mean profiles, but for our regression formulation the comparison of the rate of change across subgroups remains the goal of statistical modeling. The primary advantage of our approach is the ability to allow a general time structure, and in a parsimonious regression fashion, we can directly and simply structure comparisons in the rate of longitudinal change.
Standard approaches to estimating models for longitudinal data include the linear mixed effect (LME) model [1], that incorporates random effects to account for correlation among repeated measures, and the generalized estimating equation (GEE) approach [2], where correlation is directly modeled and semi-parametric estimation is adopted. When the time trend in the mean is assumed to be linear, both LME and GEE approaches can characterize differences in rates of change through the inclusion of a group-by-time interaction. The coefficient for the interaction term provides a direct, and simple way to compare rates across key subgroups. Typically, when a non-linear time trend is necessary, the outcome will be regressed on multiple functions of time such as with inclusion of polynomial terms or a more general parametric spline basis. In the non-linear situation, the comparison of longitudinal rates of change across subgroups requires the inclusion of multiple interactions between covariates and each function of time. In actuality, each additional interaction term models mean differences in the outcome relative to changes in the corresponding function of time, but collectively, the coefficients for the interaction terms can be considered for their impact on the rate of change. In addition, comparison of rates of change is determined by the derivative of the multiple functions of time and no longer directly characterized by key parameters such as the interaction term when time is modeled linearly. Therefore, inference and interpretation for the comparison of rates of change using linear models in a non-linear setting becomes more complex and power is reduced for the multiple degree of freedom test.
A general non-linear model framework [3] can be used for comparing rates across covariate-defined groups. Applications of non-linear longitudinal models have typically been focused in biologically motivated settings includingpharmacokinetic models, or other dynamic compartment models. For example, Wu, Ding, and De Gruttola [4] used hierarchical non-linear methods to characterize disease process dynamics based on longitudinal measures of HIV viral loads. In the model suggested by Wu et. al. [4], change in infectious T-cells over time for patients on HIV treatment is expressed in terms of the current number of infectious T-cells, and similarly for infectious and non-infectious virions. Note that, in this approach, the rate at time t is linked directly to the magnitude of the state (outcome) at time t. Non-linear models are also used for estimation of mechanistic growth models [5, 6] where the rate of change is again expressed in terms of the current state. Huang [5] discuss mechanistic growth models for characterizing growth of bacteria in relation to temperature. Infant growth curves have been modeled based on mechanistic exponential growth models such as those illustrated by Berkey [6]. Pharmacokinetics (PK) is another important area of application for non-linear models where the primary focus is on the estimation of absorption and elimination rates in early clinical testing. For example, one simple approach for estimating PK parameters is through a one-compartment non-linear model as discussed by Lindsey et. al. [7]. A relatively new research area of interest is the use of empirical dynamic methods for modeling longitudinal trends based on a differential equations model which has primarily been used for application in internet auction data [8, 9]. Also, Zhu, Taylor, and Song [10] used empirical dynamic methods to model rates of change for prostate specific antigen profiles for prostate cancer patients based on a Ornstein-Uhlenbeck process. Thus, the majority of existing non-linear methods have relied on a specific structure that is heavily motivated by the application area. In addition, these methods have not directly addressed comparing the rate structure across covariate-defined subgroups.
One approach that provides a more general comparison of longitudinal rates of change is an accelerated time (AT) model where covariates are assumed to impact the time scale and either accelerate or decelerate longitudinal progression [11–15]. Shape invariant models (SIM) are an example of AT methods and have been applied to a variety of areas [11, 12, 15]. For example, the effect of the hormone cortisol on the rate of change of circadian rhythms was estimated using SIMs by Wang, Ke, and Brown [15], and their analysis included adjustment for within individual correlation through inclusion of random effects. Brumback and Lindstrom [12] discuss an application where the position history of the tongue is recorded for participants repeatedly uttering a phrase. Brumback and Lindstrom [12] allow a general monotonic transformation of the time scale. Shape invariant models were applied to infant growth by Beath [11] for studying the effect of breastfeeding on growth among infants with asthma. Beath [11] included a scaling parameter in the model that allowed for differing magnitude of growth for the infants. In addition, Gray and Brookmeyer [13, 14] used AT models as a means to link multivariate longitudinal outcomes in treatment trials for Alzheimer’s Disease (AD). Linking multivariate outcomes for this model allows evaluation of whether a treatment accelerates or decelerates deterioration associated with underlying disease progression. An accelerated time structure is particularly useful when the ultimate magnitude of progression for an outcome is considered to be fixed, perhaps by floor or ceiling effects, and covariates are expected to potentially affect the speed at which progression occurs. Scaling terms such as those suggested by Beath [11] can be used to allow differing magnitudes, but the estimated effect of a covariate on the rate of change is still interpreted as a transformation of the time scale. In many other applications a common magnitude of ultimate disease progression is not anticipated and research generally focuses on differences in the absolute rate of change across subgroups.
In the following section, we propose a methodology for directly comparing covariate-defined subgroups in terms of the rate of change for a longitudinal outcome. We permit inference regarding rates of change while adopting a flexible specification for the reference rate as a function over time. The proposed methodology is strongly related to functional mixed effects models discussed by Guo [16]. However, the additional structure proposed by our model has the important benefit of directly making inference regarding comparisons in longitudinal rates of change. In Section 2, we outline the basic modeling framework and the induced mean structure for our longitudinal rate regression (LRR) model. Both parametric and semi-parametric modeling approaches are discussed. We detail methods for estimation using either likelihood-based or estimating equation-based approaches. Section 3 presents simulation results comparing the proposed method to a standard linear mixed model approach. Our method is illustrated in Section 4 using data on growth among infants exposed perinatally to HIV. Finally, in Section 5, discussion of potential extensions to the LRR method are considered.
2. Methods
We use Y, t, and X generically to respectively denote a longitudinal outcome, time, and a covariate defining groups of interest. We use subscripts i to specify an independent observation for i = 1, …, N and j to denote the time point of an observation with j = 1, …, ni. For convenience of notation, we assume that Y is continuous and that modeling of the expected value of the untransformed outcome is of primary interest. Specifically, we are interested in differences in the rate of change of the expected value of Y across groups defined by X. Initially, we assume that the covariate X is not time varying. We first express the expected value of Y given X and t as follows
where g(·) is a function dependent only on X and μx(·) denotes some function of t for a given value of X with the constraint that μx(0) = 0 for all values of X. In this framework, we refer to g(·) as the baseline function which defines the mean of Y at a time origin, or time zero, for a given value of X. The function μx(·) describes the change in the expected value of Y from this baseline value for each value of X. In defining the expected value of Y in this way, the rate of change of the expected value of Y is equivalent to the rate of change of μx(t).
Using the above notation, the specific aim of interest can be restated as a focus on describing the difference between and across time for all potential values of x1 and x2. In order to structure the difference in rates, we first consider a common relationship across time that assumes rates are proportional. We will also introduce proportional rate testing methods and non-proportional models that include covariate-by-time interactions, but first we assume that for any X = x there exists a parameter θ such that
| (1) |
for all values of x (and t) where μ0(t) is the time function for a preselected reference group, defined by X = 0. In this model, the rate of change in the expected value of Y for a group defined by X, relative to the rate of change in the reference group (X = 0), is given by (1 + θX) for any time t. By invoking this assumption, a regression framework can be introduced directly at the rate level through inclusion of the term θx. We will refer to this simple regression assumption as the Proportional Rate (PR) assumption. The parameter θ can be interpreted as a percent increase (decrease) in the rate of change of the mean when X = (x + 1) relative to when X = x. For example, if the value of θ is 0.1, then the group defined by X = 1 is associated with a 10% increase in the rate of change of E[Y | X] compared to the rate of change in the group defined by X = 0. Note that the reference group is used to anchor the mean (and rate of change) over time, and we refer to μ0(t) as the reference time function.
Under the PR assumption, a full specification for the mean structure of Y given X and t can be induced by integrating the rate model over the interval [0, t]. That is,
By generating a mean structure using the PR assumption, we are assuming that time periods of faster (or slower) change for an outcome occur at the same time across groups, but that groups may differ in their relative degree of change within any specific time period.
More generally, we can consider an outcome Y measured at time t, and a vector of covariates X = (X1, · · ·, Xp) where each covariate impacts the rate of change in the expected value of Y. We similarly define the conditional expected value of Y as E[Yij | Xi = x, tij = t] = g(x) + μx(t) for functions g(·) and μx(·), where μx(0) = 0 for all values of x. The extended PR assumption based on the vector of parameters θ and the resulting mean structure becomes
| (2) |
| (3) |
Various approaches can be considered for modeling the reference time function. In this paper, we outline and compare two approaches. The first approach is to specify the reference function parametrically as a linear combination of a parametric basis such as a simple polynomial basis or a regression spline basis with a small number of knots: μ0(tij) = βTTij where Tij is a vector of functions evaluated at tij. The parametric approach is simple to implement and may be beneficial for applications where the time trend is expected to be adequately expressed using a simple basis. For applications where the behavior of an outcome over time is not well understood or complex, the parametric approach may suffer from model misspecification. Therefore, we also consider a non-parametric structure for the reference time trend where the function is estimated using penalized splines. The implementation of this non-parametric approach is more complicated than the parametric approach and is discussed in the next subsection. However, the non-parametric specification offers protection against model misspecification and reduces burden for the user by requiring less a priori model specification. For all model approaches presented in this paper, we will express the baseline function as a linear combination of covariates i.e. g(Xi) = αTXi, although more general regression structures are possible.
We consider methods for estimation of the model where all mean parameters are estimated jointly. In some settings, joint estimation of the mean parameters may not be optimal for inference on the rate of change such as when longitudinal data is too sparse to estimate an accurate underlying time trend [17]. To aid in accurate estimation of a reference time function, the time trend coefficients are estimated using all the data. Therefore, the estimated reference time function for a model actually represents the time trend for the reference group based on an averaged time trend across all groups. An averaged reference trend approach is a common technique in regression models, most notably in Cox Proportional Hazards regression [18]. Estimation based solely on the reference group may also be considered particularly when strong a priori knowledge exists about the time trend among the reference group.
2.1. Penalized Spline Reference Function
Penalized splines provide a framework that can be used to estimate a smooth, non-parametric function. The method can be considered as a variant of smoothing splines [19] where a saturated parametric basis is used for function representation but the basis coefficients are subject to a penalty for estimation. The magnitude of penalization essentially controls the overall degree of freedom or flexibility in the resulting function estimator [19]. We incorporate penalized splines in order to estimate a general smooth reference time trend function, μ0(t), coupled with a parametric longitudinal rate regression structure that characterizes differences in the rate of change. The resulting semi-parametric longitudinal model is a generalization of previous methods that have demonstrated the utility of adopting penalized splines for estimation with longitudinal models [20, 21].
Given longitudinal data observed over a time interval [a, b], we estimate a reference time function for the LRR model using a penalized spline approach that requires specification of a basis structure and penalty function. First, we select knots ν1, · · ·, νq such that a < ν1 < · · · < νq < b. Typically, we specify knots at all uniquely observed time points in the data provided this is computationally feasible. Using specified knots, we construct a spline basis which we denote B1(t), · · ·, Bp(t) where p depends on q and the type of spline basis chosen e.g. a cubic B-spline basis. Then, we can express the reference time function as a linear combination of this spline basis:
| (4) |
When the number of spline functions, Bk(t) and consequently the number of coefficients, βk, is large relative to the size of the data, we introduce a penalty function, P(·), and penalty parameter, λ, into the estimation procedure to restrict and stabilize the estimation of these parameters. The penalty function and parameter are incorporated into the estimation by maximizing a penalized likelihood equation, lP (·) that is equal to the standard likelihood equation l(·) plus the penalty term. That is,
| (5) |
The penalized estimation process limits the effective degrees of freedom [22] spent on estimating these parameters. The manner by which estimation of the coefficients for μ0(t) is restricted depends on the penalty function selected. The penalty parameter controls the degree to which the estimation is restricted.
In this paper, we adopt a cubic smoothing spline penalty function for estimation of the LRR model with a non-parametric time function. The cubic smoothing spline penalty was selected since it is commonly used in practice due to the property that a cubic spline has a continuous second derivative. Modifying the estimation procedure for other penalty functions is straightforward. The cubic smoothing spline penalty is defined by the expression
where denotes the second derivative of the kth B-spline function evaluated at time t [19]. In other words, the cubic smoothing spline penalty penalizes the second derivative or the curvature of the spline function. Therefore, the degree of curvature estimated for the reference time function will vary relative to the penalty parameter, λ. When λ = 0, the curvature of the reference time function is unconstrained. As λ → ∞, curvature is reduced, and the estimated reference time function becomes more linear.
An appealing feature of the cubic smoothing spline penalty function is that it may be re-expressed into a quadratic form that is convenient for incorporating the penalty term into score and hessian equations used for estimation. The equivalent quadratic form is written as
where D is a matrix with (k, l)th entry
The entries of D can be calculated by hand or through the use of established software such as the getbasispenalty function in the fda package in R. For a given value of λ, the penalty matrix can be incorporated into the penalized likelihood, and parameter estimates can be obtained by maximizing the penalized likelihood using standard maximization procedures.
2.2. Selecting the Penalty Parameter
When using penalized splines to model an underlying time trend for the LRR model an appropriate value for the penalty parameter, λ, must be selected. Often, knowing a priori how smooth an estimated function should be and what corresponding value of λ should be chosen will be difficult. Thus, it is common to use data-driven methods to select an appropriate value for the penalty parameter. For the LRR model, we propose a penalty parameter selection procedure that is adapted from an approach for smooth curves for longitudinal data suggested by Jacqmin-Gadda et al. [23]. The procedure uses cross-validation to estimate the predicted mean squared error for a sequence of models with varying values of λ.
Let η denote the vector of parameters in the mean function of the LRR model. We use η̂−i(λ) and V̂−i(λ) to respectively denote the penalized maximum likelihood estimates (PMLEs) for the mean parameters and covariance matrix obtained from the sample with subject i omitted and with a fixed penalty, λ. Define the function fi(·) as the fitted mean vector for Yi given parameter values η. For a given value of λ, calculate the approximate cross-validation (aCV) criterion that is expressed as
| (6) |
For many applications precise estimation of the PMLEs for the mean and variance parameters for each subsample and each value of λ will be computationally intensive. Thus, Jacqmin-Gadda et al. [23] offer two suggestions for reducing computational burden. The first simplification is to assume that the variance is constant across all subsamples and values of λ. Second, Jacqmin-Gadda et al. [23] propose a one-step estimation procedure to obtain approximate PMLEs for the mean parameters. For the proposed approximation procedure, a fixed penalty parameter value, λ0, is selected and the corresponding PMLEs, η̂(λ0) = η̂0 and V̂(λ0) = V̂0, are calculated based on the full sample. Jacqmin-Gadda et al. [23] recommend selecting a value between 0 and 100 for λ0 in the approximation procedure. Then, when evaluating the predictive performance using a general penalty parameter value, λ, the cross-validation subsample that removes individual i uses V̂−i(λ) = V̂0 and η̂−i(λ) = h(η̂0) for a one-step calculation defined by the function h(·). We extend the linear model one-step estimator presented by Jacqmin-Gadda et al. [23] for our non-linear model (see Appendix A for derivation details). For our one-step estimator, the PMLEs for the mean parameters based on a sample that omits individual i can be calculated using the formula:
| (7) |
where denotes the vector of first derivatives of the mean structure with respect to the mean parameters for individual j, and Ω is a matrix with entries corresponding to the values of the penalty matrix D, described previously, for the coefficients of the reference time function and zeros everywhere else. The resulting PMLEs can be used in Equation (6) to approximate the aCV criterion for each value of lambda. By searching for a value of λ that minimizes the approximate aCV criterion, a suitable value for the penalty parameter can be selected.
The primary advantage of the approach described by Jacqmin-Gadda et al. [23] is computational simplicity since the longitudinal model only needs to be maximized once for a single initial value of λ = λ0. The reduced computational burden is achieved by two simplifications: use of a constant covariance matrix across jackknife subsamples and across values of λ; and use of a one-step estimator to approximate the PMLEs for the mean parameters. Given that the aCV criterion is essentially a Mahalanobis distance between outcome vectors Yi and fitted means, the use of a common covariance based on an intial λ* facilitates the comparison of performance of the estimated mean model when using different values of λ to contrain μ0(t). The impact of using a one-step updating relative to a fully iterated updating warrants investigation. Finally, although we describe a leave-one-out calculation, it is valid and computationally less expensive to adopt a leave-K-out procedure in order to select a penalty parameter. In the motivating example presented below we compare results using this alternative CV strategy.
2.3. Mixed Effects Model
We detail estimation for the LRR model using a natural mixed effects approach that characterizes individual variation in both the level at baseline and in the rate of change. The model is specified as follows:
| (8) |
where , Corr(b0i, b1i) = ρ, and εij ~ N (0, σ2). Thus, the mixed model specification allows for individual random intercepts and individual variation in rates of change since, for subject i,
The LRR mixed effects model naturally characterizes individual variation in longitudinal trajectories through inclusion of subject-specific (random) intercepts and rates of change. However, the inclusion of the random effect for the rate of change creates score equations for the mean parameters and variance components that are not orthogonal as in the standard linear mixed model. Details regarding calculation of the score equations and the hessian matrix for this likelihood function are provided in Appendix B. The non-orthogonality is a result of the induced interaction between the random slope and the reference time function. Due to the induced dependency, maximizing the LRR model likelihood requires special programming and has been implemented using an MLE algorithm based on Newton-Raphson methods and an LDL Cholesky Decomposition [24, 25].
2.4. Estimating Equations Approach
Alternatively, the LRR model can be estimated using semi-parametric methods. First, since the natural mixed model specification includes random effects on the linear scale, an induced marginal mean retains the same parametric form as the mean structure conditional on the random effects. Taking expectations of the outcome vector, Yi = (Yi1, · · ·, Yini), over bi and εij for the conditional mean given in Equation (8) yields a marginal mean that is expressed in vector format as
where μ0(ti) is a vector of linear combinations of a parametric basis or a penalized spline bases for the time vector ti = (ti1, …, tini) and g(Xi) = αTXi. Second, adopting a working correlation or covariance model, the solutions to the following estimating equations can be used to estimate all mean parameters
| (9) |
where Di is the vector of derivatives for the mean structure for parameters θ, β, and α; and Wi = Wi(θ, β, α, γ) is the working covariance model that is possibly dependent on some additional parameters γ. Finally, provided a consistent estimate, γ̂, for the working covariance parameters is used, then results from Liang and Zeger [2] show that solutions for θ, β, and α to the estimating equation given in Equation (9) converge in distribution to a normal distribution under mild regularity conditions (such as growth of information). The asymptotic variance is given by the standard sandwich formula:
| (10) |
The necessary regularity conditions are outlined by Liang and Zeger [2] and are explored in greater detail by Crowder [26]. The variance given by Equation (10) is typically estimated by substituting the empirical estimate of cov(Yi) into the equation.
The estimating equations approach is often attractive when the primary scientific focus is on the regression parameters since robustness to variance model and/or distributional assumptions is provided. In contrast, consistency of both point and variance estimates cannot be guaranteed in the LRR mixed effects modeling framework unless the model is correctly specified. Note that efficiency of estimation under the estimating equations approach will depend on appropriate selection of a working covariance structure. Since a mean-variance relationship can commonly occur when the primary difference in an outcome is on the rate scale, careful consideration should be given to the working covariance structure when applying this approach to the LRR model [27].
2.5. Monotonicity Constraints
In certain applications we may expect strictly non-negative (or non-positive) rates of change leading to a monotone mean function. Monotonicity is particularly common in studies of infant and adolescent growth. Thus, we consider the implications of incorporating monotone regression methods into the LRR model and discuss existing methods that can be adapted to constraint estimation for this purpose.
In the LRR model, the longitudinal behavior of an outcome is characterized by two interacting components. The reference time structure, μ0(t), describes the general trajectory of the outcome across time, and the rate structure, (1 + θTX), distinguishes the magnitude of differences across covariate-defined subgroups. In order to impose monotonicity on the model, both portions would need to be constrained but in different ways in order to maintain their functional purpose. First, to constrain μ0(t), model specification and estimation would need to ensure the reference function is monotone i.e. (or if decreasing). The problem of placing monotone constraints on an estimated, smooth function has been well studied [28–30]. A suitable approach for the LRR model is to use penalized splines with monotone constraints as discussed by Ramsay [30] and He and Shi [29] among others. Turlach [31] developed an algorithm for estimating a function with monotone constraints which is useful for a generally specified spline function. Penalized spline approaches are advantageous since they can easily be incorporated to allow a semi-parametric model.
Secondly, in order to ensure monotonicity the rate regression structure, (1 + θTX), must be constrained such that the rate for each covariate group remains positive. A simple way to enforce positive rate estimates is to modify the rate structure to characterize rate ratios rather than rate differences. To estimate rate ratios, the linear combination of rate covariates in the proportional rate assumption can be replaced by an exponentiated linear combination as follows:
| (11) |
The modified rate structure changes the interpretation of the rate parameter, θ, to represent the log rate ratio comparing two groups defined by the covariate values X = x + 1 and X = x. The exponentiated coefficient can then be interpreted as a precentage fold-change in the rate, in contrast to the percentage difference interpretation for the linear rate structure.
Imposing both monotonicity for the time structure and non-negative constraints for the rate structure, ensures the monotonicity of the overall mean structure. Such constraints will be useful for applications where monotonicity in the mean model is expected but artifacts exist in the measured data such as large imbalances in the times at which subjects are measured or large measurement error that might otherwise yield non-monotonic estimates. However, in many applications monotone solutions and estimates may result from unconstrained methods given the underlying structure of the data. In such situations it may be useful to evaluate the observed fit of the model in terms of estimated individual trajectories to verify that all (nearly all) subjects have monotone growth profiles. We illustrate such post-estimation evaluation in our analysis of the motivating example.
2.6. Diagnostics
When using the LRR model, it is appropriate to assess the adequacy of the proportional rate assumption. Standard graphical evaluation of residuals, and formal testing approaches to model checking are both feasible. First, the PR assumption can be evaluated graphically by generating standard residual plots against time for each covariate group defined by a rate covariate X. Any underlying trend in the residuals would provide evidence against the validity of the PR assumption. Graphic displays of residuals can be highly useful for providing visual validation for modeling assumptions. However, diagnostic residual plots are only subjectively interpreted. Therefore, formal tests that consider focused departures from the proportional rate assumption provide an objective model evaluation tool. Paralleling methods developed for the Cox model [32], we outline an approach for testing the adequacy of the PR assumption using a score test where the alternative is given by a linear change over time in the difference of rates of change across covariate groups. For this test, we specify an extension to the LRR method that includes a group-by-time interaction in the PR assumption:
| (12) |
In addition to detecting linear violations, the proposed structured alternative is suitable for detecting monotonic deviations from the PR assumption. Tests for more complex violations may require development of additional diagnostic tests.
If the standard PR assumption given by Equation (11) is correct, then the interaction parameter, ψ, given in Equation (12) would be zero. Thus, we test the hypothesis H0 : ψ= 0. The advantage of using a score test is that test statistic is calculated under the null permitting inference without the need for an extended (alternative model) fit. The score test only depends on the ability to compute the score equations and information for the null model. Below, we derive the needed analytic components by integrating the modified rate assumption to obtain the induced mean model. Use of integration by parts yields the following general mean structure:
where i.e. Aμ(t) is the area under our reference time function over the interval [0, t].
Here, we provide results necessary for calculating score equations for parameter ψ; all other score equations will be zero under the null hypothesis. Define
where di is a diagonal matrix whose diagonal entries are the time values associated with Yi, and μi and Aμi denote the vectors whose values are the functions μ0(t) and Aμ(t) respectively evaluated at each time value. The matrix Dψi here denotes the vector of derivatives of the mean function with respect to the parameter ψ evaluated at each time point for individual i. If θ̂, β̂, and α̂ denote the estimates from the standard rate regression model or the null model, then we express the score equation for the parameter ψ, denoted by Uψ(θ, β, α, ψ), evaluated under the null as
where D̂ψi, V̂i, and R̂i are the estimated derivative vector, variance matrix, and residual vector for Yi based on the estimates from the null model. The score test statistic can then be expressed as
where I22·1is the information for ψ under the null given by the formula based on the decomposition of the information matrix. The matrix I11 can be estimated by the hessian matrix from the null LRR model. Estimating the cross information between the score for ψ and the other mean parameters, given by I12, and the marginal information of the score for ψ, given by I22, requires taking the derivative of Uψ(θ, β, α, ψ) with respect to θ, β, α, and ψ.
For the single rate covariate test outlined above, the score statistic can be compared to a χ2 distribution with degree of freedom equal to the dimension of X. The test provides a means for testing the PR assumption based on a structured alternative. In this case, the alternative structure specifies linear changes in the rate of change due to group across times. Other structured alternatives could be considered.
2.7. Time Varying Covariates
For fixed covariates such as demographic characteristics or fixed treatment groups, the proposed LRR modeling framework can be useful for quantifying differences in rates of longitudinal change. However, there are many potential exposures of scientific interest that vary over time, and allowing incorporation of time-varying covariates into analysis is important. Although caution must be exercised with time-dependent covariate analysis (see Diggle et. al. [33], chapter 12 for overview), we outline methods for including time varying rate covariates in the LRR model. One important use of a time-dependent covariate is to allow a relaxation of the proportional rate assumption by including covariate-by-time interactions in the LRR model.
In order to characterize a LRR model with time-dependent covariates, we first consider a simple binary time varying covariate that represents an exogenous and discrete exposure that is delayed from baseline. An example exposure would be a treatment given in a controlled crossover trial. Let Xi(t) denote the covariate status for individual i who was exposed at specified time t1. That is,
Adopting the PR assumption of equation (11) with parameter θ, the induced mean structure can be obtained by dividing the integration of the time function over the key time periods associated with changes in exposure. For simplicity, we focus on the case of no baseline mean differences in the outcome across groups (i.e. g(x) = α0 for all values of x). Extension to the case of baseline differences is straightforward. The mean function at times prior to t1 will be identical to the reference mean structure up to a constant defined by the baseline function g(x). For the outcome of individual i observed at time tj ≥ t1, the expected value of Yij is calculated as
By induction, we can then extend the induced mean to the scenario involving a time varying covariate taking multiple values across multiple time points: t0 = 0, t1, · · ·, tp. For an outcome measurement time t contained in any time interval t ∈ (tk, tk+1), the mean becomes
| (13) |
The third and fourth term in equation (13) ensures that the mean function remains continuous at the time points where the covariate is changing. For covariates that only change at discrete time points, the LRR model can easily incorporate such variables into the rate model. However, if covariates are given by a continuous process then additional computational burden is required to numerically derive the induced mean function. The integration across time would need to be done with consideration of the continuous process for the time-varying covariate. Finally, for some covariates that are only measured at select times for which an underlying continuous process represents their true time-varying state, covariate values can be considered to be measured with error in between measurements using the values of the nearest measurement. Additional work is needed to incorporate the resulting covariate measurement error associated with incomplete measurement (see Carroll et. al. [34], chapter 11).
3. Simulation Studies
The LRR model using likelihood-based estimation was compared to a LME model approach in simulation studies. The LME model was chosen for comparison since it is commonly used, and can be adapted to compare rates of change by including appropriate covariate-by-time interactions. We focused evaluation on whether comparison of rates of change across groups using a direct and parsimonious LRR model provided more power than an LME approach which may require additional covariate-by-time interactions to characterize group differences. The two methods were compared where the reference trend over time was assumed to be a cubic polynomial function. A single, binary covariate was used for comparison of rates across group. The LRR and LME parameterizations can be expressed respectively as follows:
| (14) |
| (15) |
Note that the LME structure is more general in the sense that the three interaction terms allow the groups defined by X = 0 and X = 1 to differ in the outcome beyond proportional difference in the rate of change, but such differences are mean level differences that would not alter inference on the proportional difference in the rate of change relative to the given time structure. The goal of the simulation studies were to evaluate any potential gain in power to detect group differences in the rate of change of an outcome for the LRR model relative to the LME model when the groups do differ proportionally in their rate of change. Gain in power was anticipated due to the difference in degrees of freedom of the test for these two approaches. For the LRR model in Equation (14), differences in rates of change were tested by the hypothesis H0 : θ = 0, a one degree of freedom test, while the LME specification in Equation (15) required a test of the hypothesis H0 : β5 = β6 = β7 = 0, a three degree of freedom test.
Two simulations were conducted based on data generated under the LRR model and under the LME model using a mean specification that was compatible with both models. That is, using notation in Equations (14) and (15), α0 = β0, , and so forth. First we simulated data under the LRR mixed model specification given in Equation (14). However, due to the non-linear LRR specified random effects structure, standard choices for linear mixed model random effects resulted in misspecification of the covariance structure for the LME model. Therefore, robust sandwich estimators were used for the LME model under this scenario to ensure the test was the correct size. Alternatively, one may specify a more compatible variance structure for the LME model by including four random effects for intercept, linear time, quadratic time, and cubic time. We chose the sandwich variance approach since including random effects for intercept and linear time only is more common practice and the more involved random effects structure will be less likely to converge. Second, we simulated date under the LME model specified in Equation (15). Under this simulation, the random effects structure of the LRR model will be misspecified, but no adjustment for misspecification was made for this simulation since the size of the test for the LRR model was reasonably close to the nominal 5% level (see Table 1). All estimates for the LME model were calculated using the lme function in R. Simulations involved 1000 replicated datasets.
Table 1.
Parameter settings and results for two simulations comparing the LRR model to the LME model. Simulation 1 generated data based on the LRR model with a random effect for the intercept and slope. The variance for LME model was adjusted using the sandwich estimator to ensure appropriate size in simulation 1. Simulation 2 generated data based on the LME model with a random effect for the intercept and linear time. For both simulations, a cubic polynomial equation was used to model time and bivariate covariate was used to estimate differences in the rate of change of the outcome.
| Simulation 1 | Simulation 2 | |
|---|---|---|
| True Model Structure | LRR | LME |
| Sample Size | 100 | 100 |
| Time Structure ( ) | 0.11, −0.0002, −0.00005 | 0.12, −0.002, −0.00002 |
| Intercept and Main Effect (α0, α1) | 4, −0.06 | 4, 0.02 |
| Difference in Rates (θ) | −0.1 | −0.05 |
| Random Effects Covariance ( , ρ) | 0.005,0.05*,−.78 | 0.006,0.00001**,0 |
| Measurement Error Variance (σ2) | 0.005 | 0.07 |
| Size of Test (LRR, LME) | .047, .051 | .044, .041 |
| Power of Test (LRR, LME) | .637, .455 | .941, .848 |
| Failure Rate (LRR, LME) | 0, 0 | .012,.008 |
Variance for the random effect for slope.
Variance for the random effect for linear time.
Results from both simulations are presented in Table 1. For the first simulation scenario using the specified parameters and sample size given in Table 1, we find that LRR testing has 63.7% power using a focused one degree of freedom test while LME has only 45.5% power using a required three degree of freedom test. In the second simulation scenario when data was generated from the LME model, the one degree of freedom test from LRR model again showed higher power at 94.1% compared to 84.8% for the three degree of freedom test using the LME model. These simulation results demonstrate the potential advantages of a regression model that directly structures the longitudinal rate of change when this aspect is the primary target of inference.
Additional simulations (not shown) were conducted to verify that the model diagnostic test outlined in subsection 2.4 obtained proper size and had adequate power to detect violations of the proportional rate assumption. In simulations, the type I error for the score test was appropriate (observed as 4.2% for a nominal 5% level test based on 1000 replicates) and reliably detected linear violations of the PR assumption when the null model did not hold.
4. Application
The infant growth study is a secondary study from the HIVNET 012 clinical trial focusing on prevention of mother-to-child HIV transmission. Mothers were recruited during pregnancy and randomized to receive either zidovudine (AZT) or nevirapine (NEV). The first infant born of the pregnancy was then followed and tested for HIV infection. Details and results for the primary aim of the clinical trial are presented in Jackson et. al. [35]. As a secondary aim, growth among the infants was measured longitudinally. A total of 622 infants were followed for 5 years from birth and measured as many as 16 times for weight (Kg), crown-heel length (cm), and head circumference (cm). For this manuscript, we focus on weight as the outcome of interest and address whether the rate of weight change among these infants differs across groups defined by sex (314 Females, 308 Males), treatment (306 AZT, 316 NEV), and whether HIV infection was detected. To avoid confounding of treatment and HIV infection and to use HIV status as a baseline covariate, we categorize infants as HIV positive if infection was detected pre- or peri-natally, specifically defined as detection within 6 weeks from birth. This definition of baseline HIV status resulted in 60 cases of HIV.
To compare the parametric and semi-parametric modeling approaches for the LRR method outlined in Section 2, both models were run for the infant growth example. For the parametric model, the reference time trend was estimating using a linear combination of a simple regression spline basis. A natural cubic spline basis was used with knots at 150, 500, and 1100 days. In the semi-parametric model, a penalized spline equation was used to model the time structure. Knots were placed at each time point in the data for 17 knots in total. A B-spline basis with a cubic smoothing spline penalty was used to estimate the spline equation. The penalty parameter for estimation was selected using the cross-validation approach outlined in Subsection 2.2 which resulted in selected value of 676 for the current model and a value of 589 for the split rate model discussed later on. Both the parametric and semi-parametric models included the covariates sex, treatment, and baseline HIV status as main effects and rate effects. The variance structure for both models was modeled using the mixed effects approach discussed in Subsection 2.3. The mixed effects approach was selected over an estimating equations approach since the longitudinal trend in weight showed strong mean-variance relationship which could be captured more easily by a mixed effects structure. Main effect and rate effect estimates and confidence intervals for the parametric and semi-parametric models are presented in Table 2. Estimates of the coefficients of the time structure were omitted from the table since the time structures differed between the two models and because the interpretation of the individual coefficients for the time structure are not meaningful. Instead, the time structure for each model was illustrated in Figure 1.
Table 2.
Results from two LRR models for weight among infants exposed to HIV infection. The parametric model estimated the reference time trend using natural cubic spline bases with knots at 150, 500, and 1100 days. The semi-parametric model estimated the reference time trend using a penalized spline equation with knots at day 1, 1 week, 6 weeks, 10 weeks, 15 weeks, 6 months, 1 year, and every half year there after (17 knots in total). Both models provide estimates for main effects and rate effects for sex, treatment, and HIV infection status. Estimates for the coefficients of the time trend for each model were omitted from the table.
| Parametric Model | Semi-Parametric Model | |||
|---|---|---|---|---|
| Estimate | 95% CI | Estimate | 95% CI | |
| Baseline Effects | ||||
| Intercept | 3.30 | (3.22, 3.38) | 3.06 | (2.97, 3.14) |
| Sex (Male) | 0.24 | (0.16, 0.33) | 0.24 | (0.15, 0.32) |
| Treatment (Nev) | −0.13 | (−0.22, −0.04) | −0.13 | (−0.22, −0.04) |
| HIV Status | −0.03 | (−0.19, 0.12) | 0.01 | (−0.15, 0.16) |
|
| ||||
| Rate Effects | ||||
| Sex (Male) | 0.01 | (−0.01, 0.04) | 0.02 | (−0.01, 0.04) |
| Treatment (Nev) | 0.00 | (−0.02, 0.03) | 0.01 | (−0.02, 0.03) |
| HIV Status | −0.15 | (−0.20, −0.10) | −0.16 | (−0.21, −0.11) |
Figure 1.
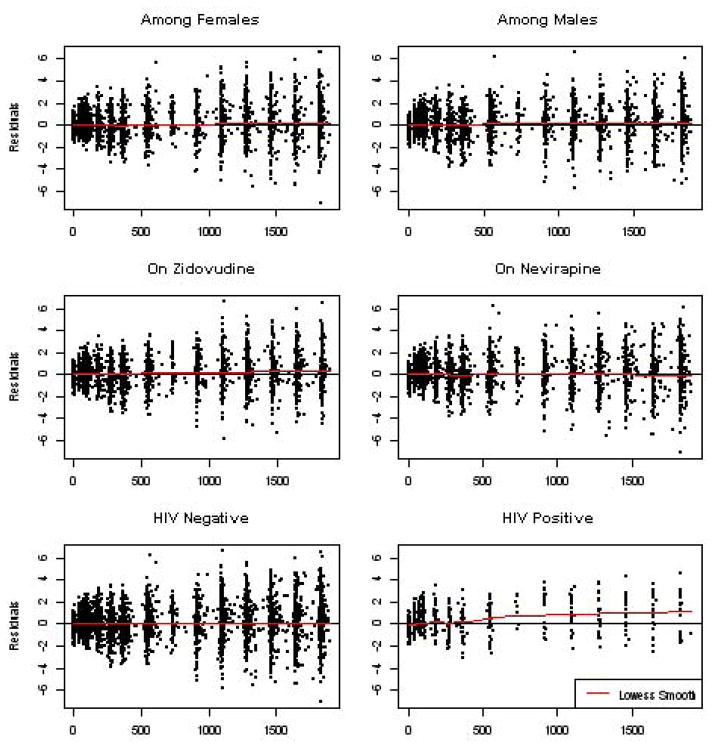
Residual plots for the model of weight among infants exposed to HIV infection across grouping variables based on the single rate LRR results from Table 2. The red line in each plot represents a lowess smooth curve for the residuals.
Model results were similar for the parametric and semi-parametric approaches (see Table 2). Mild differences in main effect estimates were presents with the largest difference for the coefficient for HIV status which reversed sign (−0.03 versus 0.01). There was also a large difference in the intercept value. There was little evidence for a difference in precision for these estimates. In general, differences in the main effects are not of great concern since the focus of the LRR model will typically be on the rate effect estimates. The rate effects for the two models were nearly identical apart from a one percentage point difference in the rate effects for sex and HIV status. For interpreting model results, we focus on model estimates for the parametric model. The main effect estimates indicated large baseline differences in mean weight associated with sex and treatment. Males were estimated to weigh 0.24 Kg more than females on average at birth (95% CI = (0.16, 0.33)). Infants whose mothers were randomized to NEV tended to be 0.13 Kg lighter than those infants on AZT (95% CI = (−0.22, −0.04)). There was little mean difference at baseline in weight among groups defined by HIV status. However, there was strong evidence of a decrease in the rate of change for weight among infants infected with HIV. Infants who were HIV positive were estimated to have a decreased rate of change in weight of 15% (95% CI = (−20%, −10%) compared to infants that were HIV negative. In other words, the LRR model estimates that, for a period of time where HIV negative infants would be expect to increase in weight by 1 kg, the average weight of HIV positive infants is estimated to increase by 0.85 kg. Therefore, the model provides evidence that HIV infection is associated with reduced growth among infants. There was little difference in the rate of change across groups defined by sex and treatment.
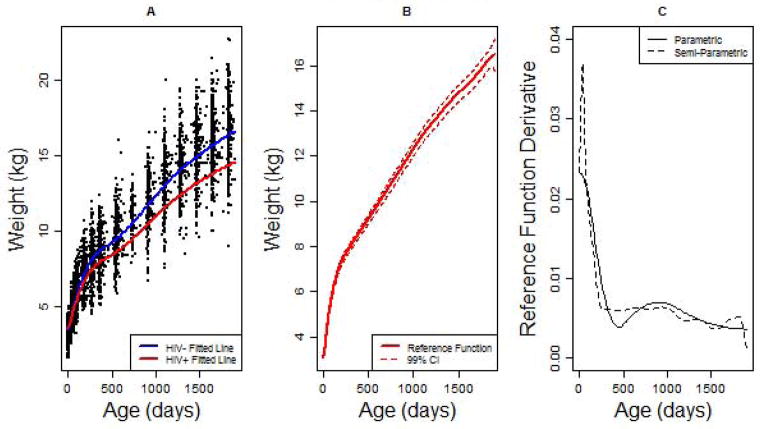
Characteristics of the estimated time trends for the parametric and semi-parametric models are illustrated in Figure 1. In Figure 1A, a scatter plot of weight across time is presented with the estimated time curves for the HIV negative and positive groups based on the parametric model. The plot illustrates the difference in the time trends resulting from the estimated 15% reduction in the rate of change for the HIV positive group. The penalized spline curve for the reference group estimated by the semi-parametric model is provided in Figure 1B along with a 99% confidence interval. In order to estimate an appropriate confidence interval for the penalized spline equation, the mean and standard error estimates must be adjusted for the bias introduced by the penalization process. The procedure used to adjust for this bias for the confidence interval presented in Figure 1B is outlined in Appendix C.
When modeling growth outcomes, an important consideration for constructing model estimates is whether such estimates reflect the natural behavior of the outcome. In longitudinal growth studies in particular, estimates are often expected to reflect the monotonic behavior of an outcome across time, and in some cases, estimation must be constrained in order to ensure such behavior. In the HIVNET growth study, the two outcomes, crown-heel length and head circumference, are examples of common anthropomorphic outcomes that would be expected to increase monotonically across time. Weight examined in infants could also be considered a monotonically increasing outcome in some applications, although weight can potentially decrease over time particularly among disadvantaged or diseased subjects such as the HIV positive children in this study. To evaluate model estimates for monotonicity in the standard LRR model, the estimates for the reference time structure and the rate effects structure must both be examined. First, the estimated time structure must be monotone or, equivalently, the first derivative of the time structure must be positive during the observed time period (or negative if decreasing). To assess monotonicity, we estimated the first derivative of the time structure for both models using a numerical derivative function. The resulting derivative curves are displayed in Figure 1C. For both models, the derivative of the time structure was positive during the observed time period though the curve for the semi-parametric model approached zero at the upper boundary. The more flexible penalized spline time structure is often unstable at the boundary due to sparsity of the data, and thus, evidence of a departure from monotonicity at the boundary may not be a serious concern. Secondly, a monotonic model would require a positive rate estimate within each group. Since all rate effect estimates are greater than −1 (see Table 2), this requirement is satisfied. Thus, the estimated mean models demonstrate a monotonically increasing longitudinal trajectory for weight.
In addition, we may wish to consider individual outcome trajectory estimates, as estimated by the random effects structure in the model, for whether they satisfy the monotonic behavior of the outcome. To ensure monotonic estimates at the individual level, we must verify that the random effect for each individual when added to the overall group rate effect does not result in a negative rate of change. For this example, it is sufficient to verify that all random effects are greater than −0.85 since that is the largest value that could result in a non-positive rate of change though only for individuals who are HIV positive. A simple approach is to examine the standard error of the random rate effect in order to consider the probability of observing a random effect that far from zero. In each model, the estimate for the standard error for the random rate effect was 0.16. Thus, a random rate effect of −0.85 would have a z-score of −5.4 which corresponds to a very small probability that this would occur. Even in a sample of 622, the probability of observing at least one random effect that small would be approximately 2 × 10−5. Therefore, departures from monotonicity at the individual level for these models are of little concern. One could also evaluate this more rigorously by carrying out the estimation of individual random effects and examining the estimated effects by group. In the event that the standard LRR model does not yield a monotonic model, one may rely on constrained estimation approaches such as those outlined in subsection 2.5 to enforce monotonicity.
To evaluate the goodness-of-fit of the LRR model, we produced residual plots for the infant data based on the fitted model. Figure 2 shows the three sets of residual plots for the covariates sex, treatment, and HIV status based on the parametric model. The residual plots show little evidence for a poor model fit except for a small lack of fit for the HIV positive group. The score test for the PR assumption is highly significant for sex and HIV status with both tests resulting in a p-value less than 0.001. The strong evidence of a deviation from the null is possibly a result of the large sample size coupled with modest departures and therefore may not be clinically relevant. The score test for treatment was not significant with a p-value of 0.15. In the residual plots for the semi-parametric model (not shown), there was little deviation from zero in the spread of the residuals, and the score tests for each covariate were non-significant. The difference in the diagnostic evaluation between the two models suggests, as would be expected, that the semi-parametric approach is more robust to model misspecification.
Figure 2.
Plots of the estimated reference time functions for the parametric and non-parametric models presented in Table 2. Plot A depicts a scatter plot of weight by age among infants exposed to HIV. The red line and blue line represent the fitted line for HIV negative and positive infants respectively based on the parametric LRR model. In Plot B, the reference time function as estimated by the penalized spline equation in the semi-parametric model is plotted with a 99% confidence interval. Plot C illustrates the estimated first derivatives of the reference time structure for the two models based on numeric derivation.
Results from the primary HIV prevention trial for the infant growth study published in Jackson et. al. [35] showed that the rate of death was significantly higher among the HIV positive infants. Our analysis simply censors follow-up at the time of death and therefore is subject to certain caveats. Given that weight is likely associated with subsequent mortality the missing data mechanism is not missing completely at random (MCAR). However, if the censoring mechanism is assumed to be dependent on past observed outcomes but not associated with unobserved outcomes then the mechanism is missing at random (MAR) and a likelihood-based analysis such as our longitudinal rate regression mixed model can yield consistent parameter estimates (see Chapter 13 of Diggle et. al. [33] and Chapters 15 and 16 of Verbeke and Molenberghs [36]). The additional caveat is that longitudinal analysis treating death as a censoring mechanism targets estimation of the longitudinal profiles that would be observed in the absence of death, and this is a hypothetical construct [37]. An analysis of dropout in this dataset showed an overall dropout rate of 28% over the entire 5 year period. There was little difference in the dropout rate based on sex and treatment, but large differences were associated with HIV status: HIV negative infants had a dropout rate of 24%; while there was 65% dropout among HIV positive infants. The difference in drop out is due primarily to the difference in death rates among HIV positive and negative infants. The statistical significance of the association between dropout and weight was evaluated using pattern mixture models estimated using a mixed effect model with an identical time structure to the presented LRR model and adjusting for sex, treatment, and HIV status (model results not shown). A statistically significant, negative association was estimated between dropout and weight. Therefore, given the missing data mechanism, we only present likelihood-based analysis of the motivating data since standard GEE would not be valid when data are MAR. Hence, in preforming model selection for the LRR method, the missing data mechanism is of important consideration as it can be highly influential on model estimates depending on the estimating approach.
We also consider a more general rate regression model by including select interactions between time and covariates in order to illustrate the LRR model under relaxation of the global proportional rate assumption. Specifically, we allow differing estimates for the rate parameters before and after two years from birth. We allow the difference in the rate to change before and after 2 years by including an interaction between each grouping variable and an indicator for whether an observation was observed after 730 days. We again ran both parametric and semi-parametric models with time structure specified similarly as before. Results from the LRR models with split rate estimates before and after 2 years are presented in Table 3. In the split rate model, the rate effect estimates can be interpreted as the estimated difference in the rate of change associated with a given grouping variable in the first 2 years from birth. The rate interaction can be interpreted as the change in the rate effect for observations after 2 years compared to observations before 2 years.
Table 3.
Results from two LRR models for weight among infants exposed to HIV infection. The parametric model estimated the reference time trend using natural cubic spline bases with knots at 150, 500, and 1100 days. The semi-parametric model estimated the reference time trend using a penalized spline equation with knots at day 1, 1 week, 6 weeks, 10 weeks, 15 weeks, 6 months, 1 year, and every half year there after (17 knots in total). Both models provide estimates for main effects, rate effects for sex, treatment, and HIV infection status. The rate structure included an interaction between the three covariates and an indicator for observations measured after 2 years from birth. The rate effects for each model can be interpreted as the difference in the rate of change associated with a given covariate prior to 2 years. The rate interaction effects estimate the change in the rate effect after 2 years. Estimates of the coefficients for the time trend of each model are omitted in the table.
| Parametric Model | Semi-Parametric Model | |||
|---|---|---|---|---|
| Estimate | 95% CI | Estimate | 95% CI | |
| Baseline Effects | ||||
| Intercept | 3.33 | (3.25, 3.42) | 3.10 | (3.01, 3.19) |
| Sex (Male) | 0.18 | (0.08, 0.27) | 0.16 | (0.07, 0.26) |
| Treatment (Nev) | −0.14 | (−0.23, −0.05) | −0.14 | (−0.23, −0.04) |
| HIV Status | −0.02 | (−0.13, 0.10) | −0.07 | (−0.23, 0.09) |
|
| ||||
| Rate Effects | ||||
| Sex (Male) | 0.05 | (0.02, 0.08) | 0.05 | (0.02, 0.08) |
| Treatment (Nev) | 0.01 | (−0.02, 0.04) | 0.01 | (−0.02, 0.04) |
| HIV Status | −0.12 | (−0.17, −0.07) | −0.12 | (−0.18, −0.07) |
|
| ||||
| Rate Interaction (After 2 years) | ||||
| Sex (Male) | −0.07 | (−0.10, −0.04) | −0.07 | (−0.09, −0.04) |
| Treatment (Nev) | −0.01 | (−0.04, 0.01) | 0.00 | (−0.03, 0.02) |
| HIV Status | −0.11 | (−0.17, −0.05) | −0.12 | (−0.17, −0.06) |
The results from the split rate model indicate a larger initial rate effect across sex groups in the first 2 years compared to the effect in the single rate model (see Table 3). The rate effect for sex is negated and perhaps inverted by the rate interaction after 2 years. The estimated difference in the rate of change based on treatment was small both before and after 2 years. Infants that were identified as HIV positive still had a large decrease in the rate of change before 2 years and an even larger deficit after 2 years. These estimated changes in the rate before and after 2 years were nearly identical between the parametric and semi-parametric models. The two models differed primarily in the intercept and main effect estimates. The alteration to the rate structure had a modest impact on main effect estimates compared to the single rate models presented in Table 2 as well. For the purposes of making inference on the rate of change, impact of rate assumptions on main effect estimates will typically not be of concern. However, some applications may wish to make simultaneous inference on rate level and mean level differences in which case the rate structure and also the reference time structure should be carefully consider for their impact on model estimates.
5. Discussion
Modeling longitudinal rates of change is important in many biomedical settings and, in particular, for pediatric applications where growth is characterized. To our knowledge, the proposed LRR method is the first attempt to focus regression directly on estimating magnitude differences in rates of change relative to a generally specified time trend. The defining characteristic of longitudinal data is that outcomes are measured over time making the study of change a natural use for such data.
We have discussed existing methods that can be used for estimating differences in rates. Linear models [1, 2] suffer from complex interpretation and potential losses in power when an outcome’s trend over time is non-linear. Methods developed for HIV viral load counts [4], mechanistic growth models [5, 6], pharmacokinetics [7], and empirical dynamic models [8–10] are tailored to settings where rates are linked to underlying states. Such approaches are typically less general in the specification of the longitudinal structure and lack in methods for differentiating the proposed rate structure across groups. However, non-linear methods [3] is a general framework that may be useful for modeling rates, and our method can be considered as a focused special case of the non-linear model proposed by Guo [16]. Accelerated time models [11–15] are another novel non-linear approach to modeling rates of change through transformations of the time scale. Applications where the magnitude of an outcome is constant but progression of the outcome can be considered to accelerate and decelerate in relation to covariate are suitable for an AT approach. In contrast, our LRR model directly links covariates to the magnitude of an outcomes progression. The method is specifically designed to improve inference on differences in the rate of change particularly under the presence of a non-linear time trend and can generally be applied to many areas of interest.
The LRR method allows for a general specification of a reference trend over time. Multiple covariates can be examined in a single comprehensive model with corresponding rate parameters that are simple to interpret even when the time trajectory for the outcome is non-linear. On the other hand, the standard linear mixed model approach will be suitable when comparing rates using linear trends in time. The mean structures for the LME and LRR models are equivalent in this setting. One limitation of the LRR method under a non-linear trend in time is the amount of data needed for estimation. Estimating differences in rates for outcomes with non-linear trends over time requires enough time points and density of data for the non-linear time trend to be adequately estimated. Thus, in settings where data is sparse or the non-linear trend is approximately linear, an appropriate linear model approach will likely perform better than the LRR method. However, the dependence on dense data exists primarily for the estimation of the reference time function since our proposed estimating procedures estimate this function jointly with the differences in the rate of change. Since the primary focus of the LRR model is on comparisons of rates of change, other estimation approaches could be considered that are less reliant on dense data across all groups. In some applications, information exterior to the group data may exist that can inform the estimation of the underlying time trend. For example, in a treatment trial, previously collected longitudinal data may exist on untreated subjects that could be used to estimate a reference time function. The estimated time trend could then be used for comparisons of rates of change between treatment and control groups in which case the rate comparison will be less dependent on having dense data for the groups in the trial.
The standard LRR method relies on a PR assumption to compare rates where it is assumed that the rate of change for any two groups differ by a fixed proportion across time. The PR assumption provides an appealing modeling structure introducing a regression framework directly on the rate level. Thus rates of change can be compared across groups in a parsimonious fashion regardless of the underlying time trend of the outcome. In addition to offering a simple interpretation for the comparison of rates, the structure induced by the PR assumption can relatively easily include random effects with an appealing individual interpretation and mean estimates that are equivalent to a marginal model estimation approach. Since the PR assumption will be unreasonable for some applications, diagnostic procedures were proposed for evaluating the assumption. Also, incorporation of time varying covariates is an effective way to relax the assumption when appropriate. However, even when the PR assumption is invalid, the standard LRR method can be a useful modeling approach for describing an averaged difference in the rate of change across groups. Further work is needed to evaluate the power of the standard LRR in scenarios where differences in rates are not proportional across time.
We applied the LRR method to examples of growth research in human subjects as studies of adolescent and juvenile development seemed to be a particularly natural use for the model. However, there are numerous other areas for which this method may be useful including treatment trials where LRR could be utilized to examine any outcome whose rate is impacted by treatment. Modeling environmental risk factors could also consider utilizing the LRR method for exposures that have an acute effect on outcomes.
Longitudinal rate regression may also be useful for applications with multivariate longitudinal outcomes. One goal with multivariate longitudinal data is to borrow information across related outcomes and across time in order to gain power to detect group differences. Structuring both the mean and the variance structure present interesting challenges in this area of methods research. One approach for specifying the mean structure is to construct a global test for group differences for a multivariate outcome [13, 14, 38]. The accelerated time model proposed by Gray and Brookmeyer [13, 14] was suggested under this premise where the acceleration parameter was estimated uniformly across correlated outcomes. The LRR method can be extended similarly to estimate a single rate parameter for a multivariate outcome measured over time. Estimating a common difference in the rate of change for multivariate outcomes is a convenient way to link outcomes since rate level differences are scale free.
Acknowledgments
This research was partially supported by the NIH grants R01 HL072966 and UL1 TR000423. The authors wish to thank the International Maternal Pediatric Adolescent AIDS Clinical Trials (IMPAACT) Group, grant UM1 AI068632, for providing access to the infant growth data from the HIVNET study, funded by National Institute of Allergy and Infectious Diseases of the NIH.
Appendix A
The one-step estimate for the mean parameters for a given subsample and under a given penalty parameter presented in Equation (7) was constructed by extending the estimate discussed by Jacqmin-Gadda et al. [23] for a linear mean model. Given a sample of size N, let fi(·) denote the mean function for an outcome vector Y evaluated for individual i, with i = 1, ···, N, that is dependent on mean parameters η. The matrix V denotes the covariance of Y which we assume to be fixed across all subsamples and for all values of the penalty parameter, λ, for the purposes of this cross-validation procedure. We use the functions Up(η) and Ip(η) to denote the score equations and information equations for the penalized likelihood for the mean parameters η with a fixed covariance matrix. Let η̂−i(λ) denote the penalized maximum likelihood estimates (PMLEs) for the subsample with the ith individual removed and a given penalty parameter value, λ. We can express the PMLEs as follows:
where is the matrix of derivatives of fj(·) with respect to the vector η. The first line of the above expression utilizes the fact that the penalized score equation will be zero when evaluated at the PMLEs. The remainder of the calculation is a result of algebraic manipulation. When the mean structure is linear in η, then and the second term in the last line is eliminated which results in the expression presented in Jacqmin-Gadda et al. [23]. However, the second term will generally not be eliminated for a non-linear mean structure as is the case for the semi-parametric LRR model. By substituting a reference estimate into the last line, the above result can be used as a one-step estimate for approximating the PMLEs for each subsample and λ value.
Appendix B
Consider a normal distribution likelihood function for a longitudinal outcome Y = (Y1, ···, Yn) measured on an individual observed at times t1i, ···, tnii. Let μ denote the mean structure and V denote the variance structure. Denote the parameters of the model generally as η, ν and ϕ where η represent parameters in the mean structure, ν represent parameters in the variance structure, and ϕ represent parameters in both the mean and variance structure. The likelihood function can then be specified as follows:
Taking the first derivative of the above equation with respect to each parameter provides the following score equations:
To calculate the hessian matrix, take the negative expected value of the derivatives of the score equations with respect to each parameter. These equations can be simplified by utilizing the properties that E[Y − μ] = 0 and E[(Y − μ)(Y − μ)T] = V. Several other properties of traces and expected values are also important in these calculations. Simplifying these equations provides the following hessian equations:
To apply these general results to the longitudinal rate regression model proposed in Subsection 2.3, we need to calculate the partial derivatives of the mean structure and variance structure with respect to each parameter specified in the model. We carry out these calculation using the following notation: let M denote the vector of length n consisting of values for μ0(t) evaluated at each time point t, X be a 1 by q + 1 matrix whose first entry is 1 and the remaining q entries are variable values for a set of variables of interest for their effect on the rate of change of Y, and Z by a 1 by r matrix of variable values for variables of interest for main effect adjustment possibly overlapping with variables in X. The parameters of the model consist of the vector β for parameters of μx(t); the vector θ of length q + 1 whose first entry is 1 and remaining entries are coefficients for the rate of change associated with variables in X; the vector α of length r consisting of coefficients for variables in Z; and variance components , ρ, and σ2 for the variation of the random intercept, the variation in the random slope, the correlation between the random effects, and the variation in the random error as specified in Equation (8). The mean and variance structure can then be expressed as follows:
The partial derivatives of these equations with respect to each parameter can then be expressed as follows:
By substituting these partial derivatives into the score and hessian equations, the score vector and hessian matrix for an individual can be calculated. By setting initial parameter values and averaging the score vector and hessian matrix across individuals, the Newton-Raphson iterations can be applied to obtain Maximum Likelihood Estimates for all parameters. An LDL Cholesky Decomposition can be used for the random effects variance structure to ensure a positive semi-definite variance structure.
Appendix C
We can re-express the form of the reference time function given in Equation (4) as a product of matrices. Let TB denote the vector with entry values corresponding to the spline basis B1(t), ···, Bp(t) evaluated at a given time and β be the vector of length p consisting of coefficients for each spline function. Then,
Given a penalized maximum likelihood estimate (PMLE) for the coefficients denoted by β̂, a (1 − α) × 100% confidence interval for μ0(·) across all values of t can be constructed based on the expression
| (16) |
where za denotes the quantile corresponding to probability a from either a normal distribution or a student-t distribution depending on sample characteristics. In order to ensure that Expression (16) provides a valid confidence interval, the distributional properties of the PMLE need to be considered.
Let η be the vector of parameters for semi-parametric LRR model, and let η̂ be the PMLE for these parameters. To describe the distributional behavior of η̂ as an estimate of η, consider that PMLE is defined by the solution to the penalized likelihood score equation i.e.
| (17) |
where U(·) is the score equation for the standard, unpenalized likelihood equation. We can relate the PMLE to the true parameter vector by considering the first-order Taylor Series approximation of the score equation based on the definition in Equation (17). That is, it follows from Equation (17) that
| (18) |
If the hessian matrix, H, for the standard likelihood equation is substituted for the derivative of the score equation where H(η) = −U(1)(η), we can derive from Equation (18) the result
| (19) |
Standard distribution theory for score equations tells us that U(η) ~ N[0, H(η)]. Thus, based on Equation (19), the PMLE will be normally distributed with mean and variance given by
The distributional results for the PMLE show that, for a fixed sample size, η̂ will be biased estimate for η with bias given by Bias(η̂) = −[H(η) + λΩ]−1 λΩη. A biased estimate was anticipated for the PMLE since the penalization of the parameters forces deviations from the unbiased maximum likelihood estimate. Since Ω has zero entries values for all entries corresponding to parameters not in the penalized spline equation, this bias is non-zero only for the estimated reference time function. However, the PMLE is a consistent estimate since λ and Ω are fixed and H(η) increases relative to increased sample size. Nonetheless, for a fixed sample size, the bias in estimating the reference time function must be corrected for when constructing a confidence interval. Therefore, we update Expression (16) to construct an asymptotically valid confidence interval based on the expression
The bias and the variance of the PMLE estimates can be approximated by substitute the PMLE estimates for the true parameter values in the respective bias and variance equations given above.
References
- 1.Laird N, Ware J. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. doi: 10.2307/2529876. [DOI] [PubMed] [Google Scholar]
- 2.Liang K, Zeger S. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. doi: 10.1093/biomet/73.1.13. [DOI] [Google Scholar]
- 3.Davidian M, Giltinan D. Nonlinear models for repeated measurement data. Chapman and Hall; 1995. [Google Scholar]
- 4.Wu H, Ding A, De Gruttola V. Estimation of hiv dynamic parameters. Statistics in Medicine. 1998;17:2463–2485. doi: 10.1002/(SICI)1097-0258(19981115)17:21<2463::AID-SIM939>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- 5.Huang L. A new mechanistic growth model for simultaneous determination of lag phase duration and exponential growth rate and a new belehdradek-type model for evaluating the effect of temperature on growth rate. Food Microbiology. 2011;28:770–776. doi: 10.1016/j.fm.2010.05.019. [DOI] [PubMed] [Google Scholar]
- 6.Berkey C. Comparison of two longitudinal growth models for preschool children. Biometrics. 1982;38:221–234. doi: 10.2307/2530305. [DOI] [PubMed] [Google Scholar]
- 7.Lindsey J, Byrom W, Wang J, Jarvis P, Jones B. Generalized nonlinear models for pharmacokinetic data. Biometrics. 2000;56:81–88. doi: 10.1111/j.0006-341X.2000.00081.x. [DOI] [PubMed] [Google Scholar]
- 8.Wang S, Jank W, Shmueli G, Smith P. Modeling price dynamics in ebay auctions using differential equations. Journal of the American Statistical Association. 2008;103:1100–1118. doi: 10.1198/016214508000000670. [DOI] [Google Scholar]
- 9.Muller H, Yao F. Empirical dynamics for longitudinal data. The Annals of Statistics. 2010;38:3458–3486. doi: 10.1214/09-AOS786. [DOI] [Google Scholar]
- 10.Zhu B, Taylor J, Song P. Semiparametric stochastic modeling of the rate function in longitudinal studies. Journal of the American Statistical Association. 2012;106:1485–1495. doi: 10.1198/jasa.2011.tm09294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Beath K. Infant growth modelling using a shape invariant model with random effects. Statistics in Medicine. 2007;26:2547–2564. doi: 10.1002/sim.2718. [DOI] [PubMed] [Google Scholar]
- 12.Brumback L, Lindstrom M. Self modeling with flexible, random time transformations. Biometrics. 2004;60:461–470. doi: 10.1111/j.0006-341X.2004.00191.x. [DOI] [PubMed] [Google Scholar]
- 13.Gray S, Brookmeyer R. Estimating a treatment effect from multidimensional longitudinal data. Biometrics. 1998;54:976–988. doi: 10.2307/2533850. [DOI] [PubMed] [Google Scholar]
- 14.Gray S, Brookmeyer R. Multidimensional longitudinal data: Estimating a treatment effect from continuous, discrete, or time-to-event response variables. Journal of the American Statistical Association. 2000;95:396–406. doi: 10.1080/01621459.2000.10474209. [DOI] [Google Scholar]
- 15.Wang Y, Ke C, Brown M. Shape-invariant modeling of cicadian rhythms with random effects and smoothing spline anova decompositions. Biometrics. 2003;59:804–812. doi: 10.1111/j.0006-341X.2003.00094.x. [DOI] [PubMed] [Google Scholar]
- 16.Guo W. Functional mixed effects models. Biometrics. 2002;58:121–128. doi: 10.1111/j.0006-341X.2002.00121.x. [DOI] [PubMed] [Google Scholar]
- 17.Bennet J, Wakefield J. Errors-in-variables in joint population pharmacokinetic/pharmacodynamic modeling. Biometrics. 2001;57:803–812. doi: 10.1111/j.0006-341X.2001.00803.x. [DOI] [PubMed] [Google Scholar]
- 18.Anderson P, Gill R. Cox’s regression model for counting processes, a large sample study. Annals of Statistics. 1982;10:1100–1120. [Google Scholar]
- 19.Fitzmaurice G, Davidian M, Verbeke G, Molenberghs G. Longitudinal Data Analysis. Chapman and Hall/CRC; 2009. [Google Scholar]
- 20.Ruppert D, Wand M, Carroll R. Semi-parametric Regression. Cambridge: Cambridge University Press; 2003. [Google Scholar]
- 21.Zhang D, Lin X, Sowers M. Semiparametric regression for periodic longitudinal hormone data from multiple menstrual cycles. Biometrics. 2000;56:31–39. doi: 10.1111/j.0006-341X.2000.00031.x. [DOI] [PubMed] [Google Scholar]
- 22.Hastie T, Tibshirani R. Generalized Additive Models. Chapman and Hall; 1990. [DOI] [PubMed] [Google Scholar]
- 23.Jacqmin-Gadda H, Joly P, Commenges D, Binquet C, Genevieve C. Penalized likelihood approach to estimate a smooth mean curve on longitudinal data. Statistics in Medicine. 2002;21:2391–2402. doi: 10.1002/sim.1225. [DOI] [PubMed] [Google Scholar]
- 24.Lindstrom M, Bates D. Newton-raphson and em algorithms for linear mixed-effects models for repeated-measures data. Journal of the American Statistical Association. 1988;83:1014–1022. doi: 10.1080/01621459.1988.10478693. [DOI] [Google Scholar]
- 25.Pinheiro J, Bates D. Unconstrained parameterizations for variance-covariance matrices. Statistics and Computing. 1996;6:289–296. doi: 10.1007/BF00140873. [DOI] [Google Scholar]
- 26.Crowder M. On consistency and inconsistency of estimating equations. Econometric Theory. 1986;2:303–330. [Google Scholar]
- 27.Davidian M, Carroll R. Variance function estimation. Journal of the American Statistical Association. 1987;82:1079–1091. doi: 10.1080/01621459.1987.10478543. [DOI] [Google Scholar]
- 28.Friedman J, Tibshirani R. The monotone smoothing of scatterplots. Technometrics. 1984;26:243–250. doi: 10.2307/1267550. [DOI] [Google Scholar]
- 29.He X, Peide S. Monotone b-spline smoothing. Journal of the American Statistical Association. 1998;93:643–650. doi: 10.2307/2670115. [DOI] [Google Scholar]
- 30.Ramsey J. Estimating smooth monotone functions. Journal of the Royal Statistical Society Series B-Statistical Methodology. 1998;60:365–375. doi: 10.1111/1467-9868.00130. [DOI] [Google Scholar]
- 31.Turlach B. Shape constrained smoothing using smoothing splines. Computational Statistics. 2005;20:81–103. doi: 10.1007/BF02736124. [DOI] [Google Scholar]
- 32.Grambsch P, Therneau T. Proportional hazards tests and diagnostics based on weighted residuals. Biometrika. 1994;81:515–526. doi: 10.1093/biomet/81.3.515. [DOI] [Google Scholar]
- 33.Diggle P, Heagerty P, Liang K, Zeger S. Analysis of Longitudinal Data. Oxford University Press; 2002. [Google Scholar]
- 34.Carroll R, Ruppert D, Stefanski L, Crainiceanu C. Measurement Error in Nonlinear Models: A Modern Perspective. Chapman and Hall/CRC Press; 2006. [Google Scholar]
- 35.Jackson B, Musoke P, Fleming T, Guay L, Bagenda D, Allen M, Nakabiito C, Sherman J, Bakaki P, Owor M, et al. Intrapartum and neonatal single-dose nevirapine compared with zidovudine for prevention of mother-to-child transmission of hiv-1 in kampala, uganda: 18-month follow-up of the hivnet 012 randomised trial. Lancet. 2003;362:859–868. doi: 10.1016/S0140-6736(03)14341-3. [DOI] [PubMed] [Google Scholar]
- 36.Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. Springer; 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kurland B, Heagerty P. Directly parameterized regression conditioning on being alive: analysis of longitudinal data truncated by deaths. Biostatistics. 2005;6:241–258. doi: 10.1093/biostatistics/kxi006. [DOI] [PubMed] [Google Scholar]
- 38.Travison T, Brookmeyer R. Global effects estimation for multidimensional outcomes. Statistics in Medicine. 2007;26:4845–4859. doi: 10.1002/sim.2983. [DOI] [PubMed] [Google Scholar]