Real-time compressive sensing spectral domain optical coherence tomography

Abstract

We developed and demonstrated real-time compressive sensing (CS) spectral domain optical coherence tomography (SD OCT) B-mode imaging at excess of 70 fps. The system was implemented using a conventional desktop computer architecture having three graphics processing units (GPUs). This result shows speed gain of 459 and 112 times compared to best CS implementations based on the MATLAB and C++ respectively and that real-time CS-SDOCT imaging can finally be realized.

Compressive sensing (CS) [1, 2] has become increasingly important in the field of medical imaging over the past decade. If data is sparse in some domain that is incoherent to the measurement domain, CS enables reliable and complete recovery of the signal from measurements less than that from the Nyquist rate requirement. Applications of CS in the optical coherence tomography (OCT) imaging have been studied by many groups [3-5] and have shown that OCT images can be reconstructed from highly under-sampled k-space data.

The less k-space data requirement by CS can facilitate minimal data acquisition, increase imaging speed and decrease storage and transfer bandwidth needs. However, regardless of which CS reconstruction algorithm is used, the reconstruction of CS OCT image takes significantly more time compared to the reconstruction of regular OCT image. This has been the major hindrance to apply this imaging technique to clinical applications that typically require either real-time or immediate image reconstruction. In this paper, we propose a practical method for achieving real-time CS SD-OCT imaging.

To achieve our goal of real-time CS SD-OCT imaging, we adopted massive parallel processing approach. Parallel computation with graphics processing units (GPU) has long been recognized as an effective way to accelerate computationally intensive task. CS reconstruction requires numerous matrix-vector multiplications which can be solved more efficiently by GPU than by CPU. GPU has been adapted to accelerate the CS reconstruction of various signals [6-8]. Compared to the CPU implementation, several orders of magnitude enhancement in speed has been commonly reported for the GPU based CS reconstruction.

In this paper, we implemented real-time CS reconstruction of the spectral domain OCT (SD OCT) images on a triple-GPUs architecture. The CS reconstruction algorithm SpaRSA [9] is programmed through the NVIDIA's Compute Unified Device Architecture (CUDA) technology [10]. High quality SD OCT images can be reconstructed at>70 frame/s, with the frame size 2048 (axial)×1000 (lateral) and stopping iteration number 10. Compared to C++ and MATLAB implementations based on CPU, CS reconstruction using the triple-GPUs architecture achieved speed enhancements of 112 and 459 times respectively.

In CS OCT imaging, the A-scan image, x is obtained with high accuracy from under-sampled linear-in-wavenumber spectral data, y_u by solving the following unconstrained nonlinear convex optimization problem:

$$\underset{\mathrm{x}}{\text{minimize}}\frac{1}{2}{\Vert {\mathbf{F}}_{\mathbf{u}}\mathbf{x}-{\mathbf{y}}_{\mathbf{u}}\Vert }_{\mathbf{2}}^{\mathbf{2}}+\tau {\Vert \mathbf{\text{Wx}}\Vert }_{\mathbf{1}}$$ (1)

where W is the sparsifying operator which transforms x to a sparse representation. F_u is the under-sampled Fourier transform matrix. τ is the regularization parameter that controls the sparsity of reconstructed A-scan. The notation ‖c‖₁ is the l₁ norm, which is defined as ‖c‖₁ = Σ_i|c_i| · ‖•‖₂ is the l₂ norm. In this paper, W is chosen to be the identity matrix because OCT signals are usually sparse enough in the spatial domain [3, 4].

The selected CS reconstruction algorithm is SpaRSA [9] which can be implemented efficiently with GPU. SpaRSA tries to solve Eq.(1) through an iterative procedure. In each iteration, SpaRSA obtains the new iterate x^k+1 from the current iterate x^k by solving the following sub problem:

$${\mathbf{x}}^{k+1}=\underset{\mathbf{z}}{min}\frac{1}{2}{\Vert \mathbf{z}-{\mathbf{u}}^k\Vert }_2^2+\frac{\tau }{{\alpha }_k}{\Vert z\Vert }_1$$ (2)

for some α_k > 0. $u^k=x^k-(1/{\alpha }_k)F_u^T(F_u{x}^k-y_u)$. $F_u^T$ is the adjoint matrix of F_u. Eq.(2) can be viewed as the quadratic separable approximation of Eq.(1) (up to a constant) [9]. Eq. (2) can be solved separately in the component of z :

$$x_i^{k+1}=\underset{z_i}{min}\frac{1}{2}{(z_i-u_i^k)}^2+\frac{\tau }{{\alpha }_k}\left|z_i\right|=\text{soft}(u_i^k,\frac{\tau }{{\alpha }_k})$$ (3)

for i ∈ [0,1, …N − 1]. N is the length of x. soft(x, a) ≙ max{|x| − a,0}× x / max{|x| − a, 0} is the complex soft-threshold function.

Inspired by Barzilai and Borwein [11], α_k is chosen as the approximation of the Hessian $F_u^T$ F_u in [9]:

$${\alpha }_k={\Vert {\mathbf{F}}_u{\mathbf{s}}^k\Vert }_2^2/{\Vert {\mathbf{s}}^k\Vert }_2^2$$ (4)

where s^k = x^k − x^k−1.

The computation procedure of the reconstruction of an A-scan on a GPU is shown in Fig. 1. β is the desired stopping iteration number. k is the current iteration number. I is the sampling mask corresponding to y_u. The procedure in Fig. 1 is different from [9] in that it uses a different stopping criterion. The reconstruction stops when the desired iteration number is achieved to avoid data divergence, which will be discussed later.

Fig. 1. computation procedure of an A-scan.

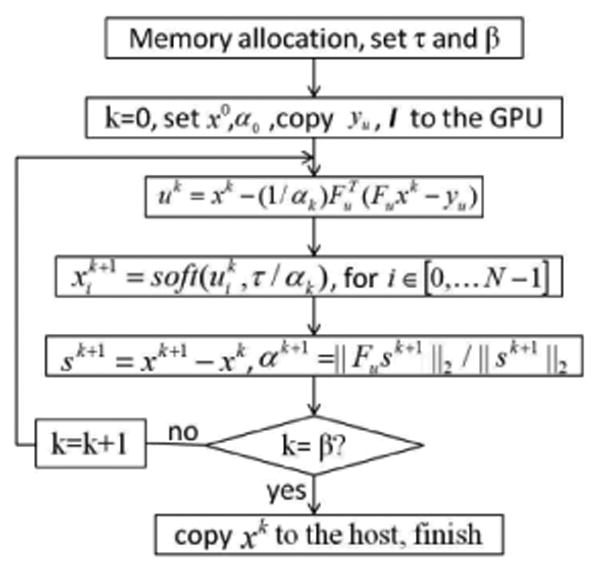
Each iteration includes the computationally extensive tasks such as one matrix-vector multiplication each by $F_u^T$ and F_u for u^k. N operations to solve Eq.(3), and two l₂ -norm computation for α_k. ( F_us^k can be obtained from the intermediate values: F_us^k = F_ux^k − F_ux^k−1). All of these can be solved efficiently through GPU.

Since the reconstructions of CS OCT A-scans are independent of each other, to maximize the computational power of a single GPU, our approach reconstructs the A-scans in one B-scan (1000 lines) together instead of sequentially.

Every computation step in Fig.1 is applied to all A-scan data simultaneously. E.g. for each iteration, instead of computing the α_k for one A-scan, our program computes the α_k for 1000 A-scans simultaneously. Thus this approach maintains a vector of α whose length is the number of A-scans. This is different from the case in which one CUDA thread reconstructs one A-scan, which limits the thread number and does too many computations on one CUDA core. The under-sampled raw A-scan spectral data are obtained using a common sampling mask.

The matrix-vector multiplications of F_u and $F_u^T$ and its efficiency is critical to the speed of the reconstruction. Although the matrix-matrix multiplication operator in the CUBLAS library [12] achieves significant acceleration, it is still too slow for achieving real-time imaging. Inspired by [7], our program takes advantage of the CUFFT library [13]. For every A-scan, F_ux^k is computed in two steps: (1) t^k = FFT (x^k); (2) under sample t^k with I. $F_u^T(F_u{x}^k-y_u)$ is computed in a similar way: (1) r^k = F_ux^k − y_u; (2) zero-padding r^k according to I, denote the result as t^k ; (3) compute the IFFT(t^k) . t^k has the same length as x in both cases. This method can be easily adapted to the multiplication of F_u and $F_u^T$ to the data of multiple A-scans since CUFFT provides the FFT operator for batch execution of multiple one-dimensional transform. Experimental results show that our implementation of the matrix-matrix multiplication is more than 10 times faster than the CUBLAS version (mainly due to the speed advantage of FFT ). For different sampling size (size of y_u ), the FFT/IFFT operator is applied to the same size data; thus the sampling rate has little effect on the reconstruction speed. The proper sampling rate should be chosen to balance the image quality and input data size. Another benefit of our implementation of the matrix-matrix multiplication is that instead of the whole sensing matrix, only the one-dimensional sampling mask (I) is stored in the GPU which is more compact.

l₂ -norm operator in the CUBLAS library cannot compute the l₂ -norm of multiple A-scan vectors simultaneously. We wrote a kernel which applies the tree-based reduction in shared memory, as advocated in reference [14]. Our implementation computes the l₂ -norms in Eq. (4) of all the A-scans simultaneously and is more than 100 times faster than computing the l₂ -norm of the A-scans sequentially using the CUBLAS l₂ -norm operator.

The one-dimensional complex soft-threshold function as well as the vector additions/subtractions can be easily implemented in parallel for multiple A-scan reconstructions on the GPU.

The stopping criterion in our program is different from that in [9]. The reconstruction of a B-scan stops when the desired iteration number (β) is achieved. In this way, the reconstruction time for any B-scan is determined solely by β and is independent of the input data as well as other parameters. When reconstructing a sequence of B-scans, fixed β will smooth the reconstruction rate. Besides, when reconstructing multiple A-scans simultaneously, inconsistent iteration numbers among A-scans are difficult to control and create a significant number of divergence branches which slows the GPU programs a lot.

Although the reconstructions of the A-scans in a B-scan stop together at β iteration, some A-scans may converge in less than β iteration while some requires more. The former case does not influence the reconstruction result or the reconstruction time. The latter case will degrade the image quality and can either be solved by increasing β or attenuated by using a sequence of decreasing τ for every iteration [7, 9]. Choosing β is a trade-off between the reconstruction speed and image quality. According to our experience, setting β to 10-20 is usually enough for a high-quality reconstruction; however, how to optimize β is still under study.

The regulation parameter determines the sparsity of the result as well as the image quality. The performance of SpaRSA generally degrades for smaller τ [7, 9], while larger τ will lead to better noise reduction and more loss of low-contrast features. As is stated above, better choice of τ will accelerate the reconstruction process by making the reconstruction converge in less iteration. How to optimize τ is still an open field in the CS reconstruction of real signals.

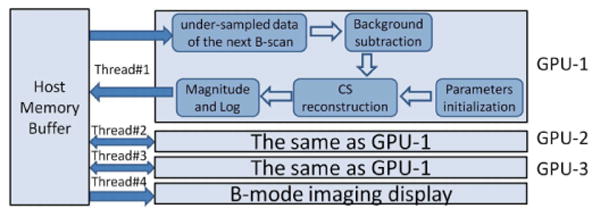
To achieve larger acceleration, we implemented CS reconstruction using three GPUs. The signal processing flow chart of the triple-GPUs architecture is illustrated in Fig. 2. Four major threads exist: three for GPU control and one for display. Each GPU is controlled by one thread which reads the under-sampled data of the next B-scan, subtracts the DC term, performs CS re-construction, then copy the result to the host computer. The fourth thread displays the B-scan reconstruction results in the order of the frame number. GPUs with similar computational power are desired to make the display smooth.

Fig. 2. triple-GPUs architecture.

K-space data from an SD OCT system is used to evaluate the program. The system uses a spectrometer having a 12-bit CMOS line scan camera (EM4, e2v, USA) with 2048 pixels at 70kHz line rate. The light source is a superluminescent laser diode (SLED) with output power of 10mW and effective bandwidth of 105nm centered at 845nm. The experimental axial resolution of the system is 4.0 μm in air while the transversal resolution is approximately 12 μm. All animal studies were conducted in accordance with the Johns Hopkins University Animal Care and Use Committee Guidelines.

A workstation with Intel Core i7 CPU (3.6GHz), 16GB RAM, Windows7 64-bit operation system is used as the host computer which contains three GPUs: GPU-1 (NVIDIA GeForce GTX 670) with 1344 stream processors, 1GHz processor clock and 2GB global memory; GPU-2 (NVIDIA Tesla C2075) with 2496 stream processors, 1.15GHz processor clock and 5GB global memory; GPU-3 which is the same as GPU-2.

For comparison, our program is also implemented on the single-GPU architecture (GPU-1) and dual-GPUs architecture (GPU-2 and GPU-3). The implementation on the single GPU architecture is similar to that on the triple-GPUs architecture except only one thread for GPU control exists. The dual-GPUs case has two threads for GPU control. C++ and MATLAB (version R2013a) implementations on CPU are also compared. They reconstruct the A-scans sequentially. The speed of our programs is evaluated with the benchmark line rate test. The same under-sampled data, parameters and algorithm (Fig. 1) are used in the comparison and the same B-scan results are obtained in all implementations with different speed. The FFT operator provided by FFTW[15] is used in the C++ implementation while MATLAB uses its built-in FFT operator. C++ program is not fully optimized (only compiled with the flag `-O2′) and no parallelization using the CPU-based multi-threading is applied. GPU programs are optimized with the CUDA Visual Profiler [16].

The under-sampled linear-in-wavenumber data set is obtained by sampling from the original k-space data set with the pre-generated k-linear sampling mask [4] and stored in the RAM. This step is not counted in the computation time which is consistent with the desired practical application in which the under-sampled data will be grabbed from the camera and stored in the RAM. The starting values are set as x⁰ = 0 and α₀ = 1 for all the A-scans. These two values do not show obvious influence on the image quality as well as computation time.

We first evaluate all the implementations on the reconstructions of OCT images of an orange. The sampling rate is 40%. τ = 2.5. The stopping iteration number is 10. The reconstruction result with 100% samples is provided in Fig. 3(a) as a reference. The CS reconstruction result is shown in Fig. 3(b). Both cases are averaged on 100 frames. As is shown by the images, the CS reconstruction result is very close to the reference image. For a quantitative assessment, the peak signal to noise ratio (PSNR) is computed for both images with definition PSNR = 10log₁₀(max²(f(x))/var). var is the intensity variance of the selected background region (the white dash rectangle areas in Figs. 3(a) and 3(b)). f(x) is the B-scan. The PSNR of Figs. 3(a) and 3(b) are 66.17dB and 75.32dB respectively. The CS reconstruction achieves 9.15dB better PSNR; it is well known to be good at reducing noise [3, 5].

Fig. 3.

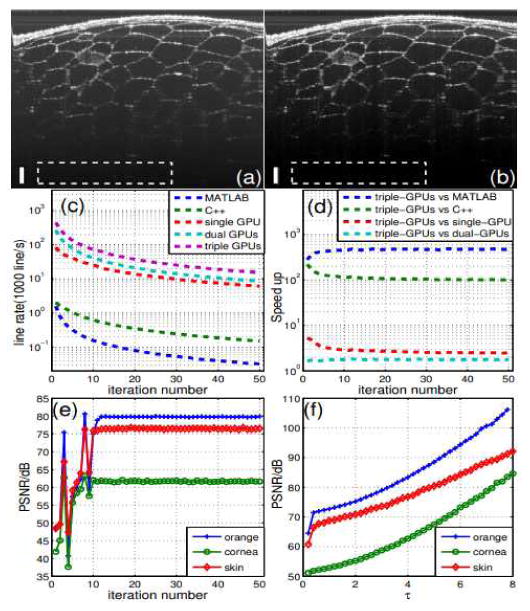
(a) original OCT image of an orange: (b) CS re construction result; (c) line rate vs iteration number; (d) speedup vs iteration number; (e) PSNR vs iteration number; (f) PSNR. vs τ. The scale bars in (a) and (b) represent 100um.

The comparison of the line rate versus stopping iteration number for different implementations is shown in Fig. 3(c). The data were obtained by applying these implementations to the reconstruction of the orange image. τ = 2.5 and sampling rate is 40%. The speedup of the implementation on the triple-GPUs architecture compared to the other implementations is illustrated in Fig. 3(d). Speedup is defined as T₀/T_t where T_t is the single B-scan reconstruction time with triple-GPUs and T_o is that of the other implementations. The triple-GPUs implementation achieves an average of 459.36, 112.02, 2.83, and 1.77 times speedup compared to those based on the MATLAB, C++, single-GPU and dual-GPUs respectively. The data in Figs. 3(c), 3(d) are averaged in 30 runs.

We screen-captured the real-time displayed scenarios from the triple-GPUs implementation, shown in Media 1. The image frames are rescaled to 512 (axial) ×500 (lateral) pixels to accommodate the monitor display. The video shows the logarithm of the rescaled B-scan and no further image processing is applied. The frame rate is 72 fps with stopping iteration number 10, τ = 2.5 and sampling rate 40%. In this paper, the term “real-time” means that the reconstruction of CS SD OCT is faster than the camera for data acquisition in the system. By using a CCD camera with randomly addressable pixels [17, 18], our program can achieve real-time reconstruction.

Then we test the programs on the OCT images of human skin and mouse cornea. The screen-captured real-time displayed scenarios from the triple-GPUs implementation are shown in Media 2 and Media 3 respectively. The image frames are processed in the same way as Media 1. The frame rate is also 72 fps with stopping iteration number 10, τ = 3.5 and sampling rate 45%. This shows that the speed of our program is independent of the imaging object which enables the development of a system that incorporates the CS technique.

To illustrate the influence of the iteration number on the image quality, the PSNR is computed for the reconstructed images of an orange, human skin and mouse cornea with different iteration numbers. τ and sampling rate are stated above. The background regions of the human skin and mouse cornea are selected similarly to that of the orange. PNSR vs. iteration number for these three samples is displayed in Fig. 3(e). As it shows, the PSNR usually converges between 10 to 20 iterations; thus setting the stopping iteration number to 10-20 (corresponding to 38-72 fps) is usually enough for a high-quality image.

Fig. 3(f) shows the PSNR versus τ for all three samples. The stopping iteration number is 10 and the sampling rate is stated above. Higher τ results in a better denoising effect and more loss of low intensity features