A Probabilistic, Dynamic, and Attribute-wise Model of Intertemporal Choice

Abstract

Most theoretical and empirical research on intertemporal choice assumes a deterministic and static perspective, leading to the widely adopted delay discounting models. As a form of preferential choice, however, intertemporal choice may be generated by a stochastic process that requires some deliberation time to reach a decision. We conducted three experiments to investigate how choice and decision time varied as a function of manipulations designed to examine the delay duration effect, the common difference effect, and the magnitude effect in intertemporal choice. The results, especially those associated with the delay duration effect, challenged the traditional deterministic and static view and called for alternative approaches. Consequently, various static or dynamic stochastic choice models were explored and fit to the choice data, including alternative-wise models derived from the traditional exponential or hyperbolic discount function and attribute-wise models built upon comparisons of direct or relative differences in money and delay. Furthermore, for the first time, dynamic diffusion models, such as those based on decision field theory, were also fit to the choice and response time data simultaneously. The results revealed that the attribute-wise diffusion model with direct differences, power transformations of objective value and time, and varied diffusion parameter performed the best and could account for all three intertemporal effects. In addition, the empirical relationship between choice proportions and response times was consistent with the prediction of diffusion models and thus favored a stochastic choice process for intertemporal choice that requires some deliberation time to make a decision.

Intertemporal choice refers to the situation in which people need to choose among two or more payoffs occurring at different times. We can find numerous examples of intertemporal choice from the economic world and our daily lives. For instance, a decision to deposit part of one’s income in a bank instead of spending the money immediately can be interpreted as an intertemporal choice. In this case, one option is to purchase some goods with the money to fulfill one’s needs instantly, while the other is to save it in order to get more money and satisfaction in the future.

Intertemporal choice has long been an intriguing topic for economists, psychologists, and decision scientists. It was introduced by Rae (1834) when addressing the issue of interest and later on elaborated by Fisher (1930), leading to the well-known discounted utility (DU) model (Samuelson, 1937). Psychologists have since put much effort into revising the DU model from a behavioral perspective. One of the most influential fruits from this endeavor is the hyperbolic discounting model (Ainslie, 1974, 1975, 1992; Mazur, 1987; Rachlin, 1989), which differs from the DU model mainly in its prediction on time consistency. Specifically, the DU model entails stationary (i.e., time-consistent) preference between two payoffs at different times when time elapses, while the hyperbolic discounting model might predict a preference reversal under the same circumstance. Meanwhile, Loewenstein, Prelec, and Thaler (Loewenstein, 1988; Loewenstein & Prelec, 1992, 1993; Loewenstein & Thaler, 1989) explored intertemporal choice in an attempt to expand related economic models to accommodate various behavioral anomalies revealed in empirical studies. Obviously, both psychological and economic research has contributed substantially to scholars’ knowledge base on this topic.

Despite a long history of intensive investigation and a rich literature, we still lack a good understanding of the underlying mechanisms of intertemporal choice, i.e. the affective and cognitive processes leading to our intertemporal decisions. Furthermore, some important properties of intertemporal choice, such as its probabilistic nature and the time taken to make these decisions, have not been systematically probed yet. Consequently, this article will examine these critical properties and offer a description of the underlying decision processes that could account for these properties by exploring diverse mathematical models. A brief review of the traditional approach to intertemporal choice and relevant findings will serve as a good starting point.

Traditional Approach to Intertemporal Choice and Relevant Findings

Intertemporal Choice from a Delay Discounting Perspective

Most traditional studies on intertemporal choice focus on how people assign subjective values or utilities to immediate or delayed payoffs. The underlying assumption is that people make an intertemporal decision by first calculating the subjective value of each option and then choosing the option with the higher subjective value. Since most people would prefer getting a payoff immediately over having it postponed into the future, it is plausible to assume that the subjective value of a payoff decreases when it is delayed. In other words, the subjective value of a delayed payoff is discounted, resulting in a concept known as delay discounting. Consequently, discovering the appropriate form of discount function that links the instantaneous utility of a payoff to its discounted utility due to delay constitutes a pivotal issue in intertemporal choice research. In following paragraphs we will discuss two most influential classes of discount functions, i.e., the exponential and hyperbolic discount functions.

Exponential discount function

The DU model and its exponential discount function were based on abstract axioms and rigorous mathematical derivations (e.g., Fisher, 1930) and thus is the most popular theory among economists studying intertemporal choice. Consider a pair of intertemporal options (v_s, t_s) and (v_l, t_l), in which v represents money amount, t represents delay duration, and v_s < v_l, t_s < t_l.¹ We will hereafter call the first option a smaller-but-sooner (SS) option and the second a larger-but-later (LL) option. Let DU represent the discounted utility of an option, u(v) be the utility of an immediate payoff of money amount v, and D(t) = exp(−kt) denote the exponential discount function with discounting parameter k. According to the DU model, a decision maker should choose the LL option when

$$\mathrm{d}={\mathrm{DU}}_{\mathrm{LL}}-{\mathrm{DU}}_{\mathrm{SS}}=\mathrm{u}\left({\mathrm{v}}_1\right)\cdot \mathrm{D}\left({\mathrm{t}}_1\right)-\mathrm{u}\left({\mathrm{v}}_{\mathrm{s}}\right)\cdot \mathrm{D}\left({\mathrm{t}}_{\mathrm{s}}\right)=\mathrm{u}\left({\mathrm{v}}_1\right)\cdot \exp (-{\mathrm{kt}}_1)-\mathrm{u}\left({\mathrm{v}}_{\mathrm{s}}\right)\cdot \exp (-{\mathrm{kt}}_{\mathrm{s}})$$ (1)

is positive, and choose the SS option when d is negative. The value of k should be positive to guarantee delay discounting, and larger values of k indicate more rapid discounting. The exponential discount function entails constant discount rates over time and thus the same ratio of discounted utilities between two payoffs when time passes. Consequently, it implies that the sign of d will not change as time passes and thus the property of time consistency, which is usually a required condition in economic analysis as a demonstration of rationality (Strotz, 1955).

Hyperbolic discount function

In reality, however, people usually do not behave as consistently as suggested by economic theories. When intertemporal choice is of concern, it means that people tend to shift their preference towards the later option when two intertemporal options are further delayed to the same degree (Benzion, Rapoport, & Yagil, 1989; Kirby & Herrnstein, 1995; Thaler, 1981). This pattern is referred to as the common difference effect and it gives rise to time inconsistent behavior (Loewenstein & Prelec, 1992). Therefore, we need a different discounting model to accommodate this effect. One of the candidates is the hyperbolic discounting model widely adopted by psychologists interested in fitting empirical data. According to this model, a decision maker should choose the LL option when

$$\mathrm{d}={\mathrm{DU}}_{\mathrm{LL}}-{\mathrm{DU}}_{\mathrm{SS}}=\mathrm{u}\left({\mathrm{v}}_1\right)\cdot \mathrm{D}\left({\mathrm{t}}_1\right)-\mathrm{u}\left({\mathrm{v}}_{\mathrm{s}}\right)\cdot \mathrm{D}\left({\mathrm{t}}_{\mathrm{s}}\right)=\mathrm{u}\left({\mathrm{v}}_1\right)∕(1+{\mathrm{kt}}_1)-\mathrm{u}\left({\mathrm{v}}_{\mathrm{s}}\right)∕(1+{\mathrm{kt}}_{\mathrm{s}})$$ (2)

is positive, and choose the SS option when it is negative. In this formulation, D(t) = 1/(1+kt) is the hyperbolic discount function with discounting parameter k. The reasonable value range of k and its interpretation are the same as those in the exponential discount function. Unlike the exponential discount function, however, the hyperbolic discount function predicts decreasing discount rates over time and thus could account for the time inconsistency in intertemporal choice typically found in empirical data (e.g., Ainslie & Herrnstein, 1981; Christensen-Szalanski, 1984; Green, Fisher, Perlow, & Sherman, 1981; Millar & Navarick, 1984; Thaler, 1981). Researchers have also investigated a number of similar but different models, including a two-parameter hyperboloid model (Green, Fry, & Myerson, 1994; Myerson & Green, 1995) and a two-parameter hyperbola model (Rachlin, 2006). See McKerchar et al. (2009) for a comparison of the aforementioned models.

Other Important Effects in Intertemporal Choice

Besides the phenomenon of time inconsistency and the related common difference effect, researchers in various domains have also examined some other effects in intertemporal choice. For example, Kirby and Maraković (1996) studied the impact of reward size on the discounting parameter in the hyperbolic discount function and found that it is a decreasing function of the size of the delayed reward. Similar results were reported by Green, Myerson, and McFadden (1997) and Chapman and Winquist (1998). This relationship between the discounting parameter in the hyperbolic discount function and the size of the delayed reward is usually termed as the magnitude effect in intertemporal choice. This effect suggests that larger dollar amounts suffer less from delay discounting than smaller ones (Loewenstein & Prelec, 1992).

In an attempt to put intertemporal and risky choice under a common theoretical framework, Prelec and Loewenstein (1991) summarized the analogy between these two research topics in terms of various related effects and proposed a set of assumptions to account for these effects. The magnitude effect in intertemporal choice is just such an effect, whose counterpart in risky choice is the so-called peanuts effect, i.e., risk-taking for small gains and risk aversion for large gains (Markowitz, 1952). To explain the magnitude effect, Prelec and Loewenstein put forward an assumption of increasing proportional sensitivity, which suggests that multiplying the values on a specific attribute across all alternatives by a constant greater than one will shift more weight to the attribute. For example, if a person has no preference between receiving 10 dollars now and receiving 20 dollars in 20 days, then the assumption of increasing proportional sensitivity implies that the person would prefer receiving 200 dollars in 20 days to receiving 100 dollars now. This is due to the fact that the two reward amounts are multiplied by a common constant, i.e., 10, and thus reward magnitude becomes more important in the decision. Consequently, the option with the higher value on the attribute will become more attractive.

The assumption of increasing proportional sensitivity can be applied to the attribute of delay duration as well. According to this assumption, if the delay durations of both options are increased by a common multiplicative constant, delay duration will become more decisive and the option with a shorter delay (i.e. the more desirable option in terms of delay duration) will become preferable. For example, if a person has no preference between receiving 10 dollars in 10 days and receiving 20 dollars in 20 days, then the assumption entails that the person would prefer receiving 10 dollars in 20 days to receiving 20 dollars in 40 days. We label this as the delay duration effect. This effect has not been as intensively studied as the magnitude effect, but it deserves a close look if we want to obtain a comprehensive understanding of intertemporal choice and develop cognitive models accordingly. In fact, the delay duration effect provides a quite useful tool to demonstrate the probabilistic nature of intertemporal choice, which is one of the major goals of this article.

Alternative Approaches to Intertemporal Choice

Although intertemporal choice has long been studied from a discounting perspective and various effects have been explored, leading to several distinct models, most of the conclusions and interpretations of intertemporal choice are based on several unquestioned but fundamental background assumptions. First, most existing models on intertemporal choice, including the hyperbolic discounting model and its variants, assume a deterministic view on human choice behavior. According to this view, when required to make choices between the same pair of options repeatedly, an individual should always have the same preference and thus choose the same option. Second, to the best of our knowledge, all existing models are static in the sense that they do not provide an account for the time associated with the underlying dynamic processes resulting in the explicit responses. Third, most existing models presume that intertemporal choice is accomplished in an alternative-wise manner (but see Scholten & Read [2010]). Such an approach demands that people first calculate the utility of each option separately and then make a choice by comparing their utilities. This is actually one of the core assumptions of the delay discounting perspective on intertemporal choice. In summary, most traditional models of intertemporal choice assume a deterministic, static, and alternative-wise view, which might impose unnecessary constraints on this topic. Therefore, we intend to transcend these boundaries in this article to introduce a different and potentially more accurate account of intertemporal choice. First, let us explore several possible alternatives to the traditional approach.

Deterministic vs. Probabilistic Approaches

A probabilistic approach to intertemporal choice, which does not assume perfect consistency in people’s preference between a pair of options presented repeatedly, is a reasonable alternative to the traditional deterministic approach. Although the probabilistic nature of intertemporal choice has not been carefully examined yet, it is quite easy to find its counterpart in risky choice literature. Ever since the early days of behavioral studies on risky choice, strong support for its probabilistic property has been reported. For example, Mosteller and Nogee (1951) demonstrated that individuals were often inconsistent in their preferences for simple gambles over repeated occasions. The deterministic perspective on risky choice requires that the preference function in observed choice proportion assume a step form with a leap from zero to one at the point where an individual had no preference between the two options. The empirical preference function, however, was strikingly similar to the smooth, gradually increasing S-shaped psychometric function typically obtained from psychophysics studies. This result suggested that a deterministic model would be insufficient to account for the complexity of human risky choice. It might well be the case that the same pattern of gradual change should occur in intertemporal choice. Consequently, the three effects discussed above would unfold in a probabilistic rather than deterministic manner.

Static vs. Dynamic Approaches

Although static models of human decision-making are easier to construct than dynamic models and are capable of explaining a number of empirical results, their silence on response time renders them less informative than dynamic models. Unfortunately, no previous models on intertemporal choice have ever attempted to address the important measure in psychological research of the decision time associated with a specific choice. However, decision time not only provides important information about how people make explicit responses, but it can also be utilized to distinguish between models with similar predictions on choice probabilities. Moreover, the probabilities found with intertemporal choice may change systematically as a function of deliberation time as they do with risky decisions (Diederich, 2003). A number of dynamic stochastic models of decision-making have been proposed and applied to empirical results of preferential choice (e.g., Usher & McClelland, 2004; Krajbich, Armel, & Rangel, 2010). Among them, decision field theory (DFT) by Busemeyer and colleagues (Busemeyer & Townsend, 1992, 1993; Johnson & Busemeyer, 2005; Roe, Busemeyer, & Townsend, 2001) has achieved the widest range of application and is the principal dynamic theory on risky choice. As a dynamic model, it describes in detail the deliberation process when one needs to choose among several competing options. Given the similarity between intertemporal choice and risky choice (Prelec & Loewenstein, 1991), it is quite likely that the deliberation process assumed by DFT can also be utilized to account for the effects in intertemporal choice.

Alternative-wise vs. Attribute-wise Approaches

Finally, the traditional approach to intertemporal choice assumes an alternative-wise perspective, which is consistent with the concept of utility maximization frequently invoked in choice theories, such as Expected Utility Theory (von Neumann & Morgenstern, 1944) and Cumulative Prospect Theory (Tversky & Kahneman, 1992). However, some computational models of risky choice suggest that people actually employ an attribute-wise approach to decision making. Such an approach assumes that people first compare options within each attribute and then aggregate the results to make a decision. Examples include the priority heuristic (Brandstätter, Gigerenzer, & Hertwig, 2006) and the proportional difference model (Gonzalez-Vallejo, 2002). Similarly, DFT also assumes an attribute-wise approach in the sense that differences within various attributes across options are the building blocks of the preference accumulation process. Given the apparent analogy between intertemporal and risky choice, it is very likely that people adopt an attribute-wise strategy to choose between intertemporal options.

In fact, Scholten and Read (2010) proposed a tradeoff model of intertemporal choice, i.e., an attribute-wise model based on direct differences in money and delay dimensions to accommodate some anomalies that elude the alternative-wise delay discounting approach. We use the term direct difference to denote the simple difference within a certain attribute, as opposed to the proportional or relative difference in the proportional difference model discussed later. For example, for the SS and LL options mentioned above, the direct difference in the money attribute is just v_l-v_s. In more complicated cases, certain forms of transformation may be applied to attribute values before direct differences are drawn. According to the tradeoff model, intertemporal choices are made by directly weighing time differences against money differences. Specifically, a decision maker will have no preference between an SS option, (v_s, t_s), and an LL option, (v_l, t_l), if

$${\mathrm{Q}}_{\mathrm{T}\mid \mathrm{V}}\left(\mathrm{w}\right({\mathrm{t}}_1)-\mathrm{w}({\mathrm{t}}_{\mathrm{s}}\left)\right)={\mathrm{Q}}_{\mathrm{V}\mid \mathrm{T}}\left(\mathrm{u}\right({\mathrm{v}}_1)-\mathrm{u}({\mathrm{v}}_{\mathrm{s}}\left)\right)$$ (3)

where u and w are two intra-attribute weighing functions and Q_T|V and Q_V|T are two inter-attribute weighing functions. The left side of Equation 3 represents the advantage of the SS option along the delay attribute while the right side of Equation 3 represents the advantage of the LL option along the money attribute. The tradeoff model is essentially deterministic and static, although simple probabilistic generalization is possible. One goal of this article is to extend the tradeoff model by incorporating a probabilistic and dynamic structure so that more general models can be developed and tested.

Probabilistic Choice Models

In this section, we will introduce five classes of probabilistic choice models that can be utilized to build probabilistic models of intertemporal choice.

Constant Error Model

The simplest possible probabilistic model, i.e., constant error model, assumes that people have a true preference between each pair of options but a fixed chance of choosing the undesirable alternative due to “trembling hand” (Harless & Camerer, 1994). Consequently, the choice probability of the option with a higher true utility is always 1 − ε and the choice probability of the other option is always ε. The parameter ε represents the chance of “hand trembling” and is typically assumed to be below 0.5. When two options have the same true utility, each alternative has a choice probability of 0.5 according to a constant error model. When manipulating a factor such as time delay of an option, this model predicts an abrupt change in choice probability at the crossing point of the factor where the true preference changes direction.

Fechner Model

A more sophisticated class of probabilistic choice models is the Fechner models (Becker, DeGroot, & Marschak, 1963). These models imply that people do have true preferences but are susceptible to processing errors (Loomes & Sugden, 1995). According to a Fechner model, the probability of choosing option A from a pair of options {A, B} equals

$$\mathrm{P}(\mathrm{A}\mid \{\mathrm{A},\mathrm{B}\left\}\right)=\mathrm{Pr}({\mathrm{u}}_{\mathrm{A}}-{\mathrm{u}}_{\mathrm{B}}+\epsilon >0)$$ (4)

where u_A and and u_B are the true utilities of the two options and ε represents the random amount of processing error. By assigning a proper distribution to the error term, we can determine the choice probability in Equation 4. For example, a logistically distributed error term will lead to the commonly used logistic model,

$$P(A\mid \{A,B\left\}\right)=1∕(1+\exp (-g(u_A-u_B))=1∕(1+\exp (-g\cdot d))$$ (5)

where d = u_A − u_B denotes the difference in true utility between the two options and g is a free parameter.

Random Utility Model

Another way to develop probabilistic models of intertemporal choice is by introducing random components into the traditional deterministic models to generate corresponding random utility models (e.g., Becker, DeGroot, & Marschak, 1963). The major difference between deterministic and random utility models lies in the way that the utility of a given option is assigned. According to a deterministic interpretation of utility, any option is associated with a fixed utility across repeated trials. To the contrary, a random utility model assumes that the utility of a given option might vary across repeated trials and thus people’s preference between the same pair of options may change from time to time. Both classes of models assume that people always choose the option with the higher utility at a given instant. Mathematically, the probability of choosing option A from a pair of options {A, B} equals

$$\mathrm{P}(\mathrm{A}\mid \{\mathrm{A},\mathrm{B}\left\}\right)=\mathrm{Pr}({\mathrm{U}}_{\mathrm{A}}>{\mathrm{U}}_{\mathrm{B}}\mid \{\mathrm{A},\mathrm{B}\left\}\right)$$ (6)

in which U_A and U_B are the random utilities of options A and B respectively.² Since random utility models are static, they are not appropriate for fitting response time data.

One common practice when applying such models in real situations is to specify the joint distribution function of the random utilities from which we can derive the choice probability in Equation 6. A frequently used distribution in this case is the multivariate normal distribution with independent components. If we can further assume that the variances of random utilities of different options are the same, then the resultant random utility model is actually a Thurstone Case V model (Thurstone, 1927). Specifically, this model assumes that U_A − U_B ~ N (d, σ²), in which d = μ_A − μ_B is the difference in mean utility between the two options and σ is a measure of the variability in utility difference. Therefore,

$$P(A\mid \{A,B\left\}\right)=\Phi \left(\frac{d}{\sigma }\right)$$ (7)

where Φ represents the cumulative distribution function of a standard normal distribution. In more complicated cases, the variances of random utilities of different options might be contingent upon idiosyncratic features of these options and thus differ from one another. Equation 7 is still valid under this circumstance but σ would vary among different pairs of options. In general, Equation 7 is called a Probit model.

Another way to generate random utility models is to introduce variability into the principal parameter of the corresponding deterministic models, such as the k parameter in either the DU model or the hyperbolic discounting model. Each possible value of the parameter leads to a given utility on a specific option and thus a certain preference relation between any pair of options.³ Consequently, the binary choice probability in Equation 6 could be determined from the distribution of the principal parameter and the deterministic model. The resultant random utility model is usually called a random preference model (Loomes & Sugden, 1995).

Proportional Difference Model

The Proportional Difference (PD) model (Gonzalez-Vallejo, 2002) is yet another probabilistic but static model of choice behavior. According to the PD model, when people need to choose between a pair of options with multiple attributes, they first compute the proportional difference within each attribute and then rely on a linear combination of these differences to obtain a general evaluation of each option. For the aforementioned pair of SS and LL options, the proportional difference within the money attribute is defined as (v_l−v_s)/v_l, and the proportional difference within the delay attribute is defined as (t_l−t_s)/t_l. Since the LL option is superior to the SS option on the money attribute but less attractive on the delay attribute, the first proportional difference represents the relative advantage of the LL option while the second represents the relative advantage of the SS option. Consequently, subtracting the second difference from the first one produces a general evaluation for the LL option. This overall evaluation will then serve as the mean of a normal distribution, based on which the choice probability of the LL option can be determined. The other two quantities required for determining the choice probability are a parameter on personal decision threshold, δ, and the standard deviation, σ, of the normal distribution; both are free parameters in the model. Specifically,

$$\mathrm{P}(\mathrm{LL}\mid \{\mathrm{SS},\mathrm{LL}\left\}\right)=\Phi \left(\right(\mathrm{d}-\delta )∕\sigma )$$ (8)

in which d = (v_l−v_s)/v_l − (t_l−t_s)/t_l represents the overall advantage of the LL option over the SS option, and Φ is the cumulative distribution function of a standard normal distribution as in Equation 7. In this article, we will also call proportional differences “relative differences” since they represent relative advantages.

The PD model differs from random utility models in two important aspects. First, the parameter d in Equation 8 is derived from within-attribute comparisons, i.e., the two proportional differences, while the same parameter in Equation 6 is calculated from within-alternative quantities, i.e., the utilities of the two options. Second, the PD model involves one more parameter, δ, which represents the degree to which a decision maker differentially weighs the two attributes (Gonzalez-Vallejo, 2002). On the other hand, both random utility models and the PD model are static and thus do not specify any predictions for response time data. The same is true for the Fechner models and constant error models.

Diffusion Models

Diffusion models are specific cases of sequential sampling models with continuous time and varying amounts of evidence. One of the key assumptions of sequential sampling models is an evidence or preference accumulation process. Specifically, evidence for and against each option is sampled and accumulated sequentially during the deliberation stage until the preference strength for one of the options reaches a threshold. At that time, a decision is made to choose the exact option whose accumulated preference strength reaches the threshold, and the deliberation time, along with the time for other non-decisional components, determines the actual response time. See Ratcliff and Smith (2004) for a review and comparison of sequential sampling models for binary decisions.

Usually there are five parameters involved in the implementation of diffusion models to binary choice tasks. The first one is the parameter of mean drift rate, d, which reflects the mean rate of preference accumulation for a specific option. Next, the diffusion parameter, σ, reflects the amount of variability in the instantaneous rate of preference accumulation. A non-zero σ is necessary for a probabilistic model of binary choice since otherwise the trajectory of accumulated preference over time will be a straight line determined solely by the mean drift rate, resulting in deterministic choice and response time on a single trial.⁴ The third parameter, θ, represents the threshold on preference strength; it determines when the accumulation process should stop. The higher the threshold, the longer it takes to make a choice. The fourth parameter, z, is the initial preference level before the accumulation process starts; it can be viewed as a measure of bias towards a specific option. The binary choice probability of a specific option given the values on d, σ, θ, and z is (Ratcliff, 1978; Busemeyer & Diederich, 2009),

$$\mathrm{Pr}(\mathrm{d},\sigma ,\theta ,\mathrm{z})=(1-\exp (-2\mathrm{d}(\theta +\mathrm{z})∕{\sigma }^2)∕(1-\exp (-4\mathrm{d}\theta ∕{\sigma }^2)).$$ (9)

The last parameter, T_er, represents the amount of time associated with non-decisional components in a specific task, and it is required for fitting response time data. See Ratcliff (1978) and Busemeyer and Diederich (2009) for the formula of probability density function of decision time.

Probabilistic Models of Intertemporal Choice

We have hitherto reviewed two alternative-wise models of intertemporal choice (i.e., the DU and hyperbolic discounting models), two attribute-wise models of intertemporal choice (i.e., the PD model and tradeoff model), three common classes of probabilistic but static choice models (i.e., random utility models, the Fechner models, and constant error models), and a prominent probabilistic and dynamic approach to choice behavior (i.e., diffusion models). With these resources, we could generate a variety of probabilistic models that might reflect the affective and cognitive processes underlying explicit intertemporal choices. We considered these classes of models for intertemporal choice since they are either a source of new perspective on intertemporal choice, such as the PD model and tradeoff model, or widely employed in risky choice research, such as the random utility models. Following is a summary of all the models we explored in the three studies reported below. Most of the models could be categorized in terms of how they transform objective value and time into subjective ones, their core theories, and their stochastic specifications. See Appendix A for a comprehensive summary table of all the models reported in this article.

Transformations of Objective Value and Time

It is widely recognized that the subjective value or utility of a monetary payoff is not identical to its objective value or amount. Consequently, researchers have examined various forms of utility function that connects objective and subjective values (e.g., Stott, 2006). Among them, the power utility function might be the most popular substitute for an identity utility function (e.g., Kahneman & Tversky, 1979; Tversky & Kahneman, 1992). By contrast, the nonlinear relationship between objective and subjective times was not well incorporated into intertemporal choice models until recently (e.g., Takahashi, Oono, & Radford, 2008; Zauberman, Kim, Malkoc, & Bettman, 2009). To emphasize the important difference between objective and subjective times, we proposed a time transformation function p(t) to convert objective times into subjective ones. We used this transformation function to replace the t variable in traditional models to reflect the impact of the difference on intertemporal preferences. For all the models examined in this article, we used either identity transformation functions (i.e., u(v) = v and p(t) = t) or power transformation functions (i.e., u(v) = v^α and p(t) = t^β) on both money and delay attributes.⁵

Core Theories

The deterministic special case of a probabilistic model is called its core theory (Loomes & Sudgen, 1995). In the reported studies, we explored four distinct core theories involving different comparison modes. On the one hand, we incorporated the time transformation function into the DU and hyperbolic discounting models to generate two alternative-wise core theories. Specifically, we rewrote Equation 1 as

$$\mathrm{d}={\mathrm{DU}}_{\mathrm{LL}}-{\mathrm{DU}}_{\mathrm{SS}}=\mathrm{u}\left({\mathrm{v}}_1\right)\cdot \exp (-\mathrm{kp}({\mathrm{t}}_1\left)\right)-\mathrm{u}\left({\mathrm{v}}_{\mathrm{s}}\right)\cdot \exp (-\mathrm{kp}({\mathrm{t}}_{\mathrm{s}}\left)\right)$$ (10)

and rewrote Equation 2 as

$$\mathrm{d}={\mathrm{DU}}_{\mathrm{LL}}-{\mathrm{DU}}_{\mathrm{SS}}=\mathrm{u}\left({\mathrm{v}}_1\right)∕(1+\mathrm{kp}({\mathrm{t}}_1\left)\right)-\mathrm{u}\left({\mathrm{v}}_{\mathrm{s}}\right)∕(1+\mathrm{kp}({\mathrm{t}}_{\mathrm{s}}\left)\right)$$ (11)

to create deterministic models on intertemporal choice. We will hereafter call these two models generalized discounted utility model and generalized hyperbolic discounting model respectively. Note that both the DU model (see Equation 1) and hyperbolic discounting model (see Equation 2) assume virtually an identity time transformation function. When power transformation functions are used, Equation 11 actually leads to a generalization of Rachlin’s (2006) two-parameter hyperbola model.

On the other hand, we proposed two attribute-wise core theories on intertemporal choice inspired by the tradeoff model and PD model. According to these core theories, people make an intertemporal decision by choosing the option with a positive overall evaluation measured as a weighted average of its advantage and disadvantage. We further assumed that the advantage/disadvantage of an option can be calibrated in either a direct way as in the tradeoff model or a relative way as in the PD model. Let w denote the weight on the money attribute and (1−w) the weight on the delay attribute. For the aforementioned pair of SS and LL options, we defined the overall evaluation of the LL option as

$$\mathrm{d}=\mathrm{w}\cdot \left(\mathrm{u}\right({\mathrm{v}}_1)-\mathrm{u}({\mathrm{v}}_{\mathrm{s}}\left)\right)-(1-\mathrm{w})\cdot \left(\mathrm{p}\right({\mathrm{t}}_1)-\mathrm{p}({\mathrm{t}}_{\mathrm{s}}\left)\right)$$ (12)

when considering direct differences, and

$$\mathrm{d}=\mathrm{w}\cdot \left(\mathrm{u}\right({\mathrm{v}}_1)-\mathrm{u}({\mathrm{v}}_{\mathrm{s}}\left)\right)∕\mathrm{u}\left({\mathrm{v}}_{\mathrm{s}}\right)-(1-\mathrm{w})\cdot \left(\mathrm{p}\right({\mathrm{t}}_1)-\mathrm{p}({\mathrm{t}}_{\mathrm{s}}\left)\right)∕\mathrm{p}\left({\mathrm{t}}_{\mathrm{s}}\right)$$ (13)

when considering relative differences. From a cognitive perspective, we can interpret the parameter w as the amount of attention allocated to the money attribute, and 1−w the corresponding amount to the delay attribute. We will hereafter call any model based on Equation 12 a weighted additive difference model with direct differences and any model based on Equation 13 a weighted additive difference model with relative differences. Equation 13 differs from the PD model in that the smaller rather than larger values on both attributes are used on the denominators to derive relative differences. We made this change because people tend to use the SS option as a reference point in intertemporal choice (Weber et al., 2007) and thus it seems more appropriate to use the smaller values as normalizers.⁶

Stochastic Specifications

We applied seven different stochastic choice functions to each core theory discussed above to generate probabilistic models. Among them, five specifications resulted in static models and the other two produced dynamic diffusion models.

Constant error models

The first class of static stochastic models we explored in the studies was constant error models. We examined this class of models to check whether trembling hand or other random errors was the major reason for probabilistic choices shown in the empirical studies reported below.

Logistic models

The second stochastic choice function came from the logistic model, i.e., Equation 5. Specifically, the parameter d was calculated from Equations 10-13 and the parameter g was freely estimated.

Probit models with fixed σ

The third stochastic choice function came from Thurstone’s Case V model (i.e., Equation 7). Specifically, to determine the choice probability of the LL option, we put the d values calculated from Equations 10-13 into Equation 7 and assumed that the parameter σ in Equation 7 was unrelated to attribute values and thus freely estimated.

Probit models with varied σ

The fourth stochastic specification also used Equation 7 as its choice function but involved a different assumption on the parameter σ. For alternative-wise models explored in this article, we assumed that the longer a payoff is delayed, the more uncertain its (random) utility will be. This is consistent with the intuition that the utility of a delayed payoff is harder to evaluate than that of an immediate payoff. Mathematically, we set

$$\sigma =\sqrt{c\cdot \left(p\right(t_s)+p(t_l\left)\right)}$$ (14)

to reflect this property; the parameter c was a proportional constant to be freely estimated.

For attribute-wise models (i.e., weighted additive difference models), we assumed that the probability of sampling from or attending to a specific attribute at any time equals the corresponding attention weight. This sampling process produces variability from which one can derive a standard deviation equal to

$$\sigma =\sqrt{w\cdot {\left(u\right(v_l)-u(v_s\left)\right)}^2+(1-w)\cdot {\left(p\right(t_s)-p(t_l\left)\right)}^2-d^2}$$ (15)

for models with direct differences, and

$$\sigma =\sqrt{w\cdot {\left[\right(u\left(v_l\right)-u\left(v_s\right))∕u(v_s\left)\right]}^2+(1-w)\cdot {\left[\right(p\left(t_l\right)-p\left(t_s\right))∕p(t_s\left)\right]}^2-d^2}$$ (16)

for models with relative differences. With Equations 10 - 16, we could again put relevant quantities into Equation 7 to calculate the choice probability of the LL option.

Random preference models

The last static specification we explored in the studies led to a special class of random preference models. We assumed that the discounting parameters in Equations 10 and 11 and the attention weight parameters in Equations 12 and 13 are random rather than fixed variables. We could interpret this class of models as if a person’s discount rate or amounts of attention on money and delay attributes vary from trial to trial. With appropriate distributional assumptions on discounting and attention weight parameters (see Appendix B for details) as well as Equations 10-13, we could calculate the choice probability of the LL option for each pair of intertemporal options.

Diffusion models

We derived the last two stochastic specifications from diffusion models and used Equation 9 as the choice probability function. Since these classes of models also provided an explicit account of the response time associated with a specific choice, we could also fit them to the choice and response time data simultaneously. Specifically, the d parameter in Equation 9 was calculated from Equations 10-13; the z parameter was fixed at zero to generate simplified unbiased models;⁷ and the θ parameter was set to be proportional to σ. The rationale for the last setting was that the more uncertain the instantaneous amount of evidence produced by the two options is (i.e., the larger σ is), the higher the preference threshold should be to guarantee a reasonably high choice probability of the option with a positive d, i.e., the option chosen by the core theory. Consequently, the proportional constant θ* (=θ/σ) was the actual free parameter to estimate. Conceptually, we can interpret the attribute-wise diffusion models as if a decision maker samples as evidence the difference in either money or delay attribute at a time and switches between these two dimensions to accumulate evidence until an evidence or preference threshold is reached to trigger an explicit choice. A similar interpretation can be applied to the alternative-wise diffusion models. The two stochastic specifications differed in their treatment of the σ parameter. In the simpler case σ was a freely estimated parameter, while in the more complicated case σ was calculated as in the Probit models with varied σ (i.e., Equations 14 - 16). Finally, T_er was treated as a free parameter when response time was of concern. Note that the attribute-wise diffusion models with varied σ were actually derived from DFT which assumes a mechanism of attention shift between attributes in addition to a sequential sampling approach as in diffusion models.

Summary of Goals for the Current Article

The current article is intended to fulfill three major goals. The first is to determine whether or not people’s intertemporal choices are essentially probabilistic, like their risky choices. The second is to determine whether an attribute-wise as opposed to alternative-wise choice model can better account for the probabilistic nature of intertemporal choice and the relevant effects. The third is to compare various attribute-wise diffusion models using both choice and response time data simultaneously to obtain more support for the winning model. To our best knowledge, this is the first time that response time in intertemporal choice tasks has been seriously examined and modeled.

General Method

Overview

We conducted a sequence of three experiments to demonstrate the probabilistic nature of intertemporal choice and test various models. A broad range of intertemporal choice pairs were used in these experiments so that the delay duration effect, the common difference effect, and the magnitude effect could be revealed in a probabilistic manner. That is to say, the observed choice proportion of the LL options (or, equivalently, the SS options) would change gradually while attribute values varied as required by those effects.

Stimuli

Because previous research on delay discounting revealed substantial individual differences in discount rate, it was necessary to generate different intertemporal choice pairs for each participant so that actual choice proportions would cover a wide range. Therefore, for each participant, we used an adjustment procedure to generate three pairs of approximately indifferent options, one for each of the aforementioned intertemporal effects. Here by approximately indifferent we mean that the two options in each pair have about the same choice probability, instead of suggesting that preferences are deterministic.

Based on the approximately indifferent pair for each effect, we then created a large number of formal questions whose attribute values were systematically varied to meet the condition of the effect. Specifically, for formal questions associated with the delay duration effect, the longer delays were always three times (in Experiment 1) or twice (in Experiments 2 and 3) as long as the shorter delays, and the shorter delays were varied between 1 to 40 days to trigger the delay duration effect. On the other hand, the reward amounts in these questions were quite similar to (in Experiments 1 and 2) or exactly the same as (in Experiment 3) those in the approximately indifferent pair. We used similar manipulations to generate formal questions for the common difference effect and magnitude effect as well. Specifically, for formal questions associated with the common difference effect, we systematically varied the delay durations while keeping a constant interval between shorter and longer delays across questions. For the magnitude effect, we systematically varied the reward amounts while keeping a constant ratio between the smaller and larger rewards across questions. On the other hand, the reward amounts for questions associated with the common difference effect and the delay durations for questions associated with the magnitude effect were quite similar to (in Experiments 1 and 2) or exactly the same as (in Experiment 3) those in the approximate indifferent pairs. See Table 1 for a sample of formal questions a typical participant answered in the first session of Experiment 1 and Appendix C for more details of the question generation procedure. The three approximately indifferent pairs for this typical participant were ($18, 20 days) versus ($36, 60 days) for the delay duration effect, ($17, 20 days) versus ($32, 60 days) for the common difference effect, and ($20, 8 days) versus ($40, 47 days) for the magnitude effect. We will describe the grouping method later on in the data analysis section.

Table 1. Sample Formal Questions for a Typical Participant in the First Session of Experiment 1.

Effect	Group	Smaller reward(dollars)	Shorter delay(days)	Larger reward(dollars)	Longer delay(days)
Delay duration	1	17	2	35	6
	1	17	2	36	6
	1	18	2	35	6
	1	18	2	36	6
	10	17	37	35	111
	10	17	37	36	111
	10	18	37	35	111
	10	18	37	36	111
Common difference	1	16	1	31	41
	1	16	1	32	41
	1	17	1	31	41
	1	17	1	32	41
	10	16	36	31	76
	10	16	36	32	76
	10	17	36	31	76
	10	17	36	32	76
Magnitude	1	2	7	4	46
	1	2	7	4	47
	1	2	8	4	46
	1	2	8	4	47
	10	37	7	74	46
	10	37	7	74	47
	10	37	8	74	46
	10	37	8	74	47

Participants

Participants were volunteers recruited at a public research university via advertisement on notice boards. For each participant, one intertemporal choice pair was randomly picked from his/her question set and the person was paid according to his/her choice in that question in addition to a small base payment. The date of payment was determined by the delay duration of the option each participant chose in the randomly selected question. For example, if a participant chose an option with a delay duration of 20 days, then he/she would get the payment 20 days after finishing the whole study. Specifically, the participant was given a receipt with the amount of payment and time delay right after completing the study and would stop by the psychology building in 20 days to get real money. See Appendix D for the instructions for participants concerning the payment schedule.

Procedure

Each experiment consisted of a practice section, an adjustment procedure and subsequent formal session(s). The experimental setting was realized by a set of programs in MATLAB together with the Cogent toolbox to record both choice responses and response times. The practice section was provided at the beginning of each experiment for participants to get familiar with the intertemporal choice task, followed by the adjustment procedure generating approximately indifferent pairs. Participants indicated their choices by clicking a mouse button on the same side as the selected options. Questions in the formal session(s) were presented in a random order. To minimize the fatigue effect, major and contingent short breaks were inserted into each experiment. Participants were instructed to take into account all pieces of information involved in each question and think them over before making a choice. They were also informed of the specific payment plan when they signed a consent form. Finally, equally-spaced filler questions with a dominated option, i.e., a smaller reward with a longer delay, were presented to detect inattention. A warning sign would pop up if participants chose the dominated option, asking for more attention and providing participants with an optional contingent break. See Figure 1 for screenshots of the experimental software used in the current research.

Figure 1.

Screenshots of the experimental software. The top panel shows the display in Experiments 1 and 2 and the bottom panel shows the display in Experiment 3. The SS options were always shown on the left and the LL options were always on the right in the first two experiments, while in Experiment 3 the positions of options were randomized across trials.

Data Analysis

Choice patterns for the questions related to various intertemporal effects

To demonstrate the probabilistic nature of intertemporal choice, we first investigated the choice patterns for questions associated with different intertemporal effects. For each participant and effect, we grouped relevant questions with the same values on the target attribute (i.e., delay duration for the delay duration and common difference effects and reward amount for the magnitude effect) together and ordered the groups accordingly. For example, question groups related to the delay duration effect were ordered so that the first group contained questions with the shortest delays, the last group consisted of questions with the longest delays (see Table 1), and intermittent groups contained questions with moderate delay durations. We then computed the choice proportion of the LL options in each group as an estimate of the corresponding choice probability.⁸ Under this circumstance, the probabilistic perspective on intertemporal choice would predict a gradual and monotonic change in choice proportion across the subsequent groups for a specific effect, but the deterministic perspective suggests that there would be only one moderate (between 0 and 1 exclusively) choice proportion across the groups (see Appendix E for proof concerning the delay duration effect as an example). For each participant and effect, we ran a logistic regression with target attribute value serving as the predictor and the choice proportion of LL options as dependent variable and counted the number of groups with moderate choice proportion. A significant slope in the logistic regression together with more than one moderate choice proportion would indicate a gradual and monotonic change in choice proportion.⁹ We also conducted an aggregate analysis for each effect using average results across participants.

Relationship between choice proportions and response times

One critical prediction of diffusion models is that extreme choice probabilities are associated with short response times. Empirically, this entails an inverse U-shaped relationship between the choice proportions of LL options and average response times within our question groups. Since we would explore a variety of diffusion models in these experiments, it was important to first test this prediction to provide evidence for using diffusion processes in these models. To show the existence of the inverse U-shaped relationship, we calculated the actual choice proportion of LL options and mean response time for each question group. The results from all participants and effects were then categorized into five equal-interval bins in terms of actual choice proportion. After that, we averaged the mean response times associated with extreme choice proportions (i.e. below 0.2 or above 0.8) and those associated with moderate choice proportions (i.e. between 0.2 and 0.8) for each participant to get two related measures and ran a related samples t test to compare the average response times associated with extreme and moderate choice proportions across participants. We also compared mean response times associated with extreme and moderate choice proportions at an individual level to show that the relationship was not an artifact of aggregation.

Model fitting and comparisons

For all the models explored in this research, maximum likelihood estimation was used to estimate the relevant parameters and a Bayesian information criterion (BIC) index was calculated as an index for model selection. Specifically, the log likelihood of the observed result predicted by a model using the exact money amounts and delay durations presented on each trial was summed across trials to produce the summed log likelihood, denoted as LogL. The SIMPLEX algorithm was employed (using the fminsearch function in Matlab) to find the maximum likelihood estimates of the parameters for each participant. See Appendix B for more details on the model fitting procedure. The models differed in number of parameters, and to account for this model complexity when comparing models, a BIC index was computed which introduces a penalty term for the number of parameters in a model. The BIC is defined by −2LogL + ln(N) · p, where p = number of parameters and N = total number of trials used to produce the sum in LogL. A lower BIC value suggests a better balance between goodness-of-fit and model complexity and thus a more desirable model (Schwarz, 1978).

We first fit all the models to individual choice data to compare static and dynamic models. For this purpose, only the choice probabilities were utilized in the model fitting procedure to obtain maximum likelihood estimates of parameters and calculate BIC values. After that, various diffusion models were fit to individual choice and response time data simultaneously to further compare the diffusion models against one another and explore their capability of fitting response times. Specifically, we utilized the joint probability densities of making the actual responses with the actual amounts of time to estimate parameters. Since both choice responses and response times were taken into account, more information from the data was exploited to find the best among the competing diffusion models. We used three criteria, i.e., overall BIC value, count of lowest BIC values across participants and result of pairwise comparisons (Broomell, Budescu, & Por, 2011) to choose the best model. The first criterion showed the performance of a model when fitting all individual data; the second denoted the number of participants whose data a model fit best; while the result of pairwise comparisons indicated which model was associated with a lower BIC value on more participants than any other model when only two models were compared each time.

Model predictions

Another way to evaluate the performance of a specific model in fitting empirical data is to compare its predictions with the actual data. Consequently, we compared the actual choice proportion of the LL options for each group of questions with the best model’s prediction on the mean choice probabilities of the LL options, and the actual average response time for each group of questions with the predicted average response time. For the latter, we used the mean of predicted response time distribution given the actual response as the point estimate for each response. We also showed that the best model could recreate the inverse U-shaped relationship between mean response times and choice proportions of the LL options within question groups. In all the aforementioned analyses, we pooled individual results together to obtain an aggregate evaluation of model performance. In addition, we calculated the correlations between actual and predicted values for each participant and reported the average results. Finally, we further tested the validity of the winning model by examining its prediction on the impact of experimental manipulation on choice proportions of the LL options across question groups for each effect at both individual and aggregate levels. If this model actually captures the essence of the underlying processes producing the explicit responses, its predictions should replicate the empirical choice patterns.

Experiment 1

Method

Ten participants (5 females and 5 males) with an average age of 27 were recruited for this experiment, which consisted of four subsequent sessions spaced one week apart for each participant. The base payment was 16 dollars and participants got the full amount of money they chose in the randomly picked question. They were always paid after the last session no matter whether the random question came from the last session or not. The average payment was 42 dollars and the average delay was 34 days. Formal questions in the four sessions were comparable to one another and each session contained 150 questions for each effect. In the first two sessions, participants were instructed to make careful choices, while in the last two sessions, they were instructed to make careful but quick responses. If their responses were too fast in any session or too slow in the last two sessions, a warning sign would pop up. The thresholds on acceptable response time were mainly determined from participants’ performance in the practice section and thus varied among participants. The lower threshold was typically above 3000ms in the first two sessions and fixed at 1500ms in the last two sessions. The upper threshold in the last two sessions was at least 3000ms. Individual data from each session were analyzed separately because of the varying time constraints.

Results

Choice patterns for the questions related to various intertemporal effects

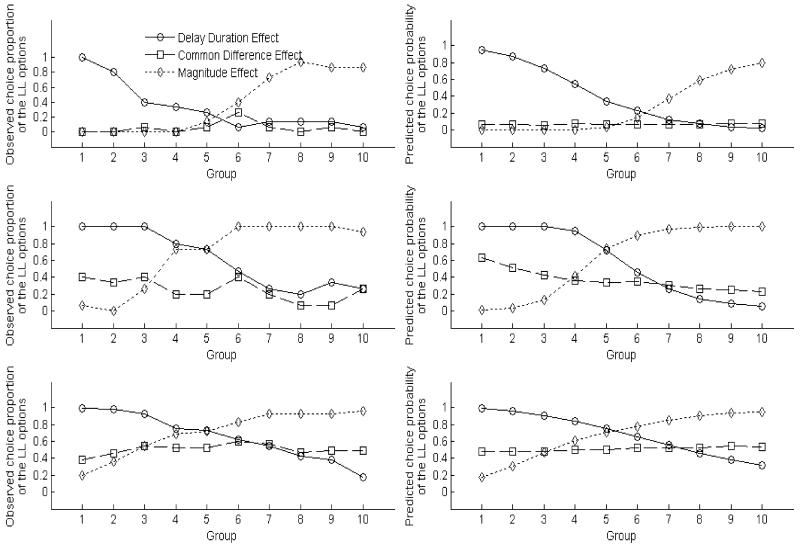
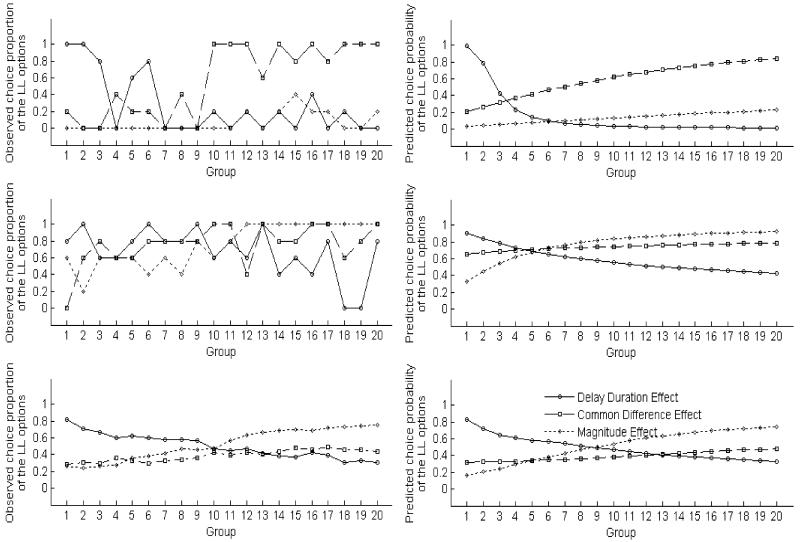
The left column of Figure 2 shows line graphs illustrating the choice patterns of two typical participants (top two panels) and the average results across participants (bottom panel) in Session 1. Each line in the panels is related to a specific intertemporal effect. Each session of this experiment contained 10 groups of questions for each participant and effect and there were 15 questions in each group. It is readily seen that in general, choice proportions did not show an abrupt change pattern suggested by a deterministic perspective (plus constant error). For example, the solid lines are associated with the delay duration effect and all of them decline gradually across groups. Recall that, for the delay duration effect, questions in the later groups had longer durations than those in the earlier ones. Therefore, the gradual change was consistent with a probabilistic interpretation of the delay duration effect. The same pattern of gradual change occurs to the dotted lines for the magnitude effect. However, the dashed lines for the common difference effect do not have a clear positive slope as suggested by that effect. Logistic regression analyses on the aggregate data also revealed a non-zero slope for groups associated with both the delay duration effect and the magnitude effect but not for those related to the common difference effect (for the delay duration effect, b = −.13, p < .01; for the magnitude effect, b = .13, p < .01; for the common difference effect, b = .006, p = .19). The choice patterns of other participants were similar to those of the typical ones shown in Figure 2, and results from other sessions were similar to those in the first one.

Figure 2.

Observed choice proportions and predicted average choice probabilities of the LL options for various intertemporal effects in the first session of Experiment 1. The left column shows the results of two typical participants (top two panels) and the average results across participants (bottom panel) in Session 1; the right column shows the corresponding predictions of the best model in Experiment 1.

Analyses on individual data revealed that, for the questions associated with the delay duration effect, all the participants exhibited a pattern of gradual monotonic change in choice proportion in at least one session and 4 participants exhibited the pattern in all sessions. Likewise, for the questions regarding the magnitude effect, 8 out of the 10 participants exhibited a pattern of gradual monotonic change in choice proportion in at least one session and 3 participants exhibited the pattern in all sessions. By contrast, only 3 participants showed a gradual monotonic change pattern in choice proportion for the questions associated with the common difference effect in at least one session and none of them showed the pattern in all sessions. In conclusion, observed choice proportions typically changed in a progressive manner in favor of a probabilistic perspective on intertemporal choice. Furthermore, the delay duration effect and magnitude effect were demonstrated in a probabilistic rather than deterministic way. The gradual change pattern was also corroborated by the fact that the constant error models turned out to fit the data very poorly for this study since they predicted an abrupt change in choice probability. We will see relevant evidence in the later section on model fitting and comparisons.

Relationship between choice proportions and response times

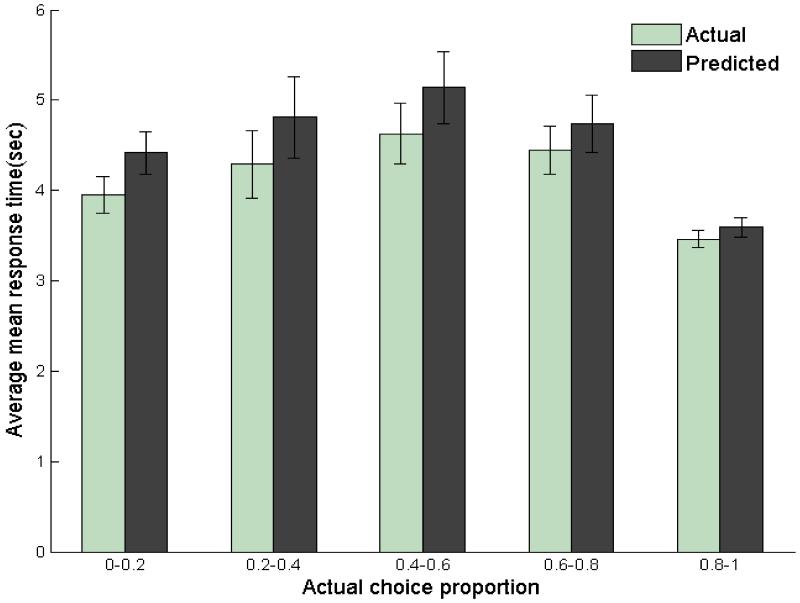
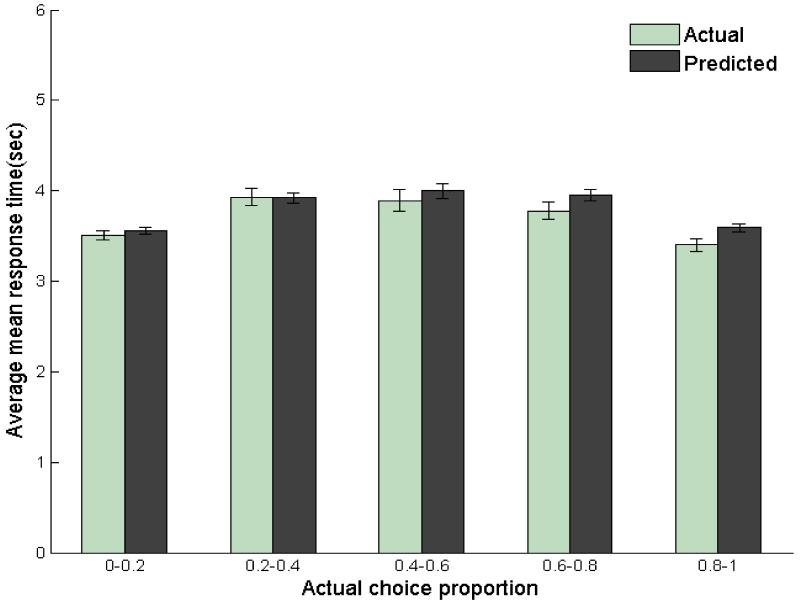
Figure 3 shows the average actual mean response times for question groups with different actual choice proportions of the LL options. Clearly the mean response times associated with extreme choice proportions (i.e. below 0.2 or above 0.8) tended to be shorter than those associated with moderate choice proportions (i.e. between 0.2 and 0.8). The difference in mean response time between groups with extreme and moderate choice proportions was significant (M_extreme = 3.56 seconds, M_moderate = 4.40 seconds, t[9] = −3.51, p < .01). Analyses on individual data also revealed the same pattern for 9 out of the 10 participants. We will discuss the average predicted mean response times later.

Figure 3.

Average mean response times for question groups with different actual choice proportions of the LL options in Experiment 1. Questions within each group had the same values on the target attribute of a specific intertemporal effect. Error bars show 95% confidence intervals.

Model fitting and comparisons

The overall BIC value of the best constant error model was 11721 and it did not produce the lowest BIC value for any participant in any session. Table 2 shows the three best models in terms of overall BIC value across participants and sessions when fitting choice data and Table 3 shows the corresponding result when considering count of lowest BIC values. Clearly the attribute-wise diffusion model with direct differences, power transformations of objective value and time, and varied σ performed the best in terms of both criteria. The result of pairwise comparisons also suggested that the above model was the best. In comparison, the performance of constant error models was quite poor.¹⁰

Table 2. The Three Best Models for Choice Data in Experiment 1 in Terms of Overall BIC Value across Participants and Sessions.

No.	Transformations of objective value and time	Core theory	Stochastic specification	No. free parameters	Overall BIC value
1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	4	9360
2	Power	Attribute-wise with direct differences	Logistic model	4	9439
3	Power	Attribute-wise with direct differences	Probit model with fixed σ	4	9593

Table 3. The Three Best Models for Choice Data in Experiment 1 in Terms of Count of Lowest BIC Values across Participants and Sessions.

No.	Transformations of objective value and time	Core theory	Stochastic specification	No. free parameters	Count of lowest BIC values
1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	4	7
2	Power	Attribute-wise with direct differences	Probit model with fixed σ	4	5
3	Power	Alternative-wise with exponential discount function	Logistic model	4	4

Since attribute-wise models performed the best in fitting choice data, we further fit attribute-wise diffusion models to choice and response time data simultaneously to check their capability of accounting for both pieces of information. Tables 4 and 5 list the resultant best models in terms of overall BIC value and count of lowest BIC values respectively. The attribute-wise diffusion model with direct differences, power transformations of objective value and time, and varied σ again performed the best, and pairwise comparisons led to the same result.

Table 4. The Three Best Attribute-wise Models for Both Choice and Response Time Data in Experiment 1 in Terms of Overall BIC Value across Participants and Sessions.

No.	Transformatio ns of objective value and time	Core theory	Stochastic specification	No. free parameters	Overall BIC value
1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	5	57344
2	Power	Attribute-wise with direct differences	Diffusion model with fixed σ	6	57717
3	Identity	Attribute-wise with direct differences	Diffusion model with fixed σ	4	59324

Table 5. The Three Best Attribute-wise Models for Both Choice and Response Time Data in Experiment 1 in Terms of Count of Lowest BIC Values across Participants and Sessions.

No.	Transformations of objective value and time	Core theory	Stochastic specification	No. free parameters	Count of lowest BIC values
1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	5	23
2	Power	Attribute-wise with direct differences	Diffusion model with fixed σ	6	12
3	Identity	Attribute-wise with direct differences	Diffusion model with fixed σ	4	5

Model predictions

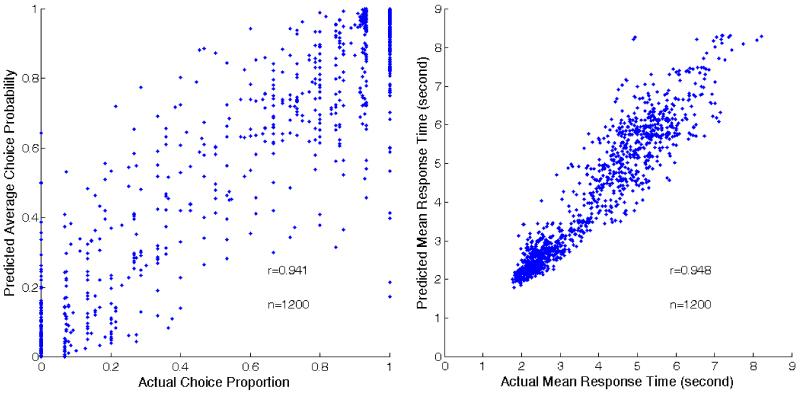
Figure 4 shows the predictions of the best model in Experiment 1 against the actual data across sessions, participants, and effects. The left panel shows the scatterplot of the predicted choice probabilities of LL options and the actual choice proportions. Each point in the scatterplot is the average associated with a group of questions with the same values on the target attribute for a specific intertemporal effect answered by an individual participant in a single session. Clearly, there was a strong correlation between the predicted average choice probabilities and the actual choice proportions for pooled data (r = .94, p < .001), with an average correlation coefficient across participants of .92.¹¹ In other words, we could use the winning model to make reasonably good predictions on the actual choice proportions. Similar results occurred when we compared the predictions on response time with the actual data. The right panel in Figure 4 shows the scatterplot of the predictions of the best model on mean response times and the actual mean response times within question groups. It is readily seen that the predictions of the model match the actual data quite well when data were pooled (r = .95, p < .001), with an average correlation coefficient across participants of .94.¹² Figure 3 also shows the average mean response times predicted by the best model for different actual choice proportions of the LL options within question groups. Clearly the same inverse U-shaped curve was reproduced by the best model.

Figure 4.

Predictions of the best model in Experiment 1. The left panel shows a scatterplot of the actual choice proportions and the predicted average choice probabilities of LL options within question groups; the right panel shows a scatterplot of the actual mean response times and predicted mean response times within question groups. Each point in the scatterplots is associated with a group of questions with the same values on the target attribute for a specific intertemporal effect answered by an individual participant in a single session.

To further test the validity of the winning model, we also examined its predictions on the impact of experimental manipulation on actual choice proportions. The right panels in Figure 2 show the corresponding predictions of the best model on the mean choice probabilities of the LL options within groups of questions for the two typical participants and the average results across participants in Session 1. It is readily seen that both individual and average predictions replicated the actual change patterns reasonably well.

Discussion

The results indicate that intertemporal choice is probabilistic in nature and that these choices require variable amounts of decision time just like risky choices do. More importantly, the choice pattern for the questions concerning the delay duration effect appeared to be beyond the means of any popular account of this topic and thus constituted a severe challenge to the deterministic perspective. According to the delay duration effect, when the ratio of delay durations is fixed as in the current experimental setting (see Table 1 for sample questions), the longer the delays are, the less preferable the LL option will be. If we assume further a deterministic perspective on intertemporal choice, there should be a single cutoff point on the shorter delay (or equivalently on the longer delay) where people become indifferent between the two options. Such a perspective also stipulates that when the shorter delay duration is below the cutoff point, people will choose the LL option for sure, and vice versa. In other words, the choice probability of the LL options should change abruptly from one to zero across the cutoff point. This is actually a typical pattern predicted by a deterministic view. Furthermore, such a pattern is consistent with both the exponential and hyperbolic discount functions as long as a deterministic approach is assumed, and it remains true even when we consider the magnitude effect (see Appendix E for mathematical proofs of these properties). When questions with the same delay durations are combined into subsequent groups, the deterministic approach suggests that only one group might have an actual choice proportion that is between 0 and 1 exclusively, and the actual proportions should jump from one to some proportion for a single group and then to zero. However, a majority of participants in Experiment 1 demonstrated a gradual rather than abrupt shift in choice proportion for the questions related to the delay duration effect. The data formed a strong piece of evidence against the deterministic assumption of intertemporal choice. Furthermore, the poor performance of constant error models excluded trembling hand or other random errors as the major reason for the probabilistic choice patterns shown in the experiment.

To incorporate the probabilistic property of intertemporal choice, we developed and tested a variety of probabilistic models on individual data. It turned out that the best model for choice data had a dynamic rather than static structure. This should not be surprising since the relationship between choice proportions and response times followed the prediction of diffusion process that extreme choice proportions are associated with quicker responses. When response time was of concern, the superiority of dynamic models became even more prominent since static models were silent on this issue.

Another finding was that in general the diffusion models based on direct differences in money amount and delay duration performed better than the diffusion models built upon relative differences, exponential discount function, or hyperbolic discount function. This suggested that people think in an attribute-wise manner and consider the simple difference in each attribute when making an intertemporal choice. Consequently, the winning model could be viewed as a probabilistic generalization of the tradeoff model proposed by Scholten and Read (2010).

Although this experiment revealed the probabilistic nature of intertemporal choice and provided a platform on which we could explore various models, it had several drawbacks which might weaken the validity of the results. First, the sample size of this experiment, i.e., 10, was relatively small compared to other studies on intertemporal choice. Second, the participants had to finish four sessions in total which were quite similar in structure and stimuli. Although successive sessions were administrated one week apart, it was possible that participants had a subtle memory of what happened in previous sessions or gradually formulated fixed strategies in later sessions. Both possibilities constitute a violation of the assumption of independence between responses, which is required for the model fitting procedure across sessions. In fact, the responses of most participants became more extreme in later sessions after they had more experience with the stimuli. Finally, the time constraints involved in the first two sessions seemed to be inappropriate in the sense that most participants had to postpone their responses in some trials to avoid the warning sign. Consequently, we refined the experimental design in the following study to resolve these issues.

Experiment 2

Method

Forty-six participants (29 females and 17 males) with an average age of 23 were recruited for this experiment, which involved only a single session. The adjustment procedure generated irregular approximately indifferent pair(s) of intertemporal options (i.e., with one option dominating the other) for nine of the participants and thus their data were analyzed separately. Among the remaining 37 participants, there were 25 women and 12 men, with an average age of about 21. Each participant was paid one-fourth of the money he/she chose in the randomly selected question in addition to a base payment of 4 dollars after the single session. The average payment was about 11 dollars and the average delay was about 39 days. There were 480 formal questions in this experiment, 160 for each effect. The ranges of attribute values in the formal questions of Experiment 2 were almost identical to those in Experiment 1. Participants were required to make careful responses and a warning sign would pop up if they responded too fast. The lower threshold on response time was set at 1500ms, which was more lenient than that in Experiment 1.

Results and Discussion

The results reported here were mainly from the 37 participants who answered intertemporal questions without a dominating option in the formal session. At the end of this section, the results from the nine participants who answered irregular questions will be briefly discussed.

Choice patterns for the questions related to various intertemporal effects

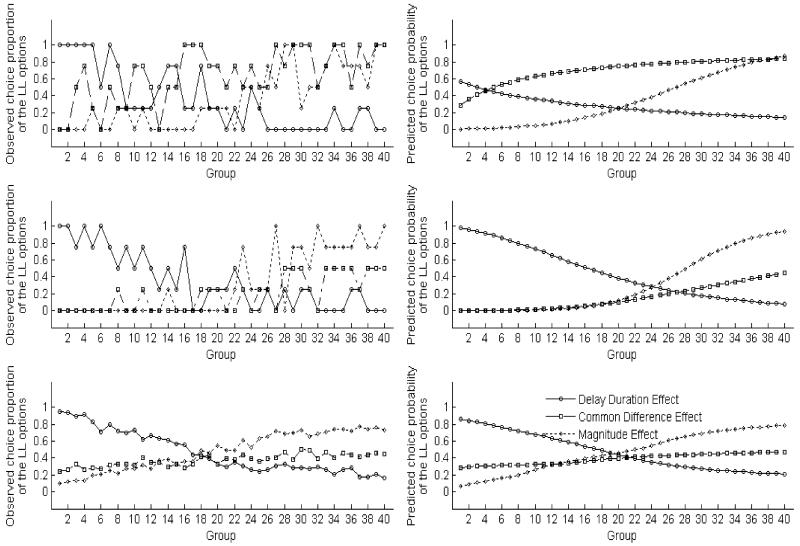
The left column of Figure 5 shows line graphs illustrating the choice patterns of two typical participants and the average results across participants in Experiment 2. In this experiment, there were 40 groups of questions for each participant and effect, 4 questions in each group. It is readily seen that, as in Experiment 1, choice proportions generally did not show an abrupt change pattern suggested by a deterministic perspective and the delay duration effect and magnitude effect occurred in a probabilistic manner. The only difference between Experiments 1 and 2 lay in the common difference effect. It can be seen from the left panels of Figure 5 that in this experiment the common difference effect appeared to be revealed at both individual and aggregate levels. Logistic regression analyses on the aggregate data also revealed a non-zero slope for groups associated with each of the three effects (for the delay discounting effect, b = −.09, p < .01; for the magnitude effect, b = .08, p < .01; for the common difference effect, b = .02, p < .01). The choice patterns of other participants were qualitatively similar to the typical ones shown in Figure 5. Analyses on individual data showed that 33, 30, and 13 out of the 37 participants exhibited a gradual monotonic change in choice proportion for the questions associated with the delay duration effect, the magnitude effect, and the common difference effect respectively. These findings again supported the probabilistic nature of intertemporal choice and these results were corroborated by the fact that the constant error models performed quite poorly in fitting these empirical data. We will see more evidence for the latter in the following section of model fitting and comparisons.

Figure 5.

Observed choice proportions and predicted average choice probabilities of the LL options for various intertemporal effects in Experiment 2. The left column shows the results of two typical participants (top two panels) and the average results across participants (bottom panel); the right column shows the corresponding predictions of the best model in Experiment 2.

Relationship between choice proportions and response times

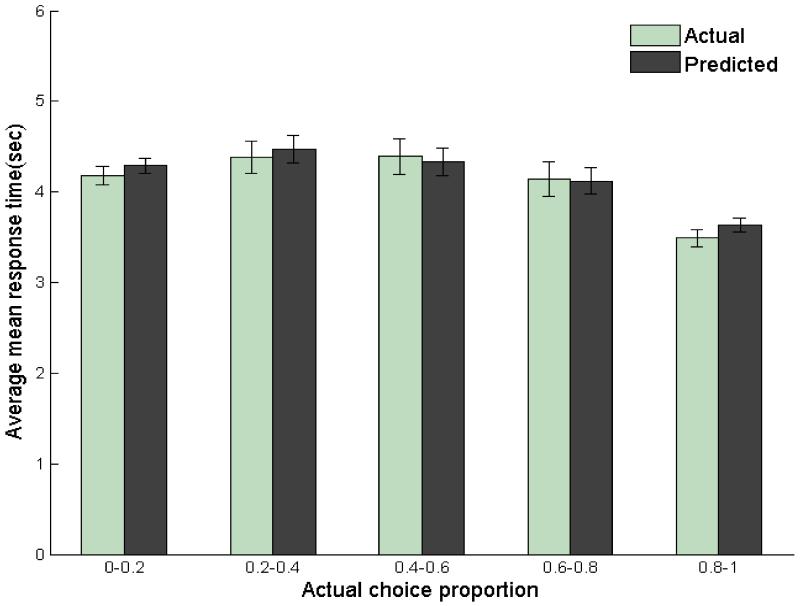
Figure 6 shows the average actual mean response times for question groups with different actual choice proportions of the LL options. As before, the mean response times associated with extreme choice proportions tended to be shorter than those associated with moderate choice proportions. The difference in mean response time between groups with extreme and moderate choice proportions was significant (M_extreme = 3.46 seconds, M_moderate = 3.90 seconds, t[36] = −7.14, p < .01). Analyses on individual data revealed the same pattern for 32 out of the 37 participants. We will discuss the average predicted mean response times later.

Figure 6.

Average mean response times for question groups with different actual choice proportions of the LL options in Experiment 2. Questions within each group had the same values on the target attribute of a specific intertemporal effect. Error bars show 95% confidence intervals.

Model fitting and comparisons

Constant error models again performed poorly when fitting choice data. The overall BIC value of the best constant error model was 14579 and it did not produce the lowest BIC value for any participant. The top half of Tables 6 and 7 list the three best models in terms of overall BIC value and count of lowest BIC values across participants when fitting only choice data in Experiments 2. It turned out that the attribute-wise diffusion model with direct differences, power transformations of objective value and time, and varied σ performed the best in terms of overall BIC value while the corresponding logistic model won in terms of count of lowest BIC values across participants. The result of pairwise comparisons also suggested that these two models were the best among all the models explored.

Table 6. The Three Best Models for Choice Data in Experiments 2 and 3 in Terms of Overall BIC Value across Participants.

Exp.	No.	Transformations of objective value and time	Core theory	Stochastic specification	No. free parameters	Overall BIC value
2	1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	4	12554
	2	Power	Attribute-wise with direct differences	Probit model with fixed σ	4	12557
	3	Power	Attribute-wise with direct differences	Logistic model	4	12599
3	1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	4	7028
	2	Power	Attribute-wise with direct differences	Probit model with fixed σ	4	7265
	3	Power	Attribute-wise with direct differences	Logistic model	4	7329

Table 7. The Three Best Models for Choice Data in Experiments 2 and 3 in Terms of Count of Lowest BIC Values across Participants.

Exp.	No.	Transformations of objective value and time	Core theory	Stochastic specification	No. free parameters	Count of lowest BIC values
2	1	Power	Attribute-wise with direct differences	Logistic model	4	10
	2	Power	Attribute-wise with direct differences	Diffusion model with varied σ	4	6
	3	Power	Attribute-wise with direct differences	Random preference model	4	3
3	1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	4	7
	2	Identity	Attribute-wise with direct differences	Probit model with varied σ	3	5
	3	Power	Attribute-wise with direct differences	Logistic model	4	3

As before, we also fit the attribute-wise diffusion models to choice and response time data simultaneously. The top half of Tables 8 and 9 list the resultant three best models in terms of overall BIC value and count of lowest BIC values across participants in Experiment 2. Clearly, the diffusion model with direct differences, power transformations of objective value and time, and fixed σ performed the best in this case. Pairwise comparisons also revealed the same result. Given its similarity to one of the best models when fitting choice data and its advantage in fitting both choice and response time data simultaneously, it seems appropriate to pick the diffusion model with fixed σ as the winning model in Experiment 2.

Table 8. The Three Best Attribute-wise Models for Both Choice and Response Time Data in Experiments 2 and 3 in Terms of Overall BIC Value across Participants.

Exp.	No.	Transformations of objective value and time	Core theory	Stochastic specification	No. free parameters	Overall BIC value
2	1	Power	Attribute-wise with direct differences	Diffusion model with fixed σ	6	68169
	2	Power	Attribute-wise with direct differences	Diffusion model with varied σ	5	68511
	3	Identity	Attribute-wise with direct differences	Diffusion model with fixed σ	4	70161
3	1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	5	42704
	2	Power	Attribute-wise with direct differences	Diffusion model with fixed σ	6	43292
	3	Power	Attribute-wise with relative differences	Diffusion model with varied σ	5	44172

Table 9. The Three Best Attribute-wise Models for Both Choice and Response Time Data in Experiments 2 and 3 in Terms of Count of Lowest BIC values across Participants.

Exp.	No.	Transformations of objective value and time	Core theory	Stochastic specification	No. free parameters	Count of lowest BIC values
2	1	Power	Attribute-wise with direct differences	Diffusion model with fixed σ	6	15
	2	Power	Attribute-wise with direct differences	Diffusion model with varied σ	5	12
	3	Power	Attribute-wise with relative differences	Diffusion model with varied σ	5	4
3	1	Power	Attribute-wise with direct differences	Diffusion model with varied σ	5	14
	2	Power	Attribute-wise with direct differences	Diffusion model with fixed σ	6	9
	3	Identity	Attribute-wise with direct differences	Diffusion model with varied σ	4	4

Model predictions

As in Experiment 1, we calculated the correlation coefficient between actual choice proportions of the LL options within question groups and the corresponding average choice probabilities predicted by the best model in Experiment 2, as well as the correlation coefficient between actual mean response times and predicted mean response times within question groups. It turned out that for aggregate data, there was a strong correlation between the actual choice proportions and predicted average choice probabilities (r = .88, p < .001), and a moderate correlation between the actual mean response times and predicted mean response times (r = .55, p < .001). Since each group contained only 4 questions in this experiment, the relatively lower correlation coefficients were not unexpected. When we raised the number of questions in each group to 16, the correlation coefficients for pooled data increased to 0.95 and 0.75 respectively. The corresponding average correlation coefficients across participants were .79 and .24 for a group size of 4 and .87 and .39 for a group size of 16. Figure 6 also shows the average mean response times predicted by the best model for different actual choice proportions of the LL options within question groups. Clearly the same inverse U-shaped curve was reproduced by the best model. Finally, the right panels in Figure 5 show the predictions of the best model on the impact of experimental manipulation on actual choice proportions. Obviously the predicted results reproduced the general change patterns in actual data reasonably well at both individual and aggregate levels.

The relatively low correlation coefficients for response time data may appear worrisome. One possible reason for this result was that, for either option in a question, the best model predicted a distribution of response time rather than a single value. This might produce a large amount of prediction error when we compared a point estimate from the predicted distribution with the actual response time even if the best model was actually the true model. The negative impact of the resultant noise on correlation coefficient got more severe when there were fewer data points as in individual data or each data point was associated with fewer questions as in this and next studies. By contrast, when the number of data points and the number of questions associated with each data point in individual data were relatively large as in Study 1, we could still use the best model to obtain quite high correlation coefficients for both choice and response time data at an individual level.

Overall, we replicated the results of Experiment 1 with a refined experimental design in this study. One new finding in Experiment 2 was that the common difference effect also occurred in a probabilistic way, which was obscured in Experiment 1 perhaps due to the small sample size. Another possible reason for the weak demonstration of the common difference effect was that the range of delays explored in the current studies might severely abate the effect. Previous research on the common difference effect has typically involved delays that differed by at least 1 year when studying human participants. To make the real payment more credible to participants, we intentionally limited the range of delay durations so that they could be fulfilled within 6 months. Under this circumstance, the common difference effect might be too weak to bring about a statistically significant result. It will be helpful to widen the range of delay durations in future studies to demonstrate the common difference effect probabilistically.

Results of participants answering irregular questions

For the nine participants whose approximately indifferent pair(s) contained a dominated option (e.g., the reward amounts were the same but one option had a shorter delay), the formal pairs generated from the approximately indifferent pair(s) would also contain a dominated option. Consequently, participants tended to choose the dominating options most of the time, leading to quite extreme choice proportions. It turned out that the data of these nine participants in general demonstrated the same change patterns as those of the other participants. When various models were fit to the data, attribute-wise diffusion models with direct differences and power transformations of objective value and time again performed better than the other models.

Experiment 3

This experiment differed from the previous two in four important aspects. First, reward amount and delay duration of each option were shown on the same row and next to each other to eliminate potential bias towards an attribute-wise decision strategy (see Figure 1). Second, we employed a more concise display of formal questions by removing the instructions for careful choice (see Figure 1). Third, each group of formal questions consisted of five identical pairs of options rather than similar questions with the same values on the target attribute. In this condition, different choices in each group would provide a stronger support for the probabilistic property of intertemporal choice and a gradual monotonic change in choice proportion across individual groups associated with the delay duration effect would exclude the possibility of a reasonable deterministic account on intertemporal choice. Finally, we randomized the positions of the SS and LL options across trials to prevent participants from clicking the same mouse button continuously.

Method

Thirty-seven participants (26 females and 11 males) with an average age of 21 were recruited for this experiment, which involved a single session and had the same payment schedule and instructions as Experiment 2. There were 300 formal questions, 100 for each effect, and the ranges of attribute values were almost the same as those in Experiment 2. The average payment was about 12 dollars and the average delay was about 35 days.

Results and Discussion

Choice patterns for the questions related to various intertemporal effects

The left column of Figure 7 shows line graphs illustrating the choice patterns of two typical participants and the average results across participants in Experiment 3. In this experiment, there were 20 groups of questions for each participant and effect. As in Experiments 1 and 2, choice proportions tended to change gradually as suggested by a probabilistic perspective. Furthermore, all three effects occurred again as revealed by logistic regression analyses on the aggregate data (for the delay discounting effect, b = −.05, p < .01; for the magnitude effect, b = .07, p < .01; for the common difference effect, b = .02, p < .01).

Figure 7.

Observed choice proportions and predicted average choice probabilities of the LL options for various intertemporal effects in Experiment 3. The left column shows the results of two typical participants (top two panels) and the average results across participants (bottom panel); the right column shows the corresponding predictions of the best model in Experiment 3.

Analyses on individual data revealed that 21, 26, and 9 out of the 37 participants exhibited a gradual monotonic change in choice proportion for the questions associated with the delay duration effect, the magnitude effect, and the common difference effect respectively. Finally, all participants switched between the SS and LL options in more than one question associated with a specific intertemporal effect and 32 participants switched between the SS and LL options in more than one question associated with the delay duration effect. All these findings again supported the probabilistic perspective on intertemporal choice and the gradual change pattern was again corroborated by the poor performance of constant error models for this data.

Relationships between choice proportions and response times

Figure 8 shows the average actual mean response times for question groups with different actual choice proportions of the LL options. Obviously the same inverse U-shaped relationship occurred again. The difference in mean response time between groups with extreme and moderate choice proportions was significant (M_extreme = 3.89 seconds, M_moderate = 4.30 seconds, t[36] = −6.40, p < .01). Analyses on individual data revealed the same pattern for 34 out of the 37 participants.

Figure 8.

Average mean response times for question groups with different actual choice proportions of the LL options in Experiment 3. Each question group contained identical questions for a specific intertemporal effect. Error bars show 95% confidence intervals.

Model fitting and comparisons

The constant error models again performed poorly when fitting choice data. The overall BIC value of the best constant error model was 7999 and it produced the lowest BIC values for only 2 participants.

The bottom half of Tables 6 and 7 list the three best models in terms of overall BIC value and count of lowest BIC values across participants when fitting only choice data in Experiments 3 and the bottom half of Tables 8 and 9 list the results when fitting both choice and response time data.¹³ The attribute-wise diffusion model with direct differences, power transformations of objective value and time, and varied σ performed the best in all situations and pairwise comparisons led to the same result. Since this model was the best one in Experiment 1 as well and differed just a little bit from the best model in Experiment 2, we picked it as the winning model in this research. This is actually a DFT model assuming a sequential sampling approach and an attention shift mechanism for making intertemporal choices. Specifically, it suggests that people attend to either the money or the delay attribute at a time and evaluate the relevant direct difference between options to update their preference. This preference updating process continues over time as people switch their attention between the two attributes until the preference level of one option reaches the preference threshold to trigger a decision. The results of model comparisons suggested that both the sequential sampling approach and the attention shift mechanism were essential for the success of the winning model (see Tables 2 - 9 and Appendix A). The sequential sampling approach is also critical for explaining the inverse U-shaped relationship between choice proportions and response times.

Table 10 provides a summary of the parameter estimates from this model when it was fit to both choice and response time data. For each participant, there were at least 153 data points used to estimate the five parameters. In general, parameters w, θ* and T_er in the winning model had unimodal distributions across participants with the modes close to the mean values shown in Table 10. In contrast, more participants had extreme estimates on parameters α and β, suggesting high (or low) sensitivity to direct difference in subjective value or time. Furthermore, individual differences in w, θ* and T_er were relatively small compared with those in α and β. The mean parameters from Experiments 1 and 2 are more similar than Experiment 3 for α and β. The third experiment differed mainly from the first two with respect to how the options were displayed.

Table 10. Means and Standard Deviations (in parentheses) of Parameter Estimates from the Winning Model, i.e., the Attribute-wise Diffusion Model with Direct Differences, Power Transformations of Objective Value and Time, and Varied σa.

Exp.	Parameters
	w	θ*	α	β	Ter
1	.63(.13)	1.79(.55)	1.68(.44)	1.26(.52)	1.57(.44)
2	.51(.17)	1.69(.23)	1.20(.69)	1.11(.71)	1.26(.08)
3	.48(.18)	1.94(.61)	.94(.64)	.75(.65)	1.23(.14)

Model predictions

As in Experiments 1 and 2, we calculated the correlation coefficient between actual choice proportions of the LL options within question groups and the corresponding average choice probabilities predicted by the best model in Experiment 3, as well as the correlation coefficient between actual mean response times and predicted mean response times within question groups. There was again a strong correlation between the predicted average choice probabilities and the actual choice proportions (r = .92, p < .001) and between the predicted mean response times and actual mean response times (r = .76, p < .001). The corresponding average correlation coefficients across participants were .74 and .20. Figure 8 also shows average predicted mean response times for different actual choice proportions of the LL options within question groups. The same inverse U-shaped curve was reproduced by the best model. Finally, the right panels in Figure 7 show the predictions of the best model on the impact of experimental manipulation on actual choice proportions. The predicted results again reproduced the general change patterns in actual data reasonably well at both individual and aggregate levels.

Overall, the results of Experiment 3 replicated those from Experiments 1 and 2 with a different experimental design encouraging an alternative-wise strategy. The results from groups of identical questions also provided more support for the probabilistic nature of intertemporal choice.

General Discussion

Probabilistic and Dynamic Nature of Intertemporal Choice

Results of all three experiments reported in this article supported a probabilistic and dynamic rather than deterministic and static perspective on intertemporal choice. The probabilistic nature has long been neglected, explicitly or implicitly. For example, previous studies attempting to estimate the discount function using indifference procedures tended to treat the deviations of actual data points from the fitting line as non-systematic errors and tried to estimate the corresponding parameters by minimizing the sum of squared errors. In this way, the emphasis was on the best form of the fitting line while the deviations were regarded as a nuisance component which should be eliminated. To the contrary, the probabilistic nature of intertemporal choice revealed in this article implies that the deviations actually demonstrated this inherent property and therefore deserved the same amount of attention as the deterministic part of the fitting line itself. Furthermore, the conclusions of previous studies on the form of discount function may be misleading due to their neglect of the probabilistic nature of intertemporal choice. For instance, the advantage of the hyperbolic discount function over the exponential discount function in describing empirical data (i.e., producing a higher R²) may indeed be the consequence of the robustness of the hyperbolic form against the randomness of human intertemporal choice. All in all, a probabilistic view on intertemporal choice may shed new light on this research area and therefore change our understanding in a fundamental way.

Another important implication of these studies comes from the finding that extreme choice proportions tended to associate with relatively short response times while moderate choice proportions, which suggested more difficult decisions, were usually accompanied by longer response times. This suggests that people’s explicit intertemporal choice is governed by an underlying dynamic process which takes various amounts of deliberation time to reach different decisions. Therefore, we developed a number of dynamic models, i.e., diffusion models, and compared them with static models using various stochastic specifications by fitting each model to choice data. The results, especially those of the most refined study, i.e., Experiment 3, favored a dynamic perspective on intertemporal choice. Future research should pay more attention to the dynamic nature of intertemporal choice in order to develop and apply a more realistic account of this topic. Finally, taking decision time into consideration may also help discriminate among models and improve parameter estimation since we can employ more information from empirical data in this case. For example, in Experiment 3, results from fitting only choice data and those from fitting choice and response time data simultaneously favored the same DFT model. The converging evidence provided more support for the winning model and its attribute-wise and dynamic approach to intertemporal choice.

Why Hyperbolic Discount Function does not Fit Best

Given the success and popularity of the hyperbolic discount function in previous research, one may wonder why probabilistic models built upon this discount function performed poorly. There are four possible explanations for this result. First, as discussed in Scholten and Read (2010), the delay discounting approach is unable to account for a number of anomalies which an attribute-wise model can handle. This suggests that the hyperbolic discount function may be inherently defective as the core of an intertemporal choice model. Second, previous research in favor of the hyperbolic discount function only examined the indifferent pairs and thus ignored a large portion of the probabilistic information in the dataset. When all the data are taken into account as in the current research, the hyperbolic model may become less useful. Third, the probabilistic nature of intertemporal choice was never explored in previous studies on the appropriate form of discount function, and thus the resultant success under the deterministic framework did not necessarily guarantee a good model. Finally, almost all of the questions in the current research involved two delayed options, while the typical form of questions used in traditional research investigating the form of discount function was a combination of immediate and delayed payoffs. An alternative-wise strategy may be more efficient and feasible than an attribute-wise strategy for traditional question form since people have to evaluate discounted utility only once in those questions. It will be valuable in the future to explore the performance of alternative-wise models with the traditional question form.

A General Framework for Explaining the Three Intertemporal Effects Simultaneously

We have shown that the attribute-wise diffusion model with direct differences, power transformations of objective value and time, and varied σ, i.e., a DFT model, could reproduce the patterns of gradual change in actual choice proportion when attribute values were manipulated as required by the three intertemporal effects. In fact, this model provides a general framework for explaining the delay duration effect, common difference effect, and magnitude effect simultaneously. Specifically, direct differences involved in this model set up a basis for accounting for the delay duration effect and magnitude effect, while the assumption that direct differences are sampled after applying power transformations enables the model to explain the common difference effect.

Mathematically, the delay duration effect and magnitude effect are equivalent if we treat reward amount and delay duration as two independent and exchangeable attributes. This is actually one implicit assumption of the weighted additive difference models. When reward amounts or delay durations of two options are increased proportionally, the associated direct difference will increase for sure, regardless of the specific value of the exponent in the power transformation function. This will, in turn, make the LL option (for the magnitude effect) or the SS option (for the delay duration effect) more attractive. That is to say, it becomes more likely that the corresponding decision threshold will be reached first after the attribute values are changed according to the specification of the effects.

On the other hand, the best model offers an explanation for the common difference effect as well when its exponent in the power transformation function of objective time is smaller than 1. Under this condition, increasing both delays by a common additive constant will reduce the direct difference between the two perceived delay durations. This will in turn make the LL option more attractive because its disadvantage due to a longer delay is lessened. In summary, the attribute-wise diffusion model with direct differences, power transformations of objective value and time, and varied σ is able to account for all three intertemporal effects with a single general framework based on the preference accumulation process. This result again demonstrates the power of diffusion models in general and DFT models in particular to account for various effects of preferential choice simultaneously.

Conclusion

This article describes three empirical studies aimed at demonstrating the probabilistic and dynamic properties of intertemporal choice and exploring a variety of brand-new models to accommodate these important features. The results strongly supported the general conclusions that intertemporal choice is probabilistic and dynamic in nature just like other preferential choices and that it is a stochastic process that unfolds over time. Furthermore, the attribute-wise diffusion model involving direct differences, power transformations of objective value and time, and varied diffusion parameter appeared to perform better than various other probabilistic models of intertemporal choice, including static models such as constant error models and Probit models, alternative-wise models built upon exponential or hyperbolic discount function, and attribute-wise models considering relative differences. The winning model also reproduced the empirical data on choice and response time quite well and provided a single general framework for the delay duration effect, common difference effect, and magnitude effect in intertemporal choice simultaneously. The success of the winning model suggested that people process intertemporal choice by accumulating evidence from sampling simple subjective differences in money and delay dimensions with differential weights.

Appendix A

A Comprehensive Summary of All Reported Models and Relevant Results of Model Fitting and Comparisons in Study 3

Model	Transformations of objective value and time	Core theory	Stochastic specification	No. free parametersa	Overall BIC value in Study 3a	Count of lowest BIC values in Study 3a
1	Identity	Alternative-wise with exponential discount function	Constant error model	2/-	9324/-	0/-
2	Identity	Alternative-wise with exponential discount function	Probit model with fixed σ	2/-	12449/-	0/-
3	Identity	Alternative-wise with exponential discount function	Probit model with varied σ	2/-	12259/-	0/-
4	Identity	Alternative-wise with exponential discount function	Logistic model	2/-	12585/-	0/-
5	Identity	Alternative-wise with exponential discount function	Random preference model	2/-	11466/-	1/-
6	Identity	Alternative-wise with exponential discount function	Diffusion model with fixed σ	3/-	12477/-	0/-
7	Identity	Alternative-wise with exponential discount function	Diffusion model with varied σ	3/-	12490/-	0/-
8	Identity	Alternative-wise with hyperbolic discount function	Constant error model	2/-	9678/-	0/-
9	Identity	Alternative-wise with hyperbolic discount function	Probit model with fixed σ	2/-	9371/-	1/-
10	Identity	Alternative-wise with hyperbolic discount function	Probit model with varied σ	2/-	10300/-	0/-
11	Identity	Alternative-wise with hyperbolic discount function	Logistic model	2/-	9765/-	0/-
12	Identity	Alternative-wise with hyperbolic discount function	Random preference model	2/-	12369/-	3/-
13	Identity	Alternative-wise with hyperbolic discount function	Diffusion model with fixed σ	3/-	9675/-	0/-
14	Identity	Alternative-wise with hyperbolic discount function	Diffusion model with varied σ	3/-	10105/-	0/-
15	Identity	Attribute-wise with direct differences	Constant error model	2/-	8727/-	2/-
16	Identity	Attribute-wise with direct differences	Probit model with fixed σ	2/-	8919/-	0/-
17	Identity	Attribute-wise with direct differences	Probit model with varied σ	1/-	9499/-	5/-
18	Identity	Attribute-wise with direct differences	Logistic model	2/-	9282/-	2/-
19	Identity	Attribute-wise with direct differences	Random preference model	2/-	9187/-	2/-
20	Identity	Attribute-wise with direct differences	Diffusion model with fixed σ	3/4	9129/44451	0/3
21	Identity	Attribute-wise with direct differences	Diffusion model with varied σ	2/3	8802/44592	1/4
22	Identity	Attribute-wise with relative differences	Constant error model	2/-	9839/-	2/-
23	Identity	Attribute-wise with relative differences	Probit model with fixed σ	2/-	10602/-	0/-
24	Identity	Attribute-wise with relative differences	Probit model with varied σ	1/-	10494/-	1/-
25	Identity	Attribute-wise with relative differences	Logistic model	2/-	10838/-	0/-
26	Identity	Attribute-wise with relative differences	Random preference model	2/-	10857/-	0/-
27	Identity	Attribute-wise with relative differences	Diffusion model with fixed σ	3/4	10811/4702 7	0/0
28	Identity	Attribute-wise with relative differences	Diffusion model with varied σ	2/3	9837/45701	1/3
29	Identity	Attribute-wise with proportional differences	Probit model with fixed σ and fixed decision threshold δ	2/-	9194/-	0/-
30	Power	Alternative-wise with exponential discount function	Constant error model	4/-	8973/-	0/-
31	Power	Alternative-wise with exponential discount function	Probit model with fixed σ	4/-	7816/-	0/-
32	Power	Alternative-wise with exponential discount function	Probit model with varied σ	4/-	7836/-	0/-
33	Power	Alternative-wise with exponential discount function	Logistic model	4/-	7799/-	0/-
34	Power	Alternative-wise with exponential discount function	Random preference model	4/-	8229/-	0/-
35	Power	Alternative-wise with exponential discount function	Diffusion model with fixed σ	5/-	8082/-	0/-
36	Power	Alternative-wise with exponential discount function	Diffusion model with varied σ	5/-	8106/-	0/-
37	Power	Alternative-wise with hyperbolic discount function	Constant error model	4/-	8758/-	2/-
38	Power	Alternative-wise with hyperbolic discount function	Probit model with fixed σ	4/-	7845/-	0/-
39	Power	Alternative-wise with hyperbolic discount function	Probit model with varied σ	4/-	7896/-	1/-
40	Power	Alternative-wise with hyperbolic discount function	Logistic model	4/-	7827/-	0/-
41	Power	Alternative-wise with hyperbolic discount function	Random preference model	4/-	7959/-	0/-
42	Power	Alternative-wise with hyperbolic discount function	Diffusion model with fixed σ	5/-	8115/-	0/-
43	Power	Alternative-wise with hyperbolic discount function	Diffusion model with varied σ	5/-	8173/-	0/-
44	Power	Attribute-wise with direct differences	Constant error model	4/-	7999/-	2/-
45	Power	Attribute-wise with direct differences	Probit model with fixed σ	4/-	7265/-	1/-
46	Power	Attribute-wise with direct differences	Probit model with varied σ	3/-	8546/-	0/-
47	Power	Attribute-wise with direct differences	Logistic model	4/-	7329/-	3/-
48	Power	Attribute-wise with direct differences	Random preference model	4/-	7330/-	0/-
49	Power	Attribute-wise with direct differences	Diffusion model with fixed σ	5/6	7508/43292	0/9
50	Power	Attribute-wise with direct differences	Diffusion model with varied σ	4/5	7028/42704	7/14
51	Power	Attribute-wise with relative differences	Constant error model	4/-	9924/-	0/-
52	Power	Attribute-wise with relative differences	Probit model with fixed σ	4/-	9570/-	0/-
53	Power	Attribute-wise with relative differences	Probit model with varied σ	3/-	9504/-	0/-
54	Power	Attribute-wise with relative differences	Logistic model	4/-	9427/-	0/-
55	Power	Attribute-wise with relative differences	Random preference model	4/-	9305/-	0/-
56	Power	Attribute-wise with relative differences	Diffusion model with fixed σ	5/6	9763/45541	0/1
57	Power	Attribute-wise with relative differences	Diffusion model with varied σ	4/5	9093/44172	0/3

^aThe value before slash is for fitting only choice data; the value after slash is for fitting both choice and response time data. A dash indicates either the relevant model was not suitable for fitting response time data or we did not fit the model to response time data in this article.

Appendix B

Details of the Model Fitting Procedure

The first step in the model fitting process was to prune the data from each participant in terms of response time so that outliers were excluded from further analyses. Specifically, any choice with a response time shorter than 1500ms or longer than 10000ms was removed. We set the lower bound to ensure that participants had sufficient time to sample all the information presented on the screen, and chose the upper bound to avoid the impact of extremely long response times on parameter estimation when response time was taken into account. It turned out that most response times were below the upper bound.

For the attribute-wise models, the attentional weight parameters were constrained between .05 and .95 to avoid practically meaningless extreme values; for the alternative-wise models, the parameter k was set to be positive. The exponents in the power transformation functions were limited between .01 and 2. The non-decisional component of response time, T_er, was constrained by an upper limit equal to the shortest response time produced by an individual when the data of that individual were fit. For the PD model, the parameter on personal decision threshold was constrained between −20 and 20 and the range of the standard deviation was between .001 and 20. For Probit and diffusion models with fixed σ, the parameter σ was set to be positive. For logistic models, the parameter g was set to be positive. For random preference models, we assumed that exp(-k) in the generalized discounted utility model follows a truncated normal distribution between 0 and 1, the natural logarithm of the k parameter in the generalized hyperbolic discounting model follows a normal distribution, and the w parameters in the weighted additive difference models follow a truncated normal distribution between 0 and 1. With these limitations in place, the various models were fit to individual data and compared to one another using the BIC index.

Appendix C

Question Generation Procedure

To generate an appropriate set of formal questions for each participant, an adjustment procedure was administrated in each study to find three approximately indifferent pairs of options. Since the approximately indifferent pairs varied across participants, the formal questions generated from them also differed among participants. In the adjustment procedure, we fixed three of the four attribute values in questions associated with each effect and let the remaining one vary from trial to trial according to participants’ response to the previous question for the same effect. Specifically, in Experiment 1, for the questions related to the delay duration effect, the shorter delays were fixed at 20 days; the longer delays were fixed at 60 days; and the larger rewards were always 36 dollars. The remaining attribute value, i.e., the smaller reward amount, was initially set at 20 dollars and then altered contingent on participants’ responses. For example, if one chose the LL option in a specific question, the smaller reward amount would increase in the next question associated with the delay duration effect, and vice versa. The procedure continued until a tiny change in the smaller reward amount would lead to a choice reversal, and the pair of options in the last question was viewed as an approximately indifferent pair. Similarly, for the questions related to the common difference effect, the shorter delays were fixed at 20 days; the longer delays were fixed at 60 days; and the larger reward amounts were always 32 dollars. The smaller reward amount started from 16 dollars and again changed according to participants’ previous response. Finally, for the questions concerning the magnitude effect, the smaller rewards, the larger rewards, and the short delays were fixed at 20 dollars, 40 dollars, and 8 days respectively. The longer delay was initially set at 20 days and changed in the same manner as for the other two effects.

The same procedure was also implemented in Experiments 2 and 3. Specifically, for the questions related to the delay duration effect, the shorter delay was fixed at 20 days, the longer delay was fixed at 40 days, and the larger reward amount was fixed at 35 dollars. The remaining attribute value, i.e., the smaller reward amount, was initially set at 20 dollars and was changed on the basis of the participants’ responses. For the questions related to the common difference effect, the shorter delay, the longer delay, and the larger reward were fixed at 20 days, 50 days and 32 dollars respectively. The smaller reward amount started from 16 dollars and again changed according to participants’ previous response. Finally, for the questions concerning the magnitude effect, the smaller reward, the larger reward, and the shorter delay were fixed at 20 dollars, 40 dollars, and 12 days respectively. The longer delay was initially set at 30 days and was changed in the same manner as for the other two effects.

After finding the approximately indifferent pairs for each participant, the experimental software proceeded to generate formal questions based on the approximately indifferent pairs. Specifically, in Experiment 1, the LL option in each formal question concerning the delay duration effect always had a delay three times as long as that of the SS option as in the approximately indifferent pair, and the shorter delays ranged between 1 day and 40 days, leading to 40 pairs of delay durations. The reward amounts in the approximately indifferent pair were then changed a little bit to generate 15 pairs of reward amounts in formal questions that were slightly different but practically the same. The purpose of this change was to minimize the potential impact of memory by preventing participants from answering the same questions repeatedly. Furthermore, the tens digits of the smaller and larger rewards in these questions were always the same to make the questions look more similar to one another. Finally, the 40 pairs of delay durations and the 15 pairs of reward amounts were factorially combined to generate 600 formal questions. The same method was employed to generate formal questions for the common difference effect and magnitude effect. Specifically, the delay durations in the questions concerning the common difference effect and the reward amounts in the questions associated with the magnitude effect varied systematically, while the reward amounts in the questions concerning the common difference effect and the delay durations in the questions associated with the magnitude effect were quite similar to those in the approximately indifferent pairs.

The same procedure was followed in Experiment 2 with two minor changes. First, for the questions concerning the delay duration effect, the delays of LL options were twice as long as those of the SS options. Second, 4 rather than 15 slightly different pairs of reward amounts (for the delay duration effect and common difference effect) or delay durations (for the magnitude effect) were created from the approximately indifferent pairs to generate formal questions. Experiment 3 had virtually the same design as Experiment 2 with regard to stimulus structure except that the exact reward amounts (for the delay duration effect and common difference effect) or delay durations (for the magnitude effect) from the approximately indifferent pairs were utilized to generate formal questions and each pair of options were presented five times. Although each participant answered different questions, due to the same question generating procedure, question sets for different participants were similar to one another.

Appendix D

Instruction for Participants Concerning the Payment Schedule

Experiment 1:

You will receive payment for taking part in this study. There will be four sessions in the study; you will be paid $4 for each session you take part in. You will get the payment when you finish the whole study. If you quit prior to the completion of the whole study, you will still get $4 for each session you participate. Besides, you will get a bonus no matter whether you finish the whole study or not. Specifically, one of the intertemporal choice questions you answer in the study will be randomly selected and the bonus will be offered accordingly. For example, if the randomly selected question requires you to show your preference between receiving $5 in 2 days and receiving $8 in 10 days and the latter is chosen, then a bonus of $8 will be given to you 10 days after you finish the whole experiment or decide to quit. Please treat the delays in each question as if they were counted from the time you think over the question although you will get the bonus only when you finish the study or even later.

Experiments 2 and 3:

You will receive payment for participating in this study. You will get a base payment of $4 for your participation. If you quit prior to the completion of the whole study, you will still get the base payment. Besides, you will get a bonus no matter whether you finish the whole study or not. Specifically, one of the intertemporal choice questions you answer in the study will be randomly selected and a quarter of the actual amount of money you choose will be offered as a bonus. For example, if the randomly selected question requires you to show your preference between receiving $5 in 2 days and receiving $8 in 10 days and the latter is chosen, then a bonus of $2 (.25*8), together with the base payment, will be given to you 10 days after you finish the whole experiment or decide to quit. Please think over each question as if you would get the full amount of money after the specified delay according to your choice.

Appendix E

Proof of the Delay Duration Effect as an Indication of the Probabilistic Nature of Intertemporal Choice

It was found in all three experiments that choice proportions of the LL options changed gradually when delay durations were increased proportionally. We interpreted this as a demonstration of the probabilistic nature of intertemporal choice. We will show the validity of this deduction by proving its converse-negative proposition that a deterministic approach entails an abrupt change in choice proportion under this circumstance given either the exponential or hyperbolic discount function. We will also show that the converse-negative proposition is still true even if the magnitude effect is taken into account.

First of all, suppose a decision maker has no preference between two intertemporal options, (v_a, t_a) and (v_b, t_b), and 0 < v_a < v_b, 0 < t_a < t_b. With the exponential discount function and a deterministic perspective, we have

$$DU(v_a,t_a)=u\left(v_a\right)\times \exp (-k{t}_a)=u\left(v_b\right)\times \exp (-k{t}_b)=DU(v_b,t_b)$$

in which DU(v, t) represents the discounted utility of an option and k > 0. If both delays are multiplied by a constant m greater than 1, the new SS option, (v_a,mt_a) will be more preferable to the new LL option, (v_b,mt_b), since

$$\begin{array}{c}\hfill DU(v_a,m{t}_a)=u\left(v_a\right)\times \exp (-km{t}_a)\hfill \\ \hfill =u\left(v_a\right)\times \exp (-k{t}_a)\times \exp (-k(m-1\left)t_a\right)=u\left(v_b\right)\times \exp (-k{t}_b)\times \exp (-k(m-1\left)t_a\right)\hfill \\ \hfill >u\left(v_b\right)\times \exp (-k{t}_b)\times \exp (-k(m-1\left)t_b\right)=u\left(v_b\right)\times \exp (-km{t}_b)=DU(v_b,m{t}_b).\hfill \end{array}$$

When the magnitude effect is taken into account, the same result will occur given the exponential discount function. In this case, the indifference between two original options implies that

$$DU(v_a,t_a)=u\left(v_a\right)\times \exp (-k_a{t}_a)=u\left(v_b\right)\times \exp (-k_b{t}_b)=DU(v_b,t_b).$$

Because u(v_a) < u(v_b), we have exp(−k_at_a) > exp(−k_bt_b). Consequently, for the new pair of options (v_a, mt_a) and (v_b, mt_b),

$$\begin{array}{c}\hfill DU(v_a,m{t}_a)=u\left(v_a\right)\times \exp (-k_{a}m{t}_a)\hfill \\ \hfill =u\left(v_a\right)\times \exp (-k_a{t}_a)\times \exp (-k_a(m-1\left)t_a\right)=u\left(v_b\right)\times \exp (-k_b{t}_b)\times \exp (-k_a(m-1\left)t_a\right)\hfill \\ \hfill >u\left(v_b\right)\times \exp (-k_b{t}_b)\times \exp (-k_b(m-1\left)t_b\right)=u\left(v_b\right)\times \exp (-k_{b}m{t}_b)=DU(v_b,m{t}_b).\hfill \end{array}$$

In other words, the new SS option will again be preferred over the new LL option.

For the hyperbolic discount function, the indifference between (v_a,t_a) and (v_b,t_b) implies that

$$DU(v_a,t_a)=\frac{u\left(v_a\right)}{1+k{t}_a}=\frac{u\left(v_b\right)}{1+k{t}_b}=DU(v_b,t_b),$$

and thus

$$\frac{u\left(v_a\right)}{u\left(v_b\right)}=\frac{1+k{t}_a}{1+k{t}_b}.$$

When both delays are increased proportionally,

$$\frac{DU(v_a,m{t}_a)}{DU(v_b,m{t}_b)}=\frac{u\left(v_a\right)∕(1+km{t}_a)}{u\left(v_b\right)∕(1+km{t}_b)}=\frac{1+k{t}_a}{1+k{t}_b}\times \frac{1+mk{t}_b}{1+mk{t}_a}=\frac{1+k(t_a+m{t}_b)+m{k}^2{t}_a{t}_b}{1+k(t_b+m{t}_a)+m{k}^2{t}_a{t}_b}.$$

Because t_a < t_b and m > 1, we have t_a + mt_b > t_b + mt_a. Therefore,

$$\frac{1+k(t_a+m{t}_b)+m{k}^2{t}_a{t}_b}{1+k(t_b+m{t}_a)+m{k}^2{t}_a{t}_b}>1,$$

indicating that the new SS option is preferable to the new LL option. When the magnitude effect is taken into account, the indifference between two original options implies that

$$DU(v_a,t_a)=\frac{u\left(v_a\right)}{1+k_a{t}_a}=\frac{u\left(v_b\right)}{1+k_b{t}_b}=DU(v_b,t_b).$$

Because u(v_a) < u(v_b), we have 1 + k_at_a < 1 + k_bt_b and thus k_at_a < k_bt_b. Consequently,

$$\frac{DU(v_a,m{t}_a)}{DU(v_b,m{t}_b)}=\frac{u\left(v_a\right)∕(1+k_{a}m{t}_a)}{u\left(v_b\right)∕(1+k_{b}m{t}_b)}=\frac{1+k_a{t}_a}{1+k_b{t}_b}\times \frac{1+m{k}_b{t}_b}{1+m{k}_a{t}_a}=\frac{1+(k_a{t}_a+m{k}_b{t}_b)+m{k}_a{k}_b{t}_a{t}_b}{1+(k_b{t}_b+m{k}_a{t}_a)+m{k}_a{k}_b{t}_a{t}_b}>1$$

since k_at_a + mk_bt_b > k_bt_b + mk_at_a. All in all, increasing both delays proportionally will make the SS option more attractive than the LL option, given that participants are indifferent between the original pair. Similar reasoning can be invoked for the situation in which the original two options are not equally appealing. In this case, the ratio of discounted utilities will increase when both delays are increased proportionally. The monotonic change pattern guarantees that, when both delays are increased in a proportional way, there exists only one cutoff point on the shorter delay duration (or, equivalently, on the longer delay duration) at which people are indifferent between the SS and LL options. Thus, for any pair with shorter delays, the LL option should be chosen, and for any pair with longer delays, the SS option should be chosen. That is to say, the choice probability of the LL option is expected to change from 1 to 0 at the cutoff point. When similar questions with the same values on the target attribute for a specific effect are combined into groups as in Experiments 1 and 2, a deterministic approach suggests that only one group might have a choice proportion that is between 0 and 1 exclusively. When identical questions are grouped together as in Experiment 3, a deterministic approach is completely incompatible with a pattern of gradual change in choice proportion across individual groups associated with the delay duration effect. Since most participants did produce the gradual change pattern, the probabilistic nature of intertemporal choice is self-evident.