Performance on the Iowa Gambling Task: From 5 to 89 Years of Age

Abstract

The present study focuses on the role of frequency bias and expected value on the learning processes driving performance on the Iowa Gambling Task (IGT) in individuals between 5 and 89 years of age. As in previous studies, children performed poorly on the IGT, were increasingly influenced by frequency of losses during learning, and constantly changed their decisions. Decision-making strategies changed after childhood from erratic behavior to more consistent strategies that promoted expected value of deck choices. Performance deficits as well as a loss frequency bias were found in older adults. However, age-related deficits were distinct between children and older adults. Cognitive modeling analysis indicated that older adults were more likely to forget about recent outcomes and were more consistent than children when selecting decks. Cognitive ability was associated with a modeling parameter for memory as well as IGT performance, suggesting the involvement of a cognitive component in young and middle-aged adult decision making. The interactions of modeling parameters suggested that cognitive changes were the cause of lowered performance in older adults. These analyses suggest critical developments in decision processes during the adolescent years and decline in a cognitive process leading to decision-making deficits after age 60.

Decision making is a crucial ability that impacts the quality of life from childhood to old age. Age-related trends in decision making have traditionally motivated separate groups of researchers: one group that devotes its attention to the acquisition of adult decision ability from childhood and adolescence and another group that focuses on decline in decision ability from adulthood to the end of life. Researchers often utilize identical laboratory tasks to evaluate decision-making ability without integrating information from different parts of the life span to support their hypotheses. Nevertheless, research in one part of life-span development might benefit by extending findings from other areas to increase interpretability. The present study focuses on life-span decision making on the Iowa Gambling Task (IGT), a learning-based decision task commonly utilized by both early life and late life decision researchers.

The IGT is currently the most frequently cited assessment of experiential decision making, as indicated by 558 and 611 search hits on PsycINFO and Scopus databases in 2013. The IGT was developed by Bechara, Damasio, Damasio, and Anderson (1994) to study the observed decision-making deficits caused by ventromedial prefrontal cortex lesions. During the IGT, cards are freely sampled from four deck choices associated with specific reward structures (i.e., monetary gain followed by possible loss after a selection). Individuals must gradually learn about these reward structures without explicitly learning payoffs from each deck, as successive selections on any one deck result in varying wins and losses. Actual payoff structures on the IGT mirror short-term and long-term prospects because each deck has two factors: expected value and loss frequency (see Table 1). When individuals are overly focused on short-term prospects, they focus on the deck with infrequent losses and high immediate wins (Deck B). Finding and selecting the decks that have positive expected value regardless of loss frequency is most advantageous and involves focusing on long-term prospects rather than immediate payouts or losses. For this reason, performance reported in past studies was usually assessed by taking the proportion of advantageous selections over 100 selections (usually Decks C and D).

Table 1.

IGT Deck Characteristics

Characteristic	Deck A	Deck B	Deck C	Deck D
Mean gain	125.00 (100%)	125.00 (100%)	62.50 (100%)	62.50 (100%)
Mean loss	187.50 (75%)	187.50 (10%)	31.25 (75%)	31.25 (10%)
Net score	−250	−250	+250	+250

Note. The table depicts the general structure of the IGT used in the current study. Numbers outside parentheses indicate average wins over 10 trials. Numbers in parentheses indicate percentage of trials involving gain or loss. Net score is the total amount won (+) or lost (−) after 10 selections from the deck. IGT = Iowa Gambling Task.

Improvement and decline in learning ability with age are thought to be major contributors of age-related performance on the IGT. Studies of child and adolescent performance on the IGT have reported general improvements in IGT performance with age (Cassotti, Houde, & Moutier, 2011; Cauffman et al., 2010; Crone & Van der Molen, 2004; Hooper, Luciana, Conklin, & Yarger, 2004). These studies usually indicate that adults (18–25 years old) perform better than adolescents (13–15 years old), and adolescents perform better than children (6–12 years old) by quickly learning about expected value over the course of several trials. Cauffman and colleagues (2010) also found that adults evaluate negative outcomes with greater accuracy than adolescents on a modified IGT, suggesting that distinct developments in learning ability occur between adolescence and adulthood. Studies of older adult decision making on the IGT have reported mixed findings. Early studies found no performance differences between young adults and older adults but instead found different learning strategies with age (Lamar & Resnick, 2004; MacPherson, Phillips, & Della Sala, 2002; Wood, Busemeyer, Koling, Cox, & Davis, 2005). Specifically, IGT learning strategies change in older adults and involve rapid forgetting of feedback coupled with recency effects (Wood et al., 2005). Contrary to earlier studies, however, some recent findings indicate the beginnings of performance decline in the mid-50s and 60s (Baena, Allen, Kaut, & Hall, 2010; Denburg, Tranel, & Bechara, 2005; Fein, McGillivray, & Finn, 2007; Isella et al., 2008; for the single exception, see Henninger, Madden, & Huettel, 2010). A recent meta-analysis performed by Mata, Josef, Samanez-Larkin, and Hertwig (2011) confirmed many of the latter findings, although the age-related decline in performance was not as strong on the IGT as on other experiential decision tasks. Overall, most researchers agree that some learning-related improvement occurs between childhood and adulthood and that decline occurs in older adults.

However, recent evidence suggests that learning ability may not be the primary influence on decision making during the IGT. Many researchers have questioned the construct validity of the IGT as a measure of experiential decision making in healthy participants due to common selection preferences that do not support any learning theory (Buelow & Suhr, 2009; Chiu & Lin, 2007; Fernie, 2007; Lin, Chiu, Lee, & Hsieh, 2007; Steingroever, Wetzels, Horstmann, Neumann, & Wagenmakers, 2013). Steingroever, Wetzels, Horstmann, and colleagues (2013) demonstrated that normal participants in several different studies were biased to select from decks with infrequent losses. Furthermore, performance within groups was highly variable, and not all participants developed strategies that resulted in appropriate exploitation of decks following exploration. Indeed, Crone and Van der Molen (2004) reported that all children and young adults in their study increasingly preferred choices associated with lower frequency of punishment during the task (loss frequency bias). A follow-up study by Crone, Bunge, Latenstein, and Van der Molden (2005) found that developmental differences in performance between ages 7 and 15 occur because of the availability of low punishment frequency decks (e.g., 10% of selections result in loss) and not because children become confused by the many options available or misunderstand task instructions. That is, punishment frequency was found to be the cause of fewer good selections before adolescence. With new insights about the frequency bias, Huizenga, Crone, and Jansen (2007) revisited the Crone and Van der Molen data and found that young children and some adolescents learned to prefer these infrequent punishment decks over several selections. Adults preferred low punishment frequencies early in the task but increasingly preferred positive expected value over trials (for similar findings, see Cassotti et al., 2011). However, low frequency preference does not seem to stop changing after young adulthood. MacPherson and colleagues (2002) found that punishment frequencies highly influenced older adults’ decision making, such that they were reluctant to select from decks with relatively small but frequent penalties (i.e., Decks A and C). These results indicate a secondary developmental trend in the elderly involving loss frequency that seems to overshadow the trend involving improved learning ability.

A major question left unanswered by previous research involves the nature of experiential decision making across the life span and if decision making is associated with processes that are differentially affected by aging. Both development and decline must be examined to determine if frequency bias and expected outcome contribute to performance differentially across the life span. Thus, it is necessary to compare child and adolescent decision making to older adult decision making. This study seeks to expand current understanding of differences in experiential decision making for the maturational period between 5 and 89 years of age by applying multiple analysis methods to a large data set. An initial goal of this study is to determine if changes in processes subserving IGT performance change at different times during the life span. This involves describing the effects that frequency and expected value have on deck preferences during the life span. However, analysis of deck preferences cannot fully explain how normal individuals make decisions during the IGT. A second goal of this study is the examination of learning strategies as a function of age. We reason that consistent decision making despite negative feedback should indicate purposeful decisions and learning. Strategic adjustment to feedback allows examination of learning by providing an additional behavioral component that can be examined with age (i.e., win-shift and loss-stay) and provides a possible moderator to preferential decision behavior if not an outright indicator of learning ability. A third goal involves examining four cognitive models of IGT performance and evaluating parametric information from the most effective of these models with respect to strategic and cognitive data. Cognitive models involve theory-driven approaches to data, and parameters from these models may be used to examine cognitive contributions to task performance. A final goal involves examining the effects of cognitive processes (i.e., shifting, inhibition, working memory, fluid reasoning, processing speed, and episodic memory) on strategies and decisions made on the IGT during development. Relating specific strategies to cognitive variables will show how decision preferences and strategies are related to cognition.

Method

Participants

Participants (N = 1,583) were recruited from the Colorado Springs, Colorado, metropolitan area. Participants between 18 and 59 years of age were recruited from psychology classes at the University of Colorado at Colorado Springs (UCCS). Older adults (60–89 years of age) were recruited through a registry of volunteers from the UCCS Gerontology Center. Children (5–17 years of age) were recruited from families of students and previous participants. All individuals completed the IGT, and many completed additional cognitive tasks. Table 2 shows participant demographics for individuals divided into five age groups (5–10, 11–16, 17–29, 39–59, and 60–89). The basis for selection of different age groups is given in the online supplemental materials. Students received extra credit for participation; adults 60 years of age or older received $10 per hour of participation, and children and adolescents between 5 and 17 years of age received $5 per hour of participation. Participants included in this study reported no history of neurological disease, head trauma, learning disability, psychiatric illness, or drug use that they thought might affect their cognition. All participants reported fair or good health on a questionnaire administered prior to neuropsychological testing.

Table 2.

Demographic Information

Age group	n	% male/female	Mean full scale IQ (SD)	Mean years of education (SD
5–10	174	49/51	119.53 (14.60)	2.65 (1.80)
11–16	171	48/52	114.77 (15.40)	7.63 (1.90)
17–29	664	27/73	112.54 (11.30)	14.03 (1.40)
30–59	281	25/75	120.00 (9.60)	15.06 (1.80)
60–89	293	31/69	120.40 (14.90)	14.90 (2.40)

Note. The 155 subjects in the Wood, Busemeyer, Koling, Cox, and Davis (2005) study are part of the current data set and were treated identically, receiving the same cognitive test versions and subject to the same testing situations. Full scale IQs were derived from a subset of individuals who were assessed using all Wechsler Abbreviated Scale of Intelligence subtests.

Procedures

Participants were told that they would be given several tests of general cognitive functioning including memory and reasoning tests. All testing was carried out in quiet testing rooms at UCCS or at the Gerontology Center. Participants attended multiple testing sessions, and the necessary time to complete the assessments used in this study did not exceed two 1- to 2-hr sessions. After testing was complete, participants were debriefed and provided feedback regarding their test performance. This study was approved by the UCCS institutional review board committee, and all participants gave informed consent. Treatment of all participants was consistent with American Psychological Association ethical standards (American Psychological Association 2002).

Measures

Iowa Gambling Task

Participants were assessed using a standard computerized version of the IGT identical to the version distributed by Psychological Assessment Resources (Bechara, 2007). Participants were told that the game involved a long series of card selections from four decks of cards. Participants received $2,000 of virtual currency and were instructed to use this money to gamble on the four decks, marked A, B, C, and D. Participants were free to switch from one deck to another as often as they wished, so long as a deck had not run out of cards (60 cards per deck). If a deck ran out of cards, it would no longer be available to select. Experimenters informed participants that selections would always result in immediate gains, but occasionally losses would follow gains. Participants were instructed to win as much money as possible or avoid losing as much as possible by staying away from the worst decks. Finally, the experimenter informed participants that they had to win enough to repay the virtual loan at the end of the task. However, there were no consequences for failing to repay the loan.

Deck selections resulted in an array of feedback: a smiling face with a pleasant sound for gains, a frowning face with an unpleasant sound for losses, a horizontal green bar for accumulated winnings, and a horizontal red bar for losses and amount owed. The green bar, a visual measure of the amount of money currently held, increased in length with gains, decreased in length with losses, and by default started at $2,000. The red bar, a visual measure of the amount of money currently owed back to the experimenter, increased in length when the green bar was reduced to $0 (signifying an additional loan of $2,000) and by default started at $2,000. The money won and lost was shown after each selection. Deck arrangements were identical for each participant: Decks A and B had high gains but incurred net losses over time, whereas Decks C and D had low gains but incurred net gains over time. Decks A and C resulted in losses on 75% of selections, whereas Decks B and D resulted in losses on 10% of selections. After 100 selections, the task ended. The 100 selections were scored by subtracting disadvantageous choices from advantageous choices: (C + D) − (A + B). The total number of advantageous choices was also computed for five blocks of 20 choices.

Additionally, cognitive and neuropsychological measures used in examination of the relationship between cognition and IGT performance are briefly described.

Reaction time

Participants were administered a computerized reaction time test for simple, choice, and conditional reaction times (Teng, 1990). Participants used a handheld gaming controller and were instructed to respond as quickly and accurately as possible to < or > stimuli by pressing the left or right trigger, respectively. The test displayed 16 right and then 16 left arrows at varying interstimulus intervals to assess motor response time and then used both arrows (appearing randomly one at a time) for 36 trials to assess choice reaction time. Reaction time was the average amount of time it took to make a correct response in the choice task minus the average motor response time: (motor response time left + motor response time right)/2.

Matrix Reasoning

The Wechsler Abbreviated Scale of Intelligence (Psychological Corporation, 1999), a shortened version of the Wechsler Adult Intelligence Scale–Third Edition, contains the Matrix Reasoning subtest as a measure of fluid intelligence. The subtest is a multiple-choice task in which participants must complete complex patterns (matrices) one at a time by inferring the rules from each design and then selecting the best answer from five possibilities. The number of correct responses on Matrix Reasoning uncorrected for age was used in the current investigation for the fluid intelligence variable.

Wisconsin Card Sorting Task (WCST)

A computerized version of the WCST developed by Colorado Assessment Tests was used to assess set shifting (Feldstein et al., 1999). During the WCST, participants match cards that contain shapes of varying color, form, and number to four key cards. The key cards contain all possible shapes (star, triangle, circle, plus), all possible numbers of symbols (one to four), and all possible colors (red, blue, green, yellow) in the set. Participants infer a matching rule (color, shape, or number) based on immediate feedback after matching. Shifting was assessed by measuring the number of perseverative errors (continuing to match based on a key card dimension after a change in matching principle) made throughout the task following the Heaton scoring method (Heaton, Chelune, Talley, Kay, & Curtiss, 1993).

Stroop task

A shortened version of the Stroop task (from Stroop, 1935) was used to assess stimulus inhibition. During the Stroop task, participants are asked to read words in black ink, read words in different colors, name the ink color of dots, and finally name ink colors in the presence of conflicting color words (mismatch). The experimenter recorded the amount of time spent in each section. Inhibition time was the amount of time (in seconds) it took to state the color of the mismatched color items minus the time to read the mismatched color items.

N-back

A verbal N-back task (from Kirchner, 1958) was used to assess working memory updating (a commercial version of the test is available from Sanzen Neuropsychological Assessment Tests, https://neuropsychological-assessment-tests.com). During the N-back task, letters are presented one at a time, and participants are asked to identify whether each presented stimulus is the same as a previously presented stimulus by pressing yes or no keys. This test spans from one stimulus back to three stimuli back. For each N-back, participants are first given a practice set of 10 stimuli and then a test comprising 100 stimuli. The percentage of stimuli that were responded to correctly (i.e., yes when an identical stimulus occurred three back and no when a stimulus did not occur three back) during the 2-back task was used as the variable for working memory updating.

Memory cards

A computerized memory cards task (Eskritt & Lee 2002) was administered to assess visuospatial episodic memory. During memory cards, 24 boxes hide a set of 12 pairs of cartoon images. Clicking on a box reveals the image underneath for 10 s. If a participant reveals two cards with the same image, the images disappear, leaving empty boxes. Otherwise, the boxes return to their original state, occluding the images. After all pairs have been found, the task restarts. This process repeats a total of five times and after 20 min repeats a final time (during the final presentation, the pairs stay face up after they are found). The percentage of pairs found without mismatch was recorded after the fifth attempt and again after the delay period. The delay measure ment was used as the variable for episodic memory.

Results

Deck Preferences Across the Life Span

Previous research indicates that a substantial subset of normal individuals select decks on the basis of loss frequency preference (Decks B + D) without ever considering net outcomes of decks (Decks C + D). As a result, the traditional analysis of net outcome preference alone insufficiently explains decision behavior. Alter natively, each deck attribute might be analyzed simultaneously to understand deck preference. Effects of deck attributes may be assessed in this manner using the number of choices on each deck in an analysis of variance (ANOVA): Because all possible deck combinations exist, decks may be categorized along dimensions of loss frequency (high/low) and net outcome (high/low). This allows for analysis of interactive effects of deck attributes with age or trial block that may provide information on the rate of learning. Based on previous findings, we predict that children, adolescents, and older adults will be less influenced by net outcome than young and middle-aged adults. Older adults should be more influenced by loss frequency than net outcome. Furthermore, loss frequency preference should be heightened in adolescents who are able to determine good choices as well as adults but are impaired in their ability to detect bad choices (Cauffman et al., 2010).

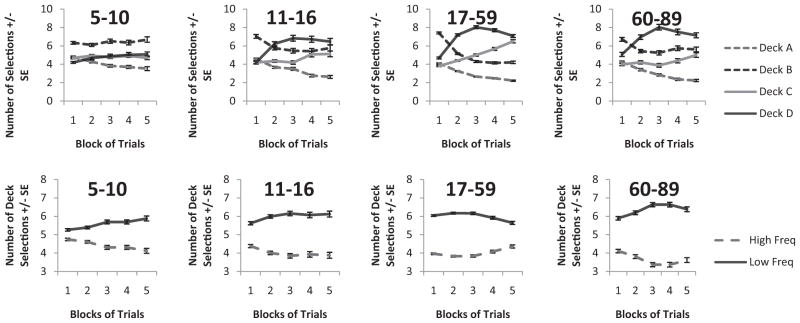
A four-way mixed ANOVA was performed on the number of deck selections across five blocks of 20 trials for the five age groups. Blocks and deck types were the repeated measures factors, and age group was the between-subjects factor. Deck types were further categorized along two dimensions: loss frequency (75% vs 10%) and net outcome (disadvantageous vs. advantageous). Be cause the number of trials per block and the total number of selections for all age conditions had fixed values, all main effects and interactions that did not include a deck type factor (frequency or net outcome) were excluded in a custom analysis. Greenhouse Geisser adjustments were made to the degrees of freedom when the sphericity assumption was violated. For the purposes of visu alizing life-span differences on the IGT, deck selections over 100 trials are shown by decade in Figure 1. A summary of the full ANOVA is presented in Table 3, and plots of deck selections by block for the different age groups are shown in the upper portion of Figure 2. Groups 17–29 and 30–59 were combined in Figure 2, as all results for these groups were identical in this analysis. Each term was examined with a Bonferroni post hoc test.

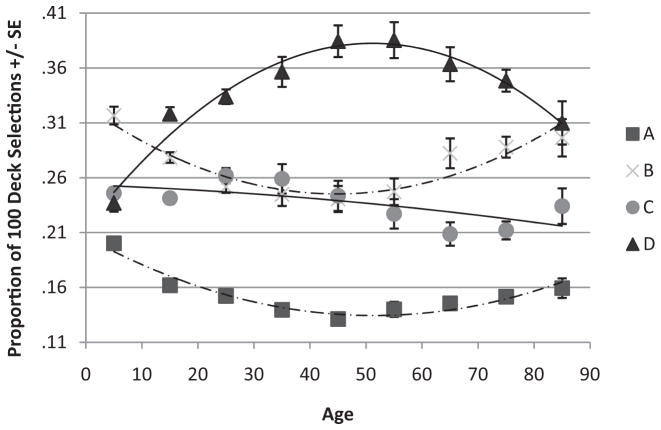
Figure 1.

Proportion of deck selection over 100 trials by decade. C and D trend lines are solid, A and B trend lines are dashed. Global maximum for D selections = 45.7 years.

Table 3.

Summary of Analysis of Variance Results for Deck Preferences

Terms	df	F	MSE	${\mathrm{\eta }}_{\mathrm{p}}^2$
Net outcome	1, 1578	229.04**	35.76	.13
Net Outcome × Age	4, 1578	37.71**	35.76	.09
Net Outcome × Age × Block	13, 5257	12.14**	13.99	.03
Loss frequency	1, 1578	844.25**	29.57	.35
Loss Frequency × Age	4, 1578	13.65**	29.57	.03
Loss Frequency × Age × Block	13, 5132	5.77**	13.60	.01
Net Outcome × Loss
Frequency × Age	4, 1578	10.60**	28.57	.03
Net Outcome × Loss
Frequency × Age × Block	14, 5566	2.96**	13.72	.01

Note. The dependent variable is the number of deck selections on individual decks per block. Net outcome = expected value (negative or positive); Loss frequency = frequency of loss (10% or 75%).

^**p < .001.

Figure 2.

Deck preferences and loss frequency preference by block for each age group. Low loss frequency decks are darker than high loss frequency. Freq = frequency.

As expected, a main effect of net outcome indicated a general preference for Decks C and D over Decks A and B ( ${\mathrm{\eta }}_{\mathrm{p}}^2=.15$). A two-way interaction of net outcome and age also indicated that this was more characteristic of young–middle-aged adults (ages 17–59) than children, adolescents, and older adults (5–16, 60–89). Finally, a three-way interaction of net outcome, block, and age indicated that these preferences were more frequent in the latter blocks of the task (Blocks 3–5). Block is introduced here as an analogy to learning rate; an interaction between net outcome and block at different ages indicates that the learning rate is different for these ages. By the 60th trial, individuals 17–59 surpassed individuals 5–16 and 60–89 years of age in average performance. In total, ages 17–59 learned high net outcome preferences faster than ages 11–16 and 60–89, and children 5–10 learned slower than all other groups. Trend analysis across age categories revealed that overall IGT performance (Decks C + D) changed as a quadratic function of age.

The main effect of loss frequency indicated that the decks with the lowest punishment frequencies (i.e., Decks B and D) were selected most often over the 100 trials ( ${\mathrm{\eta }}_{\mathrm{p}}^2=.35$). The interaction between loss frequency and age revealed individuals ages 30–89 preferred low frequency of loss selections more than other age groups (ps < .03), and individuals ages 5–10 were least likely to select decks based solely on loss frequency compared to other age groups. However, a three-way interaction between loss frequency, block, and age suggested that this effect changed as a function of trial block (see lower portion of Figure 2); although children’s preferences were not initially influenced by loss frequency, their appreciation for low frequency decks increased over trials. Adolescents through older adults (ages 11–59) were initially attracted to low loss frequency, and this trend did not change significantly over trials. In the oldest age group, the frequency bias was similar to that in children as low punishment preferences increased slowly over time, yet this group was also attracted to low punishment frequencies during the first block. This idea is expressed by the degree of line separation between low and high frequency decks shown in Figure 2; although deck preference is clearly dichotomized by the presence of different loss frequencies at all ages, the extent of the dichotomy is more evident early in the task in young and older adults than in children, and thus, not all individuals are equally biased by loss frequency. Trend analysis across age categories revealed that frequency selection changed as an increasing linear function of age. Alternatively, visual inspection of data suggested that decline occurred so late that the ANOVA model was unable to accommodate for it. The age cutoff may have suppressed a significant quadratic trend.

Finally, a three-way interaction between loss frequency, net outcome, and age was qualified by a four-way interaction between loss frequency, net outcome, block, and age. Children had the strongest interactive effect of choice characteristics, as indicated by a significant loss frequency by net gain interaction, F(1, 174) = 69.00, MSE = 18.19, p < .001, ${\mathrm{\eta }}_{\mathrm{p}}^2=.29$. This interaction was also evident in adolescents (ages 11–16; ${\mathrm{\eta }}_{\mathrm{p}}^2=.05$), although the effect did not meet the significance criterion of .001 (p = .005). The four-way interaction indicated that conjoint effects of deck attributes changed over the course of the task for all individuals older than 10. Specifically, age groups with significant four-way inter actions were likely to change their initial preferences from the single dimension of low frequency (i.e., Deck B) to consider both net gain and loss frequency (i.e., Deck D). The four-way interactive effects were largest for middle-aged adults: 11–16, ${\mathrm{\eta }}_{\mathrm{p}}^2=.05$;17–29, ${\mathrm{\eta }}_{\mathrm{p}}^2=.05$;30–59, ${\mathrm{\eta }}_{\mathrm{p}}^2=.06$;60–89, ${\mathrm{\eta }}_{\mathrm{p}}^2=.03$. In young and middle-aged adults, this indicated a greater preference for net outcome with learning, whereas, in older adults, this indicated a greater preference for loss frequency with learning.

Discussion of Deck Preferences Across the Life Span

Loss frequency explained more variance than net outcome, as more cards were usually selected from Deck B than from Deck C during the task. However, age modified the effects of deck attributes on deck preference. Young and middle-aged adults preferred high net outcome more than children, adolescents, and older adults. Middle-aged and older adults preferred low frequency decks more than children, adolescents, and young adults. Therefore, preference for low punishment frequency increases as a linear function of age, whereas preference for net outcome occurs as a quadratic function of age. Preferences were also modified by age and learning. Children and older adults learned to prefer low loss frequency decks over blocks, whereas adolescents, young adults, and middle-aged adults preferred these decks from the initial block. Preference for low frequency decks over blocks led older adults to select fewer cards from high net outcome decks. Finally, interactions between deck properties suggested that children uniquely learned to select from Deck B over blocks, possibly due to the high gains and low frequency of losses in this deck.

These results suggest a composite effect of learning processes (i.e., processes associated with loss frequency and net outcome) on age-related differences in IGT performance. Contrary to our predictions, early life preferences are only partially driven by loss frequency and must be learned over several trials; children are ultimately driven by selective preferences toward decks with a mix of high wins and uncommon losses (e.g., Deck B). With age, this gradually shifts to learning which decks will result in better outcomes over time. Finally, in accordance with our predictions, the influence of loss frequency continues to increase with age and appears to overcome the effect of net outcome in older adults.

A limitation of this analysis is the use of arbitrarily defined (i.e., binned) age groupings and trial blocks. Data averaged across blocks and individuals must be understood as averaged strategies. Indeed, preferences often do not extend beyond a single deck, and preferences for individual cases are often ambiguous. The consequence is that performance for one individual may be associated with opposite trends than expected in his or her age group. This criticism of IGT results has been noted by Steingroever, Wetzels, Horstmann, and colleagues (2013) as reflected by variance in performance in typical IGT analyses. Ultimately, more information than deck preferences is needed to determine how individuals are selecting decks and achieving high performance. One method to achieve this goal involves examining changes in deck selection according to experienced feedback.

Rationale for Analysis of Strategic Movement

Strategic movement represents a possible component that biases child and adolescent learning toward low frequency preferences. For example, shifting from a deck after every loss (i.e., high loss aversion) but staying after wins will inevitably result in preference for low loss frequency decks. This may represent an explicit strategy or may be intuitive for individuals taking the IGT (Cassotti et al., 2011). Consistency (less shifting, more staying) on the IGT is expected to improve over the life span, as previous studies have found older adults to be more consistent than young adults but less able to flexibly shift between disadvantageous and advantageous decks (Wood et al., 2005; Zamarian, Sinz, Bonatti, Gamboz, & Delazer, 2008). The effects of strategic movement measures are also expected to differ depending on age. If individuals are truly learning on the basis of frequency or expected value, early life and late life individuals are expected to prefer loss frequency with more consistent decision making, whereas young and middle-aged adults are expected to prefer net outcome decisions with consistency.

Outcome-behavior models, such as win-stay/loss-shift, may not be specific enough to explore learning of deck preferences, as deck characteristics (e.g., loss frequency and net gain) and trial appear to be relevant in decision making at all ages. Inclusion of all of this information potentially results in the creation of a large number of variables. However, as many as half of these variables are redundant because they are inversions (e.g., probability of win-stay is an inversion of win-shift). Win-shift and loss-stay were utilized in the present study to prevent confusion, as some researchers have traditionally identified win-stay and loss-shift variables as true strategies (i.e., win-stay/loss-shift strategy; Cassotti et al., 2011). This method also has more utility near the end of the task when win-stay may be more likely than loss-stay, and the latter variable may indicate more about an individual. Furthermore, it was assumed that the mere occurrence of a loss on a trial was enough to affect behavior, as opposed to net loss. A loss was defined as any trial where a monetary loss was indicated by the computer program.

$$[{\mathit{WinShift}}_{jk}]=\frac{{\sum }_{k=1}^{99}{\mathit{WinShift}}_{jk}}{{\sum }_{k=1}^{99}{\mathit{Win}}_{jk}}.$$ (1)

$$[{\mathit{LossStay}}_{jk}]=\frac{{\sum }_{k=1}^{99}{\mathit{LossStay}}_{jk}}{{\sum }_{k=1}^{99}{\mathit{Loss}}_{jk}}.$$ (2)

The probability of moving (shift/stay) after an outcome (win/loss) is given as the sum of movements up to an outcome for Deck j at Trial k divided by the sum total instances of win or loss outcome events for Deck j at Trial k. For example, if an individual continuously shifted decks before any losses occurred for the first four selections, the value of WinShift for each of those decks up to Trial 5 would be 100%. If the individual then selected Deck A for a second time (another win) but continued to select Deck A afterward, the value of WinShift for Deck A would be updated to 50%. After the third selection of Deck A (a loss), the person shifts to another deck, and WinShift does not update, while LossStay updates to 0% for Deck A. It is necessary to divide by the total number of wins or losses for a deck because these events depend on previous decisions for each case; certain individuals may have experienced fewer wins or losses on a deck than others, and therefore, it is useful to capture movement information relative to previous experiences. Scores for each strategy metric ranged from 0 (no use of strategy) to 1 (maximal use of strategy).

Analysis of Strategic Movement Results and Discussion

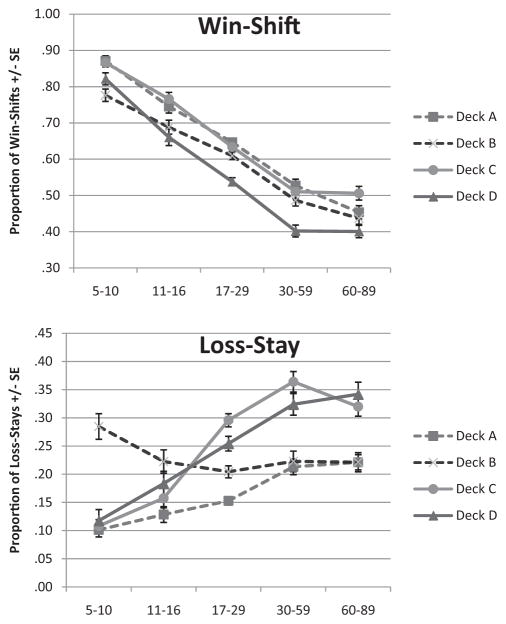
Figure 3 shows win-shift and loss-stay information (99th trial) for each deck and age grouping. Results for a mixed ANOVA on win-shift information revealed a lifelong trend involving decreasing win-shift behavior independent of deck type, F(4, 1578) = 96.62, p < .001, ${\mathrm{\eta }}_{\mathrm{p}}^2=.20$. Middle-aged adults were not different than older adults in loss-stay behavior, but both groups made significantly fewer shifts than children, adolescents, and young adults. Results for a mixed ANOVA on loss-stay information revealed a lifelong trend involving increasing loss-stay behavior, F(4, 1578) = 21.20, p < .001, ${\mathrm{\eta }}_{\mathrm{p}}^2=.05$. This effect was also modified by deck type, F(10.3, 4070) = 14.23, p < .001, ${\mathrm{\eta }}_{\mathrm{p}}^2=.04$. Loss-stay for Deck B slightly decreased with age, Deck A selection loss-stay slightly increased with age, and loss-stay on Decks C and D increased significantly with age, peaking in middle adulthood. It is important to keep in mind that the latter finding, dramatically illustrated in Figure 3, reflects age group behavior rather than individual behavior (i.e., see Steingroever, Wetzels, Horstmann, et al., 2013, for discussion of variance on the IGT). Effects of strategic movement on deck preference were examined within each age group (see Table 4). Findings were much more complex than our basic hypotheses about frequency and expected value. Consistent selections often indicated learned preference for Deck B in children, whereas inconsistency favored more Decks A + C selections, indicating that frequency preference is of central concern in children. Adolescents were similar to children in preferring frequency, except they tended to make more Deck D selections. Indeed, after childhood, nearly all individuals tended to select from Deck D, and this tendency was only modified by degree of consistency. As individuals became more consistent (high loss-stay), they were more likely to select on the basis of expected value, whereas inconsistency resulted in an even distribution of deck selections. Therefore, our hypothesis that consistency moderates frequency or net outcome preference depending on age was partially supported. It was not supported for the elderly, who were instead closer to younger adults, but selected more from Deck D as a result of consistency. This is detected as both an increase in net outcome and frequency preference (ambiguous) for older adults.

Figure 3.

Proportion of win-shift and loss-stay decisions by deck over 100 trials. Decks A and B are represented with dashed lines.

Table 4.

Correlations of Strategic Movement Measures With Deck Preference

Age group	Measure	A	B	C	D	N
5–10	Win-shift	.31**	−.32**	.41**	−.18*	174
	Loss-stay	.18*	.20*	−.05	−.29**	174
11–16	Win-shift	.51**	.01	.20*	−.38**	171
	Loss-stay	−.30**	−.14	.26**	.05	171
17–29	Win-shift	.50**	.23**	−.02	−.38**	664
	Loss-stay	−.41**	−.45**	.55**	−.01	664
30–59	Win-shift	.42**	.29**	−.03	−.36**	281
	Loss-stay	−.33**	−.39**	.56**	−.09	281
60–89	Win-shift	.54**	.12*	.07	−.39	293
	Loss-stay	−.38**	−.40**	.37**	.23*	293

Note. Deck preference is over 100 trials; strategic movement metrics are for Trial 99 collapsed on all decks. Bold formatting indicates significant differences in correlation compared to adults (ages 17–59).

^*p < .05.

^**p < .001.

In general, a linear decline in win-shift coupled with an increase in loss-stay occurred over the life span, although loss-stay improved for net outcome decks only. This casts doubt on a true win-stay/loss-shift strategy as an explanation of any age effect on the IGT. Furthermore, strategic movement appears to moderate the effects of age on deck preference. Except for children, higher consistency was nearly universally associated with a net gain preference (Decks C and D). Level of consistency indicated that children and adolescents were primarily learning frequency, whereas all other age groups primarily learned net outcome selections (Deck C or D). Therefore, strategic movement metrics might be utilized in future studies to indicate the presence of learning. In addition to the general strategic findings presented here, the online supplemental materials describe an age group breakdown of strategies as determined by cluster analysis and complement the finding that children tend to make inconsistent decisions. Findings from the following computational analysis are also incorporated into this cluster analysis.

Rationale for Computational Models

Many researchers have attempted to account for learning in the IGT by utilizing computational modeling. Computational models have been demonstrated as a powerful method of determining whether theoretical frameworks fit IGT data (Ahn, Busemeyer, Wagenmakers, & Stout, 2008; Busemeyer & Stout, 2002; Cheng, Sheu, & Yen, 2009; Wetzels, Vandekerckhove, Tuerlinckx, & Wagenmakers, 2010; Yechiam & Busemeyer, 2005). Although the goal of modeling is to predict decision outcomes and extrapolate cognitive parameters as neurological and psychological constructs, currently there is no consensus on which model best fits experimental IGT data (Steingroever, Wetzels, & Wagenmakers, 2013). Nevertheless, cognitive models purportedly involve all processes necessary in decision making, and examination of these models is a necessary step in elucidating the processes that contribute to decision making. If strategic movement moderates age-related differences in deck preference, as in the previous analysis, then cognitive modeling should reveal how strategic processes (e.g., consistency) interact with other parameters and result in these age effects.

It is predicted that the selection consistency parameters will increase over the life span. Furthermore, cognitive parameters such as memory should decline in older adults (Wood et al., 2005). Cognitive parameters (recency) should also be associated with net outcome preferences, while strategic parameters (consistency, loss aversion) should be associated with loss frequency preferences.

Prospect-Valence Learning (PVL) Model

Computational reinforcement learning models are based on three assumptions: Each individual evaluates positive and negative payoffs based on a utility function, learns about expected future payoffs from previous evaluations based on an updating or learning function, and determines which decks to select based on a probabilistic choice rule. The models used in the current study were based on a prospect utility function (see Ahn et al., 2008),

$$u(t)=\left\{\begin{array}{c}x{(t)}^{a}ifx(t)\ge 0\\ -\left|x{(t)}^a\right|ifx(t)<0\end{array}\right\},$$ (3)

where x(t) is the net amount won or lost on Trial t, α is an attention-weight parameter that establishes the shape of the utility function for an individual (0.01 < α < .9999), and λ is a loss aversion parameter (0.01 < λ < 5). As α approaches 0, the shape of the function becomes more stepwise, and decision makers place less value on feedback information. A value of λ below 1 indicates greater sensitivity to gain than loss, while a λ value above 1 indicates increased sensitivity to losses compared to gains and greater likelihood of shifting after losses. The utility function modifies a learning rule concerning the subjective value applied to each deck. Two rules examined in the current study were Rescorla Wagner (delta learning) and decay-reinforcement rules.

$$\text{Delta}\text{learning}\text{rule}:E_j(t)=E_j(t-1)+A·d_j(t)·[u(t)-E_j(t-1)].$$ (4)

$$\text{Decay}-\text{reinforcement}\text{rule}:E_j(t)=A·E_j(t-1)+d_j(t)·u(t).$$ (5)

These rules represent the learned expectancy for Deck j on Trial t On each trial the expected utility for the chosen deck is updated, while other decks remain unchanged (delta rule), or are discounted by an updating parameter (decay rule). δ_j(t) is a dummy variable that is 1 whenever Deck j is chosen on Trial t and 0 otherwise. For the delta learning rule, A is an updating parameter between 0 and 1 that determines how much the expectancy of a selected deck is modified by the discrepancy between the current utility and the expected utility from the previous trial, [u(t) − E_j(t − 1)]. For the decay-reinforcement rule, all expectancies are discounted, and only the utility of the selected deck is added to that deck’s expectancy. A is a recency parameter between 0 and 1 that deter mines how much expectancies from the previous trial are discounted. As A approaches 0, previous expectancies are discounted more. Individual deck utilities are then inserted into the choice rule function, which represents the choice on the following trial.

$$Pr[D(t+1)=j]=\frac{e^{\mathrm{\theta }(t)·E_j(t)}}{{\sum }_{k=1}^4{e}^{\mathrm{\theta }(t)·E_k(t)}}.$$ (6)

This rule modifies the deck expectancies by θ(t), the sensitivity to the choice probabilities. As sensitivity increases, choices become more deterministic and informed by expectancies. Ahn and colleagues (2008) suggested that sensitivity could either change with learning (i.e., a trial-dependent rule) or remain constant over time (i.e., a trial-independent rule). The trial-dependent learning rule is given by

$$\mathrm{\theta }(t)={(t/10)}^{\mathrm{c}},$$ (7)

where −5 < c < 5. High c values indicate more deterministic choices with increasing trial, while low c values indicate random choices with increasing trial. The trial-independent choice rule is given by

$$\mathrm{\theta }(t)=3^{\mathrm{c}}-1,$$ (8)

where 0 < c < 5. The trial-independent choice rule suggests that choice consistency is not contingent on trial. In both cases, higher c values indicate more consistency and deterministic choices, and lower values indicate random choices.

Models were evaluated using a one-step-ahead prediction method, where choices on the following trial were predicted based on previous choices and outcomes of those choices. Predictions over 100 trials (or until the trial where one deck runs out of cards) were combined, and parameters were estimated in such a way that maximized the log likelihood (LL) of the data fit to the model for each individual. This was accomplished by fitting parameters to a grid using 50 starting points and finding the values of each parameter that would maximize the LL of the function for all 50 iterations (for further details on modeling computations, see Ahn et al., 2008). The LL of the model for each individual was also compared to the LLs of baseline models for the same individuals, and comparisons were adjusted for model complexity using the Bayesian information criterion (BIC). The baseline model assumed that consecutive selections were statistically independent and that deck selections were made using only information about the overall proportion of selections from each deck. Therefore, a cognitive model could only outperform a baseline model if it explained learning that occurred from one trial to the next.

PVL Model Results and Discussion

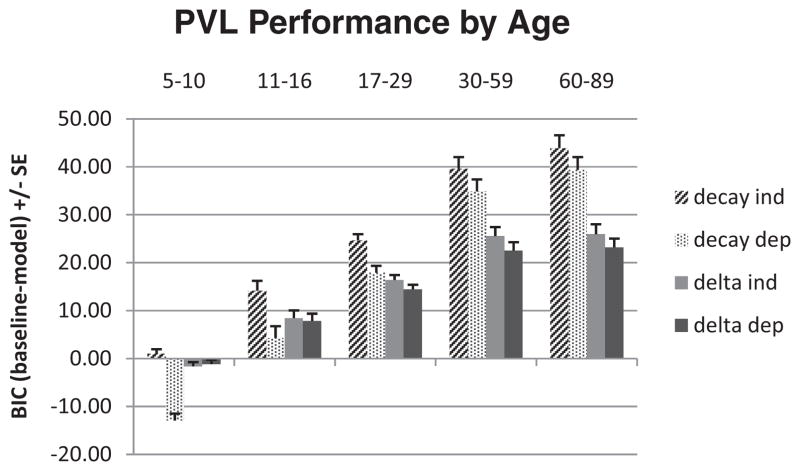
Figure 4 shows PVL model performance by age group. No model successfully characterized learning in children or adolescents, but for young, middle-aged, and older adults, the decay-reinforcement learning model coupled with the trial-independent choice rule was most successful as determined by BIC (baseline-model) estimates. The decay-reinforcement model was least effective in characterizing learning when individuals shifted decks often, as would be expected if decisions were truly random (see the online supplemental materials for a detailed examination of model predictions by age). In addition to the problem of modeling children, parameters for the decay-independent model were often located on the boundaries of parameter space. As a result, all cases with parameters stuck on boundary space or below age 17 were selected out of further analyses (see the online supplemental materials for further information).

Figure 4.

Model evaluation using Bayesian information criteria by age group. Decay = decay reinforcement rule; delta = delta learning rule; dep = trial-dependent choice rule; ind = trial-independent choice rule.

Correlations between modeling parameters and age were examined first. Attention (alpha) and loss aversion (lambda) parameters did not reliably change with age (ps > .05), while recency and consistency were negatively, r(480) = −.20, p < .001, and positively, r(480) = .17, p < .001, correlated with age, respectively. Parameters and age were also examined in a regression predicting net outcome and loss frequency selections for all remaining 482 cases. Main effects of linear age and parameters accounted for 22% of the variance in high net outcome selections, F(5, 476) = 27.41, p < .001, and 10% of the variance in low loss frequency selections, F(5, 476) = 10.92, p < .001. It was found that age significantly predicted fewer net outcome selections (β = −.12, p = .003) and that higher recency and consistency both predicted more net outcome selections (β = .23, p < .001, and β = .44, p < .001, respectively). Age predicted more loss frequency selections (β = .16, p < .001), while attention (alpha) and consistency significantly predicted fewer loss frequency selections (β = −.23, p < .001, and β = −.19, p = .005, respectively). These findings indicate that selection consistency strongly relates to deck preference. Indeed, win-shift and loss-stay variables were found to be highly correlated with the consistency parameter (rs = −.66 and .52, respectively) and loss aversion parameter (lambda; rs = .40 and −.31, respectively). High memory for previous feedback represented another characteristic of net outcome preference, suggesting the involvement of a cognitive component. Importantly, frequency preference did not explicitly require a cognitive component but was affected by attentiveness and behavioral consistency. In other words, many adults may arrive at frequency preference by using their basic skills and perhaps minimal attentiveness, whereas those who arrive at net outcome preference are more cognitively involved in the task. These findings largely support our hypothesis that consistency parameters increase over the life span, while cognitive parameters decrease (Wood et al., 2005). Cognitive parameters (recency) were also associated with net outcome preferences, but strategic parameters were not limited to association with only loss frequency preference. As in the strategic analysis, consistency was positively related to net outcome preference and negatively related to loss frequency preference. Loss aversion was not supported as a relevant parameter in loss frequency preference, but loss aversion effects may have been moderated by other parameters such as memory or attention.

Although model findings were largely consistent with expected findings (lower memory, greater consistency with age; Wood et al., 2005), newer models must account for decision instability in children and adolescents for these models to be of particular use in clinical settings. PVL models failed to provide effective estimations of child and/or adolescent learning. Because a large portion of children and adolescents was characterized by unstable decision making, decision making could not be modeled in these individuals. Selection stability (number of switches) was also strongly related to model performance, indicating a limitation of cognitive modeling for developmental groups. Use of maximum-likelihood estimation (MLE) is a limitation of this analysis, as subject data were not mutually informed during parameter estimation. This increased the noise and likely reduced the efficacy of estimation procedure (scatterplots for parameters revealed model over fitting). One alternative involves use of a Bayesian hierarchical approach, which has been shown to outperform the MLE approach (Ahn, Krawitz, Kim, Busemeyer, & Brown, 2011; Wetzels et al., 2010). However, this approach is more applicable to smaller data sets and assumes group-level distributions when it is unclear how many groups are present in the data set. Newer models, such as win-stay/loss-shift, have also been shown to outperform reinforcement learning models, at least in older adult populations, and may complement traditional learning models by determining the cause of decision instability (Worthy, Hawthorne, & Otto, 2013; Worthy & Maddox, 2012). Nevertheless, the current model contributes to understanding the cause of performance decline in older adults with the assumption that parameters represent a mix of theoretical cognitive and motivational processes.

Cognitive Correlates of Strategy, Modeling, and IGT Performance

Researchers have a strong interest in the role of cognitive abilities in learning high net outcome decisions (Toplak, Sorge, Benoit, West, & Stanovich, 2010). Working memory, set shifting, behavioral inhibition, episodic memory, reaction time, and/or general intelligence tasks may provide evidence of a theoretical cognitive process in decision making. These tasks encompass a general selection of cognitive tasks commonly applied to IGT analysis (Toplak et al., 2010) and are also relevant in life-span cognition research (Salthouse, Atkinson, & Berish, 2003; Salthouse & Davis, 2006). Based on previous associations of cognition with IGT performance, we expected small to moderate correlations. We also predicted that cognitive variables would be associated with consistent decision making (low win-shift or high loss-stay). Furthermore, the recency parameter in the PVL model explicitly suggests a memory component unlike attention, consistency, or loss aversion parameters, which suggest behavior independent of cognition.

Table 5 shows cognitive variables in a correlation matrix with net outcome selections, loss frequency selections, and strategic movement metrics. All correlations were age controlled to partial out shared age-related variance. In general, correlations were small and in many cases not significant. Reaction time was found to be the least useful cognitive metric, whereas N-back was found to be the most useful. Better performance on WCST, N-back, and matrices subtests positively correlated with IGT performance (Decks C + D), suggesting that cognitive ability does relate to good performance to a small extent. Similarly, performance on cognitive tasks was positively correlated with consistent decision making in the form of lower win-shift and higher loss-stay at the end of the IGT. No cognitive variables were associated with number of loss frequency selections (Decks B + D). When examining cognitive relationships with modeling parameters, better performance on all cognitive measures was significantly associated with recency (rs < .20), but no other parameters. However, after selecting out cases that were on parameter boundaries and removing children and adolescents from the sample size, these correlations disappeared. Therefore, much more work is necessary in building newer cognitive models before validation can occur. Nevertheless, early results are promising and indicate that at least one of the PVL parameters may involve cognitive processes.

Table 5.

Correlations Between Cognitive Variables, Deck Preferences, and Strategic Movement

Variable	C+D	B+D	Shift	Stay	df
Reaction time	−.10*	−.02	.09	−.07	959
Stroop	−.19**	−.07	.22**	−.17**	920
Matrices	.23**	.05	−.21**	.17**	936
WCST	−.21**	−.04	.19**	−.18**	1,255
2-back	.29**	.00	−.20**	.22**	920
Memory	.11*	.04*	−.11*	.10	1,292

Note. All correlations were controlled for age. C+D = high net outcome selections; B+D = low loss frequency selections; Shift = win-shift on Trial 99; Stay = loss-stay on Trial 99; Stroop = Part D − Part B time; WCST = Wisconsin Card Sorting Task perserverative errors.

^*p < .05.

^**p < .001.

Overall, attempts to link cognitive abilities to IGT performance have, at best, resulted in small effects (Toplak et al., 2010). We expected to successfully link IGT performance to cognitive abilities by using a large sample. Indeed, better cognition was found to result in net outcome preferences and did not affect loss frequency preference. Nevertheless, cognitive effects in the current analysis were small (i.e., rs < .3). The weak relationship between our measures of cognition and IGT performance is not surprising given the findings of complex interactions obtained in the PVL model. As of yet, relationships between cognitive variables and modeling parameters remain unclear. The relationship between cognition and the modeling parameters may have been lowered due to inconsistent decision making, which was shown to confound parameter estimation. That is, the relationship could have been weakened due to low reliability of modeling parameters at the level of individual subjects—another indication of the problem of variability in the IGT task. Until a model is found that can account for high switching, it is likely that correlations will remain low between parameters and cognitive ability. Nevertheless, relationships between specific modeling parameters are an initial step in validating computational procedures for examining the IGT and are necessary for wide usage of computational procedures in clinical settings.

General Discussion and Conclusion

Results in the present study were largely consistent with many previous findings. As expected, IGT performance increased from childhood to adulthood and declined in older adults (Baena et al., 2010; Cassotti et al., 2011; Cauffman et al., 2010; Crone & Van der Molen, 2004; Denburg et al., 2005; Fein et al., 2007; Hooper et al., 2004; Isella et al., 2008). Not all studies of IGT performance with the elderly detect a decline in performance (Henninger et al., 2010; Lamar & Resnick, 2004; MacPherson et al., 2002; Wood et al., 2005). As noted in the PVL analysis, the IGT has numerous theoretical components that may interact during decision making. These interactions explain why age may have only a small effect when examining deck preference. Several psychological constructs may influence deck preference, and some of these, such as consistency in decision making, may compensate for memory processes lost as a result of aging. Similar to previous reports, no substantial relationship between cognitive tasks and IGT performance was detected (Brand, Recknor, Grabenhorst, & Bechara, 2007; Del Missier, Mäntylä, & Bruine de Bruin, 2012; Henninger et al., 2010; Stocco, Fum, & Napoli, 2009; Toplak et al., 2010). Nevertheless, the findings obtained in four different analyses provide the first complete picture of life-span developmental trends in experiential decision making on the IGT from childhood to old age.

IGT Performance by Children and the Elderly

A basic review of developmental literature suggests that children, adolescents, and the elderly make similar decisions. However, in-depth analysis of deck preference suggests that a dual-process framework of the IGT in which loss frequency is separate from net outcome preference provides a clearer understanding of the differences in early and late life decision making. Furthermore, the IGT is sensitive to both strategic judgment in children and cognitive deficits in older adults. Children and adolescents utilize an impulsive strategy, whereas older adults utilize a relatively stable strategy that is a combination of loss avoidance and maximization of gain. However, many older adults experience cognitive decline (Salthouse & Davis, 2006), and modeling analysis suggested that loss frequency preference in older adults was in part due to poor memory for feedback. Future models must account for the high instability in children and adolescent groups to provide an unambiguous answer about the development of experiential learning. In the absence of improved behavioral models, researchers are strongly encouraged to examine additional behavioral metrics on the IGT involving strategic movement (e.g., win-shift and loss-stay), as opposed to focusing only on traditional performance metrics and deck choices. Overall, the results of these analyses indicate that research questions regarding IGT performance need to shift toward relative decision stability during development.

The IGT as an Experimental Assessment Tool

The IGT is frequently used to assess decision making in normal individuals, yet it has been increasingly criticized in recent years. Some of the earliest criticism occurred in the studies of decision making by children and elderly (Crone & Van der Molen, 2004; Huizenga et al., 2007; MacPherson et al., 2002). Many of these authors found the traditional performance metric of advantageous deck proportion provided less information in assessing decision ability than examination of individual decks by trial. Punishment frequency bias was also detected in early development and aging studies (Crone & Van der Molen, 2004; MacPherson et al., 2002).

Steingroever, Wetzels, Horstmann, and colleagues (2013) also noted this frequency bias and provided a carefully considered evaluation and critique of the IGT. They suggested that the interpretation of IGT findings depends on three assumptions: (a) Normal participants learn to choose advantageous decks over disadvantageous decks, (b) normal participants show similar deck choices, and (c) normal participants show initial exploration of decks followed by exploitation of advantageous decks. These assumptions are frequently violated in normal populations and potentially invalidate comparison of normal and impaired populations. All three of these assumptions were violated in the present study, indicating that several behavioral metrics need to be considered when interpreting performance. However, even after considering variability in each of these assumptions, age effects were still present. For example, a subset of adults learned to make advantageous decisions and to follow an explore-exploit learning pattern. Examination of performance in children represented an extreme and shows that some populations are clearly distinguished from normal adults: Children appear homogeneous as an age group yet display anomalous and inconsistent decision making. Variability in responses occurred in all age groups except children, and every group utilized some degree of frequency bias, consistent with critiques by Lin, Song, Chen, Lee, and Chiu (2013). Nevertheless, frequency bias could not account for all age-related variability, especially variability between children and adults.

Serious concerns have also been raised about the punishment and reward structure of the IGT in a series of articles by Lin and Chiu (Chiu, & Lin, 2007; Lin et al., 2007). Chiu and Lin (2007) found that the high frequency loss Decks A and C are not equivalent in terms of actual frequency of losses when considering immediate outcome (win − loss). In a block of 10 trials, Deck A will have five loss trials while Deck C will have an average 2.5 draws and 1.25 losses. Individuals may prefer Deck C because of its favorable gain-loss frequency rather than its favorable net gain outcome. Lin and colleagues (2007) also took note of a prominent Deck B phenomenon in which participants failed to suppress a Deck B preference in the later stages of the game. However, in the current study, the degree of frequency bias changed over the life span, indicating that loss frequency preference is only one factor contributing to task performance and does not completely explain an age effect. Nevertheless, the reward structures of the original task may cause individuals to prefer specific decks for reasons other than net outcome. Issues regarding IGT reward structure need to be addressed as they may affect selection patterns in some groups.

Although responses were highly variable across the life span, decision patterns did not appear random. Researchers may opt to control some of the variability in performance by manipulating task parameters such as loss frequency or preventing participants from switching decks at their own discretion (see Cauffman et al., 2010). Nevertheless, the original IGT represents a potentially important research tool in the investigation of processes related to decision making and should not be discarded in the absence of any singularly compelling explanation of decision behavior (i.e., cognition, frequency bias, or personality).

The IGT as a Clinical Assessment Tool

Use of the IGT as a clinical tool is automatically suspect due to criticism of the IGT as a valid experimental paradigm. Several researchers strongly indicate that caution must be exercised when interpreting clinical data in normal adults (Buelow & Suhr, 2009; Chiu & Lin, 2007; Fernie, 2007; Lin et al., 2007, 2013; Steingroever, Wetzels, Horstmann, et al., 2013). Beyond this warning, there exists the problem of differentiating clinical deficits when using the IGT. For example, the finding that a cognitive parameter moderates IGT performance indicates that populations that share cognitive impairments may perform poorly on the IGT. Similarly, for the same reason that strategic movement moderates IGT performance, individuals with noncognitive impairments but with other behavioral deficits (e.g., impulsive behavior) may also perform poorly (Bechara et al., 1994). Despite the number of limitations of modeling in the current study, cognitive modeling continues to provide the most realistic possibility for establishing the IGT as a clinical assessment (Busemeyer & Stout, 2002). Importantly, IGT modeling may represent a valuable approach to detecting unique impairments in several different clinical populations. Differences in clinical deficits assessed through the IGT remain unclear in the absence of additional information, such as that provided by modeling.

Limitations and Conclusion

As this study has demonstrated, the complexity of the IGT warrants unique investigation. However, emphasis on the IGT in most studies detracts from the possibility of alternative decision components contributing to behavior during the life span (e.g., descriptive decision making; Mata et al., 2011). Other decision-making assessments such as the Game of Dice or the Balloon Analogue Risk Task may deserve greater attention in experimental situations as these tasks appear more sensitive to individual processing components (Brand, Labudda, & Markowitsch, 2006; Lejuez et al., 2002). Another limitation involves sampling of college-aged individuals. Students received extra credit instead of monetary compensation, which children, adolescents, and older adults received. Because multiple processes appear to contribute to IGT performance, any differences in test administration may result in minute changes in decision parameters, such as motivation or attention to feedback. A final limitation is the use of cross-sectional sampling to make inferences about cognitive development. Cross-sectional sampling does not control for interindividual variability that may arise for different groups across the life span. However, longitudinal assessment is also problematic because the IGT is subject to practice effects (Lin et al., 2013; Xiao et al., 2013).

Despite these limitations, the present study clearly demonstrates the differences in experiential decision making that occur across the life span. A major difference in decision-making rationale associated with increased consistency was found to occur in late adolescence. This difference was more prevalent in many of the adults who exhibited a skill reflecting advantageous experiential decision making as opposed to a frequency preference. A final difference occurred in late adulthood, when individuals retained adult levels of consistency but preferred low loss frequency more than net outcome decisions. Differences in experiential decision making across the life span were reflected in deck preferences, decision strategies, cognitive models, and cognitive correlates. The IGT was found to be a sensitive indicator of distinct age-related deficits in decision making in early and late life. Future research utilizing the IGT should recognize that traditional assumptions involving IGT performance do not hold in normal adult populations and that basic deck-selection metrics do not adequately assess performance in all individuals.