Abstract
When the sensory consequences of an action are systematically altered our brain can recalibrate the mappings between sensory cues and properties of our environment. This recalibration can be driven by both cue conflicts and altered sensory statistics, but neither mechanism offers a way for cues to be calibrated so they provide accurate information about the world, as sensory cues carry no information as to their own accuracy. Here, we explored whether sensory predictions based on internal physical models could be used to accurately calibrate visual cues to 3D surface slant. Human observers played a 3D kinematic game in which they adjusted the slant of a surface so that a moving ball would bounce off the surface and through a target hoop. In one group, the ball's bounce was manipulated so that the surface behaved as if it had a different slant to that signaled by visual cues. With experience of this altered bounce, observers recalibrated their perception of slant so that it was more consistent with the assumed laws of kinematics and physical behavior of the surface. In another group, making the ball spin in a way that could physically explain its altered bounce eliminated this pattern of recalibration. Importantly, both groups adjusted their behavior in the kinematic game in the same way, experienced the same set of slants, and were not presented with low-level cue conflicts that could drive the recalibration. We conclude that observers use predictive kinematic models to accurately calibrate visual cues to 3D properties of world.
Keywords: 3D slant, calibration, psychophysics, stereopsis
Introduction
To effectively control our behavior, our sensorimotor systems need to maintain external accuracy with respect to the world. Previous research has shown that perceptual attributes can be recalibrated after extended experience of altered sensory feedback, such as when wearing laterally displacing or magnifying prisms (von Helmholtz, 1925; McLaughlin and Webster, 1967; Adams et al., 2001). There are, however, many possible causes of the recalibration. In addition to changing the sensory consequences of a person's actions, prisms introduce low-level cue conflicts and alter the overall statistics of incoming sensory data. Both of these are known to cause recalibration, but in both instances this can either increase or decrease a cue's external accuracy (Ernst et al., 2000; Atkins et al., 2001; Adams et al., 2004; Burge et al., 2010; Seydell et al., 2010; van Beers et al., 2011). This is possible because neither the perceptual estimates provided by a cue, nor the reliability associated with those estimates, can signal whether a cue is well calibrated (Smeets et al., 2006; Ernst and Di Luca, 2011; Scarfe and Hibbard, 2011).
Despite these challenges to accurate calibration, human observers exhibit expert knowledge of the physics governing the environment, such as mass, gravity, and object kinematics (Battaglia et al., 2013; Smith and Vul, 2013; Smith et al., 2013). Knowledge describing these dynamics could provide the error signals required to maintain accurate calibration. Our experiment was designed to test this idea. To do this we manipulated the kinematics of a 3D game in which observers altered the slant of a surface so that a ball would bounce off the surface and through a target hoop. By altering the bounce angle of the ball we were able to make the surface behave as if it had a different slant to that signaled by visual cues. This allowed us to determine whether observers' expectations of the ball's bounce, based on an understanding of object kinematics, could drive recalibration of perceived 3D surface slant.
We also examined slant recalibration when the ball's altered bounce was coupled with the ball spinning in such a way that it could “explain away” its altered trajectory (Battaglia et al., 2010; Shams and Beierholm, 2010; Clark, 2013). The role of internal physical models and sensory prediction has been most closely studied in the domain of visuomotor control where it has been shown that error signals based on sensory prediction can be used to update information about the current body state (Wolpert et al., 1998; Cressman and Henriques, 2011; Henriques and Cressman, 2012). More recently, research has suggested that internal models of physical laws may be a much more general part of our perceptual experience than previously thought (Hamrick et al., 2011; Battaglia et al., 2013; Smith and Vul, 2013; Smith et al., 2013). The experiments reported here provide an unambiguous test of the extent to which sensory prediction, based on internal physical models, can be used to calibrate sensory cues so that they provide accurate information about the world.
Materials and Methods
Apparatus.
Stimuli were displayed on a spatially calibrated, gamma corrected, CRT (1600 × 1024 pixels, 85 Hz refresh rate) viewed at a distance of 50 cm in a completely dark room. At this distance the monitor spanned ∼51 × 34 degrees of visual angle. Eye height was matched to the vertical center of the CRT and head position maintained directly in front of the center of the monitor with a chin rest. Stereoscopic presentation was achieved using Stereographics Crystal Eyes CE-3 shutter goggles. All stimuli were tailored to the interocular distance of each observer and were rendered in OpenGL using MATLAB and the Psychtoolbox extensions (Brainard, 1997; Pelli, 1997; Kleiner et al., 2007). Stimuli were rendered in red to exploit the fastest phosphor of the monitor. No cross-talk between the two eyes view was visible.
Participants.
There were 12 participants in total (9 male, 3 female). Six participants were assigned to each condition (four males and two females in condition one, five males and one female in condition two). All participants were naive to the purpose of the experiment, except for P.S. Sample size was determined on the basis of the consistency of the effects across participants in a pilot study. The University of Reading Research Ethics Committee approved the study.
Kinematic ball game.
Observers performed two different tasks: a 3D kinematic ball game and a frontoparallel slant judgment task. In the kinematic game they had to adjust the slant of a disparity-defined surface on-line with a mouse so that a moving checkerboard-textured ball (2 cm diameter) bounced off the surface and through a target hoop (Fig. 1), Rendered distance to the surface matched that of the screen. The surface was elliptical with a fixed width of 10 cm, but with a variable height selected from a uniform distribution of 7.5–12.5 cm (when frontoparallel, this equated to 8.58 and 14.25 degrees, respectively). Varying the height degraded the use of vertical angular subtense as a cue to slant. The dot density of the surface was 0.6 dots per cm2. Each dot had a diameter of 3.4 pixels (∼0.11 degrees) and was positioned with subpixel precision. The slant of the surface could be adjusted by ±50 degrees around its horizontal axis using lateral mouse movements.
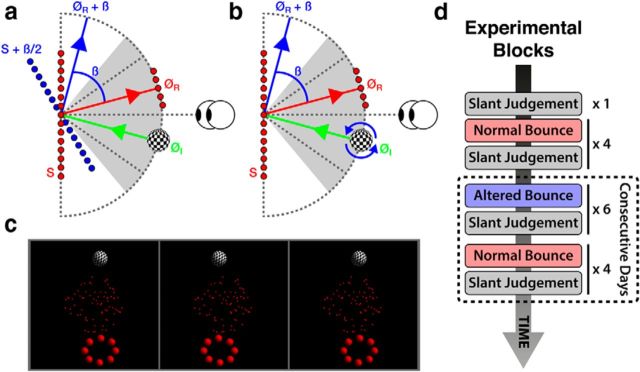
Figure 1.
Schematic illustration of the kinematic ball task for (a) the nonspinning ball and (b) the spinning ball. During the experiment on each trial the position of the ball took a random position within a ±50 degree range on an imaginary circle 12 cm in diameter, centered on the center of the slanted surface. This range is represented by the shaded region in a and b. Similarly, on each trial the hoop took a different random position within a ±35 degrees range on the same imaginary circle. This range is represented by the dashed diagonal lines in a and b. c, Stereogram of the ball game stimuli (left and middle images for divergent fusion, middle and right image for crossed fusion). d, Sequence of experimental blocks during the experiment.
There were 80 trials in each block. On each trial, the starting position of the ball took a random value within ±50 degrees of straight ahead, on an imaginary circle with a radius of 12 cm centered on the center of the slanted surface (Fig. 1a,b, shaded region). The position of the hoop took a random value between ±35 degrees of straight ahead on the same imaginary circle (Fig. 1a,b, diagonal dashed lines). The ball and hoop took random positions within different angular ranges to ensure that when the ball's bounce bias was introduced (see below) observers could always get the ball directly through the hoop, i.e., they were never given an impossible task. The orientation of the ball around its center (in all three dimensions) was randomized on each trial. The target hoop consisted of eight balls (1 cm in diameter) equally spaced around a circle 4 cm in diameter and was always rendered tangential to the imaginary radius on which it was placed. The hoop and checkerboard-textured ball were illuminated with a single point light source off to the upper right. The random-dot surface was unaffected by this light source.
At the beginning of each trial, the checkerboard ball would pause for 1 s in its starting position before launching directly toward the center of the surface at a constant speed of 6 cm s−1. Initially, for the first four blocks, the ball bounced off the surface vertically with a mirror reflection, such that ∅R = ∅I (Fig. 1). This is, to a first approximation, how nonspinning balls and planar surfaces behave in real life. For the next six blocks of trials, a bias was added to the ball's bounce such that ∅R = ∅I + β (exaggerated for the purpose of illustration in Fig. 1). The value of β was 15 degrees (sign consistent for a single observer, but counterbalanced across observers). During this period, for any slant Si, the surface now behaved as if it had a slant of Si + β/2. For the final four blocks of trials, the bounce bias was removed. Observers reported that, throughout the experiment, they remained entirely unaware of the introduction and removal of β despite having to adapt their behavior in the game to continue getting the ball through the hoop (for further discussion see Results, Equivalence of the learning signal across groups).
After bouncing off the surface, the ball continued moving at the same speed as before the bounce until its center intersected the imaginary circle upon which it started. The game then paused for 1 s to give observers feedback about the magnitude of their error. If the center of the ball passed within the hoop's radius the hoop turned a lighter shade of red, if it passed within 1.25–1.5 times its radius it stayed the same shade of red, and if it passed outside this range it turned a darker shade of red. An error of zero was achieved if the ball passed directly through the hoop. It was predicted that, if high-level knowledge can drive sensory recalibration in addition to adapting behavior, observers might also recalibrate their perception of slant with introduction and removal of β. This would happen if observers assumed the laws of kinematics governing the task were invariant over time and instead used errors in the bounce task to infer that their encoding of slant from disparity had slipped out of calibration.
Spinning ball.
In a separate condition, for a separate set of observers, everything was identical to that described above except that when the scene appeared the checkerboard ball began spinning around its horizontal axis at a speed of 300 degrees/s. The ball's spin was in the same direction as the bias added to its bounce. The aim here was that observers would have to adapt their behavior in the game in the same way, because β was the same, and would therefore experience the same set of surface slant; however, the ball's spin might offer an alternative physical explanation for its altered bounce and thus remove any need for recalibration. Discounting of this sort need not be a binary decision, but could instead reflect the degree of certainty the observer has that the alternative explanation is valid. This type of process has been termed “explaining away” in the context of Bayesian decision theory and can be modeled within a probabilistic framework (Battaglia et al., 2011).
Frontoparallel slant judgment task.
To track any recalibration of slant that occurred, all observers completed a frontoparallel slant judgment task interleaved between game blocks (Fig. 1d). In this task, observers judged whether a random dot stereogram of a slanted surface (identical to that used in the kinematic ball game) was sloped toward or away from them (top near–bottom far, and top far–bottom near, respectively). During this task, the hoop and ball were not present, but the surface was otherwise identical to that used in the kinematic ball game, including the variation in its vertical height on each trial. At the start of each trial, a fixation point 13 pixels (∼0.42 degrees) in diameter was presented for 1 s centrally in the plane of the screen. The 3D slanted surface was then presented, also for 1 s. This was replaced by the fixation point, which remained on the screen until observers indicated their response by pressing one of two keyboard buttons. Keyboard responses were used to avoid any carryover effects from using the mouse for the ball-bounce task.
The slant of the surface was varied using the method of constant stimuli (seven slant values, each presented in a randomized order 33 times). The number of slant values and number of repetitions had provided well fit psychometric functions in a pilot study. The slant range and slant center was manually adjusted for each observer as needed throughout the experiment to ensure that their point of subjective equality (PSE) remained within the range and that the function encompassed high and low performance levels to obtain a good psychometric function fit (Wichmann and Hill, 2001a, b; Prins and Kingdom, 2009; Kingdom and Prins, 2010). This was essential as different observers adapted their perception of slant by different magnitudes and these differences could not be predicted a priori (Fig. 4, described in more detail later in the text). We note also, that we chose a task that observers could understand readily and unambiguously; indeed, subjectively, all found the task exceptionally easy to complete.
Figure 4.
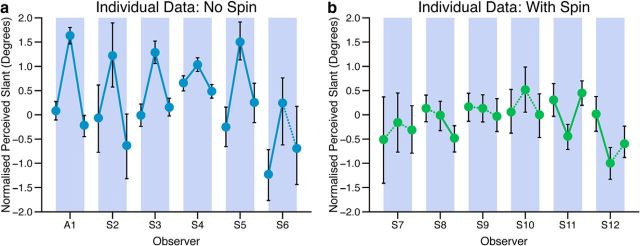
Recalibration effect for each observer in the (a) nonspinning ball and (b) spinning ball groups. This is in the same format as Figure 3c, and shows the slant perceived as frontoparallel at the end of each phase of the experiment, i.e., sessions 5, 11, and 15, as highlighted in Figure 3a and b. Error bars show bootstrapped 95% confidence intervals from the psychometric function fit. Solid lines show differences between PSEs at the p < 0.05 level, dashed lines show no significant difference. Participant labeled A1 is P.S. Blue bands delineate the data from each observer.
Procedure.
There were 14 sessions (Fig. 1d) each lasting around half an hour. Each session consisted of two separate tasks: first, the 3D kinematic game and second, the frontoparallel, slant judgment task. The exception to this was the first session, which had an additional block of slant judgment trials before the first block of ball task trails. To maximize the chances of measuring any recalibration, the last 10 sessions had to be completed over consecutive days. Furthermore, given that sleep can enhance the effects of perceptual learning with stereoscopic stimuli (van Ee, 2001), observers were encouraged to spread these last 10 sessions over a full working week of 5 d. Therefore, typically, each observer completed the last 10 blocks, 2 blocks per day for 5 consecutive days.
Results
Kinematic ball game
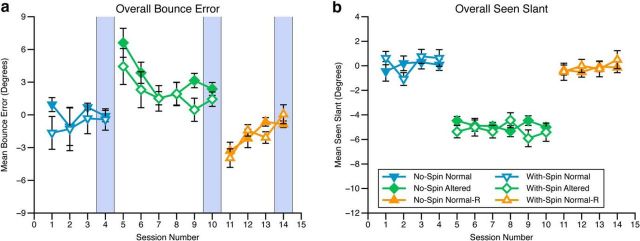
Observers' average error across blocks of the ball game was calculated, as well as the average slant presented throughout the task (Fig. 2). Because half of the observers experienced a positive bounce bias and half a negative bounce bias, in all graphs, for those observers where β was negative we have multiplied their data by −1. As can be seen, observers in the two conditions (nonspinning and spinning ball) learned to change their behavior in response to the altered bounce in the same way and at the same rate over the full course of the experiment, including with the introduction and removal of β (Fig. 2a). This was confirmed by a between-subjects ANOVA, with experimental block as a within-subjects factor, which showed that there was a significant main effect of experimental phase (F(5,50) = 10.44, p < 0.001), but no significant effect of group (F(1,10) = 0.9, p = 0.37), and no interaction (F(5,50) = 1.41, p = 0.24). As a result of this, observers in each group experienced the same slants during the ball game (Fig. 2b; this is also true if medians are used instead of means). We can therefore be confident that any differences in recalibration observed across the two groups cannot be caused by differences in the slants seen during the ball game or differences in the way observers in each group learned to respond to the altered bounce. For example, there is no evidence in our data that the ball spinning disrupted how observers adapted to its altered bounce. Indeed, the magnitude of β was specifically selected on the basis of piloting so that this would not occur.
Figure 2.
a, Mean bounce error across sessions during the ball bounce task. b, Mean seen slant during each session of the ball bounce task (note: Normal-R = Normal bounce regained). Error bars show SEM. The blue vertical stripes highlight the final block of each phase of the experiment. These are included on the data plots to ease comparison across this figure and Figure 3.
Recalibration of perceived slant
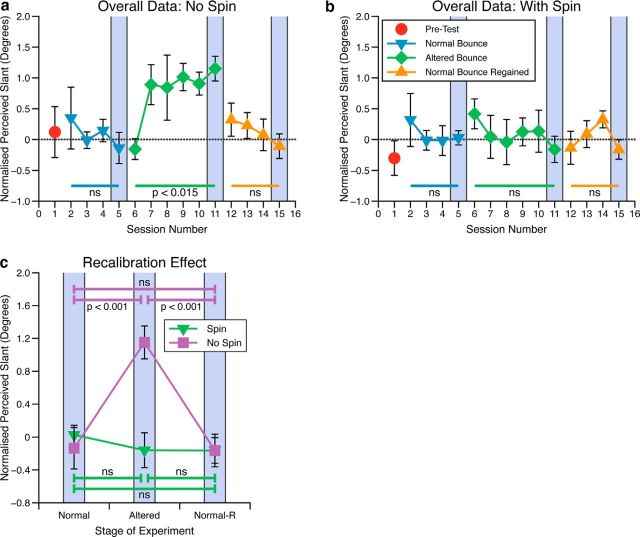
Cumulative Gaussian functions were fitted to the slant judgment data by a maximum likelihood procedure in MATLAB using the Palamedes software package (Prins and Kingdom, 2009; Kingdom and Prins, 2010; Prins, 2012). The PSE and 95% confidence intervals were estimated via bootstrapping. The PSE represents the slant that observers would perceive as frontoparallel. Figure 3 shows the mean PSEs for observers in each group across the 15 sessions. Here, to remove any small constant biases in perceived frontoparallel, each observer's data have been normalized to the mean slant seen as frontoparallel across blocks 3–5 (mean shift of 0.46 degrees across observers). Additionally, as for the ball game data, where β was negative the observer's data have been multiplied by −1 to make the bounce biases' polarity comparable across observers.
Figure 3.
Slant perceived as frontoparallel, normalized across observers, as measured with the frontoparallel slant judgment task interleaved between ball bounce blocks. This is shown for (a) the nonspinning ball group and (b) the spinning ball group. c, Overall recalibration effect averaged across observers in each group. This represents the slant perceived as frontoparallel at the end of each phase of the experiment, i.e., sessions 5, 11, and 15, as highlighted in a and b. Error bars all show SEM.
Effects over time
As can be seen in Figure 3a, when the bounce bias was introduced (blocks 6–11) observers in the nonspinning ball group recalibrated their perception of slant so that a perceptually frontoparallel surface became more like the surface that behaved like a frontoparallel surface in the ball game. Upon removal of the bounce bias observers were able to more rapidly switch back to the previous sensory mapping for perceived slant, as would be predicted by previous research (Welch et al., 1993; van Dam et al., 2013). Consistent with this, within-subjects ANOVA showed that for the nonspinning ball condition there was no significant recalibration across sessions in the normal bounce phase (F(3,15) = 0.43, p = 0.73, ns), there was significant recalibration during the altered bounce phase (F(5,25) = 3.54, p < 0.015), and no significant recalibration over the phase where the normal bounce was regained (F(3,15) = 0.84, p = 0.49, ns). In contrast, with the spinning ball there was no significant recalibration in any phase of the experiment (normal bounce phase: F(3,15) = 0.33, p = 0.81, ns; altered bounce phase: F(5,25) = 2.03, p = 0.11, ns; and when the normal bounce was regained: F(3,15) = 3.11, p = 0.06, ns).
Perceived slant after full experience
We would expect the maximum learning effect to be evident at the end of each phase of the experiment where the bounce was altered, i.e., after blocks 11 and 15. Figure 3c shows the slant perceived as frontoparallel in these cases compared with that in block five, which was the last block of the normal bounce phase, before introduction of the altered bounce. As can be seen, with a nonspinning ball, experience of a biased bounce resulted in significant recalibration of perceived slant; however, this recalibration was eliminated when the introduction of the bounce bias was coupled with the ball spinning. Between-subjects ANOVA showed there to be a significant main effect of condition (spinning vs nonspinning ball; F(1,30) = 6.39, p < 0.017) and experimental phase (normal bounce, altered bounce, and normal bounce regained, F(2,30) = 6.26, p < 0.005), as well as a significant condition by phase interaction (F(2,30) = 8.41, p < 0.001). This interaction arose because perceived frontoparallel was the same after each phase of the experiment with the spinning ball, but not with the nonspinning ball (Fig. 3c).
Consistency of effects over observers
We were interested in how consistent the recalibration effect was across observers. In Figure 4 we plot perceived slant at the end of each phase of the experiment, for each observer, in each condition. Here error bars show bootstrapped 95% confidence intervals around the perceived slant PSEs. As can be seen visually, the predicted recalibration effect was highly consistent across all observers in the no-spin condition. In contrast, the recalibration effect was absent in all observers in the spinning ball condition. To test this statistically, on a per observer basis, we used a bootstrapped likelihood ratio (LR) test to compare the PSEs generated by each observer at the end of each stage of the experiment (Kingdom and Prins, 2010; i.e., normal bounce phase compared with altered bounce phase, and altered bounce phase compared with normal bounce regained phase).
For each observer, we first determined the likelihood of the data from both conditions assuming a single psychometric function, with a single PSE (1PSE model), versus two separate psychometric functions, with different PSEs and, potentially, different slopes (2PSE model). The 1PSE model assumes that there is no effect of adaptation and that any difference between the data in the two conditions is simply due to sampling noise. In contrast, the 2PSE model assumes that the difference between PSEs is due to a significant recalibration effect and not just sampling noise. The ratio of these two likelihoods (1PSE/2PSE) gives us the LR, which is a measure of the relative goodness of fit of the 1PSE and 2PSE models. If there is indeed no difference between conditions (i.e., no recalibration effect), a generative 1PSE model needs to be able to generate an LR as small as that derived from the experimental data (Kingdom and Prins, 2010).
To assess this we used the Palamedes toolbox (Prins and Kingdom, 2009) to simulate each observer in an experiment with the same stimulus intensities as in the real experimental conditions, 1000 times, each time generating responses in accordance with the 1PSE model and recalculated the LR. From these simulations we determined the probability with which an observer whose PSEs do not differ (1PSE model) could generate an LR as small as that generated by a real observer in the experiment. This determines the solid and dashed lines in Figure 4. Solid lines indicate that 5% or less of the 1000 simulations of the 1PSE model produced an LR less than or equal to that of the experimental data (i.e., a difference at the p < 0.05 level). Conversely, dashed lines indicate no significant difference (p > 0.05). From this analysis it is clear that the group effects we report are also highly robust and consistent across individual observers in the experiment.
Equivalence of the learning signal across groups
The experiment was designed, as far as possible, to equate the learning signal across the two experimental conditions. One possible difference that it is important to exclude is that the spinning ball simply caused observers to be more uncertain as to its trajectory and that this provided a weaker learning signal for recalibration. It has been shown previously that participants in both groups adapted in the same way and at the same rate to the altered bounce (Fig. 2). This suggests that the learning signal was equally effective in both conditions. However, the reliability of the learning signal can also be examined directly by looking at the variability of participants' behavior in each group. Specifically, if it really were participant uncertainty about the ball's trajectory that determined the extent of slant recalibration, participants in the spinning ball group should show greater variability in the ball task during the altered bounce phase, and, regardless of group, those participants who were more variable should show less recalibration of slant.
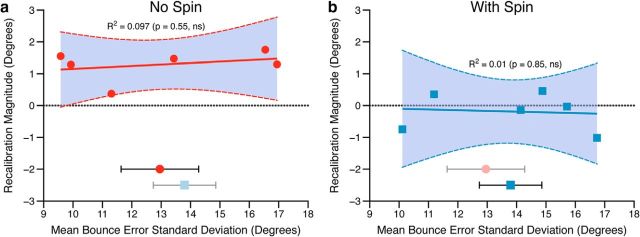
As a measure of variability, the mean SD of bounce errors was calculated across participants in each group during the altered bounce phase of the experiment, i.e., across the whole period in which they experienced the learning signal that triggered the initial recalibration. As can be seen in Figure 5, there was on average no difference in variability across groups (between-subjects t test, t = 0.5, p = 0.63, ns), and no relationship between how variable an observer was during the ball task and the magnitude of their recalibration of slant (magnitude of recalibration being calculated as the difference between the PSE in block 15 and PSE in block 11, just as in Fig. 4). This was true for both the spinning ball (R2 = 0.01, p = 0.85, ns) and nonspinning ball groups (R2 = 0.097, p = 0.55, ns). We can therefore conclude that the magnitude of slant recalibration was not determined by differences in the variability of the learning signal across groups. Note also that our conclusions remain unchanged if an alternative measure of variability, such as the SD in the last altered bounce block, is used.
Figure 5.
The extent of individual observers' recalibration of slant as a function of their variability in the 3D kinematic game. The magnitude of recalibration is calculated as perceived slant after block 11 minus perceived slant after block 5 (just as in Fig. 4). This is plotted against the average SD of bounce errors in the ball game during the altered bounce phase of the experiment. This is shown for (a) the nonspinning ball group and (b) the spinning ball group. The solid line in both plots shows a least-squares linear fit to the data, with 95% confidence intervals of the fit shown with dashed lines (statistics of linear regression inset). The dotted horizontal lines show zero recalibration. In the lower part of both a and b the group mean bounce error SD during the altered bounce phase of the experiment is shown for both groups, with less opacity for the condition shown on each graph. Symbols for averages match those of the individual data. Error bars show SEM.
Despite this analysis, some might argue that the mere fact that the spinning ball trials are noticeably “different” in some unspecified way might disrupt the learning signal required for slant recalibration, while leaving no measurable effect on observers' behavior. While this is possible, without specifying a putative mechanism for this disruption this would be hard, if not impossible, to objectively test. Furthermore, exactly the same criticism applies to similar experiments that explore explaining away (Knill and Kersten, 1991; Battaglia et al., 2010). This is due to the fact that for explaining away to occur there always has to be a difference between conditions, i.e., a signal that does the “explaining” in one condition that is absent in another condition. One can therefore always counter that an unspecified and unknown property of that signal, other than that identified, could account for the explaining away. We have therefore taken the pragmatic approach of equating the reliability of the learning signal across groups and demonstrating that there is no statistical difference between experimental conditions and no relationship between uncertainty in the learning signal and the magnitude of slant recalibration.
It is also worth noting that in pilots for this experiment, if the bounce bias was too large participants immediately noticed it and attempted to consciously “correct” for it. This resulted in highly erratic behavior and no recalibration of slant. It was therefore essential that observers did not consciously detect the altered bounce. With the magnitude of β used, this was the case for all of the observers. What observers did notice was that in some blocks they missed the hoop more often, but they universally attributed this to having a “bad day” or “bad block of the game.” None had any idea that this drop in performance was caused by a biased bounce. Of course, failing to notice an altered bounce consistent with a 7.5 degree difference in slant is very different from distinguishing two slants separated by 7.5 degrees, as in a slant threshold task.
Discussion
Our results show that human observers recalibrate their perception of 3D surface slant when they experience altered visual feedback consistent with a surface having a different slant to that signaled by disparity cues. Observers therefore appear to have assumed that the physical laws governing the kinematic task were invariant over time and used prediction errors caused by the altered bounce to recalibrate their perception of slant to bring it back into alignment with the physical behavior of the surface. Furthermore, when an alternative for the altered feedback presented itself (the ball spinning), this pattern of recalibration was eliminated, suggesting that observers used the ball's spin to explain away (Battaglia et al., 2010) its altered bounce. Importantly, the recalibration we observed (or lack thereof, in the case of the spinning ball) could not be accounted for in terms of response biases, low-level cue conflicts, uncertainty in the learning signal, or alterations to the statistics of incoming sensory data. It was especially important to exclude these in our experiment as they have been shown in the past to cause recalibration (Ernst et al., 2000; Atkins et al., 2001; Burge et al., 2010), and this control has not been possible in previous research using traditional techniques such as prism adaptation (Ogle, 1950; Pick et al., 1969; Adams et al., 2001).
The use of error signals based on sensory prediction has long been studied in the domain of visuomotor control (Blakemore et al., 1998; Wolpert et al., 1998; Blakemore et al., 2001). Within this domain there are similarities between explaining away (Battaglia et al., 2010), as described here, and a mechanism that has been termed “credit assignment” (Berniker and Kording, 2008). Credit assignment acts to assign motor errors across different effectors or actions for the purposes of recalibration (Franklin and Wolpert, 2011; Wolpert and Landy, 2012). However, the importance of sensory prediction in calibrating cues, including those to 3D object properties, has not been fully appreciated until now. Our results suggest that the ability to compare incoming sensory signals to expected values, in this case using predictive kinematic models (Smith and Vul, 2013; Smith et al., 2013), is a critical component in keeping visual cues such as slant from disparity well calibrated. This is understandable given that cues themselves carry no information about their accuracy (Berkeley, 1709; Smeets et al., 2006; Burge et al., 2010; Ernst and Di Luca, 2011; Scarfe and Hibbard, 2011; Zaidel et al., 2011).
We see two additional areas where sensory prediction may be important: first, in determining how novel cues to object properties are learned and, second, in determining when existing cues to object properties should be combined. Previous research has shown that novel cues to object properties can be learned through a process of paired association with existing “trusted” cues (Haijiang et al., 2006; Ernst, 2007). However, this type of learning cannot guarantee that the learned cue is providing accurate information about the world. One way in which this could be achieved is by learning cues that provide behavioral predictability, even in the absence of correlations with existing trusted cues. Once learned, past behavior could also indicate whether cues are likely to have a common cause and hence should be combined. Previous research has shown that cues that are spatially (Gepshtein et al., 2005) and temporally (Parise et al., 2012) correlated are more likely to be combined. However, spurious correlations could also arise with discrepant sensory stimuli that should remain segregated. Using behavioral predictability as a cue to a common cause would avoid this problem.
It is worth noting that the recalibration we observed was not sufficient to completely account for the behavior of the ball (it was ∼16% of “full” recalibration). This is consistent with previous studies demonstrating explaining away (Battaglia et al., 2010, 2011). The extent of explaining away is likely to be affected by numerous variables that influence the observer's beliefs about the causal structure of the stimuli (Körding et al., 2007; Battaglia et al., 2011). As discussed in the Materials and Methods section, explaining away need not necessarily be an all-or-none phenomenon. Our data indicate a significant difference between the spinning and nonspinning ball cases (Figs. 3c, 4), demonstrated by testing the null hypothesis that there is no recalibration. However, given an appropriately rich dataset, a full Bayesian model could test a much wider range of outcomes that include a variable degree of explaining away.
There is debate about the extent to which the realism of stimuli is helpful in distinguishing between hypotheses in experiments (De Gelder and Bertelson, 2003; Felsen and Dan, 2005; Rust and Movshon, 2005; Battaglia et al., 2013; Scarfe and Hibbard, 2013). However, in our experiment the fact that observers used the ball's spin to explain away the need for recalibration, even with a simplified simulation of kinematics, suggests that the information provided to observers was sufficient for them to infer the causal structure of the stimuli and use this to determine the extent of sensory recalibration.
It is also important to note that observers had far greater experience of real-world physics between experimental sessions than they did of the altered physics within experimental sessions, so the magnitude of recalibration was unlikely to fully account for the ball's altered bounce. This is consistent with previous research on perceptual learning and sensory adaptation of 3D object properties (Adams et al., 2004; Ernst, 2007). As such, it suggests that the learning we observed must have been context specific; otherwise observers' experience of real-world physics between sessions would have overridden any learning driven by altered physics within sessions. This type of specificity has been demonstrated in previous studies on perceptual learning where an adaptation state can be yoked to the context in which it was learned (Welch et al., 1993; Martin et al., 1996; Osu et al., 2004; Kerrigan and Adams, 2013; van Dam et al., 2013).
We also note that it is an open question as to whether the recalibration observed altered the mapping between disparity and perceived slant, or the mapping between perceived slant and the observer's response. Previous research suggests that perceptual learning and adaptation may be driven by both cue-specific and cue-invariant mechanisms (Adams et al., 2001; Ivanchenko and Jacobs, 2007). However, the fact that observers remained consciously unaware of the altered bounce and that the recalibration was measured in a different task, with a different mode of response, provides evidence in favor of the hypothesis that recalibration altered the mapping between disparity and perceived slant. It is also clear that, in addition to perceptual recalibration, some response recalibration also occurred, as observers in the spinning ball group were able to improve their performance in the altered bounce phase of the experiment in exactly the same way as the no-spin group, despite the fact that they exhibited no recalibration of perceived slant.
Overall, our results, together with those on visuomotor adaptation, highlight the fact that cues are simply arbitrary patterns of sensory data that allow us to make accurate predictions about their hidden world causes (Berkeley, 1709; Gibson, 1950). This predictability is embodied in our understanding of physical laws (Smith and Vul, 2013; Smith et al., 2013) and our own bodily mechanics (Wolpert et al., 1998). Throughout our discussion we have drawn the distinction between sensory cues and error signals produced by a discrepancy between predicted and observed sensory feedback. While this distinction has been profitable (Atkins et al., 2001, 2003; Cressman and Henriques, 2011; Henriques and Cressman, 2012), ultimately, a close iterative relationship between the two must exist, as the only information available from which to derive error signals is that provided by the senses (von Helmholtz, 1925; Gregory, 1980; Knill and Richards, 1996; Rao and Ballard, 1999; Clark, 2013). The spatial and temporal invariance of the physics governing the world is one way to constrain possible solutions to this open-ended self-calibration problem.
Footnotes
This work was supported by the Wellcome Trust (086526/A/08) and EPSRC (EP/K011766/1). We thank Loes van Dam, Paul Hibbard, Marc Ernst, and Mario Kleiner for helpful discussion.
The authors declare no competing financial interests.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/3.0), which permits unrestricted use, distribution and reproduction in any medium provided that the original work is properly attributed.
References
- Adams WJ, Banks MS, van Ee R. Adaptation to three-dimensional distortions in human vision. Nat Neurosci. 2001;4:1063–1064. doi: 10.1038/nn729. [DOI] [PubMed] [Google Scholar]
- Adams WJ, Graf EW, Ernst MO. Experience can change the ‘light-from-above’ prior. Nat Neurosci. 2004;7:1057–1058. doi: 10.1038/nn1312. [DOI] [PubMed] [Google Scholar]
- Atkins JE, Fiser J, Jacobs RA. Experience-dependent visual cue integration based on consistencies between visual and haptic percepts. Vision Res. 2001;41:449–461. doi: 10.1016/S0042-6989(00)00254-6. [DOI] [PubMed] [Google Scholar]
- Atkins JE, Jacobs RA, Knill DC. Experience-dependent visual cue recalibration based on discrepancies between visual and haptic percepts. Vision Res. 2003;43:2603–2613. doi: 10.1016/S0042-6989(03)00470-X. [DOI] [PubMed] [Google Scholar]
- Battaglia PW, Di Luca M, Ernst MO, Schrater PR, Machulla T, Kersten D. Within- and cross-modal distance information disambiguate visual size-change perception. PLoS Comput Biol. 2010;6:e1000697. doi: 10.1371/journal.pcbi.1000697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battaglia PW, Kersten D, Schrater PR. How haptic size sensations improve distance perception. PLoS Comput Biol. 2011;7:e1002080. doi: 10.1371/journal.pcbi.1002080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battaglia PW, Hamrick JB, Tenenbaum JB. Simulation as an engine of physical scene understanding. Proc Natl Acad Sci U S A. 2013;110:18327–18332. doi: 10.1073/pnas.1306572110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berkeley G. An essay towards a new theory of vision. Cirencester, UK: The Echo Library; 1709. [Google Scholar]
- Berniker M, Kording K. Estimating the sources of motor errors for adaptation and generalization. Nat Neurosci. 2008;11:1454–1461. doi: 10.1038/nn.2229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blakemore SJ, Wolpert DM, Frith CD. Central cancellation of self-produced tickle sensation. Nat Neurosci. 1998;1:635–640. doi: 10.1038/2870. [DOI] [PubMed] [Google Scholar]
- Blakemore SJ, Frith CD, Wolpert DM. The cerebellum is involved in predicting the sensory consequences of action. Neuroreport. 2001;12:1879–1884. doi: 10.1097/00001756-200107030-00023. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10:433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Burge J, Girshick AR, Banks MS. Visual-haptic adaptation is determined by relative reliability. J Neurosci. 2010;30:7714–7721. doi: 10.1523/JNEUROSCI.6427-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav Brain Sci. 2013;36:181–204. doi: 10.1017/S0140525X12000477. [DOI] [PubMed] [Google Scholar]
- Cressman EK, Henriques DY. Motor adaptation and proprioceptive recalibration. Prog Brain Res. 2011;191:91–99. doi: 10.1016/B978-0-444-53752-2.00011-4. [DOI] [PubMed] [Google Scholar]
- De Gelder B, Bertelson P. Multisensory integration, perception and ecological validity. Trends Cogn Sci. 2003;7:460–467. doi: 10.1016/j.tics.2003.08.014. [DOI] [PubMed] [Google Scholar]
- Ernst MO. Learning to integrate arbitrary signals from vision and touch. J Vis. 2007;7(5):1–14. doi: 10.1167/7.5.7. [DOI] [PubMed] [Google Scholar]
- Ernst MO, Di Luca M. Multisensory perception: from integration to remapping. In: Trommershauser J, Körding KP, Landy MS, editors. Sensory cue integration. New York: Oxford UP; 2011. pp. 224–250. [Google Scholar]
- Ernst MO, Banks MS, Bülthoff HH. Touch can change visual slant perception. Nat Neurosci. 2000;3:69–73. doi: 10.1038/71140. [DOI] [PubMed] [Google Scholar]
- Felsen G, Dan Y. A natural approach to studying vision. Nat Neurosci. 2005;8:1643–1646. doi: 10.1038/nn1608. [DOI] [PubMed] [Google Scholar]
- Franklin DW, Wolpert DM. Computational mechanisms of sensorimotor control. Neuron. 2011;72:425–442. doi: 10.1016/j.neuron.2011.10.006. [DOI] [PubMed] [Google Scholar]
- Gepshtein S, Burge J, Ernst MO, Banks MS. The combination of vision and touch depends on spatial proximity. J Vis. 2005;5(11):1013–1023. doi: 10.1167/5.8.1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson JJ. The perception of the visual world. Boston: Houghton Mifflin; 1950. [Google Scholar]
- Gregory RL. Perceptions as hypotheses. Philos Trans R Soc Lond B Biol Sci. 1980;290:181–197. doi: 10.1098/rstb.1980.0090. [DOI] [PubMed] [Google Scholar]
- Haijiang Q, Saunders JA, Stone RW, Backus BT. Demonstration of cue recruitment: change in visual appearance by means of Pavlovian conditioning. Proc Natl Acad Sci U S A. 2006;103:483–488. doi: 10.1073/pnas.0506728103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamrick J, Battaglia PW, Tenenbaum JB. Internal physics models guide probabilistic judgments about object dynamics. Proceedings of the 33rd Annual Conference of the Cognitive Science Society.2011. [Google Scholar]
- Henriques DY, Cressman EK. Visuomotor adaptation and proprioceptive recalibration. J Mot Behav. 2012;44:435–444. doi: 10.1080/00222895.2012.659232. [DOI] [PubMed] [Google Scholar]
- Ivanchenko V, Jacobs RA. Visual learning by cue-dependent and cue-invariant mechanisms. Vision Res. 2007;47:145–156. doi: 10.1016/j.visres.2006.09.028. [DOI] [PubMed] [Google Scholar]
- Kerrigan IS, Adams WJ. Learning different light prior distributions for different contexts. Cognition. 2013;127:99–104. doi: 10.1016/j.cognition.2012.12.011. [DOI] [PubMed] [Google Scholar]
- Kingdom FAA, Prins N. Psychophysics: a practical introduction. London: Academic; 2010. [Google Scholar]
- Kleiner M, Brainard D, Pelli D. What's new in Psychtoolbox-3? Perception. 2007;36:Abstr. doi: 10.1068/v070821. [DOI] [Google Scholar]
- Knill DC, Kersten D. Apparent surface curvature affects lightness perception. Nature. 1991;351:228–230. doi: 10.1038/351228a0. [DOI] [PubMed] [Google Scholar]
- Knill DC, Richards W. Perception as Bayesian inference. Cambridge: Cambridge UP; 1996. [Google Scholar]
- Körding KP, Beierholm U, Ma WJ, Quartz S, Tenenbaum JB, Shams L. Causal inference in multisensory perception. PLoS One. 2007;2:e943. doi: 10.1371/journal.pone.0000943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin TA, Keating JG, Goodkin HP, Bastian AJ, Thach WT. Throwing while looking through prisms. 2. Specificity and storage of multiple gaze-throw calibrations. Brain. 1996;119:1199–1211. doi: 10.1093/brain/119.4.1199. [DOI] [PubMed] [Google Scholar]
- McLaughlin SC, Webster RG. Changes in the straight-ahead eye position during adaptation to wedge prisms. Percept Psychophys. 1967;2:37–44. doi: 10.3758/BF03210064. [DOI] [Google Scholar]
- Ogle KN. Researches in binocular vision. Philadelphia: W. B. Saunders Company; 1950. [Google Scholar]
- Osu R, Hirai S, Yoshioka T, Kawato M. Random presentation enables subjects to adapt to two opposing forces on the hand. Nat Neurosci. 2004;7:111–112. doi: 10.1038/nn1184. [DOI] [PubMed] [Google Scholar]
- Parise CV, Spence C, Ernst MO. When correlation implies causation in multisensory integration. Curr Biol. 2012;22:46–49. doi: 10.1016/j.cub.2011.11.039. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–442. doi: 10.1163/156856897X00366. [DOI] [PubMed] [Google Scholar]
- Pick HL, Warren DH, Hay JC. Sensory conflict in judgments of spatial direction. Percept Psychophys. 1969;6:203–205. doi: 10.3758/BF03207017. [DOI] [Google Scholar]
- Prins N. The psychometric function: the lapse rate revisited. J Vis. 2012;12(6):25. doi: 10.1167/12.6.25. pii. [DOI] [PubMed] [Google Scholar]
- Prins N, Kingdom FAA. Palamedes: Matlab routines for analyzing psychophysical data. 2009. http://www.palamedestoolbox.org.
- Rao RP, Ballard DH. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci. 1999;2:79–87. doi: 10.1038/4580. [DOI] [PubMed] [Google Scholar]
- Rust NC, Movshon JA. In praise of artifice. Nat Neurosci. 2005;8:1647–1650. doi: 10.1038/nn1606. [DOI] [PubMed] [Google Scholar]
- Scarfe P, Hibbard PB. Statistically optimal integration of biased sensory estimates. J Vis. 2011;11(7):12. doi: 10.1167/11.7.12. pii. [DOI] [PubMed] [Google Scholar]
- Scarfe P, Hibbard PB. Reverse correlation reveals how observers sample visual information when estimating three-dimensional shape. Vision Res. 2013;86:115–127. doi: 10.1016/j.visres.2013.04.016. [DOI] [PubMed] [Google Scholar]
- Seydell A, Knill DC, Trommershäuser J. Adapting internal statistical models for interpreting visual cues to depth. J Vis. 2010;10(4):1.1–27. doi: 10.1167/10.4.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shams L, Beierholm UR. Causal inference in perception. Trends Cogn Sci. 2010;14:425–432. doi: 10.1016/j.tics.2010.07.001. [DOI] [PubMed] [Google Scholar]
- Smeets JB, van den Dobbelsteen JJ, de Grave DD, van Beers RJ, Brenner E. Sensory integration does not lead to sensory calibration. Proc Natl Acad Sci U S A. 2006;103:18781–18786. doi: 10.1073/pnas.0607687103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith KA, Vul E. Sources of uncertainty in intuitive physics. Top Cogn Sci. 2013;5:185–199. doi: 10.1111/tops.12009. [DOI] [PubMed] [Google Scholar]
- Smith KA, Dechter E, Tenenbaum JB, Vul E. Physical predictions over time. Proceedings of the 35th Annual Meeting of the Cognitive Science Society; 2013. pp. 1–6. [Google Scholar]
- van Beers RJ, van Mierlo CM, Smeets JB, Brenner E. Reweighting visual cues by touch. J Vis. 2011;11(10):20. doi: 10.1167/11.10.20. pii. [DOI] [PubMed] [Google Scholar]
- van Dam LC, Hawellek DJ, Ernst MO. Switching between visuomotor mappings: learning absolute mappings or relative shifts. J Vis. 2013;13(2):26. doi: 10.1167/13.2.26. pii. [DOI] [PubMed] [Google Scholar]
- van Ee R. Perceptual learning without feedback and the stability of stereoscopic slant estimation. Perception. 2001;30:95–114. doi: 10.1068/p3163. [DOI] [PubMed] [Google Scholar]
- von Helmholtz H. Helmholtz's treatise on physiological optics. Bristol, UK: Thoemmes; 1925. [Google Scholar]
- Welch RB, Bridgeman B, Anand S, Browman KE. Alternating prism exposure causes dual adaptation and generalization to a novel displacement. Percept Psychophys. 1993;54:195–204. doi: 10.3758/BF03211756. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Percept Psychophys. 2001a;63:1293–1313. doi: 10.3758/BF03194544. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: II. Bootstrap-based confidence intervals and sampling. Percept Psychophys. 2001b;63:1314–1329. doi: 10.3758/BF03194545. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Landy MS. Motor control is decision-making. Curr Opin Neurobiol. 2012;22:996–1003. doi: 10.1016/j.conb.2012.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert DM, Miall RC, Kawato M. Internal models in the cerebellum. Trends Cogn Sci. 1998;2:338–347. doi: 10.1016/S1364-6613(98)01221-2. [DOI] [PubMed] [Google Scholar]
- Zaidel A, Turner AH, Angelaki DE. Multisensory calibration is independent of cue reliability. J Neurosci. 2011;31:13949–13962. doi: 10.1523/JNEUROSCI.2732-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]