Human L3L4 intervertebral disc mean 3D shape, modes of variation, and their relationship to degeneration

Abstract

Intervertebral disc mechanics are affected by both disc shape and disc degeneration, which in turn each affect the other; disc mechanics additionally have a role in the etiology of disc degeneration. Finite element analysis (FEA) is a favored tool to investigate these relationships, but limited data for intervertebral disc 3D shape has forced the use of simplified or single-subject geometries, with the effect of inter-individual shape variation investigated only in specialized studies. Similarly, most data on disc shape variation with degeneration is based on 2D mid-sagittal images, which incompletely define 3D shape changes. Therefore, the objective of this study was to quantify inter-individual disc shape variation in 3D, classify this variation into independently-occurring modes using a statistical shape model, and identify correlations between disc shape and degeneration. Three-dimensional disc shapes were obtained from MRI of 13 human male cadaver L3L4 discs. An average disc shape and four major modes of shape variation (representing 90% of the variance) were identified. The first mode represented disc axial area and was significantly correlated to degeneration (R² = 0.44), indicating larger axial area in degenerate discs. Disc height variation occurred in three distinct modes, each also involving non-height variation. The statistical shape model provides an average L3L4 disc shape for FEA that is fully defined in 3D, and makes it convenient to generate a set of shapes with which to represent aggregate inter-individual variation. Degeneration grade-specific shapes can also be generated. To facilitate application, the model is included in this paper’s supplemental content.

Introduction

Intervertebral disc shape influences both nutrient transport and spine mechanics (Fujiwara et al., 2000; Magnier et al., 2009; Meijer et al., 2011; Niemeyer et al., 2012; Niosi and Oxland, 2004), and shape changes are involved in disc degeneration (Berlemann et al., 1998; Pappou et al., 2007; Pfirrmann et al., 2006; Videman et al., 2008; Videman et al., 2007). The mechanical consequences of disc degeneration and the treatments meant to address it are often investigated with finite element analysis (FEA). However, due to lack of multi-subject 3D shape information in the literature, investigators typically use a 3D geometry from on a single subject (El-Rich et al., 2008; Rundell et al., 2009) or a simplified geometry extrapolated from vertebral bone morphometry (point-to-point distances) (Kim et al., 2001; Kim, 2000; Meijer et al., 2011; Meijer et al., 2010; Niemeyer et al., 2012; Panjabi et al., 1992; Rohlmann et al., 2006; Rundell et al., 2009; Smit, 1996; Yan et al., 2011). Morphometry of the disc itself is also available, based on 2D mid-sagittal MRI (Boos et al., 1996; Fujiwara et al., 2000; Kwok et al., 2012) or dissected discs (Beckstein et al., 2008; Brinckmann and Grootenboer, 1991; Keller et al., 1987; Nachemson et al., 1979; O’Connell et al., 2007; Porter et al., 1989). These lists are representative, not exhaustive. The common factor is that all these studies use morphometry, which only defines distances between specific points. If morphometry is used to construct a 3D shape for FEA, the resulting shape is underdetermined, and the gaps must be filled in by guesswork. A 3D single-subject image produces a fully determined shape, but may not be representative. A solution to this dilemma would be greatly beneficial.

Since variation in intervertebral disc shape causes corresponding variation in spine mechanics (Campana et al., 2007; Farfan et al., 1972; Galbusera et al., 2011; Keller et al., 2005; Meijer et al., 2011; Meijer et al., 2010; Niemeyer et al., 2012; Schmidt et al., 2013), it is important to include inter-individual shape variation in FEA studies of the intervertebral disc. However, the effort involved in doing so for a morphometry-based geometry relegates such a task to specialized studies (Meijer et al., 2011; Niemeyer et al., 2012). There is a need for a parameterization of 3D intervertebral disc shape variation that can be conveniently incorporated into FEA models.

Relations between degeneration and 3D disc shape are also incompletely examined, as prior studies of degeneration and disc shape used morphometry, usually with 2D sagittal images (Battié et al., 2008; Benneker et al., 2005; Berlemann et al., 1998; Luoma et al., 2001; Pfirrmann et al., 2006; Pfirrmann et al., 2001; Videman et al., 2008; Videman et al., 2006; Videman et al., 1995). As above, this poses difficulty for FEA of degenerate discs. Additionally, 2D or morphometric analysis may overlook degeneration-related shape variation outside the imaging plane or away from the morphometric markers.

This study was designed to improve upon these three issues by (1) quantifying inter-individual 3D shape variation of the L3L4 disc, (2) parameterizing this variation with a minimum number of parameters, and (3) identifying relationships between 3D shape and degeneration. The L3L4 disc was chosen because FEA studies often target it specifically (Bono et al., 2007; Dahl et al., 2010; Kim and Choi, 2009; Kim, 2000; Lee et al., 2000; Meijer et al., 2011; Niemeyer et al., 2012; Rohlmann et al., 2006; Rundell et al., 2009). 3D disc shapes were measured from MRI, the mean shape was computed, and the shape variation was decomposed and parameterized as independent principal components. Importantly, this decomposition is made without any a priori assumptions about the kinds of shape variation in the data. The resulting shape model facilitates examination of relationships between disc shape and degeneration and provides convenient means to incorporate inter-individual shape variation in disc FEA studies.

Materials and Methods

Samples

Thirteen fresh-frozen spines were obtained from donor human cadavers via National Disease Research Interchange. After thawing, the spines were imaged intact by T2-weighted MRI in order to assign degenerative grades (Pfirrmann scale) (Pfirrmann et al., 2001), which has been validated as having good inter-rater reliability (Kettler and Wilke, 2006). The grades were averaged between three graders. Following T2 imaging, L3L4 discs were dissected (with the surrounding bone attached), vacuum-sealed in plastic, and stored frozen. The samples remained sealed in plastic throughout the study to avoid swelling or shrinking due to exposure to water or air. Donors ranged from 50–93 years of age (average 67.5 years) and were all male. Degenerative grade was 2.3–5.0 (mean 3.3).

Image Segmentation

High-resolution MRI was acquired for shape analysis. In preparation for imaging, the samples were thawed and surrounded (outside their encasing plastic) with 2% agarose, which has similar magnetic susceptibility to tissue. Images were acquired using a 7T Siemens whole-body MRI scanner and a custom transmit/receive RF coil programmed with a 3D FLASH sequence (TE = 3.7 ms; TR = 9 ms) (Moon et al., 2013). Voxel size was 200 μm isotropic.

Discs were segmented from the high-resolution images using Convert3D and ITK-SNAP (Yushkevich et al., 2006). Each MR image was preprocessed with N3 intensity inhomogeneity correction, 2:1 resampling, and Gaussian smoothing (Figure 1). ITK-SNAP’S active contour tool was used to create an initial automatic segmentation. Segmentation was completed manually. The segmentations were aligned to a common anatomical coordinate system using Matlab. Translational alignment was accomplished by moving the centroid to the origin. For rotational alignment, the major axes were used to define the aligned coordinate system (algorithm in Supplemental Information) (Gonzalez and Woods, 2002; Petrou and Petrou, 2010).

Figure 1.

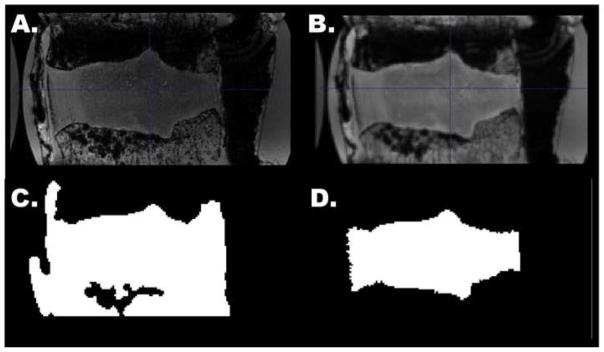
Mid-sagittal slice of a 3D disc MRI, illustrating image processing steps. The initial image (a) was bias corrected and smoothed (b). An automatic segmentation was generated in ITK-SNAP (c), then manually corrected (d).

Shape Analysis

A shape model was created from the disc segmentations using principal components analysis (PCA) according to established methods (Tsai et al., 2003). First, each segmentation was converted to a signed distance function, which encodes a shape as an image of distance from the shape boundary. The mean shape Φ₀ was obtained by calculating the mean of the signed distance functions. Subtracting the mean disc shape from each original shape forms a set of residuals, from which were calculated the principal components (PCs) of variation Φ_i. The PCs were ordered by the amount of variance they represent (PC 1 representing the most variance) and normalized by their standard deviations. Each PC represents an independent mode of disc shape variation. Since the dataset contained 13 discs, the shape model defines 12 PCs and one mean shape. Each PC is orthogonal to all the others; together they form a basis which spans the same 3D shape space as the original dataset. Any shape in the original dataset, or any shape in-between, can be represented as the sum of the mean shape and a weighted linear combination of the PCs: $\mathrm{\Phi }={\mathrm{\Phi }}_0+{\displaystyle \sum _{i=1}^{12}}{w}_i{\mathrm{\Phi }}_i$. The scalar weighting factors w_i compactly and completely define the shape. To give the weights physical meaning, we expressed w_i as fractions of the standard deviation σ_i for each Φ_i.

To aid in comparison to prior work, morphometric measurements of disc axial area, width, depth (anterior-posterior distance), and height were made directly from the 3D disc segmentation. Axial area was measured from the disc’s projection into the anterior-posterior/left-right plane. Width was measured as the distance between the most extreme points on the left-right axis. Depth was measured as the anterior-posterior distance at the mid-sagittal plane. Height was defined as the volume divided by the axial area.

Leave-One-Out Analysis

In order to determine if the shape model was stable (not unduly influenced by outlier discs), a leave-one-out analysis (a type of cross-validation) was performed (Morra et al., 2008; Xie et al., 2005; Yang, 2004). The PCA procedure was repeated excluding each disc in turn, creating 13 reduced models. The PCs in each reduced model were compared with the full model using vector dot products. A dot product of zero indicates maximum change; a dot product of one indicates no change. If the model is stable, the inclusion or exclusion of any single disc will have little effect.

Statistics

Relationships between degenerative grade and disc shape, represented by both the shape model (weights w_i) and morphometry (axial area, depth, width, and height), were tested by Pearson correlation. The significance level (α) was set to 0.05, and the power (β) was 0.8 to detect Pearson R² = 0.5, as we did not expect degeneration-related shape changes to be subtle. Summary statistics are reported as mean ± standard deviation (s.d.).

Results

Physical Meaning of the Shape Model

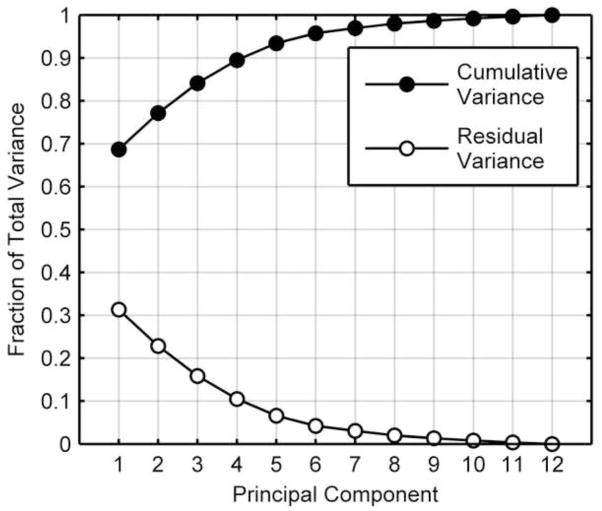
The shape model includes a mean shape and encodes shape variability using a set of principal components (PCs). The observed mean shape was overall qualitatively normal, but did have a slight asymmetry between the posterolateral margins (Figure 2). Each PC represents a distinct kind of shape variation. The majority (70%) of shape variation in the dataset was represented by PC 1 (Figure 3). PCs 1–4 together are sufficient to represent 90% of the variability in disc shape, and so were selected for analysis.

Figure 2.

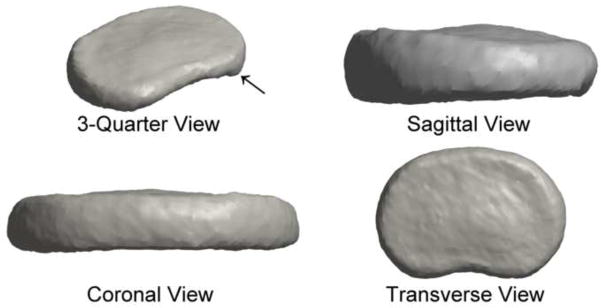
The mean disc shape displayed the expected kidney-bean shape of an intervertebral disc. The shape was nearly symmetric, with a slight protrusion at the inferior posterolateral margin (arrow).

Figure 3.

Cumulative shape variance represented by the principal components. The first four principal components represented ~90% of the total variance of intervertebral disc shape. PC 1 alone accounted for ~70% of the variance.

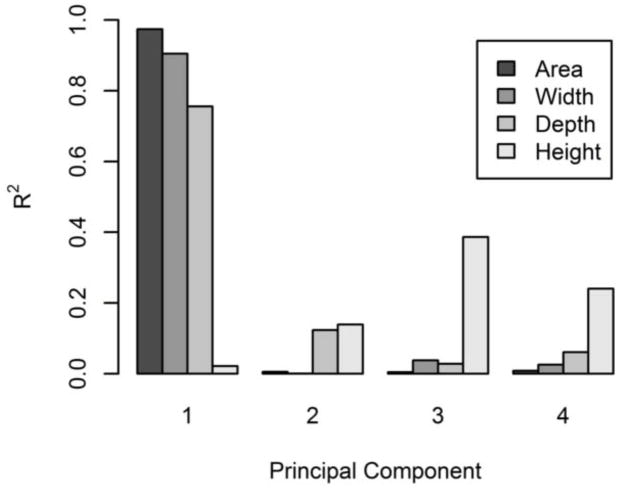
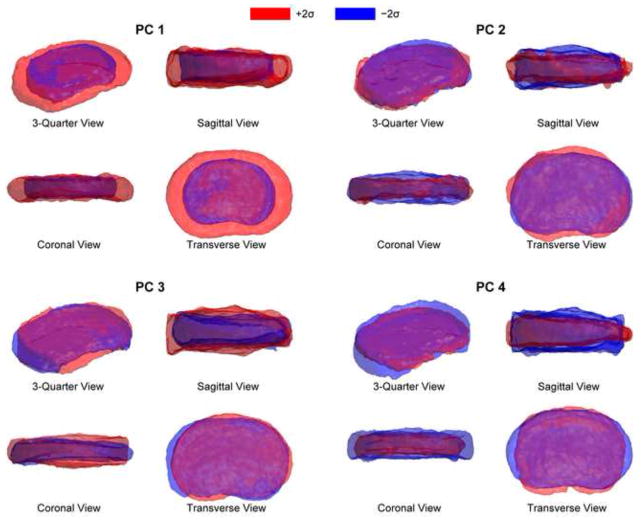
In terms of geometry, PC 1 represents variability in axial area (R² = 0.97), but is unrelated to disc height (R² = 0.02) (Figure 4). Increased PC 1 indicates increased axial area, a shallower or nonexistent posterior notch, and rounded sides (Figure 5). PCs 2–4 are all somewhat related to disc height, as well as more complicated shape variations. Increased PC 2 indicates protrusion of the anterior, left, and posterolateral margins and increased height (Figures 4 and 5). Increased PC 3 indicates uniform bulging of the left margin and increased disc height. PC 3 has the strongest relationship to disc height, representing ~40% of the height variation (Figure 4). Increased PC 4 indicates increased depth, decreased width, and decreased disc height (Figure 5). The kind of height variability encoded by PC 3 includes left-right asymmetry, whereas PCs 2 and 4 represent uniform height variation.

Figure 4.

Correlation between shape model PCs and disc morphometry. PC 1 was strongly related to axial area, width, and anterior-posterior depth. PC 3 had the strongest relationship to disc height, with PCs 2 and 4 somewhat related to disc height.

Figure 5.

Each principal component encodes a different kind of shape variation, illustrated here by adding ± 2 s.d. of PCs 1–4 to the mean shape. PC 1 encodes variation in axial area. PCs 2–4 each encode a different form of disc height variation, mixed with other kinds of variation.

Morphometry

Morphometric measurements of each disc were made for comparison with prior work and to aid in explicating the shape model. Height, depth, width, and axial area are given in Table 1.

Table 1.

L3L4 disc morphometry. Statistics for Brinckmann and Grootenboer (1991) and Keller et al. (1987) were calculated by pooling reported measurements of individual discs. Where possible, measurements were selected that match the demographics of the current data set. For Nachemson et al. (1979) the reported standard deviations include non-L3L4 levels & Marfan syndrome discs, as only means were reported by subset. The entries for Panjabi et al. (1992) are the average of the reported superior and inferior vertebral endplate dimensions. n.d. = no data.

Reference	Sex	Age (years)	Height (mm)	Width (mm)	Depth (mm)	Area (cm2)
This study	Male	50–93	10.2 ± 1.9	63.3 ± 6.8	42.2 ± 5.2	23.3 ± 4.5
Nachemson et al. (1979)	Mixed	21–60	16.0 ± 0.3	54 ± 8	40 ± 6	15.9 ± 3.1
Showalter et al. (2012)	Male	22–42	10.9 ± 0.8	55 ± 2	38 ± 2	19.2 ± 1.8
Brinckmann and Grootenboer (1991) and Keller et al. (1987)	4 M, 1 F	37–82	10.6 ± 1.0	n.d.	n.d.	22.2 ± 5.6
Amonoo-Kuofi et al. (1991)	Male	50–64	7.5 ± 0.6	n.d.	42.7 ± 1.9	n.d.
Panjabi et al. (1992)	8 M, 4 F	19–59	n.d.	47.3 ± 1.2	35.1 ± 1.2	12.6 ± 0.6

Effect of Degeneration

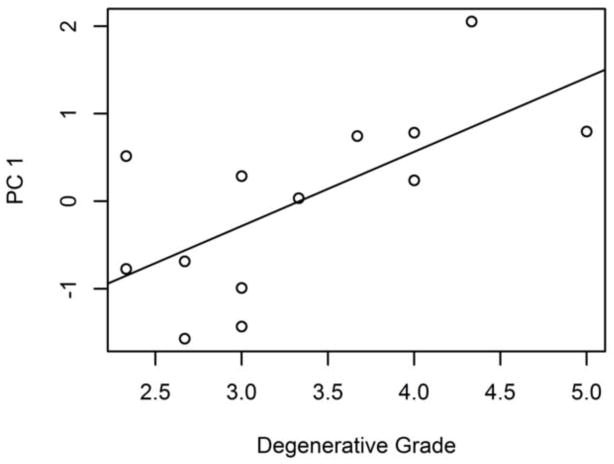
The effect of degeneration on disc shape was identified by correlating the modes of shape variation with degenerative grade. Of all the modes of shape variation identified by the shape model, only PC 1 was significantly correlated to degeneration (r = 0.66 (95% CI 0.18, 0.89); intercept = −2.8 ± 1.0, slope = 0.85 ± 0.29) (Figure 6), indicating that degenerate discs tend to have larger axial area. This result is corroborated by the morphometric measures (Figure 7)—degenerative grade was correlated with axial area (r = 0.74 (95% CI 0.32, 0.92); intercept = 9.7 ± 3.8 cm², slope = 4.1 ± 1.1 cm²), width (r = 0.60 (95% CI 0.07, 0.86); intercept = 46.8 ± 6.8 mm, slope = 5.0 ± 2.0 mm), and depth (r = 0.85 (95% CI 0.55, 0.95); intercept = 24.2 ± 3.5 mm, slope = 5.4 ± 1.0 mm).

Figure 6.

PC 1 is moderately correlated (R² = 0.44) with degenerative grade.

Figure 7.

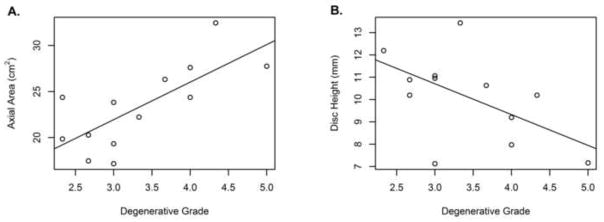
Intervertebral disc morphometry was correlated with degeneration, (a) Axial area increased with degeneration (r = 0.74 (95% CI 0.32, 0.92)). (b) Height decreased with degeneration (r = −0.58 (95% CI −0.86, −0.05)).

Degeneration was also correlated with height (r = −0.58 (95% CI −0.86, −0.05); intercept = 14.8 ± 2.0 mm, slope = −1.4 ± 0.6 mm). Note that the Pfirrmann scale does consider height loss as part of the score, so some correlation with height is expected.

Leave-one-out analysis

A leave-one-out analysis was conducted to check if the shape model was unduly influenced by outlier discs. Reduced models were created by excluding each disc in turn and repeating the shape analysis. The boundary of the mean shape moved an average distance of 0.10 mm (range 0.04–0.12 mm), less than the image resolution. The stability of each mode of shape variation was evaluated by its dot products between the full model and reduced models (Table 2). PC 1 exhibits negligible change with the exclusion of any single disc. The exclusion of disc #5 or #6 produced large apparent changes in PCs 2 and 3, but this is actually caused by the two vectors swapping rank. Reversing the swap, the PC 2 dot products are 0.58 and 0.68 and the PC 3 dot products are 0.90 and 1.00. Still, PC 3 is sensitive to disc #10, which had an unusually short depth relative to its width. Overall, while PCs 2–4 may change meaning slightly between datasets (and PCs > 4 may greatly change meaning) the meaning of the mean shape and PC 1 is consistent.

Table 2.

Dot products between full and reduced model PCs. PC 1 does not change between the full and reduced models, indicating that PC 1’s definition is not distorted by any outlier disc shapes. The remaining PCs are somewhat sensitive to the influence of particular discs.

Excluded Disc	PC 1	PC 2	PC 3	PC 4
1	1.00	1.00	0.99	0.72
2	1.00	0.95	0.83	0.87
3	1.00	1.00	1.00	0.99
4	1.00	1.00	1.00	0.99
5	0.98	0.41	0.42	0.71
6	1.00	0.07	0.05	0.73
7	1.00	0.96	0.87	0.94
8	1.00	0.99	0.99	0.90
9	1.00	1.00	1.00	1.00
10	1.00	0.98	0.32	0.36
11	1.00	1.00	0.96	0.93
12	1.00	1.00	0.99	0.99
13	1.00	0.99	0.99	0.93
mean	1.00	0.87	0.80	0.85
s.d.	0.01	0.29	0.32	0.18

Discussion

Shape and degeneration

This study quantified intervertebral disc shape variation from 3D MRI of a set of human L3L4 discs. The most significant finding was that degeneration is associated with greater disc axial area. Variation in axial area (PC 1) accounts for most (70%) of the overall variation in disc shape (Figure 3). The correlation between disc area and degeneration (R² = 0.44) therefore accounts for a large part (~30%) of disc shape variation. This correlation was confirmed, independent of the shape model, by basic morphometry. The use of 3D images was advantageous in this respect, as in 2D it is ambiguous whether a bulge is local or global (Kalichman, 2010; Milette et al., 1999; Videman et al., 2008). This correlation between degeneration and axial area could be explained as either degeneration causing whole-disc bulging or larger discs being more prone to degeneration (Brinckmann and Grootenboer, 1991; Milette et al., 1999; Videman et al., 2007; Yates et al., 2010).

Although disc height is typically regarded as a single parameter (Berlemann et al., 1998; Pfirrmann et al., 2006), the shape model identified three distinct height-related modes of shape variation. Only PCs 2 (uniform height change) and 4 (altered axial aspect ratio plus uniform height change) had an indication (trend) of being related to degeneration (r ≈ 0.4, p ≈ 0.1 for both). PC 3 (left-right wedging), despite having the strongest relationship to height (Figure 4), had no significant correlation with degenerative grade. Height changes may be more pronounced for the L4L5 disc (Battié et al., 2004). The existence of multiple types of height-related variation should be considered in future investigations of disc biomechanics and classification of degeneration phenotype, as these modes of height loss would affect spine mechanics in dissimilar ways.

Model consistency and limitations

The morphometric measurements from this study are consistent with previous work (Table 1), with differences in reported height attributable to procedure (caliper measurement of whole motion segments in (Nachemson et al., 1979) and lateral radiography in (Amonoo-Kuofi, 1991)). The lesser disc area in (Nachemson et al., 1979) may be due to including female discs in the average. The CT-derived vertebral body measurements from Panjabi et al. (1992) are much smaller than measurements of the disc, which may have implications for spine FEA based on these measurements (Meijer et al., 2011; Meijer et al., 2010; Niemeyer et al., 2012). We recommend using both disc- and vertebral body-specific measurements when possible. The remaining disc-specific studies are consistent with the present study and each other.

As demonstrated by the leave-one-out analysis, the current sample size is sufficient to clearly establish the definition of the mean shape and PC 1 and that multiple modes of height-related variation (PCs 2–4) exist. The statistical power was sufficient to identify a correlation between PC 1 and degeneration.

The primary limitation of this study is the subpopulation used (aged, male, L3L4, and moderately to severely degenerate). However, the use of consistent gender and level eliminated these factors as sources of variation, maximizing statistical power to detect degeneration effects. The use of cadaver discs is also a limitation, as the fluid within the disc redistributes after death (Johnstone et al., 1992). It is possible that this redistribution affects disc shape, though this effect remains unquantified. A further limitation is the use of Pfirrmann grading to quantify disc degeneration. Pfirrmann grading mixes several possibly-independent degenerative changes (reduced nucleus image intensity, loss of contrast between nucleus and annulus, and decreased height). However, it is validated, and there is no better alternative (Kettler and Wilke, 2006). The shape model also does not include the internal structures of the disc, such as the nucleus. The success of the shape model in the present context justifies future studies extending it to a broader population and other anatomical targets.

Application to computer simulations

The 3D statistical shape modeling approach used in this study has three important advantages that make it ideal for use in finite element analysis (FEA), which is an important tool to explore the biomechanical (Fagan et al., 2002; Goto et al., 2002; Natarajan et al., 2006; Schmidt et al., 2013; Schroeder et al., 2010; Schroeder et al., 2007; Schroeder et al., 2006) or biological (Magnier et al., 2009; Malandrino et al., 2011; Soukane et al., 2007; Zhu et al., 2012) aspects of disc degeneration. First, it provides an average L3L4 disc shape, with a complete 3D definition, that represents multiple people (Figure 8a). This is a major advance in improving the representativeness of computer simulations.

Figure 8.

The shape model can be used to generate physiologically representative meshes for finite element analysis. (A) The mean shape, shown here as an example mesh, is the simplest representative shape. The nucleus pulposus, in blue, is defined using data from O’Connell et al. (2007). (B) Since PC 1 is correlated with degeneration, PC 1 can be scaled and summed with the mean shape to create representative shapes for specific degeneration grades. Other linear combinations of principal components can also be used, depending on the application. All shapes in this figure are plotted using the same scale.

Second, the shape model provides a single parameter (PC 1) that can represent 70% of the inter-individual variation from this average shape. An investigator running a simulation of the disc could thus run analysis for the mean shape ± 1 s.d. PC 1 to obtain an estimate of how the result of the simulation would vary between individuals. Other PCs could be also used to obtain a more precise result. Since the PCs are ranked according to their variance (Figure 3) and have clear physical meaning (Figure 5), it is easy to select the appropriate number of PCs for the application. Each PC can be varied independently or together, depending on the desired complexity.

Third, the model can be used to construct shapes representing specific degeneration grades by adding the appropriate weight of PC 1 (Figure 8b); using the correlation in Figure 6, we represented grade 2 discs as Φ₀ − 1.13σ₁Φ₁, grade 3 as Φ₀ − 0.28σ₁Φ₁, and grade 4 as Φ₀ + 0.56σ₁Φ₁.

In conclusion, the shape model offers a convenient and powerful option for incorporating shape variation in future disc FEA studies. Without using the shape model, incorporating inter-individual shape variation in a simulation study requires constructing many subject-specific models, running the simulation on each, and calculating summary statistics on the simulation results. This process is extremely laborious. Consequently, shape variation has only been included in a few studies, and then only in terms of simplified CAD-like geometry with assumed independence between geometric measures (Meijer et al., 2011; Meijer et al., 2010; Niemeyer et al., 2012). The shape model vastly reduces the time required to simulate inter-individual variation; additionally, it represents the 3D disc anatomy without any simplification, and the independence between PCs reflects actual independence in the dataset. The necessary data to use the shape model is provided in the supplemental digital content for this paper.