Artificial neural network based characterization of the volume of tissue activated during deep brain stimulation

Abstract

Objective

Clinical deep brain stimulation (DBS) systems can be programmed with thousands of different stimulation parameter combinations (e.g. electrode contact(s), voltage, pulse width, frequency). Our goal was to develop novel computational tools to characterize the effects of stimulation parameter adjustment for DBS.

Approach

The volume of tissue activated (VTA) represents a metric used to estimate the spatial extent of DBS for a given parameter setting. Traditional methods for calculating the VTA rely on activation function (AF)-based approaches and tend to overestimate the neural response when stimulation is applied through multiple electrode contacts. Therefore, we created a new method for VTA calculation that relied on artificial neural networks (ANNs).

Main Results

The ANN-based predictor provides more accurate descriptions of the spatial spread of activation compared to AF-based approaches for monopolar stimulation. In addition, the ANN was able to accurately estimate the VTA in response to multi-contact electrode configurations.

Significance

The ANN-based approach may represent a useful method for fast computation of the VTA in situations with limited computational resources, such as a clinical DBS programming application on a tablet computer.

Introduction

Deep brain stimulation (DBS) is an established clinical treatment for a range of neurological disorders. Successful application of DBS technology requires the identification of a therapeutic stimulation parameter setting in each patient (Moro et al., 2006). Clinical DBS devices enable thousands of different parameter settings to be defined, which provide flexibility to customize the stimulation to the patient. However, exploration of this parameter space is limited by a wide range of variables, such as the clinician’s experience with DBS technology, and their available time for device programming with the patient. Therefore, we proposed that patient-specific computational models of stimulation, coupled with visualization software, could represent useful tools to assist DBS clinicians (McIntyre et al., 2007). A recent clinical study supported this concept, demonstrating that prospective definition of DBS parameter settings, via calculations of the volume of tissue activated (VTA), could generate clinical outcomes that rivaled those of traditional clinical practice (Frankemolle et al., 2010).

The “gold standard” for computational prediction of neurostimulation is to couple electric field data to multi-compartment neuron models (McNeal, 1976). Unfortunately, this McNeal-based prediction method is currently too computationally intensive to be practical for most clinical applications. Therefore, simplified methods for calculating the spatial extent of axonal activation have been developed that typically rely on the second spatial difference of the extracellular voltages generated by the electrode (e.g. Rattay, 1986; Warman et al., 1992; Moffitt et al., 2004; Butson and McIntyre, 2006). These activating function (AF) based approaches are relatively accurate predictors for monopolar cathodic stimulation. However, the increased complexity of the electric fields generated during multi-contact stimulation limits generalization of the traditional AF-based approach (Peterson et al., 2011).

Previously, our group has customized AF-based approaches for clinical DBS electrodes (e.g. McIntyre et al., 2004; Butson and McIntyre, 2006; Butson et al., 2007) to enable calculation of a VTA. VTA predictor functions have also been used by a range of other groups investigating DBS (e.g. Yousif et al., 2010; Martens et al., 2011; Schmidt et al., 2013). However, we have found the performance of AF-based VTA predictor functions to be unsatisfactory in the context of bipolar or multipolar stimulation conditions. Therefore, the objective of this study was to develop a new method that improves the accuracy of VTA predictions for DBS electrodes. We explored the concept of using artificial neural networks (ANNs) to characterize the spatial extent of axonal activation for a given set of stimulation parameters. The benefits of ANNs reside in their ability to generalize complex relationships. Therefore, we hypothesized that ANNs could outperform traditional AF-based approaches for VTA estimation.

Materials and methods

The goal of this study was to develop a new method for improving the accuracy of VTA predictions for DBS electrodes. There are multiple options for developing predictor functions, each having their own advantages and disadvantages. Among the most commonly used are look-up tables, polynomial fitting, and regression analysis. Look-up tables are the easiest to implement, but require that each unique stimulation setting be modeled independently. Polynomial and regression-based predictor functions are effective at predicting monopolar stimulation; however, separate functions are typically needed for each electrode design, electrode configuration and pulse width examined (Butson and McIntyre, 2006). In contrast, ANNs are able to characterize complex multi-parameter relationships with high accuracy. Furthermore, ANNs allow dynamic changes to the model inputs and outputs without requiring significant changes to its underlying structure. Additionally, once trained, ANNs are efficient in making predictions in real-time. As a result, ANNs represent a potential alternative to AF-based approaches for predicting the spatial extent of neural activation.

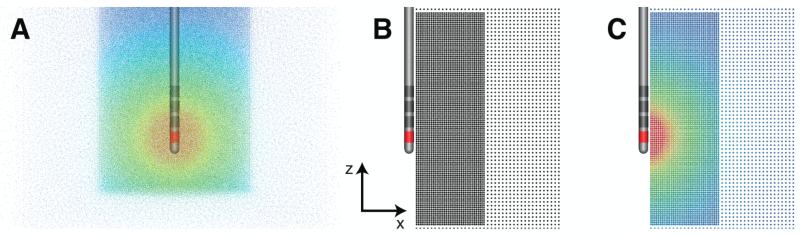
Our ANN predictor function was created to estimate neural activation based on results derived from finite element models (FEM) of the electric fields generated by DBS electrodes. We evaluated a wide range of stimulation settings and electrode configurations (Table 1), directly coupling the DBS electric field to multi-compartment cable models of myelinated axons. The DBS FEM was created with a three-dimensional multi-resolution mesh using COMSOL 3.4 (Comsol Inc., Burlington, MA). A virtual Medtronic 3389 DBS electrode (Medtronic, Minneapolis, MN), was centered within the FEM mesh (Fig. 1A). The model explicitly represented the capacitance and voltage drop at the electrode-electrolyte interface, as well as an encapsulation layer of tissue surrounding the DBS electrode (Chaturvedi et al., 2010). The bulk tissue medium was modeled as homogeneous and isotropic with a conductivity of 2 S/m. The encapsulation layer (0.5 mm thick) was set to one of three values to represent low (0.680 S/m), medium (0.128 S/m), or high (0.066 S/m) impedance conditions (Butson et al., 2006). The electrode capacitance was set to 3.3 μF (Butson and McIntyre, 2005), while the voltage drop at the electrode-tissue interface was set to 42% (Miocinovic et al., 2009).

Table 1.

Range of stimulation settings and electrode configurations used in this study.

electrode:	Medtronic 3389
frequency:	130 Hz
pulse-widths:	60, 90, 120, 150, 180, 210, 450 μs
amplitudes:	−1, −2, −3, −4, −5, −6, −7, −8, −9, −10 V
impedances:	low (0-749), medium (750-1250), high (1251+) Ω
contact configurations:	4 monopolar, 18 two-contact

Figure 1.

Electric field and axon models. (A) Finite element model consisting of the Medtronic 3389 DBS electrode lead centered within a multi-resolution FEM mesh. The extracellular voltage is shown for a −1 V stimulation through contact 0 (red - high voltage; blue - low voltage). (B) Points represent the axon model distribution. The axons have straight trajectories that project along the y-axis. (C) Voltage distribution interpolated from the FEM mesh to each axon model.

To estimate axonal activation from DBS, we used a population of 6803 axon models positioned adjacent to and perpendicular to the electrode (Fig. 1B). The geometrical and biophysical parameters of the individual axon models have been previously described (McIntyre et al., 2002). The position and orientation for the axons were chosen to estimate the vertical and lateral aspects of the stimulation spread. Volumetric spread was then estimated by rotating the activation surface about the electrode shaft to create a three-dimensional VTA. These axons were distributed at 0.25 mm intervals in a region close to the electrode, and at 0.5 mm intervals further away. The axon population was positioned 1 to 10 mm horizontally from the center of the electrode shaft, and −10 to 18 mm from the bottom of the electrode shaft (Fig. 1B). The lower resolution axon population continued to encompass a region 28 mm lateral from the center of the electrode shaft and −19 to 28 mm in the vertical direction (Fig. 1B). We also varied the axon diameter (2.0, 5.7, 7.3, 8.7, and 10.0 μm) to investigate its effects on neural activation. Each axon model, regardless of diameter, consisted of 21 nodal compartments, except the 2.0 μm diameter axons that contained 51 nodal compartments due to its much shorter internodal distance.

Axonal response to DBS

The threshold for action potential initiation of each axon was determined using NEURON 6.2 (Hines and Carnevale, 1997). We calculated the extracellular voltage within the FEM mesh and interpolated those voltages onto the myelinated axon models using SCIRun (Scientific Computing and Imaging Institute, University of Utah, Salt Lake City, UT). The population of axons that elicited propagating action potentials from the stimulation defined our McNeal-based “gold standard” of activation for that setting. Monopolar and multi-contact settings were evaluated using 4620 unique stimulation configurations for each population of axons for each axon diameter analyzed.

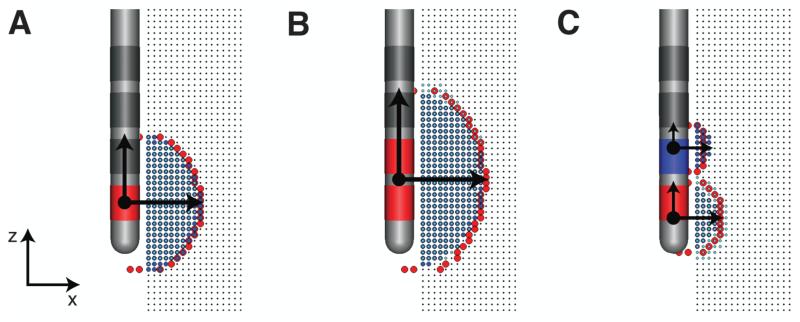
We grouped and characterized the location of the directly activated axons for each stimulation parameter setting tested, and for each active contact (cathode or anode) used in the simulation (Fig. 2A). Adjacent cathodic active regions were merged into a single active region (Fig. 2B). A constrained optimization algorithm (Boyd and Vandenberghe, 2004) was used to find the parameters defining a 2D ellipse that best described each active region (Fig. 2C).

Figure 2.

Definition of active region(s). (A) monopolar stimulation. (B) two-contact stimulation with two adjacent cathodes. (C) two-contact stimulation with one cathode and one anode. The boundary of all active regions are shown in red. Horizontal and vertical arrows describe the horizontal (a) and vertical (c) spreads of activation, respectively. The dot(s) represents the center (z) of the active region(s).

ANN-based predictor functions

We used ANNs developed in MATLAB (Mathworks Inc., Natick, MA) to model the spread of activation for monopolar and two-contact stimulation. Each predictor function used two feed-forward ANNs to parameterize neural activation. One feed-forward ANN described the size of each activation region (Table 2). A second ANN determined the placement of each activation region along the electrode shaft (Table 2).

Table 2.

Inputs and outputs for each of the two artificial neural networks used to create each novel predictor function, one for monopolar and another for two-contact.

inputs	outputs
	ANN 1	ANN 2
fiber diameter (□) - (μm)	horizontal spreads	activation centers
pulse-width (pw) - (μs)	(a0,a1,a2,a3,) - (mm)	(z0,z1,z2,Z3,) - (mm)
voltage (V) - (volts)	vertical spread
impedance (Z) - (Ω)	(c0,c1,c2,c3,) - (mm)
contact 0 configuration (cc0 )*
contact 1 configuration (cc1 )*
contact 2 configuration (cc2 )*
contact 3 configuration (cc3 )*
ellipse 0(e0 )D
ellipse 1 (e1)D
ellipse 2 (e2)D
ellipse 3 (e3)D

^*−1 (cathode), 0 (dormant), +1 (anode)

^D(active region, ellipse present), 0 (inactive)

Architecturally, each ANN received 12 inputs describing the stimulation parameters and electrode configurations (Table 2). After performing a sensitivity analysis on its architecture, we found that one hidden layer with 20 elements using a sigmoid transfer function and a linear output layer produced accurate results (i.e., low training and validation RMS errors), while still being computationally efficient (Lujan and Crago, 2009). Both networks were trained using the Levenberg-Marquardt algorithm on 70% of the stimulation settings, and their corresponding ellipse parameters were fit to match the McNeal-based data. The remaining 30% of the McNeal-based data were used for validation and assessing the performance of the ANN-based predictor functions. Weights were initialized with random values. While training, the backpropagation algorithm is presented with training data and novel validation data, after which the error between the actual and expected results is calculated (training error and validation error, respectively). Overtraining the neural network can lead to decreased performance and an inability to generalize the ellipse parameters accurately. To prevent ANN overtraining, training was terminated if the validation error became larger than the training error.

Performance evaluation

We evaluated the accuracy of the trained ANN predictor functions by comparing the spatial spread of their predicted ellipses to the remaining McNeal-based data set, within a single plane. In addition, we compared the ANN-based predictions to AF-based predictions. We calculated false-positives (FP, type I errors) and false-negatives (FN, type II errors) in axon activation for all stimulation settings and electrode configurations (Table 1). A type I error corresponds to spatial regions where the predicted activation regions overshoots the gold standard and incorrectly marks axons as being active. A type II error resulted from an underestimation of neural activation. Total error was defined by the sum of prediction errors normalized by the number of active axons (AA) in the McNeal-based data set, for the given stimulation parameter setting being evaluated: Error = (FP + FN) / AA.

Results

Axon activation prediction errors

ANNs were trained to define the spatial extent of stimulation and the center of activation along the electrode shaft. These ANN-based predictor functions were created separately for both the monopolar and two-contact stimulation cases. Two ANNs were used for each complete predictor function. The first ANN described the size of the ellipse(s), while the second ANN described center of the ellipse(s). Training of the first ANN yielded a 0.990 and 0.987 coefficients of determination (R²-value) for the monopolar and two-contact cases, respectively. Training the second ANN had an R²-values of 0.992 (monopolar) and 0.988 (two-contact).

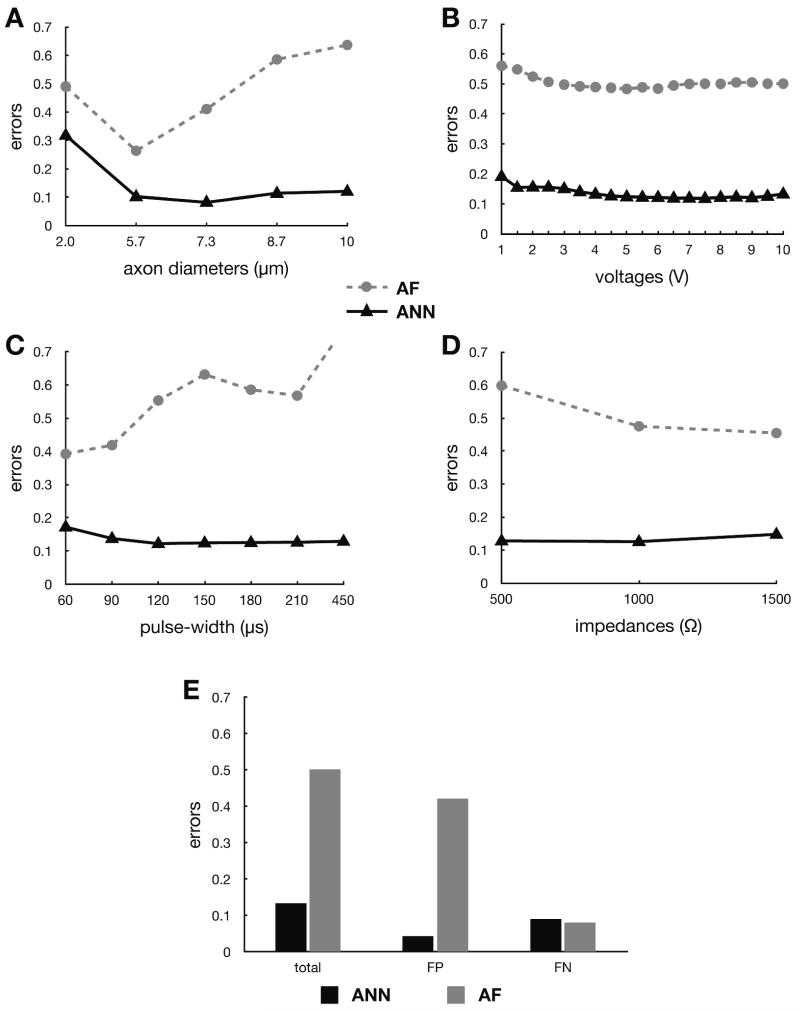
Figure 3 shows the error in prediction of axonal activation for both the ANN-based and AF-based predictor functions for monopolar cathodic stimulation settings. This stimulation configuration represents the lowest possible error opportunity for the AF-based predictor function, as this is the stimulation configuration for which it was designed to operate in. For fiber diameters greater than 2.0 μm, the ANN-based predictor function has an error of 0.13 ± 0.03 (mean ± std) regardless of the parameter being varied. Neither the ANN nor AF-based predictors had errors that were affected by increasing the voltage amplitude or impedance. On the other hand, the error for the AF-based predictor became greater at larger fiber diameters and longer pulse-widths. The AF-based predictor function had its lowest error when using 5.7 μm diameter axons, which corresponds to the original axon diameter used to develop this predictor function (Butson and McIntyre, 2006). To better understand the origin of the error associated with predictor functions, we examined the individual type I (overestimation) and type II (underestimation) errors (Fig. 3E). The ANN-based approach slightly underestimated activation, while the AF-based predictor function overestimated activation.

Figure 3.

Activation error comparisons between the ANN-based predictor function (solid line) and the AF-based predictor function (dashed line) for monopolar stimulation as a function of (A) axon diameter, (B) voltage, (C) pulse-width, and (D) clinical impedance. (E) Predictor function errors, false-positives (FP, type I errors) and false-negatives (FN, type II errors), for monopolar stimulation are also compared.

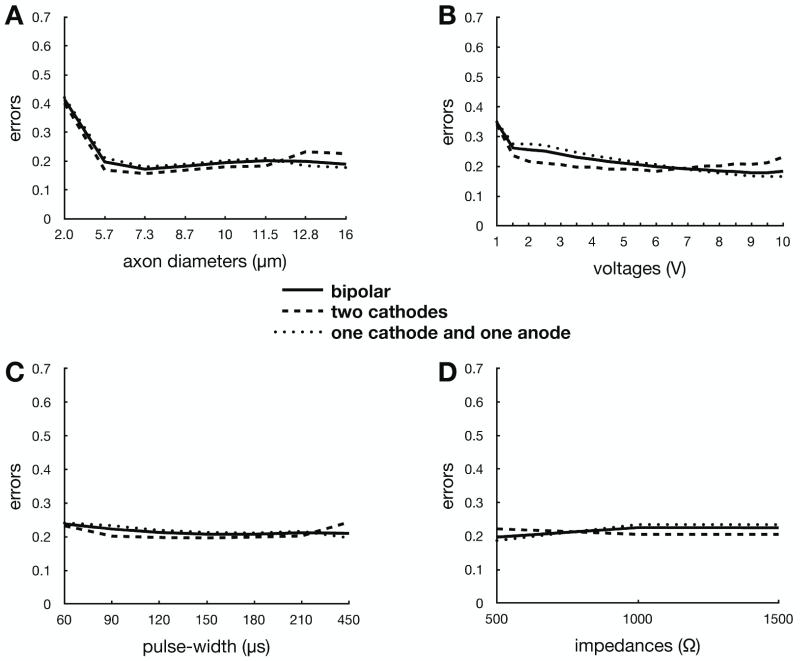
When considering stimulation delivered through two contacts on the same electrode (i.e., two cathodes or anode/cathode stimulation), the ANN-based prediction errors nearly doubled (Fig. 4). However, this error was still lower than the AF-based error for monoplar stimulation, and the AF-based system is only accurate when used in the context of monopolar cathodic stimulation. In contrast, the ANN-based predictor behavior for two-contact stimulation was analogous to monopolar stimulation across the entire range of stimulus amplitudes, pulse widths, electrode impedances, and axon diameters. Similarly, there were no major differences in prediction error when comparing stimulation through two cathodes or one anode and one cathode combinations.

Figure 4.

ANN-based prediction error for all two-contact stimulation (solid line) as a function of (A) axon diameter, (B) voltage, (C) pulse-width, and (D) clinical impedance. This error was also analyzed for two cathodes only (dashed line), as well as traditional “bipolar” one cathode / one anode (dotted line) only.

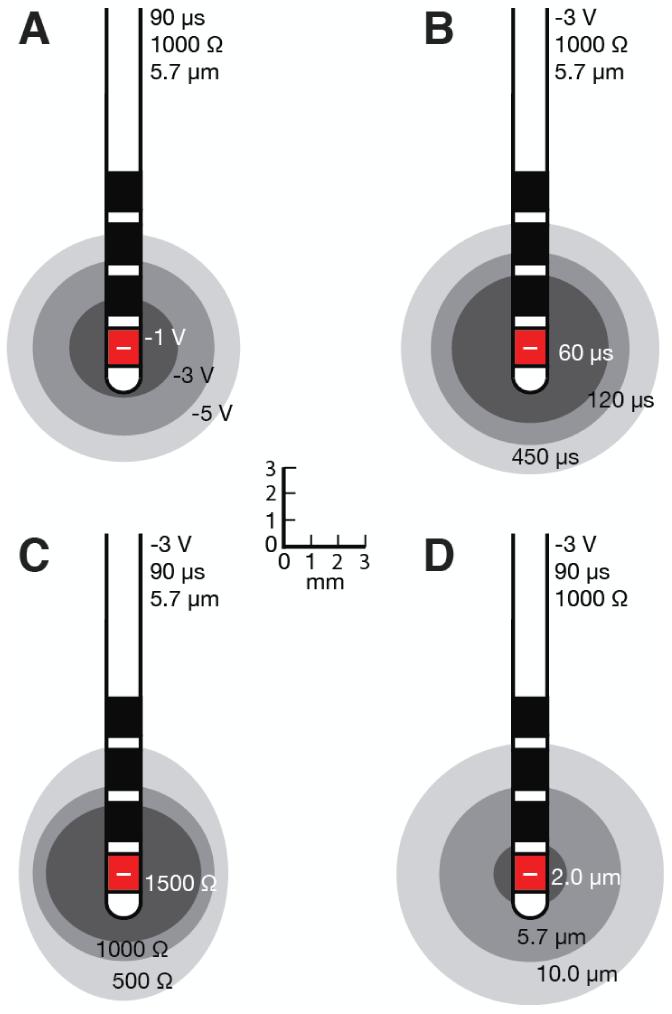
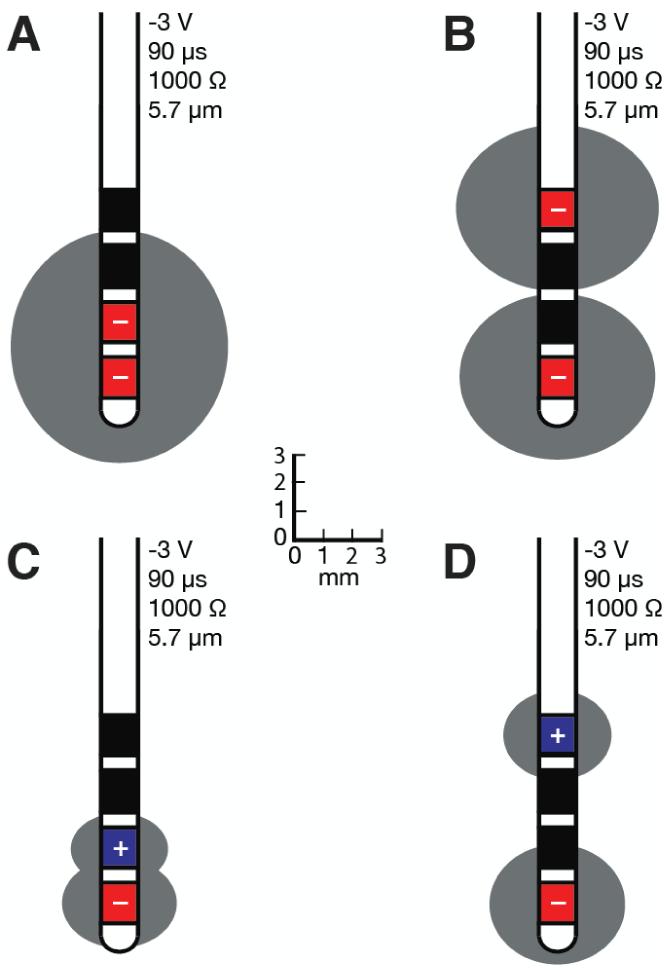
The spatial extent of axonal activation is affected by many factors. The ANN-based predictor function enables comparisons for varying voltage amplitudes, pulse-widths, impedances, and axon diameters (Fig. 5). As expected, higher stimulation voltages, longer pulse-widths, and lower impedances increase the spatial spread of activation and the corresponding VTA (Table 3). More importantly, changes in axon diameter have a large effect on the VTA (Fig. 5D). When multiple contacts are active, the VTA can take a wide range of shapes and sizes (Fig. 6). Multiple cathodes can generate large activation volumes (Fig. 6A, B), while bipolar stimulation (cathode and anode) substantially decreases the overall VTA (Fig. 6C, D).

Figure 5.

Volumes of tissue activated when a monopolar cathode at contact 0, with (A) varying voltages, (B) pulse-widths, (C) impedances, and (D) axon diameters.

Table 3.

Quantifying the impact of these various parameters on the spatial spread of activation and the volume of tissue activated (V - voltage, pw - pulse-width, Z - impedance, [c₀, c₁, c₂, c₃] - contact configurations, a - horizontal spread of activation, c - vertical spread of activation).

Stimulation configuration					spread (mm)		volume (mm3)
V (V)	Pw (μs)	Z (Ω)	φ(μm)	[C0, C1, C2, C3]	a	c
−1	90	1000	5.7	[−1000]	1.97	1.81	29
−3	90	1000	5.7	[−1000]	3.32	3.21	148
−5	90	1000	5.7	[−1000]	4.27	4.18	318
−3	60	1000	5.7	[−1000]	2.86	2.72	93
−3	120	1000	5.7	[−1000]	3.63	3.53	195
−3	450	1000	5.7	[−1000]	4.73	4.61	432
−3	90	500	5.7	[−1000]	3.83	4.67	287
−3	90	1000	5.7	[−1000]	3.32	3.21	148
−3	90	1500	5.7	[−1000]	2.83	2.51	84
−3	90	1000	2.0	[−1000]	1.32	1.17	9
−3	90	1000	5.7	[−1000]	3.32	3.21	148
−3	90	1000	10.0	[−1000]	4.9	4.80	482
−3	90	1000	5.7	[−1 −1 0 0]	3.69	3.95	225
−3	90	1000	5.7	[−1 0 0−1]	3.32	2.81	130
					3.44	2.81	139
−3	90	1000	5.7	[−1 1 0 0]	1.93	1.50	23
					1.63	1.20	13
−3	90	1000	5.7	[−1001]	2.29	2.02	45
					1.82	1.50	21

Figure 6.

Volumes of tissue activated during two-contact stimulation for (A) adjacent cathodes, (B) farthest away cathodes, (C) adjacent cathode / anode, and (D) distant cathode / anode.

Discussion

To achieve the best possible therapeutic outcomes, present-day clinical DBS programming requires multiple programming sessions to identify a suitable set of stimulation parameters (Moro et al., 2006). Due to time constraints, only a small subset of the stimulation parameter space is thoroughly explored during each clinical session, making optimal therapeutic benefits sometimes difficult to achieve. Recently, computational models have been introduced to address this limitation and aid in the search for therapeutic stimulation parameters settings (McIntyre et al., 2007). These models are capable of estimating the spatial extent of neural activation, or VTA, which has been successfully used clinically to identify theoretically optimal DBS parameter settings in Parkinson’s disease patients (Frankemolle et al., 2010). Historically, these VTA models have relied on an AF-based approach that is only be suitable for monopolar cathodic stimulation predictions (Butson and McIntyre, 2006). Therefore, we set out to develop a new method for predicting neural activation that could be used to explore more complex electrode configurations with limited prediction error.

Predictor evaluation

Artificial neural networks represent a useful tool for predicting the VTA because of their ability to approximate the non-linear changes in the electric field produced by complex electrode configurations and stimulation settings. When compared to a typical AF-based predictor, the ANN-based predictor function was more accurate over the entire range of stimulation settings (Fig. 3). We noted that the error was highest in both monopolar and two-contact stimulation cases when activating 2.0 μm diameter axons. Presumably this was the case because there were fewer 2.0 μm diameter axons directly activated for each stimulation setting, so even a small number of false-positive or false-negative errors could lead to a large overall error. More importantly, unlike for the AF-based predictor, the ANN prediction errors remained relatively consistent across the entire parameter space despite large changes in voltage amplitudes, pulse-widths, and impedances.

Study limitations

While the ANN-based predictor functions performed well, they lack a first principles connection to the biophysical interpretation of the method, which does exist for AF-based predictor functions (Rattay, 1986). In addition, the representation of ANN-based activation regions did have limitations under some stimulation settings and electrode configurations. For example, at high voltages (e.g., >3 V) with non-adjacent cathodes, the active regions were represented by two smaller ellipses that did not entirely capture neural activation at their overlapping boundaries. However, using higher-order equations and/or combinations of single equations to define these complex active regions could potentially minimize this type of error. In addition, similar ANN-based predictor functions could theoretically be created for any number of active contacts or alternative electrode designs.

It should also be noted that the VTA prediction used in this study were calculated in the context of a highly idealized brain tissue environment. For example, straight axons, orientated perpendicular to the electrode, within the context of an isotropic bulk tissue medium. The impact of these assumptions has been addressed in numerous studies (e.g. Chaturvedi et al., 2010; Yousif et al., 2010; Schmidt et al., 2013). However, for all the shortcomings of simplified VTA predictions, they do appear to represent a viable tool for clinical DBS parameter selection (Frankemolle et al., 2010).

Conclusions

The use of ANN-based predictor functions provides the flexibility to characterize DBS axonal activation for a wide range of stimulation settings and contact configurations. The flexibility of ANNs should also enable customization of the technique to novel electrode designs and stimulation paradigms. Application of this methodology may someday have clinical utility by providing fast VTA simulation for visual feedback in clinical software interfaces designed for customizing patient-specific DBS parameter settings.