A simple generative model of collective online behavior

Significance

One of the most common strategies in studying complex systems is to investigate and interpret whether any “hidden order” is present by fitting observed statistical regularities via data analysis and then reproducing such regularities with long-time or equilibrium dynamics from some generative model. Unfortunately, many different models can possess indistinguishable long-time dynamics, so the above recipe is often insufficient to discern the relative quality of competing models. In this paper, we use the example of collective online behavior to illustrate that, by contrast, time-dependent modeling can be very effective at disentangling competing generative models of a complex system.

Abstract

Human activities increasingly take place in online environments, providing novel opportunities for relating individual behaviors to population-level outcomes. In this paper, we introduce a simple generative model for the collective behavior of millions of social networking site users who are deciding between different software applications. Our model incorporates two distinct mechanisms: one is associated with recent decisions of users, and the other reflects the cumulative popularity of each application. Importantly, although various combinations of the two mechanisms yield long-time behavior that is consistent with data, the only models that reproduce the observed temporal dynamics are those that strongly emphasize the recent popularity of applications over their cumulative popularity. This demonstrates—even when using purely observational data without experimental design—that temporal data-driven modeling can effectively distinguish between competing microscopic mechanisms, allowing us to uncover previously unidentified aspects of collective online behavior.

The recent availability of datasets that capture the behavior of individuals participating in online social systems has helped drive the emerging field of computational social science (1), as large-scale empirical datasets enable the development of detailed computational models of individual and collective behavior (2–4). Choices of which movies to watch, which mobile applications (“apps”) to download, or which messages to retweet are influenced by the opinions of our friends, neighbors, and colleagues (5). Given the difficulty in distinguishing between potential explanations of observed behavior at the individual level (6), it is useful to examine population-level models and attempt to reproduce empirically observed popularity distributions using the simplest possible assumptions about individual behavior. Such generative models have arisen in a wide range of disciplines—including economics (7, 8), evolutionary biology (9, 10), and physics (11). When studying generative models, the microscopic dynamics are known exactly, so it is possible to explore the population-level mechanisms that emerge in a controlled manner. This contrasts with studies driven by empirical data, in which confounding effects can always be present (6). The value of explanations based on mechanisms has long been appreciated in sociology (12–14), and they have recently received increased attention due to the availability of extensive data from online social networks (15–18).

One well-studied rule for choosing between multiple options is cumulative advantage (also known as preferential attachment), in which popular options are more likely to be selected than unpopular ones. This leads to a “rich-get-richer” agglomeration of popularity (7, 9, 19–22). Bentley et al. (5, 23, 24) proposed an alternative model, in which members of a population randomly copy the choices made by other members in the recent past. As a result, products whose popularity levels have recently grown the fastest are the most likely to be selected (whether or not they are the most popular overall). In the present paper, we show that models of app-installation decisions that are biased heavily toward recent popularity rather than cumulative popularity provide the best fit to empirical data on the installation of Facebook apps. We use the model to identify the timescales over which the influence of Facebook users upon each others’ choices is strongest, and we argue that the interaction between these timescales and the diurnal variation in Facebook activity yields many of the observed features of the popularity distribution of apps. More generally, we illustrate how to incorporate temporal dynamics in modeling and data analysis to differentiate between competing models that produce the same long-time (i.e., after transients have died out) behavior.

We use the Facebook apps dataset that was first reported in ref. 15 by Onnela and Reed-Tsochas. These data include the records, for every hour from June 25, 2007 to August 14, 2007, of the number of times that every Facebook app (of the n = 2,705 total available during this period) was installed. At the time, Facebook users had two streams of information about apps: a “cumulative information” stream gave an “all-time best-seller” list, in which all apps were ranked by their cumulative popularity (i.e., the total number of installations to date), and a “recent activity information” stream consisted of updates provided by Facebook on the recent app installation activity by a user’s friends. Users could also visit the profiles of their friends to see which applications a friend had installed.

The data thus consist of N time series n_i(t), where the “popularity” n_i(t) of app i at time t is the total number of users who have installed app i by hour t of the study period. The discrete time index t counts hours from the start of the study period (t = 0) to the end (t = t_max ≡ 1,209). The distribution of n_i values is heavy-tailed (SI Appendix, Fig. S1), so the popularities n_i(t) of the apps cover a very wide range of scales. Facebook apps first became available on May 24, 2007, corresponding to t ≈ −720 in our notation. By time t = 0, when the data collection began, 980 apps had already launched (with unknown launch times); the remaining apps in our dataset were launched during the study period. Among the latter, we pay particular attention to those for which we have at least t_LES ≡ 650 h (i.e., more than one-half of the data collection window) of data. We call these apps the “launched-early-in-study” (LES) apps. Denoting by t_i the launch time of app i, the 921 LES apps i are those that satisfy t_i > 0 and t_i < t_max − t_LES = 559. We set t_i = 0 for apps that were launched before the study period.

To measure the change in app popularity during hour t, we define the “increment” in popularity of app i at time t as f_i(t) = n_i(t) − n_i(t − 1) [with f_i(t) = 0 for t ≤ t_i] (15). The total app installation activity of users during hour t is then as follows:

$$F\left(t\right)={\displaystyle \sum _{i=1}^N{f}_i\left(t\right)}.$$ [1]

We show in SI Appendix, section SI1 that F(t) has large diurnal fluctuations superimposed on a linear-in-time aggregate growth.

We define the “age-shifted popularity” ${\tilde{n}}_i\left(a\right)=n_i\left(t_i+a\right)$ and “age-shifted increment” ${\tilde{f}}_i\left(a\right)=f_i\left(t_i+a\right)$ of app i at age a to enable comparison of apps when they are the same age (i.e., at the same number of hours after their launch). An examination of the trajectories of the largest LES apps reveals that their popularity grows exponentially for some time before reaching a steady-growth regime in which ${\tilde{n}}_i\left(a\right)$ increases approximately linearly with age. The corresponding age-shifted increment functions ${\tilde{f}}_i\left(a\right)$ reach a “plateau” at large a, although they have a superimposed 24-h oscillation (SI Appendix, Figs. S3 and S4). To study the entire set of LES apps, we scale the increment ${\tilde{f}}_i$ of app i by its temporal average ${\tilde{\mu }}_i=\left({\displaystyle {\sum }_{a=1}^{t_{\text{LES}}}\hspace{0.17em}{\tilde{f}}_i\left(a\right)}\right)/t_{\text{LES}}$ over the first t_LES = 650 observations for each app. This weights very popular apps and other (less popular) apps in a similar manner (25). For a given set $\mathrm{ℐ}$ of LES apps, we define the “mean scaled age-shifted growth rate” as follows:

$$r\left(a\right)={\langle \frac{{\tilde{f}}_i\left(a\right)}{{\tilde{\mu }}_i}\rangle }_{\mathrm{ℐ}},$$ [2]

where 〈⋅〉 denotes an ensemble average over all apps in the set $\mathrm{ℐ}$.

The mean scaled age-shifted growth rate reveals several interesting features (Fig. 1A). First, at large ages (e.g., a ≥ 150 h), the function r(a) has 24-h oscillations superimposed on a nearly constant curve. The behavior of r(a) is very different for smaller ages; we dub this the “novelty regime,” as it represents the (approximately 1-wk) time period that immediately follows the launch of apps. The r(a) curve for the entire LES set is similar to those found by splitting the LES set into two disjoint subsets based on ordered launch times—the 460 applications with earlier launch times (t_i ≤ 260; early-launch) and the 461 applications with later launch times (t_i ≥ 261; late-launch). The small difference between the r(a) curves for these cases gives an estimate of the inherent variability within the data and sets a natural target for how well stochastic simulations can fit the data. We find similar results for other subsets of the same size (SI Appendix, section SI3).

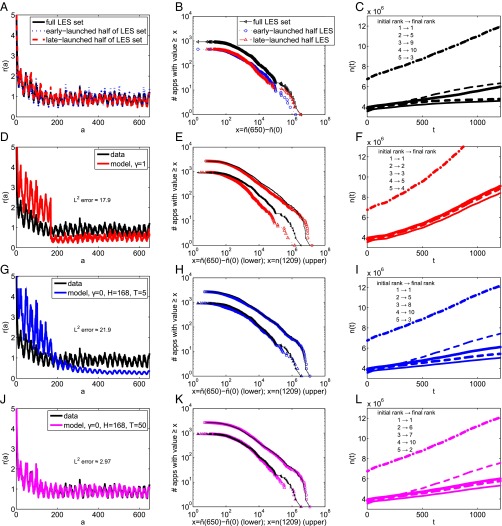
Fig. 1.

(Left) Mean scaled age-shifted growth rate r(a), (Center) distributions of app popularity, and (Right) popularity over time for the top-five apps, showing turnover. (A and B) Behavior of the entire LES set of applications and its two subsets (which are described in the text); (C) trajectories of the top-five apps in the dataset (ordered by popularity at t = 0; note apps that were not in the t = 0 top-five are not shown here but can be seen in SI Appendix, Fig. S7). (D–F) Cumulative-information model (γ = 1), for which (E) shows popularity distributions at t = t_max (upper symbols) and for LES app growth to age a = t_LES (lower symbols); empirical data are in black. (G–I) Recent-activity model with short memory (γ = 0, H = 168, T = 5). (J–L) Recent-activity model with long-memory (γ = 0, H = 168, T = 50).

To directly measure the growth of new apps in their first t_LES hours, we show the distribution of ${\tilde{n}}_i\left(t_{\text{LES}}\right)-{\tilde{n}}_i\left(0\right)$ for the entire LES set in Fig. 1B. We also show the corresponding distributions for the two LES subsets (early and late launch). The similarity of distributions for early-born apps and late-born apps implies that the launch time, at least in the period that we examined, does not have a strong effect on the growth of new apps. This contrasts with Yule–Simon models of popularity (7, 21, 26) and related preferential-attachment models used to model citations (11). In these models, early-born apps have more time to accumulate popularity and hence exhibit a different aging behavior to later-born apps (27).

In Fig. 1C, we examine changes in the rank order of the top-5 list of apps by plotting the trajectories of the largest apps (ranked by their popularity at time t = 0) over the duration of the study (and see SI Appendix, Fig. S7, for plots of top-10 lists). Reproducing realistic levels of turnover in such lists is a challenging test for models of popularity dynamics (24, 28).

The popularity dynamics for the novelty regime seem to be app-specific (Fig. 1A and SI Appendix, Fig. S4), but a simple model can satisfactorily describe the postnovelty regime. We introduce a general stochastic simulation framework with a “history-window parameter” H and consider an app to be within its “history window” for the first H hours that data on the app are available. The history window of LES apps extends from their launch time to H hours later; for non-LES apps, we define the history window to be the first H hours (t = 0 to t = H) of the study. We conduct stochastic simulations by modeling F(t) computational “agents” in time step t, each of whom installs one app at that time step. We take the values of F(t) from the data (Eq. 1). Note that our simulated agents do not correspond directly to Facebook users, as we do not have data at the level of individual users. In reality, a Facebook user can, for example, install several different apps during an hour; in our simulations, however, such actions would be modeled by the choices of several agents.

We simulate the choices of the agents as follows. First, for any app i that is in its history window at time t, we copy the increment f_i(t) directly from the data. This determines the choices of F_H(t) of the agents, where F_H(t) is the number of installations of all apps that are within their history window at time t. Each of the remaining F(t) − F_H(t) agents then installs any one of the apps that are not in their history window. An installation probability p_i(t) is allocated based on model-specific rules (see below), and the F(t) − F_H(t) agents each independently choose app i with probability p_i(t). These rules ensure that the total number of installations in each hour exactly matches the data and that the history window of each app is reproduced exactly.

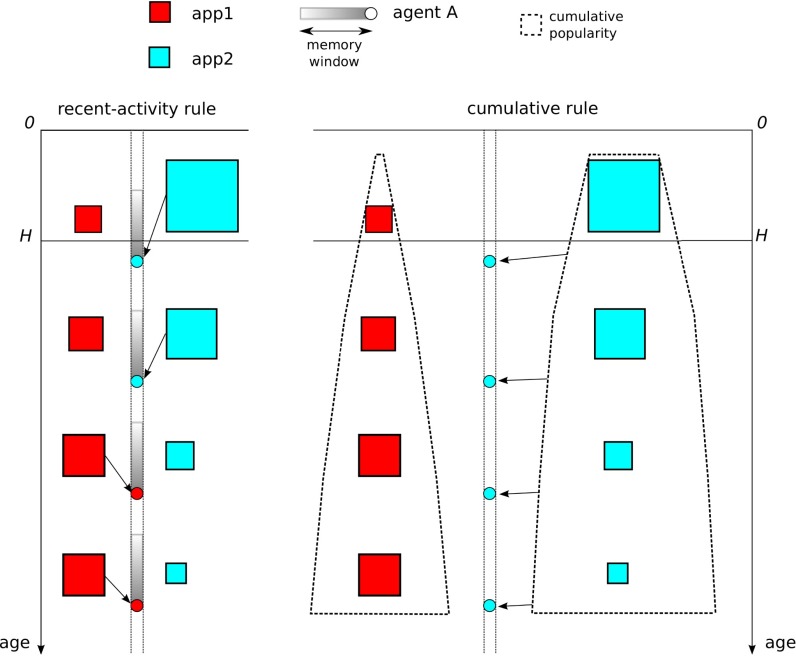
We investigate several possible choices for p_i(t) by comparing the results of simulations with the characteristics of the data highlighted in Fig. 1 A–C. The history-window parameter H plays an important role in capturing the app-specific novelty regime. However, if H is very large, then most of the simulation is copied directly from the data and the decision probability p_i(t) becomes irrelevant. It is therefore desirable to find models that fit the data well while keeping H as small as possible. Motivated by the information available to Facebook users during the data collection period, we propose a model based on a combination of a “cumulative rule” $p_i^c\left(t\right)$ and a “recent activity rule” $p_i^r\left(t\right)$. See the schematic in Fig. 2.

Fig. 2.

Schematic of the model. The squares indicate the number of installations at time t of two example apps; their size represents the number of installations of an app in a particular hour. The circles represent agents, and the arrows indicate the adoption of an app. In the history window (ages 0 to H), we copy the installation history directly from the data. Outside of the history windows, we simulate the actions of F(t) agents by assigning probabilistic rules for how they choose which app to install. An agent who uses (Left) the recent-activity rule at a given time copies the choice of an agent who acted in the recent past, so apps that were recently more popular are more likely to be chosen. By contrast, an agent who uses (Right) the cumulative rule at a given time installs the app with the larger number of accumulated installations. We represent this cumulative popularity using the dashed contour, which increases in width with time as more installations occur.

An agent who uses the cumulative rule at time t chooses app i with a probability proportional to its cumulative popularity n_i(t − 1), yielding the following:

$$p_i^c\left(t\right)=K\hspace{0.17em}{n}_i\left(t-1\right),$$ [3]

where the constant K is determined by the normalization ${\displaystyle {\sum }_i{p}_i^c\left(t\right)}=1$. In contrast, an agent who follows the recent-activity rule at time t copies the installation choice of an agent who acted in an earlier time step, with some memory weighting (Eq. 4 below). Consequently, apps that were recently installed by many agents [i.e., apps with large f_i(τ) values for τ ≈ t] are more likely to be installed at time step t even if these apps are not yet globally popular [i.e., n_i(t − 1) can be small]. In reality, the information available to Facebook users on the recent popularity of apps was limited to observations of the installation activity of their network neighbors. As we lack any information on the real network topology, we make the simplest possible assumption: that the network is sufficiently well-connected (see ref. 29 for a study of Facebook networks from 2005) to enable all agents in the model to have information on the aggregate (system-wide) installation activity. When applying the recent-activity rule, an agent chooses app i with a probability proportional to the recent level of that app’s installation activity:

$$p_i^r\left(t\right)=L{\displaystyle \sum _{\tau =0}^{t-1}W\left(t-\tau \right)f_i\left(\tau \right)},$$ [4]

where L is determined by the normalization ${\displaystyle {\sum }_i{p}_i^r\left(t\right)}=1$. The “memory function” W(τ) determines the weight assigned to activity from τ hours ago and thereby incorporates human-activity timescales (30). In SI Appendix, we consider several examples of plausible memory functions and also examine the possibility of heterogeneous app fitnesses.

If our dataset included the early growth of every app, then a constant weighting function W(t) ≡ 1 would reduce $p_i^r$ to $p_i^c$. However, because of our finite data window, many apps have large values of n_i(0), so we cannot capture the cumulative rule by using a suitable weighting function in the recent-activity rule. Instead, we introduce a tunable parameter γ ∈ [0, 1] so that the population-level installation probability p_i used in the simulation is a weighted sum,

$$p_i\left(t\right)=\gamma \hspace{0.17em}{p}_i^c\left(t\right)+\left(1-\gamma \right)p_i^r\left(t\right),$$ [5]

that interpolates between the extremes of γ = 0 (recent-activity rule) and γ = 1 (cumulative rule). The model ignores externalities between apps, an assumption that is supported by the results of ref. 15.

To explore our model, we start by considering the case γ = 1, in which agents consider only cumulative information. In Fig. 1 D–F, we compare the results of stochastic simulations with the data (Fig. 1 A–C) using a history window of H = 168 h (i.e., 1 wk). Clearly, the cumulative model does not match the data well. Although the app popularity distributions at t = t_max are reasonably similar (Fig. 1E), the largest popularities are overpredicted by the model. By contrast, the popularity of the LES apps—which include many of the less popular apps—is underpredicted. In particular, their mean scaled age-shifted growth rate has a lower long-term mean than that of the data (Fig. 1D). Recall from Eq. 2 that each app’s increments are scaled by their temporal average ${\tilde{\mu }}_i$ before ensemble averaging to calculate r(a). As a result, any error in predicting the value of ${\tilde{\mu }}_i$ has an effect on the entire r(a) curve. This explains why, for example, the values of r(a) for a < H are overpredicted in Fig. 1D, despite the fact that the increments in this regime are copied from the data. The corresponding temporal averages are too low, so the scaled increment values are too high. In Fig. 1F, we illustrate that the ordering among the top-five apps does not change in time for this model, so it does not produce realistic levels of app-popularity turnover (Fig. 1C and SI Appendix, Fig. S7). In SI Appendix, sections SI6 and SI7, we demonstrate that several alternative models based on cumulative information also match the data poorly.

We next consider the case in which γ is small, so recent information dominates (5, 24). In Fig. 3, we show results for stochastic simulations using an exponential response-time distribution $P\left(t\right)=\left(1/T\right)e^{-t/T}$ to determine the weights W(t) assigned to activity from t hours earlier for varying history-window lengths H and response-time parameters T. The colors in the (H, T) parameter plane represent the L² error, which is given by the L² norm of the difference between the simulated r(a) curve and the r(a) curve from the data. A value of 3.11 is representative of inherent fluctuations in the data (SI Appendix, section SI3), and the bright colors in Fig. 3 represent parameter values for which the difference between the model’s mean growth rate and the empirically observed growth rate is less than the magnitude of fluctuations present in the data. Observe that the model requires a history window of approximately 1 wk (i.e., H ≈ 168 h) to match the data. As γ increases, cumulative information is weighted more heavily, and the region of “good-fit” parameters moves toward larger T and larger H (SI Appendix, section SI3). As noted previously, large-H models trivially provide good fits (because they mostly copy directly from data), but the γ = 0 case provides a good fit to the data even with a relatively short history window H.

Fig. 3.

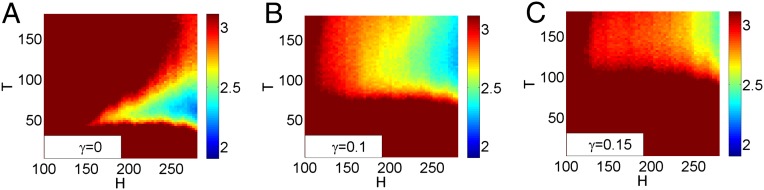
Parameter planes showing the L² error (SI Appendix, section SI3) for the r(a) curve for the recent-activity–dominated model described in the text. The parameter H is the length of the history window, and T is the mean of the exponential response-time distribution. For each point in the plane, we average values of the L² error over 24 realizations. We show all values above 3.11 as dark red.

In Fig. 1 G–I, we compare model results with data for parameter values H = 168, T = 5, and γ = 0 (i.e., the “recent-activity, short-memory” case). This reproduces the app popularity distributions of the data rather well, but the mean scaled age-shifted growth rates are markedly different. In contrast, Fig. 1 J–L compare model results with data for parameter values H = 168, T = 50, and γ = 0 (i.e., the “recent-activity, long-memory” case). These parameters are just inside the good-fit region of Fig. 3A, so the r(a) curve in Fig. 1J matches the data well. Moreover, the popularity distributions at t = t_max and at age t_LES (Fig. 1K) are both reasonably matched by the model, which also allows realistic turnover in the top-10 list (Fig. 1L and SI Appendix, Fig. S7). These considerations highlight the importance of using temporal data to develop and fit models of complex systems. Distributions at single times can be insensitive to model differences, and the r(a) curves are crucial for distinguishing between competing models. In SI Appendix, section SI4, we show that the recent-activity (γ = 0) case still gives good fits to the data if the exponential response-time distribution is replaced by a lognormal, gamma, or uniform distribution.

Another noteworthy feature of the recent-activity case is its ability to produce heavy-tailed popularity distributions in stochastic simulations even if no history is copied from the data (H = 0). Even if all apps initially have the same number of installations, random fluctuations lead to some apps becoming more popular than others, and the aggregate popularity distribution becomes heavy-tailed (10, 23, 24, 31). In SI Appendix, section SI5, we show that this situation is described by a near-critical branching process, for which power-law popularity distributions are expected (32–36).

Our model suggests that app adoption among Facebook users was guided more by recent popularity of apps (as reflected in installations by friends within 2 days) than by cumulative popularity. The fact that the model is a near-critical branching process might help to explain the prevalence of heavy-tailed popularity distributions that have been observed in information cascades on social networks, such as the spreading of retweets on Twitter (4, 17, 18) or news stories on Digg (37). The branching-process analysis is also applicable to the random-copying models of Bentley et al. (5, 23, 24). Although most random-copying models consider only short (e.g., single time-step) memory (5, 23), the simulation study of ref. 24 includes a uniform response-time distribution and demonstrates the role of memory effects in generating turnover. As shown in Fig. 1 and detailed in SI Appendix, section SI7, generating realistic turnover of rank order in the top-10 apps is a significant challenge for all models based on cumulative information, even those that include a time-dependent decay of novelty (38, 39). In SI Appendix, section SI9, we show that our model can also explain the results of the fluctuation-scaling analysis of the Facebook apps data in ref. 15 that highlighted the existence of distinct scaling regimes (depending on app popularity).

Our approach also highlights the need to address temporal dynamics when modeling complex social systems. Online experiments have been used successfully in computational social science (1), but it is challenging to run experiments in online environments that people actually use (as opposed to creating new online environments with potentially distinct behaviors). If longitudinal data are available, as in the present case, it is possible to evaluate a model’s fit based not only on long-time behavior but also on dynamical behavior. Given that several models successfully produce similar long-time behavior, the investigation of temporal dynamics is critical for distinguishing between competing models. As more observational data with high temporal resolution from online social networks become available, we believe that this modeling strategy, which leverages temporal dynamics, will become increasingly essential.