The fossilized birth–death process for coherent calibration of divergence-time estimates

Significance

Divergence time estimation on an absolute timescale requires external calibration information, which typically is derived from the fossil record. The common practice in Bayesian divergence time estimation involves applying calibration densities to individual nodes. Often, these priors are arbitrarily chosen and specified yet have an excessive impact on estimates of absolute time. We introduce the fossilized birth–death process—a fossil calibration method that unifies extinct and extant species with a single macroevolutionary model, eliminating the need for ad hoc calibration priors. Compared with common calibration density approaches, Bayesian inference under this mechanistic model yields more accurate node age estimates while providing a coherent measure of statistical uncertainty. Furthermore, unlike calibration densities, our model accommodates all the reliable fossils for a given phylogenetic dataset.

Abstract

Time-calibrated species phylogenies are critical for addressing a wide range of questions in evolutionary biology, such as those that elucidate historical biogeography or uncover patterns of coevolution and diversification. Because molecular sequence data are not informative on absolute time, external data—most commonly, fossil age estimates—are required to calibrate estimates of species divergence dates. For Bayesian divergence time methods, the common practice for calibration using fossil information involves placing arbitrarily chosen parametric distributions on internal nodes, often disregarding most of the information in the fossil record. We introduce the “fossilized birth–death” (FBD) process—a model for calibrating divergence time estimates in a Bayesian framework, explicitly acknowledging that extant species and fossils are part of the same macroevolutionary process. Under this model, absolute node age estimates are calibrated by a single diversification model and arbitrary calibration densities are not necessary. Moreover, the FBD model allows for inclusion of all available fossils. We performed analyses of simulated data and show that node age estimation under the FBD model results in robust and accurate estimates of species divergence times with realistic measures of statistical uncertainty, overcoming major limitations of standard divergence time estimation methods. We used this model to estimate the speciation times for a dataset composed of all living bears, indicating that the genus Ursus diversified in the Late Miocene to Middle Pliocene.

A phylogenetic analysis of species has two goals: to infer the evolutionary relationships and the amount of divergence among species. Preferably, divergence is estimated in units proportional to time, thus revealing the times at which speciation events occurred. Once orthologous DNA sequences from the species have been aligned, both goals can be accomplished by assuming that nucleotide substitutions occur at the same rate in all lineages [the “molecular clock” assumption (1)] and that the time of at least one speciation event on the tree is known, i.e., one speciation event acts to “calibrate” the substitution rate.

The goal of reconstructing rooted, time-calibrated phylogenies is complicated by substitution rates changing over the tree and by the difficulty of determining the date of any speciation event. Substitution rate variation among lineages is pervasive and has been accommodated in several ways. The most widely used method to account for rate heterogeneity is to assign an independent parameter to each branch of the tree. Branch lengths, then, are the product of substitution rate and time, and usually measured in units of expected number of substitutions per site. This solution allows estimation of the tree topology—which is informative about interspecies relationships—but does not attempt to estimate the rate and time separately. Thus, under this “unconstrained” parameterization, molecular sequence data allow inference of phylogenetic relationships and genetic distances among species, but the timing of speciation events is confounded in the branch-length parameter (2–4). Under a “relaxed-clock” model, substitution rates change over the tree in a constrained manner, thus separating the rate and time parameters associated with each branch and allowing inference of lineage divergence times. A considerable amount of effort has been directed at modeling lineage-specific substitution rate variation, with many different relaxed-clock models described in the literature (5–19). When such models are coupled with a model on the distribution of speciation events over time [e.g., the Yule model (20) or birth–death process (21)], molecular sequence data can inform the relative rates and node ages in a phylogenetic analysis.

Estimates of branch lengths in units of absolute time (e.g., millions of years) are required for studies investigating comparative or biogeographical questions (e.g., refs. 22, 23). However, because commonly used diversification priors are imprecise on node ages, external information is required to infer the absolute timing of speciation events. Typically, a rooted time tree is calibrated by constraining the ages of a set of internal nodes. Age constraints may be derived from several sources, but the most common and reliable source of calibration information is the fossil record (24, 25). Despite the prevalence of these data in divergence time analyses, the problem of properly calibrating a phylogenetic tree has received less consideration than the problem of accommodating rate variation. Moreover, various factors may lead to substantial errors in parameter estimates (26–31). When estimating node ages, a calibration node must be identified for each fossil. For a given fossil, the calibration node is the node in the extant species tree that represents the most recent common ancestor (MRCA) of the fossil and a set of extant species. Based on the fossil, the calibration node’s age is estimated on an absolute timescale. Thus, fossil data typically can provide valid minimum-age constraints only on these nodes (24, 27), and erroneous conclusions may result if the calibration node is not specified properly (26).

Bayesian inference methods are well adapted to accommodating uncertainty in calibration times by assuming that the age of the calibrated node is a random variable drawn from some parametric probability distribution (10, 14, 29, 31–35). Although this Bayesian approach properly propagates uncertainty in the calibration times through the analysis (reflected in the credible intervals on uncalibrated node ages), two problems remain unresolved.

First, these approaches, as they commonly are applied, induce a probability distribution on the age of each calibrated node that comes from both the node-specific calibration prior and the tree-wide prior on node ages, leading to an incoherence in the model of branching times on the tree (35, 36). Typically, a birth–death process of cladogenesis is considered as the generating model for the tree and speciation times (20, 21, 37–40), serving as the tree-wide prior distribution on branch times in a Bayesian analysis. The speciation events acting as calibrations then are considered to be drawn from an additional, unrelated probability distribution intended to model uncertainty in the calibration time. This procedure results in overlaying two prior distributions for a calibration node: one from the tree prior and one from the calibration density (35, 41). Importantly, this incoherence is avoided by partitioning the nodes and applying a birth–death process to uncalibrated nodes conditioned on the calibrated nodes (32), although many divergence time methods do not use this approach. Nevertheless, a single model that acts as a prior on the speciation times for both calibrated and uncalibrated nodes is a better representation of the lineage diversification process and preferable as a prior on branching times when using fossil data.

Second, the probability distributions used to model uncertainty in calibration times are poorly motivated. The standard practice in Bayesian divergence time methods is to model uncertainty in calibrated node ages by using simple probability distributions, such as the uniform, log-normal, gamma, or exponential distributions (29). When offset by a minimum age, these “calibration densities” (35) simply seek to characterize the age of the node with respect to its descendant fossil. However, the selection and parameterization of calibration priors rarely are informed by any biological process or knowledge of the fossil record (except see refs. 42–44). A probability model that acts as a fossil calibration prior should have parameters relevant to the preservation history of the group, such as the rate at which fossils occur in the rock record, a task that likely is difficult for most groups without an abundant fossil record (43, 45). Consequently, most biologists are faced with the challenge of choosing and parameterizing calibration densities without an explicit way to describe their prior knowledge about the calibration time. Thus, calibration priors often are specified based on arbitrary criteria or ad hoc validation methods (46), and ultimately, this may lead to arbitrary or ad hoc estimates of divergence times.

We provide an alternative method for calibrating phylogenies with fossils. Because fossils and molecular sequences from extant species are different observations of the same diversification process, we use an explicit speciation–extinction–fossilization model to describe the distribution of speciation times and recovered fossils. This model—the fossilized birth–death (FBD) process—acts as a prior for divergence time dating. The parameters of the model—the speciation rate, extinction rate, fossil recovery rate, and proportion of sampled extant species—interact to inform the amount of uncertainty for every speciation event on the tree. These four parameters are the only quantities requiring prior assumptions, compared with assuming separate calibration densities for each fossil. Analyses of simulated data under the FBD model result in reliable estimates of absolute divergence times with realistic measures of statistical uncertainty. Moreover, node age estimates are robust to several biased sampling strategies of fossils and extant species—strategies that may be common practice or artifacts of fossil preservation but heavily violate assumptions of the model.

Results and Discussion

A Unified Model for Fossil and Extant Species Data.

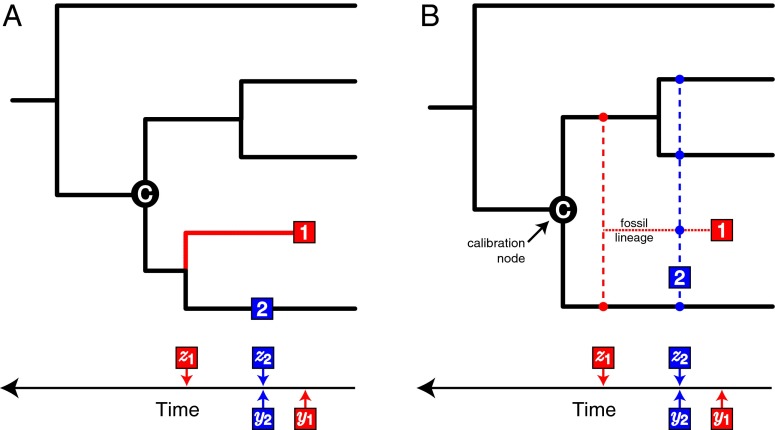
The process of diversification under the FBD model (first introduced in refs. 47, 48) starts with a single lineage at time x₀ (stem age) before the present. The model assumes a constant speciation rate λ and a constant extinction rate μ. Recovered fossils appear along lineages of the complete species tree according to a Poisson process with parameter ψ. Finally, each extant species is sampled with probability ρ. This process gives rise to complete FBD trees with extinct and extant tips and fossil occurrences along the branches. Deleting all lineages without sampled extant or fossil descendants leads to the resolved FBD tree (Fig. 1A), in which the precise relationships of the fossil and extant lineages are depicted. Pruning all lineages without sampled extant descendants leads to the reconstructed phylogeny, i.e., trees representing only extant species relationships (Fig. 1A, black). We denote the age of the i^th internal node in the reconstructed phylogeny with x_i (for i ∈ 1, …, n − 1).

Fig. 1.

Representations of fossils on (A) a resolved FBD tree and (B) an unresolved FBD tree. (A) The phylogeny of four extant species and two sampled fossils, in which the true phylogenetic relationships are known [the resolved FBD tree described in Stadler (47)]. Each fossil has observed age y and attachment time z, which is the point at which the fossil links to the tree. Fossil 1 (red), the youngest fossil specimen, is descended from node C via speciation at time z₁ and occurs on an extinct lineage, such that y₁ < z₁. Fossil 2 (blue) lies directly on a lineage in the extant tree; therefore, y₂ = z₂ and fossil 2 is the ancestor of a sampled, present-day taxon. (B) The unresolved FBD tree on which the precise phylogenetic relationships of the fossils are ignored and the two fossil specimens are used to calibrate the extant tree. Both fossils calibrate a single internal node, C, based on prior knowledge that fossils 1 and 2 are descendants of the calibration node. All other nodes are uncalibrated. Because fossil 1 (red) attaches to the extant tree via speciation, where y₁ < z₁, the unobserved speciation event is assumed to occur at any lineage that is descended from C and that intersects with z₁ (small red ●). The attachment time of fossil 2 (blue) is equal to the age of the fossil; thus, fossil 2 represents a direct ancestor of any lineage descended from node C that intersects with time z₂ (small blue ●), including any “ghost” lineages leading to other fossil taxa (e.g., the dotted red line leading to fossil 1).

Using the resolved FBD tree requires explicit representation of the phylogenetic relationships of both extant and fossil taxa (Fig. 1A). Accordingly, methods based on the resolved FBD tree are appropriate for describing the distribution of speciation times and tree topologies when used in “tip-dating” approaches, in which sequence data—either molecular or discrete morphological characters—are available for both extant and extinct taxa (49–54). However, suitable data matrices of discrete morphological characters for both living and fossil taxa are unavailable for many groups in the tree of life. Instead, biologists may have access to the times of fossil occurrences and their taxonomic identification based on only a few diagnostic characters. In these cases, fossils still are useful for calibrating a molecular phylogeny of extant species provided that calibration nodes are identified correctly. Conventional calibration approaches for Bayesian divergence time estimation require that prior densities be parameterized for each calibrated node (29), a task that presents a challenge for most biologists performing these analyses.

The FBD model overcomes several of the major limitations associated with standard node calibration for phylogenetic datasets unsuitable for tip dating by allowing ambiguity in the precise phylogenetic placement of fossils while still considering them part of a unified macroevolutionary process. We introduce unresolved FBD trees, an alternative construction of the fossil/extant lineage topology (Fig. 1B). Like tip-dating or using resolved FBD trees, divergence time estimation of the unresolved FBD tree allows for inclusion of all reliable fossil taxa available for the group of interest and eliminates the need for ad hoc calibration prior densities without requiring combined character data for both modern and fossil species.

We obtain an unresolved FBD tree from a resolved FBD tree by ignoring the exact placement of fossils in the sampled tree. This is accomplished by removing all fossils from the resolved FBD tree, keeping the attachment time to the resolved FBD tree and a calibration node for each fossil (Fig. 1B) while ignoring the attachment lineage. The age of fossil f is denoted with y_f, and the attachment time of f is z_f. The calibration node is defined as the branching event in the reconstructed tree that is the most recent known ancestor of the fossil and a set of extant species (node C in Fig. 1). For any fossil, if y_f < z_f, then fossil f attaches to the resolved FBD tree by way of speciation and induces an unobserved lineage in the unresolved FBD tree. Foote (55) described models to assess the probability of ancestor–descendant pairs in the fossil record; in the unresolved FBD tree, this pattern is possible when y_f = z_f, such that fossil f lies directly on a branch and is an ancestor of sampled extant or fossil taxa (Fig. 1B).

In summary, the unresolved FBD tree contains all branching and sampling time information of the resolved FBD tree; however, the precise attachment lineages of the fossils are not specified. Thus, the precise topology of the resolved FBD tree is ignored when calculating the probability of the unresolved FBD tree by summing over the probabilities of all possible resolved FBD trees that can induce a given unresolved FBD tree (Methods; Eq. 1). Importantly, because we do not know whether a given fossil is the direct ancestor of a lineage in the resolved FBD tree or whether it lies on an unobserved lineage, we average over all possible resolved FBD tree realizations using numerical methods. To use the FBD model as a prior for divergence time dating, we calculate the probability density for obtaining a particular unresolved FBD tree, conditioning on the root (crown) age of the tree, x₁ (Eq. 1).

The unresolved FBD tree probability is central to our Bayesian divergence time estimation method implemented in the program DPPDiv (https://github.com/trayc7/FDPPDIV) (19, 31, 56). This approach estimates unresolved FBD trees—specifically, divergence times—from molecular sequence data for extant species together with fossil occurrence times. The user provides only the sequence data, extant tree topology, fossil ages, and calibration nodes for each fossil. Thus, this approach is suitable for analyzing a wide variety of datasets, provided that at least one fossil taxon is known for the group. We use Markov chain Monte Carlo (MCMC) to approximate the posterior distribution of unresolved FBD trees conditional on the extant species tree topology and calibration node assignments for each fossil specimen. Note that like calibration density methods, divergence time estimation under the unresolved construction of the FBD model requires that the fossil be assigned correctly to a calibration node in the extant tree that is truly older than the fossil age. However, in contrast to calibration density approaches that require the user to choose and parameterize a prior density for each calibrated node, the only input assumptions required when applying the FBD model are prior information on the FBD model parameters (λ, μ, ψ, ρ, x₁), parameters of the GTR + Γ substitution model (e.g., general time reversible model with gamma-distributed rate heterogeneity), and parameters of the model of branch rate variation (i.e., relaxed-clock model). We used both simulated and empirical data to evaluate the accuracy, precision, and robustness of divergence time estimation under the FBD model. Our simulation results show that integrating fossil information into the diversification model yields accurate inferences of absolute node ages. Furthermore, the FBD model provides coherent measures of statistical uncertainty that lead to more straightforward interpretation compared with standard practices for node calibration.

Analyses of Simulated Data.

We generated tree topologies and sets of fossils under a forward-time simulation of the FBD model. Our results are focused on a set of simulations with the following conditions: r = 0.5, d = 0.01, and ψ = 0.1, where r is the turnover rate such that r = μ/λ, the diversification rate is d = λ − μ, and ψ is the Poisson rate of fossilization events (see Methods for details; SI Appendix, Fig. S1 shows a single simulation replicate). Each of our 100 simulation replicates comprised a tree topology for 25 extant species with corresponding sequence data (GTR + Γ, strict molecular clock), and a complete set of fossil ages. Each fossil is associated with a calibration node representing the most recent branching event in the reconstructed tree ancestral to the fossil. We then subsampled each set of complete fossils, so that only a percentage, ω, of the fossils were present. We produced four different fossil subsets under different values of ω: 5%, 10%, 25%, and 50% (henceforth we use the notation ω_P to indicate ω = P%). Additionally, for sets of ω₁₀ fossils (across 100 replicates: median = 17 fossils), we created a set of ‘calibration fossils’ (ω_cal10), where, for each calibrated node, only the oldest fossils were retained (median = 9 fossils). We created the ω_cal10 fossils to compare node calibration under the FBD model with commonly used calibration density approaches which do not consider all available fossils.

We estimated absolute node ages for trees of 25 extant species under the FBD model using each set of fossils: ω₅, ω₁₀, ω₂₅, ω₅₀, and ω_cal10. For comparison, we estimated node ages under three different calibration-density approaches using the ω_cal10 set of fossils, each assuming an exponential calibration density (see Methods). The fixed-scaled calibration density method scaled the expected value of each exponential prior density based on the age of the calibrating fossil. Another calibration density was created where the expected age of the calibrated node was equal to the true age (fixed-true). The third calibration-density approach applied a hyperprior to the rate parameters of exponential distributions, such that the nodes are calibrated by a mixture of exponentials (31). The fixed-true calibration density is expected to perform well and represent an ideal prior density parameterization. The hierarchical, hyperprior calibration density approach has been evaluated using simulated data and yields accurate estimates of node ages (31). The fixed-scaled approach treats the fossil calibration densities in an arbitrary fashion that may be similar to the strategies used to parameterize these priors in practice. We selected a scale value that can result in overly informative calibration densities for some nodes and diffuse densities for others. For each analysis, we estimated absolute node ages in the program DPPDiv (19, 31, 56), conditioning on the true tree topology and assuming a GTR+Γ model of sequence evolution and a strict molecular clock (true models). We chose to simulate and estimate data under a single-rate, strict clock model to evaluate the FBD model while reducing the uncertainty from the branch rate prior.

We compared the node age estimates under the FBD model with the three calibration density analyses (fixed scaled, fixed true, and hyperprior). Our results show that estimates of absolute node ages are more reliable under the FBD model relative to calibration density approaches with acceptable cost regarding precision. Fig. 2A shows the coverage probabilities for node age estimates under the FBD model, using both the ω₁₀ and ω_cal10 sets of fossils and for the calibration density analyses, using only the ω_cal10 fossils. The coverage probability (CP) is the proportion of nodes for which the true value falls within the 95% credible interval (95% CI). When calculated across all nodes, the CP for ages estimated under the FBD model was 0.96 for the ω₁₀ fossils and 0.97 for the ω_cal10 fossils, indicating robust inference under the FBD process (SI Appendix, Table S1). On average, the more reliable calibration density approaches had high coverage using the ω_cal10 fossils, with CP = 0.93 under the hyperprior calibrations and CP = 0.904 when the expectation of the calibration density was equal to the true calibration node age (fixed true). By contrast, the calibration densities parameterized based on the magnitudes of fossil ages (fixed scaled) had relatively poor coverage: CP = 0.68. In Fig. 2A, we show CP as a function of the true node age by creating bins of 150 nodes and computing the CP for each bin. The node age estimates under the FBD model show consistently high CPs for both the ω₁₀ and ω_cal10 sets of fossils. In comparison, hyperprior and fixed-true calibration density analyses show slightly reduced CPs for older nodes, and the fixed-scaled calibration densities have very low CPs as node age increases.

Fig. 2.

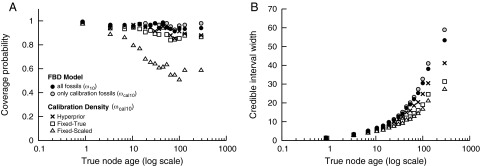
The results for 100 replicate trees simulated under the FBD model with μ/λ = 0.5, λ − μ = 0.01. Node age estimates are summarized for analyses under the FBD model by using all available fossils sampled randomly (10%; ω₁₀) from the total number of simulated fossils (●). These results are compared with divergence time estimates on the set of calibration fossils (ω_cal10) under the FBD model (), with a hyperprior on calibration density parameters (×), with a fixed calibration density where the expected value is equal to the true node age (□), and for a fixed calibration density scaled based on the age of the fossil (△). Both the coverage probability and precision (95% CI width) are shown as a function of the true node age (log scale), where the nodes were binned so that each bin contained 150 nodes and the statistics were computed within each bin. (A) The coverage probability is the proportion of nodes in which the true value falls within the 95% CI. (B) The average size of the 95% CIs for each bin was computed to evaluate precision.

Fig. 2B illustrates the precision of divergence time estimates by depicting the average 95% CI width for increasing node age. These results show that estimates under the FBD model are less precise (larger 95% CIs) relative to the calibration density methods. Therefore, inference under the FBD model yields conservative estimates of node ages, with high CPs combined with large 95% CIs. In contrast, the precision of node-age estimates under calibration density methods is driven primarily by the variance of calibration priors (4). Importantly, however, the average widths of the 95% CIs are smaller with the ω₁₀ set of fossils compared with the reduced set of calibration fossils, ω_cal10 (Fig. 2B). Thus, as more fossils are added, precision under the FBD model increases.

We investigated the effect of different levels of fossil sampling under the FBD model. Fig. 3 shows the results for node age estimation for different values of ω: 5%, 10%, 25%, and 50%. Overall, we do not observe large changes to the coverage of estimates using different sets of fossils, with CPs remaining consistently high (Fig. 3A). However, when we examine the precision of node age estimation under the FBD model, we find that as the density of sampled fossils increases, the precision of divergence time estimates also increases (Fig. 3B).

Fig. 3.

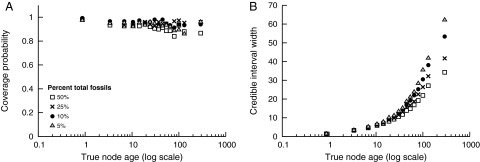
The results for 100 replicate trees simulated under the FBD model with μ/λ = 0.5, λ − μ = 0.01. Node age estimates are summarized for analyses under the FBD model by using sets of fossils comprising fossils sampled from the total number of simulated fossils. Fossils were sampled at different percentages: 5% (), 10% (●), 25% (×), and 50% (□). Both the coverage probability and precision (95% CI width) are shown as a function of the true node age (log scale), where the nodes were binned so that each bin contained 150 nodes and the statistics were computed within each bin. (A) The coverage probability is the proportion of nodes in which the true value falls within the 95% CI. (B) The average size of the 95% CIs for each bin was computed to evaluate precision.

Our simulation results make a strong case for node age calibration under the FBD model. Furthermore, these patterns—high CPs, with increased fossil sampling leading to increased precision—are consistent under different simulation conditions. In particular, we focused on varying the turnover rate, r = μ/λ, leaving the Poisson rate of fossilization at ψ = 0.1 while changing the diversification rate, d = λ − μ, to ensure that the expected root age was approximately equal to 200 (varying d changes the timescale of trees generated under a given value of r). In SI Appendix, Figs. S2 and S3 and Table S1, the results for r = 0.1 and r = 0.9 exhibit patterns similar to those shown in Figs. 2 and 3, with high coverage across all estimates (SI Appendix, Table S1).

Much like conventional calibration approaches, estimates of absolute node ages under the FBD model are informed by the distribution, sampling, and phylogenetic placement of fossils. However, unlike calibration density methods, inference is improved as additional fossils are applied to already-calibrated nodes. The FBD model also is robust to explicit violation of model assumptions concerning sampling (namely, biased fossil sampling and biased extant species sampling do not bias the divergence time estimates for the investigated cases explored in detail in SI Appendix, section S.3.2), provided that the fossils are placed correctly and cover a wide range of node ages. Fundamentally, our results highlight the importance of thorough fossil sampling for robust and accurate node age estimation.

Analysis of Biological Data.

We assembled a phylogenetic dataset of all living bears (Ursidae) plus two outgroup species (Canis lupus and Phoca largha). The sequence data for the complete mitochondrial genomes (mtDNA) and the nuclear interphotoreceptor retinoid-binding protein gene (irbp) were downloaded from GenBank (SI Appendix, Table S2) and aligned using MAFFT (57). Preliminary analysis of these data using MrBayes v3.2 (58) yielded the same topology (for the overlapping set of taxa) reported in two recent studies (59, 60); we then conditioned our divergence time analyses on this topology.

To estimate absolute speciation times, we compiled a set of fossil ages from the literature (SI Appendix, Table S3). This set of fossils included five fossils belonging to the family Canidae (assigned to calibrate the root), five fossils classified as Pinnipedimorpha (assigned to date the MRCA of P. largha and Ursidae), and 14 fossils in the family Ursidae. Information regarding the phylogenetic placement of the ursid fossils was based on phylogenetic analyses of morphological data (61) as well as analyses of mtDNA for extinct Pleistocene subfossils (59). With these data, we estimated divergence times under the FBD model using five stem-fossil ursids, six fossils in the subfamily Ailuropodinae (pandas and relatives), the giant short-faced bear (Arctodus; Pleistocene), and two fossil representatives of the genus Ursus: the Pliocene U. abstrusus fossil and the Pleistocene cave bear subfossil U. spelaeus (SI Appendix, Table S3). The ages of most fossils are imprecise and therefore represented in the literature as age ranges. Because the FBD model assumes that the fossil is associated with a single point in time, we then sampled the age for each fossil from a uniform distribution of its given range (SI Appendix, Table S3). Given sufficient fossil sampling, this approach is intended to approximate random recovery. It would be preferable, however, to treat the ages of fossils as random variables by placing prior densities on fossil occurrence times conditional on their estimated age ranges, a feature planned for future implementations of the FBD model.

Using DPPDiv, we estimated speciation times in calendar time units for all living bears, as well as deep nodes in the caniform tree. We used a GTR+Γ model of sequence evolution and applied a relaxed-clock model to allow substitution rates to vary across the tree. The relaxed-clock model we used assumes that lineage-specific substitution rates are distributed according to a Dirichlet process prior (DPP) such that branches fall into distinct rate categories, yet the number of categories and the assignment of branches to those categories are random variables (19). For the FBD model, we assumed putatively noninformative, uniform priors on all rate parameters. Additionally, because our simulations demonstrated that node age estimation is robust to extant species sampling, we specified ρ = 1. We ran three independent chains, each for 20 million iterations. We used the program Tracer (62) to verify that the three independent runs converged on the same stationary distribution for all parameters. Furthermore, we confirmed that the sequence data were informative on branch rates and node times by comparing the MCMC samples from the three different runs to samples under the prior (i.e., without sequence data).

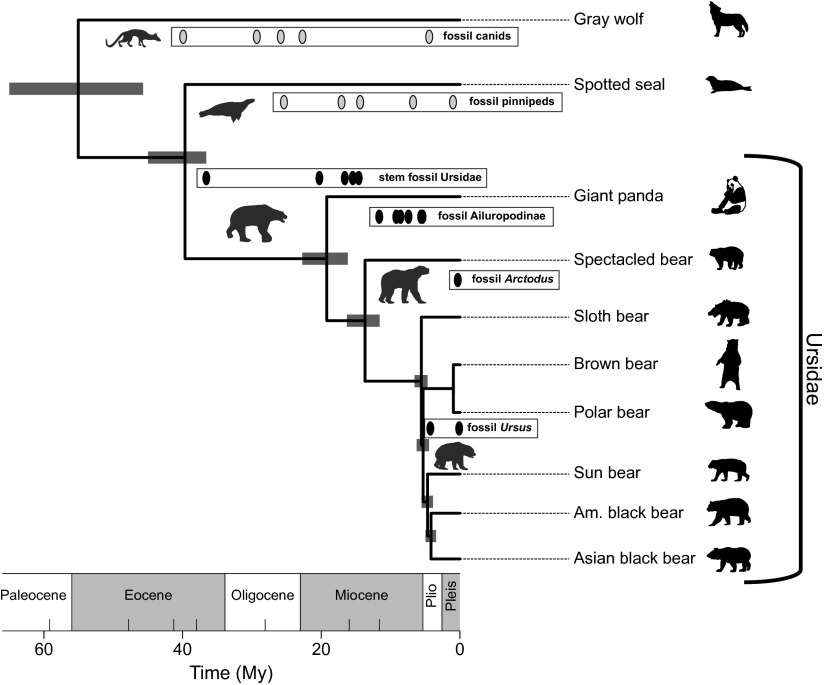
We used tools in the Python library DendroPy (63) to summarize the divergence times sampled by MCMC from the three independent runs. The divergence times of all living bears and occurrence times of calibrating fossils are summarized in Fig. 4. On average, the node ages estimated under the FBD model are consistent with the ages estimated by Krause et al. (59), with overlapping 95% CIs for all common nodes (SI Appendix, Fig. S.10), suggesting the radiation of the genus Ursus occurred in the late Miocene to mid Pliocene (Fig. 4). In contrast, dos Reis et al. (60) uncovered much older ages for all nodes except for the node representing the MRCA of Canidae and Ursidae (the root in Fig. 4). Their results indicate a much earlier origin of crown ursids, with much of the diversification of present-day Ursus occurring in the mid- to late Miocene. Our analyses were most similar to those of Krause et al. (59), who estimated divergence times using mitochondrial genomes under a global molecular clock. This gene region dominated our alignment, and analyses under the DPP model indicate low among-lineage substitution rate variation with a median of two rate categories (95% CI = 1–4 rate categories). Furthermore, although they used calibration densities, the common fossils, U. abstrusus and Parictis montanus, between our study and that of Krause et al. (59) appear to strongly influence absolute node ages. In contrast, dos Reis et al. (60) estimated divergence times for 274 mammals by using a two-step approach in which they first used nuclear genomes to estimate the node ages for 36 species, then used the posterior estimates to inform analyses of 12 mitochondrial protein genes for all 274 species. Their analysis of the 36-taxon tree included only two carnivores, Canis familiaris and Felis catus; thus, the age estimates of the bears in the 274-species tree were uncalibrated yet informed by the ages of all other nodes in the mammal tree.

Fig. 4.

The divergence times of extant bears and two caniform out-groups estimated under the FBD model. The branch lengths are in proportion to the mean branch time in millions of years. Horizontal node bars represent the 95% CI for node ages. In each labeled box, the ovals indicate the fossil occurrence times. The fossils in the family Ursidae are all indicated with black ovals, whereas the out-group fossils are shaded light gray. Ursus (including Melursus and Helarctos) species include the sloth bear, brown bear, polar bear, sun bear, American black bear, and Asian black bear. (Silhouette images available at http://phylopic.org/.)

The dissimilar divergence time estimates resulting from distinctly different Bayesian methods and datasets reveal that the speciation times within the caniforms may still be an open question. Moreover, elucidating the time-calibrated phylogeny of this group calls for a more comprehensive approach that includes more species and sequence data (as in ref. 60) in conjunction with a mechanistic diversification model that allows for inclusion of the rich fossil history of the group.

Conclusions

By modeling extant species data and fossil data as outcomes of the same macroevolutionary process, we provide a coherent framework for calibrating phylogenies. In particular, the FBD model integrates fossil information into the lineage-based diversification process, overcoming many of the limitations of calibration density methods. Standard calibration density approaches using fossils have inherent flaws that may lead to biased estimates of node ages and measures of uncertainty, particularly when applied using fixed parameters (31). Fundamentally, the prior densities used to calibrate nodes are not derived from any underlying biological process but instead are intended to characterize the biologist’s uncertainty in the age of the calibrated node with respect to its oldest descendant fossil. As a result, estimates of absolute speciation times are driven by the choice and parameterization of these calibration densities. The FBD model considers calibrating fossils and extant species as part of a unified diversification process and provides a more mechanistic model for lineage divergence times.

Our simulations show that estimates under the FBD model have greater coverage compared with the most robust calibration approaches. This result holds even compared with estimates using calibration densities centered on the true value (an ideal but unrealistic scenario). In particular, the FBD model, assuming constant speciation, extinction, and fossilization rates, also provides reliable estimates when its assumptions are violated in the data, namely biased sampling of fossils or extant species—scenarios that probably are very common. Importantly, because increasing the number of calibrating fossils results in a corresponding increase in the precision of node age estimates, the FBD model is better at capturing statistical uncertainty in the timing of speciation events. By contrast, the precision of node age estimates under calibration density approaches is controlled entirely by the precision of the prior distributions on calibrated nodes, particularly in the case of fixed calibration densities. Thus, the FBD model eliminates one of the greatest challenges imposed on biologists applying Bayesian divergence time methods: choosing and parameterizing calibration densities for multiple nodes.

Phylogenetic analysis under a unified model of diversification uses all the fossils available for a group. This feature represents another significant advantage over traditional approaches that condense all the fossil information associated with a given node to a single minimum age estimate. Our results highlight the importance of thorough fossil sampling; therefore, every reliably identified and dated fossil species is useful and may improve estimation of both node ages and parameters of the diversification model. In fact, inclusion of fossil lineages in macroevolutionary studies leads to more accurate inferences of patterns of speciation and extinction (64) and rates of phenotypic trait evolution (65). This factor underscores the importance of carefully curated and analyzed paleontological collections, thus motivating collaboration with experts on extinct organisms and critical assessment of fossil specimens (66). Moreover, comprehensive models such as the FBD have the potential to address interesting questions about diversity through time and harness the wealth of information available in online databases such as the Paleobiology Database (http://paleodb.org).

Alternative sources of calibrating information often are applied to date species phylogenies, particularly when fossil information is unavailable. Therefore, it is important to note that the FBD model is explicitly for fossil calibration. Nonfossil calibration times typically are derived from biogeographical dates or node age estimates from previous studies (e.g., secondary calibrations). Thus, the FBD model is not an appropriate prior for calibration with these data, and calibration density approaches still are necessary. For these analyses, hierarchical calibration models (31) and methods that condition on node calibrations (32, 35, 41) are recommended.

The FBD model offers a rich basis for the development of complex, biologically informed models of macroevolution that incorporate both modern and fossil species. Improving the integration of fossil data with extant-species data in a phylogenetic framework is an important step toward enhancing our understanding of evolution and biodiversity. As morphological datasets uniting fossil and modern species become available, methods based on the FBD model will be necessary to answer macroevolutionary questions in a phylogenetic context.

For the purpose of divergence time dating, we can view the constant rates of speciation, extinction, and fossilization in the FBD model as nuisance parameters over which the MCMC integrates out, and our simulated datasets with biased sampling still returned reliable divergence time estimates. However, when going beyond phylogenetic reconstruction, and actually inferring the macroevolutionary dynamics (i.e., inferring the variation in speciation, extinction, and fossilization), we must model rate variation explicitly. In fact, modifications of the FBD model that accommodate variation in diversification and sampling parameters already are useful for analysis of infectious disease data (53, 54, 67, 68). The phylogenetic patterns of rapidly evolving viruses modeled by these processes are analogous to macroevolutionary patterns of lineage diversification. Mechanistic diversification models that account for biological factors and properties of the fossil and geologic records may provide a better understanding of lineage diversification across the tree of life.

Methods

The Probability of an FBD Tree.

We assume an FBD process is a model of speciation, extinction, and fossilization that gives rise to extant and extinct species and fossils. This process starts with one species at time x₀ in the past. At all time points, each species speciates with rate λ and goes extinct with rate μ. At speciation, we arbitrarily assign one species descendant the label “right” and one descendant the label “left” to distinguish between the two lineages. This assignment gives rise to oriented trees, objects that are very convenient for calculating tree likelihoods (69). Observed fossils are produced along lineages with rate ψ (i.e., fossilization plus observation is a Poisson process). Extant species are sampled from all species with probability ρ. This model gives rise to complete FBD trees, i.e., trees on the sampled and nonsampled extant species, the fossils, and the extinct species lineages. Pruning all unsampled extinct and extant lineages from the complete tree yields the sampled, resolved FBD tree. Stadler (47) introduced the FBD model and provided the details for calculating the probability of a resolved FBD tree. Note that pruning the tree further by removing all lineages without sampled extant species descendants yields the reconstructed tree introduced in Nee et al. (70).

A resolved FBD tree makes the phylogenetic relationships of the fossils and sampled extant species explicit. However, these relationships are quite uncertain for many fossil specimens; thus, we introduce the unresolved FBD tree. In the unresolved FBD tree, the precise phylogenetic topology relating any fossil f to the resolved extant phylogeny is not specified; only the fossil’s calibration node, its age y_f, and the time z_f at which the fossil attaches to the tree are considered (Fig. 1B). For the purposes of estimating species divergence times using fossils, we condition the process on the crown (root) age of the clade x₁ instead of the stem age x₀ (SI Appendix, section S.1.1).

For our FBD calibration method, we calculate the probability of an unresolved FBD tree $\mathcal{T}$: f[$\mathcal{T}$|λ, μ, ψ, ρ, x₁], where the probability of the topology, internal node ages, and fossil attachment times (summarized in $\mathcal{T}$) for n extant species and m calibrating fossils is conditional on the hyperparameters of the FBD model (λ, μ, ψ, ρ) and the age of the root node (x₁). To state f[$\mathcal{T}$|λ, μ, ψ, ρ, x₁], we define additional notation (SI Appendix, Table S5). Let $\mathcal{V}$ be the set of internal node indices in the reconstructed (extant species) phylogeny, $\mathcal{V}$ = (1, …, n−1), labeled such that 1 is the index representing the root of the tree, with internal node indices increasing toward the present (i.e., labeled in preorder sequence), and the age for any internal node i is x_i (for i ∈ $\mathcal{V}$). The occurrence times and calibration nodes in the extant tree are provided for m sampled fossil specimens. For any given FBD tree, k of m fossils lie directly in the branches and therefore are ancestor fossils (e.g., fossil 2 in Fig. 1). Accordingly, m − k of m fossils attach in the FBD tree at a speciation event and thus induce unobserved lineages. We denote the vector of fossil calibration indices as $\mathcal{F}$ = (1, …, m); y_f is the age of fossil f obtained from the fossil record and z_f is the time at which the fossil attaches to the unresolved FBD tree, either forming a new lineage via speciation or as an ancestor fossil (for f ∈ $\mathcal{F}$).

The probability of a resolved FBD tree is provided in equation 5 of Stadler (47). Importantly, the probability of the resolved FBD tree is invariant to changing the attachment lineage (in the FBD tree) of fossil f at time z_f; therefore, we multiply the resolved FBD tree probability by the number of possible attachment lineages γ_f to obtain the unresolved FBD tree probability (e.g., for fossil 1 in Fig. 1B, there are two lineages to which the fossil might attach, γ₁ = 2). Moreover, for any fossil where z_f > y_f, because the fossil may attach as either the left or right lineage at the speciation event in the resolved FBD tree [as our tree probability is on so-called oriented trees (69)], we multiply the probability by a factor of 2. Finally, if the fossil is an ancestral fossil, where z_f = y_f, we do not account for a speciation event; thus, ${\mathcal{I}}_f$ is the indicator function for fossil f, where ${\mathcal{I}}_f=0$ if the fossil is ancestral, otherwise ${\mathcal{I}}_f=1$.

Given the notation defined above and the FBD probability defined by Stadler (47), we obtain the probability of an unresolved FBD tree,

$$f\left[\mathcal{T}|\mathrm{\lambda },\mathrm{\mu },\mathrm{\psi },\mathrm{\rho },x_1\right]=\frac{1}{{\left(\mathrm{\lambda }\left(1-{\widehat{p}}_0\left(x_1\right)\right)\right)}^2}\frac{4\mathrm{\lambda \rho }}{q\left(x_1\right)}{\displaystyle \prod _{i\in \mathcal{v}}\frac{4\mathrm{\lambda \rho }}{q\left(x_i\right)}}{\displaystyle \prod _{f\in \mathrm{ℱ}}{\mathrm{\psi \gamma }}_f{\left(2\mathrm{\lambda }\frac{p_0\left(y_f\right)q\left(y_f\right)}{q\left(z_f\right)}\right)}^{{\mathrm{ℐ}}_f}},$$ [1]

with

$$\begin{array}{c}{c}_1=\left|\sqrt{{\left(\mathrm{\lambda }-\mathrm{\mu }-\mathrm{\psi }\right)}^2+4\mathrm{\lambda \psi }}\right|,\\ c_2=-\frac{\mathrm{\lambda }-\mathrm{\mu }-2\mathrm{\lambda \rho }-\mathrm{\psi }}{c_1},\\ q\left(t\right)=2\left(1-c_2^2\right)+e^{-c_{1}t}{\left(1-c_2\right)}^2+e^{c_{1}t}{\left(1+c_2\right)}^2,\\ p_0\left(t\right)=1+\frac{-\left(\mathrm{\lambda }-\mathrm{\mu }-\mathrm{\psi }\right)+c_1\frac{e^{-c_{1}t}\left(1-c_2\right)-\left(1+c_2\right)}{e^{-c_{1}t}\left(1-c_2\right)+\left(1+c_2\right)}}{2\lambda },\\ {\widehat{p}}_0\left(t\right)=1-\frac{\mathrm{\rho }\left(\mathrm{\lambda }-\mathrm{\mu }\right)}{\mathrm{\lambda \rho }+\left(\mathrm{\lambda }\left(1-\mathrm{\rho }\right)-\mathrm{\mu }\right)e^{-\left(\mathrm{\lambda }-\mathrm{\mu }\right)t}}.\end{array}$$

Note that p₀(t) is the probability that a lineage at time t in the past has no sampled extant species or sampled fossil descendants, and ${\widehat{p}}_0\left(t\right)$ is the probability that a lineage at time t in the past has no sampled extant species descendants and arbitrarily many fossil descendants. Further, we define p₁(t) as the probability that an individual alive at time t before the present has precisely one sampled extant descendant and no sampled fossil descendants (47), and we have $p_1\left(t\right)=\frac{4\rho }{q\left(t\right)}$. We state alternative FBD tree probabilities in SI Appendix, detailing conditioning on the stem age x₀ (SI Appendix, section S.1.1) and when there are no sampled ancestors (SI Appendix, section S.1.1). Additionally, we discuss the parameters needed to write down the FBD probability in SI Appendix, section S.1.3.

MCMC Approximation Under the FBD Model.

We implemented the FBD model in a Bayesian framework for estimating species divergence times on a fixed tree topology by building the model into an existing program, DPPDiv (version 1.1; https://github.com/trayc7/FDPPDIV) (19, 31, 56). The input data ($\mathcal{D}$) are as follows:

τ	Extant-species tree topology
X	DNA sequences for n extant species
y = (y1, …, ym)	Vector of occurrence times for m fossils
$\mathcal{C}$	Calibration nodes in τ for all fossils

Note that these are the same input data required for divergence time estimation using calibration density approaches (29, 31, 32). We use MCMC to approximate the joint posterior distribution of internal node ages and fossil attachment times ($\mathcal{T}$) together with all other model parameters.

The FBD model acts as a prior on speciation times, explicitly assuming that this model generated $\mathcal{T}$. Additionally, we assume prior distributions on parameters of the model of sequence evolution and on the substitution rates associated with each branch in the tree. These models correspond to the exchangeability rates and nucleotide frequencies of the GTR model, the shape parameter of the gamma distribution on site rates, and the parameters of the relaxed-clock model describing lineage-specific rate variation across the tree. The implementation of these models is described in detail in Heath et al. (19), and we use the notation θ to represent these parameters. Using this framework, we sample from the posterior distribution of unresolved FBD trees:

$$f\left[\mathcal{T},\mathrm{\lambda },\mathrm{\mu },\mathrm{\psi },\mathrm{\rho },\mathrm{\theta },x_1|\mathcal{D}=\left(\mathrm{\tau },X,\mathcal{C},\mathit{y}\right)\right]=\frac{f\left[X|\mathcal{T},\mathrm{\theta }\right]f\left[\mathcal{T}|\mathrm{\lambda },\mathrm{\mu },\mathrm{\psi },\mathrm{\rho },x_1\right]f\left[\mathrm{\lambda },\mathrm{\mu },\mathrm{\psi },\mathrm{\rho },x_1,\mathrm{\theta }\right]}{f\left[\mathcal{D}\right]}.$$

We note that f[X|$\mathcal{T}$, θ] is the likelihood of the tree and sequence model parameters, which we calculate with Felsenstein’s pruning algorithm (71, 72); f[$\mathcal{T}$|λ, μ, ψ, ρ, x₁] is the prior probability of the unresolved FBD tree given in Eq. 1; and f[λ, μ, ψ, ρ, x₁,θ] is the prior distribution on the model parameters and hyperparameters (specified by the user). Because we use the numerical method MCMC, we avoid computation of the normalizing constant f[$\mathcal{D}$].

Our implementation of the FBD model assumes that μ ≤ λ; otherwise, the process will go extinct with probability 1. Furthermore, instead of the parameters λ, μ, and ψ, we use the following parameterization:

d = λ − μ	Net diversification rate
r = μ/λ	Turnover
s = ψ/(μ + ψ)	Probability of fossil observation before species extinction

Importantly, we can recover λ, μ, and ψ via

$$\mathrm{\lambda }=\frac{d}{1-r},\hspace{1em}\mathrm{\mu }=\frac{rd}{1-r},\hspace{1em}\mathrm{\psi }=\frac{s}{1-s}\frac{rd}{1-r}.$$

The d, r, s, ρ parameterization has the advantage that r, s, ρ ∈ [0,1] and only d is on the interval (0, ∞), whereas the parameterization using λ, μ, ψ, ρ requires a prior on an unbounded interval (0, ∞) for the three parameters λ, μ, ψ.

We used standard MCMC proposals for operating on the parameters and hyperparameters of the FBD model (d, r, s, ρ, and x₁) and sequence substitution model (θ), changing the ages (x) of internal nodes, and updating the attachment ages of the fossils (z). These proposal mechanisms are described in greater detail in previous implementations of Bayesian inference software (7, 8, 11, 14, 19, 32, 58, 73, 74), and all were available previously in DPPDiv.

We formulated reversible-jump MCMC (rjMCMC) proposals to sample fossil attachment configurations and to determine whether fossils lie directly on lineages (ancestral fossils) or represent “tip fossils” by attaching to the resolved FBD tree via speciation (Fig. 1B). Moves that cause a fossil to become ancestral to an extant species, as well as reciprocal moves changing an ancestral fossil to one that forms an extinct lineage, result in a dimensionality change to the unresolved FBD tree by altering the number of speciation events; therefore, rjMCMC (75) proposals are needed to sample from the posterior distribution. In SI Appendix, section S.2, we outline our rjMCMC proposals on the fossil attachment configurations. These proposals, which are similar to the polytomy proposals of Lewis et al. (76), result in a probability mass for each fossil f on the state where y_f = z_f. Ultimately, our MCMC framework allows us to sample ages of nodes in the extant tree while marginalizing over the fossil attachment times and FBD model hyperparameters.

Simulation Study: Data Generation.

Trees, fossils, and sequences.

We evaluated the performance—accuracy, precision, and robustness—of absolute node-age estimation under the FBD model using simulated data. Complete tree topologies and branch times were generated under a constant-rate birth–death process conditional on n = 25 extant species by using the generalized sampling approach (77, 78) (simulation source code: https://github.com/trayc7/FossilGen). Three separate sets of simulated trees were generated, each with 100 replicates, such that the turnover rate (r = μ/λ) varied among the sets: (A) r = 0.1, (B) r = 0.5, and (C) r = 0.9. The rate of diversification (d = λ − μ) was adjusted so that the expected root age (x₁) was approximately equal to 200: (A) d = 0.0134, (B) d = 0.0106, and (C) d = 0.0041.

An absolute fossil history was generated on each complete phylogeny according to a continuous time Poisson process with rate ψ = 0.1. At this step in our forward-time simulation model, the Poisson rate, ψ, represents the rate of fossilization opportunity over the tree; thus, this set of fossils is the complete fossil record without accounting for preservation and recovery. The complete tree with absolute fossil history corresponds to a simulation of a complete FBD tree (47) (SI Appendix, Fig. S1). Trees generated under this model with ψ = 0.1 produced dense fossil records for each of our simulations (SI Appendix, Table S4). We chose to vary the turnover parameter, r, because this value controls the branching time distribution in reconstructed trees (79) as well as the distribution of fossils. Under high values of r, more lineages exist on which fossilization events may occur, resulting in more sampled fossils on these trees that are not ancestors of extant species. Conversely, trees with low turnover will produce fewer fossils, with a greater proportion of fossils lying directly on branches of the extant tree. For each fossil, a calibration node was identified. This node represented the most recent node in the extant tree that was ancestral to the fossil.

We simulated DNA sequence data for every extant tip, for every simulation replicate. Sequences were generated under the GTR substitution model (80) with gamma-distributed rate heterogeneity among sites (81, 82) in the program Seq-Gen (83). For details about simulation parameters, see SI Appendix, section S.3.1.

Random fossil recovery.

Without question, fossils available for calibrating biological datasets never represent the absolute fossil history. We addressed this for each set of simulations by randomly sampling a percentage, ω, of the total fossils. This strategy produced four sets of calibration fossils for each simulation replicate—ω₅ = 5%, ω₁₀ = 10%, ω₂₅ = 25%, and ω₅₀ = 50%—and was applied across the three different simulation conditions (A, B, and C).

Because we planned to compare divergence time estimates under the FBD model to calibration density approaches, we additionally constructed a set of calibration fossils. The calibration fossils were taken from the ω₁₀ sample by selecting the oldest fossil specimen available for each calibration node. Additionally, if fossil f was assigned to date node i and fossil g was assigned to node j, fossil f was removed if x_i > x_j and y_f < y_g. Calibration density approaches condense the available information in the fossil record; thus, the ω_cal10 set of fossils resulted in fewer calibrating ages compared with the ω₁₀ set (SI Appendix, Table S4).

Nonrandom sampling and uncertain fossil placement.

We additionally investigated the impact of nonrandom sampling on estimates of node ages (for details, see SI Appendix, section S.3.2). Specifically, we emulated preservation-biased fossil recovery (SI Appendix, section S.3.2.1) as well as fossil sampling from discrete stratigraphic intervals (SI Appendix, section S.3.2.2). Additionally, we generated datasets with two different nonrandom extant species sampling schemes (SI Appendix, section S.3.2.3). Under taxonomy-driven sampling, the extant species were sampled to maximize diversity, thus emulating species trees of higher-level taxa. A second sampling strategy produced sets of taxa representing concentrated in-group sampling with a distant out-group. Because divergence time estimation relies on correctly assigning the fossils to calibration nodes, we also examined the impact of increased uncertainty in the fossil placement (SI Appendix, section S.3.2.4 for methods and results).

Simulation Study: Divergence Time Analyses.

General priors and MCMC details.

We estimated species divergence times for each simulation replicate and fossil subset using the Bayesian inference program DPPDiv (19, 31, 56). Each analysis, regardless of the calibration model, conditioned divergence times on the true extant species topology, assuming a strict molecular clock with a GTR+Γ substitution model. We applied standard prior distributions on the parameters and hyperparameters of the clock and substitution models (19, 31).

Each analysis was run using a single Markov chain of 2 million iterations, sampling every 100th step, with the first 500,000 iterations discarded as burn-in before the MCMC samples were summarized. Because we ran ∼2,200 MCMC analyses, it was not feasible to perform convergence diagnostics on every replicate analysis. However, because we evaluated performance under a unified framework, in which all models are implemented in the same program with consistent priors and sampling mechanisms for overlapping parameters, summary statistics over 100 replicates are very informative about the accuracy and precision of node age estimates across our different simulation treatments and analyses. Nevertheless, for a subset of our analyses (five for each type of analysis), we evaluated the MCMC samples in the program Tracer (62) and confirmed that the Markov chains effectively sampled the stationary distributions.

Node age inference under the FBD model.

We performed divergence time analyses under the FBD model on every simulation replicate for each fossil-sampling and taxon-sampling treatment. Our implementation of the FBD model has four hyperparameters: d, r, s, and ρ. Because we are interested only in estimating node ages and not in inferring the parameters of the diversification model, we chose uniform prior densities on d, r, and s to marginalize over a wide range of possible values. The diversification rate d may take any value on the interval (0, ∞); however, because they are not likely in nature, we did not simulate under extremely large values. Thus, we place a proper, uniform prior distribution on d with an arbitrarily chosen upper limit: Unif(0,30000). The turnover (r) and fossilization (s) parameters can each take values only on the interval (0,1), and we simply chose Unif(0,1) prior densities for each of these parameters. The bulk of our simulated datasets included all extant taxa; therefore, we fixed the probability of sampling parameter to ρ = 1. It is important to note, however, that although we assume that the uniform priors on the diversification parameters are noninformative, in reality such prior densities—particularly diffuse, truncated uniform priors—often are highly informative because they place significant prior mass on regions in parameter space with very low posterior probability (84, 85). Accordingly, future implementations of this model will include development of alternative hyperprior densities for these parameters. Nevertheless, our simulation analyses indicate that node age estimates are robust to these uniform hyperpriors.

Node age inference using calibration densities.

Calibration density approaches require that only a single fossil be assigned to each calibrated node. Thus, the set of calibration fossils ω_cal10 constructed from the 10% sample for both the random and preservation-biased subsets was used to estimate absolute node ages by using three different node-calibration densities: (i) fixed scaled, (ii) fixed true, and (iii) hyperprior. Each of the calibration density analyses assumed an exponential prior distribution, with the methods differing in the parameterization of the prior density. The exponential distribution is characterized by a single rate parameter ε, which dictates both the mean (ε⁻¹) and variance (ε⁻²) of the prior density. Calibration priors typically describe the duration between the calibrated node and its fossil descendant. The fossil acts as a hard, minimum bound on the age of the node; thus, the calibration density is offset by the age of the fossil.

The fixed-scaled analysis applied a fixed-parameter exponential distribution to each calibrated node, where for any node i calibrated by the fossil f, the rate of the prior density was scaled by the age of the fossil y_f such that the rate of the exponential was $\mathit{ϵ}={\left(\frac{1}{5}{y}_f\right)}^{-1}$. Thus, for very young fossils the expected age of the calibrated node $\left(\mathbb{E}\left[x_i\right]=y_f+\frac{1}{5}{y}_f\right)$ would be smaller compared with the expectation for nodes calibrated by older fossils. By scaling the calibration density based on the fossil age, we attempted to model the arbitrary parameterization of fossil prior distributions common in divergence time estimation analyses.

The fixed-true calibration prior represents an ideal albeit unrealistic case in which the density is parameterized such that the expected age of the calibrated node is equal to its true age. Under this calibration prior, for any node i with true age $x_i^{\ast }$ and calibrated by fossil f with age y_f, the rate parameter of the exponential density was fixed to $\mathit{ϵ}={\left(x_i^{\ast }-y_f\right)}^{-1}$. When applied as a zero-offset calibration prior, the fixed-true parameterization is expected to result in accurate node age estimates because the expected age of the node is equal to the true value $\left(\mathbb{E}\left[x_i\right]=x_i^{\ast }\right)$.

The hierarchical calibration density approach uses a hyperprior on the rate parameters of exponential distributions (31). This method results in robust estimates of node ages and assumes that the vector of ε-rates for all calibrated nodes is drawn from a Dirichlet process model. By allowing the rates of exponential calibration densities to be random variables using MCMC, calibration node ages are sampled from a mixture of prior distributions. Furthermore, this approach accounts for uncertainty in these hyperparameters and reduces the user’s burden with regard to parameter specification. For these analyses, we specified a prior mean of three for the number of ε-rate categories and set the remaining hyperparameters to those of Heath (31).

All calibration density methods require a prior on node ages. This prior is applied to both calibrated and uncalibrated nodes and describes the distribution of speciation events over time. For all analyses using calibration priors (fixed scaled, fixed true, and hyperprior), we assumed a constant-rate reconstructed birth–death process (i.e., an FBD model with ψ = 0) (39, 40) as a prior on speciation times. This model has three hyperparameters on which we applied the following priors: d ∼ Unif(0, 30000), r ∼ Unif(0, 1), and ρ = 1.