Key Concepts and Limitations of Statistical Methods for Evaluating Biomarkers of Kidney Disease

Abstract

Interest in developing and using novel markers of kidney injury is increasing. To maintain scientific rigour in these endeavors, a comprehensive understanding of statistical methodology is required to rigorously assess the incremental value of novel biomarkers in existing clinical risk prediction models. Such knowledge is especially relevant, because no single statistical method is sufficient to evaluate a novel biomarker. In this review, we highlight the strengths and limitations of various traditional and novel statistical methods used in the literature for biomarker studies and use biomarkers of AKI as examples to show limitations of some popular statistical methods.

The surge in biomarker development for various kidney diseases calls for appropriate application of statistical evaluation methodology to rigorously assess emerging biomarkers and their inclusion in disease classification models in clinical care.¹ The development of biomarkers into diagnostic or prognostic tests can be categorized into three broad phases: discovery, performance evaluation, and impact determination when added to existing clinical measures.² Each phase requires a unique study design and statistical considerations to accurately accomplish research objectives. In this review, we will discuss strengths and limitations of the statistical tests used for assessing clinical value and use of biomarkers after successful discovery. We will use examples of novel kidney injury biomarkers in the setting of perioperative AKI to highlight key concepts. The methodology and framework described herein broadly apply to the development of biomarkers in other diseases. Because the focus of this review is on biomarkers of diagnosis and prognosis, statistical methods related to other potential applications of biomarkers (exposure, treatment responsiveness, etc.) will not be addressed.

The statistical methodology required for assessing biomarker performance differs from the classic methods used in epidemiology or therapeutic research. For example, in the biomarker discovery stage, we focus on measures of association (e.g., odds ratios and relative risks) rather than classification or discrimination (e.g., true-positive rates [TPRs] and false-positive rates [FPRs]). At the end of successful biomarker discovery and early human validation, we advance candidate biomarkers with potential for clinical identification of the disease of interest. During this phase, the statistical methods quantify the classification potential of the biomarker. The focus is to show the biomarker’s ability to discriminate between diseased and nondiseased patients better or earlier than the current clinical risk factors, explore clinical covariates associated with the biomarker, and establish scenarios or subgroups in which biomarker testing criteria could be applied. In the final phase of biomarker development, the objective is to determine the additional value of the biomarker when used to expand existing clinical models.

Statistical Methods to Quantify Classification Potential of the Biomarker

After biomarker discovery, it is necessary to evaluate the classification performance, especially for biomarkers that will be used for diagnostic purposes. In general, the first step adopted by most researchers is to quantify the classification performance with TPRs, FPRs, and receiver operating characteristic (ROC) curves. In the medical literature, these rates are also referred to as sensitivity (TPR) and specificity, which is the true negative rate and calculated as 1−FPR. We summarize these performance metrics in Table 1.

Table 1.

Summary of traditional and novel measures

Statistical Metric	Description	Advantages	Disadvantages
Association
Odds ratio or relative risk	Quantifies association between biomarker and outcome	Well known in medical community; useful for categorical or continuous biomarkers	Influenced by how biomarker is modeled; not possible to compare with different biomarker distributions
Performance
ROC curve	Visual description of discriminatory performance for every possible biomarker cutoff	Rank-based (no transformation required if biomarker is skewed); visual comparison of biomarkers	Biomarker must be continuous
AUC	Summary measure of the ROC curve	Single measure to summarize entire curve	Interpretation is not clinically relevant
TPR and FPR	TPR, proportion of cases correctly identified by biomarker as cases; FPR, proportion of controls incorrectly identified by biomarker as cases	Interpretation is clinically intuitive	Must consider both metrics together; does not summarize entire biomarker performance but rather, performance at one threshold value
Incremental value
Multivariable significance test	Summarizes the evidence against the null hypothesis that that marker has no incremental value	Useful for categorical or continuous biomarkers; shows if biomarker is a risk factor	Does not indicate whether the incremental value of a biomarker is substantial or clinically important
∆AUC	Difference in the AUC between two prediction models	Compares models and not biomarkers; single summary measure	Interpretation is not clinically relevant
∆TPR, ∆FPR, or NRI (two way)	For a given risk threshold, ∆TPR (or NRI event) is the change in the proportion of cases correctly identified, and ∆FPR (or NRI nonevent) is the change in the proportion of controls incorrectly identified	Directly links to improvement in biomarker discrimination	Must specify risk thresholds, which may not be well defined in clinical setting
NRI three-way categorical	Enumerates cases and controls with improved or worsening reclassification by examining changes in risk categories	Compares models and not individual variables	Dependent on choice of categories; does not distinguish types of reclassifications that have different clinical implications
NRI>0	Enumerates cases and controls with improved or worsening reclassification defined by any change in predicted probabilities after the addition of the biomarker to the risk prediction model	Biomarkers differentially distributed can be compared; easy to calculate	Not directly linked to clinical use, undefined range of meaningful improvement; very small change in predicted probability is counted as a meaningful change in reclassification
IDI	Difference in discrimination slopes	Compares models and not individual variables; biomarkers differentially distributed can be compared	Sensitive to differences in event rates; undefined range of meaningful improvement
Relative IDI	Ratio of IDI and the discrimination slope in the baseline clinical model	Relative scale improves interpretability for the biomarker contribution; biomarkers differentially distributed can be compared	Undefined range of meaningful improvement

If we compare the classification assigned by the biomarker with the true disease status, the results can be categorized as a true positive, false positive, true negative, or false negative. The TPR is the proportion of diseased patients that the biomarker correctly classifies as diseased patients, and the FPR is the proportion of nondiseased patients that the biomarker incorrectly classifies as diseased patients. The range of possible values for both the TPR and FPR is between zero and one. A good biomarker has high TPR and low FPR. The ROC curve—a single curve plotted on a graph with the FPR on the horizontal axis and the TPR on the vertical axis—provides a complete description of the biomarker classification performance as the disease-positive cutoff changes. ROC curves can, thus, guide the selection of cutoffs for diagnosis of a disease.³

The area under the ROC curve (AUC) is probably the most widely used summary index. The AUC ranges from 0.5 (the area under the diagonal line representing discrimination based on random chance) to 1 (the area of the entire square representing perfect discrimination). The AUC can be interpreted as the probability of the biomarker value being higher in a diseased patient compared with a nondiseased patient if the diseased and nondiseased pair of patients is randomly chosen. Often, the optimal classification threshold is defined as the cut point with the maximum difference between the TPR and FPR [e.g., the Youden Index calculated as maximum (TPR−FPR) or equivalently, maximum (sensitivity+specificity−1)]. TPR and FPR must be reported together, and there is always a tradeoff in the selection of TPR versus FPR. Occasionally, the partial area under the curve can be used to describe the classification performance within a range of FPR values. For example, certain settings in which treatment is harmful may require very low FPR values (e.g., ≤0.1); therefore, only the AUC between FPR values of 0 and 0.1 would be of interest.

Although ROC curves and their summary measures are widely used, there are several limitations. The interpretation of the AUC is not directly clinically relevant, because patients do not present as pairs of randomly selected cases and controls. ROC curves are well established for continuous values of biomarkers and binary outcomes, but the statistical methodology for ROC curves is still evolving for continuous outcomes (e.g., Δcreatinine), ordinal outcomes (e.g., acute kidney injury network stages),⁴ and time to event outcomes (e.g., months to ESRD).^5,6 Furthermore, the AUC of a new biomarker is highly dependent on its comparison with the gold standard. In the presence of an imperfect gold standard, such as serum creatinine for the cases of AKI and CKD, the classification potential of the new biomarker may be falsely diminished.^7,8

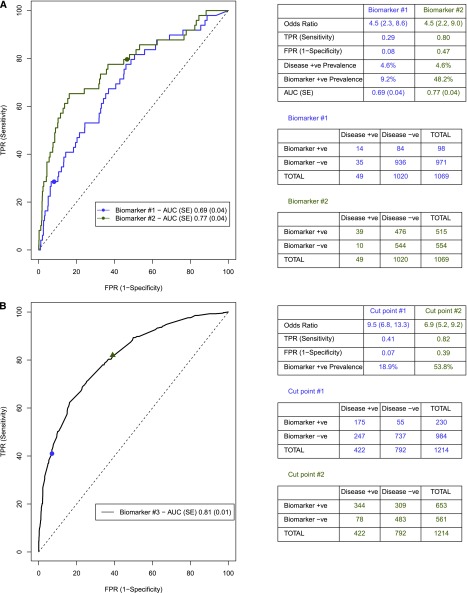
Traditional epidemiologic metrics, such as odds ratios, quantify the association between the biomarker and outcome but not the discriminatory ability of the biomarker to separate cases from controls, because odds ratios are not directly linked to TPR and FPR levels.⁹ Figure 1A shows that, for a given odds ratio, multiple combinations of TPR and FPR can exist. Similarly, for a given biomarker, the AUC will remain constant, but the odds ratio will differ depending on the selection of the cutoff point of the biomarker (Figure 1B).

Figure 1.

Relationship between ROC curve and odds ratios. (A) Odds ratios are not directly linked to TPR and FPR. Biomarkers #1 and #2 have different AUCs (0.69 and 0.77, respectively) for AKI (4.6% prevalence rate). For each biomarker, we can find a threshold value where both biomarkers have an odds ratio of 4.5, but the TPR and FPR values differ (0.29 and 0.08 versus 0.80 and 0.47, respectively). (B) Selection of cut point influences metrics to evaluate biomarker performance. Cut point #1 has a higher odds ratio, lower TPR, lower FPR, and lower biomarker+ve prevalence rate than cut point #2 (odds ratio, 9.5 versus 6.9; TPR, 0.41 versus 0.82; FPR, 0.07 versus 0.39; biomarker+ve prevalence, 18.9% versus 53.8%, respectively). +ve, positive; −ve, negative.

Statistical Methods to Evaluate the Incremental Value of Biomarkers

Frequently, the classification potential of a biomarker is not adequate alone, which is especially true in settings in which clinical measures or clinical risk models are already in use to facilitate clinical decisions. In such scenarios, it is of interest to determine the contribution of the biomarker to an existing multivariable clinical risk model. Also, if the marker will be used predominantly for predictive purposes, it is of interest to determine the potential of improvement in the clinical risk prediction model with the addition of a novel biomarker. There are several methods to assess the contribution of the new marker that are discussed below and summarized in Table 1. For simplicity of discussion, we assume that we are evaluating the incremental value of a biomarker as an extension of a clinical risk prediction model.

Incremental Value

Before evaluating the incremental performance of the biomarker, it is essential that the underlying clinical risk prediction model is well calibrated. Good calibration means that risk prediction model-based event rates correspond to those rates observed in clinical settings, which can be assessed using plots (scatter plot of observed versus predicted risk). The most fundamental requirement for a new marker is independent relation to the outcome of the study after adjusting for existing variables in the risk prediction model. In several instances, the biomarker may be related to one or more clinical factors, and its independent association may be diminished in the presence of that clinical factor. For some biomarkers, such as plasma neutrophil gelatinase-associated lipocalin, the association with the outcome of AKI diminishes markedly after the addition of postoperative change in serum creatinine.¹⁰ In practical terms, if we are using a logistic regression model, this finding means looking at the coefficient (or β) and P value for the biomarker in the multivariable clinical risk model. Statistical significance may be inferred from the P value, and the strength of clinical association can be measured by the effect size.¹¹ The interpretation of the magnitude and direction of the effect size should take several factors, such as the study design, clinical setting, and clinical relevance, into consideration. In large studies, a biomarker may have a significant P value but a small effect size that is not clinically significant. We, therefore, suggest balancing the interpretation of statistical and clinical significance by considering the effect size of the biomarker association with the outcome and the P value after adjusting for existing clinical measures.

With multivariable models that account for relevant clinical factors, the effect size of the biomarker from these models does not necessarily provide a complete understanding of the added contribution of the new marker in the context of risk prediction. Effect size is usually presented as metrics of odds ratios, relative risks, or hazard ratios or absolute risk difference. As shown in Figure 1, these effect sizes are not linked to discriminatory performance. Hence, researchers have to move beyond associations and explore other measures for understanding the incremental value of the biomarker in risk prediction. The metrics of improvement in discrimination and risk classification are the two additional aspects that must be evaluated for a new biomarker to understand its contribution to a risk prediction model.

An important step in this process, often overlooked when evaluating the classification performance of a biomarker, is to determine the existence of other factors or variables that influence a biomarker’s prediction performance and whether they are related to the outcome of interest.^12–14 It is important to explore such factors by examining the distribution of the biomarker in the nondiseased patients. Factors to consider may be related to patient demographics (e.g., age, race, and sex), clinical parameters (e.g., protein in urine, oliguria, and CKD), or sample processing details (e.g., collection time, freezing time, and length of storage). If there are variables associated with biomarker performance, then diagnostic accuracy can be assessed separately (e.g., biomarker performance was determined in adults and children separately in the Translational Research Investigating Biomarker Endpoints (TRIBE)-AKI consortium cohort), or more sophisticated methods for adjustment can be applied.^15–17 Knowledge of these parameters may allow the investigator to expand the use of this biomarker into other clinical settings.

Improvement in Discrimination

As discussed above, the AUC, which corresponds to the C statistic of the risk prediction model, is a common method to assess discrimination performance of binary outcomes. Thus, the increment in the C statistic or change in AUC (ΔAUC) is applied to quantify the added value offered by the new biomarker. The widely used method by DeLong et al.¹⁸ is designed to nonparametrically compare two correlated ROC curves (clinical model with and without the biomarker); however, it has recently been shown that the test may be overly conservative and may occasionally produce incorrect estimates. Begg et al.¹⁹ have used simulations to show that the use of same risk predictors from nested models while comparing AUCs with and without risk factors leads to grossly invalid inferences. Their simulations reveal that the data elements are strongly correlated from case to case, and the model that includes the additional marker has a tendency to interpret predictive contributions as positive information, regardless of whether the observed effect of the marker is negative or positive. Both of these phenomena lead to profound bias in the test. It is also recommended not to pursue additional hypothesis testing on the ΔAUC after showing that the test of the regression coefficient is significant.^20,21 Researchers have observed that ΔAUC depends on the performance of the underlying clinical model. For example, good clinical models are harder to improve on, even with markers that have shown strong association.²² In Table 2 using data from TRIBE-AKI, we show that a biomarker with an AUC of 0.67 exhibits a change in C statistic of 0.13 when the underlying clinical model has an AUC of 0.54, but the change in C statistic is only 0.02 when the clinical model is 0.66.

Table 2.

Magnitude of ∆AUC depends on AUC of baseline model

Variable	Demographic Modela (AUC=0.54)	Full Clinical Modelb (AUC=0.66)
+ Biomarker #1 (AUC=0.59)	0.07	0.02
+ Biomarker #2 (AUC=0.67)	0.13	0.04
+ Biomarker #3 (AUC=0.77)	0.25	0.19

The table presents the ∆AUC when each biomarker is added to the baseline model (demographic or full clinical model). The models are predicting AKI (>50% increase in serum creatinine or dialysis) after cardiac surgery.

^aDemographic model is comprised of age, race, and sex.

^bFull clinical model is comprised of age, sex, preoperative eGFR, elective surgery (yes or no), white race, diabetes, and hypertension.

Because good clinical models did not show an improvement in AUC after adding new risk factors, Pencina et al.^23–26 devised alternative metrics for evaluating reclassification with novel biomarkers.^23–26 The proposed new metrics, integrated discrimination improvement (IDI) and net reclassification index (NRI), are becoming widely used and discussed below.

Improvement in Reclassification

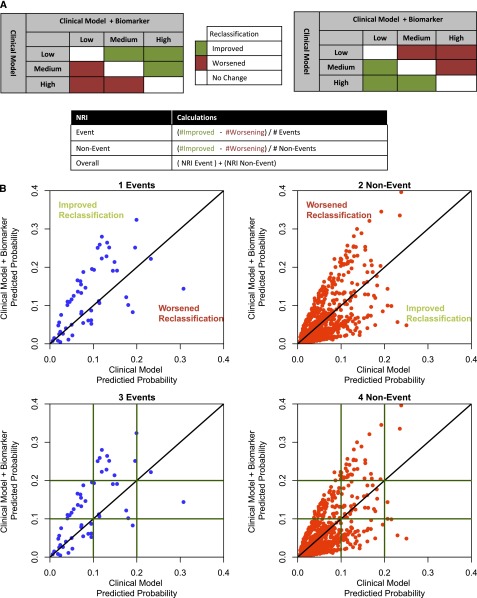
A reclassification table is created to show how many subjects change risk categories by adding a biomarker to the risk model. In this table, an upward movement in categories for subjects with the event suggests improved classification, and a downward movement indicates worse reclassification (Figure 2A). The reclassification and interpretation is opposite for subjects without the outcome. The overall improvement in reclassification, referred to as the NRI, is quantified as the sum of the following two difference: (1) the proportion of individuals moving up minus the proportion of individuals moving down for those individuals with the outcome and (2) the proportion of individuals moving down minus the proportion of individuals moving up for those individuals without the outcome. NRI, thus, combines four proportions (upward and downward movement in both event and nonevent groups) and can have a minimum value of −2 and a maximum value of 2. It should be remembered that NRI itself is not a proportion—a common mistake in the literature—but rather, an index that combines four proportions.

Figure 2.

Concepts of NRI. (A) Event and nonevent categorical NRI calculation. (B) Continuous NRI (NRI>0) and the relationship between continuous and categorical NRI. Continuous NRI scatter plots have the predicted probabilities from the clinical model+biomarker on the vertical axis (y axis) and the predicted probabilities from the clinical model on the horizontal axis (x axis). (B, 1 Events) For events, an increase in predicted probabilities with the addition of the biomarker to the clinical model is an improvement in reclassification (above the y=x line) and a decrease in predicted probabilities is a worsening in reclassification (below the y=x line). (B, 2 Non-Event) The opposite is true for nonevents; increase in predicted probabilities is worse (above the y=x line) and decrease in predicted probabilities is an improvement in reclassification (below y=x line). (B, 3 Events; 4 Non-Event) Relationship between categorical and continuous NRI. The horizontal and vertical green lines identify the risk categories used for a three-category NRI calculation (low risk<10%, medium risk=10%–20%, high risk>20%). The scatter plot shows areas where the improvement or worsening of classification differs between categorical NRI and NRI>0.

Since the introduction of NRI, there have been various modifications to improve this metric. One of the earliest suggestions was to report NRI separately for events (NRI_e) and nonevents (NRI_ne) instead of reporting an overall NRI.²⁷ This dichotomization proved beneficial, because a biomarker frequently improves reclassification only of participants with the disease or vice versa. The range for both NRI_e and NRI_ne metrics individually range from −1 to 1. Often, useful information is lost with reporting of overall NRI, and in cases of low disease occurrence, the overall NRI would weigh the disease and the nondisease groups equally. Based on the disparate clinical consequences, it would be desirable to report both NRI_e and NRI_ne separately. When there are two risk categories, low and high, NRI_e is equal to the change in the TPR (proportion of the events assigned to the high-risk category). Similarly, NRI_ne for the two-risk category is the change in the proportion of nonevents, which corresponds to a change in the FPR.²⁸ Categorical NRI is highly dependent on the number of categories. This metric also introduces issues, because higher numbers of categories would lead to increased movement of persons across categories with addition of the new biomarker, thus inflating the NRI value.

Another suggestion by some statisticians is to weight the NRI by prevalence of events to understand the total value in the population. The weighting extends the NRI_e and NRI_ne interpretation to the whole population. The population-weighted NRI can be calculated as Rho(NRI_e)+(1−Rho)NRI_ne, in which Rho denotes the prevalence of the disease.²⁹ However, as with overall NRI, weighted NRI similarly leads to a loss of information by combining the two groups.

In the above discussion, we assume that there is an underlying clinical model with well defined risk categories (such as the Framingham risk model) on which the biomarker must improve. However, for several diseases, such as AKI and CKD, there is no accepted clinical prediction model with established risk categories. In this situation, Pencina et al.²⁴ suggest calculating the continuous NRI (NRI>0) for which no categories are needed. In the calculation of continuous NRI, the change caused by the addition of the biomarker in the predicted probability, regardless of whether upward or downward, is counted (Figure 2B). Similar to example above, continuous NRI can be obtained for event and nonevent components. Because every person will be reclassified, the values of NRI>0 are much larger than those values of categorical NRIs (Figure 2B). However, the presence of categories in the discussion above substantially reduces reclassification and gives points only when a person changes categories. Continuous NRI is, thus, highly inflated, and several statisticians have discouraged its use.^29,30 For purposes of quantification of NRI>0, Pencina et al.²⁶ have designated values of <0.20, 0.40, and >0.60 for adding a weak, intermediate, and strong independent predictor, respectively. However, others have shown that NRI>0 suffers from some of the same problems as AUC and is not clinically interpretable.²⁹

The continuous NRI was originally proposed to overcome the problem of selecting categories in applications in which they do not naturally exist, which has several consequences. First, most changes in predicted risk do not translate into changes in clinical management; therefore, the interpretation of the continuous NRI is different from that of the category-based NRI. Second, the continuous NRI is often positive for relatively weak markers, and it is strongly affected by miscalibration, especially in the setting of external validation. As such, the continuous NRI is less suitable for head-to-head comparisons of competing models, unless these models have been developed from the same data or are correctly calibrated.³¹ However, the continuous NRI does provide a consistent message across different models and therefore, is marker-descriptive rather than model-descriptive.²⁹ In general, we do not recommend the use of continuous NRI and would encourage investigators to apply it only in special situations and along with reporting other metrics of marker assessment.

IDI

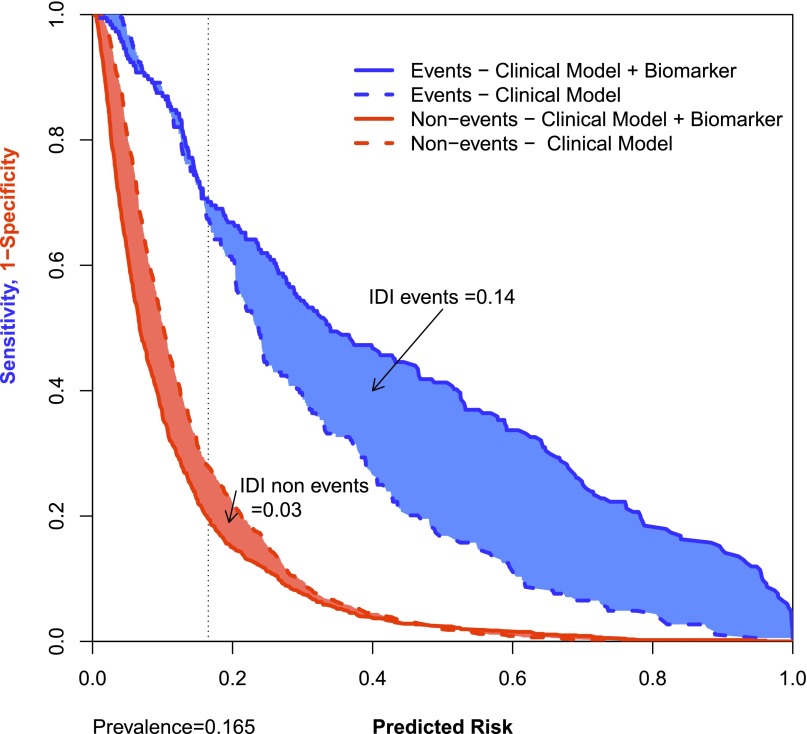
The IDI metric is independent of category and separately considers the actual change in calculated risk of each individual for those individuals with and without events. Unlike NRI, IDI does not take into account the direction of change and can be conceptualized as a metric that provides the difference in discrimination slopes or the difference of average probabilities between events and nonevents.²³ Also, unlike NRI, IDI is dependent on calibration of the underlying clinical model. For overall assessment of biomarkers, IDI is a better metric than NRI, because it aggregates the magnitude of reclassification. For example, a biomarker receives more weight if it reclassifies risk in someone with an outcome from 55% to 80% than it would from 55% to 60%, although both would be counted as the same increment in continuous or categorical NRI. There are no established criteria for the interpretation of the magnitude of the IDI. As a result, the metric of relative IDI is calculated as the IDI divided by the discrimination slope of the clinical model and may be easier to interpret. If the relative IDI>(1/number of predictors) in the clinical model, it can be inferred that the biomarker has provided some incremental value beyond existing clinical measures. Pickering and Endre³² have suggested graphical methods for presentation of NRI and IDI combined for events and nonevents. For example, this risk assessment plot can provide a visual presentation of the IDI by comparing the performance of an existing clinical model (or reference model) and the clinical model with the addition of a biomarker (the new model). The IDI for events is the sum of the region between the line of sensitivity versus the predicted risk of the clinical model and the clinical model+biomarker (Figure 3). Similarly, the IDI for nonevents is the sum of the region between the line of 1−specificity and the predicted risk. The overall IDI is the sum of the IDI for events and the IDI for nonevents.

Figure 3.

Risk assessment plot. Risk assessment plot for a clinical model (dashed lines) and the clinical model with the addition of a biomarker (solid lines) to predict AKI. The blue lines are sensitivity versus the predicted risk, and the red lines are 1–specificity versus the predicted risk. An improvement in reclassification for an event moves upward and to the right from the clinical model (dashed blue line) to clinical model+biomarker (solid blue line). For a nonevent, downward and to the left movement denotes an improvement in reclassification from the clinical model (dashed red line) to the clinical model+biomarker (solid red line). The sum of the blue shaded region is the IDI for events, and the sum of the red shaded region is the IDI for nonevents.

Clinical Use and Decision Analytic Measures

If a biomarker improves clinical risk prediction, the next important consideration is its impact on clinical management.³³ Does the new biomarker improve the outcomes of patients who receive the test? Cost-effectiveness, decision, and net benefit analyses need to be subsequently performed.³⁴ For assessment of the potential clinical use of promising markers, decision analytic approaches are needed before a formal cost-effectiveness analysis, which encompasses changes in costs and clinical outcomes in more detail. Decision analytic measures incorporate the prevalence of the disease in the population, the gain in TPRs and FPRs because of the new biomarker, and the benefit and harm related to over- and underdiagnosis. However, the use of such decision analytic measures is limited by the fact that weights for harms and benefits are not firmly established in most fields of medicine, although a range of decision thresholds can be considered in a sensitivity analysis with visualization in a decision curve. One such method of decision curve analysis has easy-to-use software and wide practical application.³⁵ These metrics have not been used abundantly in nephrology, because there are no approved treatments for AKI or CKD.

Conclusions

We discussed several statistical measures that can be used at various phases in biomarker development. There is no one measure that can be used for accepting or refuting a biomarker, because each statistical method has its own strengths and weaknesses. In addition, different methods have different properties and applicability as discussed above. Biomarker development is also a phased process, which inherently requires the use of a variety of statistical methods to fulfill different objectives. In the early phases, association assessment using techniques such as logistic regression may be sufficient, because the goal is to advance the promising biomarkers to the next phases. Incremental values of biomarkers cannot be reliably assessed at this stage. At the later phases of development, the primary purpose is to determine the added discriminatory value and incremental benefit provided by the biomarker to traditional clinical measures.

Thus, investigators need to choose methods based on the limitations of the statistical measure, biomarker phase of development, hypothesis being tested, sample size, and clinical question. As we discussed, although ROC curves may be conservative in terms of discovering a new biomarker, NRI may be too aggressive when the marker may not provide predictive information. As with most summary statistics, the NRI should not be interpreted on its own but in the context of complementary statistical measures. If a marker is not associated with the outcome or does not yield an increase in the AUC, a positive NRI should not be expected.³⁶ In rare instances in which it does occur, random chances or differences in calibration between the models are the most likely causes. Thus, biomarker reporting guidelines suggest reporting of multiple metrics for full assessment of a novel biomarker.³⁷ Investigators should veer away from statistical abstractions, such as the NRI and AUC, and rather, move to illustrating the consequences of using a marker or model in straightforward clinical terms.³⁸

In addition to prognostic information and improvement in risk prediction, it is also conceivable that the current biomarkers under investigation in AKI or CKD may be used to provide valuable information as exposure biomarkers (e.g., cotinin levels for tobacco exposure) or predictors of treatment responsiveness (e.g., estrogen receptor status for endocrine therapy in breast cancer). Testing for other applications of biomarkers may require alternate study designs and statistical methods. Ultimately, investigators and the nephrology community are optimistic that novel biomarkers will have important applications and improve risk prediction models. In turn, they will allow researchers to design more efficient clinical trials for promising interventional agents and clinicians to improve the management of kidney diseases.

Disclosures

None.