Abstract
Recently, brain connectivity networks have been used for classification of Alzheimer's disease and mild cognitive impairment (MCI) from normal controls (NC). In typical connectivity‐networks‐based classification approaches, local measures of connectivity networks are first extracted from each region‐of‐interest as network features, which are then concatenated into a vector for subsequent feature selection and classification. However, some useful structural information of network, especially global topological information, may be lost in this type of approaches. To address this issue, in this article, we propose a connectivity‐networks‐based classification framework to identify accurately the MCI patients from NC. The core of the proposed method involves the use of a new graph‐kernel‐based approach to measure directly the topological similarity between connectivity networks. We evaluate our method on functional connectivity networks of 12 MCI and 25 NC subjects. The experimental results show that our proposed method achieves a classification accuracy of 91.9%, a sensitivity of 100.0%, a balanced accuracy of 94.0%, and an area under receiver operating characteristic curve of 0.94, demonstrating a great potential in MCI classification, based on connectivity networks. Further connectivity analysis indicates that the connectivity of the selected brain regions is different between MCI patients and NC, that is, MCI patients show reduced functional connectivity compared with NC, in line with the findings reported in the existing studies. Hum Brain Mapp 35:2876–2897, 2014. © 2013 Wiley Periodicals, Inc.
Keywords: mild cognitive impairment, Alzheimer's disease, functional connectivity network, graph kernel, multiple thresholds
INTRODUCTION
Alzheimer's disease (AD) is the most common form of dementia in elderly population worldwide. It is predicted that the number of affected people will double in the next 20 years, and 1 in 85 people will be affected by 2050 [Brookmeyer et al., 2007]. Thus, accurate diagnosis of AD, especially its early stage, such as mild cognitive impairment (MCI), is very important for possible early treatment and possible delay of the progression of disease. Existing studies have shown that MCI subjects progress to clinical AD at an annual rate of ∼10–15%, while the healthy normal controls (NC) develop dementia at an annual rate of 1–2% [Petersen et al., 2001]. So far, many methods have been developed to identify predictive biomarkers of AD or MCI from different neuroimaging modalities [Filippi and Agosta, 2011; Fjell et al., 2010; Haller et al., 2010; Sperling et al., 2011; Zhang and Shen, 2012a,b].
In the past decade, modern magnetic resonance imaging (MRI) [e.g., functional MRI (fMRI) and diffusion MRI], and neurophysiological [e.g., electroencephalograph (EEG) and magnetoencephalograph (MEG)] techniques have provided efficient and non‐invasive ways to map the patterns of structural and functional connectivity of the human brain [Robinson et al., 2010; Sporns, 2011; Xie and He, 2011]. Structural brain connectivity is referred to as the anatomical connection pattern between different neuronal elements [Bassett and Bullmore, 2009; He et al., 2009; Rubinov and Sporns, 2010]. However, functional brain connectivity is referred to as the functional association pattern among brain regions, which can be obtained by measuring the temporal correlations between spatially remote neurophysiological events from fMRI and EEG/MEG data [Kaiser, 2011; Wang et al., 2013]. Recent applications of brain connectivity networks include exploring the anatomical and functional connectivity relationship between brain regions [Honey et al., 2009; Zhou et al., 2006] and also the connectivity abnormality in neurodegenerative diseases (e.g., MCI and AD) for identifying biomarkers for diagnosis [Morbelli et al., 2010; Pievani et al., 2011; Stam et al., 2009; Wang et al., 2013].
It is reported that structural and functional abnormalities can be observed in the brains of AD and MCI patients [Busatto et al., 2003; Filippi and Agosta, 2011; Sperling et al., 2003; Xie and He, 2011]. Recent studies have suggested that, in addition to the regional disturbance of brain structure and function, neurodegenerative diseases (e.g., AD and MCI) are also associated with the abnormalities in connections between different brain regions [Bai et al., 2012; Delbeuck et al., 2003; Morbelli et al., 2010; Palop et al., 2006; Pievani et al., 2011; Stam et al., 2009; Wang et al., 2013]; see [Kaiser, 2011; Xie and He, 2011; Ye et al., 2011] for review. For instance, small‐world characteristics are disrupted in the functional brain networks of AD, implicating disruptive system integrity associated with specific cognitive states caused by the disease [Sanz‐Arigita et al., 2010; Stam et al., 2007]. Moreover, functional connectivity is shown decreased between the hippocampus and other regions of AD and MCI brains [Bai et al., 2009; Supekar et al., 2008; Wang et al., 2007]. However, some studies found increased connectivity between the frontal lobe and other brain regions in early AD and MCI [Gould et al., 2006; Stern, 2006].
Network analysis provides a new way for exploring the association between brain functional deficits and the underlying structural disruption related to brain disorders [Kaiser, 2011; Sporns et al., 2005; Wee et al., 2011]. Due to the increasing reliability of network characterization through neurobiologically meaningful and computationally efficient measures [Kaiser, 2011; Rubinov and Sporns, 2010], learning connectivity characteristics of network from neuroimaging data shows great promise for identifying image‐based biomarkers. Recently, connectivity networks have been used for analysis of AD and MCI. Applications of network‐based analysis tools in neuroimaging can be divided into two categories: (1) Studies focusing on specific hypothesis‐driven tests, for example, on the small‐world network [He et al., 2009; Liu et al., 2012b; Sanz‐Arigita et al., 2010], default mode network [Greicius et al., 2004, 2007, 2009; Petrella et al., 2011], and hippocampus network [Bai et al., 2009; Li et al., 2002; Wang et al., 2006b] and (2) Studies focusing on machine learning based methods for individual‐based classification [Chen et al., 2011; Wee et al., 2011; 2012b; Ye et al., 2011; Zhou et al., 2011].
In the first category, studies mainly focus on network dysfunction perspective of neurodegenerative diseases using graph theoretical analysis [Buldu et al., 2011; He and Evans, 2010; Xie and He, 2011], to demonstrate the topological differences of the brain networks between patients and NC. While these studies in general support the hypothesis of disconnection syndrome in AD and MCI, they cannot be automatically used to discriminate MCI and AD from NC at individual level [Seeley et al., 2009; Supekar et al., 2008; Wang et al., 2007]. However, in the second category, machine learning methods are used to train classification models to identify diseased subjects from NC [Craddock et al., 2009; Richiardi et al., 2012; Shen et al., 2010; Wang et al., 2006a]. For instance, Wee et al. [2011] proposed an effective network‐based classification framework to identify accurately MCI patients from NC by using a collection of measures derived from white matter (WM) connectivity networks. Shen et al. [2010] designed a data‐driven classifier based on machine learning to discriminate schizophrenic patients from NC. In network‐based classification approaches, it involves two main steps: (1) extracting meaningful features from the connectivity network, followed by feature selection to select the most discriminative feature subset and (2) training a classifier using the chosen features. However, the extracted features, such as local network measures [Wee et al., 2011, 2012a,b] and the weights between the region‐of‐interest (ROI) pairs [Chen et al., 2011], are usually concatenated into a long feature vector for subsequent feature selection and classification, without considering the disease‐related topological information such as local and global topological information of the network. To some extent, this may deteriorate the final classification performance.
In this article, we propose a network‐based classification framework to identify accurately MCI patients by using a collection of local measures of connectivity networks and topological information, derived from functional connectivity networks. The key of our approach involves using a new tool, that is, graph kernel [Shervashidze et al., 2011; Vishwanathan et al., 2010], to directly measure the topological similarity between functional connectivity networks. Specifically, we first apply multiple thresholds to generate multiple thresholded connectivity networks, to reflect different levels of topological structure of the original connectivity network. (Here, different thresholds determine their corresponding different levels of topological structure. In other words, the thresholded connectivity networks with larger threshold often preserve fewer connections and thus are sparser in connection.) Then, for each thresholded connectivity network, we derive its corresponding subnetwork by filtering out irrelevant ROI features, followed by a new recursive feature elimination method based on graph kernel (namely, RFE‐GK), where in each iteration the subnetworks are derived by using the current surviving ROI features and also the support vector machine (SVM) with graph kernel is adopted to select the most discriminative ROI features. Finally, we use multikernel SVM to fuse all features from multiple thresholded networks for final classification of MCI from NC. It is worth noting that the idea of using multiple thresholded connectivity networks has also been investigated in several recent works, that is, in Zanin et al. [2012]. However, one of the main differences between our method and the work of Zanin et al. [2012] is that our method uses a multiple‐kernel learning technique to combine network properties from multiple thresholded networks, while Zanin et al. determined only one best thresholded network representation by exploring the classification performance on multiple possible thresholds. Moreover, our method uses a new graph‐kernel tool to measure directly the topological similarity between connectivity networks, which is one of our major contributions and was not investigated in Zanin et al. [2012].
METHOD
Data Acquisition
In this study, 12 amnestic MCI patients and 25 NC were recruited. Demographic information of the participants is shown in Table 1. Informed consent was obtained from all participants, and the experimental protocols were approved by the institutional ethics board. All the recruited subjects were diagnosed by expert consensus panels. Data acquisition was performed using a 3.0‐Tesla GE Signa EXCITE scanner. FMRI images of each participant were acquired with the following parameters: flip angle = 77°, TR/TE =2000/32 ms, imaging matrix = 64 × 64, FOV = 256 × 256 mm2, 34 slices, 150 volumes, and voxel thickness = 4 mm. During scanning, all subjects were instructed to keep their eyes open and stare at a fixation cross in the middle of the screen, which lasted for 5 min. It is worth indicating that in our study, we did not use extra techniques or devices to measure whether subjects actually kept their eyes open during the scan. Although existing studies have reported that the sleep alterations or early sleep (with eyes open) in neurological and psychiatric patients [AASM, 2007; Ford and Kamerow, 1989] could be distinguished by recent multivariate pattern analysis methods (e.g., SVM) [Tagliazucchi et al., 2012], the full investigation on that topic is beyond the main aim in this article.
Table 1.
Characteristics of the participants used in this study
| Group | MCI | Normal |
|---|---|---|
| No. of subjects (male/female) | 6/6 | 9/16 |
| Age (mean ± SD) | 75.0 ± 8.0 | 72.9 ± 7.9 |
| Years of education (mean ± SD) | 18.0 ± 4.1 | 15.8 ± 2.4 |
| MMSE (mean ± SD) | 28.5 ± 1.5 | 29.3 ± 1.1 |
Overview
Figure 1 shows the framework of the proposed method for connectivity‐networks‐based classification, which contains three main steps: (1) image preprocessing and functional connectivity networks construction, (2) feature extraction and feature selection, and (3) classification. For clarity of notations, we have listed the main symbols used in this article in the Supporting Information Table S1.
Figure 1.
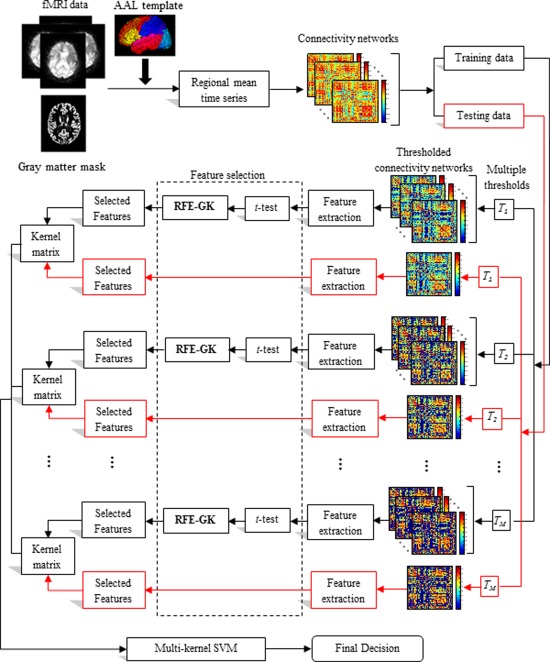
The proposed classification framework. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
The preprocessing steps of the fMRI images, which include slice timing correction and head‐motion correction, were performed using Statistical Parametric Mapping software package (SPM8, http://www.fil.ion.ucl.ac.uk.spm). The first 10 acquired fMRI images of each subject were discarded to ensure magnetization equilibrium. The remaining 140 images were first corrected for the acquisition time delay among different slices before they were realigned to the first volume of the remaining images for head motion correction. Since the regions of ventricles and WM contain a relatively high proportion of noise caused by the cardiac and respiratory cycles [Van Dijk et al., 2010], we only used BOLD signals extracted from gray matter (GM) tissue to construct functional connectivity network. Accordingly, we first segmented the T1‐weighted image of each subject into GM, WM, and cerebrospinal fluid (CSF). GM tissue of each subject was then used to mask their corresponding fMRI images to eliminate the possible effect from WM and CSF in the fMRI time series.
The first scan of fMRI time series was coregistered to the T1‐weighted image of same subject. The estimated transformation was then applied to other fMRI scans of the same subject. The brain space of fMRI scans for each subject was then parcellated into 90 ROIs by warping the automated anatomical labeling [Tzourio‐Mazoyer et al., 2002] template to the subject space using the deformation fields estimated via a deformable registration method called HAMMER [Shen and Davatzikos, 2002]. For each subject, the mean time series of each individual ROI was then computed by averaging the GM‐masked fMRI time series over all voxels in the particular ROI.
In this study, the GM‐masked mean time series of each region was band‐pass filtered within frequency interval [ Hz] since the fMRI dynamics of neuronal activities are most salient within this frequency interval. It is reported in [Zuo et al., 2010] that the frequency band of (0.027–0.073 HZ) demonstrated significant higher test‐retest reliability than other frequency bands. It provides a reasonable trade‐off between avoiding the physiological noise associated with higher frequency oscillations [Cordes et al., 2001] and the measurement error associated with estimating very low frequency correlations from limited time series [Achard et al., 2008; Fornito et al., 2010]. Here, the band‐pass filtering was implemented using the discrete fast Fourier transform function provided by the MATLAB package.
We adopted Pearson correlation coefficients to compute the functional connectivity between the ROI pairs. For each subject, a functional connectivity network was constructed with the vertices of network corresponding to the ROIs and the weight of edges corresponding to the correlation coefficients. Fisher's r‐to‐z transformation was applied on the elements of the functional connectivity network (matrix) to improve the normality of the correlation coefficients as
| (1) |
where r is the Pearson correlation coefficient and z is approximately a normal distribution with standard deviation , where n is the number of ROIs. Moreover, to extract the meaningful network measures, all negative correlations have been removed from the obtained functional connectivity networks.
Since the functional connectivity networks are intrinsically fully connected, we threshold each connectivity network with different values in order to reflect different levels of topological structure of the original connectivity network. The weighted clustering coefficients of each ROI in relation to the remaining ROIs were then extracted from each thresholded connectivity network as features for subsequent feature selection and classification. We adopted a two‐stage approach to select the optimal features for MCI classification. Specifically, a statistical t‐test was first performed to screen out some less important features in discrimination between MCI patients and NC, and then followed by the recursive feature elimination with graph kernel (denoted as RFE‐GK), to further select the most discriminative features. Figure 2 illustrates the flowchart of the proposed RFE‐GK approach. Finally, multikernel SVM was adopted for final classification based on the selected ROI features.
Figure 2.
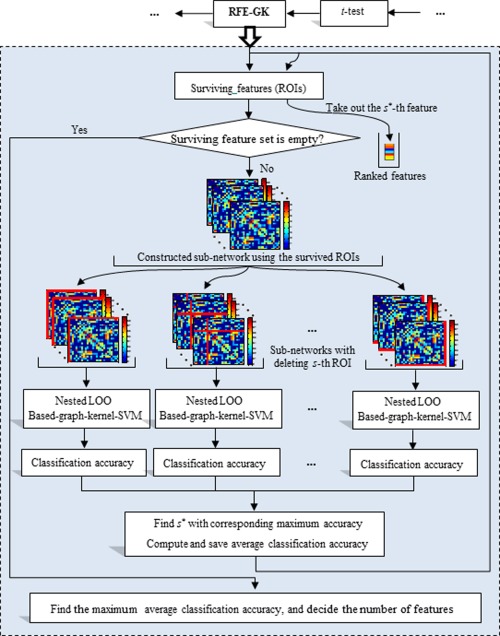
Flowchart of the proposed RFE‐GK method. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Graph Kernel
Kernel‐based learning methods work by first mapping the data into a higher dimensional feature space, and then searching for linear relations among the mapping data points [Scholkopf and Smola, 2002]. The mapping is performed implicitly by specifying the kernel function between subjects. Given two subjects (vectors) x and , the kernel can be defined as , where is a mapping function that maps data from data space to feature space. The common kernel functions are linear function and Gaussian radial basis function (RBF). These are given by, respectively:
| (2) |
| (3) |
Roughly speaking, kernel can be seen as a similarity measure between a pair of subjects. Once a kernel is defined, many learning algorithms such as SVM can be applied. Besides working on feature vector, kernel can also work on more complex data types, for example, graph, with the corresponding kernel called as graph kernel, which captures the semantics inherent in the graph structure [Shervashidze et al., 2011; Vishwanathan et al., 2010]. A number of methods have been proposed to construct graph kernel, including walk‐based [Gartner et al., 2003; Kashima et al., 2003], path‐based [Alvarez et al., 2011; Borgwardt and Kriege, 2005], subtree‐patterns‐based [Harchaoui and Bach, 2007; Shervashidze and Borgwardt, 2009], and limited‐size‐subgraph‐based [Horvath et al., 2004; Shervashidze et al., 2009] kernels. Graph kernel has been successfully applied to a variety of problems such as image classification [Camps‐Valls et al., 2010; Harchaoui and Bach, 2007], protein function prediction [Borgwardt et al., 2005; Zhang et al., 2011b], etc. More recently, some researchers also applied graph kernel for neuroimaging studies. For example, Mokhtari et al. adopted the graph kernel to discriminate between attentional cueing task and rest states from functional connectivity networks [Mokhtari et al., 2012; Shahnazian et al., 2012].
Weisfeiler‐Lehman subtree kernel
We first introduce the notations of graph kernel. A graph is an ordered pair comprising a set V of vertices together with a set E of edges. An undirected graph is one in which edges have no orientation. A labeled graph is a graph whose vertices are each assigned with an element from an alphabet L. A walk is a finite sequence of neighboring vertices, while a path is a walk such that all its vertices are distinctive. A subtree is a subgraph of a graph, which has no cycles (i.e., any two vertices are connected by exactly one simple path). Subtree pattern extends the notion of subtree by allowing repetitions of nodes and edges. However, these same nodes (edges) are treated as distinct nodes (edges). Figure 3 illustrates some examples for these notations. It is worth noting that (1) the subtree kernel between two graphs is computed using the derived subtree patterns, rather than their subtrees, (2) the graph used in this article is the undirected graph.
Figure 3.
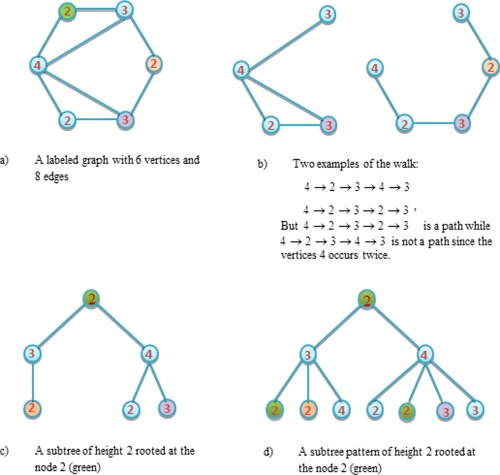
Example of some notations about graph. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Graph kernel is one kind of kernel constructed on graphs that measures the topological similarity between graphs. More formally, given a pair of graphs G and H, a graph kernel can be defined as , which takes into account the topology of graphs G and H. Typical graph kernels measure the common subgraph such as paths and walks [Harchaoui and Bach, 2007; Ramon and Gärtner, 2003]. Recently, Shervashidze et al. [2011] proposed an effective subtree‐based method to construct the graph kernel. The key concept of their graph kernel is based on the Weisfeiler‐Lehman test of isomorphism. Given two graphs, the basic process of the 1‐dimensional Weisfeiler‐Lehman test is as follows: if these two graphs are unlabeled graph, that is, vertices of the graph have not been assigned labels, every vertex in each graph is first labeled with the number of edges that are connected to that vertex. Then, at each subsequent step (or iteration), the label of each vertex is updated based on its previous label and the label of its neighbors, that is, parallelly augment the label of each vertex in the graph with the sorted set of node labels of neighboring nodes, and compress these augmented labels into new, shorter labels. This process proceeds iteratively until the node label sets of the two graphs differ, or the number of iteration reaches its predefined maximum value, h. If the sets of new created labels are identical after h iterations, we cannot determine whether these two graphs are isomorphic.
Give a pair of graphs G and H, let be the set of initial labels of G and H, and be the set of letters that occurs as node labels in G and H at the end of the i‐th iteration of the Weisfeiler‐Lehaman test of isomorphism. Assume all are pairwise disjointed. Without loss of generality, assume every is ordered, then the Weisfeiler‐Lehman subtree kernel of two graphs is defined as [Shervashidze et al., 2011]:
| (4) |
where
and
with and are the number of occurrences of the letter in G and H, respectively. It can be proved that this kind of kernel is positive definite and the computational complexity for N graphs is [Shervashidze et al., 2011], where n and l are the numbers of nodes and edges of graphs, respectively.
Figure 4 illustrates the construction process of the Weisfeiler‐Lehman subtree kernel with h = 1. Here, is considered as the set of letters. It is worth noting that the compressed labels denote the subtree patterns. For instance, for a node on graph G, if the compressed label is 10, that means there is a subtree pattern of height 1 rooted at this node, where the root has the label 3 and its neighbors have the labels of 2, 3, and 4, respectively. Intuitively, the Weisfeiler‐Lehman subtree kernel accounts for the original and compressed labels (i.e., the subtree patterns) in two graphs. According to this definition, the graph kernel embeds local and global graph topological information into kernel. In our method, we compute the graph kernel based on the above definition on a pair of connectivity networks that are thresholded at same level across different subjects, as shown in Figure 2.
Figure 4.
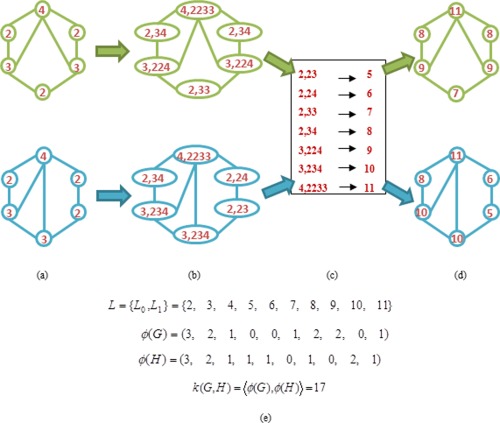
Illustration of the construction process of the Weisfeiler‐Lehman subtree kernel with h = 1 for two graphs G and H. Here, (a) the initial labeled graph G and H, (b) augmented labels on graph G and H, (c) label compression, (d) relabeled graph G and H, and (e) computation of the kernel on Graph G and H. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Feature Extraction
In machine learning and image processing, feature extraction and feature selection are a special form of dimensionality reduction. Feature extraction is a dimensionality reduction approach that projects (linear or nonlinear) D‐dimensional vector onto d‐dimensional vector ( ), while feature selection is an approach that selects a small subset of original features. The aim of feature extraction and feature selection is to prevent the curse of dimensionality problem [Guyon and Elisseeff, 2003] and to identify the relevant features that leads to better performance of learning models.
In the connectivity networks (matrices), there exist a large number of low level features (i.e., , where n is the total number of ROIs) but with small subject size. To reduce the dimension of data and to find out the biomarkers for MCI diagnosis, it is crucial to extract meaningful features from the connectivity networks. The connectivity networks can be characterized at different levels, ranging from properties characterizing a whole network at global scale to properties of network components at local scale [Kaiser, 2011; Rubinov and Sporns, 2010]. Since our aim is to identify MCI patients from NC, the weighted clustering coefficient [Rubinov and Sporns, 2010], which conveys the topological information of single node as well as the weighted information of adjacent edges, was extracted from connectivity network. However, since functional connectivity networks are intrinsically fully connected, to reflect different levels of topological structure of the original connectivity network, we simultaneously threshold the connectivity network with different predefined values.
Given the connectivity network (matrix) , and the threshold , the connectivity network was thresholded by using the following formulation:
| (5) |
where n and M are the numbers of ROIs and thresholds, respectively. Therefore, for each given threshold , we can obtain a new connectivity network , which will be used for subsequent feature extraction.
The clustering coefficient, a local measure of individual node, was extracted from the thresholded network as [Rubinov and Sporns, 2010]:
| (6) |
where is the number of neighboring node around node i. These extracted clustering coefficients were treated as features and used for subsequent feature selection.
It is worth noting that (1) for each thresholded connectivity network, each node (ROI) corresponds to one feature, hence there are totally n features, (2) for each subject, there are totally M different thresholded connectivity networks, and therefore we totally extract M groups of features, as shown in Figure 1.
Feature Selection
In our studies, we adopted a two‐stage feature selection strategy. Specifically, a standard t‐test, which has been widely used in the neuroimaging analysis, was first performed to screen out those features that are not significant for discrimination between MCI patients and NC. For instance, given training subjects, the P‐value of each feature was first computed via t‐test, and those features with P‐value larger than a given threshold will be omitted. Furthermore, to preserve the topological information of connectivity networks in feature selection, we used graph‐kernel based recursive feature elimination (RFE‐GK) for further selection of discriminative ROI features.
In the standard RFE method, linear or RBF kernel is used for SVM classification, without considering the topological information of network. Since each feature corresponds to a ROI or node, a subnetwork can be constructed according to the selected features (ROIs) in the previous feature selection step (i.e., t‐test). Then, the graph kernel, instead of conventional linear or RBF kernel, was used to preserve the network topological information. Figure 2 illustrates the flowchart of the proposed RFE‐GK approach. Specifically, for each thresholded connectivity network, we performed the following steps. First, we set the features selected at the first feature selection step (i.e., t‐test) as the initial surviving features, and used them to construct the subnetwork with corresponding connections in the thresholded connectivity network. Then, for each node s in subnetwork, we removed it from the network and computed graph kernel on the new subnetworks (i.e., after removing s‐th node and corresponding edges) to measure the topological similarity between different subjects. Next, a SVM classifier with the above computed graph kernel was trained on training subjects through leave‐one‐out (LOO) cross‐validation. Feature (ROI) that is the least important for classification will be removed from the surviving features set. The process was repeated until the surviving feature set is empty. Algorithm 1 illustrates the detailed procedure of the proposed RFE‐GK method.
Algorithm 1. Recursive Feature Elimination with Graph Kernel (RFE‐GK).
Input:
Training subjects and threshold , where is the i‐th connectivity network, is corresponding class label, and N is the number of training subjects.
Output:
Selected features (ROIs)
Initialize:
Subset of surviving features (ROIs) , ranked feature (ROI) list , and average accuracy list ; Here d is the number of surviving features in previous feature selection step;
Construct the thresholded network with threshold for connectivity network ,
Repeat
Initialize a temporary list ;
For each
Let ;
For each pair of and , , construct two sub‐networks using set , and compute the graph kernel on two sub‐networks;
Train SVM via LOO cross‐validation and get the accuracy c,
Update list
End for
Find s * with corresponding maximum accuracy, and update ranked feature list F=[s *,F];
Update the average accuracy list , where is the average accuracy of C;
Eliminate s * from S
Until
Find with corresponding maximum average accuracy in U. Assuming that is the P‐th value in U, we then select top P features in F as selected features
It is worth noting that our proposed RFE‐GK method is different from the standard RFE‐SVM [Guyon et al., 2002], which eliminates features through ranking based on weight vector of a linear SVM. In our proposed method, features are eliminated based on classification accuracy in a wrapper‐like approach. Moreover, there are two other key differences between the proposed method and the standard RFE‐SVM, that is, (1) the former uses graph kernel that preserves the topological (structural) information of data while the latter uses standard kernel on vector‐type data without considering the structural information and (2) the former can automatically determine a group of stable features, as well as its number, by computing the maximum average accuracy, while the latter needs to decide the number of features by using other approach.
Classification
Finally, in the classification step, a linear SVM classifier was adopted to identify MCI patients from NC by using the features selected in the feature selection step. To deal with multiple thresholded connectivity networks available in each subject, we used multikernel SVM technique [Zhang and Shen, 2012a; Zhang et al., 2011a] to combine multiple kernels constructed from different thresholded connectivity networks. Given a series of training connectivity networks represented as with corresponding class labels , , where N is the number of training subjects. Generally, the mixed kernel can be learned through a linear combination of multiple basis kernels as below:
| (7) |
where is a basis kernel, and are two selected features for training subjects and on the m‐th thresholded connectivity network, respectively, and is a nonnegative weighting parameter with . Different from the existing multikernel learning methods [Kloft et al., 2011; Sonnenburg et al., 2006] that jointly optimize the weighting parameter together with other SVM parameters, we adopted a coarse‐grid search approach through cross‐validation on the training samples to determine the optimal . After obtaining the optimal , the multiple kernels will be combined into a mixed kernel, and standard SVM will be then performed to identify the MCI patients from NC.
Implementation Details
In our study, we adopted the LOO cross‐validation to evaluate the performance of classifier. Specifically, for all subject samples, one was left out for testing, and the remaining were used for training (see Fig. 1). This entire process was repeated for each subject, thereby yielding an unbiased estimate of classification error rate. In the proposed classification framework, each brain image was parcellated into 90 ROIs, where a connectivity network was then constructed according to these ROIs. Five different values (i.e., T = [0.20,0.30,0.38,0.40,0.45], with 0.38 as the average value of connectivity strength between all ROIs across all training subjects), were used to threshold the connectivity network. The corresponding average connection density (i.e., the fraction of present connections to possible connections) of each threshold is located in interval [40% 75%], which is to some extent consistent to the average connection density interval of [25% 75%] used in [Zanin et al., 2012], which demonstrated higher classification performance. Moreover, 90 features were extracted from each thresholded connectivity network. For each extracted feature , we adopted a common feature normalization scheme, that is, , where and are respectively the mean and standard deviation of the i‐th feature across all training subjects. Here, and will be used to normalize the corresponding feature of each test subject.
For feature selection step, a statistical t‐test was first performed with five different thresholds for five different thresholded networks, respectively. In our experiment, the P‐values were learned based on the training subjects via the inner LOO cross‐validation. Specifically, at each LOO cross‐validation, we varied P‐value with [0.05 0.08 0.10 0.12 0.15] and computed the classification accuracy on training subjects via the inner LOO cross‐validation. The P‐value with the best classification performance (on the inner LOO cross‐validation) will then be used. Afterwards, our proposed RFE‐GK method was performed to select the most discriminative ROI features. Here, the SVM was implemented based on the LIBSVM library [Chang and Lin, 2001], by using the default parameter values (i.e., C = 1). At the classification step, the optimal weighting parameter was learned based on the training subjects through a grid search, using the range from 0 to 1 at a step size of 0.1, via another LOO cross‐validation.
It is worth noting that the nested LOO cross‐validation strategy used enhances the generalization power of the classifier. For example, the inner cross‐validation loop was performed on the training data to determine certain parameters while the outer cross‐validation loop was used to evaluate the generalizability of SVM models using unseen subjects.
RESULTS
Comparison on Classification Performance
In our experiments, we evaluated the performance of different methods by measuring the classification accuracy, sensitivity, specificity, area under receiver operating characteristic (ROC) curve (AUC), and balanced classification accuracy. Specifically, the accuracy measures the proportion of subjects that are correctly predicted among all subjects, the sensitivity represents the proportion of patients that are correctly predicted, and the specificity denotes the proportion of NC that are correctly predicted. The ROC curve is a plot of the sensitivity [Sen(c)] versus 1‐specificity [1‐Spe(c)] over all possible values (c) of the marker. Besides, to avoid the possible inflated performance estimation on the unbalanced datasets, we also compute the balanced classification accuracy, which can be defined as the arithmetic mean of sensitivity and specificity. Classification performances of the proposed and other connectivity‐network‐based methods are summarized in Table 2. Figure 5 shows the ROC curves of different methods. Here, we compared our method with several feature selection methods including: (1) t‐test, (2) hybrid t‐test and standard RFE‐SVM [including both linear kernel (RFE‐LK) and RBF kernel (RFE‐RBF)], that is, a t‐test was first performed and then followed by the standard RFE‐SVM to select the most discriminative features. For further comparison, we also combined all 90‐dimensional feature vectors extracted from five thresholded connectivity networks into a long 540 (=5 × 90) dimensional feature vector, and then perform different hybrid feature selections (i.e., t‐test and standard RFE‐SVM), denoted as VEC‐RFE‐LK and VEC‐RFE‐RBF corresponding to the linear and RBF kernels, respectively. Finally, standard SVM is performed on the above selected features for classification. It is worth noting that (1) all experiments were performed via LOO cross‐validation, (2) in both Table 2 and Figure 5, “combined” denotes methods using all thresholded connectivity networks, while T 1, T 2, T 3, T 4, and T5 denote methods only using one individual thresholded connectivity network.
Table 2.
Classification performance of different methods
| Methods | T 1 | T 2 | T 3 | T 4 | T 5 | Combined | |
|---|---|---|---|---|---|---|---|
| ACC (%) | VEC‐RFE‐LK | – | – | – | – | – | 83.8 |
| VEC‐RFE‐RBF | – | – | – | – | – | 73.0 | |
| t‐test | 75.7 | 78.4 | 64.9 | 64.9 | 64.9 | 81.1 | |
| RFE‐RBF | 78.4 | 73.0 | 67.6 | 73.0 | 78.4 | 86.5 | |
| RFE‐LK | 83.8 | 70.3 | 64.9 | 78.4 | 64.9 | 86.5 | |
| RFE‐GK | 86.5 | 83.8 | 75.7 | 75.7 | 64.9 | 91.9 | |
| BAC (%) | VEC‐RFE‐LK | – | – | – | – | – | 83.7 |
| VEC‐RFE‐RBF | – | – | – | – | – | 71.4 | |
| t‐test | 75.5 | 77.5 | 61.0 | 61.0 | 61.0 | 81.7 | |
| RFE‐RBF | 73.2 | 71.4 | 56.5 | 62.7 | 71.0 | 85.7 | |
| RFE‐LK | 85.9 | 67.2 | 58.9 | 75.4 | 61.0 | 87.9 | |
| RFE‐GK | 87.9 | 81.5 | 71.2 | 73.4 | 61.0 | 94.0 | |
| SEN (%) | VEC‐RFE‐LK | – | – | – | – | – | 83.3 |
| VEC‐RFE‐RBF | – | – | – | – | – | 66.7 | |
| t‐test | 75.0 | 75.0 | 50.0 | 50.0 | 50.0 | 83.3 | |
| RFE‐RBF | 58.3 | 66.7 | 25.0 | 33.3 | 50.0 | 83.3 | |
| RFE‐LK | 91.7 | 58.3 | 41.7 | 66.7 | 50.0 | 91.7 | |
| RFE‐GK | 91.7 | 75.0 | 58.3 | 66.7 | 50.0 | 100.0 | |
| SPE (%) | VEC‐RFE‐LK | – | – | – | – | – | 84.0 |
| VEC‐RFE‐RBF | – | – | – | – | – | 76.0 | |
| t‐test | 76.0 | 80.0 | 72.0 | 72.0 | 72.0 | 80.0 | |
| RFE‐RBF | 88.0 | 76.0 | 88.0 | 92.0 | 92.0 | 88.0 | |
| RFE‐LK | 80.0 | 76.0 | 76.0 | 84.0 | 72.0 | 84.0 | |
| RFE‐GK | 84.0 | 88.0 | 84.0 | 80.0 | 72.0 | 88.0 | |
| AUC | VEC‐RFE‐LK | – | – | – | – | – | 0.85 |
| VEC‐RFE‐RBF | – | – | – | – | – | 0.79 | |
| t‐test | 0.84 | 0.86 | 0.74 | 0.71 | 0.68 | 0.86 | |
| RFE‐RBF | 0.68 | 0.77 | 0.75 | 0.65 | 0.76 | 0.83 | |
| RFE‐LK | 0.87 | 0.82 | 0.70 | 0.79 | 0.72 | 0.89 | |
| RFE‐GK | 0.85 | 0.86 | 0.77 | 0.78 | 0.60 | 0.94 |
Note: T 1, T 2, T 3, T 4 and T 5 denote using the individual thresholded connectivity network, respectively, while “combined” denotes using all thresholded connectivity networks; ACC represents classification accuracy; BAC represents balanced accuracy of classification; AUC represents the area under receiver operating characteristic curve; SEN represents sensitivity; SPE represents specificity; VEC‐RFE‐LK and VEC‐RFE‐RBF represent the hybrid feature selection with the t‐test and standard RFE‐SVM on combined feature vector, using linear kernel and RBF kernel, respectively; t‐test represents the feature selection method based on statistic t‐test; RFE‐LK and RFE‐RBF represent the hybrid feature selection methods with t‐test and standard RFE‐SVM, using linear kernel and RBF kernel, respectively; RFE‐GK represents the proposed feature selection method.
Figure 5.
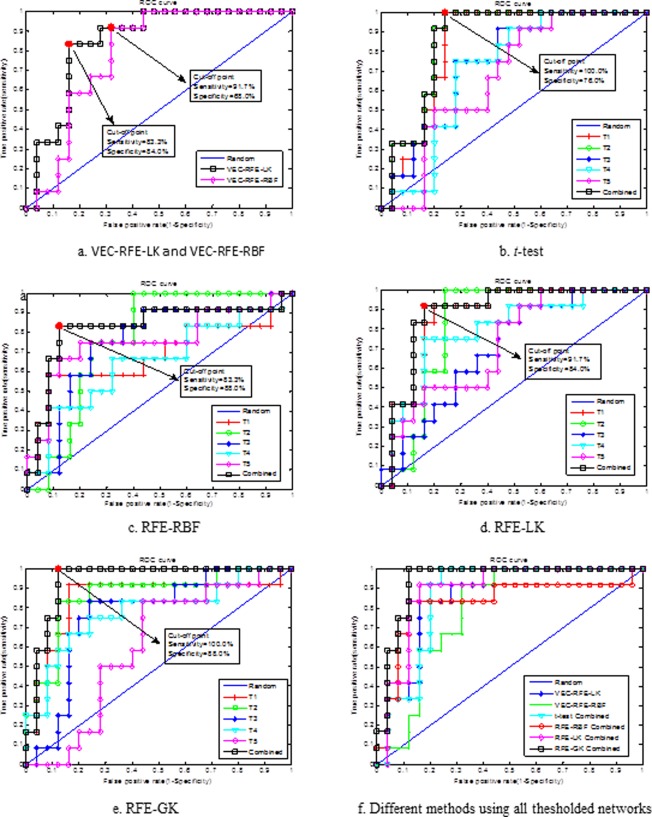
ROC curves of different methods. (a–e) Show the ROC curve of each feature selection method when using single thresholded connectivity network or all thresholded connectivity networks. (f) Shows the ROC curves of different feature selection methods when using all thresholded connectivity networks, for better comparison of their performances. Here, T1, T2, T3, T4, and T5 denote, respectively, using single thresholded connectivity. The red dot denotes the cut‐off point corresponding to the Youden index. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
As can be seen from Table 2 and Figure 5, the proposed method performs the best in all performance measures including the classification accuracy, balanced accuracy, sensitivity, specificity, and AUC value. Specifically, our method achieves a classification accuracy of 91.9%, a balanced accuracy of 94.0%, an AUC of 0.94, and a sensitivity of 100.0%, while for other connectivity‐network‐based feature selection methods, the best accuracy is only 86.5%, the best balanced accuracy is 87.9%, the best AUC is 0.89, and the best sensitivity is 91.7%. Obviously, by including the topological information through graph kernel, our proposed method achieves consistently better performance than the existing methods. In addition, it is worth noting that our method achieves a perfect sensitivity, that is, it successfully classified all the MCI patients. Table 2 also indicates that the combination of multiple thresholded connectivity networks performed significantly better than using any single thresholded connectivity network alone.
Moreover, Table S2 in the Supporting Information gives the classification results on each test subject as well as the combination weights of five thresholded connectivity networks. In addition, to investigate further the generalizability of the obtained SVM classifier, we recorded the number of support vectors (SVs) after the learning process. Table S3 in the Supporting Information gives the number of SVs used in each LOO cross‐validation of each method. As we can see from Supporting Information Table S3, our proposed method achieves the smallest average number of SVs compared with other methods.
Finally, we further employed other statistical measures to evaluate the diagnostic power of the various methods. Specifically, we used Yonden index (J) [Fluss et al., 2005], positive predictive value (PPV), and negative predictive value (NPV):
where TP, TN, FP, and FN denote true positive, true negative, false positive, and false negative, respectively. Table 3 summarizes these statistical measures of different methods at the point of Yonden index, and Figure 5 plots the cut‐off point corresponding to the Youden index for different methods. As can be seen from both Table 3 and Figure 5, our proposed method achieves the best performance on all above statistical measures.
Table 3.
Statistical measures of performance of different methods at the point of Yonden index
| Methods | J | TP | FP | PPV (%) | NPV (%) |
|---|---|---|---|---|---|
| VEC‐RFE‐LK | 0.67 | 10 | 4 | 71.4 | 91.3 |
| VEC‐RFE‐RBF | 0.60 | 11 | 8 | 57.9 | 94.4 |
| t‐test | 0.76 | 12 | 6 | 66.7 | 100.0 |
| RFE‐RBF | 0.71 | 10 | 3 | 76.9 | 91.7 |
| RFE‐LK | 0.76 | 11 | 4 | 73.3 | 95.5 |
| RFE‐GK | 0.88 | 12 | 3 | 80.0 | 100.0 |
The Most Discriminative Regions
In this subsection, we evaluated the discriminative power of the selected features. Since the selected features are different in each LOO cross‐validation fold, we choose those features with the highest occurrence frequency in all LOO cross‐validation as the most discriminative features for classification.
Table 4 shows the top twelve ROIs with the highest frequency in different thresholded connectivity networks. The result shows that the most discriminative regions obtained using our proposed method include the inferior temporal gyrus, anterior cingulate gyrus, amygdala, insula, orbitofrontal cortex, heschl gyrus, rectus gyrus, and precentral gyrus, which are consistent with previous studies. Figure 6 shows the top 19 ROIs that are selected from all thresholded networks, as listed in Table 4.
Table 4.
Top selected ROIs
| T 1 | T 2 | T 3 |
|---|---|---|
| L olfactory cortex | L inferior temporal gyrus | L anterior cingulate gyrus |
| R inferior temporal gyrus | L olfactory cortex | L olfactory cortex |
| L inferior temporal gyrus | R inferior temporal gyrus | R middle cingulate |
| L anterior cingulate gyrus | R gyrus rectus | L amygdala |
| R supramarginal gyrus | R amygdala | L calcarine sulcus |
| L supplementary motor area | R precentral gyrus | R olfactory cortex |
| L orbital part of inferior frontal gyrus | L gyrus rectus | L middle cingulate |
| L gyrus rectus | L orbital part of inferior frontal gyrus | R inferior temporal gyrus |
| R gyrus rectus | L supplementary motor area | L orbital part of inferior frontal gyrus |
| R amygdale | R supramarginal gyrus | R amygdala |
| R precentral gyrus | L anterior cingulate gyrus | L heschl gyrus |
| R anterior cingulate gyrus | R anterior cingulate gyrus | L gyrus rectus |
| T 4 | T 5 | All |
| L olfactory cortex | L amygdala | R precentral gyrus |
| R middle cingulate | R middle cingulate | L orbital part of inferior frontal gyrus |
| R olfactory cortex | L orbital part of inferior frontal gyrus | L supplementary motor area |
| L gyrus rectus | L olfactory cortex | L olfactory cortex |
| L anterior cingulate gyrus | R olfactory cortex | R olfactory cortex |
| L amygdala | L gyrus rectus | L gyrus rectus |
| R inferior temporal gyrus | L anterior cingulate gyrus | R gyrus rectus |
| L orbital part of inferior frontal gyrus | R inferior temporal gyrus | L insula |
| R amygdala | R anterior cingulate gyrus | L anterior cingulate gyrus |
| L inferior temporal gyrus | L insula | R anterior cingulate gyrus |
| L calcarine sulcus | L inferior temporal gyrus | L middle cingulate |
| R anterior cingulate gyrus | L calcarine sulcus | R middle cingulate |
| L amygdale | ||
| R amygdale | ||
| L calcarine sulcus | ||
| R supramarginal gyrus | ||
| L heschl gyrus | ||
| L inferior temporal gyrus | ||
| R inferior temporal gyrus |
Note: T 1, T 2, T 3, T 4, and T 5 denote, respectively, using single thresholded connectivity network, while “All” denotes the ROIs from all thresholded connectivity networks; L and R represent left and right, respectively.
Figure 6.
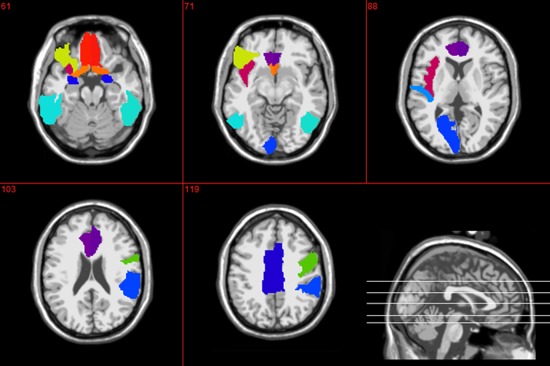
Top 19 regions that were selected using the proposed method. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
To visualize the discriminative power of the selected features, the locality preserving projection (LPP) approach [Belkin and Niyogi, 2002; He and Niyogi, 2003] that preserves the intrinsic geometrical structure of the data and implicitly emphasizes the natural clusters in the data (i.e., it makes the neighboring points in the ambient space nearer in the reduced representation space, and far away points in the ambient space further in the reduced representation space) was adopted to project the selected features into a 2‐D space. Specifically, for each feature selection method we selected the top 12 features with the highest frequency in LOO cross‐validation and then projected them into a 2‐D space using LPP. Figure S1 in the Supporting Information shows the 2‐D visualization results of LPP approach. As can be seen from Supporting Information Figure S1, feature selection methods enhance the discriminative ability of the selected features compared with the whole feature set.
The Connectivity Analysis
To analyze the connectivity strength between selected ROIs and to visually show the differences on connectivity networks for MCI patients and NC, we computed the average connectivity network based on all 19 ROIs selected in Table 4. Specifically, for each group, an average connectivity network was constructed based on all 19 selected ROIs with the connection as the average of weights (i.e., connectivity strength) of corresponding edge in connectivity networks for subjects in the same group. Figure 7 graphically shows the average connectivity networks (matrix). Colors in Figure 7a,b represent connectivity strength, while colors in Figure 7c represent the connectivity strength difference between MCI and NC groups on certain ROIs. As can be seen from Figure 7, in most cases the connectivity strengths in MCI group are smaller than those in NC group.
Figure 7.
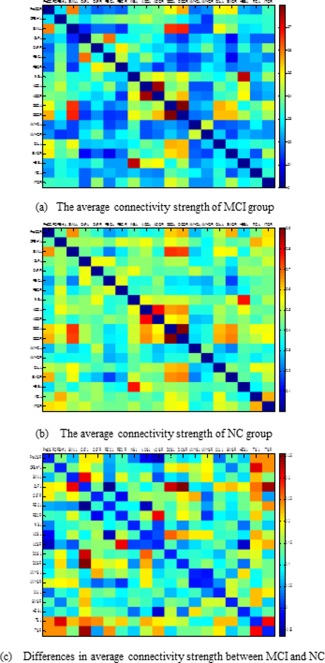
Visualization on average connectivity networks (matrices) constructed using 19 selected ROIs in Table 3. Here, colors in (a) and (b) represent the connectivity strength, while the color in (c) represents the difference of connectivity strength between MCI and NC. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
However, to visualize the topology of network for MCI and NC, an average connectivity subnetwork was constructed for each group, according to the selected ROIs in each thresholded connectivity network. Moreover, the threshold value that was used to threshold connectivity network was also used to threshold the corresponding average connectivity subnetwork. Figure 8 shows those thresholded averaged connectivity subnetworks. Each red node denotes a brain ROI, and the edge denotes the connectivity between ROI pairs. The thickness of edge is proportional to the weight of edge between ROI pairs, and T 1, T 2, T 3, T 4, and T5 denotes the individual thresholded connectivity network, respectively. Compared with NC group, we can observe significant reduction in connections in the MCI group. These results suggest possible disruptions in connectivity between these regions, as reported in previous studies.
Figure 8.
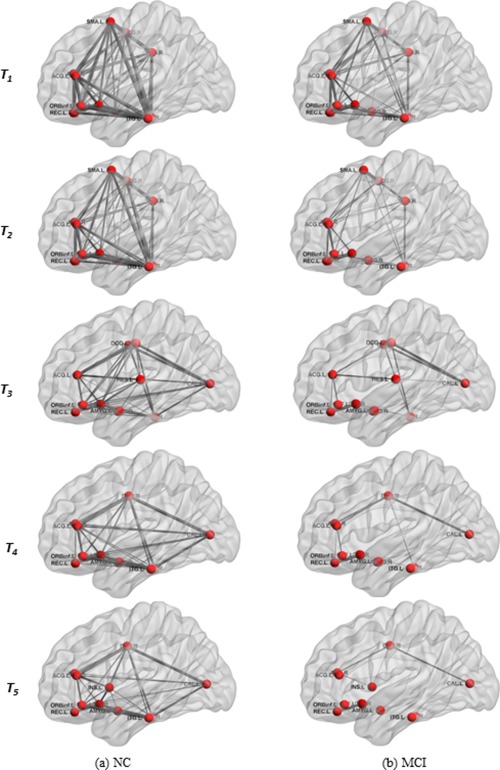
Thresholded average connectivity subnetwork based on top 12 selected ROIs (as listed in Table 3) for NC (a) and MCI (b) groups. T1, T2, T3, T4, and T5 denote using ROIs from the corresponding thresholded connectivity network. (PCG.R = R precentral gyrus, ORBinf.L = L orbital part of inferior frontal gyrus, SMA.L = L supplementary motor area, OLF.L = L olfactory cortex, OLF.R = R olfactory cortex, REC.L = L gyrus rectus, REC.R = R gyrus rectus, INS.L = L insula, ACG.L = L anterior cingulate gyrus, ACG.R = R anterior cingulate gyrus, MCG.L = L middle cingulate, MCG.R = R middle cingulate, AMYG.L = L amygdala, AMYG.R = R amygdala, CAL.L = L calcarine sulcus, SMG.R = R supramarginal gyrus, HES.L = L heschl gyrus, ITG.L = L inferior temporal gyrus, ITG.R = R inferior temporal gyrus; L = Left, R = Right). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
DISCUSSION
In this article, we proposed a connectivity networks‐based classification framework to identify automatically the MCI patients from NC. The key of the proposed method involves the use of a new topological graph kernel‐based approach to select the most discriminative features for classification. The classification performance was evaluated via LOO cross‐validation to ensure the generalization of classifier. The obtained results show that our proposed method can significantly improve the classification performance of the connectivity‐network based classification method.
Significance of Results
Recently, connectivity‐network‐based classification methods have been proposed for diagnosis of neurodegenerative diseases. However, the topological information from network, which may potentially further improve prediction accuracy, is not fully utilized in the existing connectivity‐based classification methods. Our study demonstrated that, by including the topological information, the proposed method can achieve much improved performance in identifying MCI subjects from NC. In particular, our method can achieve a perfect sensitivity (i.e., correctly classifying all MCI subjects) compared with other methods (for example, in [Wang et al., 2013] a sensitivity of 86.5% is obtained, and in [Chen et al., 2011] a sensitivity of 93% is obtained). This is important for clinical applications because there are different costs for misclassifying a normal person to be a patient, compared with the case of misclassifying a patient to be a healthy person. Obviously, compared with the former, the latter may cause more severe consequences and thus has higher misclassification cost. Hence, it is advantageous for a classifier to provide higher sensitivity rate.
The regions selected in the course of classification by our method are in agreement with previous studies, which include the inferior temporal gyrus [Han et al., 2011; Lenzi et al., 2011], anterior cingulate gyrus [Davatzikos et al., 2011; Grady et al., 2003; Han et al., 2011], amygdala [Davatzikos et al., 2011], insula [Davatzikos et al., 2011; Grady et al., 2003], orbitfrontal cortex [Han et al., 2011; Wee et al., 2012a], heschl gyrus [Liu et al., 2012b], rectus gyrus [Wee et al., 2012b], and precentral gyrus [Lenzi et al., 2011]. However, we also analyzed the connectivity between the selected brain regions and found that the MCI patients have lower functional connectivity when compared with the healthy subjects. This finding is consistent with previous studies. For example, Bai et al. [2011] explored the properties of whole‐brain networks and found the evidence of reduced connectivity in the MCI group. Wang et al. [2013] investigated the topological architecture of the functional connectome in MCI patients and found abnormal structure as shown by an increase of characteristic path length and impaired functional connectivity between different functional modules. Supekar et al. [2008] reported that AD patients had reduced clustering in the brain functional networks. Other studies suggested a loss in small‐world characteristics (i.e., high degree of clustering and short path length) in subjects with MCI and AD [Liu et al., 2012b; Sanz‐Arigita et al., 2010; Yao et al., 2010]. These changes in connectivity may further indicate that some ROIs are affected by the disease and their functional connectivity between ROIs are thus disrupted, which is consistent with the evidences of early functional abnormalities in MCI patients [Feng et al., 2012; Liu et al., 2012b; Wang et al., 2013]. Therefore, it is reasonable to speculate that these decreased connectivity led to decreased functional integration and information processing capability of the brain, which may account for cognitive deficits in patients.
Overall, our results show that the proposed method can automatically and effectively identify the MCI patients from NC, and provide empirical evidence for disrupted network organization in MCI at nodal and connectional levels.
Functional Connectivity Network and Identification of MCI
Functional connectivity analysis is a technique for in vivo examination of brain regions cooperating during rest or task performance and provides a measure of the temporal correlation between neurophysiological activities in different brain regions [Bai et al., 2009; Friston et al., 1996]. Recent studies have shown that higher cognitive processing is not isolated to specific brain regions, but instead resulting from the interactions of different brain regions [Bai et al., 2009; Huang et al., 2010]. Numerous studies have suggested that the neurodegenerative diseases such as AD and MCI are related to a large‐scale, highly connected functional network, rather than solely on one single isolated region [Damoiseaux et al., 2012; Filippi and Agosta, 2011; Grady et al., 2001; Kiuchi et al., 2009; Kuceyeski et al., 2012; Liu et al., 2012a; Rose et al., 2000; Sanz‐Arigita et al., 2010; Stam, 2010; Xie and He, 2011; Xie et al., 2006]. Therefore, this concept provides an important alternative to make use of the characteristics of functional connectivity to identify the AD or MCI patients from NC, and to understand better the underpinnings of MCI and AD pathology.
Recently, some works on identifying MCI based on extracting features from connectivity network have been reported [Chen et al., 2011; Wee et al., 2011, 2012a,b]. For example, in [Wee et al., 2012a] a multispectrum approach was proposed to characterize the blood oxygenation level dependent (BOLD) signals with multiple frequency sub‐bands, where local clustering coefficients were then extracted from these networks as features for classification. Also, in [Chen et al., 2011] the averaged low‐frequency BOLD signal time course was computed for 116 ROIs, and the Pearson product moment correlation coefficients of pairwise ROIs were used to classify subjects. As can be seen from Table 4, the proposed method achieves the best accuracy.
Effect of Feature Extraction and Selection
Traditional algorithms used in machine learning are often susceptible to the well‐known problem of the curse of dimensionality [Guyon and Elisseeff, 2003]. In these situations, it is often beneficial to reduce the dimension of the data to improve the efficiency and accuracy of data analysis. In addition, from a statistical point of view it is desirable that the number of training subjects should significantly exceed the number of features. In theory, the number of subjects needs to be increased exponentially with the number of features if inference is to be made about the data [Cunningham, 2008]. Feature extraction and selection, which are often applied as a data pre‐processing step or part of the data analysis to simplify the data model, are the two most commonly used approaches for dimensionality reduction. In this study, we adopted both approaches to pre‐process our data to improve the performance of classifier and to find out the biomarkers for identifying MCI from NC.
To evaluate the effect of feature extraction and selection, we performed three additional experiments. (1) Without feature extraction from connectivity network and without feature selection (Exp 1). Specifically, we directly converted the connectivity network (matrix) into a vector, instead of extracting features from connectivity network. Then a linear SVM was trained to classify the MCI from NC based on the aligned vectors. (2) Without feature extraction from connectivity network (matrix) but with feature selection (Exp 2). Specifically, we converted the connectivity network (matrix) into a vector, and a simple feature selection method based on statistic t‐test was performed. Then, a linear SVM was used to classify the MCI patients from NC. (3) With feature extraction but without feature selection (Exp 3). Specifically, the features (i.e., the clustering coefficient) were first extracted from the thresholded connectivity network before they were combined into a long vector and used for MCI classification. The experimental results are summarized in Table 6. As can be seen from Table 6, the method in the first experiment obtains the worst classification performance, because of the following disadvantages: (1) the aligned vectors have huge features (here 90 × 89/2 = 4005), which may cause the problem of overfitting on training; (2) some useful information (e.g., topology) of connectivity is lost in matrix‐to‐vector transformation. The results in the second experiment are the best, indicating that the feature selection can improve the classification accuracy. These three methods are, however, inferior to the proposed method, indicating the importance of employing both feature extraction and feature selection.
Table 6.
Classification performance without‐feature‐extraction and/or without‐feature‐selection
| Experiment | ACC (%) | BAC (%) | AUC |
|---|---|---|---|
| Exp 1 | 64.86 | 48.00 | 0.50 |
| Exp 2 | 70.27 | 65.00 | 0.80 |
| Exp 3 | 64.86 | 48.00 | 0.56 |
Table 5.
Comparison on classification performance of different functional connectivity network based methods
Effect of Threshold
In AD/MCI studies threshold‐based method has been used for exploring topological properties of functional connectivity network [Liu et al., 2012b; Sanz‐Arigita et al., 2010; Supekar et al., 2008]. To determine an appropriate threshold, network properties are often explored over a range of thresholds. For example, Supekar et al. [2008] adopted thresholds ranging from 0.01 to 0.99 with an increment of 0.01 to explore the “small‐world” properties of functional connectivity networks in AD. Recently, Zanin et al. [2012] proposed an approach to determine the best threshold by exploring the classification performance on the whole range of applicable thresholds. Compared with the single threshold based methods, our method has the following advantages; (1) avoiding testing over a range of thresholds to find the optimal one: (2) combining network properties from multiple thresholded networks for classification by using the multiple‐kernel learning technique.
To investigate the effect of threshold on final classification performance, we performed the following experiment on nonthresholded networks. Specifically, we first extracted features (i.e., the local clustering coefficients) directly from the original connectivity network (i.e., nonthresholded connectivity networks). Then, we performed the hybrid feature selection (i.e., t‐test and standard RFE‐SVM with linear kernel) to select the most discriminative features. Finally, a linear SVM was trained for classification. The obtained classification accuracy is 72.9%, with a balanced accuracy of 67.0% and an AUC value of 0.82. Obviously, these results are much lower than those of our methods as shown in Table 2, which validates the efficacy of our proposed multithreshold approach for functional connectivity network based classification.
Effect of Image Preprocessing Step
In this subsection, we investigate the effect of image preprocessing step for final classification. First, to check whether motion parameters are the same in the two groups (i.e., MCI patients and NC), we performed two‐sample t‐test on the six standard head motion parameters between patient and control groups. The results show that the head motion profiles are matched between two groups (P > 0.2182 in any direction), and none of the subjects in the study have a displacement >3 mm and an angular rotation >3 degrees in any direction. Furthermore, the mean motion metric, as mentioned in [Van Dijk et al., 2012], has been used to evaluate the head motion between two groups, and no significant (P > 0.05) difference was observed based on two‐sample t‐test.
Then, we performed another set of experiments on the same dataset but using the image preprocessing steps descriebd in [Van Dijk et al., 2012], except for global signal regression due to controversy in this preprocessing step. The details of image preprocessing are provided in the Supporting Information. In the experiments, we adopted the same setting as before except for using different sets of thresholds T = [0.0, 0.1, 0.15, 0.2, 0.25]. The corresponding average connection density of these thresholds is located in the interval [38%, 65%]. In the Supporting Information, Table S4 gives the classification results, and Supporting Information Table S5 shows the top twelve selected ROIs in five thresholded connectivity networks.
As can be seen from Supporting Information Table S4 and Table 2, overall two different image‐preprocessing steps achieve comparable performances in terms of classification accuracy and balanced accuracy. Significant improvements can still be observed when using different image‐preprocessing method, which confirms that our proposed method performs better than the compared methods. In addition, comparing Supporting Information Table S5 with Table 4, we find that the most of discriminative regions obtained with two different preprocessing steps are consistent.
Limitations
This study is limited by following factors. First, during the network construction, the definition of nodes and edges is a critical step. Previous studies have demonstrated that network nodes can be defined using both anatomical and/or functional brain atlases and image voxels, but the constructed network exhibited significantly different topological properties [Hayasaka and Laurienti, 2010; He and Evans, 2010; Sanabria‐Diaz et al., 2010; Wang et al., 2009; Zalesky et al., 2010]. This study does not analyze the impact of different brain parcellation atlases on classification performance. Second, the performance of our proposed method may be affected by the unbalanced data. A classifier will normally try to adapt itself for better prediction of the majority class. Although the sensitivity has been improved by our proposed method, the proposed framework at its current stage is not designed to handle this issue. Full investigation focusing on handling unbalanced data will be our future work. Third, in our study, we investigated only the classification between MCI and NC, and did not test the ability of the proposed framework to identify AD from NC, and more importantly the multiclass classification of AD, MCI, and NC. Many multiclass classification methods are available [Duda et al., 2001] and can be tested, which will be our future work. Another limitation of our current study is the limited sample size. In the future, we will evaluate our proposed method with larger dataset.
CONCLUSION
In this article, we have proposed a connectivity networks‐based classification framework to identify automatically MCI patients from NC. The core of the proposed method involves a novel topological graph kernel based feature selection method. Specifically, the graph kernel was used to measure the topological similarity between two networks of subjects. Moreover, multiple thresholds were used to threshold the functional connectivity network, and multiple kernel learning approach was adopted to combine features that were selected from multiple thresholded connectivity subnetworks. Experimental results show not only the significant improvement of classification performance in terms of accuracy, AUC value, and sensitivity, but also the great potential of our method in detecting ROIs and functional connectivity that are sensitive to disease pathology.
Supporting information
Supporting Information
This article was published online on 13 September 2013. An error was subsequently identified. This notice is included in the online and print versions to indicate that both have been corrected 20 March 2014.
References
- AASM (2007): The AASM Manual For The Scoring Of Sleep And Associated Events‐Rules, Terminology And Technical Specifcations. Chicago: American Academy of Sleep Medicine. [Google Scholar]
- Achard S, Bassett DS, Meyer‐Lindenberg A, Bullmore E (2008): Fractal connectivity of long‐memory networks. Phys Rev E Stat Nonlin Soft Matter Phys 77:036104. [DOI] [PubMed] [Google Scholar]
- Alvarez MA, Qi X, Yan C (2011): A shortest‐path graph kernel for estimating gene product semantic similarity. J Biomed Semantics 2:3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai F, Zhang Z, Watson DR, Yu H, Shi Y, Yuan Y, Zang Y, Zhu C, Qian Y (2009): Abnormal functional connectivity of hippocampus during episodic memory retrieval processing network in amnestic mild cognitive impairment. Biol Psychiatry 65:951–958. [DOI] [PubMed] [Google Scholar]
- Bai F, Liao W, Watson DR, Shi Y, Wang Y, Yue C, Teng Y, Wu D, Yuan Y, Jia J, Zhang Z (2011): Abnormal whole‐brain functional connection in amnestic mild cognitive impairment patients. Behav Brain Res 216:666–672. [DOI] [PubMed] [Google Scholar]
- Bai F, Shu N, Yuan YG, Shi YM, Yu H, Wu D, Wang JH, Xia MR, He Y, Zhang ZJ (2012): Topologically Convergent and divergent structural connectivity patterns between patients with remitted geriatric depression and amnestic mild cognitive impairment. J Neurosci 32:4307–4318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Bullmore ET (2009): Human brain networks in health and disease. Curr Opin Neurol 22:340–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belkin M, Niyogi P (2002): Laplacian eigenmaps and spectral techniques for embedding and clustering In: Dietterich TG, Becker S, Ghahramani Z, editors. Advances in Neural Information Processing Systems 14, Cambridge, MA: MIT Press. [Google Scholar]
- Borgwardt KM, Kriege H‐P (2005): Shortest‐path kernels on graphs. In Proceedings of the International Conference on Data Mining. pp 74–81, Houston, USA, November 27, 2005.
- Borgwardt KM, Ong CS, Schonauer S, Vishwanathan SVN, Smola AJ, Kriegel HP (2005): Protein function prediction via graph kernels. Bioinformatics 21:I47–I56. [DOI] [PubMed] [Google Scholar]
- Brookmeyer R, Johnson E, Ziegler‐Graham K, Arrighi HM (2007): Forecasting the global burden of Alzheimer's disease. Alzheimers Dement 3:186–191. [DOI] [PubMed] [Google Scholar]
- Buldu JM, Bajo R, Maestu F, Castellanos N, Leyva I, Gil P, Sendina‐Nadal I, Almendral JA, Nevado A, del‐Pozo F, Boccaletti S (2011): Reorganization of functional networks in mild cognitive impairment. PLoS One 6:e19584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busatto GF, Garrido GE, Almeida OP, Castro CC, Camargo CH, Cid CG, Buchpiguel CA, Furuie S, Bottino CM (2003): A voxel‐based morphometry study of temporal lobe gray matter reductions in Alzheimer's disease. Neurobiol Aging 24:221–231. [DOI] [PubMed] [Google Scholar]
- Camps‐Valls G, Shervashidze N, Borgwardt KM (2010): Spatio‐spectral remote sensing image classification with graph kernels. IEEE Geosci Remote Sensing Lett 7:741–745. [Google Scholar]
- Chang CC, Lin CJ (2001): LIBSVM: A library for support vector machines.
- Chen G, Ward BD, Xie C, Li W, Wu Z, Jones JL, Franczak M, Antuono P, Li SJ (2011): Classification of Alzheimer disease, mild cognitive impairment, and normal cognitive status with large‐scale network analysis based on resting‐state functional MR imaging. Radiology 259:213–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes D, Haughton VM, Arfanakis K, Carew JD, Turski PA, Moritz CH, Quigley MA, Meyerand ME (2001): Frequencies contributing to functional connectivity in the cerebral cortex in "resting‐state" data. AJNR. Am J Neuroradiol 22:1326–1333. [PMC free article] [PubMed] [Google Scholar]
- Craddock RC, Holtzheimer PE III, Hu XP, Mayberg HS (2009): Disease state prediction from resting state functional connectivity. Magn Reson Med 62:1619–1628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham P (2008): Dimension reduction. Machine Learning Techniques for Multimedia: Case Studies on Organization and Retrieval. Germany: Springer. pp 91–112.
- Damoiseaux JS, Prater KE, Miller BL, Greicius M.D (2012): Functional connectivity tracks clinical deterioration in Alzheimer's disease. Neurobiol Aging 33:828 e819–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davatzikos C, Bhatt P, Shaw LM, Batmanghelich KN, Trojanowski JQ (2011): Prediction of MCI to AD conversion, via MRI, CSF biomarkers, and pattern classification. Neurobiol Aging 32:2322 e2319–2327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delbeuck X, Van der LM, F., C. , 2003. Alzheimer's disease as a disconnection syndrome? Neuropsychol Rev 13:79–92. [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG: Pattern Classification. Wiley-Interscience, (2001). [Google Scholar]
- Feng Y, Bai L, Ren Y, Chen S, Wang H, Zhang W, Tian J (2012): FMRI connectivity analysis of acupuncture effects on the whole brain network in mild cognitive impairment patients. Magn Reson Imaging 30:672–682. [DOI] [PubMed] [Google Scholar]
- Filippi M, Agosta F (2011): Structural and functional network connectivity breakdown in Alzheimer's disease studied with magnetic resonance imaging techniques. J Alzheimers Dis 24:455–474. [DOI] [PubMed] [Google Scholar]
- Fjell AM, Walhovd KB, Fennema‐Notestine C, McEvoy LK, Hagler DJ, Holland D, Brewer JB, Dale AM (2010): CSF biomarkers in prediction of cerebral and clinical change in mild cognitive impairment and Alzheimer's disease. J Neurosci 30:2088–2101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fluss R, Faraggi D, Reiser B (2005): Estimation of the Youden Index and its associated cutoff point. Biom J 47:458–472. [DOI] [PubMed] [Google Scholar]
- Ford DE, Kamerow DB (1989): Epidemiologic study of sleep disturbances and psychiatric disorders. JAMA 262:1479–1484. [DOI] [PubMed] [Google Scholar]
- Fornito A, Zalesky A, Bullmore ET (2010): Network scaling effects in graph analytic studies of human resting‐state FMRI data. Front Syst Neurosci 4:22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Fletcher P, Liddle PF, Frackowiak RS (1996): Functional topography: Multidimensional scaling and functional connectivity in the brain. Cerebral cortex 6:156–164. [DOI] [PubMed] [Google Scholar]
- Gartner T, Flach PA, Wrobel S (2003): On graph kernels: Hardness results and efficient alternatives. Sixteenth Annual Conference on Computational Learning Theory and Seventh Kernel Workshop, COLT, Washington, DC,USA, August 24, 2003.
- Gould RL, Arroyo B, Brown RG, Owen AM, Bullmore ET, Howard RJ (2006): Brain mechanisms of successful compensation during learning in Alzheimer disease. Neurology 67:1011–1017. [DOI] [PubMed] [Google Scholar]
- Grady CL, Furey ML, Pietrini P, Horwitz B, Rapoport SI (2001): Altered brain functional connectivity and impaired short‐term memory in Alzheimer's disease. Brain 124:739–756. [DOI] [PubMed] [Google Scholar]
- Grady CL, McIntosh AR, Beig S, Keightley ML, Burian H, Black SE (2003):. Evidence from functional neuroimaging of a compensatory prefrontal network in Alzheimer's disease. J Neurosci 23:986–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V (2004): Default‐mode network activity distinguishes Alzheimer's disease from healthy aging: Evidence from functional MRI. Proc Natl Acad Sci USA 101:4637–4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Martinez O, Keller KE, Fletcher EM, Menon V, DeCarli C (2007): Reduced default mode network connectivity in patients with mild cognitive impairment. Neurology 68:A329–A329. [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF (2009). Resting‐state functional connectivity reflects structural connectivity in the default mode network. Cerebral cortex 19:72–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyon I, Elisseeff A (2003): An introduction to variable and feature selection. J Machine Learning Res 3:1157–1182. [Google Scholar]
- Guyon I, Weston J, Barnhill S, Vapnik V (2002): Gene selection for cancer classification using support vector machines. Machine Learn 46:389–422. [Google Scholar]
- Haller S, Nguyen D, Rodriguez C, Emch J, Gold G, Bartsch A, Lovblad KO, Giannakopoulos P (2010): Individual prediction of cognitive decline in mild cognitive impairment using support vector machine‐based analysis of diffusion tensor imaging data. J Alzheimers Dis 22:315–327. [DOI] [PubMed] [Google Scholar]
- Han Y, Wang J, Zhao Z, Min B, Lu J, Li K, He Y, Jia J (2011): Frequency‐dependent changes in the amplitude of low‐frequency fluctuations in amnestic mild cognitive impairment: A resting‐state fMRI study. Neuroimage 55:287–295. [DOI] [PubMed] [Google Scholar]
- Harchaoui Z, Bach F (2007): Image classification with segmentation graph kernels. IEEE Conference on Computer Vision and Pattern Recognition pp 1–8 612–619, Minneapolis, Minnesota, USA, June 18, 2007.
- Hayasaka S, Laurienti PJ (2010): Comparison of characteristics between region‐and voxel‐based network analyses in resting‐state fMRI data. Neuroimage 50:499–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Niyogi P (2003). Locality preserving projections. Proceedings Advances in Neural Information Processing Systems Conference, Vancouver and Whistler, Canada, December 8, 2003.
- He Y, Evans A (2010): Graph theoretical modeling of brain connectivity. Curr Opin Neurol 23:341–350. [DOI] [PubMed] [Google Scholar]
- He Y, Chen Z, Gong G, Evans A (2009): Neuronal networks in Alzheimer's disease. Neuroscientist: Review 15:333–350. [DOI] [PubMed] [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P (2009): Predicting human resting‐state functional connectivity from structural connectivity. Proc Natl Acad Sci USA 106:2035–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horvath T, Gartner T, Wrobel S (2004): Cyclic pattern kernels for predictive graph mining. In Proceedings of the International Conference on Knowledge Discovery and DataMining, Seattle, WA, USA, August 22, 2004.
- Huang SA, Li J, Sun L, Ye JP, Fleisher A, Wu T, Chen KW, Reiman E, Initia ADN (2010): Learning brain connectivity of Alzheimer's disease by sparse inverse covariance estimation. Neuroimage 50:935–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser M (2011): A tutorial in connectome analysis: Topological and spatial features of brain networks. Neuroimage 57:892–907. [DOI] [PubMed] [Google Scholar]
- Kashima H, Tsuda K, Inokuchi A (2003): Marginalized kernels between labeled graphs. In Proceedings of the 20‐th International Conference on Machine Learning (ICML). Washington, DC, USA, August 21, 2003.
- Kiuchi K, Morikawa M, Taoka T, Nagashima T, Yamauchi T, Makinodan M, Norimoto K, Hashimoto K, Kosaka J, Inoue Y, Inoue M, Kichikawa K, Kishimoto T (2009): Abnormalities of the uncinate fasciculus and posterior cingulate fasciculus in mild cognitive impairment and early Alzheimer's disease: A diffusion tensor tractography study. Brain Res 1287:184–191. [DOI] [PubMed] [Google Scholar]
- Kloft M, Brefeld U, Sonnenburg S, Zien A (2011): l(p)‐Norm Multiple Kernel Learning. J Machine Learn Res 12:953–997. [Google Scholar]
- Kuceyeski A, Zhang Y, Raj A (2012): Linking white matter integrity loss to associated cortical regions using structural connectivity information in Alzheimer's disease and fronto‐temporal dementia: The Loss in Connectivity (LoCo) score. Neuroimage 61:1311–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenzi D, Serra L, Perri R, Pantano P, Lenzi GL, Paulesu E, Caltagirone C, Bozzali M, Macaluso E (2011): Single domain amnestic MCI: A multiple cognitive domains fMRI investigation. Neurobiol Aging 32:1542–1557. [DOI] [PubMed] [Google Scholar]
- Li SJ, Li Z, Wu GH, Zhang MJ, Franczak M, Antuono PG (2002): Alzheimer disease: Evaluation of a functional MR imaging index as a marker. Radiology 225:253–259. [DOI] [PubMed] [Google Scholar]
- Liu Z, Zhang Y, Bai L, Yan H, Dai R, Zhong C, Wang H, Wei W, Xue T, Feng Y, You Y, Tian J (2012a). Investigation of the effective connectivity of resting state networks in Alzheimer's disease: A functional MRI study combining independent components analysis and multivariate Granger causality analysis. NMR Biomed 25:1311–1320. [DOI] [PubMed] [Google Scholar]
- Liu Z, Zhang Y, Yan H, Bai L, Dai R, Wei W, Zhong C, Xue T, Wang H, Feng Y, You Y, Zhang X, Tian J (2012b): Altered topological patterns of brain networks in mild cognitive impairment and Alzheimer's disease: A resting‐state fMRI study. Psychiatry Res 202:118–125. [DOI] [PubMed] [Google Scholar]
- Mokhtari F, Bakhtiari SK, Hossein‐Zadeh GA, Soltanian‐Zadeh H (2012): Discriminating between brain rest and attention states using fMRI connectivity graphs and subtree SVM. SPIE Med Imaging. [Google Scholar]
- Morbelli S, Drzezga A, Perneczky R, Frisoni G, Caroli A, Van Berckel BN, Ossenkoppele R, Guedj E, Didic M, Brugnolo A, Sambuceti G, Rodriguez G, Nobili F (2010): Resting‐state brain metabolic connectivity in amnestic MCI‐AD converters and healthy controls. A joint project of the European Alzheimer's Disease Consortium (EADC). Eur J Nuclear Med Mol Imaging 37:S259–S260. [Google Scholar]
- Palop JJ, Chin J, Mucke L (2006): A network dysfunction perspective on neurodegenerative diseases. Nature 443:768–773. [DOI] [PubMed] [Google Scholar]
- Petersen RC, Doody R, Kurz A, Mohs RC, Morris JC, Rabins PV, Ritchie K, Rossor M, Thal L, Winblad B (2001): Current concepts in mild cognitive impairment. Arch Neurol 58:1985–1992. [DOI] [PubMed] [Google Scholar]
- Petrella JR, Sheldon FC, Prince SE, Calhoun VD, Doraiswamy PM (2011): Default mode network connectivity in stable vs progressive mild cognitive impairment. Neurology 76:511–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pievani M, Agosta F, Galluzzi S, Filippi M, Frisoni GB (2011): Functional networks connectivity in patients with Alzheimer's disease and mild cognitive impairment. J Neurol 258:170–170. [Google Scholar]
- Ramon J, Gärtner T (2003): Expressivity versus efficiency of graph kernels. Trees and sequences. Technical report, First International Workshop on Mining Graphs.
- Richiardi J, Gschwind M, Simioni S, Annoni JM, Greco B, Hagmann P, Schluep M, Vuilleumier P, Van De Ville D (2012): Classifying minimally disabled multiple sclerosis patients from resting state functional connectivity. Neuroimage 62:2021–2033. [DOI] [PubMed] [Google Scholar]
- Robinson EC, Hammers A, Ericsson A, Edwards AD, Rueckert D (2010): Identifying population differences in whole‐brain structural networks: A machine learning approach. Neuroimage 50:910–919. [DOI] [PubMed] [Google Scholar]
- Rose SE, Chen F, Chalk JB, Zelaya FO, Strugnell WE, Benson M, Semple J, Doddrell DM (2000): Loss of connectivity in Alzheimer's disease: An evaluation of white matter tract integrity with colour coded MR diffusion tensor imaging. J Neurol Neurosurg Psychiatry 69:528–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010): Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 52:1059–1069. [DOI] [PubMed] [Google Scholar]
- Sanabria‐Diaz G, Melie‐Garcia L, Iturria‐Medina Y, Aleman‐Gomez Y, Hernandez‐Gonzalez G, Valdes‐Urrutia L, Galan L, Valdes‐Sosa P (2010). Surface area and cortical thickness descriptors reveal different attributes of the structural human brain networks. Neuroimage 50:1497–1510. [DOI] [PubMed] [Google Scholar]
- Sanz‐Arigita EJ, Schoonheim MM, Damoiseaux JS, Rombouts SA, Maris E, Barkhof F, Scheltens P, Stam, C.J. , 2010. Loss of 'small‐world' networks in Alzheimer's disease: Graph analysis of FMRI resting‐state functional connectivity. Plos One 5:e13788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholkopf B, Smola A (2002): Learning with Kernels. The MIT Press. [Google Scholar]
- Seeley WW, Crawford RK, Zhou J, Miller BL, Greicius MD (2009): Neurodegenerative diseases target large‐scale human brain networks. Neuron 62:42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahnazian D, Mokhtari F, Hossein‐Zadeh G (2012): A method based on the granger causality and graph kernels for discriminating resting state from attentional task. Int Conf Biomed Eng 83–88. [Google Scholar]
- Shen D, Davatzikos C (2002): HAMMER: Hierarchical attribute matching mechanism for elastic registration. IEEE Trans Med Imaging 21:1421–1439. [DOI] [PubMed] [Google Scholar]
- Shen H, Wang LB, Liu YD, Hu DW (2010): Discriminative analysis of resting‐state functional connectivity patterns of schizophrenia using low dimensional embedding of fMRI. Neuroimage 49:3110–3121. [DOI] [PubMed] [Google Scholar]
- Shervashidze N, Borgwardt KM (2009): Fast subtree kernels on graphs. Adv Neural Inform Process Syst 22:1660–1668. [Google Scholar]
- Shervashidze N, Vishwanathan SVN, Petri T, Mehlhorn K, Borgwardt KM (2009): Efficient graphlet kernels for large graph comparison. In Proceedings of International Conference on Artificial Intelligence and Statistics, Florida, USA, April 16, 2009. [Google Scholar]
- Shervashidze N, Schweitzer P, van Leeuwen EJ, Mehlhorn K, Borgwardt KM (2011): Weisfeiler‐Lehman Graph Kernels. J Machine Learn Res 12:2539–2561. [Google Scholar]
- Sonnenburg S, Ratsch G, Schafer C, Scholkopf B (2006): Large scale multiple kernel learning. J Machine Learn Res 7:1531–1565. [Google Scholar]
- Sperling RA, Bates JF, Chua EF, Cocchiarella AJ, Rentz DM, Rosen BR, Schacter DL, Albert MS (2003). fMRI studies of associative encoding in young and elderly controls and mild Alzheimer's disease. J Neurol Neurosurg Psychiatry 74:44–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperling RA, Aisen PS, Beckett LA, Bennett DA, Craft S, Fagan AM, Iwatsubo T, Jack CR, Kaye J, Montine TJ, Park DC, Reiman EM, Rowe CC, Siemers E, Stern Y, Yaffe K, Carrillo MC, Thies B, Morrison‐Bogorad M, Wagster MV, Phelps CH (2011): Toward defining the preclinical stages of Alzheimer's disease: Recommendations from the National Institute on Aging‐Alzheimer's Association workgroups on diagnostic guidelines for Alzheimer's disease. Alzheimers Dementia 7:280–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O (2011): From simple graphs to the connectome: Networks in neuroimaging. Neuroimage 62:881–886. [DOI] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Kotter R (2005): The human connectome: A structural description of the human brain. Plos Comput Biol 1:245–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam CJ (2010): Use of magnetoencephalography (MEG) to study functional brain networks in neurodegenerative disorders. J Neurol Sci 289:128–134. [DOI] [PubMed] [Google Scholar]
- Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P (2007): Small‐world networks and functional connectivity in Alzheimer's disease. Cerebral Cortex 17:92–99. [DOI] [PubMed] [Google Scholar]
- Stam CJ, de Haan W, Daffertshofer A, Jones BF, Manshanden I, van Cappellen van Walsum AM, Montez T, Verbunt JP, de Munck JC, van Dijk BW, Berendse HW, Scheltens P (2009): Graph theoretical analysis of magnetoencephalographic functional connectivity in Alzheimer's disease. Brain 132:213–224. [DOI] [PubMed] [Google Scholar]
- Stern Y (2006). Cognitive reserve and Alzheimer disease. Alzheimer Dis Assoc Disord 20:112–117. [DOI] [PubMed] [Google Scholar]
- Supekar K, Menon V, Rubin D, Musen M, Greicius MD (2008): Network analysis of intrinsic functional brain connectivity in Alzheimer's disease. Plos Comput Biol 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, von Wegner F, Morzelewski A, Borisov S, Jahnke K, Laufs H (2012): Automatic sleep staging using fMRI functional connectivity data. Neuroimage 63:63–72. [DOI] [PubMed] [Google Scholar]
- Tzourio‐Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M (2002): Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single‐subject brain. Neuroimage 15:273–289. [DOI] [PubMed] [Google Scholar]
- Van Dijk KRA, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL (2010): Intrinsic functional connectivity as a tool for human connectomics: Theory, properties, and optimization. J Neurophysiol 103:297–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk KRA, Sabuncu MR, Buckner RL (2012): The influence of head motion on intrinsic functional connectivity MRI. Neuroimage 59:431–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vishwanathan SVN, Schraudolph NN, Kondor R, Borgwardt KM (2010): Graph Kernels. J Machine Learn Res 11:1201–1242. [Google Scholar]
- Wang J, Wang L, Zang Y, Yang H, Tang H, Gong Q, Chen Z, Zhu C, He Y (2009): Parcellation‐dependent small‐world brain functional networks: A resting‐state fMRI study. Hum Brain Mapp 30:1511–1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Zuo X, Dai Z, Xia M, Zhao Z, Zhao X, Jia J, Han Y, He Y (2013): Disrupted functional brain connectome in individuals at risk for Alzheimer's disease. Biol Psychiatry 73:472–481. [DOI] [PubMed] [Google Scholar]
- Wang K, Jiang T, Liang M, Wang L, Tian L, Zhang X, Li K, Liu Z (2006a): Discriminative analysis of early Alzheimer's disease based on two intrinsically anti‐correlated networks with resting‐state fMRI. Med Image Comput Comput Assist Interv 340–347. [DOI] [PubMed] [Google Scholar]
- Wang K, Liang M, Wang L, Tian L, Zhang X, Li K, Jiang T (2007): Altered functional connectivity in early Alzheimer's disease: A resting‐state fMRI study. Hum Brain Mapp 28:967–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Zang Y, He Y, Liang M, Zhang X, Tian L, Wu T, Jiang T, Li K (2006b): Changes in hippocampal connectivity in the early stages of Alzheimer's disease: Evidence from resting state fMRI. Neuroimage 31:496–504. [DOI] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Li W, Denny K, Browndyke JN, Potter GG, Welsh‐Bohmer KA, Wang L, Shen D (2011): Enriched white matter connectivity networks for accurate identification of MCI patients. Neuroimage 54:1812–1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Denny K, Browndyke JN, Potter GG, Welsh‐Bohmer KA, Wang LH, Shen DG (2012a): Resting‐state multi‐spectrum functional connectivity networks for identification of MCI patients. PLoS One 7:e37828. doi: 10.1371/journal.pone.0037828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Zhang DQ, Denny K, Browndyke JN, Potter GG, Welsh‐Bohmer KA, Wang LH, Shen DG (2012b). Identification of MCI individuals using structural and functional connectivity networks. Neuroimage 59:2045–2056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie S, Xiao JX, Gong GL, Zang YF, Wang YH, Wu HK, Jiang XX (2006): Voxel‐based detection of white matter abnormalities in mild Alzheimer disease. Neurology 66:1845–1849. [DOI] [PubMed] [Google Scholar]
- Xie T, He Y (2011): Mapping the Alzheimer's brain with connectomics. Front Psychiatry 2:77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao Z, Zhang Y, Lin L, Zhou Y, Xu C, Jiang T (2010): Abnormal cortical networks in mild cognitive impairment and Alzheimer's disease. Plos Comput Biol 6:e1001006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye JP, Wu T, Li J, Chen KW (2011): Machine Learning Approaches for the Neuroimaging Study of Alzheimer's Disease. Computer 44:99–101. [Google Scholar]
- Zalesky A, Fornito A, Harding IH, Cocchi L, Yucel M, Pantelis C, Bullmore ET (2010): Whole‐brain anatomical networks: Does the choice of nodes matter? Neuroimage 50:970–983. [DOI] [PubMed] [Google Scholar]
- Zanin M, Sousa P, Papo D, Bajo R, Garcia‐Prieto J, del Pozo F, Menasalvas E, Boccaletti S (2012): Optimizing functional network representation of multivariate time series. Sci Rep 2:630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Wang Y, Zhou L, Yuan H, Shen D (2011a): Multimodal classification of Alzheimer's disease and mild cognitive impairment. Neuroimage 55:856–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Shen D (2012a): Multi‐modal multi‐task learning for joint prediction of multiple regression and classification variables in Alzheimer's disease. Neuroimage 59:895–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Shen D (2012b): Predicting future clinical changes of MCI patients using longitudinal and multimodal biomarkers. Plos One 7:e33182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Lin H, Yang Z, Li Y (2011b): Neighborhood hash graph kernel for protein‐protein interaction extraction. J Biomed Inform 44:1086–1092. [DOI] [PubMed] [Google Scholar]
- Zhou C, Zemanova L, Zamora G, Hilgetag CC, Kurths J (2006): Hierarchical organization unveiled by functional connectivity in complex brain networks. Phys Rev Lett 97:238103. [DOI] [PubMed] [Google Scholar]
- Zhou L, Wang Y, Li Y, Yap PT, Shen D (2011): Hierarchical anatomical brain networks for MCI prediction: Revisiting volumetric measures. Plos One 6:e21935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo XN, Di Martino A, Kelly C, Shehzad ZE, Gee DG, Klein DF, Castellanos FX, Biswal BB, Milham MP (2010): The oscillating brain: Complex and reliable. Neuroimage 49:1432–1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


