Theoretical comparison of wall-derived and erythrocyte-derived mechanisms for metabolic flow regulation in heterogeneous microvascular networks

Abstract

The objective of this study is to compare the effectiveness of metabolic signals derived from erythrocytes and derived from the vessel wall for regulating blood flow in heterogeneous microvascular networks. A theoretical model is used to simulate blood flow, mass transport, and vascular responses. The model accounts for myogenic, shear-dependent, and metabolic flow regulation. Metabolic signals are assumed to be propagated upstream along vessel walls via a conducted response. Arteriolar tone is assumed to depend on the conducted metabolic signal as well as local wall shear stress and wall tension, and arteriolar diameters are calculated based on vascular smooth muscle mechanics. The model shows that under certain conditions metabolic regulation based on wall-derived signals can be more effective in matching perfusion to local oxygen demand relative to regulation based on erythrocyte-derived signals, resulting in higher extraction and lower oxygen deficit. The lower effectiveness of the erythrocyte-derived signal is shown to result in part from the unequal partition of hematocrit at diverging bifurcations, such that low-flow vessels tend to receive a reduced hematocrit and thereby experience a reduced erythrocyte-derived metabolic signal. The model simulations predict that metabolic signals independent of erythrocytes may play an important role in local metabolic regulation of vascular tone and flow distribution in heterogeneous microvessel networks.

local flow regulation at the microvascular level enables the cardiovascular system to maintain adequate perfusion throughout tissue under conditions of varying metabolic demand (10, 25). Disruption of flow regulation mechanisms can lead to areas of inadequate oxygen delivery and impaired oxygen extraction (30). Local control of blood flow is achieved by variations in the degree of contraction (tone) of vascular smooth muscle in vessel walls, particularly in arterioles, resulting in diameter changes.

Several factors influence vascular tone. Hemodynamic factors include responses to wall shear stress as well as changes in transmural pressure. Increases in wall shear stress are sensed by endothelial cells and typically result in vasodilation (decreased tone), whereas increases in transmural pressure lead to vasoconstriction (increased tone) due to the myogenic response (23). Metabolic factors also affect tone. Arterioles typically respond to hypoxia by vasodilation, with multiple mechanisms thought to be responsible for this effect. Metabolites including ATP, NO, and potassium are typically released in response to hypoxia. The rate of release of ATP from erythrocytes has been found to be inversely related to hemoglobin saturation, supporting the hypothesis that erythrocytes act as oxygen sensors (12). Other potential sources for metabolic signals include parenchymal cells, which release vasodilatory substances under conditions of hypoxia, and the vessel wall (22). Possible metabolites arising from tissue include carbon dioxide (resulting in decreased pH) and adenosine, a breakdown product of ATP (4). Endothelial cells also release metabolites under hypoxic conditions, including NO, prostaglandins, EDHF, and adenosine. Another possible mechanism involves a direct effect of hypoxia on smooth muscle cell function causing vasodilation (28).

As well as acting locally, vasoactive stimuli can generate responses that are propagated upstream and lead to constriction or dilation of the vessels that supply the region experiencing a metabolic stimulus. These conducted responses play an essential role in coordinating changes in arteriolar diameters so that blood flow can be modulated according to the metabolic needs of the tissue (3, 26, 27).

The contributions of these various mechanisms to regulation of blood flow in skeletal muscle and their effects on oxygen delivery have previously been investigated using a theoretical model that assumes homogeneous network properties (1, 6). In this “representative segment” model, all vessels of a given class are considered to have identical characteristics. Real microvascular networks, however, exhibit significant heterogeneity, which leads to substantial variations in convective and diffusive oxygen transport and may cause local mismatch between metabolism and perfusion. The structural heterogeneity of microvascular networks results in multiple parallel flow pathways with various lengths, leading to the possibility of shunting or maldistribution of blood flow if regulatory mechanisms are stressed or impaired (18, 19). For example, administration of adenosine leads to increased blood flow and vasodilation but decreased extraction in working muscle (5). As another example, sepsis results in a state of increased overall blood flow but with impaired regulation and decreased oxygen extraction, leading to tissue hypoxia and organ failure (14). Other mechanisms related to heterogeneity in consumption and delivery include the sequential activation of microvascular units in skeletal muscle and capillary recruitment with increasing workload (13).

The objective of this study is to compare the effectiveness of signals derived from erythrocytes and signals derived from the vessel wall for the metabolic regulation of blood flow in a microvascular network with a realistic heterogeneous structure. In such networks, non-uniform partition of erythrocytes and plasma (phase separation) occurs at diverging microvascular bifurcations, resulting in non-uniform hematocrit distribution. Therefore, a further objective is to explore the effect of phase separation on flow regulation by the erythrocyte-dependent mechanism. A theoretical model for microvessel networks that simulates blood flow, mass transport, and vascular responses including myogenic, shear-dependent, and metabolic effects is used.

METHODS

Network structure.

Previous theoretical models of flow regulation in microvascular networks have generally assumed either a single flow pathway or multiple identical flow pathways in parallel (1, 6, 8, 29). For example, Fig. 1A shows the representative segment model used by Arciero et al. (1) to simulate flow regulation in skeletal muscle. In that model, several compartments are connected in series, and each compartment consists of a number of identical segments connected in parallel. In the present study, the model is modified by replacing the small arteriole, capillary, and small venule compartments with a heterogeneous network structure derived from detailed experimental observations of rat mesentery (20), as shown in Figs. 1B and 2. This network contains 388 nodes and 546 segments. Arterial and venous segments are connected to the main inlet and outlet vessels of these networks to form a complete flow pathway through the tissue, including larger vessels that are also capable of active flow regulation. Addition of these segments results in a network with 392 nodes and 550 segments.

Fig. 1.

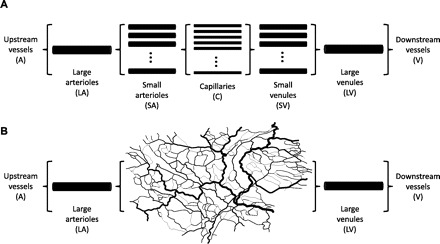
Schematic illustration of network models for blood flow regulation. A: representative segment model used in previous analysis (1). B: modified representative segment model used in present study. Small arterioles, capillaries, and small venules are replaced by a heterogeneous network derived from observations of rat mesentery.

Fig. 2.

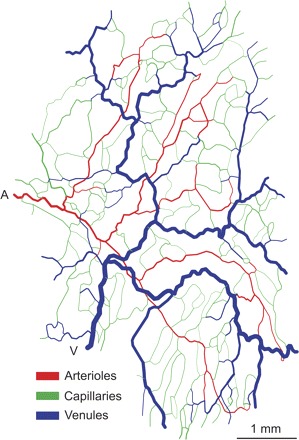
Microvascular network used in simulations, derived from observations of rat mesentery. Red, regulating, oxygen-exchanging segments (arterioles); green, nonregulating oxygen-exchanging segments (generally capillaries); blue, nonregulating non-oxygen-exchanging segments (venules); A, main arteriolar inflow; V, main venular outflow.

For the purposes of the model, all vessels in the network are designated as one of three types: arterioles, capillaries, and venules. The morphological designation, which does not coincide with the topological classification used in previous studies (17), is used to ensure that the arterioles constitute a single connected tree and are sufficiently large to possess vascular smooth muscle. Vessels smaller than a specified cutoff diameter (8.4 μm) (31) are identified as capillaries. All arterial vessels above this diameter comprising a contiguous tree are classified as arterioles and assumed to be vasoactive, with active responses as described below. Similarly, all venous vessels above this diameter comprising a contiguous tree are classified as venules. Arterioles and capillaries are assumed to participate in oxygen exchange. Capillaries and venules are assumed to act as fixed flow resistances (1). The resulting distribution of arterioles, capillaries, and venules in the network is shown in Fig. 2.

The mesentery typically shows little or no activity with regard to acute flow regulation. However, similarly comprehensive structural data sets for microvascular networks in more vasoactive tissues such as skeletal muscle are not currently available. It is therefore assumed here that the structural heterogeneity observed in mesenteric networks is representative of that present in skeletal muscle. Values of oxygen consumption characteristic of skeletal muscle are used in conjunction with this network structure for simulations of hemodynamics and oxygen transport.

Hemodynamics.

Flow through the network is initially calculated assuming a prescribed flow at the main inlet vessel and a prescribed pressure at the main outflow vessel. Flow conditions at other boundary nodes are considered to be proportional to the arterial inflow. Internal node pressures are calculated iteratively at each time step by imposing conservation of mass at each node, with flows calculated in each segment assuming Poiseuille's law with an effective viscosity dependent on vessel hematocrit and segment diameter (21). Phase separation is assumed to take place at each diverging bifurcation. The dependence of hematocrit in each daughter vessel on the segment flow and diameters and the hematocrit in the parent vessel is based on previously developed empirical relationships (16). Because segment flow resistance depends on hematocrit, the flow and hematocrit distributions are interdependent. Flows and hematocrits are therefore calculated using an iterative method. Inlet and outlet pressure values are initially set to 100 and 12.91 Torr, respectively, representing normal perfusion. At each time step, the pressure drop across the network is adjusted to maintain a desired rate of network perfusion.

Flow regulation.

The arterioles are assumed to regulate flow by myogenic, shear-dependent, and metabolic mechanisms. Metabolic signals generated in all vessels are propagated upstream to the arterioles via conducted responses. The diameter of each regulating segment is represented as a function of time by a model that incorporates vessel wall mechanics and vascular smooth muscle tone (1, 6). Key features of this model are that the vasoactive signal for tone generation depends on the balance between competing vasodilator and vasoconstrictor stimuli and that the level of vascular smooth muscle activation has maximal and minimal levels, with saturating behavior at high net levels of vasodilator or vasoconstrictor signals. For each arteriolar segment, the wall tension is assumed to consist of a passive component T_pass and an active component T_act such that

$$T_{\text{total}}=T_{\text{pass}}+A\cdot T_{\text{act}}^{\max }$$ (1)

where the activation A characterizes the level of vascular tone. The values of A satisfy 0 ≤ A ≤ 1, where A = 0 represents absence of vascular tone and A = 1 represents maximal vasoconstriction. For a vessel of diameter D, the passive wall tension component T_pass is given by

$$T_{\text{pass}}=C_{\text{pass}}\exp \left[C_{\text{pass}}^{\prime }\left(D/D_0-1\right)\right]$$ (2)

where C_pass and C′_pass are constants, and D₀ represents the passive vessel diameter at a pressure of 100 Torr (6). The active component T_act^max generated by the vascular smooth muscle in each vessel is given by

$$T_{\text{act}}^{\max }=C_{\text{act}}\exp \left[-{\left(\frac{D/D_0-C_{\text{act}}^{\prime }}{C_{\text{act}}^{″}}\right)}^2\right]$$ (3)

where C_act, C′_act, and C′′_act are parameters characterizing the active component of the myogenic response (6). The dependence of activation on vasoactive signals is expressed by introducing a target activation A_total where

$$A_{\text{total}}=\frac{1}{1+\exp \left(-S_{\text{tone}}\right)}$$ (4)

The total vasoactive signal S_tone represents the net effects of the myogenic, shear-dependent, and metabolic responses on vascular smooth muscle tone:

$$S_{\text{tone}}=C_{\text{myo}}{T}_{\text{cur}}-C_{\text{shear}}{\tau }_{\text{wall}}-S_{\text{CR}}+C_{\text{tone}}^{″}$$ (5)

where S_CR represents the conducted (metabolic) response signal, τ_wall is the wall shear stress, and C_myo, C_shear, and C′′_tone are constants (1, 7). Here, T_cur = PD/2 is the current wall tension, where P is the average intravascular pressure.

The time-dependent behavior of the diameter D and activation A in each segment are calculated by integrating the system

$$\frac{\text{d}D}{\text{d}t}=\frac{1}{{\tau }_{\text{d}}}\frac{D_{\text{c}}}{T_{\text{c}}}\left(T_{\text{cur}}-T_{\text{total}}\right)$$ (6)

$$\frac{\text{d}A}{\text{d}t}=\frac{1}{{\tau }_{\text{a}}}\left(A_{\text{total}}-A\right)$$ (7)

where τ_d and τ_a are the respective time constants for changes in D and A and the subscript c refers to the control state (6). In some cases, these solutions approach steady-state behavior, but oscillatory behavior is also possible (2).

Oxygen transport.

Oxygen consumption for each arterial and capillary segment is calculated using zero-order kinetics for a surrounding tissue sleeve of width 18.8 μm, resulting in a linear decrease in oxygen saturation along the length of each vessel. The width of the sleeve corresponds to an overall capillary density of 500 mm⁻², typical of skeletal muscle (1). A fixed rate of oxygen consumption is assumed per length of vessel, until oxygen is fully depleted. The Hill equation is used to estimate oxygen saturation as a function of Po₂. Dissolved oxygen is not considered. No oxygen exchange is assumed to take place in venous segments, resulting in constant saturation along each venous segment. For vessels entering the network, arbitrarily chosen values for Po₂ are assigned according to vessel type: Po₂ = 50 Torr is used for venular inlet vessels, Po₂ = 75 Torr for capillaries, and Po₂ = 100 Torr for small arterioles as well as the feed artery. Oxygen demand M is fixed at a baseline value of 8.28 ml O₂·100 ml⁻¹·min⁻¹, corresponding to moderate exercise (1).

Conducted metabolic response.

Metabolic signals are assumed to be generated in all segments by two alternative mechanisms: ATP release by erythrocytes (12) and signals originating from vessel walls. In either case, signals are assumed to be conducted upstream to the arterioles, where they influence the generation of vascular tone (12). In the erythrocyte-dependent mechanism, the conducted metabolic signal for each segment is determined by the mean local ATP concentration, C_ATP. In the wall-dependent mechanism, the signal is assumed to be a decreasing function of the local oxygen tension, P_O2^mid. The local metabolic signal S_loc is thus:

$$S_{\text{loc}}=C_{\text{rbc}}^{\text{meta}}\cdot C_{\text{ATP}}+C_{\text{wall}}^{\text{meta}}\cdot C_{\text{ATP}}^{\text{0}}\cdot \frac{P_0}{P_0+P_{{\text{O}}_2}^{\text{mid}}}$$ (8)

where C_rbc^meta and C_wall^meta are parameters describing the strength of the responses to the two types of signal, and C_ATP⁰ (representing arterial inflow ATP concentration) serves as a scaling factor for C_wall^meta. The parameter P₀ gives the level of oxygen tension at which a half-maximal, wall-derived signal is generated. A value of 1 Torr is assumed, corresponding to the estimated Michaelis constant for tissue oxygen consumption (24). Under this assumption, the wall-derived signal rises rapidly as intravascular oxygen levels approach low levels of ∼1 Torr. The conducted signal S_CR (Eq. 3) is assumed to act analogously to an electrical current along the vessel expressed per unit circumference and is propagated upstream with exponential decay according to a length constant L_met. In each segment, it is augmented according to the local metabolic signal S_loc. Signals are combined at converging bifurcations and divided at diverging bifurcations, relative to the direction of conduction. In each case, circumference-based weighting is used, such that the product of the signal and the circumference in the parent vessel equals the sum of the corresponding products in the daughter vessels. Virtual segments distal to boundary outflow nodes are used to generate the conducted signals at outflow nodes.

Reference state.

A reference state is established for the network, representing a moderate degree of vascular tone at a moderate level of consumption. In the reference state, the measured diameters of the arterioles are multiplied by a constant factor (0.869 in this case), so that the pressure drop and tissue perfusion match those in the control state of the representative segment model, representing conditions in skeletal muscle (1); this state is referred to as a physiological reference state since the specified arteriolar diameters are proportional to those observed in the original experimental network (20). Passive diameters D₀ are calculated to satisfy the condition T_cur = T_total. Values of C_tone^″ are calculated by the following procedure, which is designed to establish a physiologically realistic heterogeneous distribution of vessel tone within the arteriolar network in the reference state and thereby permit testing of the effectiveness of different flow regulation mechanisms. First, the total hemodynamic signal in each arteriolar segment is computed in the reference state:

$$C_{\text{hemo}}^{\prime }=C_{\text{myo}}{T}_{\text{cur}}-C_{\text{shear}}{\tau }_{\text{wall}}$$ (9)

A linear regression of this quantity vs. vessel diameter is then performed, and a value C_hemo^″ is obtained from the regression line for each segment based on its diameter. The value of C_tone^″ in each segment is defined as:

$$C_{\text{tone}}^{″}=S_{\text{CR}}-C_{\text{hemo}}^{″}+C_{\text{0}}^{″}$$ (10)

where C₀^″ is constant for all segments. According to Eqs. 5 and 9, this implies that

$$S_{\text{tone}}=C_{\text{hemo}}^{\prime }-C_{\text{hemo}}^{″}+C_{\text{0}}^{″}$$ (11)

in the reference state. The values of S_tone are distributed around C₀^″ with a distribution that reflects the variations of hemodynamic stimuli within the network. The use of values of C_hemo^″ derived from the linear regression of C_hemo^″ with diameter ensures that the values of C_hemo^′−C_hemo^″ and hence S_tone are not correlated with diameter. For simulations in which the assumptions about the mechanisms of metabolic flow regulation are varied, the value of C₀^″ is adjusted to maintain the target perfusion. Otherwise, variations in overall perfusion would mask the relevant effects of changing the regulatory mechanisms.

Network dynamics.

The time-dependent variations in the vascular tone and diameter of the arterioles are predicted by integrating Eqs. 6 and 7 with respect to time using a predictor-corrector method. This system can result in diameter oscillations consistent with vasomotion (2). A period of 200 s is simulated for each case. After 100 s, the system variables typically approach either a steady-state or oscillatory behavior around a stable baseline. Time averages over the period from t = 100 s to t = 200 s are used to represent the eventual state of the system.

RESULTS

Effects on network oxygenation parameters of varying the strength of the erythrocyte-derived signal and the wall-derived signal are shown in Fig. 3. The left column shows results of regulation by an erythrocyte-derived signal in the absence of a wall-derived signal. The coefficient of correlation between predicted oxyhemoglobin saturation in each segment and the corresponding value in the physiological reference state shows a slight increase with increasing metabolic signal strength. Oxygen deficit, defined as the anoxic length fraction of oxygen exchanging vessels, decreases slightly, and oxygen extraction, defined as oxygen consumption relative to convective oxygen flux in the main inflow arteriole, rises. Excluding the effect of phase separation by assigning a fixed hematocrit to all vessels in the network shows a stronger effect, with increasing signal strength resulting in a decreased oxygen deficit and increased extraction. These results show that an erythrocyte-derived metabolic signal provides the capability for local regulation of blood flow in heterogeneous networks, as shown previously in homogeneous network structures (1). However, this capability is significantly reduced when the phase separation behavior of blood in diverging bifurcations is taken into account.

Fig. 3.

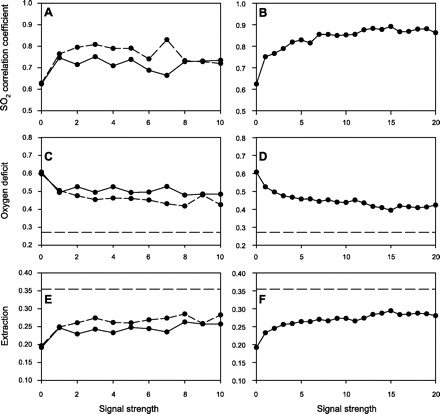
Effects of metabolic flow mechanisms on oxygen transport parameters. Left: erythrocyte-derived signal, with phase separation (solid curves) and without phase separation (dashed curves). Right: wall-derived signal. A and B: correlation between predicted oxygen saturation values after flow regulation with those computed in reference (physiological) state. C and D: oxygen deficit [fraction of vessel length with zero oxygen content (or anoxic length fraction of oxygen-exchanging vessels)]. E and F: extraction (oxygen consumption relative to convective supply in main arteriole). Horizontal dashed lines show corresponding values for the reference (physiological) state.

Figure 3, right, shows the effect of regulation by a wall-derived metabolic signal in the model. As the strength of the signal is increased, the correlation of saturation values with the values in the physiological reference state improves to ∼0.9. The oxygen deficit decreases and the extraction increases, both approaching but not attaining their values in the physiological reference state. These results show that, for the parameter values and conditions considered, a wall-derived metabolic signal results in more effective metabolism-perfusion matching than an erythrocyte-dependent mechanism, with a lower oxygen deficit and increased correlation between saturation values after regulation and those computed in the reference state.

Figure 4 shows distributions of hematocrit and saturation in all vessels of the network under different models for metabolic flow regulation. Figure 4, A and B, illustrates the effect of excluding metabolic flow regulation. Compared with the physiological state shown in Fig. 4, G and H, eliminating metabolic regulation impairs the ability of the network to redistribute flow to hypoxic areas, resulting in regions with low hematocrit and low saturation. The effect of an erythrocyte-derived metabolic signal at a signal strength C_rbc^meta = 10 is shown in Fig. 4, C and D. The erythrocyte-derived signal does not lead to substantial redistribution of flow to hypoxic areas but does result in a 48% decrease in the number of zero hematocrit vessels and a 20% decrease in the number of low saturation vessels. Figure 4, E and F, shows the effect of a wall-derived metabolic signal at a signal strength C_wall^meta = 20. The numbers of vessels with near-zero hematocrit and saturation are reduced by 67% and 32%, respectively, relative to the case with no flow regulation (Fig. 4, A and B) and are also reduced relative to the case with an erythrocyte-derived signal (Fig. 4, C and D), although the number of such vessels remains higher than in the physiological reference state (Fig. 4, G and H).

Fig. 4.

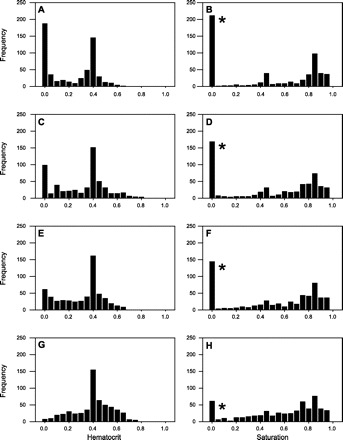
Effects of metabolic flow regulation mechanisms on hematocrit (left) and saturation (right) distributions for all vessels in the network. A and B: no metabolic regulation. C and D: erythrocyte-derived signal, C_rbc^meta = 10. E and F: wall-derived signal, C_wall^meta = 20. G and H: reference (physiological) state. *Vessels with zero hematocrit are assumed to have zero saturation.

DISCUSSION

Metabolic regulation of blood flow is critical to the ability of the circulatory system to meet tissue needs, particularly for oxygen, yet the mechanisms by which this is achieved have not been fully elucidated. Proposed mechanisms for metabolic regulation include oxygen-dependent release of ATP by erythrocytes as well as metabolites originating from the vessel wall and/or tissue under conditions of hypoxia. This study uses theoretical simulations to investigate the effectiveness of these mechanisms in regulating flow in heterogeneous microvascular networks.

Previous theoretical studies of metabolic flow regulation have generally considered homogeneous networks, in which all flow pathways are equivalent and no unequal hematocrit partition occurs at diverging bifurcations (1, 6, 8, 29). In such a model, a metabolic signal originating solely from ATP release by erythrocytes was found to be capable of maintaining and modulating blood flow according to metabolic demands (1). The present study, based on a heterogeneous network structure, reveals limitations of an erythrocyte-dependent mechanism. In this study, the initial reference state is established with heterogeneous vessel tone. Flow regulation in the absence of metabolic signaling leads to substantial numbers of vessels with near-zero hematocrit and saturation (Fig. 4, A and B), resulting in high oxygen deficit and low extraction. Metabolic regulation by an erythrocyte-derived signal leads to modest reduction in the numbers of low-hematocrit and low-saturation segments, but the resulting decrease in hypoxic fraction and increase in extraction are smaller than those predicted for metabolic regulation by a wall-derived signal, implying that erythrocyte-derived signals are less effective in terms of metabolism-perfusion matching under these conditions.

Insight into the reasons for this behavior can be obtained by considering the effects of the unequal partition of hematocrit in diverging bifurcations on the characteristics of the system when regulation by an erythrocyte-dependent mechanism is assumed. This phase separation behavior leads to large variations in hematocrit among vessels in microvascular networks, including the occurrence of channels with no erythrocytes (20). If this phase separation is excluded, such that all segments have equal hematocrit, metabolic regulation by the erythrocyte-derived signal leads to more improvement in the oxygen transport characteristics of the network (dashed curves in Fig. 3). The decreased effectiveness of erythrocyte-derived metabolic signaling relative to wall-derived signaling is thus partly a consequence of the unequal partition of hematocrit in heterogeneous networks, which leads to the occurrence of low hematocrits in some low-flow vessels. If the metabolic response is dependent only on saturation-dependent ATP release from erythrocytes, the metabolic signal may decrease instead of increasing with decreasing flow in a particular pathway due to the decrease in hematocrit resulting from phase separation at the diverging bifurcations upstream of the flow pathway (22). This mechanism can lead to the formation of flow channels with low or zero hematocrit and hypoxia in the vessels and surrounding tissue (Fig. 5). In the network simulations, it was found that hypoxic vessels were frequently those with low or zero hematocrit.

Fig. 5.

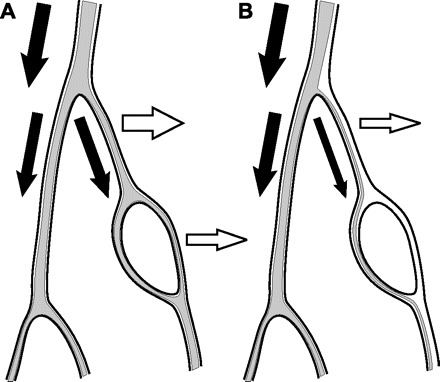
Schematic showing effects of hematocrit partition in diverging bifurcations (phase separation) on generation of erythrocyte-derived signals. A: if flow is divided equally at the initial bifurcation (filled arrows), both vessels receive approximately the same hematocrit and can produce erythrocyte-derived metabolic signals (open arrows). B: if flow decreases in one branch (filled arrows), hematocrit drops in that branch due to phase separation behavior, leading to a reduced capability of generating erythrocyte-derived metabolic signals (open arrow). If flow regulation is dependent on erythrocyte-derived signals, this branch may then further constrict, leading to further flow reduction.

Compared with the results of an erythrocyte-derived signal, metabolic regulation by a wall-derived metabolic signal led to improved oxygen transport characteristics in the network. Such a signal does not depend on the presence of erythrocytes and is therefore not subject to the same instability as the erythrocyte-derived signal. The results of these simulations suggest that erythrocyte-independent signals play an important role in metabolic regulation in heterogeneous networks. A similar result was obtained in studies of structural adaptation (22), where the presence of a wall signal results in improved tissue oxygenation. Experimental observations corroborate the involvement of erythrocyte-independent mechanisms in metabolic flow regulation. Evidence of conducted vasodilation as a result of anoxia in the absence of red blood cells has been demonstrated in mouse cremaster arterioles (15). The mechanism in this case is thought to be mediated by ATP-sensitive potassium channels, as evidenced by the abrogation of this response with glibenclamide.

These results do not, however, contradict the involvement of an erythrocyte-dependent signal in the metabolic regulation of blood flow. The saturation-dependent release of ATP by erythrocytes has its maximum sensitivity to oxygen levels in the range where the saturation curve is steepest, in the region of the animal's P₅₀. An erythrocyte-dependent mechanism would therefore potentially be effective in maintaining vessel oxygen levels in this range, which is needed to provide an adequate diffusion distance for oxygen into surrounding tissue. Since our oxygen transport model does not take account of limitation of diffusion distance on oxygen delivery, it would not be expected to show how maintenance of vessel oxygen levels in this range would contribute. Consideration of a spatially variable oxygen diffusion field throughout the tissue, with Michaelis-Menten oxygen utilization kinetics (24), would result in a more complex but realistic model, which could be used to examine the effects of combined erythrocyte-dependent and wall or tissue-dependent metabolic signals.

In view of the crucial importance of blood flow regulation for many aspects of physiological function, it is likely that multiple mechanisms are involved. A wall-dependent metabolic signal, with sensitivity at low oxygen levels, may serve to avoid hypoxia and ensure erythrocyte supply to most capillaries. Acting in parallel, an erythrocyte-dependent mechanism, with sensitivity at moderate oxygen levels, may then serve to bring capillary Po₂ high enough to provide adequate gradients for diffusion into tissue, particularly at higher consumption rates. The wall-dependent mechanism is expected to be dominant under conditions characterized by decreased perfusion pressure and/or arterial oxygenation content, as well as pathological conditions such as sepsis, in which increased flow heterogeneity and an increased number of plasma channels with poor oxygen supply can result in organ failure (9, 11).

The present model utilizes a vascular architecture derived from the mesentery to investigate regulation of oxygen supply to skeletal muscle. Obvious differences exist between the geometry of mesenteric and skeletal muscle vasculatures, such as the parallel alignment of capillaries (with muscle fibers) that occurs in skeletal muscle but not in mesentery. The simplified model for oxygen transport used here does not use information regarding the geometrical arrangement of the vessels and depends only on their lengths, flow rates, and connectivity. This model thereby minimizes the impact of network geometry. The mesenteric network provides a multigeneration arteriolar tree that can be used to demonstrate the effects of network heterogeneity on local flow regulation.

In conclusion, metabolic flow regulation based on a wall-derived signal is predicted by this model simulation to lead to better metabolism-perfusion matching than regulation based on an erythrocyte-dependent mechanism under conditions in which there is an unequal hematocrit distribution in heterogeneous networks. Advances in experimental investigations, together with models including more realistic simulations of oxygen transport, are needed to obtain improved understanding of the contributions of multiple mechanisms to the local metabolic regulation of blood flow under a wide range of conditions.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: T.K.R., A.R.P., and T.W.S. conception and design of research; T.K.R. performed experiments; T.K.R. and T.W.S. analyzed data; T.K.R. and T.W.S. interpreted results of experiments; T.K.R. and T.W.S. prepared figures; T.K.R. drafted the manuscript; T.K.R., A.R.P., and T.W.S. edited and revised the manuscript; T.K.R., A.R.P., and T.W.S. approved the final version of the manuscript.