On The Role of Physiological Fluctuations in Quantitative Gradient Echo MRI – Implications for GEPCI, QSM and SWI

Abstract

Purpose:

Physiological fluctuations in biological tissues adversely affect MR images if present during signal acquisition. This problem is especially important for quantitative MRI. The goal of the studies reported in this paper was to reduce the contributions of physiological fluctuations in quantitative MRI based on T2* tissue relaxation properties. Specifically, in this paper we deal with GEPCI, QSM and SWI techniques and propose methods allowing for substantial improvement of their results.

Methods:

We used a navigator imbedded in a multi-gradient-echo sequence to record and correct MR signal phase fluctuations at each phase encoding step. All GEPCI, QSM and SWI images were then reconstructed from a single acquisition. We employed a keyhole-type approach to further average out effects of physiological fluctuations. Voxel spread function technique was used to correct for macroscopic field inhomogeneities.

Results:

Brains of normal subjects and subjects with multiple sclerosis were studied. We demonstrated that our employed strategies substantially reduced the width of the R2*=1/T2* distribution within human brains and significantly improved quantification of tissue damage in multiple sclerosis. We also showed improved quality of the SWI and QSM images.

Conclusion:

The strategies employed in this paper greatly reduced physiologically-induced artifacts in GEPCI, QSM and SWI, improving the reliability of these techniques.

Introduction

Conventional MRI techniques such as T1-weighted (T1W) and T2-weighted (T2W) imaging provide good contrast between different tissues and have been successfully used in MRI. However, the tissue contrast of these techniques depends not only on the tissue-specific relaxation characteristics, but also on the parameters of pulse sequences used for data acquisition. This non-quantitative nature of these methods can affect detection of tissue pathology and can also reduce efficiency of applying these techniques in multi-center clinical trials. In contrast to these conventional techniques, many new quantitative techniques that rely on different tissue properties (T1 and T2 relaxation, water diffusion, etc.) have been explored in recent years. These methods providing quantitative measurements of tissue MR parameters are less inter-site dependent and can be more suitable for multi-center clinical trials (1,2). In this paper we focus on techniques that explore tissue-specific T2* relaxation properties and characteristic frequency shifts, i.e. techniques based on Gradient Recall Echo (GRE). In comparison to spin-echo (SE) techniques, GRE techniques have many advantages. First of all, the acquisition is much faster, and therefore suffers from fewer motion artifacts. Secondly, due to the low flip angle used in GRE sequences, they have lower RF power deposition and are more suitable for high-field MRI. Most importantly, since GRE sequences do not use 180° refocusing pulses, they are sensitive to the tissue-specific magnetic susceptibility properties (3,4) that are being exploited in a number of techniques, such as functional MRI (5-7), susceptibility-weighted imaging (SWI) (e.g. (8,9)), quantitative susceptibility mapping (QSM) (e.g. (10-13)), and gradient echo plural contrast imaging (GEPCI) (14-16). Herein we focus mostly on GEPCI technique that is based on a GRE sequence with multiple gradient echoes and allows simultaneous generation of naturally co-registered multi-contrast images (T1-weighted or spin density images, T2* or R2* maps and frequency maps) from a single MR scan. By combining these basic GEPCI images, additional images can be generated, such as SWI-like images, GEPCI-SWI images, T1f images, Fluid suppressed T2* (FST2*) images and SWI-T2* images (16). Exploring these multi-contrast images has a potential for improving tissue and lesion characterization, including quantitative analyses (15). Quantitative histogram analysis could be very useful in clinical studies. It can help to monitor disease progression which otherwise would be difficult to characterize on images. It also can be used to detect the global behavior of brain tissues and in selected ROIs. Using a multi gradient echo approach also provides advantages for SWI and QSM, as both SWI and frequency maps are generated from the same acquisition as for GEPCI images (16).

Although it has many advantages, obtaining quantitative tissue characteristics using GRE-based techniques also creates challenges. Among them are the effects of tissue-nonspecific macroscopic field inhomogeneities, resulting mostly from tissue-air interfaces, and the effects on MR signal due to physiological fluctuations. The former issue has been addressed recently by our group by developing a voxel spread function (VSF) method which can be used to correct for macroscopic field inhomogeneities in GRE experiments (17). This method has already been successfully verified in both computer simulated and in vivo human studies (17). The latter problem – signal alterations due to physiological fluctuations -is the subject of the current paper. Physiological fluctuations such as changes in the blood flow and blood oxygenation level, as well as the respiration-induced organs’ (such as lungs, chest and diaphragm) motion, induce fluctuations of the local magnetic fields in the tissue and consequently local resonance frequencies, f₀(r). They have been demonstrated as an important factor that influences brain MRI image quality (18-22). Hence, they can also affect the accuracy of quantitative tissue MR parameters’ evaluation.

In the studies reported herein, two methods were incorporated into the GEPCI technique to reduce the effects of physiological fluctuations. First, we employed a navigator-based technique akin to the one used previously for correcting the effects induced by f₀ fluctuations (23). This technique was first introduced in (24) and further implemented in (25,26), demonstrating substantial reduction of the motion-induced artifacts and improvement of image quality. Detailed results of the spatial distribution of respiration-induced f₀ fluctuations in the human brain caused by changes in the chest volume during respiration have been reported in theoretical (27) and experimental studies (20). Second, we employed a keyhole-type method. The keyhole technique (28) was initially designed to accelerate MRI scans to obtain dynamic images. Here, we employed a keyhole-based method which combined high-resolution and low-resolution datasets by taking the average of the k-space center to further reduce physiological fluctuations, thereby improving image quality. By incorporating all three correction strategies, navigator-based fluctuation correction, keyhole-based correction, and VSF field inhomogeneities correction, into GEPCI technique we demonstrated substantial improvements in the accuracy of quantitative GEPCI measurements (R2* and frequency shifts) and in the quality of the subsequent images based on these quantitative measurements, including those based on SWI and QSM.

Methods

Image acquisition

All studies were approved by the IRB of Washington University in St. Louis. Images were collected from two healthy volunteers (subject 1 and subject 2), and two subjects with multiple sclerosis (MS), one with secondary progressive course (SPMS, subject 3) and one with primary progressive course (PPMS, subject 4), using a 3T Trio MRI scanner (Siemens, Erlangen, Germany) equipped with a 12-channel phased-array head coil. Two datasets were collected for each subject: one of high resolution data with a matrix size of 40×192×512 (slice, phase, read) and a voxel resolution of 3×1×1 mm³ and one of low resolution data with a matrix size of 20×96×512 and the same FOV. Both datasets used three dimensional (3D) multi-gradient-echo sequences with a flip angle of 30°, TR = 50 ms and total acquisition times of 6 min 30 sec and 1 min 30 sec, respectively. For each acquisition, 11 echoes were collected with first echo time TE₁ = 4ms and echo spacing ΔTE = 4ms. The last echo was used as a navigator echo by applying additional magnetic field gradients to unwind the spatial encoding gradients before it. Data were also collected from a phantom filled with NiSO₄-dopped water.

f₀ fluctuation correction

We used navigator echoes to monitor and correct the f₀ fluctuations. This procedure was similar to that used in. (23), though in our approach the navigator was placed after all gradient echoes were acquired (in (23) navigator was placed before gradient echoes). First Inverse Fourier Transform was applied to the navigator signal (k_x-space) along the readout direction (x) to produce images projected on this direction (25,26). Then for each spatial point x of this image and each phase encoding step, the phase difference between the N-th (ϕ_N(x)) and the first (ϕ₁(x)) spatial encoding step was calculated. Finally, the correction was applied to each phase encoding step with gradient echo time TE, according to the equation:

$$S_N^c(x,TE)=S_N(x,TE)\cdot e^{-i\frac{{\varphi }_N\left(x\right)-{\varphi }_1\left(x\right)}{11\cdot \Delta TE}}$$ (1)

where $S_N^c(x,TE)$ and S_N(x, TE) are the signals in k-space after and before correction, respectively. Here we assume that the frequency f₀ did not change during the 50-ms time when 11 consecutive gradient echoes were acquired. Thus, phase correction for each echo can be calculated using relationship $\Delta \varphi =-\frac{{\varphi }_N\left(x\right)-{\varphi }_1\left(x\right)}{T{E}_{NAV}}\cdot TE=-\frac{{\varphi }_N\left(x\right)-{\varphi }_1\left(x\right)}{11\cdot \Delta TE}\cdot TE$. Here, TE_NAV is the echo time of the navigator echo. This procedure was applied to each RF channel independently.

Keyhole-type k-space center averaging

New k-space data were generated after applying the f₀ fluctuation correction using the same reference phase ϕ₁(x) to both high-resolution and low-resolution datasets. The k-space of low-resolution data was combined with the central part (size of 20×96×512) of the k-space of high-resolution data by taking the average of these two.

Image generation

After applying the Fourier transform to the corrected k-space data, data from different channels were combined for each voxel in a single data set S(TE) using a strategy developed in (16,29):

$$\begin{array}{c}\hfill S\left(TE\right)=\frac{1}{M}\sum _{m-1}^M{\lambda }_m\stackrel{‒}{S}\left(T{E}_1\right)S_m\left(T{E}_n\right)\hfill \\ \hfill {\lambda }_m=\frac{1}{M}\sum _{l=1}^M{\sigma }_l^2∕{\sigma }_m^2\hfill \end{array}$$ (2)

where the sum is taken over all channels (m), S̄ denotes complex conjugate of S, λ_m are weighting parameters, and σ_m are noise amplitudes (r.m.s.). We omitted the index corresponding to voxel position for clarity. This algorithm allowed for the optimal estimation of quantitative parameters, such as MR signal decay rate constants and also removed the initial phase incoherence between channels. The data are analyzed on a voxel-by-voxel basis using the following theoretical model:

$$S\left(TE\right)=S_0^2\cdot e^{-R_2^{\ast }\cdot TE}\cdot e^{i2\pi f\cdot (TE-T{E}_1)}\cdot F\left(TE\right)$$ (3)

where f is a local signal frequency and F(TE) is the F-function describing the influence of macroscopic magnetic field inhomogeneity effects on MR signal (4). Herein, we employed a Voxel Spread Function (VSF) algorithm developed in (17) for evaluation of F-function. With our choice of TR and flip angle, S₀ represents T1-weighted images. Numerous methods have been proposed to separate effects of the macroscopic field inhomogeneities from tissue specific local frequency shifts, such as high-pass filtering (9), projection onto dipole fields (PDF) (30), sophisticated harmonic artifact reduction for phase data (SHARP) (31), polynomial fitting (32), and others. Here we used the “PDF” (30) method to remove the effect of background field inhomogeneities on tissue specific frequency maps. The filtered frequency maps were then used to generate a frequency mask FM (16) by setting negative values to unity and normalizing positive values to be ranged from 0 to 1, which is similar to the phase mask created in a standard SWI procedure (8). Then, SWI-like, GEPCI-SWI, T2*-SWI and $FS{T}_2^{\ast }$ images were generated according to (16):

$$\begin{array}{cc}\hfill & S_{SWI-like}\left(TE\right)=S_0\cdot e^{-R{2}^{\ast }\cdot TE}\cdot F{M}^4;\hfill \\ \hfill & S_{GEPCI-SWI}\left(TE\right)=e^{-R{2}^{\ast }\cdot TE}\cdot F{M}^4;\hfill \\ \hfill & S_{T_2^{\ast }-SWI}=FS{T}_2^{\ast }\cdot S_{GEPCI-SWI};\hfill \\ \hfill & S_{FS{T}_2^{\ast }}=T_2^{\ast }\cdot M_{CSF}^n\hfill \end{array}$$ (4)

Where $FS{T}_2^{\ast }$ is a $T_2^{\ast }$ map with suppressed CSF signal obtained by multiplying the T2* map with a CSF mask (M_CSF) several times. The CSF mask is generated from the T1-weighted image. S₀ values (T1-weighted MR signal) are plotted in a histogram where the highest peak corresponding to WM is fitted to a Gaussian function with a peak position value (X0) and standard deviation (STD). All pixels with S₀ values that are higher than (X0 − 1.96×STD) are considered as from the non-CSF region and their values are set to unity in M_CSF. All other pixels that have smaller values are normalized from 0 to 1, as described in (16). QSM maps are calculated using morphology enabled dipole inversion (MEDI) methods described in (33-36).

MS scoring

Previously, our lab introduced the concept of R2*-based calculation of quantitative tissue damage score (TDS) and tissue damage load (TDL) in MS, and showed improved correlations between these scores and the standard measures of clinical disability (15). To calculate these scores, a mask was generated containing both “normal appearing white matter” (NAWM) and tissue within obvious MS lesions. Then, a Gaussian function was fitted to the upper half of the R2* distribution histogram of NAWM to determine the width, σ, and the position of the center, $R{2}_c^{\ast }$, of this distribution. TDS (for each voxel) and TDL were then calculated using equations:

$$\begin{array}{cc}\hfill & TDS=\frac{R{2}_c^{\ast }-R{2}^{\ast }}{R{2}_c^{\ast }};\hfill \\ \hfill & TDL=V\cdot \sum _{i=1}^{N}TD{S}_i\hfill \end{array}$$ (5)

Where N represents the total number of voxels in the MS white matter lesions and V is the voxel volume (mm³). MS lesions are defined as voxels having $R{2}^{\ast }>R{2}_c^{\ast }-1.96\sigma \left(15\right)$ (15).

Results

Fig. 1 shows examples of f₀ fluctuations detected with navigator echo of high resolution data for a phantom (a) and two healthy control subjects (b & c). For all examples, there was a small global frequency drift through the entire scan. This frequency drift was less than 0.5 Hz for phantom data and about 3 Hz for human subjects. For human subjects, in addition to the frequency drift, there were periodic fluctuations with a time scale of about 4 seconds. These fluctuations originated from subjects’ respiration-induced B₀ field changes inside the brain during the scan. For a healthy volunteer (subject 2: Fig. 1c), in addition to the normal respiration-induced fluctuations (with a time scale of seconds), there was a large variation (with a time scale of minutes) in the middle of the scan. This variation resulted in rather severe artifacts in the R2* map, shown in Fig. 2.

Fig. 1.

Physiologically induced f₀ fluctuations for high-resolution data. Examples are from phantom (a) and two healthy subjects. For each dataset only data from a single channel are shown.

Fig. 2.

Comparison of R2* maps (selected from subject 2). (a) without any correction; (b) with F-function field inhomogeneities correction; (c) with keyhole-based correction; (d) with navigator-based correction; (e) with all corrections. Short arrows on the top show the area affected by macroscopic field inhomogeneities, arrows in the middle show the area affected by physiological fluctuations.

Fig 2 compares the R2* maps of a healthy subject (subject 2) before and after corrections. Macroscopic field inhomogeneity induced artifact was substantially reduced by applying VSF correction (short arrows). After applying navigator-based and keyhole-based corrections, the R2* values of the deep gray matter areas of the two hemispheres become more symmetric. This is also evident by comparing the R2* distributions of the deep gray matter areas of the two hemispheres, as shown in Fig. 3.

Fig. 3.

R2* histograms of deep gray matter area (caudate nucleus, putamen and globus pallidus) before (a) and after (b) correction (squares: right hemisphere; circles: left hemisphere). After correction, R2* histograms of the two hemispheres became more symmetric. Data derive from subject 2, a healthy volunteer.

This finding was further demonstrated by results shown in Fig. 4. By comparing panel (a) and (b), one can find that the bright “cloud-like” artifacts were not related to magnetic field inhomogeneities (they still remained after applying F-function correction) and were caused by physiological fluctuations. These artifacts were reduced after keyhole correction and were practically eliminated by navigator-based correction. The two MS lesions (indicated by long arrows in Fig. 4) in the centrum semiovale became apparent after applying both the navigator-based and Keyhole-based corrections. In addition, navigator-based and Keyhole-based corrections also improved visualization of blood vessels, as indicated by short arrows in Fig. 4. Prior to these corrections, MS lesions and these blood vessels were hidden by the intrusive strong “cloud-like” artifacts.

Fig. 4.

(a) R2* map without any corrections; (b) R2* map with F-function correction; (c) R2* map with keyhole-based correction; (d) R2* map with navigator-based correction; (e) R2* map with all corrections. Long arrows point to MS lesions (dark on R2* map) and short arrows indicate blood vessels. Images were selected from subject 4, a patient with PPMS.

Additionally, physiologically induced artifacts can dramatically affect the global R2* distribution of the whole brain, as shown in Fig. 5. After applying VSF correction, the R2* distribution of the whole brain NAWM and cortical gray matter was only slightly shifted to the left. This reflects the fact that we were using high resolution imaging and apply advanced shimming techniques standard on Siemens scanner. As a result, most parts of the brain were not affected by field inhomogeneities and only several specific areas at the air/tissue interfaces required correction which had little effect on a global R2* distribution. However, the navigator-based correction greatly changed the R2* distribution, not only by shifting the distribution to the left (smaller R2*), but also making the distribution much tighter. The Keyhole-based correction further reduced the effects of physiologically induced artifacts, which provided the sharpest distribution. These improvements will be especially important for quantitative methods, such as GEPCI, when applied to quantifying tissue damage in MS.

Fig. 5.

R2* histograms of NAWM (a & b) and cortical gray matter (c & d) of the whole brain, calculated using non-Hanning filtered (a & c) and Hanning filtered (b & d) data. Black lines: data without any correction; red lines: data with F-function correction; magenta lines: data with keyhole-based corrections; green lines: data with navigator-based corrections; blue lines: data with all corrections. Data were selected from subject 4.

Fig. 6 shows a selected slice of GEPCI-T1W image and GEPCI-R2* map from subject 3. Color coded TDS scores of lesions (calculated using the corrected dataset) have been superimposed on the T1W image. The visible physiologically induced artifacts of this MS patient (subject 3) were less pronounced than for the other MS patient (subject 4). However, these artifacts still produced substantial errors in the R2* distribution, affecting the GEPCI scoring results. After applying all the corrections, the R2* distribution of the entire white matter (with lesions) became tighter ($R{2}_c^{\ast }$ = 19.5 s⁻¹, σ=2.0 s⁻¹, Fig. 7), compared to the R2* distribution ($R{2}_c^{\ast }$ = 19.5 s⁻¹, σ=2.4 s⁻¹) before correction. By applying only the VSF correction, the R2* distribution had a center at 19.5 s⁻¹ and a width of 2.4 s⁻¹, similar to the distribution without any correction. Thus, for this particular slice the narrowing of the distribution was not a result of correcting the macroscopic field inhomogeneities but was due to the correction of physiologically induced artifacts. That is, the center of the R2* distribution did not change after corrections, but the distribution width was reduced. As a result, the TDS values of the lesions barely changed while the TDL value of this specific slice changed substantially. In Fig. 7, the NAWM R2* values fitted well with a Gaussian function. The tail at left derives primarily from the low R2* values in the lesion areas. The tail on the right is due to the high R2* values of the corpus callosum area, which contains highly aligned myelinated axon bundles perpendicular to the main magnetic field. Dashed lines in Fig. 7 represent threshold values. All pixels with R2* values below this threshold were considered as MS lesions. Due to the substantial changes of the distribution parameters upon corrections, the TDL calculated from the corrected dataset had a value of 380 mm³ compared to 320 mm³ before correction. This 60 mm³ difference in TDL values might affect the correlations of quantitative GEPCI scores with clinical tests.

Fig. 6.

(a) T1-weighted image with superimposed lesion TDS, (b) R2* map from the same slice. (Data from subject 3, a patient with SPMS).

Fig. 7.

R2* distribution of white matter area (with lesions) selected from the slice shown in Fig. 6 before (a) and after (b) corrections. Upper halves of both distributions are fit to Gaussian function (solid lines). Dashed lines represent threshold values for lesion definition. Data were selected from subject 3.

Another useful application of GEPCI technique in MS has been its ability to simultaneously visualize small central veins and MS lesions (Fig. 8). Recently, T2*-weighted imaging was used for detecting small parenchymal veins within MS lesions (37-41). Due to the lower SNR and lower resolution, detecting small veins using 3 T scanners is more difficult than with 7 T scanners (37) and most studies have used high field strength magnets for this purpose. However GEPCI T2*-SWI images (16,39) at 3T were able to co-localize veins and MS lesions. By applying the current corrections, a T2* map with vein-lesion contrast enhancement (as shown in Fig. 8d) with improved quality of T2*-SWI images was produced, thus improving the detection of small central veins within MS lesions.

Fig. 8.

Demonstration of a small central vein in a MS lesion. (a) fluid suppressed T2* map (FST2*) before correction; (b) FST2* map after correction; (c) T2*-SWI image after correction; (d) profiles of dashed lines shown in (a), (b) and (c), black solid line corresponds to figure (a); gray solid line corresponds to figure (b); dashed line corresponds to figure (c).

Thus far, we have shown that reduction of the effects induced by physiological fluctuations improved GEPCI-R2* (or T2*) measurements and improved the quality of subsequent images. In the following, we demonstrate that physiological fluctuations can also hinder accurate measurements of frequency maps (Fig. 10a) and subsequent images (such as SWI and QSM) that are based on frequency maps (shown in Fig. 9 and Fig. 10).

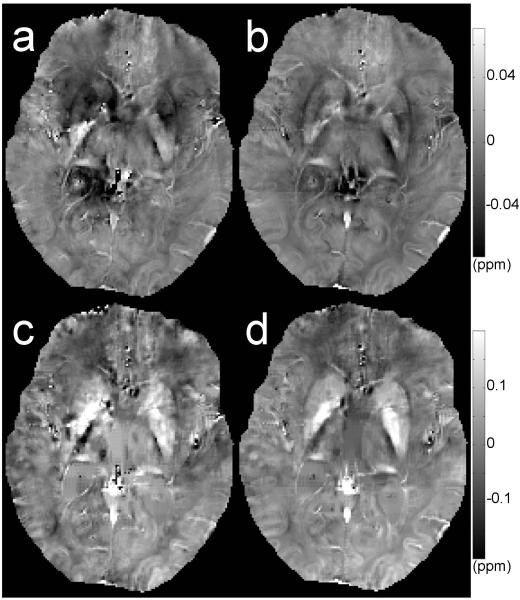
Fig. 10.

Axial section through several deep gray matter structures, including the caudate, putamen, globus pallidus and thalamus. Frequency (a, b) and QSM (c, d) maps before (a, c) and after (b, d) correction. Data selected from subject 4. QSM maps are calculated using method described in (34).

Fig. 9.

SWI-like (a, b) and GEPCI-SWI (c, d) images before (a, c) and after (b, d) corrections. Arrows show examples with substantial improvement in visibility of blood vessels. Data were selected from subject 4. GEPCI-SWI show better contrast of blood vessels in the areas occupied by CSF, e.g. ventricles.

As shown in Fig. 9b and d, the applied corrections greatly improved the visibility of blood vessels on SWI-like and GEPCI-SWI images, which otherwise were not readily visible (9a and c) due to the strong physiologically induced artifacts. By comparing with SWI-like images, GEPCI-SWI images showed better contrast of blood vessels within the ventricle region.

Corrections employed in this paper also improved the quality of QSM maps (as shown in Fig. 10). QSM is sensitive to iron concentration, thus sensitive to those iron-rich regions of the basal ganglia such as caudate nucleus, putamen and globus pallidus. In Fig. 10c, the anatomical structures of the deep gray matter regions on the QSM map were greatly disturbed by the physiologically induced artifacts; this artifact was substantially improved by applying our correction scheme (Fig. 10d).

Discussion

In this paper, we incorporated three correcting strategies into GEPCI technique and demonstrated substantial improvements to the GEPCI quantitative maps and images, as well as to corresponding SWI and QSM images. We identified two major factors creating artifacts in GEPCI measurements. One was tissue-nonspecific macroscopic field inhomogeneities, and the second was physiological fluctuations. Then, we demonstrated that these artifacts could be effectively reduced by employing specifically targeted correction strategies. The macroscopic field inhomogeneity artifacts were reduced by using VSF correction as proposed previously (17), and the artifacts caused by the physiological fluctuations were substantially improved by utilizing navigator-based and Keyhole-based corrections.

Fig. 1 shows examples of f₀ fluctuations using one phantom dataset and in two human subjects. These fluctuations were accompanied by a global frequency drift which was less than 0.5 Hz in phantom data, but larger in human data. All human data also showed periodic fluctuations having a time scale of a few seconds, which were attributed to respiration induced field changes within the brain, as discussed previously (20,27). However, in one human dataset (subject 2) we also found a large variation having a time scale of minutes that was most likely caused by changes in brain metabolism during data acquisition. In this paper, we demonstrated that correction of all these fluctuations improved the quantitative measurements and quality of acquired images.

Many neurological diseases, such as Alzheimer’s, Parkinson’s and Multiple Sclerosis are accompanied by local changes of iron concentration within the deep gray matter of the brain (42-47). R2*, SWI and QSM images are sensitive to iron distribution in brain tissues and have been used to detect iron deposition in vivo. However, these images can be affected by physiologically induced artifacts, as shown herein (Fig. 2, Fig. 9 & Fig. 10). For one healthy human subject in our studies, the images of deep gray matter area of the left hemisphere were severely blurred and the R2* values inside this area were unauthentic. After applying corrections as described, these artifacts were greatly reduced, providing more reliable R2* values (Fig. 2). Similar effects were observed on the SWI (Fig. 9) and QSM (Fig. 10) data from subject 4 with MS.

Recent research suggests that multicenter trials using R2*-based techniques are feasible if the inter-center data variability would be less than the inter-subject variability (1). Here we show that physiological fluctuations induce artifacts can greatly distort R2* maps and introduce large variability to R2* mapping, which would present problems for clinical trials. Application of the correcting strategies described here resulted in more accurate and reliable R2* maps, needed for future application of R2* in multi-center clinical trials.

We also showed that physiological fluctuations not only cause visible artifacts but also affect the global distribution of R2* (Fig. 3, Fig. 5 & Fig. 7). Correcting this would be crucial for accurate quantitation using methods such as GEPCI. Due to the substantial artifactual changes in the R2* distribution, GEPCI scores with appropriate corrections (15) might provide better correlations with clinical assessments. The described correcting strategies are not only useful for GEPCI but can also be applied to other techniques that employ MR relaxometry as a quantitative tool.

It is known that most, if not all, white matter MS lesions develop around small veins. (37,40,41). Moreover, demonstration of a central vein may help to differentiate MS lesions from other non-MS lesions seen (48). Due to its sensitivity to tissue specific magnetic susceptibility, T2* (or R2*) contrast is suitable for detecting veins and, in the past few years T2*-weighted images have been used for identifying perivenous white matter MS lesions (37,38,40,41). T2* maps generated by GEPCI technique can detect perivenous white matter lesions in MS. Comparing with conventional T2*-weighted images, T2* maps do not depend on scanner settings, and thus can provide tissue-specific information. In this and a prior study, we successfully used fluid suppressed T2* image (FST2*) to detect small central veins in MS lesions (16). Although central veins can be clearly defined using 7T MRI, they are difficult to identify using 3T MRI (37). Out results showed that employing the GEPCI T2*-SWI images along with the new strategies for improving image quality allowed co-localization of veins and MS lesions, thus providing a readily available tool for detecting central veins in MS lesions using 3T MRI.

Signal phase (or frequency shift) is another parameter that is generated by gradient echo MRI that can provide quantitative tissue-specific information. The exact nature of signal phase is not fully understood and has been the subject of debates (see for example (49-52)). However, signal phase (or frequency shift) is important; several imaging techniques such as susceptibility weighted imaging (SWI) (8,9,53) and quantitative susceptibility mapping (QSM) (10-13,51) rely on accurate frequency/phase maps. Our data show substantial improvement in the quality of frequency maps after application of the described corrections.

Conclusion

The goal of our study was to evaluate the role of physiological fluctuations in quantitative MRI based on T2* tissue relaxation properties and MR signal frequency shifts. Specifically, we addressed the effects of such artifacts on GEPCI, QSM and SWI techniques, and proposed methods to overcome these artifacts. We proposed a navigator imbedded in a multi-gradient-echo sequence to record and correct MR signal phase fluctuations at each phase encoding step. All GEPCI, QSM and SWI images were then reconstructed from the corrected data of a single acquisition. We employed a keyhole-type approach to further average out effects of physiological fluctuations. VSF (voxel spread function) technique was used to correct for macroscopic field inhomogeneities. We demonstrated that the employed strategies substantially reduced the width of the R2*=1/T2* distribution within a human brain, indicating that significant improvement in tissue damage measurement in multiple sclerosis and other neurological diseases would be expected. We also showed improvement in the visual quality of SWI and QSM images, and in subsequent GEPCI images. We conclude that use of the correcting strategies employed in this paper has potential to greatly reduce physiologically-induced artifacts in GEPCI, QSM and SWI, making the quantitative value of these techniques more accurate and reliable.