Haplotype Kernel Association Test as a Powerful Method to Identify Chromosomal Regions Harboring Uncommon Causal Variants

Abstract

For most complex diseases, the fraction of heritability that can be explained by the variants discovered from genome-wide association studies is minor. Although the so-called ‘rare variants’ (minor allele frequency [MAF] < 1%) have attracted increasing attention, they are unlikely to account for much of the ‘missing heritability’ because very few people may carry these rare variants. The genetic variants that are likely to fill in the ‘missing heritability’ include uncommon causal variants (MAF < 5%), which are generally untyped in association studies using tagging single-nucleotide polymorphisms (SNPs) or commercial SNP arrays. Developing powerful statistical methods can help to identify chromosomal regions harboring uncommon causal variants, while bypassing the genome-wide or exome-wide next-generation sequencing. In this work, we propose a haplotype kernel association test (HKAT) that is equivalent to testing the variance component of random effects for distinct haplotypes. With an appropriate weighting scheme given to haplotypes, we can further enhance the ability of HKAT to detect uncommon causal variants. With scenarios simulated according to the population genetics theory, HKAT is shown to be a powerful method for detecting chromosomal regions harboring uncommon causal variants.

Introduction

Genetic association studies have provided insights into the genetic architecture of complex diseases [WTCCC, 2007; Hardy and Singleton, 2009]. However, for most complex diseases, the fraction of heritability that can be explained by the variants discovered from association studies remains minor [Maher, 2008; Manolio et al., 2009; Eichler et al., 2010; Gibson, 2012]. Although the so-called ‘rare variants’ (minor allele frequency [MAF] < 1%) have attracted increasing attention, they are unlikely to account for much of the ‘missing heritability’ because very few people may carry these rare variants [Pihur and Chakravarti, 2010]. The best bet of genetic variants to fill in the ‘missing heritability’ includes two sources: uncommon causal variants (MAF < 5%) that are generally untyped in association studies using tagging single-nucleotide polymorphisms (SNPs) or commercial SNP arrays, and common causal variants with small genetic effects that cannot be detected via conventional statistical analyses [Manolio et al., 2009; Eichler et al., 2010; Yi et al., 2011]. Indeed, existing association studies such as genome-wide association studies (GWAS) or candidate-gene association studies (CGAS) are not designed to capture uncommon causal variants [Wray et al., 2011]. The emergence of next-generation sequencing technologies has allowed for the mapping of all genetic variants across the human genome [Hawkins et al., 2010]. However, the cost of sequencing remains high [Sboner et al., 2011]. Genome-wide sequencing is especially expensive for large sample sizes that are required for association studies [Sampson et al., 2012]. In the current stage, GWAS and CGAS data are still much more widely available than next-generation sequencing data [WTCCC, 2007; Li et al., 2010].

The widely used single-marker analysis that is implemented on each tagging SNP (usually with MAF ≥ 5%) is underpowered for detecting uncommon causal variants [Gusev et al., 2011], because the information of uncommon causal variants is not easy to be represented by common SNPs. Haplotypes, combinations of multiple adjacent alleles on a single chromosome, may act as ‘superalleles’ and serve as better tagging markers for uncommon causal variants that are generally not genotyped in GWAS or CGAS [Lin et al., 2012b]. For case-control studies with unrelated subjects, haplotype frequencies are often compared between cases and controls with a likelihood-ratio statistic [Zhao et al., 2000; Epstein and Satten, 2003; Becker et al., 2005]. To deal with continuous traits, a regression framework has been introduced to relate inferred haplotype frequencies to observed phenotypes [Zaykin et al., 2002]. Moreover, score tests based on generalized linear models have been proposed to deal with a variety of traits [Schaid et al., 2002]. Methods with use of haplotype similarity [Tzeng et al., 2003] and haplotype clustering [Molitor et al., 2003; Durrant et al., 2004; Tzeng, 2005; Tzeng et al., 2006; Browning and Browning, 2007] were also developed for GWAS or CGAS.

Modelling individual effects for all distinct haplotypes may induce many parameters and cause computation problems to the conventional likelihood-ratio test [Schaid et al., 2002]. In this work, we propose a haplotype kernel association test (HKAT) that is equivalent to testing the variance component of random effects for distinct haplotypes. Despite a large number of distinct haplotypes in a region, the signal of haplotype-trait association can be aggregated to a single variance parameter. With an appropriate weighting scheme given to haplotypes, we can further enhance the ability of HKAT to detect uncommon causal variants. We also consider the situation that a gene or a chromosomal region harbors not only uncommon causal variants but also common causal variants, and then we compare HKAT with several popular genotype or haplotype analysis methods by performing systematic simulations under a wide range of linkage disequilibrium (LD) patterns. In addition, we apply HKAT to data from a genetic association study related to human adiposity.

Materials and Methods

Haplotype Kernel Association Test (HKAT)

Let Y_i be the trait of the i^th subject (i = 1, …, n), and let x_i=[x_i,1 x_i,2 ⋯ x_i,p]' be a vector that codes p non-genetic covariates (e.g., age, gender, ethnicity, etc.) of the i^th subject. To account for haplotype ambiguity, the expectation-maximization algorithm [Dempster et al., 1977] is often used to infer the posterior distribution of haplotypes given multimarker genotypes. Let h_i=[h_i,1 h_i,2 ⋯ h_i,L]' be the i^th subject's expected frequencies of L distinct haplotypes over his/her posterior distribution of haplotypes. To relate the genetic composition to the trait, we consider a linear model for a continuous trait:

$$E(Y_i)={\alpha }_0+{\mathit{\alpha }}^{\prime }{\mathit{x}}_i+{\mathit{\beta }}^{\prime }{\mathit{h}}_i,$$ (1)

or a logistic regression model for a dichotomous trait:

$$\mathit{\text{logit}}P(Y_i=1)={\alpha }_0+{\mathit{\alpha }}^{\prime }{\mathit{x}}_i+{\mathit{\beta }}^{\prime }{\mathit{h}}_i,$$ (2)

where α₀ is the intercept term, α = [α₁ α₂ ⋯ α_p]' is the vector of regression coefficients for the p covariates, and β = [β₁ β₂ ⋯ β_L]' is the vector of regression coefficients for the L distinct haplotypes.

To test if any of the haplotypes are associated with the trait, the null hypothesis is H₀ : β = 0, i.e., H₀ : β₁ = β₂ =⋯ = β_L = 0. However, the commonly used likelihood-ratio test is computationally intensive and underpowered especially when some haplotypes are of low frequency. To reduce the number of parameters for distinct haplotypes, we assume that β_j is a random effect following an arbitrary distribution with a mean of zero and a variance of w_jτ, where τ is a variance component and w_j is a pre-specified weight for the jth distinct haplotype. Therefore, τ is a common parameter for all of the distinct haplotypes and w_j's (j = 1, …, L) are pre-specified weights for these distinct haplotypes. To test whether the regression coefficients of the L distinct haplotypes are all zero (H₀ : β = 0) is equivalent to test whether the variance component is zero (H₀ : τ = 0). The score statistic to test H₀ : τ = 0 is

$$T_{\mathit{\text{HKAT}}}={(\mathit{y}-\widehat{\mu })}^{\prime }{\mathit{H}}^{\prime }{\mathit{W}}_{\mathit{H}}\mathit{H}(\mathit{y}-\widehat{\mathit{\mu }}),$$ (3)

where y is the vector of traits of all the n subjects, μ̂ is the predicted mean of y under the null hypothesis (H₀ : τ = 0), H is the haplotype frequency matrix with the i^th column as h_i, and W_H is a diagonal matrix with the (j, j)-th element to be the pre-specified weight for the jth distinct haplotype (w_j). This test is referred to as the haplotype kernel association test (HKAT).

According to the theory of quadratic forms of normal variables [Scheffe, 1959], T_HKAT is asymptotically distributed as a mixture of χ² variables: ${\sum }_{i=1}^{\varpi }{\lambda }_i{\chi }_{1,i}^2$, where ${\chi }_{1,i}^2$'s are independent χ² variables with one degree of freedom, and λ₁ ≥ λ₂ ≥ ⋯ ≥ λ_ϖ are the ordered eigenvalues of the matrix ${\mathit{P}}_0^{1/2}{\mathit{H}}^{\prime }{\mathit{W}}_{\mathit{H}}\mathit{H}{\mathit{P}}_0^{1/2}$ (with the rank of ϖ). To reduce the bias that may be caused by a small sample size, we use the restricted maximum likelihood estimator of the variance component [Zhang and Lin, 2003] and therefore the matrix P₀ = V̂⁻¹ − V̂⁻¹ X̃ (X̃′ V̂⁻¹ X̃)⁻¹ X̃′ V̂⁻¹, where X̃ = [1 X] is a n × (p + 1) matrix and V̂ is a diagonal matrix with the (i, i)-th element to be the estimated variance of μ̂_i. For a continuous trait, $\widehat{\mathit{V}}={\widehat{\sigma }}_0^2\mathit{I}$ where ${\widehat{\sigma }}_0^2$ is the mean squared error under the null hypothesis and I is an n×n identity matrix. For a dichotomous trait, V̂ = diag (μ̂₁(1 − μ̂₁), μ̂₂ (1 − μ̂₂), ⋯, μ̂_n (1 − μ̂_n)) where μ̂_i = logit⁻¹ (α̂₀ + α̂′ x_i) is the estimated probability of being a case under the null hypothesis. The distribution of T_HKAT can be approximated by the three-moment approximation method [Imhof, 1961; Zhang, 2005; Allen and Satten, 2007, 2009; Pan, 2009; Tzeng et al., 2009], and the P-value of the observed HKAT test statistic is given by

$$P({\chi }_b^2>(T_{\mathit{\text{HKAT}}}-c_1)\times \sqrt{\frac{b}{c_2}}+b),$$ (4)

where $c_j={\sum }_{i=1}^{\varpi }{\lambda }_i^j$, $b=\raisebox{1ex}{$c_2^3$}\!\left/ \!\raisebox{-1ex}{$c_3^2$}\right.$, and ${\chi }_b^2$ is the χ² distribution with b degrees of freedom.

Genotype Kernel Association Test (GKAT)

To investigate the association of genetic variants in a chromosomal region with the disease, we can use genotypes to bypass the haplotype-phasing stage. Let g_i be a vector of genotype scores of the i^th subject at the set of markers in the chromosomal region. Under the assumption of additive genetic model, the possible elements of g_i are 0, 1, and 2, representing the number of copies of the minor allele. The vector g_i can be recoded accordingly if dominant or recessive genetic models are considered. In Equations (1) and (2), if we substitute h_i with g_i, the score statistic to test whether the variance component of genotypes is zero will be

$$T_{\mathit{\text{GKAT}}}={(\mathit{y}-\widehat{\mathit{\mu }})}^{\prime }{\mathit{G}}^{\prime }{\mathit{W}}_G\mathit{G}(\mathit{y}-\widehat{\mathit{\mu }}),$$ (5)

where G is the genotype matrix with the i^th column to be g_i, and W_G is a diagonal matrix with the (j, j)-th element to be the weight given to the jth genetic variant. This test is referred to as the genotype kernel association test (GKAT). Similarly, T_HKAT is asymptotically distributed as a mixture of χ² variables: ${\sum }_{i=1}^{{\varpi }^{\prime }}{\lambda }_i{\chi }_{1,i}^2$, where ${\chi }_{1,i}^2$'s are independent χ² variables with one degree of freedom, and λ₁ ≥ λ₂ ≥ ⋯ ≥ λ_ϖ′ are the ordered eigenvalues of the matrix ${\mathit{P}}_0^{1/2}{\mathit{G}}^{\prime }{\mathit{W}}_G\mathit{G}{\mathit{P}}_0^{1/2}$ (with the rank of ϖ′).

The test statistic of GKAT is equivalent to that of the popular sequence kernel association test (referred to as ‘SKAT’) [Wu et al., 2011], except the weight given to genetic variants, i.e. W_G in Equation (5). In SKAT, the weight given to the jth variant is w_j = Beta (p_j; a_1, a₂)², where p_j is the MAF of the jth variant, and a_1, and a₂ are suggested to be set at 1 and 25, respectively [Wu et al., 2011]. We call the test in Equation (5) GKAT rather than SKAT [Wu et al., 2011], because we want to distinguish the situations of using SKAT and GKAT. SKAT has been proposed by Wu et al. [2011] for analyzing sequencing data, whereas GKAT is used to analyze genotyped SNPs in GWAS or CGAS.

W_H and W_G

In Equations (3) and (5), W_H and W_G are diagonal matrices with weights given to distinct haplotypes and SNPs, respectively. If mutations are rare, the distribution of the frequency (p) of the mutant allele is f(p) ∝ p⁻¹ [Wright, 1931; Crow and Kimura, 1970; Kimura, 1983; Hill et al., 2008]. A causal allele may be a mutant allele or an ancestral allele, so the frequencies of causal alleles follow a U-shaped distribution; i.e. f(p) ∝ p⁻¹ + (1 − p)⁻¹ = [p (1 − p)]⁻¹ [Hill et al., 2008]. Therefore, a straightforward weight given to a genetic variant with MAF of p_j is [p_j (1 − p_j)]⁻¹. To avoid obtaining an extreme weight given a p_j very close to 0, we follow Madsen and Browning [2009] to estimate frequencies as ${\widehat{p}}_j=\frac{(m_j+1)}{(2n_j+2)}$, where m_j is the number of minor allele observed for the jth SNP and n_j is the total number of subjects genotyped for that SNP. In the following, GKAT is evaluated with W_G = diag ([p̂₁ (1 − p̂₁)]^−k, ⋯, [p̂_L (1 − p̂_L)]^−k), where L is the number of loci in the chromosomal region and $k=0,\frac{1}{2}$, and 1, respectively. According to the different levels of k, the test is referred to as GKAT0, GKAT1/2, or GKAT1, respectively. As mentioned above, k = 1 is a straightforward choice given the U-shaped distribution for a causal allele [Hill et al., 2008]. The choice of $k=\frac{1}{2}$ is based on Madsen and Browning's [2009] weight given to genetic variants. In addition, k = 0 represents a same weight given to all variants, regardless of their MAFs.

Parallel to GKAT, HKAT is evaluated at W_H = diag([f̂₁ (1 − f̂₁)]^−k, ⋯, [f̂_L (1 − f̂_L)]^−k), where L here is the number of distinct haplotypes in the chromosomal region and $k=0,\frac{1}{2}$, and 1, respectively. The test is referred to as HKAT0, HKAT1/2, or HKAT1, respectively. In W_H, f_h is the frequency of haplotype h, estimated with ${\widehat{f}}_h=\frac{(C_h+1)}{(2n+2)}$, where C_h is the number of haplotype h among all of the n subjects. When haplotype phases are ambiguous, C_h can be inferred from unphased multimarker genotypes using the expectation-maximization algorithm [Dempster et al., 1977], under the assumption of Hardy-Weinberg equilibrium [Excoffier and Slatkin, 1995; Hawley and Kidd, 1995; Long et al., 1995].

When dealing with case-control studies, some researchers [Madsen and Browning, 2009; Li et al., 2010; Lin et al., 2012b] have proposed using only unaffected subjects to estimate MAFs or haplotype frequencies. However, weights dependent on traits (affected or unaffected) will inflate type-I error rates [Lin and Tang, 2011], especially for the HKAT1 test. Suppose the count of some distinct haplotype is five in the pooled sample and that, by chance, these five haplotypes are all contributed by the affected subjects. If we calculate the frequencies and consequent weights with only the unaffected subjects, this haplotype will be even more up-weighted (i.e., more than if it were weighted independently of the traits) and this artificial association will be amplified. This phenomenon will jeopardize the validity of the HKAT1 test, in which a larger magnitude of weight (k = 1) is given to haplotypes. Therefore, we use the whole sample to estimate MAFs (in GKAT) or haplotype frequencies (in HKAT).

Simulation study

Following Li et al.'s simulation [2010] and using the Cosi program [Schaffner et al., 2005], we generated 500 data sets each containing 10,000 chromosomes of 1 Mb regions. The chromosomes were generated according to the LD patterns of the HapMap CEU samples, and an ∼50 kb causal region was randomly picked from the 1 Mb region for each data set. Within each causal region, we randomly selected d variants (d = 5, 10, 20, 30, or 40) as causal variants. When evaluating the performance of different methods for detecting uncommon causal variants, the causal variants were chosen from the variants with population MAFs ranging from 0.1% to 5%. In addition, a gene may harbor both uncommon and common causal variants, and therefore we also consider the scenario with causal variants having population MAFs ranging from 0.1% to 30%. Minor alleles were treated as causal alleles, which might be deleterious or protective (or, increase or decrease the trait values, when continuous traits are simulated). We let r_isk % of the d causal variants increase the disease risk, while the remaining (1- r_isk) % decrease the disease risk (or increase/decrease the value of a continuous trait). The value of r_isk was evaluated at 5, 20, 50, 80, and 100, respectively. To mimic the selection of tagging SNPs based on the HapMap CEU data, for each data set, we randomly chose 120 from the 10,000 chromosomes and paired them as 60 subjects. Based on the LD patterns of the 60 subjects, we used the H-clust method [Rinaldo et al., 2005; Roeder et al., 2005] to select tagging SNPs with the conventional criteria, i.e. r² > 0.8 (only one SNP selected from a group of SNPs in LD with r² > 0.8) and MAF > 5% [Barrett and Cardon, 2006; Keating et al., 2008]. These tagging SNPs were served as genotyped genetic variants in our simulations. For each simulated data set, a 20-tagging-SNP window that encompasses the causal region was chosen as a multimarker set used for analysis.

Dichotomous traits

Population genetics theories and empirical studies all support the assumption that the effect sizes of causal variants tend to be inversely related to their allele frequencies [Park et al. 2011; Bodmer and Bonilla, 2008; Eyre-Walker, 2010; Weetman et al., 2010; Ramsey et al., 2012]. Therefore, following previous studies [Madsen and Browning, 2009; Li et al., 2010; Lin et al., 2012b], we let the genotype relative risk (GRR) of the jth causal variant be

$${\mathit{\text{GRR}}}_j={(\frac{{\mathit{\text{PAR}}}_j}{(1-{\mathit{\text{PAR}}}_j)·{\mathit{\text{MAF}}}_j}+1)}^{{(-1)}^{I({\xi }_j=1)}},$$ (6)

where PAR_j and MAF_j are the population attributable risk (PAR) and the population MAF of the jth causal variant, respectively. The indicator function I(ξ_j = 1) is 1 or 0 according to whether the jth causal variant is protective or deleterious. Given PAR, the relationship between MAF and GRR is shown in Supplementary Figure S1. In addition, Supplementary Figures S2 and S3 present the distributions of MAFs and GRRs of the causal variants in our 500 simulated data sets, respectively.

To generate the genotypes of an individual, we randomly selected two chromosomes from the remaining 9,880 (= 10,000–120) chromosomes. The disease status of an individual with chromosomes {H₁, H₂} was determined by

$$P(\mathit{\text{affected}}|\{H_1,H_2\})=f_0\times \prod _{k=1}^2\prod _{j=1}^d{\mathit{\text{GRR}}}_j^{I(H_{k,j}=a_j)},$$ (7)

where f₀ was the baseline penetrance and was fixed at 10% [Li et al., 2010; Lin et al., 2012b], and a_j was the minor allele of the jth causal variant. The total sample size was set at 2,000. Considering that cases are usually more difficult to recruit and so many studies have fewer cases than controls [WTCCC, 2007; Zhernakova et al., 2007; Barrett et al., 2011; Macgregor et al., 2011; Sawcer et al., 2011], we let the 2,000 subjects be composed of 400 cases and 1,600 controls (a balanced case-control design with equal numbers of cases and controls will be discussed later). After generating the disease status based on Equation (7), the genotypes of the causal variants that were not selected as tagging SNPs were removed from our analysis data sets. When all of the causal variants were uncommon (MAF < 5%), almost all of them were removed from the multimarker set because the tagging SNPs were selected with the criterion of MAF > 5% [Barrett and Cardon, 2006; Keating et al., 2008]. When the causal variants were selected from those having MAFs ∈[0.1%, 30%], some common causal variants (MAF > 5%) might be reserved in the multimarker set if they were selected as tagging SNPs.

Continuous traits

In addition to dichotomous traits, we also simulated continuous traits. The trait value (Y) was generated by

$$Y=10C_1+10C_2+{\beta }_1{g}_1+{\beta }_2{g}_2+\cdots +{\beta }_d{g}_d+e,$$ (8)

where C₁ was a continuous covariate following a standard normal distribution, C₂ was a dichotomous covariate taking a value of 0 or 1 each with a probability of 0.5, g_j was the number of causal allele on the j^th causal variant (g_j = 0, 1, or 2), β_j was the effect size of the j^th causal variant, and e was the random error. The random error, e, was assumed to have a normal distribution with a mean of zero and a variance of V_e. The effect sizes β's and V_e were determined so that the ‘marginal heritability’ (the heritability of each causal variant, notated as h² and $h^2=\frac{\mathit{\text{Var}}({\beta }_j{g}_j)}{\mathit{\text{Var}}(Y)}=\frac{\mathit{\text{Var}}({\beta }_j{g}_j)}{\mathit{\text{Var}}(10C_1+10C_2)+\mathit{\text{dVar}}({\beta }_j{g}_j)+V_e}$ for j = 1,…,d) was fixed at 0.05%, 0.1%, 0.15%, or 0.2% under the alternative hypothesis. The actual values of V_e and β's were not critical. Once V_e was specified, β's were determined via the setting of the marginal heritability. We first assigned an arbitrary value to V_e, and we then obtained β_j(j = 1,…,d) from

$$\mathit{\text{Var}}({\beta }_j{g}_j)={\beta }_j^2·2·{\mathit{\text{MAF}}}_j·(1-{\mathit{\text{MAF}}}_j)=\frac{h^2·[V_e+\mathit{\text{Var}}(10C_1+10C_2)]}{1-d·h^2}=\frac{h^2·(V_e+125)}{1-d·h^2}.$$ (9)

The relationship between β's and the MAFs of causal variants is shown in Supplementary Figure S4. The total sample size was set at 2,000. After generating the traits, the genotypes of the causal variants that were not selected as tagging SNPs were removed from our analysis data sets.

Tests under comparison

We compared the three HKAT tests (HKAT0, HKAT1/2, HKAT1) and the three GKAT tests (GKAT0, GKAT1/2, GKAT1) with a global score test for haplotypes (hereinafter referred to as ‘global’) and a test based on the maximum score statistic over all haplotypes (hereinafter referred to as ‘max’), both of which have been widely used for haplotype association analyses [Schaid et al., 2002]. The global tests the overall effect of all haplotypes, while max tests the effect of the most significant haplotype. When performing global and max, the haplotypes with counts less than 5 were lumped into a single baseline group, according to the default of the package ‘haplo.stats’ [Schaid et al., 2002]. To allow the HKAT tests to be robust to genotyping errors, we merged haplotypes having a count less than 5 with their most similar haplotypes having a count larger than 5, where ‘5’ was chosen to lead to a parallel comparison on HKAT, global, and max. Under the assumption of Hardy-Weinberg equilibrium [Excoffier and Slatkin, 1995; Hawley and Kidd, 1995; Long et al., 1995], we used the ‘haplo.em’ function in the ‘haplo.stats’ package [Schaid et al., 2002] to infer haplotype phases from unphased multimarker genotypes with the expectation-maximization algorithm [Dempster et al., 1977]. The jth element of h_i=[h_i,1 h_i,2 ⋯ h_i,L]' in Equation (1) is determined by $h_{i,j}=\frac{1}{2}\sum _{k\ne j}\text{Pr}(H_j,H_k|{\mathit{g}}_{\mathit{i}})+\text{Pr}(H_j,H_j|{\mathit{g}}_{\mathit{i}})$, where Pr(H_j, H_k | g_i) is the posterior distribution of haplotype pairs (H_j, H_k)given multimarker genotypes g_i. In this way, all possible haplotype pairs were considered with their posterior probabilities. To have a better control of type-I error rates, phasing cases and controls together (instead of phasing them separately) was suggested [Lin and Huang, 2007]. Therefore, we phased the pooled sample of cases and controls when dichotomous traits were evaluated.

In addition to global and max, we used the R package ‘SKAT’ to perform the popular sequence kernel association test (referred to as ‘SKAT’) [Wu et al., 2011], as well as the optimal test (referred to as ‘SKAT-Op’) [Lee et al., 2012], which optimally combines the burden tests [Li and Leal, 2008; Madsen and Browning, 2009; Morris and Zeggini, 2010; Price et al., 2010; Lin et al., 2011] and SKAT [Wu et al., 2011]. Both SKAT and SKAT-Op were proposed for dealing with sequencing data, therefore we applied these two approaches to the full sequence (rather than merely the 20 tagging SNPs) of the analysis region. For any given data set, there were around 170∼280 observed variants in an analysis region. With consideration of cost, there is a trade-off between the number of subjects and different study designs (CGAS or next generation sequencing) [Sampson et al., 2011; Sboner et al., 2011]. Therefore, following a suggestion from an anonymous reviewer, when performing SKAT and SKAT-Op on full sequencing data, the total sample size was set at 200 (or 40 cases and 160 controls for simulations of dichotomous traits) rather than 2000.

When analyzing dichotomous traits, we also included a haplotype grouping test (referred to as ‘HG’) [Feng and Zhu, 2010; Zhu et al., 2010] and a weighted haplotype test on genotyped SNPs (referred to as ‘WHG’) [Li et al., 2010] into comparisons. First, the data are split into a training set and a testing set. HG classifies haplotypes as risk or non-risk with the training set, and then tests for associations by performing a Fisher's exact test with the testing set. WHG is based on a similar procedure, but it further boosts power to detect rare variants by weighting haplotypes according to their frequencies. For both tests, we randomly selected 30% of the sample as the training set and let the remaining 70% be the testing set, following the allocation chosen by previous studies [Li et al., 2010; Lin et al., 2012b].

Results

Type-I error rates

By setting the PAR (for dichotomous traits) or the marginal heritability (for continuous traits) at exactly 0%, we evaluated type-I error rates by performing 1,000 replications for each of the 500 simulated data sets. The P-values of global and max were obtained with 1,000-20,000 permutations by a sequential Monte Carlo algorithm [Besag and Clifford, 1991], according to the default of the package ‘haplo.stats’ [Schaid et al., 2002]. Then we evaluated type-I error rates given significance levels from 10⁻⁴ to 10⁻¹. Based on 500,000 (=500×1000) replications across the 500 simulated data sets, Figure 1 shows that all of the 12 tests (for dichotomous traits) or 10 tests (for continuous traits) are valid in the sense that their type-I error rates match the nominal significance levels.

Figure 1. Type-I error rates.

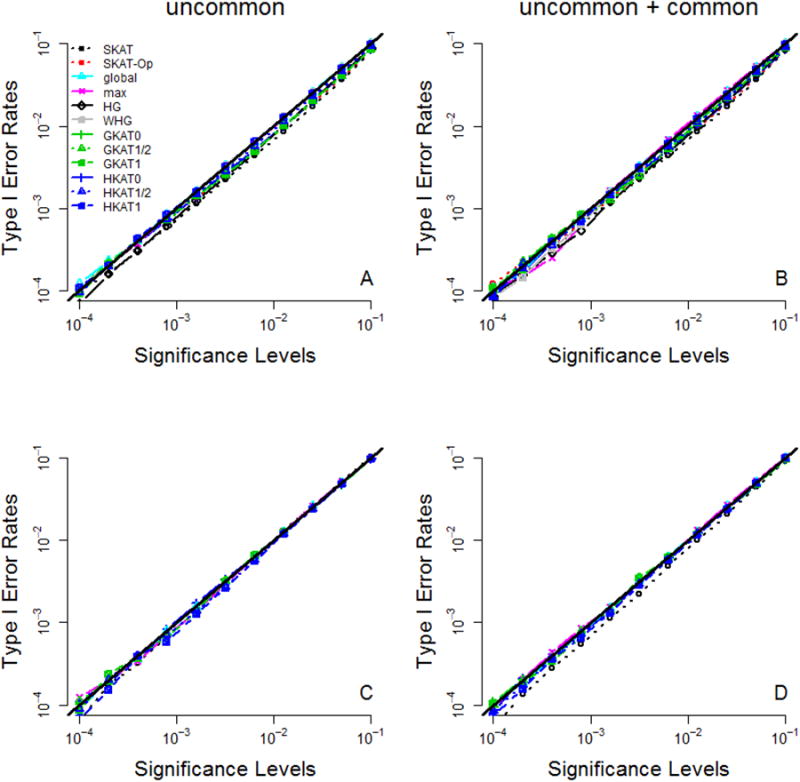
The x-axis is the nominal significance level (where the leftmost point is 10⁻⁴ and the rightmost point is 10⁻¹), and the y-axis is the type-I error rate. Panel (A): dichotomous traits and ‘uncommon’ causal variants with MAFs ∈[0.1%, 5%]; panel (B): dichotomous traits and ‘uncommon + common’ causal variants with MAFs ∈[0.1%, 30%]; panel (C): continuous traits and ‘uncommon’ causal variants with MAFs ∈[0.1%, 5%]; panel (D): continuous traits and ‘uncommon + common’ causal variants with MAFs ∈[0.1%, 30%]. The curves of all the tests are on the line y = x (the black bold line).

Power comparisons

When we evaluated power, a total of 100 replications were performed under each scenario (each combination of r_isk, PAR or marginal heritability, and d) for each of the 500 simulated data sets. Figures 2 and 3 present the power averaged over the 500 data sets, given a nominal significance level of 10⁻³, for dichotomous traits and continuous traits, respectively. When the nominal significance level is set at 10⁻⁴, we get the results presented in Supplementary Figures S5-S6. HKAT1 (HKAT with a weighting order k = 1) is the most powerful test, given uncommon causal variants with MAFs ∈[0.1%, 5%] or given a mixture of uncommon and common causal variants with MAFs ∈[0.1%, 30%].

Figure 2. Dichotomous trait - Comparison of power by r_isk (the percentage of deleterious variants among the d causal variants), PAR, and d (the number of causal variants).

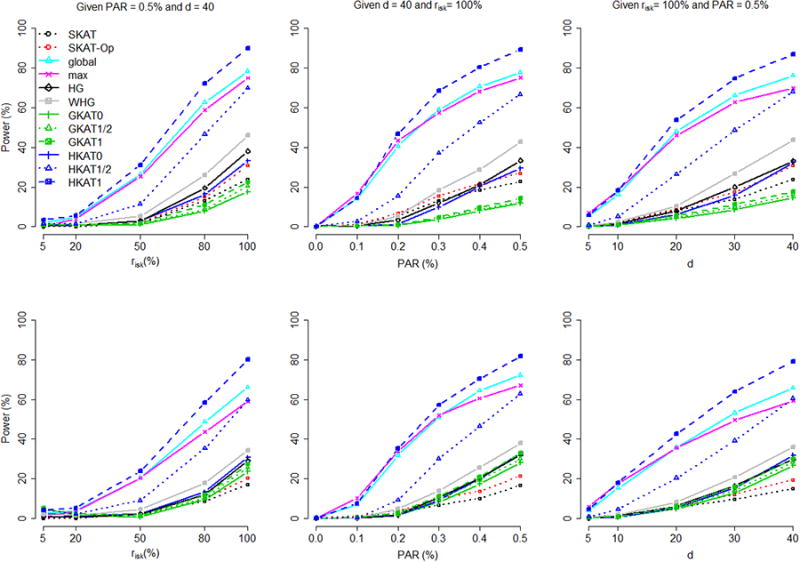
The figure shows the power comparison by r_isk (left column, given PAR = 0.5% and d = 40), PAR (middle column, given d = 40 and r_isk = 100%), and d (right column, given r_isk = 100% and PAR = 0.5%), respectively. The nominal significance level was set at 10⁻³. The top row is the result given ‘uncommon’ causal variants with MAFs ∈[0.1%, 5%]; the bottom row is the result given ‘uncommon + common’ causal variants with MAFs ∈[0.1%, 30%].

Figure 3. Continuous trait - Comparison of power by r_isk (the percentage of variants among the d causal variants that increase the trait value), the marginal heritability, and d (the number of causal variants).

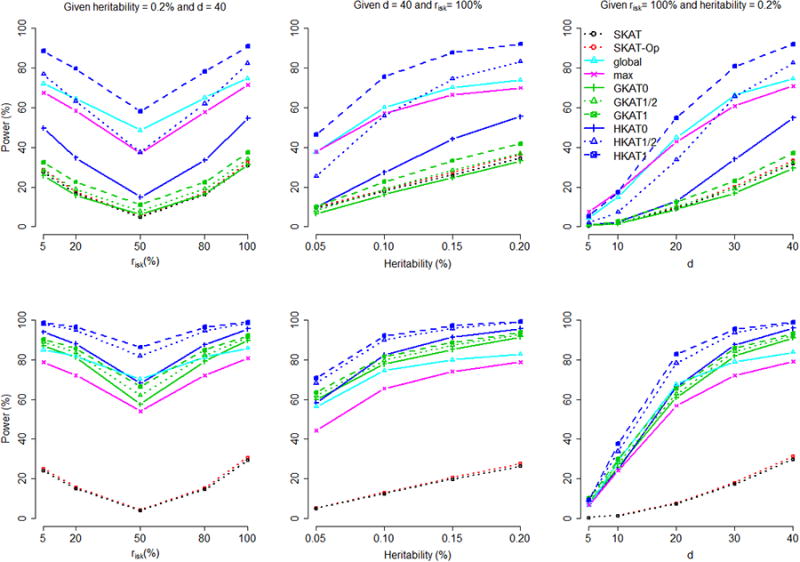
The figure shows the power comparison by r_isk (left column, given the marginal heritability = 0.2% and d = 40), the marginal heritability (middle column, given d = 40 and r_isk = 100%), and d (right column, given r_isk = 100% and the marginal heritability = 0.2%), respectively. The nominal significance level was set at 10⁻³. The top row is the result given ‘uncommon’ causal variants with MAFs ∈[0.1%, 5%]; the bottom row is the result given ‘uncommon + common’ causal variants with MAFs ∈[0.1%, 30%].

The power performance of these tests may be sensitive to (1) the percentage of rare variants among all causal variants, and (2) the LD pattern between the causal variants and the surrounding markers. With stratified analysis, we find that HKAT1 consistently outperforms other tests over all ranges of percentage of rare variants, and all ranges of average r² between causal variants and surrounding markers (data not shown).

Regarding the power performance of different levels of weighting order, k = 1 is the best, followed by $k=\frac{1}{2}$ and k = 0, for both HKAT and GKAT. This is because k = 1 setting up-weights rare haplotypes that are more likely to tag rare causal variants. As can be seen in the top rows of Figures 2-3, genotype-based tests (GKAT and SKAT [Wu et al., 2011; Lee et al., 2012], which are equivalent except for different weighting schemes given to variants) are underpowered when all causal variants are uncommon with population MAFs ∈[0.1%, 5%], because their power can only be driven by tagging SNPs (usually with MAF > 5% [Barrett and Cardon, 2006; Keating et al., 2008]) that are generally not good surrogates for uncommon causal variants. Haplotype-based tests (HKAT, global, and max) are more powerful because haplotypes can be better tags for uncommon causal variants. When some causal variants are common (so that the tagging SNPs are likely to represent the information of these common causal variants), the performance of genotype-based tests (GKAT and SKAT) improves, although it still cannot compete with HKAT (see the bottom rows of Figures 2-3). Note that our results for SKAT and SKAT-Op do not imply that they have similar performance when dealing with next-generation sequencing data in which rare variants should also be genotyped. Here we incorporated these two tests simply because of their relatedness with GKAT.

Application to a Human Adiposity Study

Next, we applied the 10 tests for continuous traits to a human adiposity study [Chung et al., 2009]. In this study, 1,982 unrelated European Americans living in the New York City metropolitan area were recruited. We investigated the association of 17 tagging SNPs in the Janus kinase 2 (JAK2) gene (located on chromosome 9p24) with body-mass index (BMI). These 17 tagging SNPs were selected from SNPs from 10,000 base pairs upstream to 10,000 base pairs downstream of JAK2's coding sequence, according to the conventional criteria of r² > 0.8 and MAF > 5%. Following Chung et al. [2009], we first adjusted the log-transformed BMI with sex, age, age², and their respective interactions. Associations of the joint additive and dominance effects of each of the 17 tagging SNPs with BMI were tested using the ordinary-least-squares regression method. Consistent with the results from Chung et al. [2009] (see their Table 3), there were six SNPs with P-values smaller than 0.05, with the smallest P-value (0.008) being observed on SNP rs3780365. However, after correcting for multiple testing, none of the six SNPs was significant at the family-wise error rate of 0.05.

We then resorted to the 10 multimarker tests. The first step was to define a ‘multimarker set’. A natural strategy is to aggregate all SNPs located in a gene [Schifano et al., 2012]. We let all the 17 SNPs in the JAK2 gene be a ‘multimarker set’ and analyze this set with the 10 multimarker tests, respectively. Among the 10 tests, GKAT0, GKAT1/2, GKAT1, and HKAT1 suggest that the JAK2 gene is associated with BMI, and the P-values are 0.025, 0.026, 0.024, and 0.025, respectively. The P-values of other six multimarker tests are all larger than 0.05.

Another commonly used strategy is to partition a gene into segments according to the LD patterns [Gabriel et al., 2002; Zhang et al., 2002; Twells et al., 2003; Han and Pan, 2010; Schifano et al., 2012]. Based on the default of Haploview [Barrett et al., 2005] to customize the haplotype blocks (the Gabriel et al.'s rule [2002]), there are two haplotype blocks in the JAK2 gene. We applied the 10 multimarker tests to the two haplotype blocks, respectively. Only HKAT1 and global suggest an association of haplotypes from the second block (rs3780365- rs2230724- rs1410779- rs3824432- rs3780372- rs10491652- rs3780379- rs966871) with BMI, and the P-values are 0.004 and 0.006, respectively.

JAK2 is involved in leptin, insulin, and ABCA1 (the adenosine triphosphate-binding cassette transporter A1) signaling pathways [Banks et al., 2000]. Disturbance in leptin and insulin signalling pathways are related to obesity and metabolic syndrome [Penas-Steinhardt et al., 2011]. It may influence body fat mass, insulin sensitivity, or serum lipid profile in humans [Ge et al., 2008]. An independent study genotyped tagging SNPs spanning JAK2 for 2,760 white female twin subjects from the St. Thomas' U.K. Adult Twin Registry [Ge et al., 2008], and it led to a similar result as that of Chung et al.'s study [2009]. That is, although some P-values of SNP-obesity association were smaller than 0.05, none of these remained significant after adjusting for multiple testing. Investigation of the tagging SNPs via HKAT may provide additional information that may be missed by single-marker analyses.

Discussion

Because the cost of sequencing remains high, association studies using SNP arrays or tagging SNPs are still among the most commonly available data types in the current stage [WTCCC, 2007; Li et al., 2010]. The aim of this study is to provide a valid and powerful statistical method for detecting disease-associated genomic regions with uncommon causal variants from contemporary GWAS or CGAS data sets, thus bypassing the genome-wide or exome-wide next-generation sequencing. Both uncommon causal variants with large effect sizes and common variants with small effect sizes are possible to contribute to the missing heritability for complex diseases [Manolio et al., 2009; Eichler et al., 2010; Yi et al., 2011]. Single-locus analysis is underpowered to detect these two types of causal variants [Stahl et al., 2010, 2012]. Because a susceptibility gene is likely to harbor multiple causal variants [Hugot et al., 2001; Ogura et al., 2001; Pritchard, 2001; WTCCC, 2007; Madsen and Browning, 2009; Wang et al., 2010], we investigate methods that can test multiple SNPs aggregately for a collective signal on traits. These methods include SKAT, which is popular and powerful for rare variant detection [Wu et al., 2010; Wu et al., 2011; Lee et al., 2012]; global and max [Schaid et al., 2002], which have been widely used for detecting haplotype-trait association; our HKAT and GKAT equipped with three levels of weighting order ( $k=0,\frac{1}{2}$, and 1). After simulating scenarios based on the population genetics theory [Wright, 1931; Crow and Kimura, 1970; Kimura, 1983; Hill et al., 2008], we find that HKAT1 is the best test to detect the signal of uncommon causal variants.

HKAT is computationally feasible, because it is based on a score test without fitting the full model (i.e., the model under the alternative hypothesis). On an Intel Xeon workstation with 3.0 GHz of CPU and 2.0 GB of memory, HKAT with a 20-SNP multimarker set on average takes ∼0.9, ∼7.0, and ∼22.8 seconds to analyze 1000, 2000, and 3000 subjects, respectively. In genetic studies, haplotype phase is usually unknown when diploid subjects are heterozygous at more than one chromosomal locus. Therefore, we inferred haplotype information with the expectation-maximization algorithm [Dempster et al., 1977], which leads inferred haplotype frequencies to maximum likelihood estimates under the assumption of Hardy-Weinberg equilibrium [Excoffier and Slatkin, 1995; Hawley and Kidd, 1995; Long et al., 1995]. There are two common uses of the inferred haplotypes in downstream analyses. One way is to use the most likely haplotype pair, which has the highest posterior probability among all possible haplotype pairs of a subject. The most likely haplotype pair is assigned probability 1 and all other possible haplotype pairs are assigned probabilities 0. This common practice is intrinsically biased because the most likely haplotype pair is not necessarily the true haplotype pair of that subject [Lin and Huang, 2007]. Another way is the expectation substitution approach [Zaykin et al., 2002; Stram et al., 2003]. That is, a subject's expected frequencies of haplotypes are treated as observed and directly used in downstream analyses. Under the null hypothesis of no haplotype effects, similar to previous methods [Schaid et al., 2002; Zaykin et al., 2002; Stram et al., 2003], the resulting score statistic (i.e., HKAT statistic in Equation (3)) is unbiased and gives correct type-I error rates (see Figure 1). Employing this expectation substitution approach, although the variability of the estimated haplotype frequencies is not explicitly incorporated in the variance of the HKAT statistic, the HKAT test is shown to be valid.

The HKAT and GKAT proposed here are applicable to CGAS or GWAS. An issue is how to select a set of SNPs to be included in a multimarker test. Natural strategies include aggregating all SNPs located in a gene or within a haplotype block [Feng and Zhu, 2010; Lin et al., 2012a; Schifano et al., 2012], as we have shown in the analysis for the human adiposity study. Haplotype-based methods such as HKAT are justifiable to analyze haplotype blocks, which are discrete chromosome regions containing SNPs in high LD [Cardon and Abecasis, 2003]. Another strategy is to use sliding windows [Guo et al., 2009; Wang et al., 2012]. In general, multimarker analyses with larger window sizes may allow for measuring sharing over longer genomic sequences and lead to more power gains [Allen and Satten, 2009; Lin et al., 2012b].

The HKAT and GKAT can be applicable to continuous or dichotomous traits. In our simulation for dichotomous traits, we considered an unbalanced case-control design with 20% cases and 80% controls. For a balanced case-control design (with 50% cases and 50% controls), HKAT1 has a similar performance with global. However, HKAT1 is still more advantageous than global in computational feasibility, because no permutation is required for HKAT1. By contrast, global needs permutations to obtain reliable P-values when the frequencies of some haplotypes are low [Schaid et al., 2002; Lin et al., 2012b].

Our work shows that in GWAS using commercial SNP arrays or CGAS using tagging SNPs, the haplotype-based methods (e.g., HKAT, global [Schaid et al., 2002], max [Schaid et al., 2002], HG [Feng and Zhu, 2010; Zhu et al., 2010], and WHG [Li et al., 2010]) are more promising than the genotype-based methods (e.g., GKAT, SKAT [Wu et al., 2011], and SKAT-Op [Lee et al., 2012]) in detecting uncommon causal variants. Among haplotype-based methods, HKAT is further shown to be more powerful than HG [Feng and Zhu, 2010; Zhu et al., 2010] and WHG [Li et al., 2010], because the power of HG or WHG is generally compromised due to splitting the data into two subsets (i.e., a training set and a testing set). In addition, HKAT1 outperforms global and max by up-weighting uncommon haplotypes that may be better tags for uncommon causal variants. When a gene harbors both uncommon and common causal variants, HKAT1 remains the most powerful test among all the tests we evaluate here. Note that this conclusion is based on the simulation scenario following the population genetics theory (i.e., the distribution of causal allele frequencies is U-shaped) [Wright, 1931; Crow and Kimura, 1970; Kimura, 1983; Hill et al., 2008], and in this situation k = 1 is a straightforward and reasonable weighting order. However, for any given study, the most powerful test may vary if the underlying genetic architecture departs from the population genetics theory.

At the pseudo-sequencing level (i.e., GWAS or CGAS imputed with publicly available sequencing data) [Li et al., 2010] or the sequencing level, the haplotype-based methods may not be as promising as the genotype-based methods. This deserves further investigation. In recent years, many novel methods have been proposed for rare variant identification using next-generation sequencing data [Li and Leal, 2008; Madsen and Browning, 2009; Han and Pan, 2010; Liu and Leal, 2010; Morris and Zeggini, 2010; Price et al., 2010; Basu and Pan, 2011; Lin et al., 2011; Neale et al., 2011; Wu et al., 2011; Yi et al., 2011; Yi and Zhi, 2011; Lee et al., 2012; Liu and Leal, 2012]. However, next-generation sequencing data have not been prevalent till today. By contrast, few methods have been proposed for detecting uncommon causal variants from genetic association studies genotyped with tagging SNPs or commercial SNP arrays. We here provide a haplotype-based test that is powerful to detect disease-associated regions from GWAS or CGAS.