Simulating Linkage Disequilibrium Structures in a Human Population for SNP Association Studies

Abstract

Existing simulation methods usually simulate linkage disequilibrium (LD) structures starting with an initial population that is randomly generated according to specified allele frequencies. These at random based methods might be unstable because the LD level of the initial population is generally extremely low. This study presents a new algorithm, SIMLD, to simulate genome populations with real LD structures. SIMLD begins from an initial population with possibly the highest LD level, and then the LD decays to fit the desired level through processes of mating and recombination over generations. SIMLD can produce case–control samples according to various disease models. Using empirical SNP marker information from three populations of HapMap data, we implement the proposed algorithm and demonstrate a set of experimental results.

Introduction

The International HapMap project (International HapMap Consortium 2003, 2005; http://www.hapmap.org/) has provided a public resource to help researchers perform disease gene studies. Though its continuously updated datasets are very significant in the development of statistical approaches for SNP association studies, in the study of real genome data, the lack of known disease markers makes it difficult to evaluate the performance of the approaches. A possible solution is to develop techniques to simulate samples with real genome features and known markers. This is believed to be a key step in successful efforts to find genes or single nucleotide polymorphisms (SNPs) associated with human diseases or responses to pharmaceuticals (i.e., to produce abundant simulated human genome data).

One of the most significant features of human genome data is linkage disequilibrium (LD) structure, defined as gametic phase disequilibrium, or allelic association. It is a nonrandom correlation between alleles at different loci in a chromosome population. LD exists because of the shared ancestry of contemporary chromosomes. Strong linkage between loci on the same chromosome could result in high levels of LD. Naturally, the processes of recombination and mutation often act to decay strong LD levels. For a pair of SNP alleles, LD is a measure of deviation from random association (i.e., no recombination), and it is usually measured by r² or D′ (Lewontin 1988). In recent years, LD analysis has become a topic of great interest in the field of SNP association studies and an effective approach to connect structural SNPs to phenotypes.

Generally, simulation methods are expected to generate real LD structures across the genome. Unfortunately, uncertainties in the genetic history of human populations make it difficult to implement such simulations. Various simulation methods have been developed. GenomeSIM (Dudek et al. 2006) allows users to specify many parameters to control evolutionary process and permits single-locus and multi-locus models to be associated with disease risk, but it is not clear how to get the expected LD. GenomeSIMLA (Edwards et al. 2008), an extension of GenomeSIM, can simulate real patterns of LD in both family-based and case–control datasets. Its computational complexity, however, is very high because of extremely low LD levels in the initial population. Simulation of linkage and association (SIMLA; Bass et al. 2004) and its extension (Schmidt et al. 2005) are proposed to generate pedigree data under user-specified conditions, and allow users to specify varying levels of LD among markers and between markers and disease loci. One drawback of these approaches is that they are not flexible in simulating LD structures, because markers must be selected manually to get the expected LD level based on conditional haplotype frequencies. HAP-Sample (Wright et al. 2007) is a nice Web tool that can simulate real human autosomal SNP data by resampling chromosome-length haplotypes from real data (phase I/II HapMap), and it also allows for considerable flexibility in disease models. Other methods such as Genome (Liang et al. 2007), MaCS (Chen et al. 2009), and SimuGWAS (Peng and Amos 2010) have also been developed recently. In the simulation of LD structures, many existing methods create an initial population by randomly arranging marker alleles, and then strengthen LD through processes of mating and recombination over generations. Empirically, these methods are usually unstable in converging to real LD and are computationally intensive because the LD level in the initial population is extremely low compared with the expected real one.

With these considerations, in this paper we present a new algorithm, SIMLD, to simulate genome populations with real LD structures. In comparison with existing methods, the central feature of SIMLD is that it initiates a population with the highest possible LD level, and then the LD decays gradually to fit the desired level through processes of mating and recombination. The initial population can be uniquely determined given allele frequencies, so the algorithm can avoid uncertainties of initialization and it is insensitive to starting genotypes. In each generation, mating is guided according to a distance function and crossover is supervised by a designed designator of recombination probabilities. SIMLD allows a variety of disease models and provides case–control samples. Using SNP information from three populations in phase I/II HapMap data as a basis of the LD information, we simulate a set of genome populations with the desired LD features and allele frequencies, as well as some specified disease models.

Materials and Methods

Description of SIMLD

SIMLD is freely available at http://simld.sourceforge.net/. The algorithm is implemented according to a set of parameters and a set of disease models. The parameters include chromosome population size, SNP size, simulation population (e.g., JPT/CHB, CEU, and YRI from phase I/II HapMap datasets), simulation regions, etc. The set of disease models including single-locus and multi-locus interactions is set in a disease model file. The parameters and the disease models provide information that a dataset to be simulated is assumed to be the one where the simulation population confines the LD levels among SNPs in the simulated data, and the simulated data are allowed to have genotype-phenotype association with the set of disease models in the disease model file. The real marker IDs, marker positions, and allele frequencies are gained from the prescribed phase I/II HapMap datasets, which have been incorporated in the simulation package. Exceptionally, if the number of available SNPs in HapMap datasets is less than the required number, the algorithm can randomly specify a minor allele frequency (MAF), in the range 0.01–0.5, for the remainders.

The flowchart of SIMLD in simulating case–control samples begins from an initial population with the highest possible LD level, and then the LD decays to fit the desired level through processes of mating and recombination over generations (Fig. 1). In a generation, each sample in the population will be mated with another one only once, and a pair of mated samples will give birth to two children for the next generation through crossover. This strategy can keep both the MAF of each allele and the population size unchanged over generations. The process of mating and crossover is a little different from that of meiosis, which consists of two successive nuclear divisions (Baker et al. 1976). In our method, the purpose of the crossover is to decay strong LD levels to approach the desired ones.

Fig. 1.

The flowchart of SIMLD. An initial population with the highest possible LD level is created, and then the population undergoes mating and recombination over generations to achieve the final population with the desired LD features. Subsequently, case–control samples are produced based on disease models. Output files are presented in both phased and genotype formats

After the final population has been obtained, nonredundant individuals are created by randomly selecting two chromosomes from the population. In phased data format, each allele value at one locus for an individual is “1, 2,” where “1” represents the major allele and “2” represents the minor allele. In genotype data format, we assume that there is no difference between 12 and 21. Thus, there are three possible genotypes for a SNP locus: 11, 12, and 22. For simplicity, the genotype value for the SNP is denoted as 1 (for 11), 2 (for 12), or 3 (for 22). The last step of SIMLD is to produce case–control samples based on disease models. Various models including single-locus and multi-locus interactions are allowed in the method. Users can either use default disease models or define different models by selecting disease loci and setting penetrance values.

Initialization

The initial population has a significant influence on the efficiency of data simulation. In this section, we present a novel strategy to initialize a chromosome population, by setting the initial population with the highest possible LD level. To achieve this, a particular distribution of alleles is established in the chromosome population, as demonstrated in the following example.

Assume a population consists of 20 chromosomes, each with 20 SNPs. The MAFs of the SNPs are 0.1, 0.1, 0.25, 0.25, 0.3, 0.3, 0.3, 0.4, 0.2, 0.15, 0.35, 0.25, 0.15, 0.15, 0.2, 0.35, 0.15, 0.15, 0.2, 0.2. We store the population in a matrix in which rows correspond to chromosomes and columns correspond to SNPs. To make the initial population achieve the highest possible LD level, we distribute the minor alleles in the top of the matrix (Fig. 2). The resulting LD level (mean r² × distance) of the current initial population is clearly higher than the other randomly initialized populations (Fig. 2).

Fig. 2.

Example of initializing population. Left In the matrix for storing allele sequences, each row corresponds to a chromosome and each column corresponds to an SNP. Right Mean r² as a function of distance in the population. The top curve shows the highest level of LD in the initial population; the lower curves are the LD levels of randomly generated populations

Obviously, the LD level of the population in the example (Fig. 2) greatly deviates from that of the real human genome data. However, if the minor alleles are randomly distributed in the matrix, the deviation from the real data will be even greater. When compared with random initialization, our approach shows several advantages, such as deterministic starting genotypes and that the initial population forms a basis for crossover to reduce strong LD to fit desired levels.

Processes of Mating and Recombination

To efficiently weaken LD through mating and recombination, we first design a distance function, Eq. 1, to guide the process of mating among chromosomes.

$$\mathrm{dist}({\mathrm{chr}}_i,{\mathrm{chr}}_j)=\sum _{k=1}^L\mid ({\mathrm{chr}}_{ik}-{\mathrm{chr}}_{jk})\mid ,i\ne j$$ (1)

Assume that a chromosome population is represented by Chr = {chr₁, chr₂, ..., chr_M}, where chr_i denotes the ith chromosome and chr_ik denotes the kth allele of chr_i. The mating process is performed from the first chromosome to the last one, and each chromosome will be mated only once. In the pool of chromosomes, the non-mated chromosomes are marked as free. The mate (chr^–) for chromosome chr_i is selected according to Eq. 2.

$${\mathrm{chr}}^{-}=\arg \underset{{\mathrm{chr}}_j\in {\mathrm{Chr}}^{\prime }}{\max }\left(\mathrm{dist}({\mathrm{chr}}_i,{\mathrm{chr}}_j)\right),$$ (2)

where Chr′ (a subset of Chr) is a set of free chromosomes and L is the length of chromosomes (i.e., it is the number of SNPs in the genome).

After the mating, new chromosomes will be generated based on recombination between mated chromosomes. To determine where recombination should occur, we present a designator to assign recombination probabilities (RPs) to adjacent SNPs. At the beginning, any adjacent SNP has the same RP, which usually falls in the range 0–0.5. When any crossover event occurs between adjacent SNPs A and B, the corresponding RP will be increased by a certain amount, while the RPs between the SNPs near A and B will be reduced by a certain amount. This strategy can account for recombination interference, which is an important feature of genetics in biology. In addition, some alternative approaches are available to calculate the values of RP, such as the mapping functions of Haldane (1919) and Kosambi (1944).

The RP designator incorporates four parameters, the initial RP, the distance near the recombination point, the rate of increase (i.e., how much RP should be increased), and the rate of decrease (i.e., how much RP should be decreased). We denote these parameters as Init_RP, Dist_near, Rate_in, and Rate_de, respectively. Theoretically, the four parameters not only impact the speed of simulating LD features but also influence the sizes of haplotype blocks. We test and validate the algorithm repeatedly and select the most suitable values for these parameters as default in the software package. For a clear understanding, we provide two equations to illustrate how RP value increases and decreases, assuming that the recombination probability between SNPs A and B is p: In_RP = (0.5 – p) * Rate_in, where In_RP is the increased RP between A and B; and De_RP = p_i * Rate_de, where De_RP is the decreased RP for p_i, p_i is the RP between the ith pair of SNPs near the breakpoint of A and B, and i is in the range of [1, Dist_near]. Thus, after the crossover, p is set as p + In_RP, and p_i is set as p_i – De_RP.

Termination Criteria

We use the LD level of the population to determine when the simulation process should stop. Generally, LD level is measured using mean r² or D′ by distance. To simulate LD structures in real genome data, we compare the LD levels of the simulated data with those of HapMap data. When the deviation between them reaches an acceptable level, the simulation process stops. That deviation in each generation is D(g), where g is the generation index (i.e., 1, 2, ...). Along with generations, D(g) decreases gradually to a minimum value and then might increase. When D(g) changes steadily during the latest generations, the simulation program is terminated and the generation with the minimum value of D(g) is selected as the final generation. D(g) is calculated by

$$D\left(g\right)=\sum _{i=1}^N{\left({\mathrm{LD}}_g^2\left(il\right)-{\mathrm{LD}}_h^2\left(il\right)\right)}^2,$$

where ${\mathrm{LD}}_g^2\left(il\right)$ and ${\mathrm{LD}}_h^2\left(il\right)$ denote the mean r² or D′ by distance (il) for the simulated and HapMap data at the gth generation, respectively; N is the number of segments of chromosome; and l is the segment length, calculated as the chromosome length L divided by N. Therefore, to solve the D(g) equation, we just need to define N. Generally, the longer the chromosome, the larger N might be defined.

In the simulation of LD structures, we consider the squared correlation coefficient (r²) or D′ in evaluating associations between SNPs but ignore signs of the correlation coefficients. Thus, the haplotype frequencies in the simulated population are not fixed even if the allele frequencies and LD structures are determined. Consequently, the final chromosome population is not unique due to nonunique haplotype frequencies. Given allele frequencies, the correlation between two loci can be calculated using any types of haplotypes (“1 1,” “1 2,” “2 1,” and “2 2”) such as “1 1”. If the sign of the correlation coefficient is negative, then there must be at least another correlation coefficient, which is calculated using another haplotype such as “1 2,” showing positive, and vice versa. This implies that both positive and negative correlation coefficients always exist between SNPs if they are not zero. In our method, the LD measures r² and D′ do not address the signs of correlation coefficients but allow for the diversity of haplotypes.

Simulation of Case–Control Samples

Based on the nonredundant individuals that are created in the chromosome population, SIMLD produces case–control samples according to specified disease models. Multiple disease models are allowed to generate disease status independently for each individual. To test the new algorithm, we use the SNP marker information from three populations, JPT/CHB, CEU, and YRI, in phase I/II HapMap data as substrate to simulate various genome data. For each population, we simulate four datasets (with 500, 1000, 2000, and 5000 SNPs), each with 2000 individuals. In these simulations, we limit the MAFs within 0.01–0.5. In the results of genome data simulation, we get 12 chromosome populations with the desired LD features. Particularly, in the simulation of the JPT/CHB population, we define four disease models to produce case–control samples, incorporating nine susceptibility SNPs chosen according to locus position and allele frequency (Table 1). The four disease models include 1 three-locus and 3 two-locus interactions (Tables 2, 3, 4, and 5). Other types of disease models, such as logistic function (Schmidt et al. 2005), absolute genotype specification, genotype relative risk specification, and absolute risk specification (Wright et al. 2007), could also be used in the method.

Table 1.

Nine susceptibility SNPs selected to define disease models

Disease SNP ID	Marker ID	Position	Minor allele frequency
dS1	rs2977670	713754	0.27
dS2	rs9442371	1008425	0.222
dS3	rs9442372	1008567	0.222
dS4	rs12402203	2155383	0.202
dS5	rs2643885	2211082	0.294
dS6	rs1496555	2224111	0.18
dS7	rs2843153	2235081	0.399
dS8	rs7545940	2289487	0.444
dS9	rs2840534	2293426	0.122

Table 2.

Three SNP interaction model, penetrance values for genotype combinations of SNPs dS1, dS2, and dS3

	dS1 (11)			dS1 (12)			dS1 (22)
	dS3 (11)	dS3 (12)	dS3 (22)	dS3 (11)	dS3 (12)	dS3 (22)	dS3 (11)	dS3 (12)	dS3 (22)
dS2 (11)	0.172	0.013	0.005	0.180	0.018	0.012	0.185	0.057	0.045
dS2 (12)	0.015	0.107	0.020	0.015	0.156	0.034	0.061	0.083	0.005
dS2 (22)	0.003	0.035	0.025	0.017	0.029	0.091	0.050	0.006	0.075

Genotype is indicated in parentheses: (11) and (22) are homozygous genotypes; (12) is the heterozygous genotype

Table 3.

Two-SNP interaction model, penetrance values for genotype combinations of SNPs dS4 and dS5

	dS5 (11)	dS5 (12)	dS5 (22)
dS4 (11)	0.179	0.083	0.038
dS4 (12)	0.085	0.173	0.007
dS4 (22)	0.033	0.005	0.086

Genotypes as in Table 2

Table 4.

Two SNP interaction model, penetrance values for genotype combinations of SNPs dS6 and dS7

	dS7 (11)	dS7 (12)	dS7 (22)
dS6 (11)	0.093	0.066	0.096
dS6 (12)	0.047	0.178	0.077
dS6 (22)	0.008	0.003	0.052

Genotype as in Table 2

Table 5.

Two SNP interaction model, penetrance values for genotype combinations of SNPs dS8 and dS9

	dS9 (11)	dS9 (12)	dS9 (22)
dS8 (11)	0.256	0.092	0.014
dS8 (12)	0.087	0.213	0.007
dS8 (22)	0.013	0.008	0.050

Generally, disease status greatly depends on penetrance value. The value over zero means that the genotype combination has positive association with the disease, while the value equal to zero means that the genotype combination has negative (protective) association with the disease. Since a couple of disease models have been used, heterogeneous disease has been incorporated (i.e., there are multiple factors related with the disease). To mark disease status for each individual, SIMLD first acquires the genotype combination of the susceptibility SNPs, and then determines if the individual is affected by generating a random number to compare with the corresponding penetrance value. If the random number is less than that value, the individual is affected.

After completion of the simulation, the 2000 individuals are divided into two groups, case and control. Usually, the two groups are not the same size. To conduct standard association studies, researchers may extract the same number of cases and controls from the individual population and then apply statistical methods to the case–control samples. For example, multifactor dimensionality reduction (Ritchie et al. 2001; Hahn et al. 2003) is a popular computational method to detect gene–gene and gene–environment interaction models using case–control samples.

Results

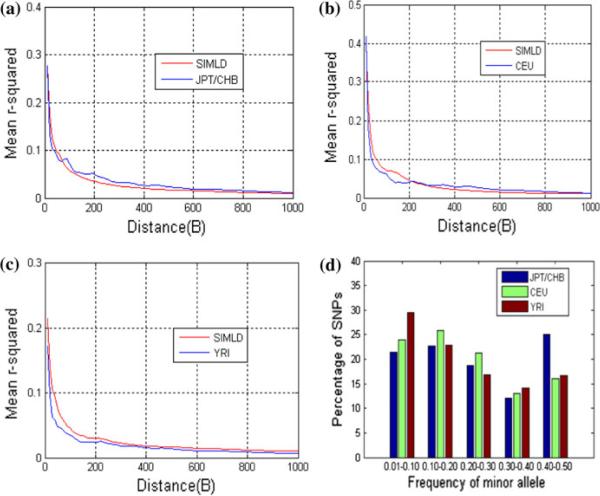
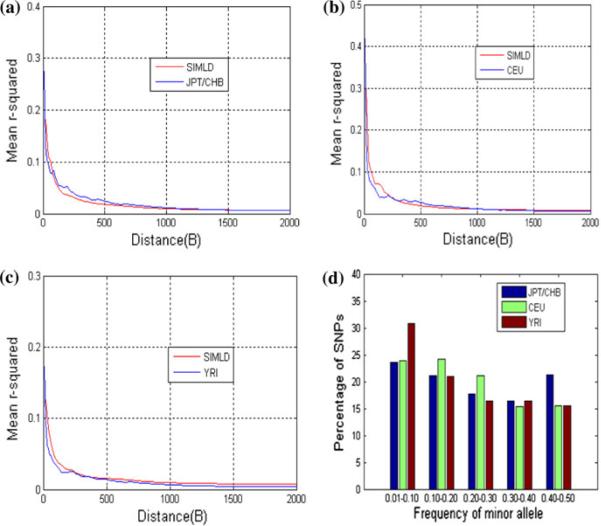
The results of the above simulation examples are described here. Table 6 lists the parameter settings for the simulation of each population. The LD levels of the simulated datasets compared with realistic datasets are presented in Figs. 3 (sim500SNPs_data), 4 (sim1000SNPs_data), 5 (sim2000SNPs_data), and 6 (sim5000SNPs_data), and triangle LD plots are compared for a sample of markers between the simulated data and real data (Fig. 3). The LD plots were made using Haploview software (Barrett et al. 2005). The numbers of cases and controls are also given for the simulation of the JPT/CHB population (Table 7).

Table 6.

Simulation algorithm parameters for three populations in this study

Parameter	JPT/CHB	CEU	YRI
Init_RP	0.0015	0.0020	0.0035
Dist_near	6 (Base)
Rate_in	0.018
Rate_de	0.020

	sim500SNPs_data	1000SNPs_data	sim2000SNPs_data	sim5000SNPs_data
N	10	20	40	100

Fig. 3.

Simulation results for sim500SNPs_data. LD (mean r²) value as a function of distance across the simulated genome region: red curves are the LD of the simulated data and blue curves are real data for a JPT/CHB, b CEU, and c YRI. d MAF distribution of the simulated 500 SNPs in the three populations. e Triangle LD plots (r²) of a sample of simulated JPT/CHB data (left) and a sample of real JPT/CHB data (right) (color figure online)

Fig. 4.

Simulation results for sim1000SNPs_data. LD (mean r²) value as a function of distance across the simulated genome region: red curves are the LD of the simulated data and blue curves are real data for a JPT/CHB, b CEU, and c YRI. d MAF distribution of the simulated 1000 SNPs in the three populations (color figure online)

Fig. 5.

Simulation results for sim2000SNPs_data. LD (mean r²) value as a function of distance across the simulated genome region: red curves are the LD of the simulated data and blue curves are real data for a JPT/CHB, b CEU, and c YRI. d MAF distribution of the simulated 2000 SNPs in the three populations (color figure online)

Fig. 6.

Simulation results for sim5000SNPs_data. LD (mean r²) value as a function of distance across the simulated genome region: red curves are the LD of the simulated data and blue curves are real data for a JPT/CHB, b CEU, and c YRI. d MAF distribution of the simulated 5000 SNPs in the three populations (color figure online)

Table 7.

Cases and controls obtained from the simulation of population JTP/CHB

Simulated dataset	Number of JTP/CHB individuals
	Cases	Controls	Total
sim500SNPs_data	870	1130	2000
sim1000SNPs_data	847	1153
sim2000SNPs_data	859	1141
sim5000SNPs_data	844	1156

In these simulations, we use mean r² to measure LD levels of genome populations. For another measure, D′, we have also compared the simulated data with real data (Supplementary Figs. 1, 2, 3, 4). Generally, it is difficult to optimize both r² and D′ measures in simulating LD features. In our results, the mean r² of the simulated data is very close to that of the real data (Figs. 3, 4, 5, and 6). In addition, Haploview software allows us to observe various haplotype blocks, including short and long block patterns, in the simulated data. Therefore, SIMLD is a valid algorithm in simulating genome data with real LD structures, and it can be used to assist investigators in exploring statistical methods for SNP association studies.

There remain, however, some deviations between the simulated data and HapMap data in terms of LD. Potential reasons for these deviations might include the following. First, the MAF in our simulation is 0.1–0.5, but the observed MAF is in the range 0–0.5. Second, genotyping errors and missing data are not considered in this approach. As for MAF, some deviations between simulated and real data might also be due to small population sizes. An estimate of the deviation for one SNP is given as

$$d=\frac{\sqrt{np}(1-p)}{n},$$

where n is the population size and p is the MAF of the SNP. Here, we assume that the number of the minor alleles (x) approximately follows a binomial distribution x ~ B (n, p), so our estimate of the SNP deviation is actually the standard deviation of the MAF.

In terms of computational complexity, SIMLD takes less than 5 min to finish the simulation of each dataset in the examples. When simulating a sample of 1500 individuals and SNP size of 500,000, it takes about 20 min. We have implemented SIMLD in C++ on a Linux system with Inter Core Duo CPU 2.16 GHz and 2 GB RAM. The major reason for the efficiency of SIMLD is that it usually needs less than ten generations to reach convergence, a great reduction in computational complexity from that of GenomeSIMLA, which often needs hundreds of generations to achieve desired LD features. SIMLD requires so few generations to achieve convergence possibly because the algorithm starts with an initial population with the highest possible LD level, which can be decreased rapidly over generations. Also, the strategies of mating and recombination among chromosomes are suitably designed.

Discussion

Success in finding disease-related genes using association or LD analysis methods depends partly on the power of genome data simulators, which can assist investigators in developing a variety of advanced methods. With that in mind, we have described a new algorithm, SIMLD, to simulate genome data with real LD structures. The central feature of SIMLD is that it begins from an initial population with the highest possible level of LD, and then decays the LD to fit a real level through mating and recombination over generations. Experimental results show that SIMLD can reach convergence within a few generations at high efficiency. Another feature of the method is that it is very flexible in incorporating various disease models to produce phenotypes for individuals.

SIMLD uses phase I/II HapMap datasets as a basis for simulating samples. Phase II HapMap, which characterizes over 3.1 million human SNPs genotyped in 270 individuals (International HapMap Consortium 2007), is a valuable resource that helps investigators perform disease-associated SNP studies and provides abundant allele information for our approach. In addition, SIMLD can be extended to simulate genome data that represent other populations in HapMap data. The population size and genome size are not limited in SIMLD as long as memory is permitted. Using simulated case–control data, users can assess the performance of various SNP association study methods. The simulated populations can also be used to feed simuGWAS (Peng and Amos 2010), which is a forward-time simulation framework based on initial populations with real marker allele frequency and LD structure. The main difference is that SIMLD focuses on the simulation of real genome data structures, but simuGWAS addresses the evolutionary process using real genome data.

Several issues still need to be addressed. In the simulation of real LD features, we have not optimized both r² and D′ measures at the same time. Thus, different haplotype structures might result from the use of different LD measures. Also, if the disease is relatively rare and the penetrance values are relatively low, it is difficult to control the size of case–control populations. One alternative approach is to extend SIMLD to simulate an entire set of cases based on the results of HAP-Sample (Wright et al. 2007), which can be extended to simulate disease mutations by selecting individuals to harbor the mutations. Finally, some disease-predisposing loci might be linked by LD, which can interfere with the estimation of the power of statistical methods. One way to reduce that influence may be to select disease-predisposing loci that are far away from each other in the genome.

In our future work we intend to improve SIMLD by addressing those issues. We also will extend SIMLD to simulate more populations such as ASW (African ancestry in Southwest USA) and CHD (Chinese in Metropolitan Denver, Colorado). Finally, we are going to design more complete and real disease models including the interactions between genes and environmental factors. Such models may bring huge challenges in the field of developing more sophisticated statistical gene mapping methods.