NUMBER AND COUNTING SKILLS IN KINDERGARTEN AS PREDICTORS OF GRADE 1 MATHEMATICAL SKILLS

1. Introduction

Mathematics difficulties (MD) are an important concern in the United States. Approximately 6 to 7% of the school age population has a mathematical disability (Barbaresi, Katusic, Colligan, Weaver, & Jacobsen, 2005; Geary, 1993). Therefore, identifying predictors of performance in the early grades should be applicable towards efforts at early identification, especially to the extent that math difficulties occur on a continuum. In choosing potential predictors, the current study was influenced by several dominant issues and notable frameworks. The first is the relative contribution of domain general versus domain specific variables in predicting math outcomes. Domain general variables that have been associated with math skill include language processes (Savage, Carless, & Ferraro, 2007), working memory (Fuchs et al., 2006; see review by Raghubar, Barnes, & Hecht, 2010), and attention (Fuchs et al., 2010a). Domain specific skills are those broadly related to number or numerosity. These include non-symbolic math knowledge such as estimation of magnitude or magnitude comparison (Landerl, Bevan, & Butterworth, 2004), symbolic knowledge such as number identification and number comparison (LeFevre et al., 2010), and counting skills and principles (Geary, 1993; 2011). Of these, counting skills appear most proximal to arithmetic and therefore may be more predictive of math outcomes than are other number predictors or domain general skills. A second recurring issue in the mathematics literature involves the role of procedural versus conceptual counting (Geary, 2004a; Praet, Titeca, Ceulemans, and Desoete, 2013). Studies that have examined both domain specific and domain general predictors (e.g., Fuchs et al., 2010a; 2010b) find support for both types of predictors and this pattern of predictors may also vary according to the mathematical outcome examined (see also Fuchs et al., 2008).

More clarification is needed regarding not only the relative contributions between domain general and domain specific skills, but also among several domain specific skills, particularly symbolic number skills (involving written numerals as in number identification and symbolic comparison; or oral numbers, as in counting). Further distinctions among domain general skill contributions are also needed. Therefore, the goal of the present study is to evaluate the role of symbolic number skills in the context of domain general variables. We do this by assessing these predictor skills in kindergarten and assessing these same students’ mathematical skills in grade 1 when these skills are being developed and of primary focus in education. In addition to previous empirical literature, our selection of predictors was informed by the theoretical frameworks of LeFevre et al. (2010), who emphasized domain general precursors of spatial attention (akin to spatial working memory), linguistic skill, and domain specific quantitative skills, as well as that of Geary (2004), who emphasized the particular role of working memory in supporting math outcomes. Below we review the role of domain general skills for mathematics, then differentiate among domain specific skills, particularly focused on symbolic number skills, and then present hypotheses.

1.1 Domain General Factors for Mathematical Development and Difficulty

As noted, language, working memory, and attention are important potential domain general factors related to math. Among language-based measures, phonological awareness (PA) has received a significant amount of attention (Krajewski & Schneider, 2009; Savage et al., 2007), in part because phonological processes may impact computation performance due to the need to create and maintain phonological representations of stem and answer associations (Logie & Baddeley, 1987). Additionally, De Smedt, Taylor, Archibald, and Ansari (2010) suggested that quality of long-term phonological representations (that PA measures) is important in predicting mathematical outcomes. Further, learning the Arabic numerals and linking them to the appropriate labels is similar to developing lexical mappings when learning to read (LeFevre et al., 2010). It is also possible that the memory representations required for mathematical computations are supported in part by the same memory systems required for decoding and reading (Geary, 1993), though the exact mechanism is not yet completely understood. Empirically, phonological awareness at ages 4 to 6 is related to computation skills at age 7 (Bryant, Maclean, Bradley, & Crossland, 1990). More specifically, De Smedt and colleagues (2010) found that phonological awareness is associated with math problems that rely on retrieval rather than procedural strategies. Also, Savage et al. (2007) found that phonological awareness at age 5 predicted math outcomes at age 11 even after controlling for early literacy skills (word reading, decoding, and letter sound knowledge). Similarly, Hecht, Torgeson, Wagner and Rashotte (2001) found phonological processes to be related to growth in math computation skills from 2^nd to 5^th grade while controlling for previous math ability, vocabulary, and reading ability. In another study in children with and without spina bifida, a neurodevelopmental disorder associated with specific math difficulties, PA at 5 years of age partially mediated the effect of group on computations and single digit arithmetic fluency at 9 years (Barnes et al., 2014).

Other aspects of language have also been noted in the literature in relation to math outcomes. For example, Koponen, Mononen, Rasanen, and Ahonen (2006) found that rapid automatized naming was related to addition, subtraction, and counting tasks in preschool children. While such factors may be relevant to math, the role of phonological awareness both mechanistically and empirically is dominant, and therefore is the focus of language assessed in this study. The impact of phonological awareness might be expected to be strongest for automatized math facts and/or mathematical outcomes with a strong verbal component (e.g., word problems).

Following the importance of working memory in relation to math outcomes proposed by Geary (2004a), we review the differential relationships of the types of working memory. Each component of the Baddeley and Hitch (Baddeley, 1986; Baddeley & Hitch, 1974) model of working memory (central executive, phonological loop, and visuospatial sketch pad) has been shown to relate to mathematical performance (Zheng, Swanson, & Marcoulides, 2011), although differential prediction has been noted (e.g., Keeler & Swanson, 2001; McLean & Hitch, 1999; Rasmussen & Bisanz, 2005). For instance, both the phonological loop and the central executive are related to mathematical problem solving ability (Rasmussen & Bisanz, 2005). The phonological loop appears to be important for counting and holding information in complex calculations (Mclean & Hitch, 1999), and for holding problem associations (Fuchs et al., 2006), given that its contents are sensitive to decay. Geary et al. (2009) found a specific role for spatial working memory; using latent class analyses, students with strong computational performance in grade 1 were also noted to have high spatial working memory performance. Barnes et al. (2014) found that visual-spatial working memory at 36 months of age partially or fully mediated the effect of group (typical and atypical development of math) at 8 and 9 years of age on math calculations and math word problems, respectively.

The complexity of the relationship of working memory to math was noted in the review by Raghubar et al. (2010), but also in a recent meta-analysis of this relationship in children between 4 and 13 years of age (Friso-van den Bos, van der Ven, Kroesbergen, & van Luit, 2013). In that meta-analyses, one result compared processing (recall/complex span) tasks to replacement (n-back) tasks and found that spatial span was more important than spatial updating, but that verbal updating was more important than verbal span, possibly due to the referencing of a constant mental map visually, but using rehearsal verbally. Children may also rely on different components of working memory at different stages of development, with a shift in reliance from visuospatial sketchpad to phonological loop with age (De Smedt et al., 2009; Hitch, Halliday, Schaafstal, & Schraagen, 1988; McKenzie, Bull, & Gray, 2003; Rasmussen & Bisanz, 2005). For example, poor performance on measures of the visuospatial sketch pad has been associated with deficits in early (preschool) non-verbal mathematics achievement (Rasmussen & Bisanz, 2005), whereas Holmes and Adams (2006) found that the central executive and the visuospatial sketchpad were more predictive of math outcomes for children in 2^nd grade than for those in 4^th grade. However, Bull, Epsy, and Wiebe (2008) found that both spatial and verbal working memory in preschool were predictive of math achievement in 1^st and 3^rd grade. Thus, while the role of working memory to math is unquestioned, its impact may be moderated by the characteristics of the measure (particularly its verbal or spatial nature), the type of math outcome, and by what other factors are considered in such prediction models. This current study, then, will consider both verbal and spatial working memory.

A third important domain general factor for math skills is attention. Attentional resources are necessary for children to initiate and direct their processing of information, comprehend, and retrieve information for different tasks (Geary, Hoard, & Hamson, 1999). A reduced ability to maintain the focus of attention as rated by teachers (behavioral inattention, Fuchs et al., 2005; 2006) is predictive of arithmetic skill (adding and subtracting single digit numbers), algorithmic computation, arithmetic word problems in first graders (Fuchs et al., 2006), and of estimation skill in children in grade 3 (Seethaler & Fuchs, 2005). Raghubar et al. (2009) found that higher levels of ratings of inattention in children in third and fourth grade were related to higher multi-digit computation and math fact errors. As well, children with mathematics difficulty are rated as more inattentive than students without such difficulties (Cirino, Fletcher, Ewing-Cobbs, Barnes, & Fuchs, 2007). Although attention may be assessed from a cognitive or a behavioral perspective, many prior studies focus on behavioral inattention. The current study adopts this perspective as well.

1.2. Domain Specific Factors for Mathematical Development and Difficulty

Number sense or numerosity may be as important to mathematics learning as phonemic awareness is to reading development (Gersten & Chard, 1999). Number sense includes non-verbal and implicit understanding of both absolute and relative magnitude of sets of non-symbolic (i.e. objects or dots) or symbolic (i.e. Arabic numerals) items (Geary et al., 2009). Models that focus on mathematical precursors utilize a wide array of factors related to quantity (Aunio et al., 2006; Jordan, Kaplan, Nabors Olah, & Locuniak, 2006; Lefevre et al., 2010). For example, LeFevre and colleagues (2010) found that non-symbolic estimation was related to mathematical concepts and computations. Jordan, Kaplan, Ramineni, & Locuniak (2009) found that number sense in kindergarten predicted calculation fluency over and above age, reading, vocabulary, working memory, and spatial reasoning, with number combinations (e.g. How much is 2 and 1?) and number knowledge (e.g. Which is bigger, 4 or 5?) being uniquely predictive. Geary et al. (2009) found that several number factors including number line estimation and conceptual counting were predictive of mathematics learning disability.

Among the array of potential number-related factors, Author (2011) identified five related latent variables, which included symbolic number comparison, non-symbolic comparison, symbolic labeling, rote counting, and counting concepts. A major distinction can be made between those number variables that utilize written Arabic numerals and therefore require extracting meaning from an alphanumeric symbol, versus those that rely on counting. In Author (2011), all factors, with the exception of non-symbolic comparison, were strongly related to small sums addition. Linguistic ability (phonological awareness and rapid automatized naming) and spatial working memory were also predictive of small sums addition, but their effect was mediated by measures of symbolic quantity, including counting. Non-symbolic factors are emphasized in many conceptualizations of number sense (e.g., Butterworth, 2005) and have been shown to relate to mathematical competence (Desoete, Ceulemans, De Weerdt, & Pieters, 2010; Mazzocco, Feigenson, & Halberda, 2011). However, it has also been suggested that symbolic factors are more predictive of mathematics (Holloway & Ansari, 2009). Further, children with MD appear to be more impaired on symbolic tasks than non-symbolic tasks (De Smedt & Gilmore, 2011). Therefore, the present study focuses specifically on symbolic predictors.

Counting per se is particularly important for later mathematics (Carrasumada, Vendrell, Ribera, & Montserrat, 2006), in part due to its explicit role in the transition to formal arithmetic in which counting is used in early calculation (Geary, 2004a). Counting also allows for the automatic use of math-related information which would permit other cognitive resources to be devoted to more complex tasks, such as problem solving (Gersten & Chard, 1999; Resnick, 1989). Counting can be further partitioned into separate but related components that are procedural versus conceptual. Poor arithmetic skills in children with MD are related to an immature understanding of the counting principles and increased procedural counting errors (Geary, 2004a). Empirically, both conceptual and procedural counting are strongly related to mathematics (Geary, 1993; Stock, Desoete, & Roeyers, 2009), but few studies compare the impact of different types of counting, or evaluate their impact against other domain specific and domain general predictors.

We follow Koponen, Aunola, Ahonen and Nurmi (2007) in defining procedural counting as the ability to correctly sequence numbers orally; in the present study, this is done without reference to external visual stimuli. Geary (2004a) suggests that procedural counting is supported by language systems, though it is associated with MD regardless of IQ or reading difficulties (Geary, 2007). Aunola, Leskinen, Lerkkanen, & Nurmi (2004) examined growth trajectories of mathematical competence (on a composite including basic arithmetic, knowledge of numbers, and word problems) in preschool to grade 2 and found that oral counting ability predicted both initial performance as well as growth; other studies also document the predictive role of procedural counting (Geary, Hoard, & Hamson, 1999; Koponen et al., 2007; Koponen, Salmi, Eklund, & Aro, 2012).

In contrast to procedural counting, conceptual counting refers to the child’s understanding of counting procedures; that is, knowledge of principles that govern how and why counting works. Gelman and Galistel (1978) described three essential (one-toone correspondence, stable order, and cardinality) and two non-essential (abstraction and order irrelevance) counting principles based on whether or not mastery of the principle is required for correct counting (Briars & Siegler, 1984; Kamawar et al., 2010; Laupa & Becker, 2004). Specific components of conceptual counting are related to mathematical outcomes at young ages (LeFevre et al., 2006; Stock et al., 2009). For example, Stock et al. (2009) found that the essential counting principles (stable order, one-to-one, and cardinality) in kindergarten predicted grade 1 arithmetic (14% variance) and math facts (5% variance). Praet, Titeca, Ceulemans, and Desoete (2013) followed 63 children from kindergarten to grade 1, and found procedural counting to be more predictive than conceptual counting of a composite grade 1 math outcome, within the context of language variables and a square estimation/counting task. Neither procedural nor conceptual counting were unique predictors when generalized language, logical thinking, the square task, and a non-symbolic comparison task were also included. The present study is similar in utilizing both procedural and conceptual counting variables in children from kindergarten to grade 1, but is broader in scope in that it also considers working memory and attention, and other symbolic number predictors, and examines more specific outcomes.

1.3 Present Study

The primary goal of this study was to evaluate the relative role of kindergarten number skills, with a particular emphasis on counting, as precursors to three types of mathematics achievement in grade 1: fluency, computation, and math problem solving, in the context of domain general predictors. We expected that both procedural and conceptual counting, as well as symbolic number variables, and domain general predictors (verbal and spatial working memory, behavioral inattention, and phonological awareness) would each be related to all of the outcomes. We also expected domain specific variables (counting and symbolic number) to be predictive even with domain general predictors included in the models. Our particular research questions focused on the specificity of the domain specific variables. That is, (1) Are counting skills, which are perhaps most proximal to the developmental sequence of early addition, more important longitudinal predictors than symbolic number predictors? There is little research that examines the relative roles of these predictors in the context of one another for various outcomes. (2) We were also interested in what type of counting skills are more relevant for which mathematical outcome, which we examined in the context of the above models. Again, there is little prior research, however, we followed Koponen et al. (2007) in expecting that conceptual counting will be more relevant for math problem solving relative to math fluency and computation, and in contrast that procedural counting will be most relevant for math fluency and computation.

2. Method

2.1 Participants

The 193 participants were from a larger study of math skills in 286 kindergarten students (referred to below as parent sample; Author, 2011). Students (48.70% female) from a single large urban district were evaluated in kindergarten (mean age = 6.16, SD = 0.32) and then again in grade 1 (mean age = 7.16, SD = 0.32). Only children who had data at both time points (and therefore were assessed on math outcomes) were included in this study. Students were from eight schools and 37 classrooms where English was the language of instruction. Participant characteristics comparing those available for the present study versus those who were not, are summarized in Table 1. Students who were unavailable did not significantly differ from those who remained in terms of age in kindergarten, socioeconomic status, sex, ESL status, or small sum addition scores (all p > .05); however, groups did differ on ethnicity. When standardized residuals were tested to examine differences by specific ethnicity (Field & Miles, 2010), the only difference that approached significance was the Caucasian group, such that there was less than expected in the group that discontinued. However, the relative distribution of ethnicity remained the same in those who remained and those who did not (African American > Caucasian > Asian > Other ethnicity).

Table 1.

Demographic Characteristics Comparing Included and Dropped Samples

Variable	Category/Scale	Included (n = 193)	Dropped (n = 93)
Age in Kinder	Years Mean (SD)	6.16 (0.32)	6.07 (0.34)
Gender	Female (%)	48.70%	48.39%
Ethnicity*	African American	43.52%	63.44%
	Caucasian	23.83%	10.75%
	Hispanic	25.39%	19.35%
	Asian	7.25%	6.45%
Language	English Second Language (%)	12.44%	5.38%
SES	Free/Reduced Lunch (%)	58.03%	66.67 %
K-BIT Verbal	Standard Score	97.61 (13.86)	--
Small Sums Addition	Total Score	4.73 (13.77)	2.93 (14.79)

Note. SES = Socioeconomic status measured by receiving a free or reduced lunch; K-BIT Verbal = Verbal IQ index from Kaufman Brief Intelligence Test given in grade 1; Small Sums Addition in Kindergarten

^*p < .01 overall.

2.2 Procedures

Students were assessed in two 30-minute sessions in their schools mostly on consecutive days by trained examiners. Students were first assessed in Spring of their Kindergarten year and again in Spring of first grade. More specific details for the Kindergarten measures, and regarding the initial time point, may be found in Author (2011).

2.3 Kindergarten Predictors

2.3.1

Counting: Procedural counting was assessed with Oral Counting and Counting Down (see Author, 2011). Oral Counting was adapted from AIMsweb, (Clarke & Shinn, 2004); test-retest reliabilities range from .78 to .80. Students count aloud from “1” for one minute. The number of correctly identified digits minus the number of errors was recorded, and converted to a numbers-per-second metric. Counting Down requires children to count down from 10, and then from 20, as quickly but as accurately as possible. Dependent measures are the times taken to say all of the numbers for each subsection, converted to a numbers-per-second metric. The median intercorrelation of these three counting speed measures in the parent sample was r = .59. The number-per-second counting scores were then z-scored against the sample and averaged into a single procedural counting composite.

Conceptual Counting was assessed with Count Out Objects and Puppet Counting. For the 5 items of the Count Out Objects measure, children see pictures of boxes and cars (5 boxes and 4 cars; 6 boxes and 7 cars; 8 boxes and 7 cars; 7 boxes and 7 cars; and 4 boxes and 4 cars) randomly displayed on a page, and are instructed to “Count out loud, ALL of the things on this page.” Immediately thereafter, the child was asked, “How many are there altogether?” Four counting errors were noted (Gelman & Gallistel, 1978): abstraction (only one type of object (e.g., cars) was counted), one-to-one correspondence (double counting an item), stable order (disruption of the counting order), and cardinality (mismatch between the final number counted and the response to the “how many” question). Some errors were of low frequency, and so a sum of error score was the dependent measure. Internal consistency from the parent sample was α = 0.68. Puppet Counting followed the procedure of Geary (Geary, Brown, & Samaranayake, 1991; Geary et. al 1999; Geary, Hoard, Byrd-Craven, & DeSoto, 2004b). The puppet counts an array of alternating red and green dots (a) correctly in typical left-to right fashion (3 trials); (b) correctly though by counting all the red dots and then all the green dots (psuedoerrors, 4 trials); or (c) incorrectly by double counting the first dot (3 trials). Double count error trials, which assess the one to one counting principle, were included in the analyses. Parent sample internal consistency for the error count trials was α = 0.80. A composite conceptual counting knowledge variable was used.

2.3.2

Symbolic Number: Symbolic Number Identification asks children to identify 15 numbers (4, 8, 3, 7, 6, 84, 17, 25, 33, 12, 79, 100, 150, 264, 333). Number correct was used in this study. Parent sample internal consistency was α = .86. A measure of symbolic number comparison (Quantity Discrimination) was adapted from AIMSweb (Clarke & Shinn, 2004) and consists of 28 pairs of Arabic numbers; in this version, children are asked to circle the greater number of the pair. Alternate form and test-retest reliability were good with a range from .85 to .93 (Clarke & Shinn, 2004; Lembke & Foegen, 2009). Both correct response and errors are recorded. The total number correct was used in this study.

2.3.3

Domain General: Spatial Working Memory (Author, 2011) consists of a series of un-nameable shapes, or a star, presented one at a time in one of four quadrants of a page. The child is asked to identify whether the shape is a star for each stimulus shown, and then to recall the position of all the shapes in a series, in sequential order. There were two practice trials and three trials with systematically increasing series lengths (blocks) of 2, 3, 4, and 5. The measure was discontinued if students incorrectly recalled the order of all three series within a block. In the parent sample, internal consistency across individual trials was α = 0.73. A total raw score was used where a point was awarded for each correct sequence recalled (maximum = 12).

Digits Backward from the Test of Memory and Learning 2^nd edition (TOMAL-2; Reynolds & Voress, 2007) was included as a measure of phonological or verbal working memory. Students were read a string of numbers and asked to repeat them in reverse order back to the examiner. Test-retest reliability for this age group was .61 (Reynolds & Voress, 2007) and internal consistency was α = 0.83. Total number correct was used.

Phonological Awareness was assessed using the Phoneme Elision subtest from the Comprehensive Test of Phonological Processing (CTOPP; Wagner, Torgesen, & Rashotte, 1999). The Phoneme Elision task involves hearing a whole word, and then being asked to remove a sound from the beginning, middle, or end of the word, and state the result, which is always a new word. Reliability in this age range is r = .82 and the parent sample internal consistency was α = 0.88. The scaled score of the subtest was used.

2.3.4 Behavioral Inattention: The Strengths and Weaknesses of ADHD and Normal Behavior (SWAN-IV; Swanson et al., 2005)

SWAN-IV is an 18-item teacher rating scale of inattention and hyperactivity/impulsivity rated on a 7-point Likert scale that ranges from −3 to +3. Each behavior corresponds to specific ADHD criteria identified in the Diagnostic and Statistical Manual of Mental Disorders-Fourth Edition, Text Revision (American Psychiatric Association, 2004) which factors into two scales, inattention and hyperactivity/impulsivity. The inattention scale was used in this study.

2.4 Grade 1 Outcome Measures

2.4.1

Fluency: A combined score across Small Sums Addition and Subtraction was used. Problems were arranged in vertical format with six rows of six problems per sheet, over two sheets. The 72 Addition items included 55 single-digit problems that sum to 9 or less, followed by 17 single digit items that sum to 18 or less (in general these later items were not attempted). . The 72 Subtraction items included 53 with minuends 1 to 9 (with all answers positive or zero), followed by 19 items with minuends of 10 or 11 (and which were in general not attempted). Students were asked to complete as many problems as they could in two minutes. A composite sum of the number correct minus the number incorrect on the addition and subtraction tests was used. The correlation for the addition and subtraction variables was r = .80, p <.0001.

2.4.2 Computation: Woodcock-Johnson-Third Edition (WJ-III) Calculation and Wide Range of Achievement Test-Third Edition (WRAT-3) Arithmetic

The WJ-III calculation subtest consists of addition and subtraction of single and multi digit problems for this age range. Test-retest reliability in this age range for this task is 0.96 (McGrew, Schrank, & Woodcock, 2007). The WRAT-3 arithmetic subtest involves symbolic number identification, counting, and number comparisons for very young children; at school age, the task requires computations that increase in difficulty. Test-retest reliability in this age range for this task is 0.87 (Wilkinson, 1993). The computation variable was created using a composite of the standard scores from the WJ Calculation subtest and the WRAT-3 Arithmetic subtest. The correlation of the WRAT-3 Arithmetic subtest with the WJ-III Calculation subtest was r = .82, p <.0001.

2.4.3

The Woodcock-Johnson - III Tests of Academic Achievement (WJ-III; Woodcock et al., 2001) Applied Problems subtest is a much more broad measure, and consists of math word problems that are presented to the subject and read out loud by the examiner. The items range in difficulty and the use of pencil and paper is allowed. Test-retest reliability in this age range for this task is 0.88 (McGrew et al., 2007). The standard score of the total correct items was used.

Math Problem Solving: Single Digit Story Problems was first developed by Riley, Greeno, and Heller (1983) and has since been adapted (Hanich, Jordan, Kaplan, & Dick, 2001; Jordan & Hanich, 2003; Riley & Greeno, 1988). The measure includes 14 items of addition and subtraction read out loud by the examiner that includes three categories of problems: change, combine, and compare. The sample internal consistency was α = 0.85. A total raw score was used where a point was awarded for each correct sequence recalled (maximum = 14).

3. Analyses and Preliminary Data Examination

The primary analytic approach was regression-based, including correlations, multiple regression, and hierarchical regression. The assumptions of regression were examined, including multicolinearity, and were not violated. After examination of zero-order correlations, models that tested hypotheses were each built in a similar fashion. The first model included the appropriate demographic variables and the domain general factors. The next two hierarchical models were run in two parallel steps to evaluate the relative contributions of the counting versus symbolic number factors. In one model, the counting variables were added first (model 2a), followed by the symbolic number variables (model 2b), whereas in the other model, the symbolic number variables (model 3a) were added first, followed by the counting variables (model 3b). Model comparisons were used to test the amount of variance attributable to each step over and above the other. The R² change for the models was evaluated by calculating an observed F value based on the sum of squares of the error term for the models and comparing it to a critical F value with the degrees of freedom associated with the full model (Maxwell & Delaney, 2003). Assumptions for all analyses (e.g., for regression this included independence, homoscedasticity, and normality of residuals) were evaluated and addressed where appropriate.

Several covariates were considered. Because lower socioeconomic status is a risk factor for learning difficulties (Duncan et al, 2007), free lunch status was evaluated. Sex differences were considered though not expected as these do not become apparent until later in academic development (Rosselli, Ardila, Matute, & Inozemtseva, 2009). Age, ethnicity, and English as Second Language (ESL) status were also considered. Free lunch status and ethnicity were related to each outcome; age was related to the computation and story problems models, and both sex and ESL status were unrelated to each outcome. Covariates that related to specific outcomes were considered; where multiple covariates were considered, a model was run without additional predictors to determine the most parsimonious set of covariates, which were trimmed where not relevant in final models.

4. Results

First, descriptive/distributional characteristics for the predictor and outcome variables are reported in Table 2. Correlations among predictors and outcomes are reported in Table 3, and document the strong relationship of each of the predictors to the outcomes of interest. These ranged from .23 to .60, with an overall median of .47 (median counting r = .44; median number r = .56; median domain general r = .47). In general, relations of these predictors were weakest for computation relative to other mathematical outcomes.

Table 2.

Descriptive Statistics for Predictor and Outcome Variables

Variable	Range	N	Mean	Std Dev	Kurtosis	Skewness
Procedural Counting	−1.46 – 2.70	191	0.06	0.81	0.52	0.58
Conceptual Counting	−2.38 – 0.88	193	0.07	0.75	0.25	−0.92
Domain Specific
Symbolic Number Identification	−3.13 – 1.24	193	0.82	0.94	0.01	−0.74
Symbolic Number Comparison	−2.29 – 2.10	192	0.04	0.98	−0.60	−048
Domain General
Verbal Working Memory	3 – 19	189	9.98	3.47	−0.26	−0.21
Spatial Working Memory	0 – 10	192	2.96	2.32	0.33	0.86
Phonological Awareness	4 – 19	185	10.04	2.95	−0.01	−0.05
Behavioral Inattention	−27 – 27	192	6.65	11.84	−0.49	−0.12
Grade 1 Outcomes
Fluency	−3.28 – 2.56	192	-	0.95	−0.82	−0.32
Computation	3.08 – 2.06	193	0.0001	0.96	0.42	−0.73
Applied Problems	69 – 151	193	- 0.0052 109.73	13.73	0.13	−0.25
Story Problems	0 – 14	189	6.86	4.481	−1.36	0.06

Note. N = number of participants; Std Dev = standard deviation; Procedural counting = z-mean of oral counting, counting down from 10 and counting down from 20; Conceptual counting = z-mean of counting errors and puppet counting errors; Digit Backwards = scaled score from the Test of Memory and Learning-2; Phonological Awareness = Phoneme Elision scaled score from the Comprehensive Test of Phonological Processing; Behavioral Inattention = Inattention scale from the Strengths and weaknesses of ADHD and normal behavior; Fluency = mean of Small Sums Addition and Small Sums Subtraction; Computation = mean of standard scores of Woodcock Johnson III Calculations subtest and Wide Range of Achievement Test Arithmetic subtest; Applied Problems = standard score from the Woodcock Johnson III subtest.

Table 3.

Correlations between Kindergarten Predictors and Grade 1 Math Outcomes

	Counting		Number		Cognitive
	1	2	3	4	5	6	7	8
1. Procedural Counting
2. Conceptual Counting	0.40
3. Symbolic Number Identification	0.63	0.36
4. Symbolic Number Comparison	0.53	0.47	0.50
5. Verbal Working Memory	0.36	0.32	0.40	0.42
6. Spatial Working Memory	0.37	0.39	0.38	0.34	0.33
7. Phonological Awareness	0.48	0.31	0.48	0.43	0.38	0.33
8. Behavioral Inattention	0.43	0.37	0.55	0.52	0.36	0.33	0.42
Outcomes
Fluency	0.42	0.44	0.60	0.55	0.46	0.36	0.46	0.47
Computation	0.33	0.37	0.52	0.45	0.38	0.27	0.47	0.35
Applied Problems	0.53	0.45	0.58	0.54	0.52	0.39	0.59	0.45
Story Problems	0.48	0.44	0.57	0.58	0.50	0.46	0.59	0.48

Note. All correlations significant at p < .0001. Abbreviations as in Table 2.

4.1 Predictions of Fluency, Computation, Applied Problems and Story Problems

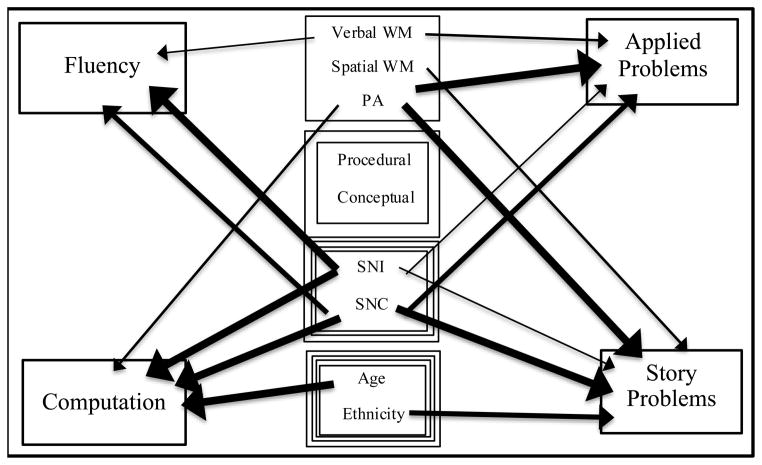
The relative predictive power of the demographic, domain specific, and domain general variables for three types of outcomes (fluency, computation, and math problem solving) was examined through hierarchical regressions. The models were built similarly for each of the four specific outcomes (Fluency, Computation, Applied Problems, and Story Problems). First we considered the most parsimonious set of covariates/demographic variables. Then, Model 1 included these relevant demographic variables and domain general variables. Model 2a added the procedural and conceptual counting variables and Model 2b added the symbolic number variables. Models 3a and 3b switch the order of the domain specific variables (i.e. adding symbolic number variables before the counting variables) to assess the difference in the R² change for these steps. Though the predictors are significantly correlated, none were extreme, and tolerance was adequate for the regression models. The results of the regression models are summarized in Tables 5 to 8, and those of the final models are pictorially represented in Figure 1.

Table 5.

Hierarchical Regression Statistics for Computation Outcome Model

	B	SE	t	β	p
Model 1
Age	−1.3367	0.1664	−8.03	−0.4597	<.0001
Behavioral Inattention	0.0139	0.0050	2.80	0.1778	0.0057
Spatial Working Memory	0.0599	0.0239	2.50	0.1537	0.0132
Verbal Working Memory	0.0347	0.0179	1.94	0.1283	0.0544
Phonological Awareness	0.0886	0.0205	4.33	0.2848	<.0001
Model 2a
Age	−1.4123	0.1637	−8.63	−0.4857	<.0001
Behavioral Inattention	0.0099	0.0050	1.98	0.1260	0.0494
Spatial Working Memory	0.0336	0.0244	1.37	0.0861	0.1711
Verbal Working Memory	0.0286	0.0175	1.63	0.1057	0.1048
Phonological Awareness	0.0771	0.0209	3.68	0.2479	0.0003
Procedural Counting	0.0513	0.0781	0.66	0.0451	0.5120
Conceptual Counting	0.2657	0.0801	3.32	0.2140	0.0011
Model 2b
Age	−1.5523	0.1495	− 10.39	−0.5338	<.0001
Behavioral Inattention	−0.0028	0.0049	−0.57	−0.0358	0.5685
Spatial Working Memory	0.0319	0.0221	1.44	0.0818	0.1508
Verbal Working Memory	0.0190	0.0159	1.20	0.0703	0.2333
Phonological Awareness	0.0413	0.0197	2.10	0.1328	0.0372
Procedural Counting	−0.0925	0.0751	−1.23	−0.0812	0.2199
Conceptual Counting	0.1372	0.0757	1.81	0.1105	0.0716
Symbolic Number Identification	0.0987	0.0223	4.44	0.3068	<.0001
Symbolic Number Comparison	0.0248	0.0053	4.68	0.3019	<.0001
Model 3a
Age	−1.5576	0.1498	− 10.40	−0.5356	<.0001
Behavioral Inattention	−0.0024	0.0049	−0.49	−0.0309	0.6243
Spatial Working Memory	0.0387	0.0214	1.82	0.0995	0.0712
Verbal Working Memory	0.0186	0.0159	1.17	0.0689	0.2440
Phonological Awareness	0.0364	0.0195	1.87	0.1168	0.0636
Symbolic Number Identification	0.0942	0.0209	4.51	0.2927	<.0001
Symbolic Number Comparison	0.0269	0.0051	5.30	0.3271	<.0001

Model 3b (See Model 2b)
Model/Model Comparison	R2 / R2 Δ	F	p
R2 Model 1	0.4593	29.56	<.0001
R2 Δ Model 2a – 1	0.0356	6.42	0.0026
R2 Δ Model 2b – 2a	0.0986	20.77	<.0001
R2 Δ Model 3b – 3a	0.0102	2.14	ns
R2 Full Model (2b/3b)	0.5957	27.84	<.0001

Note. B = parameter estimate; SE = standard error; t = t value; β = standardized estimate; p = p value. Abbreviations as in Table 2. Model 3b will have the same parameter estimates as Model 2b and therefore is not listed.

Figure 1.

Domain General, Domain Specific, and Demographic Factors Influencing Fluency, Computation, Applied Problems, and Story Problems Outcomes

Note. Thickness of the arrows represent highest to lowest p value. WM = Working Memory, PA = Phonological Awareness, Procedural = Procedural Counting, Conceptual = Conceptual Counting, SNI = Symbolic Number Identification, SNC = Symbolic Number

For Fluency (Table 4), the relevant demographics included free lunch status and ethnicity, though only ethnicity was a unique predictor. Model 1 included ethnicity and domain general predictors (verbal working memory, spatial working memory, behavioral inattention, and phonological awareness). However, ethnicity was not significant, and after trimming, the remaining model accounted for 35.7% of the variance, F (4,174) = 24.19; p < .001; each of the cognitive predictors added unique predictive value (all p < .03). Model 2a added the counting predictors, and the full model showed R² = .394, R² change = .036, p < .001. In this model, conceptual counting, but not procedural counting, was a unique predictor, along with most cognitive variables, except for spatial working memory. Model 2b added symbolic number variables (symbolic number identification and symbolic number comparison), and the full model showed R² = .495, R² change = .101, p < .001. In this model, the only significant predictors were the symbolic number variables (both p < .001), and verbal working memory, p < .041. Models 3a results were highly similar to those of Model 2b, and in Model 3b, the counting variables did not add unique variance, F (1,170) = < 1; R² change = .010.

Table 4.

Hierarchical Regression Statistics for Fluency Outcome Model

	B	SE	t	β	p
Model 1
Behavioral Inattention	0.0206	0.0055	3.73	0.2555	0.0003
Spatial Working Memory	0.0597	0.0266	2.25	0.1482	0.0259
Verbal Working Memory	0.0549	0.0202	2.72	0.1957	0.0072
Phonological Awareness	0.0713	0.0228	3.13	0.2238	0.0021
Model 2a
Behavioral Inattention	0.0162	0.0056	2.90	0.2011	0.0042
Spatial Working Memory	0.0317	0.0274	1.16	0.0788	0.2496
Verbal Working Memory	0.0485	0.0199	2.43	0.1725	0.0160
Phonological Awareness	0.0602	0.0234	2.57	0.1889	0.0109
Procedural Counting	0.0621	0.0871	0.71	0.0531	0.4772
Conceptual Counting	0.2595	0.0898	2.89	0.2034	0.0044
Model 2b
Behavioral Inattention	0.0027	0.0056	0.49	0.0340	0.6272
Spatial Working Memory	0.0265	0.0253	1.05	0.0658	0.2969
Verbal Working Memory	0.0379	0.0184	2.06	0.1350	0.0407
Phonological Awareness	0.0270	0.0222	1.21	0.0846	0.2264
Procedural Counting	−0.1013	0.0858	−1.18	−0.0867	0.2393
Conceptual Counting	0.1289	0.0866	1.49	0.1010	0.1387
Symbolic Number Identification	0.1105	0.0255	4.33	0.3352	<.0001
Symbolic Number Comparison	0.0232	0.0060	3.86	0.2749	0.0002
Model 3a
Behavioral Inattention	0.0031	0.0056	0.55	0.0384	0.5839
Spatial Working Memory	0.0323	0.0243	1.33	0.0802	0.1865
Verbal Working Memory	0.0374	0.0184	2.03	0.1332	0.0436
Phonological Awareness	0.0216	0.0219	0.99	0.0682	0.3231
Symbolic Number Identification	0.1046	0.0238	4.39	0.3173	<.0001
Symbolic Number Comparison	0.0250	0.0057	4.38	0.2958	<.0001

Model 3b (See Model 2b)
Model/Model Comparison	R2 / R2 Δ	F	p
R2 Model 1	0.3573	24.19	<.0001
R2 Δ Model 2a – 1	0.0362	5.78	<.001
R2 Δ Model 2b – 2a	0.1009	10.78	<.001
R2 Δ Model 3b – 3a	0.0095	<1	ns
R2 Full Model (2b/3b)	0.4944	20.78	<.0001

Note. B = parameter estimate; SE = standard error; t = t value; β = standardized estimate; p = p value. Abbreviations as in Table 2. Model 3b will have the same parameter estimates as Model 2b and therefore is not listed.

For Computation (Table 5), the relevant demographics included free lunch status, ethnicity, and age, though only ethnicity and age were unique predictors. Model 1 included these demographic variables and the domain general variables. Ethnicity was no longer significant and after trimming the remaining model was significant, F (5,174) = 29.56; p <.0001, R² = .46, with each of the cognitive predictors adding unique predictive value (all p < .05). Model 2a added the counting predictors, and the full model showed R² = .50, R² change = .036, p < .002. In this model, conceptual counting (p < .002), but not procedural counting, was a unique predictor, along with behavioral inattention (p < .05) and phonological awareness (p < .001). Model 2b added symbolic number variables, and the full model showed R² = .60, R² change = .099, p < .0001. In this model, the only significant predictors were the symbolic number variables (both p < .0001), and phonological awareness, p < .037. As in the Fluency models, the results of Models 3a and Model 2b were very similar except that phonological awareness was no longer significant. The counting variables did not add unique variance in Model 3b, F (2,170) = 2.14; R² change = .010.

For Applied Problems (Table 6), the relevant demographics included free lunch status and ethnicity, though only ethnicity was a unique predictor. Model 1 included ethnicity and the domain general variables. Ethnicity was no longer significant, and after trimming, the remaining model was significant, F (4,175) = 36.76; p <.0001, R² = .46, with each of the cognitive predictors adding unique predictive value (all p < .03). Model 2a added the counting predictors, and the full model showed R² = .50, R² change = .040, p < .001. In this model, both conceptual and procedural counting were unique predictors (p < .02), along with verbal working memory (p < .02) and phonological awareness (p < .0001). Model 2b added symbolic number variables, and the full model showed R² = .530, R² change = .034, p < .003. In this model, the symbolic number variables were significant predictors (both p < .05), with the same domain general variables remaining uniquely predictive (phonological awareness, p < .0001; verbal working memory, p < .02). Model 3a results were highly similar to those of Model 2b with spatial working memory also being significant (p < .05), and in Model 3b, the counting variables did not add unique variance, F (2,171) = 1.80; R² change = .010.

Table 6.

Hierarchical Regression Statistics for Applied Problems Outcome Model

	B	SE	t	β	p
Model 1
Behavioral Inattention	0.1580	0.0712	2.22	0.1398	0.0277
Spatial Working Memory	0.8894	0.3417	2.60	0.1582	0.0100
Verbal Working Memory	0.7733	0.2581	3.00	0.1984	0.0031
Phonological Awareness	1.8118	0.2927	6.19	0.4036	<.0001
Model 2a
Behavioral Inattention	0.0872	0.0715	1.22	0.0772	0.2244
Spatial Working Memory	0.4744	0.3501	1.35	0.0844	0.1772
Verbal Working Memory	0.6550	0.2520	2.60	0.1680	0.0102
Phonological Awareness	1.5408	0.2972	5.18	0.3433	<.0001
Procedural Counting	2.5389	1.1146	2.28	0.1546	0.0240
Conceptual Counting	2.7002	1.1492	2.35	0.1508	0.0199
Model 2b
Behavioral Inattention	−0.0183	0.0761	−0.24	−0.0162	0.8102
Spatial Working Memory	0.4620	0.3415	1.35	0.0822	0.1779
Verbal Working Memory	0.5698	0.2472	2.31	0.1462	0.0218
Phonological Awareness	1.2774	0.2994	4.27	0.2846	<.0001
Procedural Counting	1.4071	1.1605	1.21	0.0857	0.2270
Conceptual Counting	1.5010	1.1730	1.94	0.0843	0.1999
Symbolic Number Identification	0.6692	0.3447	1.94	0.1442	0.0538
Symbolic Number Comparison	0.2350	0.0815	2.88	0.1981	0.0044
Model 3a
Behavioral Inattention	−0.0128	0.0764	−0.17	−0.0114	0.8668
Spatial Working Memory	0.6405	0.3285	1.95	0.1139	0.0528
Verbal Working Memory	0.6032	0.2466	2.45	0.1547	0.0154
Phonological Awareness	1.3297	0.2963	4.49	0.2962	<.0001
Symbolic Number Identification	0.8779	0.3222	2.72	0.1891	0.0071
Symbolic Number Comparison	0.2823	0.0773	3.65	0.2379	0.0003

Model 3b (See Model 2b)
Model/Model Comparison	R2 / R2 Δ	F	p
R2 Model 1	0.4566	36.76	<.0001
R2 Δ Model 2a – 1	0.0399	6.85	0.0014
R2 Δ Model 2b – 2a	0.0335	6.09	0.0028
R2 Δ Model 3b – 3a	0.0099	1.80	ns
R2 Full Model (2b/3b)	0.5300	24.10	<.0001

Note. B = parameter estimate; SE = standard error; t = t value; β = standardized estimate; p = p value. Abbreviations as in Table 2. Model 3b will have the same parameter estimates as Model 2b and therefore is not listed.

For the Story Problems outcome (Table 7), the relevant demographics included free lunch status, ethnicity, and age, though only ethnicity was a unique predictor. Model 1 therefore included ethnicity and the domain general variables, and all variables were retained, and the model was significant, F (7,170) = 29.69; p <.0001, R² = .55, with each of the cognitive predictors adding unique predictive value (all p < .02). Model 2a added the counting predictors, and the full model showed R² = .567, R² change = .017, p > .05. In this model, neither conceptual nor procedural counting were unique predictors, but each of the domain general variables were (all p < .03). Model 2b added symbolic number variables, and the full model showed R² = .609, R² change = .042, p < .0001. In this model, the significant predictors were the symbolic number variables (both p < .03), spatial working memory (p < .02) and phonological awareness (p < .001). Model 3a and Model 2b were highly similar. In Model 3b, the counting variables did not add unique variance, F (2,167) = 1.15; R² change = .005.

Table 7.

Hierarchical Regression Statistics for Story Problems Outcome Model

	B	SE	t	β	p
Model 1
Ethnicity (African American)	−1.7752	0.9638	−1.84	−0.1978	0.0672
Ethnicity (Hispanic)	−2.0367	0.9933	−2.05	−0.2005	0.0419
Ethnicity (Caucasian)	0.3394	1.0059	0.34	0.0324	0.7363
Behavioral Inattention	0.0830	0.0227	3.66	0.2151	0.0003
Spatial Working Memory	0.3636	0.1099	3.31	0.1905	0.0011
Verbal Working Memory	0.2060	0.0818	2.51	0.1535	0.0128
Phonological Awareness	0.4464	0.0973	4.59	0.2954	<.0001
Model 2a
Ethnicity (African American)	−1.6963	0.9552	−1.78	−0.1890	0.0776
Ethnicity (Hispanic)	−1.7419	0.9896	−1.76	−0.1719	0.0802
Ethnicity (Caucasian)	0.4777	0.9947	0.48	0.0457	0.6317
Behavioral Inattention	0.0697	0.0230	3.03	0.1813	0.0028
Spatial Working Memory	0.2728	0.1143	2.39	0.1434	0.0181
Verbal Working Memory	0.1828	0.0814	2.25	0.1368	0.0260
Phonological Awareness	0.4090	0.0996	4.10	0.2718	<.0001
Procedural Counting	0.3751	0.3521	1.07	0.0677	0.2882
Conceptual Counting	0.6493	0.3646	1.78	0.1072	0.0768
Model 2b
Ethnicity (African American)	−1.6965	0.9172	−1.85	−0.1884	0.0662
Ethnicity (Hispanic)	−1.2485	0.9571	−1.30	−0.1231	0.1939
Ethnicity (Caucasian)	0.3810	0.9583	0.40	0.0365	0.6915
Behavioral Inattention	0.0295	0.0244	1.21	0.0762	0.2286
Spatial Working Memory	0.2685	0.1102	2.44	0.1412	0.0159
Verbal Working Memory	0.1459	0.0785	1.86	0.1091	0.0649
Phonological Awareness	0.3312	0.0984	3.37	0.2194	0.0009
Procedural Counting	−0.0344	0.3610	−0.10	−0.0062	0.9243
Conceptual Counting	0.2120	0.3668	0.58	0.0350	0.5640
Symbolic Number Identification	0.2398	0.1087	2.21	0.1530	0.0286
Symbolic Number Comparison	0.0925	0.0256	3.57	0.2318	0.0005
Model 3a
Ethnicity (African American)	−1.6199	0.9140	−1.77	−0.1799	0.0782
Ethnicity (Hispanic)	−1.2537	0.9556	−1.31	−0.1234	0.1913
Ethnicity (Caucasian)	0.3946	0.9574	0.41	0.0377	0.6806
Behavioral Inattention	0.0309	0.0244	1.27	0.0797	0.2069
Spatial Working Memory	0.2895	0.1061	2.73	0.1518	0.0070
Verbal Working Memory	0.1501	0.0784	1.91	0.1118	0.0574
Phonological Awareness	0.3237	0.0970	3.34	0.2137	0.0010
Symbolic Number Identification	0.2612	0.1013	2.58	0.1666	0.0107
Symbolic Number Comparison	0.0926	0.0245	3.78	0.2314	0.0002

Model 3b (See Model 2b)
Model/Model Comparison	R2 / R2 Δ	F	P
R2 Model 1	0.5500	29.69	<.0001
R2 Δ Model 2a – 1	0.0170	2.61	ns
R2 Δ Model 2b – 2a	0.0417	5.88	<.0001
R2 Δ Model 3b – 3a	0.0054	1.15	ns
R2 Full Model (2b/3b)	0.6087	23.19	<.0001

Note. B = parameter estimate; SE = standard error; t = t value; β = standardized estimate; p = p value. Abbreviations as in Table 2. Ethnicity t values are relative to students coded Asian. Model 3b will have the same parameter estimates as Model 2b and therefore is not listed.

5. Discussion

The goal of the present study was to evaluate the role of key domain specific factors in the context of domain general variables, for mathematical competencies. In doing so, we specifically considered the role of symbolic number predictors and both procedural and conceptual counting. Although prior studies have examined the issue of domain specific versus domain general contributions to mathematics, this study was unique in the careful selection of domain general outcomes, the comprehensiveness of the domain specific predictors examined, the variety of mathematical outcomes considered, and its doing so in a fairly large sample, and in a longitudinal fashion. The present study contributes to the literature in helping to clarify not only the dominant type of predictors important for each outcome, but also the specific variety of each.

In general, domain specific measures of both counting (median r = .44) and symbolic number (median r = .56), as well as domain general measures (median r = .47), were robustly predictive of each outcome. The only uniquely predictive demographic variables were age (for Computation) and ethnicity (for Story Problems).. Within the context of the domain general variables, review of the domain specific variables showed that conceptual counting was significantly predictive for all outcomes except story problems and procedural counting was additionally predictive of applied problems. However, when the symbolic number variables were added, these were consistently uniquely predictive, and the contributions of the counting variables became no longer significant. Though differential contribution of domain general variables to the outcomes was not specifically hypothesized, there was variability observed. Specifically, phonological awareness and working memory were more consistently predictive relative to behavioral inattention; within working memory, verbal working memory was consistently stronger than visual working memory. These conclusions are further contextualized below.

5.1 Domain General

Among domain general skills, in final models, verbal working memory was predictive of math fluency; phonological awareness was predictive of computations; verbal working memory and phonological awareness were predictive of applied problem solving; and spatial working memory and phonological awareness were predictive of story problems. These results are consistent with the literature suggesting a role for each of these skills (Barnes et al., 2014; Friso-van den Bos et al., 2013; Krajewski & Schneider, 2009; Mclean & Hitch, 1999; Raghubar et al., 2010; Rasmussen & Bisanz, 2005; Savage et al., 2007; Swanson & Jerman, 2006) factors in mathematics. Author (2011) found that the effects of both working memory and phonological awareness were completely mediated by number factors (which included all of the domain specific and counting measures evaluated here). However, that study assessed only one math outcome, small sums addition, concurrently in Kindergarten, rather than assessing a variety of outcomes longitudinally.

Friso-van den Bos et al. (2013) noted that working memory correlated more strongly with general rather than specific math measures, which they related in part to the stronger measurement properties of such general measures. In the present study, working memory had the weakest relationship to the computation outcome, although these measures exhibited strong psychometric properties. The weaker observed relationships of working memory with this measure may be related to the availability of a written work space, and the relatively low number of written problems that students in this age group are required to complete (and with a range of strategies which themselves may have variable working memory demands).

We found that in general, verbal working memory was more strongly related than spatial working memory to math outcomes (Table 3), being a unique predictor for the math fluency and applied problems outcomes. Spatial working memory has been found to be more important for math at younger (e.g., preschool) ages, and verbal working memory to be more important for math performance at older ages (De Smedt et al., 2009; Hitch, Halliday, Schaafstal, & Schraagen, 1988; Rasmussen & Bisanz, 2005). This may be related to the automatization of addition and subtraction facts (where verbal memory was significantly predictive in the current study). According to Ashcraft and Christy (1995), “small facts” (i.e. addends less than 5) are more likely to be mastered by grade 1 with mastery of “large facts” continuing through grade 6. For math problem solving, verbal working memory is key given the need to identify and manipulate problem elements. Generally, as task complexity increases (e.g. applied problems in current study) working memory is relevant because students need to work with pictures/graphs, auditory input, written input, and at times, irrelevant information that need to be integrated or discarded, as necessary. This is consistent with results from prior work (Friso-van den Bos, et al., 2013; Fuchs et al., 2010a) emphasizing domain general factors for the prediction of word problems more so than for computations. The only area for which spatial working memory exerted a stronger influence than verbal working memory was for story problems; for that measure, verbal working memory did not predict unique variance (p = .07). It is possible that the format of the questions on this task required a mental number line, especially for change-type problems (i.e., beginning with a value, and then moving up or down a line to arrive at a result), which may have emphasized spatial working memory. Another possible explanation is that for this particular task, the students had access to the text, which may have reduced the verbal working memory demands.

The current data adds to a growing literature that emphasizes linguistic factors in relation to mathematics performance (Barnes et al., 2014; Fuchs et al., 2010b; Hecht et al., 2001; LeFevre et al., 2010; Savage et al., 2007). In the current study, phonological awareness was a unique predictor for the computations outcome, and also for both applied problems and story problems; thus, it the results are consistent with the existing literature in documenting a strong role for phonological awareness in math outcomes. Language systems have been shown to support math calculations; for example, in written math calculation it is necessary to identify the numbers involved (Bryant et al, 1990; Hecht et al., 2001). Additionally, math facts are commonly taught by oral repetition in order to memorize them, which can be considered learning the oral phonological representations of the number words (Robinson, Menchetti, & Torgesen, 2002). Further, the aforementioned authors suggest that children with math difficulties struggle with tasks that involve making connections between phonological representations of numbers, rather than having a general memory deficit. That phonological awareness was not a unique predictor for our math fluency measure may be due to the fact that first grade students have not yet fully automatized math facts, as evidenced by relatively few problems correct on these measures. However, it was still the case that phonological awareness had similar zero order correlations with math fluency and computations. This may in part reflect that the processes utilized by students at this age on these two tasks were more similar than different; thus the math fluency measure may have only weakly assessed “math fact retrieval” while the calculations measure only weakly assessed “procedural computations.”

Surprisingly behavioral inattention was not uniquely predictive in any of the above models, though correlations showed that behavioral inattention was significantly related to each the outcomes (r = .35 – .48), see Table 3. A review of the inter-correlations between predictors (Table 3) shows that behavioral inattention was significantly related to the other variables (r = .33 – .55), though not at a level to represent multicolinearity. While this could help to explain the lack of significance of behavioral inattention in the regression models, it is unlikely since the strength of the correlations is similar to those of the other predictor variables (r = .31 – .63).

Another possibility is related to age as much of the literature that supports the relation of behavioral inattention and math skills has been with older children (Duncan et al., 2007; Fuchs et al., 2006; Raghubar et al., 2009; Seethaler & Fuchs, 2005). In the age range of this study (6 to 7 years old), the math problems on these measures may be less susceptible to inattentive errors. For example, the problems involve only one type of operation at a time rather than having to switch among the four operations and do not require properly aligning numbers or decimal points to solve the problems. It is possible that relationships would be stronger with outcomes requiring such switching (e.g., WJ-III Math Fluency); however, even studies with older children have failed to find a relation of behavioral inattention and errors related to switching or misalignment (Raghubar et al., 2009). The present study also accounts for many relevant factors not always found in prior studies. For example, the meta-analysis by Duncan et al., (2007) included early math and reading achievement, hyperactivity and social skills ratings, and verbal measures, but did not include phonological awareness or working memory. Further, research has demonstrated that measures of teacher and parent ratings of behavioral inattention show significant phentotypic overlap with child-based measures of working memory (Gathercole, Alloway et al., 2008; Liu & Tannock, 2007), and this may account for the lack of significant findings with behavioral inattention when working memory is also in the model.

5.2 Domain Specific

Present results are consistent with previous literature showing symbolic number variables (Gersten & Chard, 1999; Geary et al., 2009; Jordan et al., 2006; 2009; Locuniak & Jordan, 2008) to be significant predictors of complex math outcomes. Counting variables showed variable predictive power in models that considered demographics, domain general, and counting variables. Conceptual counting was a unique predictor for fluency, computation, and math problem solving, whereas procedural counting was a unique predictor only for applied problems. However, when the symbolic number predictors were added, the unique contribution of counting variables was eliminated. The reverse was not true, demonstrating the robustness of the symbolic number predictors for each of the mathematical outcomes. The results to some extent differ from Praet et al. (2013), who found procedural counting to be more predictive than conceptual counting within the context of similar factors.

It is possible that the format of the problems impacted which number variables were consistently unique predictors in the final models, more so than the counting factors. All of the math outcomes involved Arabic written numerals rather than solely mental arithmetic. Where items were read (such as story problems), students also had access to the printed question, including the numbers. Therefore, to compute the answer to the written problem 4 + 8, they must first identify the numbers involved, and if the answer is not retrieved, then counting would be required. To apply more advanced counting techniques (such as max as opposed to counting all), students must also make a judgment about the relative magnitudes of the numbers. In contrast, the counting measures were either oral or did not utilize written numbers. This may have had the effect of making the counting measures less proximal to the outcome than intended. Therefore, even though counting may be more proximal to the answer, the task also requires the number skills of identification and symbolic number comparison. Author (2011) found that both symbolic number and counting factors were related to small sums written addition, although this was a concurrent outcome in Kindergarten, and was the only mathematical outcome available. However, Koponen et al. (2007) also found a specific role for procedural counting for their fluency (single digit calculation) outcome in grade 4, whereas conceptual counting was predictive of more complex computation. That study did not include symbolic number predictors, but did include letter knowledge, which may overlap with one of the number predictors used in this study, symbolic number identification, in terms of the processes involved.

It is unknown whether aural tasks would yield differing outcomes, which may be addressed in future studies. It is also possible that the counting variables, as well as the specific counting types, may manifest themselves differently at later time points, and so this remains an open avenue of investigation. Finally, it may also be that the predictive variance for all of the symbolic number variables examined here are more shared than unique. For example, Fuchs and colleagues (2010a) showed that while different domain general and domain specific predictors were unique for computational versus problem solving outcomes in Grade 1, they also indicated that the larger portion of the prediction was shared. At any rate, it is clear that the symbolic number predictors involve multiple processes themselves, including domain general ones, and so investigating mechanisms of action for each will be an important direction.

Given their strength in prediction across the range of ability as demonstrated here, the results of this study suggest that assessment of Arabic numerals and number estimations would be useful in helping to identify children who are likely to struggle with math skills. Indeed, Rouselle and Noel (2007) found that children with math learning disabilities were impaired on symbolic magnitude comparison as compared to typically developing peers, while non-symbolic magnitude comparison was intact. These authors posit that these findings suggest the difficulty for children is not with processing numerosity in general, but rather in accessibility of symbolic magnitudes. Though the counting variables were not predictive in the context of the other domain specific factors used in the current study, these have been shown in other studies to be relevant later in a child’s education. As well, the counting variables were still highly related to each of the math outcomes, and their role is consistent with studies that emphasize counting strategies for improving number combinations and generalizing to story problems in both at-risk students in kindergarten (Dyson, Jordan, & Glutting, 2011) and in students with MD with or without comorbid RD (Fuchs et al., 2009).

Curricula vary in the extent that they emphasize conceptual relationships such as discovery learning or visual representations, versus those that emphasize number recognition, sequencing, and number combinations. For students who struggle in academic areas, an explicit and systematic focus on core skills that are most closely related to the desired outcome (i.e., words in reading, Arabic numerals in math) may be even more important (Gersten et al., 2009a; Gersten et al., 2009b). The contributions of the domain general variables were found to be relevant, though the direct versus indirect impact of these variables needs to be further assessed. Such skills (or behaviors) can still exert influence on children’s classroom performance, particularly as math skills become more differentiated and involve more problem solving or extended algorithmic procedures. Therefore, assessment of these factors (working memory, phonological awareness, and behavioral inattention) can still be beneficial in guiding interventions by identifying skills that may compound or otherwise interfere with the more direct elements of the intervention.

The current results should be interpreted in the context of its limitations. The focus of this study was on identifying predictors to a variety of math outcomes across the ability level, and so explicit identification and classification of children as having a difficulty or disability in math was beyond the scope of the present study. As mentioned in the Introduction, there is no consensus of the best way to identify children with MD. Further, using cut off scores will arbitrarily demarcate a continuous distribution and there is a lack of evidence that differential prediction is possible along a continuum. There would also be the concern of restriction of range as it is likely there would be few children at the extremes of the distribution. Nonetheless, identification of risk status is an important goal, particularly from a practical perspective, and is an area that needs further study. Another limitation regards the role of ethnicity for the story problems outcome. Although this was considered in regards to other covariates such as second language status and lunch assistance at school, measurement of more finely tuned socioeconomic variables, or home language environment, specifically regarding numeracy exposure, may better have elucidated these interrelationships. Lastly, there is a limitation in regards to the assessment of the relationship between attention and math outcomes. While no relation was found here, it is possible that a measure of cognitive attention (e.g. measuring selective, sustained, or divided attention types) would have contributed to the math outcomes in the current study. Further studies should include both cognitive and behavioral ratings of attention to clarify its relationship to these math outcomes.

In sum, this study found that: (1) while both procedural and conceptual counting are both strongly related to several types of math outcomes, patterns of counting do not convincingly distinguish between different math outcomes; (2) symbolic number factors account for much of the variance in math outcomes over and above counting factors; and (3) each outcome had distinct predictors, with more comprehensive outcomes (math problem solving) having a wider range of predictors. To the extent that predictor-outcome relationships are similar across the range of ability, these results therefore highlight the importance of linguistic variables, including both the symbolic and counting skills, in helping to identify children who are more likely to struggle with mathematics skills. Further this relationship between the symbolic number tasks and the counting skills appears to be bidirectional rather than a unidirectional causation suggesting the importance for both skills to be well developed for success with mathematics.

Highlights.

• Both types of counting skills are strongly related to math outcomes

• Patterns of counting do not convincingly distinguish between math outcomes

• Symbolic number skills account for more variance in outcomes than counting

• Each outcome had distinct predictors; comprehensive outcomes have a wider range

• The relationship between symbolic number and counting is likely bidirectional