Abstract
Accurate and consistent skull stripping of serial brain MR images is of great importance in longitudinal studies that aim to detect subtle brain morphological changes. To avoid inconsistency and the potential bias introduced by independently performing skull-stripping for each time-point image, we propose an effective method that is capable of skull-stripping serial brain MR images simultaneously. Specifically, all serial images of the same subject are first affine aligned in a groupwise manner to a common space to avoid any potential bias introduced by asymmetric transforms. A brain probability map, which encapsulates prior information gathered from a population of real brain MR images, is then warped to the aligned serial images for guiding skull-stripping via a deformable surface method. In particular, the same initial surface meshes representing the initial brain surfaces are first placed on all aligned serial images, and then all these surface meshes are simultaneously evolved to the respective target brain boundaries, driven by the intensity-based force, the force from the probability map, as well as the force from the spatial and temporal smoothness. Especially, imposing the temporal smoothness helps achieve longitudinally consistent results. Evaluations on 20 subjects, each with 4 time points, from the ADNI database indicate that our method gives more accurate and consistent result compared with 3D skull-stripping method. To better show the advantages of our 4D brain extraction method over the 3D method, we compute the Dice ratio in a ring area (±5mm) surrounding the ground-truth brain boundary, and our 4D method achieves around 3% improvement over the 3D method. In addition, our 4D method also gives smaller mean and maximal surface-to-surface distance measurements, with reduced variances.
Keywords: Consistent skull stripping, Serial MR brain images, 4D deformable surface
1. INTRODUCTION
Longitudinal data analyses are especially useful in delineating changes in brain structures during the normal aging [1], as well as in evaluating the temporal progression of neuropathology, such as Alzheimer’s disease (AD). Brain volume loss and cortical thinning are observed even in healthy subjects during aging in old individuals. Researches on changes of brain volume [2] and cortical thickness [3] is used for detecting subtle changes in brain structure in cognitively normal subjects at the risk of developing AD and in subjects with mild cognitive impairment (MCI). In the longitudinal studies, it is critical and essential that the methods do not themselves introduce any bias. Methodological biases could confound placebo-treatment comparisons in trials, and the biased measurements from a pilot study could lead to under-powering or over-powering of subsequent trials, with ethical as well as scientific and financial implications [4]. Research on potential biases introduced by the interpolation methods and registration methods is presented for consistent brain atrophy estimation [5]; while there is no related research on the potential biases introduced by the inconsistent skull stripping in the longitudinal study pipeline. In the last decade, many methods are proposed for automated skull stripping of a single brain image. For studying longitudinal changes of cortical structures in relation to brain development, aging, and diseases, more accurate and consistent skull stripping methods are required for serial brain MR images, especially for measuring subtle cortical changes. However, applying the existing methods independently for skull stripping of serial brain MR images in a longitudinal study may generate longitudinally inconsistent results and introduce bias by the interpolation and registration. As the first step in most neuroimaging processing pipelines, the bias and inconsistency in skull stripping will be propagated to the following steps, such as tissue segmentation, image registration, and group analysis.
This paper presents a new method for consistent skull stripping of serial brain MR images by using a 4D deformable-surface based approach, built on our previous work [6]. Specially, all serial brain MR images of the same subject are groupwise affine aligned to a common space to avoid any bias by asymmetric transforms. A brain probability map, which encapsulates prior information gathered from a population of real brain MR images, is warped to the groupwise affine aligned serial images for guiding the deformable surface evolution. The same initial surface meshes are placed on all aligned serial images. With the temporal smoothness constraint on each vertex, all these surface meshes evolve simultaneously for all time-point serial images, thus achieving more accurate and consistent results.
2. METHOD
2.1 Overview
The proposed method consists of the following major steps: 1) Groupwise affine alignment of all serial brain MR images of the same subject; 2) Initialization by warping a brain probability map, which is obtained by warping a set of real brain MR images with manually delineated brain masks to the template space, to the aligned serial images and placing the initial surface meshes for all serial images; 3) Consistently evolving the initial surface meshes on all serial images simultaneously using a deformable-surface method with the temporal constraint, guided by intensity information as well as the brain probability map. The details of each step are given in the following sections.
2.2 Groupwise Affine Registration
To consider all serial images of the same subject simultaneously, all serial images need to be aligned to a common space. To avoid any possible bias introduced by asymmetric registration to a specific time point, groupwise affine registration is performed on the serial images of the same subject by using the congealing method [7]. This method was first introduced by Miller et al. [8] by considering the sum of univariate entropies along pixel stacks as a joint alignment criterion. Zöllei et al. [9] further extended this method to groupwise registration of medical images using affine transforms. Here we use the open-source implementation of the congealing method in ITK by Balci et al. [7]. Specifically, it optimizes the objective function using the gradient descent algorithm combined with a line search for the step size and is efficiently implemented by using a stochastic optimization scheme embedded in a multi-resolution setting. After groupwise affine registration, all serial images of the same subject are now located in the same space.
2.3 Initialization and Parameter Estimation
A good initialization of the deformable surface is important for avoiding local minima and suboptimal solutions. To facilitate more accurate parameter estimation and better positioning of the initial deformable surface, FLIRT (for affine registration) and Demons (for non-linear registration) are employed to help mask out most of the non-brain voxels. More specifically, the ICBM high-resolution single subject template (with skull) is warped to the aligned serial images by using FLIRT, followed by Demons. The accompanying brain probability map (binarized with the threshold 0), which is obtained by warping a set of real brain MR images with manually delineated brain masks to the template space, is used to mask the image at each time point for approximate skull stripping.
After the initial skull stripping, most of the skull and scalp are removed. The resulting serial brain images are used to estimate a set of parameters for describing the image intensity distribution for each serial image: intensity minimum Gmin, intensity maximum Gmax, the intensity threshold separating brain and non-brain matters Gs, and the median intensity Gmed. All voxels with intensity between Gs and Gmax are regarded as brain voxels and are used as mass to weight the position of the voxels for the computation of the center of gravity (COG). Regarding these voxels as forming a spherical volume, the radius of the brain can be estimated. Finally, the COG and radius for all serial images of the target subject are obtained by averaging the COGs and radii obtained from all the serial images, and further used to initialize the brain surface model on all serial images.
2.4 4D Deformable-Surface-Based Skull Stripping
The 4D deformable-surface evolution is implemented by a parametric active surface, and the brain boundary is modeled by a surface tessellated using connected triangles. The surface is initialized as a sphere for all serial images using the COG and radius estimated in the previous step. From the initial position, the surface evolves gradually to the optimal position, one vertex at a time, driven by four forces as detailed below: 1) the spatial-smoothness-constrained force; 2) the intensity-based force; 3) the probability-map-guided force; and 4) the temporal-smoothness-constrained force.
For the vertex i of the k-th time-point image of a subject, the first force pertaining to the spatial smoothness constraint consists of two parts:
| (1) |
where and are the tangential and normal components of uk. For the current vertex i, uk is the difference vector between the position of the current vertex and the mean position of its one-ring neighboring vertices, which is defined as . The sole role of is to shift the vertices along the surface to keep them equally spaced; while acts parallel to the local normal nk to move the current vertex into the plane formed by its neighbors to increase the smoothness of the surface. In Equation (1), ω1 is usually set as 0.5, and ω2 is defined as a nonlinear sigmoid function adaptive to the local surface geometry (i.e., local brain curvature) [6].
The second force is from the intensity information in the surface vicinity, and it acts along the local surface normal nk. It accounts for the voxel intensity changes in the surface vicinity for each serial image, aiming to drive the surface model to move towards the real brain surface. For the vertex i, the intensity-based force imposed on the k-th time-point image of a subject is thus given as:
| (2) |
where and are the local minimum and maximum intensity of the k-th time-point image and defined by searching along the normal direction pointing inwards from the current vertex i:
| (3) |
| (4) |
where R1 and R2 represent the spatial search ranges pertaining to the minimum and maximum intensities, respectively. Lk(l) is the intensity of a voxel on the searching line with the l mm away from the current vertex. Typically, R1 is fixed on 20 mm for each image and R2 = R1/2. As described in Section 2.3, for the k-th time-point image, the image intensity minimum , the median intensity , and the threshold separating brain and non-brain matters are approximately estimated according to the intensity distribution of the initial skull-stripped brain image of the k-th time-point image. These values are used to help avoid outlier voxels that are too dark or too bright. in Equation (2) is a locally estimated intensity threshold which is used to distinguish between brain and non-brain tissues in the k-th time point image:
| (5) |
where parameter f is called the fractional intensity threshold and f ∈[0,1].
Relying on image intensity information alone to localize the brain boundary are relatively susceptible to local minima because of artifacts introduced by the noise or intensity inhomogeneity. Thus the brain probability map, encapsulating prior information gathered from a population of real brain MR images, is used to impose realistic shape and topological constraints for guiding the surface deformation, thus minimize the chances of falling into less desirable sub-optimal regions. Therefore, for the current vertex i, the third force derived from the warped brain probability map is introduced for the k-th time-point image:
| (6) |
where p ∈[0,1] is the probability value from the warped probability map.
To force temporal consistency, the temporal smoothness constraint is also imposed on the k-th time-point image at the current vertex i:
| (7) |
where Mk represents the set of the temporal neighborhood of the k-th time point, i.e., Mk = (k − 2, k − 1, k + 1, k + 2)∩(1, …,K), K is the total number of serial images of a subject, and cm.= e−(m−k)2/σ. Here σ is set as 2.73 experimentally.
Thus, at iteration t, for each vertex i in the k-th time point, its updated position is:
| (8) |
where ω3 = ω4 = 0.05 * d; ω5 = 0.1. Here d is the mean inter-vertex distance over the whole surface, calculated from each vertex to its one-ring neighboring vertices.
3. EXPERIMENTAL RESULTS
The proposed algorithm is evaluated on the ADNI dataset. 20 Health Control (HC) subjects (age range: 55~90 years) each with 4 time points (with scan time interval of 6 months or 12 months) are randomly selected and used for validation. Before skull-stripping, all images were resampled to be of dimensions 256×256×256 and resolution 1×1×1 mm3. Nonparametric nonuniform intensity normalization (N3) [10] and histogram matching were performed before group-wise alignment. To better validate the effectiveness of our method, the proposed method is compared with our previously proposed 3D brain extraction method (without temporal constraint) [6], which has demonstrated state-of-the-art performance.
3.1 Overlap Consistency
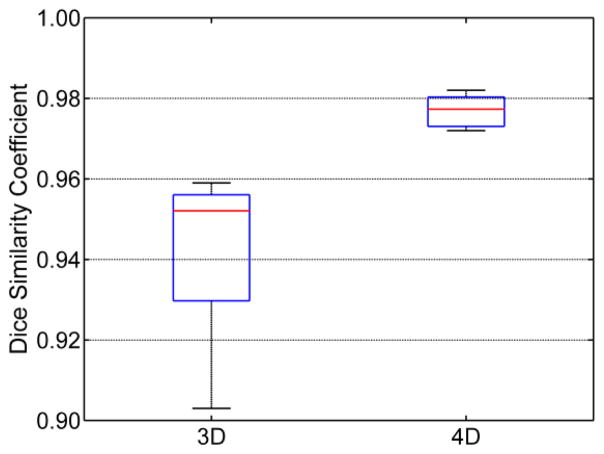
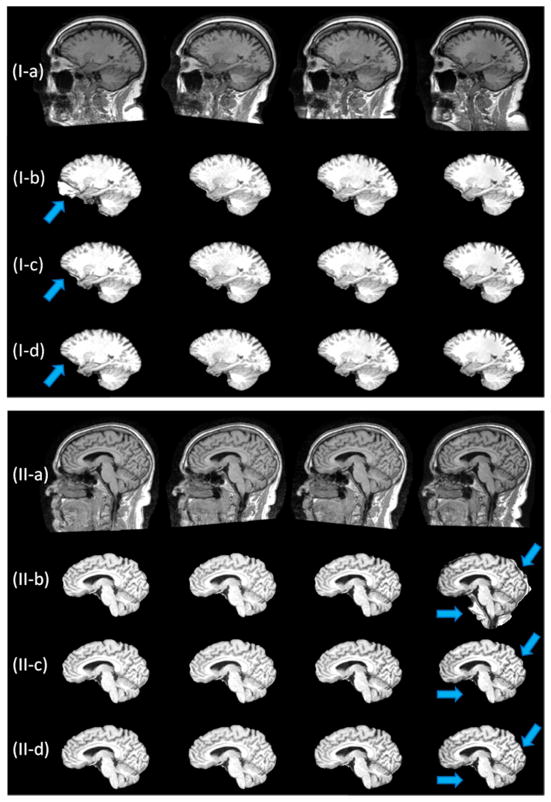
Let A and B represent for the extracted brain image and the manual skull-stripped image (ground truth), respectively. Their similarity is calculated using the Dice ratio: D(A,B) = 2|A ∩ B|/(|A| + |B|). To better show the difference between our 4D method and the 3D method, Dice ratio is calculated in the ring area (±5mm) around the ground-truth brain boundary for each time point. As can be seen from Figure 1, the proposed 4D brain extraction method has better performance than our previously proposed 3D method, with the results of the 4D method around 3% superior to the result of the 3D method. Typical skull-stripping results by our 4D method compared with our previous 3D method are shown in Figure 2, where two subjects with each having 4-time-point serial images are shown. Due to the existence of artifacts introduced by noise or intensity inhomogeneity, independent skull-stripping of each time-point image of one subject is likely causing some time-point image to be trapped into local minima during the evolution of the deformable surface, e.g., the first-time-point image in subject (I) and the fourth-time-point image in subject (II), both with some non-brain tissues unremoved. It can be observed from Figure 2 that the 4D method gives more consistent and accurate results by accounting for the longitudinal information simultaneously.
Figure 1.
Distributions of Dice ratios for the 3D and the proposed 4D methods.
Figure 2.
Typical skull-stripping results for serial brain MR images of two subjects, each with 4 time points. (a) raw images; (b) results by the 3D method; (c) results by our 4D method; (d) ground truth.
3.2 Surface-to-surface Distance
To further validate the proposed 4D method, the mean symmettric surface-to-surface distance and the maximal symmetric surface-to-surface distance are also calculated on each time point image of each subject. These measurements are used to measure the degree of mismatch between the contours of a pair of brain masks, providing information on shape differences between the results by the compared method and the ground truth. Specifically, the mean symmetric surface-to-surface distance measures for each voxel from the boundary of its estimated brain mask to the nearest boundary voxel in the ground truth and vice versa (from the voxel in the boundary of the ground truth to its nearest boundary voxel in the estimated boundary), giving a straightforward interpretation n of the skull-stripping accuracy. The maximal symmetric surface-to-surface distance takes the maximal value which is measured from each voxel in the estimated boundary to the nearest boundary voxel of the ground truth and vice versa. From Figure 3, we can see that the proposed 4D method consistently gives better results for both mean and maximal symmetric surface-to-surface distances, with less variance. Specifically, for the proposed 4D method, the mean symmetric surface-to-surface distance is around 1.1mm, compared to the value of 1.4mm by the 3D method, and the maximal symmetric surface-to-surface distance is about 5.0mm, compared to the value of 7.0mm by the 3D method.
Figure 3.
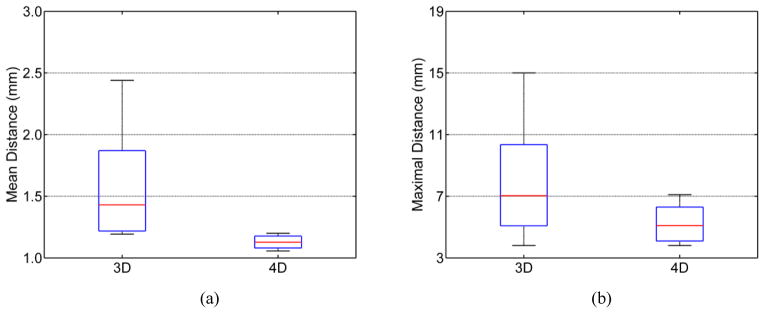
Distributions of (a) mean symmetric surface-to-surface distance and (b) maximal symmetric surface-to-surface distance for the 3D and 4D methods.
Cortical thinning is expected in the healthy elderly subjects [11], and the cortical thickness thinning in a short period of time (such as 1 year) is generally very subtle (e.g., the annual decline is around 0.5% even in some regions with significant changes [11]). To further show the consistency of our 4D method, the cortical thickness (normally with 1–5mm, with the average value around 2.5mm) is computed for the image at each time point of both the 3D and 4D skull-stripped images. To achieve this, a 4D segmentation algorithm [12] is first performed on all skull-stripped serial brain images. Then a 4D cortical surface reconstruction method [13] is further used for consistent and accurate reconstruction of inner and outer cortical surface. Figure 4 shows the trajectories of the average cortical thickness in a representative ROI (insular cortex) of all 20 subjects. The insular cortex, associated with bodily sensations and emotions, is observed an age-related decline in the gray matter volume [14], and this atrophy might contribute directly or indirectly to the cognitive deficits in the healthy elderly subjects [14]. From Figure 4, we can see that, with the temporal constraint, longitudinally more consistent results are obtained, which further confirms the advantage of our 4D method.
Figure 4.
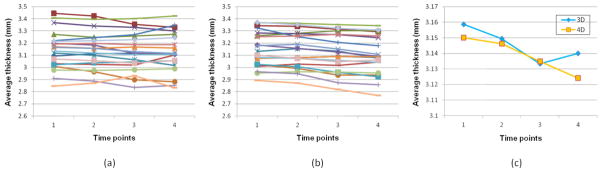
Longitudinal trajectories (4 time points) of the average cortical thickness in a representative ROI (insular cortex) of 20 subjects: (a) results by 3D method, (b) results by 4D method; and (c) the longitudinal trajectory of the average cortical thickness measured respectively by the 3D and 4D methods in this ROI.
4. CONCLUSION
We have presented in this paper a consistent 4D skull-stripping method that is capable of consistent skull-stripping of serial brain MR images. Specifically, the proposed method imposes the same initial meshes for all serial images, which simultaneously evolve to the respective target brain boundaries, with the guidance of forces from the intensity image, aligned brain probability map, and also both spatial and temporal smoothness requirements. Experimental results indicate that the proposed 4D method produces more accurate and consistent results on serial MR brain images than the 3D method.
Acknowledgments
This work was supported in part by NIH grants EB008374, EB006733, AG041721 and EB009634, and by NSFC grant (No. 61273362). Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904).
References
- 1.Resnick SM, Pham DL, Kraut MA, Zonderman AB, Davatzikos C. Longitudinal Magnetic Resonance Imaging Studies of Older Adults: A Shrinking Brain. The Journal of Neuroscience. 2003;23:3295–3301. doi: 10.1523/JNEUROSCI.23-08-03295.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Scahill RI, Frost C, Jenkins R, Whitwell JL, Rossor MN, Fox NC. A Longitudinal Study of Brain Volume Changes in Normal Aging Using Serial Registered Magnetic Resonance Imaging. Arch Neurol. 2003;60:989–994. doi: 10.1001/archneur.60.7.989. [DOI] [PubMed] [Google Scholar]
- 3.Thambisetty M, Wan J, Carass A, An Y, Prince JL, Resnick SM. Longitudinal changes in cortical thickness associated with normal aging. NeuroImage. 2010;52:1215–1223. doi: 10.1016/j.neuroimage.2010.04.258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Thompson WK, Holland D. Bias in tensor based morphometry Stat-ROI measures may result in unrealistic power estimates. NeuroImage. 2011;57:1–4. doi: 10.1016/j.neuroimage.2010.11.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Leung KK, Ridgway GR, Ourselin S, Fox NC. Consistent multi-time-point brain atrophy estimation from the boundary shift integral. NeuroImage. 2012;59:3995–4005. doi: 10.1016/j.neuroimage.2011.10.068. [DOI] [PubMed] [Google Scholar]
- 6.Wang Y, Nie J, Yap P-T, Shi F, Guo L, Shen D. Medical Image Computing and Computer-Assisted Intervention. Toronto, Canada: 2011. Robust Deformable-Surface-Based Skull-Stripping for Large-Scale Studies; pp. 635–642. [DOI] [PubMed] [Google Scholar]
- 7.Balci SK, Golland P, Wells WM. Non-rigid groupwise registration using b-spline deformation model. Proceedings of MICCAI 2007 Workshop on Open-Source and Open-Data. 2007:106–122. [Google Scholar]
- 8.Miller EG, Matsakis NE, Viola PA. Learning from one example through shared densities on transforms. Computer Vision and Pattern Recognition; Proceedings. IEEE Conference on; 2000; 2000. pp. 464–471. [Google Scholar]
- 9.Zöllei L-MEL, Grimson WEL, Wells WM., III Efficient Population Registration of 3D Data. Proceedings of the 10th IEEE International Conference on Computer Vision Workshop. 2005:291–301. [Google Scholar]
- 10.Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. Medical Imaging, IEEE Transactions on. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- 11.Fjell AM, Walhovd KB, Fennema-Notestine C, McEvoy LK, Hagler DJ, Holland D, Brewer JB, Dale AM. One-Year Brain Atrophy Evident in Healthy Aging. The Journal of Neuroscience. 2009;29:15223–15231. doi: 10.1523/JNEUROSCI.3252-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xue Z, Shen D, Davatzikos C. CLASSIC: Consistent Longitudinal Alignment and Segmentation for Serial Image Computing. NeuroImage. 2006;30:388–399. doi: 10.1016/j.neuroimage.2005.09.054. [DOI] [PubMed] [Google Scholar]
- 13.Li G, Nie J, Wu G, Wang Y, Shen D. Consistent reconstruction of cortical surfaces from longitudinal brain MR images. NeuroImage. 2012;59:3805–3820. doi: 10.1016/j.neuroimage.2011.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ohnishi T, Matsuda H, Tabira T, Asada T, Uno M. Changes in Brain Morphology in Alzheimer Disease and Normal Aging: Is Alzheimer Disease an Exaggerated Aging Process? AJNR Am J Neuroradiol. 2001;22:1680–1685. [PMC free article] [PubMed] [Google Scholar]