Mixed Messages: How Bacteria Resolve Conflicting Signals

Abstract

An elegant new study by Bollenbach and Kishony (2011) in this issue of Molecular Cell shows how bacteria resolve the apparent conflicts created when they face two signals with opposite effects on gene expression.

Imagine a graduate student with two thesis advisors. One suggests focusing on the experiments. The other suggests some mathematical modeling. What should the student do? The first strategy might involve doing a little of each, effectively “averaging” their advice. Prioritizing one mentor over the other could be a second option. Finally, when the best choice is unclear, it may be best to flip a coin. Bacteria, which live in complex environments, face similar problems and must respond optimally to multiple conflicting signals. In this issue, Bollenbach and Kishony (2011) analyze how bacteria solve these problems.

The study starts with a fundamental physiological question: how do cells respond to two signals that have opposite effects on gene expression—that is, a gene regulation conflict (Figure 1A)? One view is that cells derive an answer using a “solution manual,” or look-up table, which provides the optimal response to all possible combinations. However, the space of possible signal combinations is nearly infinite, and the information capacity of a cell’s genome is limited, making it hard to imagine how a cell could implement such a strategy. It also raises the question of how cells would respond to combinations of stimuli not previously encountered. An alternative view is that cells use simpler “rules” to determine appropriate gene expression levels in response to conflicting signals. But what do these “rules” look like, how complex are they, and to what extent can they be used to predict the response of cells to novel signal combinations?

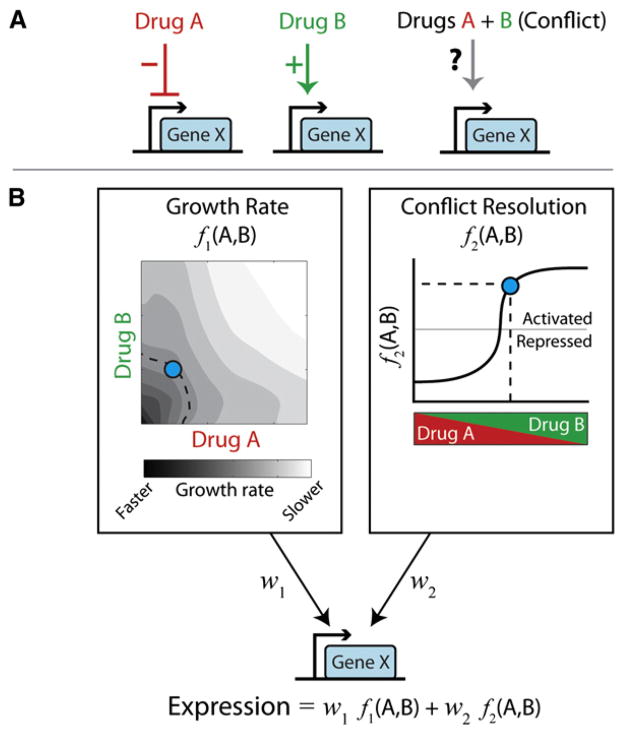
Figure 1. Gene Regulation Conflicts in Response to Drugs Are Resolved Using Simple Rules.

(A) A gene regulatory conflict (right) occurs when a cell is exposed to two drugs that have opposite effects on gene regulation (left, middle). (B) Conflict resolution is approximately represented by a weighted sum of two factors (principal components). The first component represents the response of the gene to changes in growth rate due to the drugs (heat map, left). The second component indicates the magnitude and direction of conflict response as a function of the relative concentrations of drugs A and B (x axis, right) at fixed growth rate (i.e., along the dashed line, left). The shape of these functions differs for each drug combination. However, the expression of any gene at any specific combination of drugs (blue dot) is approximately given by a weighted sum of the two effects (formula, bottom), where the weights are specific to individual genes.

These issues are increasingly critical throughout biomedical science. Single-cell organisms such as bacteria can live in extraordinarily diverse environments, in and out of hosts, and surrounded by other microbial species and the antibiotics that many of them produce. In this milieu, signal integration abilities are critical to survival. Similarly, in metazoan development, individual signaling pathways rarely work in isolation; rather, cellular responses depend on combinations of inputs from multiple pathways (Hayward et al., 2005) and even combinations of different ligands in the same pathway (Benedito et al., 2009). Finally, there is increasing excitement about the prospects of combinatorial therapies in pharmaceutical development (Keith et al., 2005). Conditions such as diabetes, heart disease, and most cancers involve many interacting genes and proteins. Thus, multifactorial diseases may respond better to multidrug combinations.

When used at sublethal concentrations, drugs—and antibiotics in particular—can induce specific cellular responses in cells (Yim et al., 2007). Considering the potential time and cost associated with testing all possible combinations of drugs, a predictive framework for understanding cellular response to drug combinations could be extremely beneficial.

Previous work examined the dynamic responses of cancer cell lines to multidrug combinations (Geva-Zatorsky et al., 2010). Using drugs that interact with different cellular targets, they found in nearly all cases that the response to a drug combination could be well described by a linear weighted average (superposition) of the effects of each drug individually. Thus, one remarkably simple way in which conflicts are resolved is by simply “averaging” the effects of the individual drugs.

Now Bollenbach and Kishony have analyzed this issue with a quantitative study of microbial responses to antibiotic combinations. To do so, they created a robotic system to comprehensively analyze microbial growth and gene expression dynamics at high throughput across two-dimensional spaces of sublethal drug concentrations for over 90 target genes. They used this system to analyze the cellular response to two pairs of drugs. In one pair, the two drugs have similar mechanisms of action, while the other pair involves different mechanisms of action. In total, nearly 20,000 drug-drug/gene measurements were collected.

In order to make sense of the resulting data, the authors used principal component analysis (PCA), a technique for analyzing high-dimensional data sets. Using PCA, the authors showed that the responses of genes across the large space of drug concentrations could be quantitatively explained in terms of just a few fundamental modes, or “principal components.” Furthermore, each of these components could be identified with a particular physiological property. The first component is determined by the effect of the drugs on cellular growth rate, while the second component represents the cellular response to the ratio of the two-drug concentrations at a fixed growth rate (Figure 1B).

Strikingly, over 95% of the gene regulation behavior could be accounted for by a weighted sum of these two components. Because the weights can be positive or negative, each individual gene may increase or decrease its expression in response to growth rate or drug ratio. Once these principal components are known for a given drug pair, the response of an arbitrary gene to any combination of drug concentrations can be computed from its specific weights, which are easily measured from exposure to each single drug alone. Note that in principle, these responses could have been much more complicated and required far more gene-specific information. Thus, cells use a strikingly simple rule to manage their responses to drug combinations, making it possible to quantitatively predict the response of cells to such combinations, even ones the cell may never have encountered before.

So how do cells resolve gene regulation conflicts? The cell’s mode of conflict resolution for each drug pair is given by the shape of its second principal component (Figure 1B, right). Interestingly, the conflict resolution mode differed qualitatively between the two drug pairs. The drugs with the same mechanism of action showed a graded dependence on the relative doses, effectively averaging the effects of the two drugs. In contrast, the other drug pair showed a much sharper dependence on the relative drug doses, effectively prioritizing the response to one drug over the other.

By extending this analysis to additional drugs, we may be able to determine how universal this behavior is, how it depends on drug mechanism, and what role epistatic drug interactions (the effect of one drug on the relative efficacy of the other) play (Loewe, 1953; Yeh et al., 2009). Indeed, it is suggestive that antagonistically interacting drugs showed a sharper conflict response curve compared to the more independently acting drugs. This may indicate that the cell responds preferentially at each drug concentration to the drug with the strongest relative impact on growth. Finally, the regulatory mechanisms through which the cell implements these conflict resolution strategies remain unclear. Because the rules of conflict resolution are so similar across genes, it is quite possible that only a small number of global regulatory molecules are involved.

A question one must always ask is: Do cellular behaviors observed at the population average level also apply at the level of individual cells? In the strongly prioritized case, the authors observed that gene expression noise, or cell-cell variability in expression (Elowitz et al., 2002), is highest when the two drugs were used at approximately equivalent doses. This shows that relative drug dosages can directly affect phenotypic variability, which in turn could influence the ability of a microbial population to survive antibiotic treatment (Balaban et al., 2004; Gefen and Balaban, 2009). Thus, it may be worthwhile to consider the effect of therapeutic drug combinations on cellular noise.

Bollenbach and Kishony’s elegant study advances our understanding of cellular responses to combinatorial inputs. Returning to the metaphor of our confused graduate student, it seems that when cells resolve conflicts, they prioritize, average, and in some cases roll the dice, all while factoring in their own growth.