Adaptive Offset Correction for Intracortical Brain Computer Interfaces

Abstract

Intracortical brain computer interfaces (iBCIs) decode intended movement from neural activity for the control of external devices such as a robotic arm. Standard approaches include a calibration phase to estimate decoding parameters. During iBCI operation, the statistical properties of the neural activity can depart from those observed during calibration, sometimes hindering a user’s ability to control the iBCI. To address this problem, we adaptively correct the offset terms within a Kalman filter decoder via penalized maximum likelihood estimation. The approach can handle rapid shifts in neural signal behavior (on the order of seconds) and requires no knowledge of the intended movement. The algorithm, called MOCA, was tested using simulated neural activity and evaluated retrospectively using data collected from two people with tetraplegia operating an iBCI. In 19 clinical research test cases, where a nonadaptive Kalman filter yielded relatively high decoding errors, MOCA significantly reduced these errors (10.6 ±10.1%; p<0.05, pairwise t-test). MOCA did not significantly change the error in the remaining 23 cases where a nonadaptive Kalman filter already performed well. These results suggest that MOCA provides more robust decoding than the standard Kalman filter for iBCIs.

I. Introduction

Intracortical brain computer interfaces (iBCIs) seek to decode intended movement from neural activity. A multielectrode array chronically implanted in the cortex records the signals and sends them to signal processing hardware and software to extract informative features and then estimate motor commands, such as raising the right arm. The technology has been tested and developed in animals [1]–[6] and in early demonstrations by people with neurological injury or disease [7]–[9]. Recent accomplishments include three dimensional, iBCI driven robotic arm reaching and grasping by neurologically intact non-human primate subjects [10] and by people with paralysis of the arms and legs [11], [12]. This recent progress offers hope that iBCIs will one day restore motor control for people with paralysis.

During iBCI setup, a calibration process is typically used to set the parameters of the decoding algorithm (filter). During calibration, the user attempts a series of instructed movements and the neural signals are recorded. The overt actions of trained non-human primates can be directly measured [1]–[6]. For people with paralysis, intended actions are assumed to match those required to accomplish the directed tasks [9], [11], [13]. With the inputs and outputs of the filter known, its internal parameters then can be estimated to capture the statistical connection between the neural recordings and intended movement.

However, sometimes during iBCI operation, the neural firing activity or the relationship between the neural signal and intended movement might change. Several studies have reported this phenomenon, called nonstationarity, in which unexpected changes occur in the statistical characteristics of the neural signals [4], [7], [14]–[20]. For instance, in monkeys, the statistical dependency between kinematics and binned counts of detected action potentials, i.e., spike counts, changed within a few minutes [15]. 84% of units underwent statistically significant changes in mean firing rates in a retrospective analysis of 22 sessions where people operated an iBCI [20]. These neural signal instabilities, combined with a nonadaptive decoding algorithm, can introduce decoding errors, rendering the iBCI less useful or even unusable until the decoder is recalibrated [17], [20].

Electrode placement [21], electrode design [22] and how the neural features are extracted from the signals [19], [23], [24] may have an effect on signal stability. However, in one study, much of the intra-day nonstationarity could not be attributed to technical artifacts suggesting that the cause is often physiological [20]. The instabilities may arise from changes in motor or cognitive states not modeled by the decoding algorithm. While modeling more states might improve decoding performance [25], accounting for all the relevant causal factors may not be feasible.

To address this problem, iBCI operation could be halted and the decoding algorithm recalibrated, for example, by the user actively using the iBCI to complete a series of pre-set exercises. Data from this “closed-loop” variant of calibration can be combined with previous calibrations to retune the filter [3], [10]–[12], [17], [26]–[28]. The more time spent calibrating the filter, however, the less time there is available for the user to make use of the iBCI. For a fully automated and practical iBCI, such interruption of iBCI use for recalibration is not desirable.

Ideally, a decoding algorithm would autonomously and “silently” (without disturbing the user) adapt to the nonstationarities that occur during iBCI operation. Differing from “closed-loop” filter recalibration techniques, this capability calls for the filter to adjust its tuning parameters without knowledge of the true motor states or objectives. To this end, an adaptive linear filter [29] and point process filters [30]–[32] have been evaluated with simulated data. Dual Kalman filtering was run offline on experimental data from monkeys [33]. In both offline and online conditions, also with monkeys, an unscented Kalman filter updated its parameters via a Bayesian paradigm [34]. In the latter two approaches, the filter’s parameters were constantly adjusted by assuming the prior motor state estimates were close to their true values.

Here, we develop an adaptive Kalman filter that adjusts an otherwise constant term, the offset vector, in the tuning model. For the first time, we present a method that can handle large, sudden nonstationarities and demonstrate improved performance over a standard, nonadaptive Kalman filter in offline analysis of data from two people with tetraplegia using an iBCI. Underlying the technique is a novel framework that employs penalized maximum likelihood estimation to implement a Multiple Offset Correction Algorithm (hereafter referred to as MOCA) in order to adapt the Kalman filter. The approach is similar to those designed to construct robust filters in the face of unknown inputs [35], [36]. Perhaps most relevant to our approach are filters built to handle large unknown impulses that are sparse in time [37], [38]. They also perform a search over a branching set of possibilities, each a solution from closed-form calculations, to determine if and when an impulse has occurred.

This report presents the general MOCA framework as well as a specific implementation. Methods and data for evaluating MOCA follow, including simulations and offline, retrospective analysis of clinical research sessions. The results demonstrate the improvement that MOCA has over its nonadaptive counterpart.

II. Decoding Methods

A. Generic Kalman Filter

The Kalman filter [39], [40] has been successfully used in iBCIs [9], [11], [13], [41], [42]. At its core, the Kalman filter assumes a Gaussian-linear model,

$${\mathit{x}}_0~\mathcal{N}({\mu }_0,P_0)$$ (1)

$${\mathit{x}}_k=A_k{\mathit{x}}_{k-1}+{\mathit{w}}_k:{\mathit{w}}_k~\mathcal{N}(0,W_k)$$ (2)

$${\mathit{z}}_k=H_k{\mathit{x}}_k+{\theta }_k+{\mathit{q}}_k:{\mathit{q}}_k~\mathcal{N}(0,Q_k)$$ (3)

where k is the time step, x is the d × 1 motor state vector, z is the m×1 neural feature vector, all model parameters reside in the matrices A_k, H_k, W_k, Q_k, μ₀, P₀ and the offset vector θ_k, and 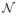(μ, Σ) is a multivariate Gaussian distribution with mean vector μ and covariance matrix Σ. The key statistical dependency between the neural features and motor states is captured by (3) and is sometimes referred to as the tuning model.

At the current time step, k = n, the filter estimates the motor state, x̂_n, given the feature history from the first time step to the present, z₁, z₂, …, z_n (or alternatively ${\{\mathit{z}\}}_1^n$). Let x_k conditioned on ${\{\mathit{z}\}}_1^{k-1}$ be written as ${\mathit{x}}_k\mid {\{\mathit{z}\}}_1^{k-1}$ or x_k|k−1. Similarly, let x_k conditioned on ${\{\mathit{z}\}}_1^k$ be written as ${\mathit{x}}_k\mid {\{\mathit{z}\}}_1^k$ or x_k|k. Using this notation, one way to arrive at the Kalman filter is to maximize the a posteriori probability density (MAP) of x_n|n,

$${\widehat{\mathit{x}}}_n=\underset{{\mathit{x}}_n}{\text{argmax}}p({\mathit{x}}_{n\mid n}).$$ (4)

Under models (1–3), x̂_n can be arrived at via recursive calculations [39], [40],

$$\begin{array}{l}{P}_{k\mid k-1}=A_k{P}_{k-1\mid k-1}{A}_k^T+W_k\\ {\widehat{\mathit{x}}}_{k\mid k-1}=A_k{\widehat{\mathit{x}}}_{k-1}\\ K_k=P_{k\mid k-1}{H}_k^T{(H_k{P}_{k\mid k-1}{H}_k^T+Q_k)}^{-1}\\ P_{k\mid k}=(I-K_k{H}_k)P_{k\mid k-1}\\ {\widehat{\mathit{x}}}_k={\widehat{\mathit{x}}}_{k\mid k-1}+K_k({\mathit{z}}_k-{\theta }_k-H_k{\widehat{\mathit{x}}}_{k\mid k-1})\end{array}$$ (5)

where, for k ∈ {1, 2, …, n} as well as initializations x̂₀ = μ₀ and P_0|0 = P₀, we have x_k|k−1 ~ 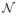(x̂_k|k−1, P_k|k−1) and x_k|k ~ 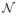(x̂_k, P_k|k).

B. Standard, Nonadaptive Kalman Filter for iBCI Applications

In the general formulation (1–3), the matrices and offset vector can change between time points. However, in iBCI applications, these parameters are usually assumed constant in time,

$${\mathit{x}}_k=A{\mathit{x}}_{k-1}+{\mathit{w}}_k:{\mathit{w}}_k~\mathcal{N}(0,W)$$ (6)

$${\mathit{z}}_k=H{\mathit{x}}_k+\theta +{\mathit{q}}_k:{\mathit{q}}_k~\mathcal{N}(0,Q).$$ (7)

Doing so simplifies the process of learning their values from calibration data. During filter calibration, the participant performs tasks where z_k is recorded and x_k is assumed known over many time steps. θ is set to the feature means over samples whose x values average out approximately to zero. Values for A and H can then be found from linear regression techniques and the resulting residuals combined to form the covariance matrices W and Q. Details about calibrating the Kalman filter for neural decoding can be found in [41], [42].

As in the generic case, x̂_n is calculated from a recursive calculation, where now all parameters are time invariant. Furthermore, K_k stabilizes over time to its steady state value, K. In the case of iBCI’s, with time steps typically separated by 100 milliseconds or less, K_k quickly converges to K [43]. Considering the filter under these steady state conditions, we arrive at our standard, nonadaptive Kalman filter,

$${\widehat{\mathit{x}}}_k=A{\widehat{\mathit{x}}}_{k-1}+K({\mathit{z}}_k-\theta -HA{\widehat{\mathit{x}}}_{k-1}).$$ (8)

C. General MOCA Framework

Changes in neural activity unrelated to movement can introduce decoding errors [20]. In order to approximately model the effects of such nonstationarities in our estimate for x̂_k, we relax the assumption of the nonadaptive Kalman filter that θ is constant in time (7),

$${\mathit{z}}_k=H{\mathit{x}}_k+{\theta }_k+{\mathit{q}}_k:{\mathit{q}}_k~\mathcal{N}(0,Q).$$ (9)

In effect, we go back to the generic Kalman filter model when it comes to the offset vector (3). The resulting, recursive Kalman filter estimate of x_k is the same as (8) only θ is replaced by θ_k.

The challenge then becomes choosing values for the θ_k’s in order to adapt the Kalman filter. In this paper we develop a penalized maximum likelihood approach for estimating the offset vector history, ${\{\theta \}}_1^n$, namely,

$${\{\widehat{\theta }\}}_1^n=\underset{{\{\theta \}}_1^n}{\text{argmax}}lnp({\{\mathit{z}\}}_1^n\mid {\{\theta \}}_1^n)-\gamma ({\{\theta \}}_1^n)$$ (10)

$$=\underset{{\{\theta \}}_1^n}{\text{argmin}}-\sum _{k=1}^{n}lnp({\mathit{z}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\theta \}}_1^n)+\gamma ({\{\theta \}}_1^n)$$ (11)

where, we define $p({\mathit{z}}_1\mid {\{\mathit{z}\}}_1^0,{\{\theta \}}_1^n)\triangleq p(z_1\mid {\{\theta \}}_1^n)$ for notational convenience. The penality term γ is necessary, because the standard maximum likelihood estimation severly overfits the offsets. The penalty term can also be used to introduce prior knowledge or other constraints into the procedure (see Section II-D).

It can be shown (see Appendix A) that (11) equates to,

$$\begin{array}{l}{\{\widehat{\theta }\}}_1^n=\underset{{\{\widehat{\theta }\}}_1^n}{\text{argmin}}\frac{1}{2}\sum _{k=1}^n{(z_k-{\nu }_k)}^T{R}_k^{-1}(z_k-{\nu }_k)+\gamma ({\{\theta \}}_1^n):\\ \begin{array}{ll}\text{for}k=1\hfill & {\nu }_k=HA{\mu }_0+{\theta }_k\hfill \\ \hfill & R_k=H({AP}_0{A}^T+W)H^T+Q\hfill \\ \text{for}k>1\hfill & {\nu }_k=HA{\widehat{\mathit{x}}}_{k-1}+{\theta }_k\hfill \\ \hfill & R_k=H(A{P}_{k-1\mid k-1}{A}^T+W)H^T+Q\hfill \\ \hfill & {\widehat{\mathit{x}}}_{k-1}=A{\widehat{\mathit{x}}}_{k-2}+K({\mathit{z}}_{k-1}-{\theta }_{k-1}-HA{\widehat{\mathit{x}}}_{k-2})\hfill \end{array}\end{array}$$ (12)

where each $p({\mathit{z}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\theta \}}_1^n)$ is 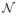(ν_k, R_k), P_k|k is computed from (5), x̂_k−1 is now the prior state estimate generated by a Kalman filter under observations for ${\{\mathit{z}\}}_1^{k-1}$ and a proposed realization of ${\{\theta \}}_1^n$, and terms not depending upon ${\{\theta \}}_1^n$ have been dropped [44].

Once ${\{\widehat{\theta }\}}_1^n$ is attained, we can run the Kalman filter, subtracting the estimated offsets from the feature vectors to arrive at an estimate for the current motor state via the recursive calculation,

$${\widehat{\mathit{x}}}_k=A{\widehat{\mathit{x}}}_{k-1}+K\left({\mathit{z}}_k-{\widehat{\theta }}_k-HA{\widehat{\mathit{x}}}_{k-1}\right).$$ (13)

Under this general strategy, a new θ history is estimated using (12) at every time step. Thus, θ̂_k is not found recursively, but rather it is computed at each time step using the full history ${\{\mathit{z}\}}_1^n$. Since the homogeneous part of (13) is the same as the original nonadaptive Kalman filter, MOCA inherits the stability properties of the nonadaptive Kalman filter. [45].

D. MOCA Implementation

1) Constraints and Choice of Penalty for ${\{\theta \}}_1^n$

We constrain our search over possible θ histories and choose a penalty both to reflect our observation that neural activity is typically stationary but, when it changes, there is a change in the average level of only a few neural features. This is embodied in the assumption that changes in offsets are sparse (e.g. few neurons are affected) and that changes in time occur rarely. The approach differs from incorporating the offsets into the hidden state, where the state transition model is linear and Gaussian. Choosing linear and Gaussian dynamics allows use of the dual kalman filter [33]. However, we find our modeling choices of sparsity and sudden shifts to better reflect the nonstationarties occurring on timescales less than a minute.

The approach also simplifies estimation of the offsets. We assume the offsets stay at their calibrated values, θ, until, at some point in the recent past, they may or may not have made a step change to a new constant value. Let the possible shift occur at k = n − τ and ξ ⊂ {1, 2, …, m} contain the indices of the offsets that have shifted. Additionally, let ϕ denote the amount each offset has shifted at k = n − τ. The relationship between the θ_k’s, θ, τ, ξ, and ϕ, is described by,

$$\begin{array}{lll}{\theta }_k\hfill & =\theta +\varphi \hfill & \text{if}k\in \{n-\tau ,n-\tau +1,n\dots ,n\}\hfill \\ \hfill & =\theta \hfill & \text{otherwise}:\hfill \end{array}$$ (14)

where ϕ_i = 0 if i ∉ ξ.

For our implementation, τ was set to 5 seconds.

To capture our belief that a few nonstationary offsets are more likely than many at any given point in time, we choose an L0 penalty,

$$\gamma ({\{\theta \}}_1^n)=\ell$$ (15)

where ℓ is the number of nonstationary offsets. The L0 penalty causes (12) to be equivalent to minimizing the Akaike information criterion [46]. For example, suppose there were 32 neural features, and we assumed only 5 of those features had nonstationary offsets (5 nonzero entries in ϕ). Then by (15), γ = 5.

2) Search Strategy for Choosing which Offsets are Nonstationary

Now that permissible values for ${\{\theta \}}_1^n$ are completely defined by ξ and ϕ, we can recast (12) as a two step minimization process, where first we propose which offsets are nonstationary and then choose the extent to which they have shifted,

$$\mathcal{E}(\xi ,{\varphi }^{\prime })\triangleq \underset{\xi }{min}\left[\underset{{\varphi }^{\prime }}{min}\frac{1}{2}\sum _{k=1}^n{(z_k-{\nu }_k)}^T{R}_k^{-1}(z_k-{\nu }_k)\right]+\ell$$ (16)

where ϕ′ contains all the nonstationary components of ϕ. For example, if m = 4 and ξ = {2, 4}, then ϕ′ = [ϕ₂ ϕ₄]^T. We can express ϕ in terms of ϕ′,

$$\varphi =B{\varphi }^{\prime }$$ (17)

where B is an m by m identity matrix with columns associated with assumed stationary offset components; that is. i : i ∉ ξ, removed. For example,

$$\begin{array}{l}\text{suppose}m=4,\xi =\{2,4\}\text{and}{\varphi }^{\prime }={[2.2-3.8]}^T\\ \text{then}B=\left[\begin{array}{ll}0\hfill & 0\hfill \\ 1\hfill & 0\hfill \\ 0\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right]\\ \text{and}\varphi ={[\begin{array}{llll}0\hfill & 2.2\hfill & 0\hfill & -3.8\hfill \end{array}]}^T.\end{array}$$

Because a complete search over all possible combinations for ξ is intractable, we instead implement the suboptimal strategy of forward stepwise search (FSS) akin to that used in linear regression under similar circumstances [47]. The algorithm initializes ξ to the null set, meaning no offsets have changed. During the first step, we propose adding one of the offsets to ξ. For each of the m candidates, the procedure estimates ϕ′ (see below) and subsequently computes 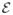. FSS then adds the candidate with the lowest 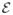to ξ. The search continues, adding only one offset component per step. The process terminates when 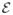cannot be improved by adding an offset ξ to or ξ contains all offsets. Figure 1 outlines MOCA’s overall approach.

Fig. 1.

Overall schematic of the multiple offset correction algorithm (MOCA). At each step in the procedure, an additional offset index, i, is added to the nonstationary set, ξ. The decision is based on improving an objective function, 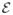, tied to maximizing the likelihood. The process terminates when either the step fails to improve 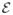or all offsets are considered nonstationary. The resulting estimates for the nonstationary offsets, ϕ̂′, are then used to correct the Kalman filter.

3) Estimation of Nonstationary Offsets

For each ξ proposed by the FSS, an optimal ϕ′ must be chosen to evaluate . We can derive an approximate, closed form solution for the inner minimization in (16) to yield an estimate for ϕ′ (See Appendix B),

$$\begin{array}{l}\widehat{{\varphi }^{\prime }}={\left(\sum _{k=n-\tau }^n{F}_k^T{R}^{-1}{F}_k\right)}^{-1}\left(\sum _{k=n-\tau }^n{F}_k^T{R}^{-1}{y}_k\right):\\ F_k\triangleq -HA\left(\sum _{j=n-\tau }^{k-1}{S}^{j-(n-\tau )}\right)KB+B\\ y_k\triangleq z_k-HA{\widehat{\mathit{x}}}_{k-1}^{(0)}-\theta \end{array}$$ (18)

where $S\triangleq (I-KH)A,{\widehat{\mathit{x}}}_{k-1}^{(0)}$ is the Kalman filter estimate at time step k under the default assumption that none of the offsets have changed; i.e., ϕ = 0, and R is a steady-state version of R_k. The latter exists because, as K_k quickly achieves the steady state value of K, then by the iterative equations above in (5) and (12), R_k also reaches R. Due to (18), θ̂_k is bounded as long as the y_k’s are bounded. This fact leads to bounded errors in estimating x_k, assuming the original nonadaptive Kalman filter is uniformly asymptotically stable (see Appendix C).

III. Simulation Test Methods

Before describing experiments with real iBCI data, we first illustrate the behavior of MOCA using a controlled scenario with simulated neural data.

A. Cursor Motion Data

In order to generate the synthetic data, the velocities of arm reaching movements performed by an able-bodied person were recorded and fed into a neural activity simulator. We constructed a 2D radial-4 center-out-and-back cursor game using the MATLAB(R) software platform (Figure 2). During each trial, the cursor was moved to within a highlighted, circular target. The game was played for 60 seconds and cursor velocities were sampled at a rate of 10 Hz.

Fig. 2.

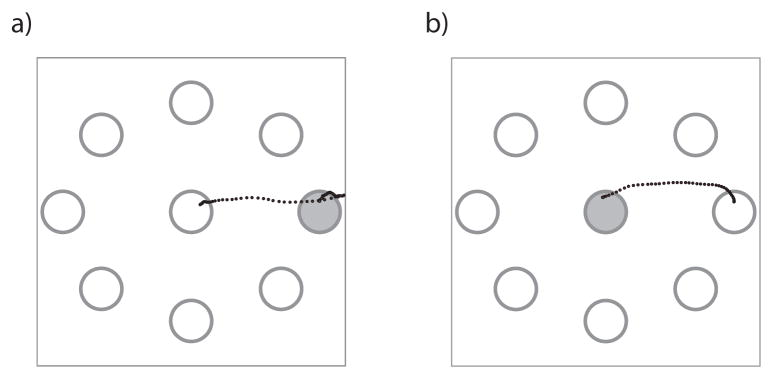
Description of the 2D radial-4 center-out-and-back cursor game used to compare the filters. a) The objective is to move the cursor (trajectory represented by the black dotted trace) to a randomly chosen, peripheral target (filled in with gray) and then b) move it back to the center target.

B. Simulated Neural Activity

The simulator contained a tuning model of the form (9) with 32 features, i.e. n_z = 32. For each feature, one movement direction, on average, generated the maximum level of activity. We distributed these preferred directions equally over the entire 360 degree range. The model was constructed so that the feature values (mean subtracted firing rates) varied between ±10 Hz. The Gaussian noise for each feature was independent of the others and their variances were all set to 10 Hz.

The simulator was run in two modes: stationary and non-stationary. Under the scenario with nonstationary offsets, the 5 features most tuned to a rightward velocity had their offsets increased by 40 Hz above their calibrated values throughout the entire simulation. This 40 Hz value was selected to generate a velocity bias that appeared similar in magnitude to the velocity biases occasionally observed in iBCI use.

C. Evaluation Procedure

Both MOCA and the standard, nonadaptive Kalman filter were run on the synthetic neural activity to estimate the cursor velocity. The models in each filter exactly matched those used by the simulator, except neither filter was informed about the 40 Hz offset increase when the simulation was run in nonstationary mode. Besides comparing traces of the estimated and true velocities, the mean absolute difference (μAD) between them was computed for both the horizontal and vertical components.

IV. Offline Clinical Research Data Test Methods

A. Study Participants

Two people with tetraplegia and anarthria due to a pontine stroke enrolled in clinical research studies where they actively controlled a computer cursor via the BrainGate2 iBCI¹ to reach circular targets [9]. One participant in the study, hereafter referred to as S3, is a woman who enrolled in the study at age 54. Participant T2, is a 65 year old man. Prior to the sessions examined here, S3 had been working with the iBCI for over 26 months; T2’s prior experience was just 2 months.

B. Implant

The implant consisted of a 10 × 10 microelectrode array (Blackrock Microsystems, Salt Lake City) inserted into the motor cortex. The hand-arm region [48] was determined by pre-operative MRI. The electrodes penetrated 1.5 mm deep in both S3 and T2 and were spaced 400 μm apart. Since four electrodes were non-active by design, a total of 96 voltage signals were recorded by the array. The array was connected via insulated gold wires to a titanium pedestal that was fastened to the skull. The pedestal functioned as a percutaneous connector through which the voltage signals were transmitted, via a cable, to amplifiers, analog-to-digital converters, as well as signal processing hardware and software on a nearby cart (see [9] for details).

C. Sessions

Participants operated the iBCI to control a cursor on a computer screen. The trials consisted of either radial-4 center-out-and-back tasks, radial-8 center-out-and-back tasks, or a random step tracking Fitts metric task. While the details of the tasks have been detailed previously [9], we briefly review the key aspects. The purpose of each trial was to move the cursor through the 2D space of the screen to reach the currently highlighted circular target and either dwell on the target for a predefined time period or select it akin to clicking with a computer mouse. For radial-4 and radial-8 variants, the targets were located at the screen’s center as well as equally distributed along the periphery. Adhering to a center-out-and-back paradigm, trial sequencing first presented a peripheral target followed by the center target (Figure 2). For the Fitts variant, the targets were presented at random locations on the screen and the size of the target randomly varied, but otherwise the tasks followed the same design as the radial-4 and radial-8 tasks.

We analyzed 20 and 22 blocks of trials from sessions with S3 and T2 respectively. Sessions explored ranged over 22 months (792 to 1447 days after implant) for S3, whereas T2 sessions spanned 8 months (68 to 270 days after implant). We chose sessions to encompass a wide range of cursor control performance.

D. Pre-Filter Signal Processing

After exiting the pedestal, all 96 voltages were immediately passed through a cable to signal processing hardware (Blackrock Microsystems, Salt Lake City). The signals then underwent amplification, an analog bandpass (0.3 Hz to 7.5 kHz), digitization (30 kHz), and highpass filtering (250 Hz). Either time and amplitude windows were used to manually sort spiking units [8] or threshold crossings were employed [11], [49], [50]. For each unit, the number of spikes in nonoverlapping 100 ms time bins were counted. Each component of the feature vector corresponded to the count of a particular unit’s spike or threshold crossing.

E. Evaluation Procedure

Both MOCA and the standard, nonadaptive Kalman filter were run offline using the recorded neural activity features to estimate the intended velocity, separate from any decoding that was done during the session to control the cursor. However, unlike the simulated data case, we did not know the true intended velocity; that is, we did not know the ground truth of how the person intended to move during each sample interval. We did, however, assume the person intended to move towards the target. Thus, we had a plausible value for the velocity’s direction, but not its magnitude. At every time step, we computed the angular error, e, between the target direction and the direction of the velocity estimated by the filters. The mean angular error (MAE) across all time steps, k ∈ {1, 2, …, n_s}, in a trial block was used to measure decoding error; that is, $\text{MAE}=\frac{1}{n_s}{\sum }_{k=1}^{n_s}\mid e_k\mid$.

V. Results

A. Simulation Tests

In both stationary and nonstationary simulation mode, MOCA’s offset corrections were recorded over time. When the simulation was in stationary offset mode, meaning the offsets did not depart from their calibrated values, MOCA’s corrections were infrequent and minor (Table I). On average, only 1.46 ± 0.57 offsets out of 32 offsets were corrected at any given time. For those offsets that were corrected, the mean correction was relatively small (0.75 ± 0.44 Hz compared to the average modulation range of 20 Hz).

TABLE I.

Distribution of corrections made by MOCA during three different situations. Because all features had an average modulation of ±10 Hz, the sizes of the false corrections made to the unperturbed offsets were relatively small.

Simulation mode	stationary sim.	nonstationary sim.
Offset type	all 32 units unperturbed 0 Hz	27 units unperturbed 0 Hz	5 units perturbed +40 Hz
correction < −2 Hz a	0.00%	0.00%	0.00%
−2 < correction < 0 Hz	2.24%	0.05%	0.00%
correction = 0 Hz	95.43%	99.93%	0.00%
0 < correction <= 3 Hz	2.33%	0.02%	0.00%
3 < correction <= 38 Hz	0.00%	0.00%	0.00%
38 < correction <= 39 Hz	0.00%	0.00%	1.96%
39 < correction <= 40 Hz	0.00%	0.00%	52.42%
40 < correction <= 41 Hz	0.00%	0.00%	42.65%
41 < correction <= 43 Hz	0.00%	0.00%	2.97%
43 < correction Hz	0.00%	0.00%	0.00%

^aThe table shows the frequency of corrections, binned by value, reported as a percentage.

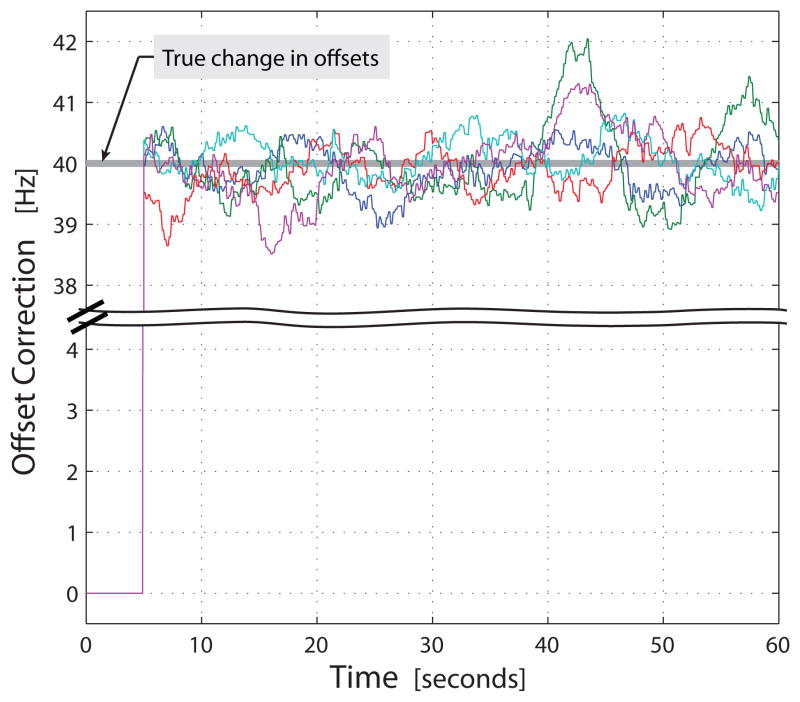
Under nonstationary conditions, MOCA corrected for all five of the increased offsets (Table I and Figure 3). Throughout the simulation, the estimate was close to the true value of 40 Hz in all five nonstationary cases. MOCA made very few corrections to the stationary offsets (0.02 ± 0.13 offsets out of 27 stationary offsets) on average and the associated values were relatively inconsequential (0.03 ± 0.23 Hz vs. an average modulation rate of 20 Hz) (Table I). In addition, MOCA rapidly adapted to the offset changes. After collecting a sufficient amount of neural activity history (τ = 5 seconds), MOCA immediately detected the 40 Hz offset change (estimates at 5 seconds: 39.52, 39.97, 40.14, 40.34, and 40.38 Hz).

Fig. 3.

MOCA’s offset corrections while the simulation ran in nonstationary mode. The colored traces indicate the corrections to 5 offsets which departed from their calibrated values by 40 Hz (highlighted by the gray line). The vertical axis between 4.5 and 37.5 Hz was removed to zoom in on areas of interest. Because MOCA must wait for a history of features to become available, it does not attempt to estimate offsets during the first 5 seconds of the simulation.

In terms of performance, MOCA was similar to the nonadaptive filter during stationary simulation mode, i.e. when no offsets were perturbed. Specifically, the filters produced similar estimates of the velocity. As measured by the mean absolute error between the estimated and actual values, their performance was within 1% of each other.

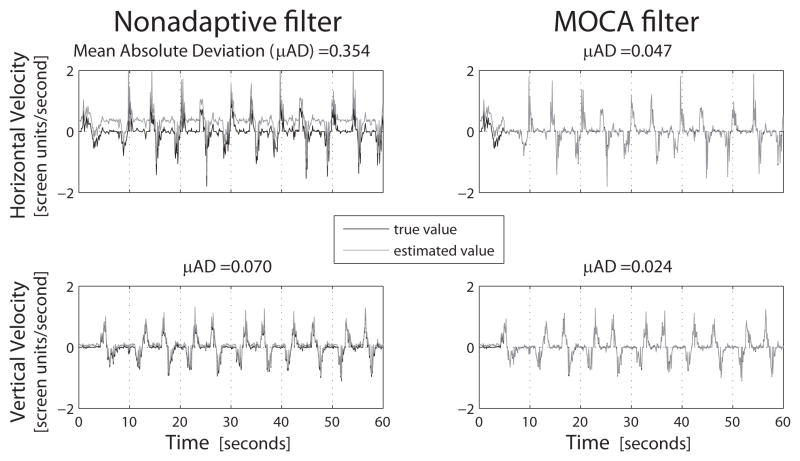
However, when 5 offsets were increased by 40 Hz from their calibrated values, the velocities estimated by the filters differed substantially. Specifically, while the nonadaptive decoder’s estimates revealed an error bias, MOCA mitigated that bias as shown in Figure 4. The mean absolute deviation dropped by nearly an order of magnitude, from 0.354 to 0.047 screen units per second in the horizontal direction under the nonadaptive filter and MOCA respectively. In the vertical dimension, the deviation fell from 0.070 to 0.024 screen units per second (both the width and height of the game area was 1.2 screen units).

Fig. 4.

Simulation traces comparing the two filters while in nonstationary mode. Black traces denote true cursor velocity over time. Similarly, gray traces provide the respective filter’s estimate of the cursor velocity. Mean absolute deviations, μAD, between the true and estimated cursor velocity along each component summarize the overall estimation accuracy. The simulation conditions cover the case where 5 of the offsets were increased from their calibrated values, requiring the decoder to adapt.

B. Clinical Research Session Tests

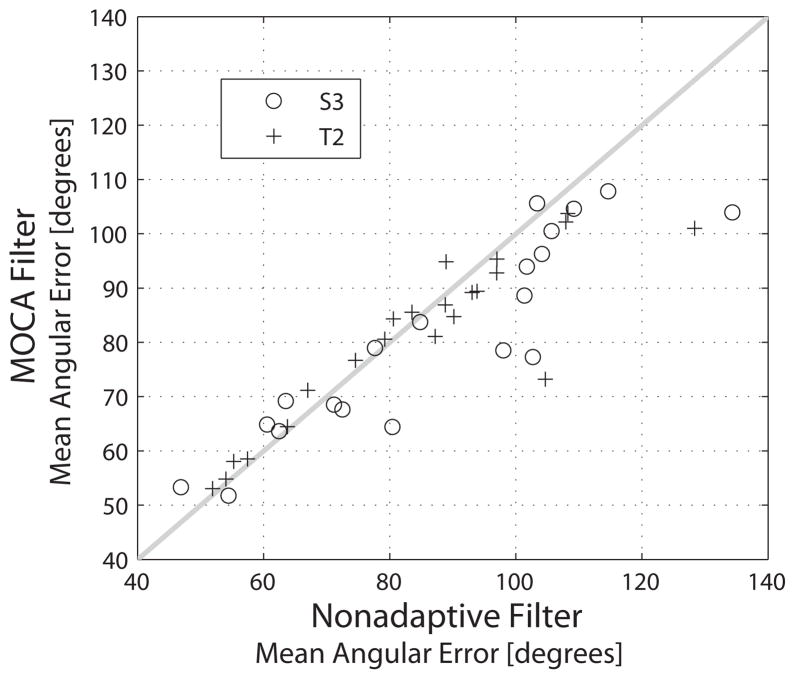
MOCA was compared to the nonadaptive Kalman filter using sessions where two individuals operated the investigational BrainGate iBCI. All filters were run offline to generate velocity estimates from the feature histories in a retrospective fashion. Use of MOCA reduced the mean angular error by 4.8 ± 8.98 degrees (p< 0.05, pairwise t-test) (Figure 5). MOCA had its greatest beneficial impact in trial blocks where the nonadaptive filter gave relatively large error and did not significantly affect cases where the nonadaptive filter reported relatively low error. Specifically, when the nonadaptive filter provided an error above 90 degrees, MOCA yielded an average reduction of 10.6 ± 10.1% (p< 0.05, pairwise t-test). Below 90 degrees, MOCA may have slightly increased error 0.01±3.83 degrees, but the findings were not statistically significant (p= 0.99, pairwise t-test).

Fig. 5.

Offline comparison between MOCA and the standard, nonadaptive Kalman filter. Each data point in the plot represents a trial block (S3 designated with black circles and T2 with black crosses). The horizontal position of each data point denotes the mean angular error from the standard filter whereas the vertical position gives the same metric when applying the MOCA variant. The light grey line is provided for reference as data points below the line indicate a lower error under the adaptive decoder.

On average, across all trial blocks, MOCA corrected 17 ± 11% of the offsets. The fraction of corrected offsets positively correlated with the nonadaptive filter’s performance error (Pearson’s correlation coefficient = 0.52; p< 0.05 t-test). Among those offsets corrected, the level of correction was relatively large. Normalized to the associated feature’s standard deviation of modulation, the average was 0.48±0.17, nearly half the level of modulation. When compared to the nonadaptive filter’s performance error, no statistically significant correlation was found (Pearson’s correlation coefficient = 0.02; p-value = 0.90, t-test). One might assume that as the error of the standard filter increases it is due to more nonstationary channels. This in turn would suggest more offsets corrected by MOCA. Taken together, the results suggest that MOCA applied a higher degree of correction to the more nonstationary blocks of trials.

MOCA’s ability to rapidly adjust modeling parameters differentiates it from other published adaptive filtering methods applied to iBCI recordings. For example, Li, et. al. applied Bayesian regression with a joint formulation to update parameters every two minutes [34]. We tested the Bayesian regression technique on the offline clinical data set and found the best performance to occur when the update interval was reduced to 30 seconds. Despite the optimization, MOCA still performed better than Bayesian regression. As compared to Bayesian regression, MOCA reduced mean angular error by −3.67 ± 10.48 degrees (p< 0.05, pairwise t-test).

VI. Discussion

In this offline analysis, MOCA provided an improvement in decoding performance when compared with the nonadaptive Kalman filter, resulting in increased robustness to the decoding of nonstationary neural signals. When control was relatively poor with the nonadaptive filter, MOCA often provided reduced error. During relatively good control under the nonadaptive Kalman filter, MOCA demonstrated no significant positive or negative impact. These findings are consistent with the hypothesis that occasionally iBCI control is degraded by nonstationarities that can be approximately modeled by offsets to the baseline firing rate. In these cases, MOCA successfully adapted the filter parameters and mitigated the effects of the nonstationarities. Furthermore, by virtue of the algorithm’s design, the adaptation took place in a few seconds.

The offline nature of the analysis presents limitations, but also may lead to an underestimate of the benefits. A decoder’s online performance can vary greatly from its offline counterpart [51]. Online, the person controlling the iBCI can try to correct for perceived errors generated by the decoding scheme. We anticipate that the adaptive method developed here would mitigate the nonstationarities sufficiently such that real time corrections made by the iBCI operator would result in a marked improvement in task performance.

MOCA was developed to address a common observation that when a person operates an iBCI, systematic changes in feature offsets can occur [20]. It is postulated that there are many other types of nonstationary behavior, such as unexpected changes in tuning direction. Modification and expansion of the presented adaptive filtering framework could be used to handle these other cases.

Finally, MOCA’s search to explore which offsets are non-stationary is a partial one. Computationally, it becomes intractable to score all possible subsets of the features (aka powerset) as there are 2^m combinations. Better search strategies or more extensive searches combined with much larger computational power might yield even greater improvement. For example, the small and occasional erroneously assigned corrections by MOCA might be eliminated by backward stepwise search.

MOCA - the presented, adaptive version of the Kalman filter - improved offline decoding performance on average in 42 sessions where two people controlled an iBCI. Furthermore, the improvements were the greatest when the effect of nonstationarities were large. The methods are derived from a penalized maximum likelihood formulation, which serves as a formal way to model nonstationarities as offsets and adds an adaptive mechanism to the Kalman filter, already a popular choice for decoding in iBCIs. Thus, beyond the immediate usefulness of the instantiated MOCA algorithm, the MOCA framework provides a foundation for constructing other offset correction algorithms in iBCIs. MOCA may also be useful in applications, beyond iBCIs, when a Kalman filter is applied in the context of nonstationary data. In such cases, the technique can quickly adapt the filter solely from the observations’ history.

Appendix A

We seek to show that (11) equates to (12). Examining (11),

$${\{\widehat{\theta }\}}_1^n=\underset{{\{\theta \}}_1^n}{\text{argmin}}-\sum _{k=1}^{n}lnp({\mathit{z}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\mathit{\theta }\}}_1^n)+\gamma ({\{\theta \}}_1^n)$$ (19)

we see that $lnp({\mathit{z}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\theta \}}_1^n)$ requires evaluation. Let ${\mathit{x}}_{k\mid k-1}\triangleq {\mathit{x}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\theta \}}_1^n$ and ${\mathit{z}}_{k\mid k-1}\triangleq {\mathit{z}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\theta \}}_1^n$. As mentioned in Section II-A, the current motor state given all prior neural features and the entire offset history follows a multivariate Gaussian distribution, i.e. x_k|k−1 ~ (x̂_k|k−1, P_k|k−1), where x̂_k|k−1 and P_k|k−1 can be produced from the recursive Kalman filter calculations (5) with x̂_1|0 = Aμ₀ and P_1|0 = AP_0|0A^T. Since q_k ~ (0, Q) and z_k|k−1 is a linear function of q_k and x_k|k−1, i.e., z_k|k−1 = Hx_k|k−1 + q_k, then p(z_k|k−1) = 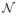(ν_k, R_k), where ν_k = HAx̂_k−1 + θ_k and R_k = H(AP_k−1|k−1A^T + W)H^T + Q.

Inserting 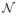(ν_k, R_k) into $lnp({\mathit{z}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\theta \}}_1^n)$ yields,

$$\begin{array}{l}lnp({\mathit{z}}_k\mid {\{\mathit{z}\}}_1^{k-1},{\{\theta \}}_1^n)=ln\left[{(2\pi )}^{-m/2}\mid R_k{\mid }^{-1/2}{e}^{-\frac{1}{2}{(z_k-{\nu }_k)}^T{R}_k^{-1}(z_k-{\nu }_k)}\right]\\ =-\frac{1}{2}{(z_k-{\nu }_k)}^T{R}_k^{-1}(z_k-{\nu }_k)+C\end{array}$$ (20)

where C is a constant with respect to ${\{\theta \}}_1^n$.

Appendix B

We seek to prove the inner minimization of ϕ′ in (16) is solved approximately by (18). Because we assume a single step change in the offsets at k = n − τ, summation terms in (16) associated with k < n − τ are constant with respect to ϕ′ and thus can be removed from the optimization,

$${\widehat{\varphi }}^{\prime }=\underset{{\varphi }^{\prime }}{\text{argmin}}\frac{1}{2}\sum _{k=n-\tau }^n{(z_k-{\nu }_k)}^T{R}_k^{-1}(z_k-{\nu }_k).$$ (21)

Next, from its definition, we note that R_k is not a function of ϕ′. Additionally, since K_k quickly achieves the steady state value of K, then by the iterative equations above in (5), R_k also reaches a steady state matrix we label as R. Thus, R⁻¹ is a precomputed constant,

$${\widehat{\varphi }}^{\prime }=\underset{{\varphi }_{\ast }}{\text{argmin}}\frac{1}{2}\sum _{k=n-\tau }^n{(z_k-{\nu }_k)}^T{R}^{-1}(z_k-{\nu }_k).$$ (22)

Thus, ϕ′ only enters into the objective function through the ν_k’s, both directly and implicitly through x̂_k−1,

$${\nu }_k=HA{\widehat{\mathit{x}}}_{k-1}+\theta +B{\varphi }^{\prime }.$$ (23)

In order to express each x̂_k−1 in terms of ϕ′, we first rearrange the recursive equation for x̂_k in (5),

$$\begin{array}{l}{\widehat{\mathit{x}}}_k=S{\widehat{\mathit{x}}}_{k-1}+K({\mathit{z}}_k-\theta )-KB{\varphi }^{\prime }:\\ S\triangleq (I-KH)A.\end{array}$$ (24)

We then can calculate the first few iterations for x̂_k in terms of ϕ̂,

$$\begin{array}{l}{\widehat{\mathit{x}}}_{n-\tau }=S{\widehat{\mathit{x}}}_{n-\tau -1}+K({\mathit{z}}_{n-\tau }-\theta )-KB{\varphi }^{\prime }\\ ={\widehat{\mathit{x}}}_{n-\tau }^{(0)}-KB{\varphi }^{\prime }:{\widehat{\mathit{x}}}_{n-\tau }^{(0)}\triangleq S{\widehat{\mathit{x}}}_{n-\tau -1}+K({\mathit{z}}_{n-\tau }-\theta )\\ {\widehat{\mathit{x}}}_{n-\tau +1}=S{\widehat{\mathit{x}}}_{n-\tau }+K({\mathit{z}}_{n-\tau +1}-\theta )-KB{\varphi }^{\prime }\\ ={\widehat{\mathit{x}}}_{n-\tau +1}^{(0)}-\mathit{SKB}{\varphi }^{\prime }-KB{\varphi }^{\prime }:{\widehat{\mathit{x}}}_{n-\tau +1}^{(0)}\triangleq S{\widehat{\mathit{x}}}_{n-\tau }^{(0)}+K({\mathit{z}}_{n-\tau +1}-\theta )\\ {\widehat{\mathit{x}}}_{n-\tau +2}=S{\widehat{\mathit{x}}}_{n-\tau +1}+K({\mathit{z}}_{n-\tau +2}-\theta )-KB{\varphi }^{\prime }\\ ={\widehat{\mathit{x}}}_{n-\tau +1}^{(0)}-(S^2+S+I)KB{\varphi }^{\prime }:{\widehat{\mathit{x}}}_{n-\tau +2}^{(0)}\triangleq S{\widehat{\mathit{x}}}_{n-\tau +1}^{(0)}+K({\mathit{z}}_{n-\tau +2}-\theta )\end{array}$$

which leads us to the general relation,

$${\widehat{\mathit{x}}}_k={\widehat{\mathit{x}}}_k^{(0)}-\left(\sum _{j=n-\tau }^k{S}^{j-(n-\tau )}\right)KB{\varphi }^{\prime }\forall n-\tau \le k\le n$$ (25)

where we note that ${\widehat{\mathit{x}}}_k^{(0)}$ is the Kalman filter estimate at time step k when ϕ = 0, that is the default assumption that none of the offsets have changed.

Substituting this finding into the definition for ν_k, we have,

$${\nu }_k=HA{\widehat{\mathit{x}}}_{k-1}^{(0)}-HA\left(\sum _{j=n-\tau -1}^{k-1}{S}^{j-(n-\tau )}\right)KB{\varphi }^{\prime }+\theta +B{\varphi }^{\prime }.$$ (26)

In order to further simplify, we again aggregate terms,

$$y_k\triangleq {\mathit{z}}_k-HA{\mathit{x}}_{k-1}^{(0)}-\theta$$ (27)

$$F_k\triangleq -HA\left(\sum _{j=n-\tau }^{k-1}{S}^{j-(n-\tau )}\right)KB+B,$$ (28)

in order to arrive at,

$${\widehat{\varphi }}^{\prime }\approx \underset{{\varphi }^{\prime }}{\text{argmin}}\frac{1}{2}\sum _{k=n-\tau }^n{(y_k-F_k{\varphi }^{\prime })}^T{R}^{-1}(y_k-F_k{\varphi }^{\prime }).$$ (29)

To minimize the objective function, $G({\varphi }^{\prime })\triangleq \frac{1}{2}{\sum }_{k=n-\tau }^n{(y_k-F_k{\nu }_k)}^T{R}^{-1}(y_k-F_k{\nu }_k)$, we compute the gradient and find the critical point,

$$\nabla G({\widehat{\varphi }}^{\prime })=\sum _{k=n-\tau }^n{F}_k^T{R}^{-1}{F}_k{\widehat{\varphi }}^{\prime }-F_k^T{R}^{(-1)}{y}_k=0$$ (30)

$${\widehat{\varphi }}^{\prime }\approx {\left(\sum _{k=n-\tau }^n{F}_k^T{R}^{-1}{F}_k\right)}^{-1}\left(\sum _{k=n-\tau }^n{F}_k^T{R}^{-1}{y}_k\right).$$ (31)

We know the critical point is a minimum because the second derivatives form the Hessian matrix, ${\sum }_{k=n-\tau }^n{F}_k^T{R}^{-1}{F}_k$ where each term is nonnegative definite, since R is positive definite.

Appendix C

To better understand error bounds, we note that (18) implies errors in estimating θ_k are bounded, if the y_k’s are bounded. Let Δθ denote the error bound on the θ_k’s. We can then compare the state estimate under a perfect estimate for the offsets, ${\widehat{\mathit{x}}}_k^{\mathit{perfect}}$, to one where the offset error is at its maximum bound, ${\widehat{\mathit{x}}}_k^{\mathit{error}}$,

$$\begin{array}{l}{\widehat{\mathit{x}}}_k^{\mathit{perfect}}=S{\widehat{\mathit{x}}}_{k-1}^{\mathit{perfect}}+K{z}_k-K{\theta }_k\forall k>0\\ {\widehat{\mathit{x}}}_k^{\mathit{error}}=S{\widehat{\mathit{x}}}_{k-1}^{\mathit{error}}+K{z}_k-K{\theta }_k-K\mathrm{\Delta }\theta \forall k>0\\ e_k\triangleq {\widehat{\mathit{x}}}_k^{\mathit{perfect}}-{\widehat{\mathit{x}}}_k^{\mathit{error}}\\ e_k=S{e}_{k-1}+k\mathrm{\Delta }\theta \forall k>0\end{array}$$ (32)

Since ${\widehat{\mathit{x}}}_0^{\mathit{perfect}}={\widehat{\mathit{x}}}_0^{\mathit{error}}={\mu }_0$, we have,

$$\begin{array}{l}{e}_1=+K\mathrm{\Delta }\theta \\ e_2=+SK\mathrm{\Delta }\theta +K\mathrm{\Delta }\theta \\ \cdots \\ e_k=\left(\sum _{j-0}^{k=1}{S}^{j}K\right)\mathrm{\Delta }\theta \end{array}$$ (33)

As k→ ∞, $e_k\to {\sum }_{j=0}^{\infty }{S}^{j}K\mathrm{\Delta }\theta$. Assuming the original nonadaptive filter is uniformly asymptotically stable, then ||S^j|| exponentially decays as a function of j [45]. By the ratio test for the series then, e_k is bounded as k → ∞.