Population Intervention Causal Effects Based on Stochastic Interventions

SUMMARY

Estimating the causal effect of an intervention on a population typically involves defining parameters in a nonparametric structural equation model (Pearl, 2000, Causality: Models, Reasoning, and Inference) in which the treatment or exposure is deterministically assigned in a static or dynamic way. We define a new causal parameter that takes into account the fact that intervention policies can result in stochastically assigned exposures. The statistical parameter that identifies the causal parameter of interest is established. Inverse probability of treatment weighting (IPTW), augmented IPTW (A-IPTW), and targeted maximum likelihood estimators (TMLE) are developed. A simulation study is performed to demonstrate the properties of these estimators, which include the double robustness of the A-IPTW and the TMLE. An application example using physical activity data is presented.

1. Introduction

Most causal inference problems are addressed by defining parameters of the distribution of the counterfactual outcome that one would obtain in a controlled experiment in which an exposure variable A is set to some prespecified value a deterministically. A widely used example of this framework is the causal effect for a binary treatment, in which the expectation of the outcome in a hypothetical world in which everybody receives treatment is compared with its counterpart in a world in which nobody does. Other common way of addressing causal problems consists in considering parameters that reflect the difference between the distribution of a counterfactual outcome in such hypothetical intervened world and the distribution of the actual outcome; these parameters are often referred to as population intervention parameters (Hubbard and van der Laan, 2005).

To estimate such exposure-specific counterfactual parameters from observational data, one has to assume that all subjects in the population have a positive probability of receiving the exposure level a under consideration. This assumption is often referred to as experimental treatment assignment, or positivity assumption and can be highly unrealistic in most cases. Additionally, when the exposure of interest is not a variable that can be directly manipulated (e.g., social or behavioral phenomena), any policy intervention targeting a change in the exposure distribution will result in a population whose exposure is stochastic rather than deterministic, and the causal effect as described in the previous paragraph loses its appeal as a measure of the gain obtained by implementing such a policy.

An example that illustrates these ideas is presented in Section 6. These data were collected by Tager, Hollenberg, and Satariano (1998) and analyzed by Bembom and van der Laan (2007) with the main goal of assessing the effect of vigorous physical activity on mortality in the elderly. First, as argued by Bembom and van der Laan (2007), experimental treatment assignment assumptions as needed to identify the causal effect of a static treatment are quite unrealistic because health problems are expected to prevent an important proportion of the population from high levels of physical activity. Second, it is clear that it is not possible to put in practice a policy in which every subject is enforced to a physical activity level dictated by a deterministic rule. Therefore, any intervention on the population that targets changes in physical activity levels will induce a random postintervention exposure. These and other reasons why deterministic interventions are not always the best approach to estimate causal effects are discussed in Korb et al. (2004) and Eberhardt and Scheines (2006). Korb et al. (2004) define an intervention on a variable A in a causal model as an action that intends to change the distribution of A. This general definition includes as special cases static and dynamic deterministic interventions (through degenerate distributions), but it also allows the definition of the causal effect in terms of a non degenerate distribution, as exploited in this article.

In our example, the question of whether higher levels of leisure-time physical activity (LTPA) cause a reduction in mortality rates in the elderly can be better addressed by considering the effect of a policy that aims to cause an increase in the mean of LTPA, possibly depending on covariates such as health status or socioeconomic level. As we will see in Section 2, this problem can be formulated by considering the effect of an intervention of the treatment mechanism. We focus the discussion on the definition and estimation of the effect of this specific type of interventions.

Despite the previous considerations, current developments and applications have almost exclusively focused on deterministic interventions. Among the few works using stochastic interventions Figure Cain et al. (2010), who used a stochastic intervention in the context of comparing dynamic treatment regimes with a grace period; and Taubman et al. (2009), who considered an intervention in the body mass index defined by a truncation of the original exposure distribution.

Other type of stochastic interventions of interest arises in applications in which the interest relies in estimating the effect of a policy that enforces the exposure level below a certain threshold. Such policies can modify the distribution of the exposure in various ways. For example, if a policy that constrains air pollution emissions below a cutoff point is put in place, it is reasonable to think that the probability mass associated with values above that cutoff in the original exposure mechanism will be relocated around the cutoff after the intervention. This is because under such a policy, high-polluting companies will not have any incentive to go below the enforced cutoff point.

Alternative threshold-like interventions can lead to a truncated version of the original density, relocating the mass above the threshold across all values of the exposure distribution below the threshold (as opposed to relocating it in the cutoff point). In fact, as proven by Stitelman, Hubbard, and Jewell (2010), the intervention obtained by considering a dichotomous version of a continuous treatment and defining a usual static intervention (e.g., the body mass index intervention in Taubman et al., 2009), corresponds to a stochastic intervention on the original continuous treatment that truncates its density below the value defining the dichotomization.

Our major goal is to introduce stochastic intervention causal parameters as a way of measuring the effect that certain policies have on the outcome of interest. As we will see, estimation of the these parameters requires weaker assumptions than estimation of other causal parameters (e.g., marginal structural models [MSM]), relaxing assumptions about positivity and consistency of the initial estimators, and thus providing a more flexible way of estimating causal effects. We will start in Section 2 by defining the parameter of interest, in Section 3 we present its efficient influence curve, and discuss the double robustness of estimators that solve the efficient influence curve equation. This section also provides the tools for defining the targeted maximum likelihood estimators (TMLE) in Section 4.3. In Section 5 we present a simulation study demonstrating consistency and efficiency properties of the estimators, and in Section 6 we present an application example.

2. Data and Parameter of Interest

Consider an experiment in which an exposure variable A, a continuous or binary outcome Y and a set of covariates W are measured for n randomly sampled subjects. Let O = (W, A, Y) represent a random variable with distribution P₀, and O₁,…, O_n represent n i.i.d. observations of O. Assume that the following nonparametric structural equation model (NPSEM, Pearl, 2000) holds:

$$W=f_W\left(U_W\right);A=f_A(W,U_A);Y=f_Y(A,W,U_Y),$$ (1)

where U_W, U_A and U_Y are exogenous random variables such that U_A ⫫ U_Y holds, and either U_W ⫫ U_Y or U_W ⫫ U_A holds (randomization assumption). The true distribution P₀ of O can be factorized as

$$P_0\left(O\right)=P_0\left(Y\right|A,W\left)P_0\right(A\left|W\right)P_0\left(W\right),$$

where we denote g₀(A|W) ≡ P₀(A|W), ${\overline{Q}}_0(A,W)\equiv E_0(Y|A,W)$, Q_W,0(W) ≡ P₀(W) and Pf = ∫fdP for a given function f.

Counterfactual outcomes under stochastic interventions are denoted by $Y_{P_{\delta }}$, and are defined as the outcome of a causal model in which the equation in the NPSEM (1) corresponding to A is removed, and A is set equal to a with probability P_δ (g₀)(A = a|W). The latter is called the intervention distribution, which we allow to depend on the true exposure mechanism g₀. Any stochastic intervention of interest can be defined in this way, and in this article we focus the discussion on the intervention distribution:

$$P_{\delta }(g_0)(A=a|W)=g_0(a-\delta (W)|W),$$ (2)

for a known function δ(W). This is a shifted version of the current treatment mechanism, where the shifting value is allowed to vary across strata defined by the covariates. As discussed in Section 6, one can be interested in the effect of a policy that encourages people to exercise more, leading to a population where the distribution of physical activity is shifted according to certain health and socioeconomic variables. As implicitly stated in (2), we will assume that the functional form of the exposure mechanism induced by the intervention differs from the original exposure mechanism only through its conditional expectation given the covariates.

2.1 Identification

Let $A_{P_{\delta }}$ denote the exposure variable under the intervened system (i.e., $A_{P_{\delta }}$ is distributed according to P_δ (g)). We have that

$$P(Y_{P_{\delta }}=y)={\displaystyle \sum }_{a\in \mathcal{A}}{\displaystyle \sum }_{w\in \mathcal{W}}P(Y_{P_{\delta }}=y|A_{P_{\delta }}=a,W=w)\times P_{\delta }(g)(A=a|W=w)P(W=w),$$

where $\mathcal{A}$ and $\mathcal{W}$ are the support of A and W, respectively. From the NPSEM (1) we have that $P(Y_{P_{\delta }}=y|A_{P_{\delta }}=a,W=w)=P(Y_a=y|A_{P_{\delta }}=a,W=w)$, where Y_a is the counterfactual outcome when the exposure is set to level a with probability one. Note also that the usual randomization assumption A⫫Y_a|W implies $A_{P_{\delta }}⫫Y_a|W$, and therefore $P(Y_a=y|A_{p_{\delta }}=a,W=w)=P(Y_a=y|W=w)$. Under the consistency assumption (A = a implies Y_a = Y) the latter quantity is identified by P(Y = y|A = a, W = w). Our counterfactual distribution can be written as

$$P(Y_{P_{\delta }}=y)={\displaystyle \sum }_{a\in \mathcal{A}}{\displaystyle \sum }_{w\in \mathcal{W}}P(Y=y|A=a,W=w)\times P_{\delta }(g)(A=a|W=w)P(W=w).$$

We define the parameter of interest as a mapping $\mathrm{\Psi }:\mathcal{M}\to R$ that takes an element in a statistical model $\mathcal{M}$ and maps it into a number in the reals. The true value of the parameter is given by the mapping evaluated at the true distribution $P_0\in \mathcal{M}$, and is denoted by ψ₀ = Ψ(P₀). Our causal and statistical parameter of interest is then given by

$$E(Y_{P_{\delta }})=\mathrm{\Psi }(P)={\displaystyle \sum }_{A\in \mathcal{A}}{\displaystyle \sum }_{W\in \mathcal{W}}\overline{Q}(A,W)P_{\delta }(g)(A|W)Q_W(W).$$ (3)

Note that this parameter depends only on $Q=(\overline{Q},g,Q_W)$. Therefore, in an abuse of notation, we will use the expressions Ψ(Q) and Ψ(P) interchangeably.

3. Efficient Influence Curve

In this section, we derive the efficient influence curve for the parameter in (3) when P_δ (g₀) is given by (2), which can be written as

$$\mathrm{\Psi }(P)={\displaystyle \sum }_{A\in \mathcal{A}}{\displaystyle \sum }_{W\in \mathcal{W}}\overline{Q}(A,W)g(A-\delta (W)|W)Q_W(W)=E_P\{\overline{Q}(A+\delta (W),W)\}.$$ (4)

The last equality can be checked by changing the index in the summation to A − δ(W). Equation (4) corresponds exactly with computing the marginal mean of Y from the joint distribution of (W, A, Y) with A replaced by A + δ(W). Note also that if δ(W) = 0, equation (4) is equal to the expectation of Y under P.

The efficient influence curve is a key element in semiparametric efficient estimation, because it defines the linear approximation of any efficient and regular asymptotically linear estimator (see Web Appendix A), and therefore provides an asymptotic bound for the variance of all regular asymptotically linear estimators (Bickel et al., 1997).

RESULT 1

The efficient influence curve of (4) is

$$D(P)(O)=\frac{g(A-\delta (W)|W)}{g(A|W)}\{Y-\overline{Q}(A,W)\}+\overline{Q}(A+\delta (W),W)-\mathrm{\Psi }(P).$$ (5)

Because this influence curve as well as the parameter of interest depend only on Q, we will also use the notations D(P)(O) and D(Q)(O) interchangeably.

Proof

See Web Appendix A.

This efficient influence curve can be decomposed in three parts corresponding to the orthogonal decomposition of the tangent space implied by the factorization of the likelihood:

$$\begin{array}{l}{D}_1(P)(O)=\frac{g(A-\delta (W)|W)}{g(A|W)}\{Y-\overline{Q}(A,W)\},\\ D_2(P)(O)=\overline{Q}(A+\delta (W),W)-E_P\{\overline{Q}(A+\delta (W),W)|W\},\\ D_3(P)(O)=E_P\{\overline{Q}(A+\delta (W),W)|W\}-\mathrm{\Psi }(P).\end{array}$$ (6)

This decomposition of the score is going to be useful later on during the construction of a TMLE of ψ₀. The following result provides the conditions under which an estimator that solves the efficient influence curve equation is consistent.

RESULT 2

Let $D(O|{\psi }_0,\overline{Q},g)$ be the estimating function implied by the efficient influence curve D(P)(O):

$$D(O|{\psi }_0,\overline{Q},g)=\frac{g(A-\delta (W)|W)}{g(A|W)}\{Y-\overline{Q}(A,W)\}+\overline{Q}(A+\delta (W),W)-{\psi }_0,$$

let w(g)(a, w) = g(a − δ(w)|w)/g(a|w), and let ${\text{sup}}_{a\in \mathcal{A}}w(g_0)(a,W)<\infty$, − a.e. We have that $E_{P_0}D(O|{\psi }_0,\overline{Q},g)=0$ if either g is such that w(g) = w(g₀), or $\overline{Q}={\overline{Q}}_0$

Proof

See Web Appendix A.

As a consequence of result 2, under regularity conditions stated in Theorem 1 of van der Laan and Rubin (2006), a substitution estimator of Ψ(P₀) that solves the efficient influence curve equation $P_{n}D(·|{\psi }_0,\overline{Q},g)$ will be consistent if either one of w(g₀) and ${\overline{Q}}_0$ is estimated consistently, and it will be efficient if and only if both w(g₀) and ${\overline{Q}}_0$ are estimated consistently. We only rely on consistent estimation of the weight function w(g₀). This consistency can be easier to obtain than consistent estimation of the density g₀, which is required for double robustness of parameters in MSM (Neugebauer and van der Laan, 2007). Because Ψ(P) depends on both ${\overline{Q}}_0$ and g, double robustness is a very unexpected result. Some intuition about it is provided by the definition of the parameter in (4): if ${\overline{Q}}_0$ is known, a consistent estimator can always be obtained by computing the empirical mean of ${\overline{Q}}_0(A+\delta (W),W)$; if the weight function w(g₀) is known, a consistent estimate of ψ₀ would be given by a weighted average of Y with weights w(g₀)(A, W).

3.1 Positivity Assumption

Alternatives to definition and estimation of causal effects in the context of continuous or categorical multilevel treatments are given by MSM and parameters like the ones presented in Petersen et al. (2010). One of the assumptions required to estimate those parameters (the positivity assumption) is given by

$$\underset{a\in \mathcal{A}}{\text{sup}}\frac{h(a)}{g_0(a|W)}<\infty ,-\mathit{\text{a.e.}},$$

for a user-specified weight function h. The function h(a) = 1 is commonly used, because it implies giving equal weights to all the possible treatment values.

From the formula of the efficient influence curve, the positivity assumption needed to identify and estimate our parameter of interest is given by

$$\underset{a\in \mathcal{A}}{\text{sup}}\frac{g_0(a-\delta (W)|W)}{g_0(a|W)}<\infty ,-\mathit{\text{a.e.}},$$ (7)

Suppose ${\text{inf}}_{a\in \mathcal{A}}{g}_0(a|W)>\in$ for some small ∈. Because the function δ is user given, we can try to define it in a way so that it is useful to answer the causal question of interest, and yet it does not produce unstable weights. As a result, the positivity assumption as needed to estimate our parameter of interest is more easily achievable than the positivity assumption as required to estimate other causal parameters for continuous exposures.

4. Estimators

In this section, we present three possible estimators for the parameter of interest. A brief review of concepts in semiparametric efficient estimation can be found in the Web Appendix A. The TMLE and the augmented inverse probability of treatment weighting (A-IPTW) estimators solve the efficient influence curve equation, and therefore, from Result 2, are consistent estimators if either one of ${\overline{Q}}_0(A,W)$ and wg₀(A|W) is estimated consistently. They are efficient if and only if both of these quantities are estimated consistently. The IPTW is inefficient, and will be consistent only if the estimator of w(g₀)(A|W) is consistent. The TMLE is expected to perform better than the A-IPTW if the positivity assumption is violated, which will be the case if the causal question of interest requires the use of a function δ that produces unstable weights in (7). The TMLE is also a better alternative than when the efficient estimating equation has multiple solutions, or its solution goes out of the natural bounds for the parameter of interest.

The estimators presented in this section require initial estimates of ${\overline{Q}}_0(A,W)$ and g₀(A|W), which can be obtained through machine learning techniques, parametric, or semi-parametric models. The consistency of these initial estimators will determine the consistency and efficiency of the estimators of ψ₀, as discussed previously. Parametric models are commonly used for the sole sake of their nice analytical properties, but they encode assumptions about the distribution of the data that are not legitimate knowledge about the phenomenon under study and usually cause a large amount of bias in the estimated parameter. As an alternative, we recommend the use of machine learning techniques such as the super learner (van der Laan, Polley, and Hubbard, 2007). Super learner is a methodology that uses crossvalidated risks to find an optimal estimator among a library defined by the convex hull of a user-supplied list of candidate estimators. One of its most important theoretical properties is that its solution converges to the oracle estimator (i.e., the candidate in the library that minimizes the loss function with respect to the true probability distribution). Proofs and simulations regarding these and other asymptotic properties of the super learner can be found in van der Laan, Dudoit, and Keles (2004) and van der Laan and Dudoit (2003).

Influence curve based variance estimators are provided for these three estimators. Consistency of the variance estimators also depends on the consistency of the initial estimates of ${\overline{Q}}_0$ and g₀. These dependencies can be avoided at the cost of computational time and effort by using bootstrapped estimates of the variance.

4.1 IPTW

Given an estimator $g_n^0$ of the exposure density, the IPTW estimator of ψ₀ is defined as

$${\psi }_{n,1}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{g_n^0(A_i-\delta (W_i)|W_i)}{g_n^0(A_i|W_i)}{Y}_i.$$

The IPTW is an asymptotically linear estimator with influence curve

$$D_{\mathit{IPTW}}(O|{\psi }_0,g_0)=\frac{g_0(A-\delta (W)|W)}{g_0(A|W)}Y-{\psi }_0;$$

therefore, the variable $\sqrt{n}({\psi }_{n,1}-{\psi }_0)$ converges in distribution to $N\{0,P_0{D}_{\mathit{IPTW}}^2(g_0)\}$, whose variance can be estimated by $P_n{D}_{\mathit{IPTW}}^2(·|{\psi }_{n,1},g_n^0)$. This variance estimator is conservative, as proved in van der Laan and Robins (2003) and corroborated in the simulation section.

4.2 A-IPTW

The A-IPTW is the value ψ_n,2 that solves the equation ${\sum }_{i=1}^{n}D(O_i|{\psi }_0,{\overline{Q}}_n^0,g_n^0)=0$, for initial estimates ${\overline{Q}}_n^0$ and $g_n^0$ of ${\overline{Q}}_0$ and g₀.

$${\psi }_{n,2}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{g_n^0(A_i-\delta |W_i)}{g_n^0(A_i|W_i)}\{Y_i-{\overline{Q}}_n^0(A_i,W_i)\}+{\overline{Q}}_n^0(A_i+\delta (W_i),W_i).$$

If the estimators ${\overline{Q}}_n^0$ and $g_n^0$ are consistent, the A-IPTW is an asymptotically linear estimator with influence curve $D(O|{\psi }_0,{\overline{Q}}_0,g_0)$. As in the case of the IPTW, the variable $\sqrt{n}({\psi }_{n,2}-{\psi }_0)$ converges in law to a random variable with distribution $N\{0,P_0{D}^2(·|{\psi }_0,{\overline{Q}}_0,g_0)\}$, whose variance can be estimated as $P_n{D}^2(·|{\psi }_{n,2},{\overline{Q}}_n^0,g_n^0)$. van der Laan and Robins (2003) (sections 2.3.7 and 2.7.1) show that inference based on this variance estimator is valid only if $g_n^0$ is consistent, providing exact inference when ${\overline{Q}}_n^0$ is consistent, and conservative inference when ${\overline{Q}}_n^0$ is inconsistent.

4.3 Targeted Maximum Likelihood Estimator

Targeted maximum likelihood estimation (van der Laan and Rubin, 2006) is a loss-based semiparametric estimation method that yields a substitution estimator of a target parameter of the probability distribution of the data that solves the efficient influence curve estimating equation, and thereby yields a double robust locally efficient estimator of the parameter of interest, under regularity conditions.

To define a TMLE for ψ₀, we need first to define three elements: (1) A loss function L(Q) for the relevant part of the likelihood required to evaluate Ψ(P), which in this case is $Q=(\overline{Q},g,Q_W)$. This function must satisfy $Q_0={\arg \min }_Q{E}_{P_0}L(Q)(O)$, where Q₀ denotes the true value of Q; (2) An initial estimator $Q_n^0$ of Q₀; (3) A parametric fluctuation Q(∈) through $Q_n^0$ such that the linear span of $\frac{d}{\mathit{d\in }}L\left\{Q\right(\in \left)\right\}{|}_{\in =0}$ contains the efficient influence curve D(P) defined in (5). These elements are defined below:

Loss Function

As loss function for Q, we will use $L(Q)=L_Y(\overline{Q})+L_A(g)+L_W(Q_W)$, where for continuous Y we set $L_Y(\overline{Q})={\{Y-\overline{Q}(A,W)\}}^2$; for binary Y we set $L_Y(\overline{Q})=Y\log \{\overline{Q}(A,W)\}+(1-Y)\log \{1-\overline{Q}(A,W)\}$, $L_A(g)=-\log g(A|W)$, and L_W(Q_W) = −log Q_W(W). It can be easily verified that this function satisfies $Q_0={\arg \min }_Q{E}_{P_0}L(Q)(O)$.

Parametric Fluctuation

Given an estimator $Q_n^k$ of Q₀, with components $({\overline{Q}}_n^k,g_n^k,Q_{W,n}^k)$, we define the (k + 1)th fluctuation of $Q_n^k$ as follows:

$$\begin{array}{l}{\overline{Q}}_n^{k+1}({\in }_1)(A,W)={\overline{Q}}_n^k(A,W)+{\in }_1{H}_1^k(A,W),\\ g_n^{k+1}({\in }_1)(A|W)=\frac{\exp \{{\in }_1{H}_2^k(A,W)\}{g}_n^k(A|W)}{{{\displaystyle \int }}_{\mathcal{A}}\exp \{{\in }_1{H}_2^k(A,W)\}{g}_n^k(A|W)}\\ Q_{W,n}^{k+1}({\in }_2)(W)=\frac{\exp \{{\in }_2{H}_3^k(W)\}{Q}_{W,n}^k(W)}{{{\displaystyle \int }}_{\mathcal{W}}\exp \{{\in }_2{H}_3^k(W)\}{Q}_{W,n}^k(W)}\end{array}$$

where $H_1^k(A,W)=g_n^k(A-\delta (W)|W)/g_n^k(A|W)$, $H_2^k(A,W)=D_2(P^k)(O)$, and H₃(W) = D₃(P^k)(O), with D₂ and D₃ defined as in (6). We define these fluctuations using a two-dimensional ∈ with two different parameters ∈₁ and ∈₂. It is theoretically correct to define these fluctuations using any dimension for ∈, as long as the condition $D(P)\in <\frac{d}{\mathit{d\in }}L\left\{Q\right(\in \left)\right\}{|}_{\in =0}>$ is satisfied, where <·> denotes linear span. The convenience of the particular choice made here will be clear once the TMLE is defined.

Targeted Maximum Likelihood Estimator

The TMLE is defined by the following iterative process:

1. Initialize k = 0.

2. Estimate ∈ as ${\in }_n^k={\arg \min }_{\in }{P}_{n}L\left\{Q_n^k\right(\in \left)\right\}$.

3. Compute $Q_n^{k+1}=Q_n^k({\in }_n^k)$.

4. Update k = k + 1 and iterate steps (ii) through (iv) until convergence (i.e., until ${\in }_n^k=0$).

First of all, note that the value of ∈₂ that minimizes the part of the loss function corresponding to the marginal distribution of W in the first step (i.e., $-P_n\log Q_{W,n}^1({\in }_2)$) is ${\in }_2^1=0$. Therefore, the iterative estimation of ∈ only involves the estimation of ∈₁. The k th step estimation of ∈₁ is obtained by minimizing $P_n\left[L_Y\right\{{\overline{Q}}_n^k\left({\in }_1\right)\}+L_A\{g_n^k\left({\in }_1\right)\left\}\right]$, which implies solving the estimating equation

$$\begin{array}{l}{S}^k({\in }_1)={\displaystyle \sum }_{i=1}^n[Y_i-\{{\overline{Q}}_n^k(A_i,W_i)+{\in }_i{H}_1^k(O_i)\left\}\right]\\ H_1^k(O_i)+D_2\left(P_n^k\right)(O_i)\\ -\frac{{\displaystyle \sum }_{A\in \mathcal{A}}{D}_2\left(P_n^k\right)(O_i)\exp \left\{{\in }_1{D}_2\right(P_n^k)(Q_i)\}{g}_n^k(A_i|W_i)}{{\displaystyle \sum }_{A\in \mathcal{A}}\exp \left\{{\in }_1{D}_2\right(P_n^k)(O_i)\}{g}_n^k(A_i|W_i)}\end{array}$$ (8)

where

$$D_2\left(P_n^k\right)(O)=Q_n^k(A+\delta (W),W)-{\displaystyle \sum }_{A\in \mathcal{A}}{Q}_n^k(A+\delta (W_i),W_i)g_n^k(A|W_i).$$

The TMLE of ψ₀ is defined as ${\psi }_{n,3}\equiv {\lim }_{k\to \infty }\mathrm{\Psi }(P_n^k)$, assuming this limit exists. In practice, the iteration process is carried out until convergence in the values of ${\in }_n^k$ is achieved, and an estimator $Q_n^{\ast }$ is obtained. The variance of ψ_n,3 can be estimated by $P_n{D}^2(·|{\psi }_{n,3},{\overline{Q}}_n^{\ast },g_n^{\ast })$, which like the A-IPTW variance estimator is consistent only if both $g_n^{\ast }$ and $Q_n^{\ast }$ are consistent, is conservative if $g_n^{\ast }$ is consistent but $Q_n^{\ast }$ is not, and is inconsistent in any other case.

5. Simulation Study

To provide an example of the finite sample properties of the estimators discussed in Section 4, a simulation study was performed. We focus on just one data-generating distribution, which provides a limited but useful situation to demonstrate our claims about consistency and efficiency.

$$\begin{array}{l}{W}_1~U\{0,1\},\\ W_2~\mathit{Ber}\{0.7\},\\ A|W_1,W_2~\mathit{\text{Poisson}}\{\exp (3+0.3\log (W_1)-0.2\exp (W_1)W_2\},\\ Y|A,W_1,W_2~N\{1+0.5A-0.2A{W}_2+2A\tan (W_1^2)-2W_1{W}_2+A{W}_1{W}_2,1\}.\end{array}$$

Assuming that we are interested in estimating the effect of a constant shift of δ(W₁, W₂) = 2, the true parameter value for this data-generating distribution is ψ₀ = 22.95, and the efficiency bound equals ${\{{\mathit{Var}}_{P_0}D(P_0\left)\right(O)\}}^{1/2}=17.81$.

For sample sizes n = 50, 100, 200, and 500, we simulated 2000 samples from the previous data-generating distribution, and estimated ψ₀ using the three estimators proposed in the previous section. As initial estimators of ${\overline{Q}}_0(A,W)$ and g₀(A|W) we considered four cases: (1) correctly specified model for both ${\overline{Q}}_0(A,W)$ and g₀(A|W), (2) incorrectly specified model for ${\overline{Q}}_0(A,W)$ but correctly specified for g₀(A|W), (3) correctly specified model for ${\overline{Q}}_0(A,W)$ but incorrectly specified for g₀(A|W), and (4) incorrectly specified model for both ${\overline{Q}}_0(A,W)$ and g₀(A|W); where misspecification of the models was performed by considering the correct distribution and link function but only main terms in the linear predictor.

TML estimation of ψ₀ was performed using the R tmle.shift() function presented in Web Appendix B. The average and variance of the estimates across the 2000 samples was computed as an approximation to the expectation and variance of the estimator (Table 1), respectively.

Table 1.

Expectation of the estimators for different sample sizes and model specifications. True value is 22.95

n	Model	TMLE	IPTW	A-IPTW
50	1	22.99	22.66	22.99
	2	22.99	22.49	22.99
	3	22.88	22.66	22.91
	4	22.01	22.49	22.04
100	1	22.95	22.81	22.95
	2	22.96	22.61	22.95
	3	22.89	22.81	22.92
	4	21.97	22.61	22.00
200	1	22.99	22.89	22.99
	2	22.99	22.68	22.99
	3	22.94	22.89	22.96
	4	21.99	22.68	22.02
500	1	22.97	22.93	22.97
	2	22.97	22.71	22.97
	3	22.93	22.93	22.96
	4	21.97	22.71	22.00

The results in Table 1 confirm the double robustness of the TMLE and A-IPTW, which had been proven analytically in Result 2. The TMLE and A-IPTW are unbiased even for small sample sizes, whereas the IPTW needs larger sample sizes to achieve unbiasedness.

Regarding the variance of the estimators, Table 2 shows that the IPTW estimator is inefficient, and its influence curve based variance estimator is very conservative. The variances of the TMLE and A-IPTW are approximately equal to the efficiency bound if the models for ${\overline{Q}}_0$ and g₀ are correctly specified, although the same equality is observed if only ${\overline{Q}}_n^0$ is misspecified. This is because, as stated in Result 2, we only need consistent estimation of the weights w(g₀)(A, W), which can be obtained through a possibly misspecified estimator of g₀. On the other hand, the variance of these estimators is considerably affected by misspecification of the model for ${\overline{Q}}_0$ (models 3 and 4), even if $g_n^0$ is correctly specified.

Table 2.

Standard error of the estimator (times $\sqrt{n}$). Expectation of the influence curve based estimator of the variance (times $\sqrt{n}$) in parentheses. Efficiency bound is 17.81

n	Model	TMLE	IPTW	A-IPTW
50	1	17.94 (17.66)	20.33 (26.80)	17.94 (17.66)
	2	17.94 (17.67)	19.16 (25.03)	17.94 (17.66)
	3	18.92 (17.81)	20.33 (26.80)	18.94 (18.08)
	4	18.21 (18.07)	19.16 (25.03)	18.25 (17.77)
100	1	17.93 (17.74)	20.36 (27.63)	17.93 (17.74)
	2	17.93 (17.75)	19.04 (25.72)	17.93 (17.75)
	3	18.96 (18.14)	20.36 (27.63)	18.98 (18.45)
	4	18.34 (18.37)	19.04 (25.72)	18.35 (18.06)
200	1	17.77 (17.77)	20.17 (28.00)	17.77 (17.77)
	2	17.77 (17.78)	18.93 (25.97)	17.77 (17.77)
	3	18.62 (18.35)	20.17 (28.00)	18.64 (18.68)
	4	17.98 (18.57)	18.93 (25.97)	18.00 (18.24)
500	1	17.38 (17.79)	20.40 (28.37)	17.39 (17.79)
	2	17.38 (17.80)	18.94 (26.24)	17.39 (17.80)
	3	18.50 (18.49)	20.40 (28.37)	18.52 (18.84)
	4	17.74 (18.71)	18.94 (26.24)	17.76 (18.36)

The fact that influence curve based variance estimators of the TMLE and A-IPTW are consistent even for misspecified $g_n^0$ can be taken to be a coincidence associated with this particular data-simulating scheme. As explained in Section 4, this type of consistency does not hold in general.

Because all estimators considered are asymptotically linear, 95% normal-based confidence intervals can be computed. Their coverage probabilities are presented in Table 3. The conservativeness of the IPTW can also be appreciated here. The consistent TMLE- and A-IPTW-based confidence intervals have perfect asymptotic coverage probability. Intervals associated to inconsistent estimators (model 4) have, as expected, confidence levels below the nominal value. In this simulation we do not observe significant differences between the TMLE and the A-IPTW.

Table 3.

Coverage probability of normal-based confidence intervals

n	Model	TMLE	IPTW	A-IPTW
50	1	0.93	0.97	0.93
	2	0.93	0.96	0.93
	3	0.92	0.97	0.92
	4	0.90	0.96	0.89
100	1	0.94	0.98	0.94
	2	0.94	0.98	0.94
	3	0.93	0.98	0.94
	4	0.89	0.98	0.89
200	1	0.95	0.98	0.95
	2	0.95	0.97	0.95
	3	0.94	0.98	0.95
	4	0.87	0.97	0.87
500	1	0.95	0.99	0.95
	2	0.95	0.98	0.95
	3	0.94	0.99	0.95
	4	0.78	0.98	0.78

6. Application

With the objective of illustrating the procedure described in the previous sections, we revisit the problem analyzed by Bembom and van der Laan (2007) of assessing the extent to which physical activity in the elderly is associated with reductions in cardiovascular morbidity and mortality, and improvement in, or prevention of metabolic abnormalities. Tager et al. (1998) followed a group of people over 55 years of age living around Sonoma, California, over a time period of about 10 years as part of a longitudinal study of physical activity and fitness (Study of Physical Performance and Age Related Changes in Sonomans—SPPARCS). The goal in analyzing the data that were collected as part of this study is to examine the effect of baseline vigorous LTPA on subsequent 5 year all-cause mortality.

In this article, we use the same measure of LTPA used by Bembom and van der Laan (2007), which is a continuous score based on the number of hours that the participants were engaged in vigorous physical activities such as jogging, swimming, bicycling on hills, or racquetball in the last 7 days, and the standard intensity values in metabolic equivalents (MET: metabolic equivalent of task) of such activities, where one MET is approximately equal to the oxygen consumption required for sitting quietly.

The primary confounding factors that we adjust for are described in Table 4. Age and gender are natural confounders, and the rest of the variables intend to account for the subject’s underlying level of general health. Of the 2092 subjects enrolled in the SPPARCS study, 40 were missing information in at least one of this variables; our analysis is based on the remaining 2052 subjects.

Table 4.

Confounders

Variable	Description
Gender	Female
	Male
Age	Age in years
Health	Self-rated health status: Excellent Fair Poor
NRB	Score of self-reported physical functioning rescaled between 0 and 1
Card	Previous occurrence of any of the following cardiac events: Angina, myocardial infarction, congestive heart failure, coronary by-pass surgery, and coronary angioplasty
Chron	Presence of any of the following chronic health conditions: stroke, cancer, liver disease, kidney disease, Parkinson’s disease, and diabetes mellitus
Smoking	Never smoked Current smoker Ex-smoker
Decline	Activity decline compared to 5 or 10 years earlier

In the sequel of this section, the vector containing the confounders will be denoted by W, the continuous MET score by A, and the indicator of 5-year all-cause mortality by Y. We are interested in estimating the effect of a policy that will produce an increase of 12 METs (corresponding, for instance, to bicycling during 3 hours at less than 10 mph per week) in the average of the conditional distribution physical activity, given the covariates. Note that our intervention could also be defined by using different values of MET in each strata defined by the covariates W.

Initial estimators of the conditional density g₀(A|W) and the conditional expectation ${\overline{Q}}_0(A,W)$ are presented below.

6.1 Initial Estimator of g₀

For the estimation of the density g₀(A|W), we consider the estimator presented in Díaz-Munoz and van der Laan (2011). We now provide a summary of the rationale behind this estimator. Consider k + 1 values α₀, α₁,…, α_k spanning the range of the data and defining k bins. Now, consider the following class of histogram-like candidate estimators of the conditional density g₀(A|W)

$$\begin{array}{l}{g}_{n,\alpha }(A=a|W)\\ =\frac{{\mathit{Pr}}_n\{A\in [{\alpha }_{m-1},{\alpha }_m)|W\}}{{\alpha }_m-{\alpha }_{m-1}},\text{for}{\alpha }_{m-1}\le a<{\alpha }_{m-1},\end{array}$$

where the choice of the α values and the number of bins index the candidates in the class. The probabilities in the numerator are estimated through the super learner. The final estimator of the density consists of a convex combination of these estimators that minimizes the crossvalidated empirical risk. For further reference and properties of this estimator in the context of estimation of causal effects, the reader is referred to the original paper.

As an example, Figure 1 shows two contrasting estimated densities g_n(A|W) for different profiles W, in which a subject with better general health status is more likely to have higher levels of physical activity. As pointed out in Díaz-Munoz and van der Laan (2011), this methodology allows the detection of high density areas in the exposure mechanism, like the one detected at zero in Figure 1a. This spike appears because this is a zero-inflated exposure, in which a large proportion of the population do not practice any amount of physical activity.

Figure 1.

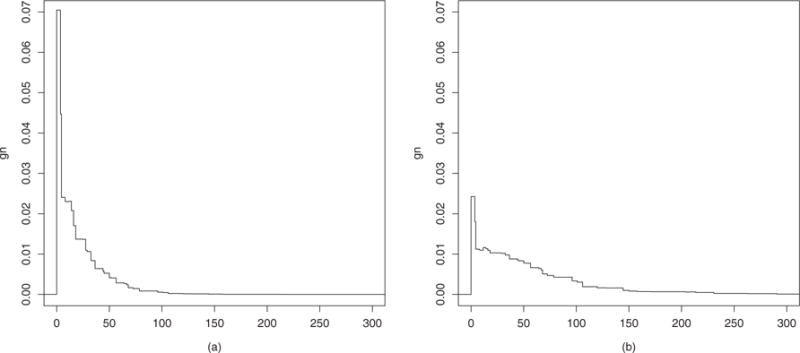
Estimated conditional density of A given the profiles: (a) age = 77, gender = female, health = fair, nrb = 0.9, card = no, smoke = ex-smoker, decline = yes, chron = yes; and (b) age = 71, gender = male, health = good, nrb = 0.88, card = no, smoke = never smoked, decline = no, chron = no.

6.2 Initial Estimator of ${\overline{Q}}_0$

For the initial estimator of ${\overline{Q}}_0$ we used the super learner (van der Laan et al., 2007). Table 5 shows the candidates used, their crossvalidated risks, and their coefficients in the final super learner predictor. To get a consistent estimator of ${\overline{Q}}_0$ the library of candidate estimators should be as large as possible. Because this is an illustrating example, we allow ourselves to use this small library.

Table 5.

Super learner output for estimation of ${\overline{Q}}_0$

	Crossvalidated risk	Coef.
Generalized linear model (GLM) main effects	0.1079	0.0000
GLM main eff. and two way interactions	0.1143	0.0835
Generalized additive model (GAM) degree 2	0.1073	0.0000
GAM degree 3	0.1071	0.9165
Bayes’ GLM main effects	0.1078	0.0000

6.3 Estimators of ψ₀

Table 6 shows the three estimates of ψ₀ with their standard errors, as described in Section 4. As an example, the TML estimated value of ψ_n,3 = 0.16 indicates that if a policy that increases the average LTPA by the equivalent of 12 METs is implemented, the estimated risk of death in the intervened population will be 16%.

Table 6.

Estimates of ψ₀

	TMLE	A-IPTW	IPTW
ψ0	0.1600(0.0104)	0.1599(0.0105)	0.1454(0.0135)
${\psi }_0^1$	−0.0179(0.0071)	−0.0179(0.0071)	−0.0324(0.0117)

If the objective is to perform a comparison with the current risk of death, we can define a population intervention parameter ${\psi }_0^1$ as

$${\psi }_0^1={\psi }_0-E_{P_0}(Y).$$

This is a parameter that compares the expected risk of death in the intervened population with the current risk of death, and therefore describes the gain obtained by carrying out the intervention of interest. For a given estimator ψ_n of ψ₀, an asymptotically linear estimator of ${\psi }_0^1$ is given by ${\psi }_n^1={\psi }_n-\overline{Y}$. Its influence curve can be computed as D¹(P)(O) = D(P)(O) − {Y − E_P(Y)}, and its variance is estimated through the sample variance of D¹(P)(O). Here D(P)(O) is the influence curve of each of the estimators defined in Section 4. The estimates of ${\psi }_0^1$ and their standard errors are presented in Table 6. Confidence intervals and p-values for hypothesis testing can be computed based on the normal approximations for asymptotically linear estimators described in Section 4 and Web Appendix A. In light of the results from the simulation section and the theoretical properties of the estimators, we rely on the TMLE and A-IPTW to measure the effect of the intervention of interest. The estimated value of ${\psi }_n^1$ means that if a policy increasing the average time of physical activity by the equivalent of 12 METs (corresponding, for instance, to bicycling during 3 hours per week at less than 10 mph) is put in place, the risk of all-cause mortality in the elderly would be reduced by 1.79%. These results are consistent with the findings of Bembom and van der Laan (2007).

7. Discussion

In this article, we define a new parameter measuring the causal effect of a population intervention that (as opposed to most of the parameters presented in the literature) accounts for the fact that in most cases the postintervention exposure continues to be a random variable. We argue that this parameter makes more intuitive sense when the objective is to assess the causal effect of policies intending to modify an exposure variable that cannot be directly intervened upon. For example, as argued in Bembom and van der Laan (2007), it makes little sense to assess the effect of a realistic policy in terms of a static intervention in which every subject in a population of elderly people is required to increase his level of physical activity to the maximum, or even to a level defined by a deterministic function of the covariates. Such interventions are never possible due to particular health conditions, physical functioning constraints, or simple inability to enforce every subject to comply with the treatment level dictated by the intervention. Hence, deterministic interventions do not provide an accurate tool to measure the causal effect of a realistic policy that renders a stochastic exposure.

Another appealing feature of the framework presented in this article is that it provides a natural way of defining and estimating causal effects for continuous variables, or discrete variables with more than two levels, which are currently defined through the specification of a working MSM (Neugebauer and van der Laan, 2007). The positivity assumption required to estimate our proposed causal parameter can be made weaker than the positivity assumption required to estimate MSM parameters.

Three estimators of the parameter were proposed, two of which are double robust to misspecification of the models for the treatment mechanism g₀ and the conditional expectation ${\overline{Q}}_0$, even when the parameter depends on these two quantities. This double robustness property is proven analytically, and corroborated in a simulation study.