A RATE FUNCTION APPROACH TO COMPUTERIZED ADAPTIVE TESTING FOR COGNITIVE DIAGNOSIS

Abstract

Computerized adaptive testing (CAT) is a sequential experiment design scheme that tailors the selection of experiments to each subject. Such a scheme measures subjects’ attributes (unknown parameters) more accurately than the regular prefixed design. In this paper, we consider CAT for diagnostic classification models, for which attribute estimation corresponds to a classification problem. After a review of existing methods, we propose an alternative criterion based on the asymptotic decay rate of the misclassification probabilities. The new criterion is then developed into new CAT algorithms, which are shown to achieve the asymptotically optimal misclassification rate. Simulation studies are conducted to compare the new approach with existing methods, demonstrating its effectiveness, even for moderate length tests.

1. Introduction

Cognitive diagnosis has recently gained prominence in educational assessment, psychiatric evaluation, and many other disciplines. Various modeling approaches have been discussed in the literature both intensively and extensively (e.g., Tatsuoka, 1983). A short list of such developments includes the rule space method (Tatsuoka, 1985, 2009), the reparameterized unified/fusion model (RUM) (DiBello, Stout, & Roussos, 1995; Hartz, 2002; Templin, He, Roussos, & Stout, 2003), the conjunctive (noncompensatory) DINA and NIDA models (Junker & Sijtsma, 2001; de la Torre & Douglas, 2004), the compensatory DINO and NIDO models (Templin & Henson, 2006), the attribute hierarchy method (Leighton, Gierl, & Hunka, 2004). Tatsuoka (2002) discussed a model usually referred to as the conjunctive DINA model that has both conjunctive and disjunctive components in its attribute specifications to allow for multiple strategies and a discussion of identifiability is also provided. See also Rupp, Templin, and Henson (2010) for more approaches to cognitive diagnosis.

Another important development in educational measurement is computerized adaptive testing (CAT), that is, a testing mode in which item selection is sequential and individualized to each subject. In particular, subsequent items are selected based on the subject’s (e.g., examinee’s) responses to prior items. CAT was originally proposed by Lord (1971) for item response theory (IRT) models as a method through which items are tailored to each examinee to “best fit” his or her ability level θ. More capable examinees avoid receiving problems that are too simple and less capable examinees avoid receiving problems that are too difficult. Such individualized testing schemes perform better than traditional exams with a prefixed set of items because the optimal selection of testing problems is examinee dependent. It also leads to greater efficiency and precision than that which can be found in traditional tests. For the traditional CAT under IRT settings, items are typically chosen to maximize the Fisher information (MFI) (Lord, 1980; Thissen & Mislevy, 2000) or to minimize the expected posterior variance (MEPV) (van der Linden, 1998; Owen, 1975).

It is natural to consider incorporating CAT design into cognitive diagnosis. The sequential nature of CAT could conceivably bring major benefits to cognitive diagnosis. First, diagnostic classification models are multidimensional with simultaneous consideration of different attributes. To fully delineate each dimension with sufficient accuracy would certainly demand a large number of items to cover all attributes. Thus, the ability to reduce test length in CAT can be attractive. Second, it is often desirable to provide feedback learning or remedial training after diagnosis; see Junker (2007). The CAT design can serve as a natural framework under which a feedback online learning system may be incorporated.

A major difference between classical IRT models and diagnostic classification models (DCM) is that the parameter space of the latter is usually discrete, for the purpose of diagnosis. Thus, standard CAT methods developed for IRT (such as the MFI or MEPV method) do not apply. Several alternative methods have already been developed in the literature. The parameter spaces of most DCMs admit a partially ordered structure (von Davier, 2005). Under such a setting, Tatsuoka and Ferguson (2003) developed a general theorem on the asymptotically optimal sequential selection of items for finite partially ordered parameter spaces. In particular, the asymptotically optimal design maximizes the convergence rate of the parameters’ posterior distribution to the true parameter. Xu, Chang, and Douglas (2003) investigated two methods based on different ideas. One method is based on the Shannon entropy of the posterior distribution. The other method is based on the Kullback–Leibler (KL) information that describes the global information of a set of items for parameter estimation. The concept of global information was introduced by Chang and Ying (1996). Cheng (2009) further extended the KL information method by taking into account the posterior distribution and the distances between the alternative parameters and the current estimate when computing the global information. Arising from such extensions are two new methods known as the posterior-weighted KL algorithm (PWKL) and the hybrid KL algorithm (HWKL). See Tatsuoka (2002) for a real-data application of CAT.

A key component in the study of CAT lies in evaluating the efficiency of a set of items, i.e., what makes a good selection of exam problems for a particular examinee. Efficiency is typically expressed in terms of the accuracy of the resulting estimator. In classic IRT, items are selected to carry maximal information about the underlying parameter θ. This is reflected by the MFI and the MEPV methods (Lord, 1980; Thissen & Mislevy, 2000; van der Linden, 1998; Owen, 1975). On the other hand, for diagnostic classification models, parameter spaces are usually discrete, and the task of parameter estimation is equivalent to a classification problem. In this paper, we address the problem of CAT for cognitive diagnosis (CD-CAT) by focusing on the misclassification probability. The misclassification probability, though conceptually a natural criterion, is typically not in a closed form. Thus, it is not a feasible criterion. Nonetheless, under very mild conditions, we show that this probability decays exponentially fast as the number of items (m) increases, that is, P(α̂ ≠ α₀) ≈ e^−m×I, where α̂ is an estimator of the true parameter α₀. We use the exponential decay rate, denoted by I, as a criterion. That is, a set of items is said to be asymptotically optimal if it maximizes the rate I (instead of directly minimizing the misclassification probability). The rate I is usually easy to compute and often in a closed form. Therefore, the proposed method is computationally efficient. In Section 3.3, we derive the specific form of the rate function for the Bernoulli response distribution that is popular in cognitive diagnosis. Based on the rate function I, we propose CD-CAT procedures that correspond to this idea. Simulation studies are conducted to compare our procedure with several existing methods for CD-CAT.

This paper is organized as follows. Section 2 provides a general introduction to the problem of CD-CAT, including an overview of existing methods. In Section 3, we introduce the idea of asymptotically optimal design and the corresponding CD-CAT procedures. We examine the connection of our new approach to previously developed methods in Section 4. Further discussion is provided in Section 5. Finally, Section 6 contains simulation studies.

2. Computerized Adaptive Testing for Cognitive Diagnosis

2.1. Problem Setting

Let the random variable X be the outcome of an experiment e. The distribution of X depends on the experiment e and an underlying parameter α. We use α₀ ∈ 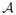to denote the true parameter and e¹, …, e^m ∈ 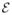to denote different experiments. In the context of cognitive diagnosis, α corresponds to the “attribute profile” or “knowledge state” of a subject, e is an item or an exam problem, and X is the subject’s response to the item e. Suppose that independent outcomes X¹, …, X^m of experiments e¹, …, e^m are collected. For each e ∈ 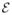and α ∈ 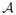, let f(x|e, α) be the probability density (mass) function of X. Throughout this paper, we suppose that the parameter space α takes finitely many values in 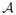= {1, …, J} and that there are κ types of experiments 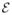= {1, …, κ}.

Let superscripts indicate independent outcomes, e.g., Xⁱ is the outcome of the ith experiment eⁱ ∈ 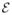. The experiments are possibly repeated, i.e., eⁱ = e^j (i.e., i.i.d. outcomes can be collected from the same experiment). Suppose that the prior distribution of the parameter α is π(α). Given the observed responses X¹, …, X^m, the posterior distribution of α is

$$\pi (\alpha \mid X^i,e^i,\text{for}i=1,\dots ,m)\propto \pi (\alpha )\prod _{i=1}^{m}f(X^i\mid e^i,\alpha ).$$ (1)

To simplify the notation, we let X_m = (X¹, …, X^m) and e_m = (e¹, …, e^m), e.g.,

$$\pi (\alpha \mid {\mathbf{X}}_m,{\mathbf{e}}_m)=\pi (\alpha \mid X^i,e^i,\text{for}i=1,\dots ,m).$$ (2)

Thus, a natural estimator of α is the posterior mode

$$\widehat{\alpha }({\mathbf{X}}_m,{\mathbf{e}}_m)=arg\underset{\alpha \in \mathcal{A}}{sup}\pi (\alpha \mid {\mathbf{X}}_m,{\mathbf{e}}_m).$$ (3)

For any two distributions P and Q, with densities p and q, the Kullback–Leibler (KL) divergence/information is

$$D_{\text{KL}}(P\Vert Q)=E_P[log(p(X)/q(X))].$$ (4)

For two parameter values α₀ and α₁, let D_e(α₀, α₁) = E_e,α0{log[f(X|e, α₀)/f(X|e, α₁)]} be the KL divergence between the outcome distributions of experiment e, where the notation E_e,α0 indicates that X follows distribution f(x|e, α₀). We say that an experiment e separates parameter values α₀ and α₁ if D_e(α₀, α₁) > 0. Note that D_e(α₀, α₁) = 0 if the two distributions f(x|e, α₀) and f(x|e, α₁) are identical and statistically indistinguishable. Otherwise, if D_e(α₀, α₁) > 0 and independently and identically distributed (i.i.d.) outcomes can be generated from the experiment e, the parameters α₀ and α₁ are eventually distinguishable. An experiment with a large value of D_e(α₀, α₁) is powerful in differentiating α₀ and α₁. To simplify the discussion, we assume that for each pair of distinct parameters α₀ ≠ α₁ there exists an experiment e ∈ 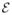that separates α₀ and α₁; otherwise, we simply merge the inseparable parameters and reduce the parameter space. This is discussed in Appendix B; see also Chiu, Douglas, and Li (2009), Tatsuoka (1991), Tatsuoka (1996) for discussions of parameter identifiability for specific models. To illustrate these ideas, we provide two stylized examples that are frequently considered.

Example 1 (Partially ordered sets, Tatsuoka and Ferguson (2003))

Consider that the parameter space 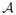is a partially ordered set with a binary relation “≤”. The set of experiment is identical to the parameter space, i.e. 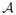= 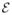. The outcome distribution of experiment e and parameter α is given by f(x|e, α) = f(x) if e ≤ α₀, and f(x|e, α) = g(x) otherwise.

The following example can be viewed as an extension of Example 1 where the distributions f and g are experiment-dependent.

Example 2 (DINA model, Junker and Sijtsma (2001))

Consider a parameter space α = (a₁, …, a_k) ∈ 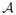= {0, 1}^k and e = (ε₁, …, ε_k) ∈ {0, 1}^k. In the context of educational testing, each a_i indicates if a subject possesses a certain skill. Each experiment corresponds to one exam problem and ε_i indicates if this problem requires skill i. A subject is capable of solving an exam problem if and only if he or she possesses all the required skills, i.e., e ≤ α, defined as ε_i ≤ a_i for all i = 1, …, k. The outcome in this context is typically binary: X = 1 for the correct solution to the exam problem and X = 0 for the incorrect solution. We let ξ = 1(e ≤ α) be the ideal response. The outcome follows a Bernoulli distribution

$$P(X=1\mid e,\alpha )=\{\begin{array}{ll}1-s_e\hfill & \text{if}\xi =1,\hfill \\ g_e\hfill & \text{otherwise}.\hfill \end{array}$$

The parameter s_e is known as the slipping parameter and g_e is the guessing parameter. Both the slipping and the guessing parameters are experiment specific. The general form of DINA model allows heterogeneous slipping and guessing parameters for different exam problems with identical skill requirements. Thus, in addition to the attribute requirements, the model also specifies the slipping and the guessing parameters for each exam problem.

In practice, there may not be completely identical items. For instance, one may design two exam problems requiring precisely the same skills. However, it is difficult to ensure the same slipping and the guessing parameters. Thus, we can only expect independent (but not identically distributed) outcomes. In the previous discussion, we assume that i.i.d. outcomes can be collected from the same experiment. This assumption is imposed simply to reduce the complexity of the theoretical development, and is not really required by the proposed CAT procedures (Algorithm 1). More discussion on this issue is provided in Remark 2.

2.2. Existing Methods for the CD-CAT

2.2.1. Asymptotically Optimal Design by Tatsuoka and Ferguson (2003)

Tatsuoka and Ferguson (2003) proposes a general theorem on the asymptotically optimal selection of experiments when the parameter space is a finite and partially ordered set. It is observed that the posterior probability of the true parameter α₀ converges to one exponentially fast, that is, 1 − π(α₀|X_m, e_m) ≈ e^−m×H as m → ∞. The authors propose the selection of experiments (items) that maximize the asymptotic convergence rate H.

In particular, the asymptotically optimal selection of experiments can be represented by the KL divergence in the following way. Let h_e be the proportion of experiment e among the m experiments. For each alternative α₁ ≠ α₀, define D_h(α₀, α₁) = h_eD_e(α₀, α₁), where h = (h₁, …, h_κ) and Σ_j h_j =1. Then the asymptotically optimal selection solves the optimization problem h^* = arg max_h[min_α1≠α0 D_h(α₀, α₁)]. The authors show that several procedures achieve the asymptotic optimal proportion h^* under their setting.

2.2.2. The KL Divergence Based Algorithms

There are several CD-CAT methods based on the Kullback–Leibler divergence. The basic idea is to choose experiments such that the distribution of the outcome X associated with the true parameter α₀ looks most dissimilar to the distributions associated with the alternative parameters. The initial idea was proposed by Chang and Ying (1996), who define the global information by summing the KL information over all possible alternatives, i.e.,

$${\text{KL}}_e({\alpha }_0)=\sum _{\alpha \ne {\alpha }_0}{D}_e({\alpha }_0,\alpha ).$$ (5)

If an experiment e has a large value of KL_e(α₀), then the outcome distributions associated with α₀ and the alternative parameters are very different. Thus, e is powerful in differentiating the true parameter α₀ from other parameters. For a sequential algorithm, let α̂_m be the estimate of α based on the first m outcomes. The next experiment is chosen to maximize KL_e(α̂_m) (Xu et al., 2003).

This idea is further extended by Cheng (2009), who proposes the weighting of each D_e(α̂_m, α₁) in (5) by the posterior probability conditional on X_m, that is, each successive experiment maximizes PWKL_e(α̂_m) = Σ_α≠α0 D_e(α̂_m, α)π(α|X_m, e_m). An α with a higher value of π(α|X_m, e_m) is more difficult to differentiate from the posterior mode α̂_m. Thus, it carries more weight when choosing subsequent items. This method is known as the posterior-weighted Kullback–Leiber (PWKL) algorithm. The author also proposes a hybrid method that adds to D_e(α̂_m, α) further weights inversely proportional to the distance between α and α̂_m, so that alternative parameters closer to the current estimate receives even more weight.

2.2.3. The SHE Algorithm

The Shannon entropy of the posterior distribution is defined as

$$H\left(\pi (·\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right)\triangleq -\sum _{\alpha \in \mathcal{A}}\pi (\alpha \mid {\mathbf{X}}_m,{\mathbf{e}}_m)log\pi (\alpha \mid {\mathbf{X}}_m,{\mathbf{e}}_m)=log\kappa -D\left(\pi (·\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\Vert U_{\mathcal{A}}(·)\right),$$

where 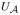is the uniform distribution on the set 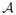and D(·||·) is the KL divergence defined in (4). Thus, the experiment that minimizes the Shannon entropy of the posterior distribution makes the posterior distribution as different from the uniform distribution as possible. In particular, let f(x^m+1|e, X_m, e_m) be the posterior predictive distribution of the (m + 1)-th outcome if the (m + 1)-th experiment is chosen to be e. The sequential item selection algorithm chooses e^m+1 to minimize the expected Shannon entropy SHE(e), where

$$\text{SHE}(e)=\int H\left(\pi \left(·\mid {\mathbf{X}}_m,X^{m+1}=x^{m+1},{\mathbf{e}}_m,e^{m+1}=e\right)\right)f\left(x^{m+1}\mid e,{\mathbf{X}}_m,{\mathbf{e}}_m\right){dx}^{m+1}.$$

The idea of minimizing the Shannon entropy is very similar to that of the minimum expected posterior variance method developed for IRT.

3. The Misclassification Probability, Optimal Design, and CAT

In this section, we present the main method of this paper. For a discrete parameter space, estimating the true parameter value is equivalent to classifying a subject into one of J groups. Given that the main objective is the estimation of the attribute parameter α, a natural goal of optimal test design would be the minimization of the misclassification probability. In the decision theory framework, this probability corresponds to the Frequentist risk associated with the zero-one loss function; see Chapter 11 of Cox and Hinkley (2000). Let α₀ denote the true parameter. The misclassification probability of some estimator α̂(X_m) based on m experiments is then

$$p({\mathbf{e}}_m,{\alpha }_0)=P_{{\mathbf{e}}_m,{\alpha }_0}\left(\widehat{\alpha }({\mathbf{X}}_m)\ne {\alpha }_0\right).$$ (6)

We write e_m and α₀ in the subscript to indicate that the outcomes X₁, …, X_i are independent outcomes from f(Xⁱ|eⁱ, α₀) respectively. Similarly, we will use E_{em, α0} to denote the corresponding expectation. Throughout this paper, we consider α̂ to be the posterior mode in (3). If one uses a uniform prior over the parameter space 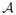, i.e., $\pi (\alpha )=\frac{1}{J}$, then the posterior mode is identical to the maximum likelihood estimate. Thus, the current framework includes the situation in which the MLE is used. Under mild conditions, one can show that p(e_m, α₀) → 0 as m → ∞. A good choice of items should admit small p(e_m, α₀). However, direct use of p(e_m, α₀) as an efficiency measure is difficult, mostly due to the following computational limitations. The probability (6) is usually not in an analytic form. Regular numerical routines (such as Monte Carlo methods) fail to produce accurate estimate of p(e_m, α₀). For instance, when m = 50, this probability could be as small as a few percentage points. Evaluating such a probability for a given relative accuracy is difficult, especially this probability has to be evaluated many times—essentially once for each possible combination of items. Therefore, (6) is not a feasible criterion from a computational viewpoint. Due to these concerns, we propose the use of an approximation of (6) based on large deviations theory. In particular, as we will show, under very mild conditions, the following limit can be established:

$$-\frac{logp({\mathbf{e}}_m,{\alpha }_0)}{m}\to I\text{as}m\to \infty .$$ (7)

That is, the misclassification probability decays to zero exponentially fast and it can be approximated by p(e_m, α₀) ≈ e^−mI. We call the limit I the rate function; it depends on both the experiment selection and the true parameter α₀. The selection of experiments that maximizes the rate function is said to be asymptotically optimal in the sense that the misclassification probability based on the asymptotically optimal design achieves the same exponential decay rate as the optimal design that minimizes the probability in (6). In addition, the rate function has favorable properties from a computational point of view. It only depends on the proportion of each type of experiments. Therefore, the asymptotically optimal proportion does not depend on the total number of experiments m, which simplifies the computation. In addition, the rate I is in closed form for most standard distributions. Minimizing the misclassification probability is equivalent to adopting a zero-one loss function. In practice, there may be other sensible loss functions under specific scenarios. In this paper, we focus on the zero-one loss function and the misclassification probability.

We emphasize that the asymptotic optimality discussed in the previous paragraph is different from the one in Tatsuoka and Ferguson (2003). In fact, these two criteria often yield different “optimal designs.” To make a difference, we refer to the latter as “Tatsuoka and Ferguson’s asymptotic optimality” and reserve the term asymptotic optimality, as specified momentarily in Definition 1, for designs that maximize the rate function I.

3.1. The Misclassification Rate Function and the Asymptotically Optimal Design

We now consider the misclassification rate function. To facilitate the discussion, we assume that m × h_e independent outcomes are collected from experiment e ∈ 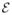. Furthermore, we assume that the proportion h_e does not change with m, except for some slight variation due to rounding. We say that such a selection of h_e is stable. Under the asymptotic regime where m → ∞, the parameter h = (h₁, …, h_κ) forms the exogenous experiment design parameter to be tuned. Under this setting, the rate function (when exists) is

$$-\frac{1}{m}logp({\mathbf{e}}_m,{\alpha }_0)\to I_{\mathbf{h},{\alpha }_0}.$$ (8)

The limit depends on the proportion of each experiment contained in h and the true parameter α₀. We establish the above approximation and provide the specific form of I_h,α0 in Theorem 2.

For two sets of experiments corresponding to two vectors h₁ and h₂, if I_h1,α0 > I_h2,α0, it suggests that the misclassification probability of h₁ decays to zero at a faster speed than h₂ and, therefore, h₁ is a better design. We propose the use of I_h,α0 as a measure of efficiency.

Definition 1

We say that an experiment design corresponding to a set of proportions h = (h₁, …, h_κ) is asymptotically optimal if h maximizes the rate function I_h,α0 as in (8).

One computationally appealing feature of asymptotically optimal design is that the asymptotically optimal proportion h generally does not depend on the particular form of the prior distribution. Since asymptotic optimality describes the amount of information in the data, item selection is relatively independent from the a priori information of the attributes.

3.2. The Analytic Form of the Rate Function

In this subsection, we present specific forms of the rate function. To facilitate discussion, we use a different set of superscripts. Among the m responses, m × h_e of them are from experiment e. Let X^e,l be the lth (independent) outcomes of type e experiments for l = 1, …, m × h_e. Note that the notation e includes all the information about an experiment. For instance, in the setting of the DINA model, e includes the attribute requirements (the Q-matrix entries) as well as the slipping and the guessing parameters.

We start the discussion with a specific alternative parameter α₁. The posterior distribution prefers an alternative parameter α₁ ≠ α₀ to α₀ if

$$\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m).$$

We insert the specific form of the posterior in (1) and the above inequality implies that

$$\frac{1}{m}\left[log\left(\pi ({\alpha }_0)\right)-log\left(\pi ({\alpha }_1)\right)\right]<\sum _{e\in \mathcal{E}}\frac{h_e}{m\times h_e}\sum _{l=1}^{m\times h_e}\left[logf\left(X^{e,l}\mid e,{\alpha }_1\right)-logf\left(X^{e,l}\mid e,{\alpha }_0\right)\right].$$ (9)

For each e, define

$$s_{{\alpha }_1}^{e,l}\triangleq logf\left(X^{e,l}\mid e,{\alpha }_1\right)-logf\left(X^{e,l}\mid e,{\alpha }_0\right),l=1,\dots ,m\times h_e$$ (10)

that is the log-likelihood ratio between the two parameter values α₀ and α₁. For a given e and different l, $s_{{\alpha }_1}^{e,l}$’s are i.i.d. random variables. Therefore, the right-hand side of (9) is the weighted sum of κ sample averages of i.i.d. random variables. Due to the entropy inequality, we have that $E_{e,{\alpha }_0}(s_{{\alpha }_1}^{e,l})=-D({\alpha }_0,{\alpha }_1)\le 0$. If equality occurs, experiment e does not have power in differentiating α₁ from α₀. This occurs often in diagnostic classification models such as the DINA model (Section 2.1, Example 2).

In what follows, we provide the specific form of the rate function for the probability

$$P\left(\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right).$$

Let g_e(s|α₁) be the distribution of $s_{{\alpha }_1}^{e,l}$ under e and α₀, and let

$$g_e(s\mid \theta ,{\alpha }_1)=g_e(s\mid {\alpha }_1)e^{\theta s-{\phi }_{e,{\alpha }_1}(\theta )}$$ (11)

be its associated natural exponential family where φ_e,α1 (θ) = log[∫ e^θs g_e(s|α₁)ds] is the log-moment-generating function. The exponential family is introduced for the purpose of defining the rate function. It is not meant for the data (response) generating process. In addition, it implicitly assumes that φ_e,α1 is finite in a neighborhood of the origin. Let

$$L_e({\theta }_e\mid {\alpha }_1)={\theta }_e{\phi }_{e,{\alpha }_1}^{\prime }({\theta }_e)-{\phi }_{e,{\alpha }_1}({\theta }_e),$$ (12)

where ${\phi }_{e,{\alpha }_1}^{\prime }$ is the derivative. We define

$$I({\alpha }_1,\mathbf{h})=\underset{{\theta }_1,\dots ,{\theta }_{\kappa }}{inf}\sum _{e\in \mathcal{E}}{h}_e{L}_e({\theta }_e\mid {\alpha }_1),\text{for}\mathbf{h}=(h_1,\dots ,h_{\kappa })$$ (13)

where the infimum is subject to the constraint that ${\sum }_{e\in \mathcal{E}}{h}_e{\phi }_{e,{\alpha }_1}^{\prime }({\theta }_e)\ge 0$. Furthermore, we define a notation

$$I_e({\alpha }_1)=I({\alpha }_1,\mathbf{h})$$ (14)

if all the elements of h are zero except for the one corresponding to the experiment e, that is, I_e(α₁) is the rate if all outcomes are generated from experiment e. Further discussion of evaluation of I(α₁, h) is provided momentarily in Remark 1.

The following two theorems establish the asymptotic decay rate of the misclassification probabilities. Their proofs are provided in Appendix A. Recall that the vector h = (h_e: e ∈ 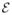) represents the asymptotic proportions, i.e., $\frac{1}{m}{\sum }_{j=1}^{m}I(e^j=e)\to h_e$ as m → ∞.

Theorem 1

Suppose that for each α₁ ≠ α₀ and each e ∈ 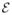, equation ${\phi }_{e,{\alpha }_1}^{\prime }({\theta }_e)=0$ has a solution. Then for every α₁ ≠ α₀, e ∈ 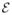, and h ∈ [0, 1]^κ s.t. h_e = 1, we have that

$$\underset{m\to \infty }{lim}-\frac{1}{m}log{P}_{{\mathbf{e}}_m,{\alpha }_0}\left(\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right)=I({\alpha }_1,\mathbf{h}).$$ (15)

Note that both I(α₁, h) and I_e(α₁) depend on the true parameter α₀. To simplify the notation, we omit the index of α₀ in the writing I(α₁, h) and I_e(α₁) because all the discussions are for the same true parameter α₀. Nonetheless, it is necessary and important to keep the dependence in mind. The rate function (15) has its root in statistical hypothesis testing. Consider testing the null hypothesis H_0: α = α₀ against an alternative H_A: α = α₁. We reject the null hypothesis if π(α₁|X_m, e_m) > π(α₀|X_m, e_m). Thus, the misclassification probability is the same as the Type I error probability. Its asymptotic decay rate I(α₁, h) is known as the Chernoff index (Serfling, 1980, Chapter 10).

Remark 1

Without much effort, one can show that the constraint for the minimization in (13) can be reduced to ${\sum }_{e\in \mathcal{E}}{h}_e{\phi }_{e,{\alpha }_1}^{\prime }({\theta }_e)=0$, that is, the infimum is achieved on the boundary. Let ( ${\theta }_e^{\ast }$: e ∈ 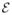) be the solution to the optimization problem. Using Lagrange multipliers, one can further simplify the optimization problem in (13) to the case in which the solution satisfies ${\theta }_1^{\ast }=\cdots ={\theta }_{\kappa }^{\ast }$. Thus, the rate function can be equivalently defined as I(α₁, h) = h_eL_e(θ|α₁), where θ satisfies ${\sum }_{e\in \mathcal{E}}{h}_e{\phi }_{e,{\alpha }_1}^{\prime }(\theta )=0$. Using the specific form of L_e in (12) and the fact that φ_e,α1’s are convex, we obtain that

$$I({\alpha }_1,\mathbf{h})=-\underset{\theta }{inf}\sum _{e\in \mathcal{E}}{h}_e{\phi }_{e,{\alpha }_1}(\theta ).$$ (16)

Thus, the numerical evaluation of I(α, h) is a one-dimensional convex optimization problem that can be stated in a closed form for most standard distributions.

While Theorem 1 provides the asymptotic decay rate of the probability that the posterior mode happens to be at one specific alternative parameter α₁, the next theorem gives the overall misclassification rate.

Theorem 2

Let p(e_m, α₀) be the misspecification probability given by (6) and define the overall rate function

$$I_{\mathbf{h},{\alpha }_0}\triangleq \underset{m\to \infty }{lim}-\frac{1}{m}logp({\mathbf{e}}_m,{\alpha }_0).$$ (17)

Then under the same conditions as in Theorem 1, I_h,α0 = inf_α1≠α0 I(α₁, h).

Here, we include the index α₀ in the rate function I_h,α0 to emphasize that the misclassification probability depends on the true parameter α₀. Thus, the asymptotically optimal selection of experiments h^* is defined as

$${\mathbf{h}}^{\ast }=arg\underset{\mathbf{h}}{sup}{I}_{\mathbf{h},{\alpha }_0}.$$ (18)

An algorithm to compute h^* numerically is included in Appendix C.

3.3. Intuitions and Examples

According to Theorem 1, for a specific parameter α₁, the probability that the posterior favors α₁ over the true parameter α₀ for a given asymptotic design h admits the approximation P(α̂(X_m, e_m) = α₁|e₁, …, e_m, α₀) ≈ e^{−m×I(α₁,h)}. Thus, the total misclassification probability is approximated by

$$p({\mathbf{e}}_m,{\alpha }_0)=P\left(\widehat{\alpha }({\mathbf{X}}_m,{\mathbf{e}}_m)\ne {\alpha }_0\mid e_1,\dots ,e_m,{\alpha }_0\right)\approx \sum _{{\alpha }_1\ne {\alpha }_0}{e}^{-m\times I({\alpha }_1,\mathbf{h})}.$$ (19)

Among the above summands, there is one (or possibly multiple) α′ that admits the smallest I(α′, h). Then the term e^{−mI(α′,h)} is the dominating term of the above sum. Note that the smaller I(α₁, h) is, the more difficult it is to differentiate between α₀ and α₁. According to the representation in (17), upon considering the overall misclassification probability, it is sufficient to consider the alternative parameter that is the most difficult to differentiate from α₀. This agrees with the intuition that if a set of experiments differentiates well between parameters that are similar to each other, it also differentiates well between less similar parameters. Thus, the misclassification probability only considers the most similar parameters to α₀. Similar observations have been made for the derivation of the Chernoff index, i.e., one only considers the alternative models most similar to the null. In practice, it is usually easy to identify these most indistinguishable parameters so as to simplify the computation of (17). For instance, in the case of the DINA model, the most indistinguishable attribute parameter must be among those that have only one dimension misspecified.

For DCM’s, the α′ is generally not unique if h^* is chosen to be asymptotically optimal. Consider the DINA model and a true parameter α₀. Let N₀ be the set of attributes closest to α₀. Each α₁ ∈ N₀ is different from α₀ by only one attribute. Thus, N₀ is the set of parameters most difficult to distinguish from α₀. The asymptotically optimal design h^* must be chosen in such a way that I(α₁, h^*) are identical for all α₁ ∈ N₀. Thus, all α₁ ∈ N₀ are equally difficult to distinguish from α₀ based on the item allocation h^*. Otherwise, one can always reduce the proportion of certain items that are overrepresented and replace them with underrepresented items. Thus, the rate can be further improved. Note that the definition of N₀ may change under the reduced parameter space. See Tatsuoka and Ferguson (2003) for such a discussion when the parameter space is a partially ordered set.

Example 3 (A simple example to illustrate α′)

Consider the DINA model with three attributes. The true attribute profile is α₀ = (1, 1, 0). There are three types of experiments in the item bank, e₁ = (1, 0, 0), e₂ = (0, 1, 0), and e₃ = (0, 0, 1). Each type of item is used to measure one attribute. The corresponding slipping and guessing parameters are (s₁, g₁) = (0.1, 0.1), (s₂, g₂) = (0.2, 0.2), and (s₃, g₃) = (0.1, 0.1). Consider a design $\mathbf{h}=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$, that is, equal numbers of items are selected for each of the three types. Then the second attribute is the most difficult to identify because its slipping and guessing parameters (s₂, g₂) are larger. In this case, the attribute parameter that minimizes I(α, h) over α ≠ α₀ and is most indistinguishable from α₀ is α′ = (1, 0, 0), which differs from α₀ in its second attribute. The asymptotically optimal design should spend more items to measure the second attribute than the other two. We will later revisit this example and compute h^*.

Example 4 (Calculations for the Bernoulli distribution)

We illustrate the calculation of the rate function for models such as the DINA with Bernoulli responses. It is sufficient to compute I(α₁, h) for each true parameter α₀ and alternative α₁ ≠ α₀. A separating experiment e will produce two different Bernoulli outcome distributions $f(x\mid {\alpha }_0,e)=p_0^x{(1-p_0)}^{1-x}$ and $f(x\mid {\alpha }_1,e)=p_1^x{(1-p_1)}^{1-x}$ where p₁ ≠ p₀. Then the log-likelihood ratio is

$$s_{{\alpha }_1}^e\triangleq logf(X\mid e,{\alpha }_1)-logf(X\mid e,{\alpha }_0)=X\left(log\frac{p_1}{1-p_1}-log\frac{p_0}{1-p_0}\right)+log\frac{1-p_1}{1-p_0}.$$

The log-moment-generating function of $s_{{\alpha }_1}^e$ under f(x|α₀, e) is

$${\phi }_{e,{\alpha }_1}(\theta )=log\left[{(1-p_1)}^{\theta }{(1-p_0)}^{1-\theta }+p_1^{\theta }{p}_0^{1-\theta }\right].$$ (20)

For the purpose of illustration, we compute I_e(α₁). The solution to ${\phi }_{e,{\alpha }_1}^{\prime }({\theta }^{\ast })=0$ is

$${\theta }^{\ast }=\left[log\frac{p^{\ast }}{1-p^{\ast }}-log\frac{p_0}{1-p_0}\right]/\left[log\frac{p_1}{1-p_1}-log\frac{p_0}{1-p_0}\right],$$

where $p^{\ast }=\frac{log(1-p_1)-log(1-p_0)}{log(1-p_1)-log(1-p_0)-log{p}_1+log{p}_0}$. Then the misclassification probability is approximated by

$$-lim\frac{logP({\widehat{\alpha }}_m={\alpha }_1)}{m}=-{\phi }_{e,{\alpha }_1}({\theta }^{\ast })=I_e({\alpha }_1).$$ (21)

The parameter θ^* depends explicitly on p₁, p₀, and φ_e,α1. Supposing that p₀ < p₁, the parameter p^* is the cutoff point. If the average response value is below p^*, then the likelihood is in favor of α₀ and vice versa.

When there are more types of items, the rate function I(α₁, h) is the sum of all the φ_e,α1 (θ) in (20) weighted by their own proportions, i.e., I(α₁, h) = − inf_θ h_eφ_e,α1 (θ). Then take the infimum over α₁ ≠ α₀ for the overall rate function I_h,α0.

Example 3 Revisited

We apply the calculations in Example 4 to the specific setting in Example 3, where α₀ = (1, 1, 0). We consider the alternative parameters closest to α₀: α₁ = (0, 1, 0), α₂ = (1, 0, 0), and α₃ = (1, 1, 1). Using the notation in (14) for each individual item and the formula in (21), we have that I_e1(α₁) = 0.51, I_e2(α₂) = 0.22, and I_e3(α₃) = 0.51.

For each h = (h_e1, h_e2, h_e3) and i = 1, 2, 3, we have that I(α_i, h) = h_ei I_ei(α_i). Thus, the asymptotically optimal allocation of experiments is inversely proportional to the rates I_ei(α_i), that is, $h_{e_1}^{\ast }=h_{e_3}^{\ast }=0.23$ and $h_{e_2}^{\ast }=0.54$.

Comparison with the KL Information

Typically, an experiment with a large KL information D_e(α₀, α₁) also has a large rate I_e(α₁). This positive association is expected in that both indexes describe the information contained in the outcome of experiment e. However, these two indexes sometimes do yield different choices of items. Consider the setting in Example 2. Let experiment e₁ have parameters s₁ = 0.1 and g₁ = 0.5 and let e₂ have parameters s₂ = 0.6 and g₂ = 0.01. Both e₁ and e₂ differentiate α₀ and α₁ in such a way that the ideal response of α₀ is negative and that of α₁ is positive. We compute the rate functions and the KL information:

$$D_{e_1}({\alpha }_0,{\alpha }_1)=0.51,D_{e_2}({\alpha }_0,{\alpha }_1)=0.46,I_{e_1}({\alpha }_1)=0.11,I_{e_2}({\alpha }_1)=\mathrm{0.19.}$$

Thus, according to the rate function, e₂ is a better experiment, while the KL information gives the opposite answer. Thus, the KL information method does not always coincide with the rate function. This is also reflected in the simulation study. More detailed connections and comparisons are provided in Section 4. A similar difference exists between Tatsuoka and Ferguson’s criterion and the rate function. Therefore, the criterion proposed in this paper is fundamentally different from the existing ideas.

Remark 2

In practice, it is generally impossible to have two responses collected from exactly the same item. The approximation of the misclassification probability can be easily adapted to the situation when all the m items are distinct. Consider that a sequence of outcomes X¹, …, X^m, has been collected from experiments e¹, …, e^m. For α₁ ≠ α₀, we slightly abuse the notation and let $s_{{\alpha }_1}^i=logf(X^i\mid e^i,{\alpha }_1)-logf(X^i\mid e^i,{\alpha }_0)$ be the log-likelihood ratio of the ith outcome (generated from experiment eⁱ) and let ${\phi }_{e^i,{\alpha }_1}(\theta )=log[E_{e_i,{\alpha }_0}(e^{\theta s_{{\alpha }_1}^i})]$ be the log-MGF. Then an analogue of Theorem 1 would be

$$P_{{\mathbf{e}}_m,{\alpha }_0}\left(\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right)\approx e^{-I_{{\mathbf{e}}_m}({\alpha }_1)},$$

where $I_{{\mathbf{e}}_m}({\alpha }_1)=-{inf}_{\theta }{\sum }_{i=1}^m{\phi }_{e^i,{\alpha }_1}(\theta )$. Furthermore, the misclassification probability can be approximated by − log p(e_m, α₀) ≈ inf_α1≠α0 I_em(α₁).

3.4. An Adaptive Algorithm Based on the Rate Function

We now describe a CAT procedure corresponding to the asymptotic theorems. At each step, one first obtains an estimate of α based on the existing outcomes, X¹, …, X^m. Then each successive item is selected as if the true parameter is identical to the current estimate.

Algorithm 1

Start with a prefixed set of experiments (e¹, …, e^m₀). For every m, Outcomes X_m = (X¹, …, X^m) of experiments e_m = (e¹, …, e^m) have been collected. Choose e^m+1 as follows:

1. Compute the posterior mode α̂_m ≜ α̂(X_m, e_m). Let α′ be the attribute that has the second highest posterior probability, that is, α′ = arg max_α≠α̂m π(α|X_m, e_m).

2. Let α₀ = α̂_m. The next item e^m+1 is chosen to be the one that admit the largest rate function with respect to α′, that is, e^m+1 = arg sup_e I_e(α′) where I_e(α′) is defined as in (14) (recall that I_e(α′) depends on the true parameter value α₀ that is set to be α̂_m).

The attribute is estimated by the posterior mode based on previous responses. Then α′ is selected to have the second highest posterior probability. Thus, α′ is the attribute profile that is most difficult to differentiate from α₀ = α̂_m given the currently observed responses X_m. Thus, the experiment e^m+1 maximizing I_e(α₁) is the experiment that best differentiates between α̂_m and α′. Thus, the rationale behind Algorithm 1 is to first find the attribute profile α′ most “similar” to α̂_m and then to select the experiment that best differentiates between the two. We implement this algorithm and compare it with other existing methods in Section 6.

4. Relations to Existing Methods

4.1. Connection to the Continuous Parameter Space CAT for IRT Models

If the parameter space is continuous (as is the case in IRT), the efficiency measure (6) and its approximation are not applicable, in that P (θ̂(X) ≠ θ₀) = 1, where θ is the continuous ability level. To make an analogue, we need to consider a slightly different probability

$$P\left(\mid \widehat{\theta }(\mathbf{X})-{\theta }_0\mid >\epsilon \mid e_1,\dots ,e_m,{\theta }_0\right)\text{for}\text{some}\epsilon >0\text{small}.$$ (22)

This is known as an indifference zone in the literature of sequential hypothesis testing. One can establish similar large deviations approximations so that the above probability is approximately e^{−mI (ε)}. Thus, the proposed measure is closely related to the maximum Fisher information criterion and expected minimum posterior variance criterion. For IRT models, θ̂(X) asymptotically follows a Gaussian distribution with mean centered around θ₀. Then minimizing its variance is the same as minimizing the probability

$$P\left(\mid \widehat{\theta }(\mathbf{X})-{\theta }_0\mid >\delta m^{-1/2}\mid e_1,\dots ,e_m,{\theta }_0\right)$$

for all δ > 0. One may consider that, by choosing ε very small in (22), in particular ε ≈ δm^−1/2, maximizing the rate function is approximately equivalent to minimizing the asymptotic variance. This connection can be made rigorous by the smooth transition from the large deviations to the moderate deviations approximations.

4.2. Connection to the KL Information Methods and Global Information

The proposed efficiency measure is closely related to the KL information. Consider a specific alternative α₁. We provide another representation of the rate function for P(π(α₁|X_m, e_m) > π(α₀|X_m, e_m)). To simplify our discussion and without loss of too much generality, suppose that only one type of experiment, e, is used and that X¹, …, X^m are thus i.i.d. The calculations for multiple types of experiments are completely analogous, but more tedious. The alternative parameter α₁ admits a higher posterior probability if ${\sum }_{i=1}^m{s}^i>log\pi ({\alpha }_0)-log\pi ({\alpha }_1)$ where sⁱ = log f (Xⁱ |α₁, e) − log f (Xⁱ |α₀, e) are i.i.d. random variables following distribution g(s). Then the rate function takes the form I_e(α₁) = − inf_θ [φ(θ)], where φ (θ) = log ∫ g(s)e^θs is the log-MGF of the log likelihood ratio. Let θ^* = arg inf_θ φ(θ) and g(s|θ) = g(s)e^θs−φ(s). With some simple calculation, we obtain that

$$I_e({\alpha }_1)=\int log\frac{g(s\mid {\theta }^{\ast })}{g(s)}g(s\mid {\theta }^{\ast })ds,$$

which is the Kullback–Leibler information between g(s|θ^*) and g(s).

Then the rate function is the minimum KL information between the log-likelihood ratio distribution and the zero-mean distribution within its exponential family. An intuitive connection between the proposed method and the existing method based on KL information is as follows. The KL, or the posterior-weighted KL method maximizes the KL information between the response distributions under the true and alternative model. Our method maximizes the KL information of the log-likelihood ratio instead of directly that of the outcome variable. This is because the maximum likelihood estimator (or the posterior mode estimator) maximizes the sum of the log-likelihoods.

The rate function in (17) is the minimum of I (α, h) over all α ≠ 3 α₀. This is different from the approach taken by most existing methods, which typically maximize a (possibly weighted) average of the KL information or Shannon entropy over the parameter space. Instead, this approach recalls Tatsuoka and Ferguson’s asymptotically optimal experiment selection, which involves maximizing the smallest KL distance.

4.3. Connection to the Tatsuoka and Ferguson’s Criterion

Using the notation in Section 2.2.1, the posterior mode converges to unity exponentially fast $\frac{1}{m}log[1-\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)]\to -H$ almost surely. This convergence implies that

$$P\left(\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)<\pi \left({\alpha }^{\prime }\mid {\mathbf{X}}_m,{\mathbf{e}}_m\right)\right)\to 0$$

as m → ∞ where α′ is the largest posterior mode other than α₀. The above probability is approximately the misclassification probability p(e_m, α₀). TF’s criterion and ours are very closely related in that a large H typically implies a small p(e_m, α₀). This is because it is unlikely for π(α₀|X_m, e_m) to fall below some level if it converges faster to unity. However, these two criteria are technically distinct. As shown later in Section 6.1, they yield different optimal designs and the corresponding misclassification probabilities could be different.

5. Discussion

Finite Sample Performance

The asymptotically optimal allocation of experiments h^* maximizes the rate function. It can be shown that h^* converges to the optimal allocation that minimizes the misclassification probability as m tends to infinity. However, for finite samples, h^* may be different from the optimal design. In addition, h^* is derived under a setting in which outcomes are independently generated from experiments whose selection has been fixed (independent of the outcome). Therefore, the theorems here answer the question of what makes a good experiment and they serve as theoretical guidelines for the design of CAT procedures. Also, as the simulation study shows, the algorithms perform well.

Results Associated with Other Estimators

The particular form of the rate function relies very much on the distribution of the log-likelihood ratios. This is mostly because we primarily focus on the misclassification probability of the maximum likelihood estimator or posterior mode. If one is interested in (asymptotically) minimizing the misclassification probability of other estimators, such as method of moment based estimators, similar exponential decay rates can be derived and they will take different forms.

Infinite Discrete Parameter Space

We assume that the parameter space is finite. In fact, the analytic forms of I_h,α0 and I (α, h) can be extended to the situation when the parameter space is infinite but still discrete. The approximation results in Theorem 2 can be established with additional assumptions on the likelihood function f (x|e, α). With such approximation results established, Algorithm 1 can be straightforwardly applied.

Summary

To conclude the theoretical discussion, we would like to emphasize that using the misclassification probability as an efficiency criterion is a very natural approach. However, due to computational limitations, we use its approximation via large deviations theory. The resulting rate function has several appealing features. First, it only depends on the proportion of outcomes collected from each type of experiment and is free of the total number of experiment m. In addition, the rate function is usually in a closed form for stylized parametric families. For more complicated distributions, its evaluation only consists of a one dimensional minimization and is computationally efficient. In addition, as the simulation study shows, the asymptotically optimal design shows nice finite sample properties.

6. Simulation

6.1. A Simple Demonstration of the Asymptotically Optimal Design

In this subsection, we consider (nonadaptive) prefixed designs selected by different criteria. We study the performance of the asymptotically optimal design h^* for a given α₀. We consider the DINA model with true attribute profile α₀ = (1, 1, 0). We also consider four types of experiments with the following attribute requirements:

$$e_1=(0,0,1),e_2=(1,0,0),e_3=(0,1,0),e_4=(1,1,0).$$

We compare the asymptotically optimal design proposed by the current paper, denoted by LYZ, and the optimal design by Tatsuoka and Ferguson (2003), denoted by TF. We consider two sets of different slipping and guessing parameters that represent two typical situations.

• Setting 1. s₁ = s₂ = s₃ = s₄ = 0.05 and g₁ = g₂ = g₃ = g₄ = 0.5. Under this setting, the asymptotically optimal proportions by LYZ are $h_1^{\text{LYZ}}=h_4^{\text{LYZ}}=0.5$ , and $h_2^{\text{LYZ}}=h_3^{\text{LYZ}}=0$; the optimal proportions by TF are $h_1^{\text{TF}}=0.3733,h_4^{\text{TF}}=0.6267$, and $h_2^{\text{TF}}=h_3^{\text{TF}}=0$.

• Setting 2. c₁ = c₂ = c₃ = c₄ = 0.05, g₁ = g₂ = g₃ = 0.5, and g₄ = 0.8. Under this selection, the asymptotically optimal proportions by LY are $h_1^{\text{LYZ}}=h_2^{\text{LYZ}}=h_3^{\text{LYZ}}=\frac{1}{3}$, and $h_4^{\text{LYZ}}=0$; the optimal proportions by TF are $h_1^{\text{TF}}=0.2295,h_2^{\text{TF}}=h_3^{\text{TF}}=0.3853$, and $h_4^{\text{TF}}=0$.

We simulate outcomes from the above prefixed designs with different test lengths m = 20, 50, 100. Tables 1 and 2 show the misclassification probabilities computed via Monte Carlo. LYZ admits smaller misclassification probabilities (MCP) for all the samples sizes. The advantage of LYZ manifests even with small sample sizes. For instance, when m = 20 in Table 2, the misclassification probability of LYZ is 13 % and that of TF is 27 %.

Table 1.

The misclassification probabilities (MCP) under Setting 1.

m	LYZ	TF
20	6.5E–02	8.5E–02
50	3.2E–03	1.0E–02
100	4.5E–05	3.7E–04

Table 2.

The misclassification probabilities (MCP) under Setting 2.

m	LYZ	TF
20	1.3E–01	2.7E–01
50	2.2E–02	3.7E–02
100	1.1E–03	5.5E–03

6.2. The CAT Algorithms

We compare Algorithm 1 with other adaptive algorithms in the literature, such as the SHE and PWKL as given in Section 2.2. We compare the behavior of these three algorithms, along with the random selection method (i.e., at each step an item is randomly selected from the item bank), in several settings.

General Simulation Structure

Let K be the length of the attribute profile. The true attribute α₀ is uniformly sampled from the space {0, 1}^K, i.e., each attribute has a 50 % chance of being positive. Each test begins with a fixed choice of m₀ = 2K items with slipping and guessing probabilities, s = g = 0.05. In particular, each attribute is tested by 2 items testing solely that attribute, i.e., items with attribute requirements of the form (0, …, 0, 1, 0, …, 0). After the prefixed choice of items, subsequent items are chosen from a bank containing items with all possible attribute requirement combinations and prespecified slipping and guessing parameters. Items are chosen sequentially based on either Algorithm 1, SHE, PWKL, or random (uniform) selection over all possible items. The misclassification probabilities are computed based on 500,000 independent simulations that provide enough accuracy for the misclassification probabilities.

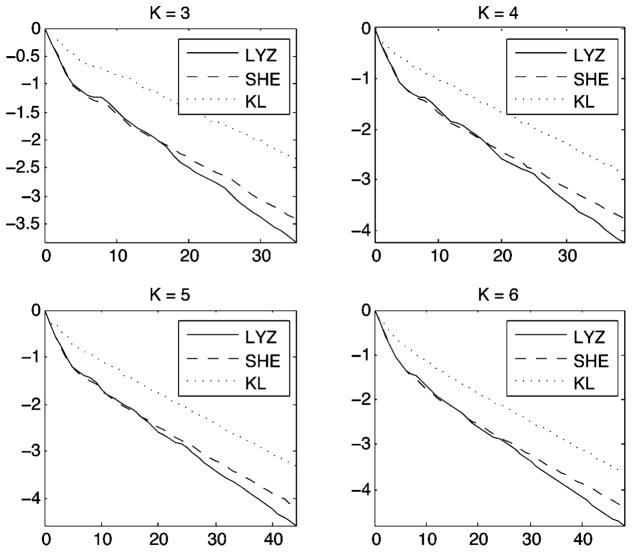
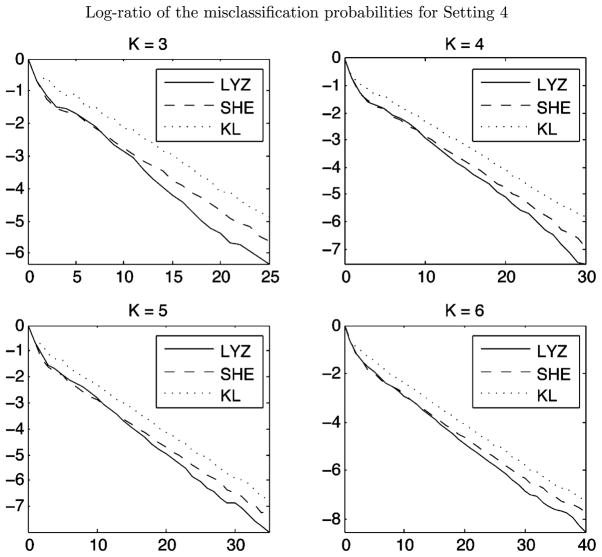
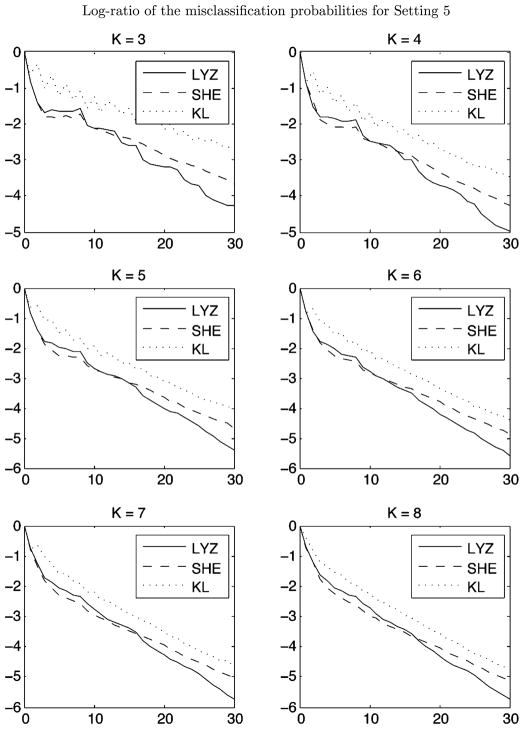
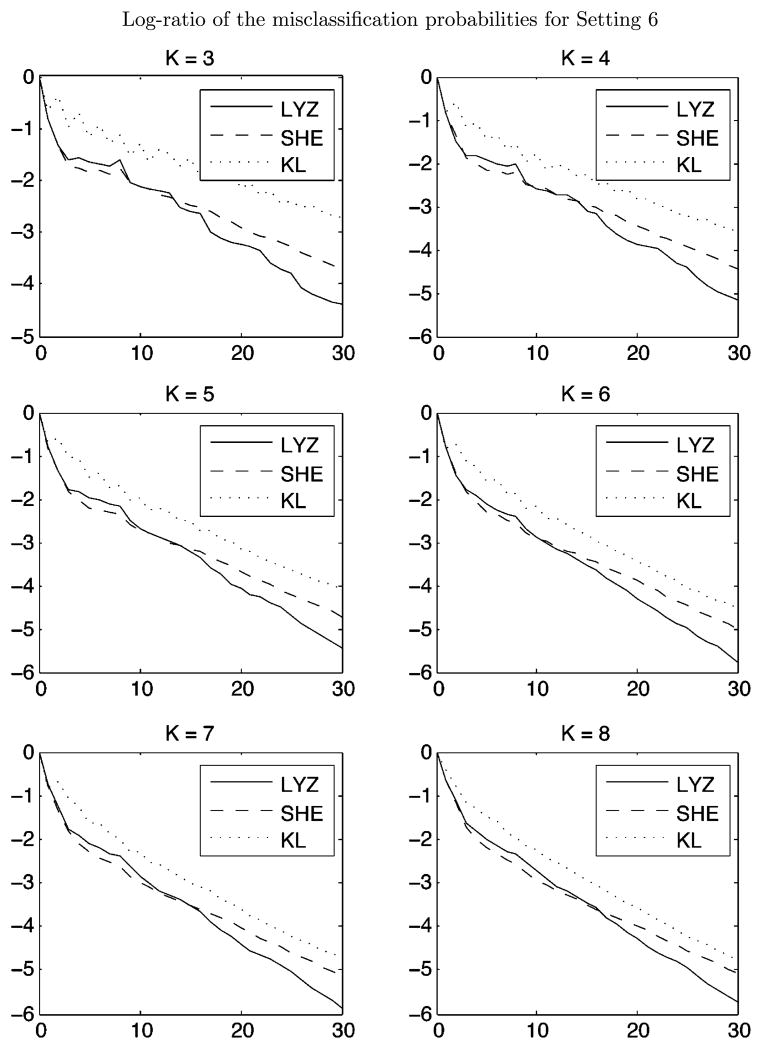
For illustration purposes, we choose the random selection method as the benchmark. For each adaptive method, we compute the ratio of the misclassification probability of that method and the misclassification probability of the random (uniform) selection method. The log of this ratio as test length increases is plotted under each setting in Figures 1, 2, 3, and 4.

Figure 1.

This plot shows the log-ratio of the misclassification probabilities of the given method and those of the random selection method. The x-coordinate is the test length, that is counted beginning with the first adaptive item (beyond the buffer).

Figure 2.

This plot shows the log-ratio of the misclassification probabilities of the given method and those of the random selection method. The x-coordinate is the test length, that is counted beginning with the first adaptive item (beyond the buffer).

Figure 3.

This plot shows the log-ratio of the misclassification probabilities of the given method and those of the random selection method. The x-coordinate is the test length, that is counted beginning with the first adaptive item (beyond the buffer).

Figure 4.

This plot shows the log-ratio of the misclassification probabilities of the given method and those of the random selection method. The x-coordinate is the test length that is counted beginning with the first adaptive item (beyond the buffer).

A summary of the simulation results is as follows. The PWKL immediately underperforms the other two methods in all settings. The SHE and the LYZ methods perform similarly early on, but eventually the LYZ method begins to achieve significantly lower misclassification probabilities. From the plots, we can see that this pattern of behavior does not change as we vary K. However, as K grows larger, more items are needed for the asymptotic benefits of the LYZ method to become apparent. In addition, the CPU time varies for different dimension and different methods. To run 100 independent simulations, the LYZ and the KL methods take less than 10 seconds for all K. The SHE method is slightly more computationally costly and takes as much as a few minutes for 100 simulations when K = 8. The specific simulation setting as given as follows.

• Setting 3. The test bank contains two sets of items. Each set contains 2^K− 1 types items containing all the possible attribute requirements. For one set, the slipping and the guessing parameters are (s, g) = (0.10, 0.50); for the other set, the parameters are (s, g) = (0.60, 0.01). Thus, there are 2(2^K − 1) types items in the bank that can be selected repeatedly. The simulation is run for K = 3, 4, 5, 6. The results are presented in Figure 1.

• Setting 4. With a similar setup, we have two different sets of the slipping and the guessing parameters (s, g) = (0.15, 0.15) and (s, g) = (0.30, 0.01). The basic pattern remains. The results are presented in Figure 2.

• Setting 5. We increase the variety of items available. The test bank contains items with any of four possible pairs of slipping and guessing parameters: (s₁, g₁) = (0.01, 0.60), (s₂, g₂) = (0.20, 0.01), (s₃, g₃) = (0.40, 0.01), and (s₄, g₄) = (0.01, 0.20); in addition, items corresponding to each of the 2^K − 1 possible attribute requirements are available. Items corresponding to a particular set of attribute are limited to either (s₁, g₁) and (s₂, g₂) or (s₃, g₃) and (s₄, g₄). Thus, combining the different attribute requirements and item parameters, there are a total of 2(2^K − 1) types of items in the bank, each of which can be selected repeatedly. The simulation is run for K = 3, 4, …, 8. The results are presented in Figure 3.

• Setting 6. We add correlation by generating a continuous ability parameter θ ~ N (0, 1). The individual α_k are independently distributed given θ, such that

  $$p({\alpha }_k=1\mid \theta )=exp(\theta )/[1+exp(\theta )],k=1,2,\dots ,K$$

  Setting 6 follows Setting 5 in all other respects. The results are presented in Figure 4.

Appendix A. Technical Proofs

Proof of Theorem 1

The proof of Theorem 1 uses standard large deviations technique and exponential change of measure. Consider a specific alternative parameter α₁ ≠ α₀. We use e ∈ 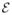to indicate different types of experiments.

Suppose that m_e independent outcomes have been generated from experiment e. Note that m_e/m → h_e. The log-likelihood ratios are as defined in (10), and follow joint distribution:

$$\prod _{e\in \mathcal{E}}\prod _{l=1}^{m_e}{g}_e\left(s_{{\alpha }_1}^{e,l}\mid {\alpha }_1\right).$$

Let A = log π(α₀) − log π(α₁). We choose θ_m such that ${\sum }_{e\in \mathcal{E}}{m}_e{\phi }_e^{\prime }({\theta }_m)=A$. Let ${\theta }_e^{\ast }$ be chosen as in the statement of the theorem. According to Remark 1, we have that ${\theta }_1^{\ast }=\cdots ={\theta }_{\kappa }^{\ast }$ and further that ${\theta }_m-{\theta }_1^{\ast }\to 0$ as m → ∞. We further consider the exponential change of measure, Q, under which the log-likelihood ratios follow joint density

$$\prod _{e\in \mathcal{E}}\prod _{l=1}^{m_e}{g}_e\left(s_{{\alpha }_1}^{e,l}\mid {\theta }_m,{\alpha }_1\right),$$ (A.1)

where g_e(s|θ, α₁) is the exponential family defined in (11).

Note that under Q or equivalently under the joint density (A.1), the $s_{{\alpha }_1}^{e,l}$’s are jointly independent. For a given experiment e, the $s_{{\alpha }_1}^{e,l}$’s are i.i.d. Following the standard results for natural exponential families, for each e, $E^Q{s}_{{\alpha }_1}^{e,l}={\phi }_e^{\prime }({\theta }_m)$, where E^Q denotes the expectation with respect to the density (A.1). The total sum has expectation

$$E^Q\sum _{e,l}{s}_{{\alpha }_1}^{e,l}=\sum _e{m}_e{\phi }_e^{\prime }({\theta }_m)=A.$$

To simplify the notation, we use Σ_e,l and Π_e,l to denote the sum and the product over all the outcomes. We write

$$\begin{array}{l}P\left(\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right)=P\left(\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right)\\ =E^Q\left(\prod _{e,l}\frac{g_e(s_{{\alpha }_1}^{e,l}\mid {\alpha }_1)}{g_e(s_{{\alpha }_1}^{e,l}\mid {\theta }_m,{\alpha }_1)};\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right).\end{array}$$

We plug in the forms of g_e(s|α₁) and g_e(s|θ, α₁) and continue the calculation:

$$\begin{array}{l}P\left(\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right)=E^Q\left(\prod _{e,l}{e}^{{\phi }_e({\theta }_m)-{\theta }_m{s}_{{\alpha }_1}^{e,l}};\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right)\\ =e^{-{\sum }_e{m}_e{L}_e({\theta }_m\mid {\alpha }_1)}{E}^Q\left(\prod _{e,l}{e}^{-{\theta }_m(s_{{\alpha }_1}^{e,l}-{\phi }_e^{\prime }({\theta }_m))};\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right),\end{array}$$

where L_e is defined as in (12). Note that ${\sum }_e{m}_e{\phi }_e^{\prime }({\theta }_m)=A$. We continue the above calculation and obtain that

$$\begin{array}{l}P\left(\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right)=e^{-{\sum }_e{m}_e{L}_e({\theta }_m\mid {\alpha }_1)}{E}^Q\left(e^{-{\theta }_m{\sum }_{e,l}{s}_{{\alpha }_1}^{e,l}+{\theta }_{m}A};\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right)\\ \le e^{-{\sum }_e{m}_e{L}_e({\theta }_m\mid {\alpha }_1)}\\ =e^{-(1+o(1))m{\sum }_e{h}_e{L}_e({\theta }_m\mid {\alpha }_1)}.\end{array}$$ (A.2)

Thus, we have shown an upper bound.

For the lower bound, by the central limit theorem, there exists ε, δ > 0 such that for m large enough, we may write the expectation term in the above display as

$$\begin{array}{l}{E}^Q\left(e^{-{\theta }_m{\sum }_{e,l}{s}_{{\alpha }_1}^{e,l}+{\theta }_{m}A};\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right)\ge E^Q\left(e^{-{\theta }_m{\sum }_{e,l}{s}_{{\alpha }_1}^{e,l}+{\theta }_{m}A};A+\sqrt{m}\delta >\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right)\\ \ge E^Q\left(e^{-{\theta }_m\delta \sqrt{m}};A+\sqrt{m}\delta >\sum _{e,l}{s}_{{\alpha }_1}^{e,l}>A\right)\\ \ge \epsilon e^{-{\theta }_m\delta \sqrt{m}}.\end{array}$$

Thus, we obtain a lower bound that

$$P\left(\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right)\ge e^{-(1+o(1))m{\sum }_e{h}_e{L}_e({\theta }_m\mid {\alpha }_1)}.$$ (A.3)

Combining (A.2), (A.3), and the fact that ${\theta }_m\to {\theta }_1^{\ast }$, we conclude the proof of Theorem 1 using the definition of I(h, α₁) in (13).

Proof of Theorem 2

Based on the proof of Theorem 1, the proof of Theorem 2 is simply an application of the Bernoulli’s inequality. Thus, we only lay out the key steps. First,

$$p({\mathbf{e}}_m,{\alpha }_0)=P\left[\underset{{\alpha }_1\ne {\alpha }_0}{\cup }\{\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\}\right].$$

Let α′ be an alternative parameter admitting the smallest rate, that is, I (α′, h) = I_{h, α0}. Thus, we have that

$$\begin{array}{l}P\left[\pi \left({\alpha }^{\prime }\mid {\mathbf{X}}_m,{\mathbf{e}}_m\right)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right]\le p({\mathbf{e}}_m,{\alpha }_0)\\ \le \sum _{{\alpha }_1\ne \alpha 0}P\left[\pi ({\alpha }_1\mid {\mathbf{X}}_m,{\mathbf{e}}_m)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right]\\ \le \kappa P\left[\pi \left({\alpha }^{\prime }\mid {\mathbf{X}}_m,{\mathbf{e}}_m\right)>\pi ({\alpha }_0\mid {\mathbf{X}}_m,{\mathbf{e}}_m)\right].\end{array}$$

We take the log on both sides and obtain that

$$-(1+o(1))I({\alpha }^{\prime },\mathbf{h})\le \frac{logp({\mathbf{e}}_m,{\alpha }_0)}{m}\le -(1+o(1))I({\alpha }^{\prime },\mathbf{h})+\frac{log\kappa }{m}.$$

Appendix B. Identifiability Issues

Throughout this paper, we assume that all the parameters are separable from each other by the set of experiments. In the case that there are two or more parameters that are not separable, we need to reduce the parameter spaces as follows. We write α₁ ~ α₂ if D_e(α₁, α₂) = 0 for all e ∈ 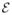. It is not difficult to verify that the binary relationship “~” is an equivalence relation. Let [α] = {α₁ ∈ 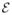: α₁ ~ α} be the set of parameters related to α by ~. Then, the reduced parameter set is defined as the quotient set

$$\stackrel{\sim }{\mathcal{E}}=\mathcal{E}/~=\{[\alpha ]:\alpha \in \mathcal{E}\}.$$

To further explain, if α₁ ~ α₂, then the response distributions are identical f (x|e, α₁) = f (x|e, α₂) for all e. We are not able to distinguish α₁ and α₂. If [α₁] ≠ [α₂], then there exists at least one e such that f (x|e, α₁) and f (x|e, α₂) are distinct distributions. Therefore, all equivalence classes in the new parameter space 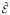are identifiable.

Appendix C. Computation of the Asymptotically Optimal Design

For some true parameter value α₀ ∈ 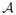, we wish to optimize

$$\underset{\mathbf{h}}{sup}{I}_{\mathbf{h},{\alpha }_0}=\underset{\mathbf{h}}{sup}\underset{\alpha \in \mathcal{A}}{inf}I(\alpha ,\mathbf{h})$$

over all nonnegative h such that Σ_j h_j = 1. Combine Equations (16), (17), and (18) to rewrite the problem as that of finding

$${\mathbf{h}}^{\ast }=arg\underset{\mathbf{h}:{\sum }_j{h}_j=1}{sup}\underset{\alpha \in \mathcal{A}}{inf}\underset{\theta }{sup}\sum _j{h}_j\left(-{\phi }_{j,\alpha }(\theta )\right).$$ (C.1)

Consider the innermost quantity as a function of h and θ. For any particular α, f_α (h, θ) = Σ_j h_j(−φ_j,α(θ)) is linear in h, and so I (α, h) = sup_θf_α(h, α) is convex in h. Additionally, the set { $\mathbf{h}\in {ℝ}_{+}^d:{\sum }_{j=1}^d{h}_j=1$} forms a (d − 1)-simplex with its d vertices at the standard basis vectors; a (d − 1)-simplex is simply a (d − 1)-dimensional polytope formed from the convex hull of its d vertices. By convexity, for each α, I (α, h) must attain its maximal value at one of these vertices. Let s_v be a generic notation for a d -dimensional simplex with vertices at v = {v₁, …, v_d }. Based on the above discussion, we can find supper and lower bounds for sup_h∈sv inf_α∈A I (α, h). In particular, we have that

$$\underset{\mathbf{h}\in s_{\mathbf{v}}}{sup}\underset{\alpha \in \mathcal{A}}{inf}I(\alpha ,\mathbf{h})\le \underset{\mathbf{h}\in s_{\mathbf{v}}}{sup}\underset{\alpha \in \mathcal{A}}{inf}\underset{\mathbf{h}\in \mathbf{v}}{sup}I(\alpha ,\mathbf{h})=\underset{\alpha \in \mathcal{A}}{inf}\underset{\mathbf{h}\in \mathbf{v}}{sup}I(\alpha ,\mathbf{h})\triangleq \text{UB}(s_{\mathbf{v}})$$

and that

$$\underset{\mathbf{h}\in s_{\mathbf{v}}}{sup}\underset{\alpha \in \mathcal{A}}{inf}I(\alpha ,\mathbf{h})\ge \underset{\mathbf{h}\in \mathbf{v}}{sup}\underset{\alpha \in \mathcal{A}}{inf}I(\alpha ,\mathbf{h})\triangleq \text{LB}(s_{\mathbf{v}}).$$

Furthermore, as I (α, h) is a continuous function of h, the two bounds converge to each other as the size of the simplex s_v converges to zero. With these constructions, now consider the following algorithm for finding h^* and I_h^*,α0. In the algorithm, we use L to denote a set, each element of which is a simplex, and “←” to denote value assignment.

Algorithm 2

Set ε > 0 indicating the accuracy level of the algorithm. Let

$${\mathbf{v}}_0=\left\{(1,0,0,\dots ,0),(0,1,0,\dots ,0),\dots ,(0,\dots ,0,1)\right\}$$

and L = {s_v0}, i.e., $s_{{\mathbf{v}}_0}=\{\mathbf{h}\in {ℝ}_d^d:\sum h_j=1\}$. Set LB ← LB(s_v0) and UB ← UB(s_v0)

Perform the following steps:

1. Let s_v^* ∈ L be the simplex with the largest UB(s_v^*), i.e.,

   $$s_{{\mathbf{v}}^{\ast }}=arg\underset{s_{\mathbf{v}}\in L}{sup}\text{UB}(s_{\mathbf{v}}).$$

   Divided s_v^* into 2^κ−1 smaller simplexes, with their vertices at either the original vertices v^* or their midpoints ${\mathbf{v}}_{\text{mdpt}}^{\ast }$ (Edelsbrunner & Grayson, 2000). Denote these 2^κ−1 subsimplexes by s_v1, …, s_v2^κ−1. A simple example for the κ = 3 case is illustrated in Figure 5.

2. Remove s_v^* from L and add s_v1, …, s_v2^κ−1 to L, i.e.,

   $$L\leftarrow (L\backslash \{s_{{\mathbf{v}}^{\ast }}\})\cup \{s_{{\mathbf{v}}_1},\dots ,s_{{\mathbf{v}}_{2^{\kappa -1}}}\}.$$

3. Let $\text{LB}\leftarrow max\{\text{LB},{sup}_{\mathbf{h}\in {\mathbf{v}}_{\text{mdpt}}^{\ast }}{inf}_{\alpha \in \mathcal{A}}I(\alpha ,\mathbf{h})\}$.

4. For each s_v ∈ L, if UB(s_v) < LB then remove s_v from L, that is, L ← L\{s_v}.

5. Set UB ← sup_sv∈L UB(s_v).

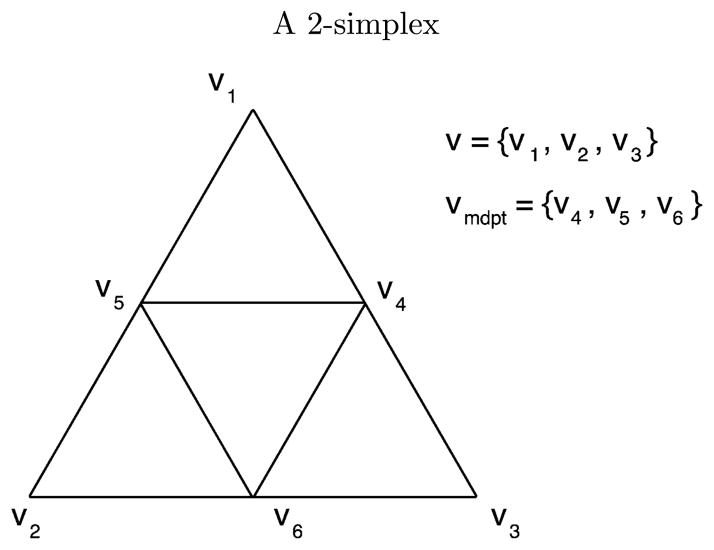
Figure 5.

This figure depicts the 2-simplex s_v with vertices v and their midpoints v_mdpt. This simplex has 4 subdivisions associated with the following sets of vertices: {v₁, v₄, v₅}, {v₂, v₅, v₆}, {v₃, v₄, v₆}, and {v₄, v₅, v₆}.

Repeat the above steps until UB – LB < ε and output

$${\mathbf{h}}^{\ast }=arg\underset{\mathbf{h}\in \mathbf{v},s_{\mathbf{v}}\in L}{sup}\underset{\alpha \in \mathcal{A}}{inf}I(\alpha ,\mathbf{h}).$$

This algorithm will efficiently solve the problem of finding the optimal h, with easily controllable error in both the objective function and h. This algorithm can in fact be used to find the maximum over the simplex of the minimum of any assortment of convex functions. In particular, this can be used to solve Tatsuoka and Ferguson’s algorithm, since the KL distance is linear (and hence convex) in h.