Abstract
During cell migration, local protrusion events are regulated by biochemical and physical processes that are in turn coordinated with the dynamic properties of cell-substratum adhesion structures. In this chapter, we present a modeling approach for integrating the apparent stochasticity and spatial dependence of signal transduction pathways that promote protrusion in tandem with adhesion dynamics. We describe our modeling framework, as well as its abstraction, parameterization, and validation against experimental data. Analytical techniques for identifying and evaluating the effects of model bistability on stochastic simulations results are shown, and implications of this analysis for understanding cell protrusion behavior are offered.
Introduction
Cell crawling over an adhesive surface is a mechanical phenomenon marked by coordinated protrusion at the cell front and retraction at the rear (Parsons et al., 2010). Fibroblasts and other migratory cells of mesenchymal lineage exhibit discrete, micron-sized adhesive contacts that are nucleated by transmembrane adhesion receptors and which form as the leading edge of a migrating cell protrudes over the surface. These adhesions are dynamic, responsive to external and intracellular forces, and conducive to assembly of molecularly diverse protein complexes. Although protrusion, adhesion, and retraction are clearly mechanical processes, they are apparently organized by the timing and partitioning of biochemical signaling pathways. This handoff from chemical regulation to mechanical actuation, together with the ability of cells to sense and respond to mechanical forces, creates a bi-directional feedback mechanism that is thought to play a critical role in controlling cell migration (Welf and Haugh, 2011). In this chapter, we discuss development and simulation of a computational model representing adhesion dynamics and adhesion-mediated signaling as both a cause and consequence of localized protrusion.
How do diverse cellular protrusion behaviors arise from the interplay among physical and biochemical subprocesses? As with any complex system, the variety of interacting molecular components and processes at work during cellular protrusion demand analytical approaches for parsing their influence on cellular behaviors, and the apparently random nature of those events suggests that stochastic computational modeling is well-suited for representing them. The key challenges include how to model the components that are not fully understood at a mechanistic level, and, for those components that are better understood, deciding how much detail to include (Mogilner, 2009). As we discuss, our approach for dealing with these challenges has been to simplify (coarse-grain) certain aspects of the system while employing phenomenological assumptions to balance the scope and desired detail of the model with computational tractability and physical understanding.
Model Synthesis
Adhesion dynamics
During active membrane protrusion in cells of mesenchymal origin, actin polymerization at the leading edge of the cell applies force on the membrane, which is balanced by immobile adhesion structures that couple with the actin network and transmit force to the substrate. These cell-matrix adhesions thus serve as mechanical linkages that enable the cell to pull itself along, but they also mediate the localization of numerous intracellular signaling proteins. The signaling properties of adhesion structures differ according to their sizes and intracellular locations. The small nascent adhesions that form at the leading edge of a cell protrusion facilitate actin polymerization through activation of Rac and certain other signaling intermediates (Cox et al., 2001); however, when these nascent adhesions mature to form larger, more stable focal adhesions, they accumulate actomyosin activity and inhibit protrusion and cell shape change either by biochemical means or by acting as firm anchors for the actin cytoskeleton (Vicente-Manzanares et al., 2007, 2011). Thus, within a local region at the cell periphery, spontaneous transitions between predominantly protrusive and adhesive phenotypes are observed.
Observation of adhesion dynamics by live-cell microscopy directly illustrates why a stochastic framework, in which adhesions are treated as discrete entities, is well suited for modeling adhesion and migration (Figure 1a). In tandem with adhesion formation and turnover, protrusion is rarely smooth with respect to time and space; it is most common to see leading edges bulge in transient, localized bursts (Machacek and Danuser, 2006; Tsukada et al., 2008). Likewise, the process of adhesion maturation occurs infrequently, and as a result there are relatively low numbers of stable adhesions that nonetheless have dramatic phenotypic effects.
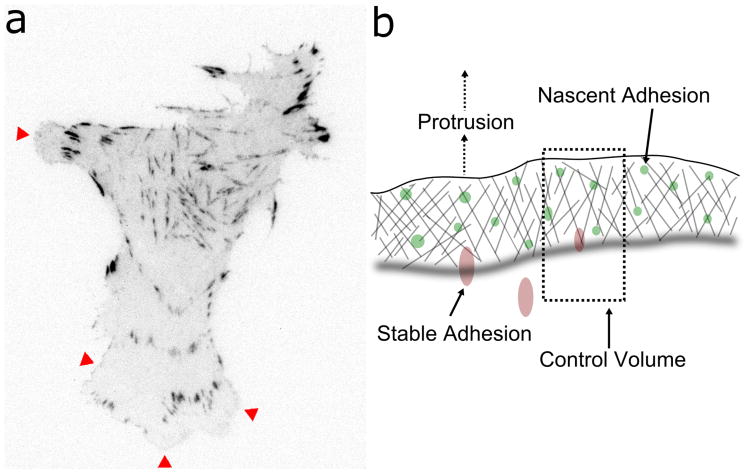
Figure 1. Stochastic nature and spatial representation of adhesions.
(a) Inverted grayscale image of a CHO.K1 cell expressing GFP-paxillin, monitored by TIRF microscopy, showing regions of nascent adhesion formation/turnover (red arrowheads) and the discrete nature of the larger, mature adhesions (adapted from (Cirit et al., 2010)). (b) Diagram illustrating the control volume for the model system and the locations of adhesions therein. Nascent adhesions are formed and move rearward relative to the leading edge as the cell protrudes, and they either mature or turn over when they reach the back edge of the lamellipodium.
To model the spatial aspects of local adhesion formation, turnover, maturation, and signaling, we consider a control volume comprising a region starting at the leading edge of a protruding region of the cell and extending rearward toward the cell center, terminating just following the boundary between the lamellipodium (LP) and the lamella (LM), as shown in Figure 1b. The LP is the region of dense, dynamic actin starting at the leading edge of the cell and extending several microns into the cell body, terminating at the location where actin depolymerization thins the dense actin network of the LP to form the LM. As the boundary between the LP and the LM moves forward relative to immobile adhesions, nascent adhesions that reach the LM-LP boundary either turn over (i.e., disintegrate) or mature to form stable adhesions (Nayal et al., 2006). As the front of a protruding region moves forward, adhesions move rearward relative to the leading edge, which is the frame of reference for the model; increases in protrusion velocity directly affect adhesion turnover by increasing the rate at which nascent adhesions reach the LM-LP boundary (Choi et al., 2008). Likewise, the effects of stable adhesions are assumed to fade with increasing distance from the cell front.
Nascent adhesions form at a rate proportional to the rate of local protrusion (Choi et al., 2008), thus placing them within the positive feedback loop, protrusion → nascent adhesion formation → Rac signaling → protrusion, which we term the core protrusion cycle (Figure 2). As explained below, nascent adhesions are assumed to mediate localized activation of Rac by one of two mechanisms, which differ in mathematical form (rate law). It is further assumed that the velocity of leading edge protrusion is a monotonically increasing function of the local Rac concentration.
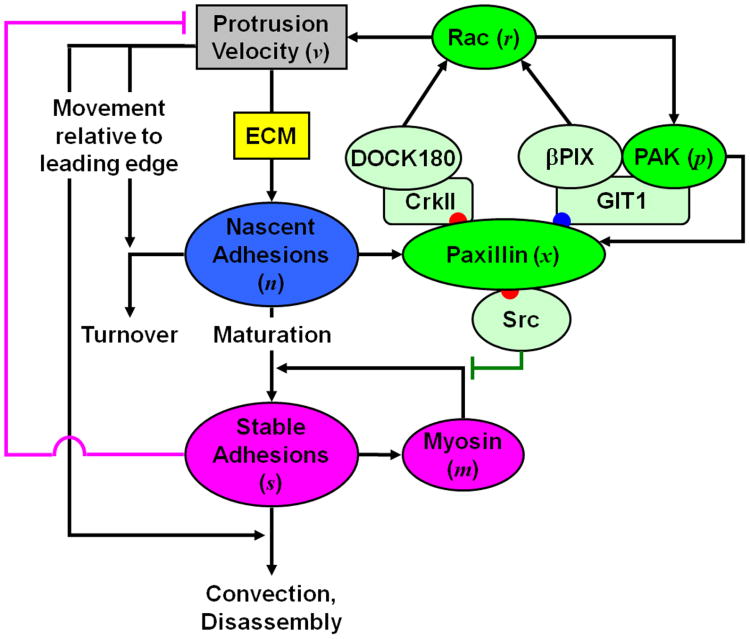
Figure 2. Conceptual model framework.
The rate of formation of nascent adhesions depends on the ECM concentration, and the rates of nascent adhesion formation and turnover depend on the velocity of membrane protrusion. Nascent adhesions promote protrusion via Rac activation, either via a pathway utilizing βPix that is reinforced by positive feedback through PAK, or through a pathway involving DOCK180. Those nascent adhesions that are not turned over mature to form stable adhesions, a process that is reinforced by myosin-mediated feedback and attenuated by Src. Stable adhesions directly antagonize protrusion, disassemble over a relatively long time scale, and have a diminishing influence on processes at the leading edge as a function of their growing distance from the leading edge during protrusion.
Experimental observations indicate that formation of stable adhesions coincides with local pauses in protrusion, and the myosin-dependent contractile processes stimulated by stable adhesions encourage adhesion maturation (Choi et al., 2008). Thus, the core protrusion cycle is subject to an opposing feedback loop whereby stable adhesions reduce the rate of nascent adhesion formation whilst enhancing the probability of nascent adhesion maturation (Figure 2). Although the effects of stable adhesions on local protrusion have not been characterized in mechanistic detail, their importance demands that these effects be included at least phenomenologically in our model.
Adhesion-mediated signaling
A host of scaffolding proteins and kinases are recruited to cell-matrix adhesions, and our focus here is on adhesion-associated signaling pathways that promote local protrusion. Paxillin is a scaffold protein recruited to nascent adhesions shortly after their formation, and once phosphorylated on specific sites, paxillin mediates binding of guanine exchange factors (GEFs) that activate Rac, which in turn enhances actin polymerization (Deakin and Turner, 2008). The Rac effector p21-activated kinase (PAK) phosphorylates paxillin on serine 273, providing a binding site for the recruitment of the scaffold protein GIT1, which forms a complex with both the Rac-GEF βPIX and PAK; this positive feedback loop involving local Rac activation, embedded within the core protrusion cycle, is apparently required for maintenance of protrusion, at least in certain cell contexts (Nayal et al., 2006). In parallel, paxillin phosphorylated on tyrosine residues 31 and 118 by focal adhesion kinase (FAK) recruits the CrkII adapter and the unconventional Rac-GEF DOCK180, further amplifying Rac activation in response to paxillin localization and phosphorylation (Smith et al., 2008; Kiyokawa and Matsuda, 2009). Paxillin phosphorylated on tyrosines 31 and 118 also mediates binding of the tyrosine kinase Src, which opposes myosin function and may thus attenuate adhesion maturation (Tsubouchi et al., 2002).
Model formulation
We are concerned with both biochemical signaling and physical processes governing adhesion dynamics and extension of the cell membrane, and how stochastic fluctuations in these processes are coupled. The appropriate level of detail therefore involves biochemical interactions and reactions at the molecular level; however, as with many biochemical systems we employ simplifying assumptions to reduce the number of adjustable model parameters and decrease the computational burden. A compromise in the degree of coarse-graining was reached by including abbreviated descriptions of biochemical mechanisms that are relatively well characterized while employing phenomenological descriptions of other important processes. For example, we model the phosphorylation of different amino acid residues on paxillin as distinct events but assume that the subsequent binding and modifications of adapter proteins and GEFs are implicit in the activation of Rac (for a discussion of kinetic model simplification, see Cirit and Haugh, 2011). Adhesion maturation is an example of a process that is less well understood, and our phenomenological approach was to treat nascent and mature adhesions as discrete entities and cast the transition between the two in terms of a probability that increases according to the local myosin activity.
The locations of adhesions relative to the leading edge and laterally along the cell contour determine the degree to which the two adhesion types influence protrusion or adhesion maturation (Figure 1b). The mechanical effects of adhesion formation and maturation are widely speculated to involve force-responsive proteins (i.e. mechanotransduction) and propagation of stress within the heterogeneous actin network (Anderson et al., 2008; Gardel et al., 2010; Parsons et al., 2010). While the molecular and physical details involved in these mechanical processes form the basis of continuing theoretical and experimental work, it seems reasonable to focus the details of a coarse-grained model on either the signaling or mechanical aspects of the system. Whereas other studies have dealt primarily with the mechanical side (Chan and Odde, 2008; Li et al., 2010; Sabass and Schwarz, 2010; Zimmermann et al., 2010; Barnhart et al., 2011), we chose to emphasize the properties of adhesion-mediated signaling.
As described above, our approach for dealing with the spatial relationships between model variables is to define a control volume that moves along with the leading edge of a cell; within a control volume, molecular species are assumed to be well mixed, and the width of the control volume is set so that the validity of this approximation is ensured. We investigated the possibility of spatial propagation along the one-dimensional leading edge contour by performing spatially extended simulations (described in detail under Computational Methods).
Model Analysis
The performance of the model was evaluated in part by comparing the qualitative behavior of model simulations at different values of the parameter representing the effect of extracellular matrix (ECM) to experiments assessing protrusion of CHO.K1 cells on different densities of the ECM protein fibronectin ([Fn]). An intermediate [Fn] (2 μg/mL coating concentration) fosters optimal cell migration speed of this cell line (Palecek et al., 1997), and the relative abundance of nascent and stable adhesions at different [Fn] apparently contributes to this optimality. As shown in both experiments and simulations, intermediate [Fn] supports maximal protrusion in conjunction with a high abundance of nascent adhesions, whereas high [Fn] supports mostly stable adhesions, and low [Fn] does not support many adhesions of either type (Cirit et al., 2010).
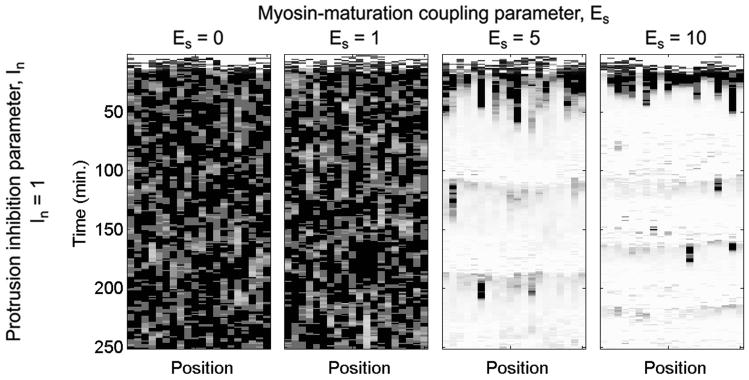
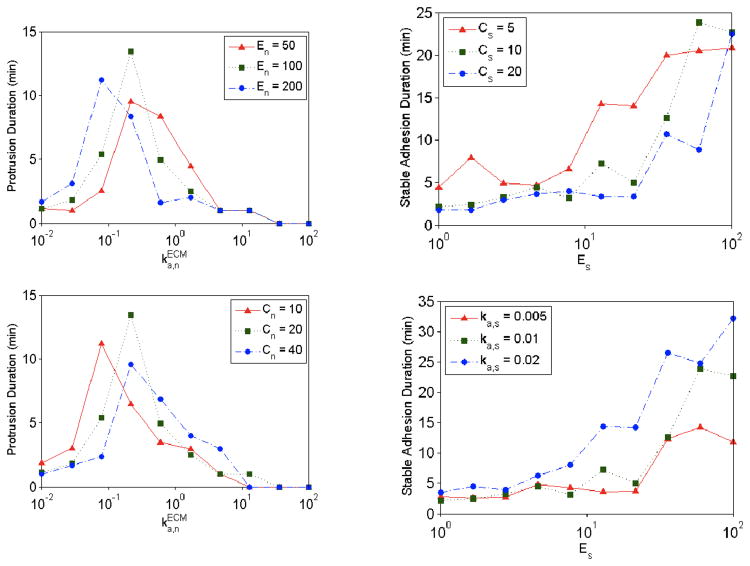
Although values for some of the model parameters were chosen based on experimental evidence, other parameters representing phenomenological relationships were varied systematically (Table 1). Figure 3a shows stochastic simulation results for the model with βPix/no DOCK180 signaling and different values of the parameters In and Es, which characterize the phenomenological effects of protrusion inhibition by stable adhesions and enhancement of adhesion maturation by myosin, respectively. Qualitative characterization of the stochastic simulation behaviors, as shown in Figure 3b, facilitates comparison of simulation results across different combinations of parameter values. The effect of myosin-mediated adhesion strengthening, modeled by the Es parameter, can be seen clearly in the spatially extended simulations shown in Figure 4 – when Es is low, protrusion dominates, but when Es is higher, the formation of stable adhesions inhibits protrusion yet allows for stochastic protrusion bursts that propagate laterally as active Rac diffuses. Another approach for characterizing stochastic simulation results is to calculate the mean lifetimes of protrusion and adhesion events occurring during an extended simulation period (1000 min was used). Protrusion events were identified as periods of time during which the dimensionless protrusion velocity v > 0.5, and adhesion events were identified as periods of time during which the number of stable adhesions was nonzero (S ≥ 1). Figure 5 shows the effect of changes to En and Cs for different values of ka,n and Es, respectively, in the model with DOCK180/no βPix signaling.
Table 1. Model parameters.
| Parameter | Description | Comment | |
|---|---|---|---|
|
|
Rate constant, N assembly | Model input; varied from 0.01–100 min-1 | |
| En | Rac → protrusion coupling | Set to 100 (≫ 1) | |
| Kv | Saturation of protrusion velocity | Set to 1; moderate saturation | |
| In | S → protrusion inhibition | Varied from 0–10 | |
| Is | Src → maturation inhibition | Varied from 0–100 | |
| kd,n | Rate constant, basal N turnover | Set to 0.1 min-1; same value as kd,s | |
| Cn | Protrusion → N turnover coupling | Set to 20 (Nayal et al., 2006) | |
| ka,s | Rate constant, basal S growth | Set to 0.01 min-1 (≪ kd,s) | |
| Es | Myosin → S growth coupling | Varied from 0–100 | |
| kd,s | Rate constant, S disassembly | Set to 0.1 min-1 (Nayal et al., 2006) | |
| Cs | Protrusion → S convection | Varied from 1–100 | |
| kd,xi | Rate constant, X dephosphorylation† | Set to 10 min-1 (arbitrarily fast) | |
| kxi | Saturation of phospho-paxillin† | Set to 1; moderate saturation | |
| po | Basal paxillin phosphorylation | Set at 0.01 (≪ 1) | |
| kd,r | Rate constant, Rac deactivation | Set at 4 min-1 (Moissoglu et al., 2006) | |
| Kp | Saturation of Pak activation | Set to 1; moderate saturation | |
| kd,m | Rate constant, myosin deactivation | Set at 4 min-1; same value as kd,r | |
| N* | Scaling factor, N | Varied from 1–10 | |
| Km | Amplification factor, S → Myosin | Set to 10 | |
| Kr | Amplification factor, Paxillin → Rac | Set to 10 | |
| Dr | Mobility coefficient, Rac | Next subvolume model; set to 15 μm2/min (Moissoglu et al., 2006) |
i denotes paxillin phosphorylation on serine 273 or tyrosines 31 and 118
Figure 3. Characterization of protrusion/adhesion phenotypes via stochastic simulation.
The model system was simulated starting with all species numbers initialized at zero. a. Protrusion velocity v is plotted as a function of time for , N* = 3, and a matrix of Es and In values as indicated. b. The same (Es, In) matrix was repeated for different values of and N* as indicated, and the apparent phenotype of each simulation is categorized qualitatively. The matrix framed with a thicker border corresponds to the simulations shown in a.
Figure 4. Spatially extended simulation results.
Spatially extended simulations were performed using the Next Subvolume Method to account for lateral diffusion of active Rac; the virtual leading edge is subdivided into 20 subvolumes, each 1.94 μm in size. Protrusion velocity is indicated in grayscale (white: v = 0; black: v = 1) as a function of time and position for a range of Es values. Adapted from (Cirit et al., 2010).
Figure 5. Characterization of stochastic simulation results.
Mean lifetimes of protrusion and adhesion events at various values for , Es, En, Cn, Cs, and ka,s were calculated. Protrusion events were identified as periods of time during which the dimensionless protrusion velocity v > 0.5, and adhesion events were identified as periods of time during which the number of stable adhesions was nonzero (S ≥ 1). Adapted from (Welf and Haugh, 2010).
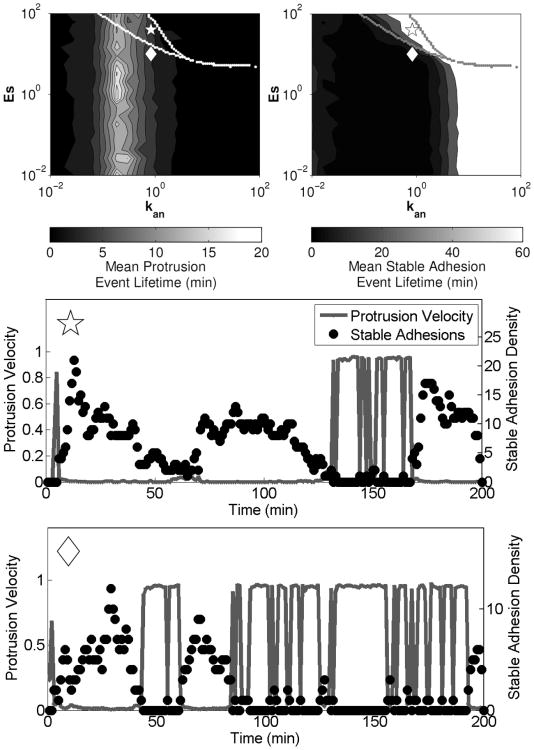
A deterministic analysis of the model equations, treating the molecular species as continua rather than as discrete entities, was also performed. Although a purely deterministic treatment was not able to produce switching between protrusive and adhesive states, the calculations proved useful in identifying conditions where the model exhibits bistability, which is related to the existence of multiple steady states (Cirit et al., 2010). In the context of our models, bistability is a condition in which both the protrusive and adhesive phenotypes are stable.. Figure 6 shows identification of regions of model bistability via phase plane analysis, with the nullclines for nascent adhesions and stable adhesions plotted in (v,s) space. Intersections of the n and s nullclines indicate fixed points in the system, and regions of bistability are shown as functions of model parameters in Figure 6b. A method for comparing regions of model bistability with stochastic model simulation results (in terms of mean protrusion or stable adhesion lifetimes) is shown in Figure 7.
Figure 6. Determination of regions of bistability by phase plane analysis.
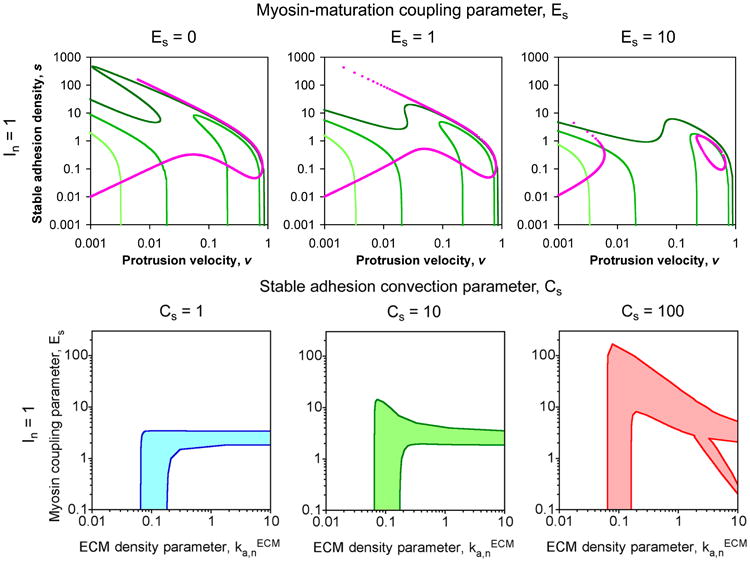
In the upper panels, the nullclines for n (green) and s (magenta) are plotted in (v, s) space. For the n-nullclines, the values of the ECM parameter are 0.03 (light green), 0.1 (green), and 0.3 (dark green) min-1. Intersections of the n- and s-nullclines are fixed points of the system. In the lower panels, the shaded region of ( ,Es) parameter space indicates where there are multiple fixed points ( values given in units of min-1). Adapted from (Cirit et al., 2010).
Figure 7. Regions of bistability overlaid on stochastic simulation results.
Mean lifetimes of protrusion and adhesion events were calculated as described in the caption for Figure 5, and regions of bistability were identified by finding the steady state(s) of the deterministic model equations numerically using different combinations of initial conditions (upper panels). Stochastic simulation results corresponding to the parameter values indicated by the symbols in the upper panels are shown in the lower panels. Results are adapted from (Welf and Haugh, 2010) with In = 10, Is = 1, and Cs = 100.
Biological Insights from the Modeling Approach
In many cell signaling systems, the coupling of multiple feedback mechanisms complicates the mapping of stimuli to cell responses. Feedback loops can give rise to nonlinear effects such as amplification, oscillation, and hysteresis (Besser and Schwarz, 2010; López, 2010). In the context of cell migration, it was of interest to investigate how feedback loops might amplify or attenuate signaling events to affect the observed stochastic switching between protrusion and adhesion phenotypes. For example, measurements of the leading-edge protrusion velocity in migrating CHO.K1 cells clearly show isolated bursts in protrusion that appear to arise randomly; monitoring the localization of adhesions in these cells confirms that a lack of protrusion is accompanied by formation of large stable adhesions (Cirit et al., 2010).
Based on our modeling studies, we can propose biochemical mechanisms that generate, through amplification of stochastic fluctuations, transient yet dramatic excursions from a particular stable state (Cirit et al., 2010; Welf and Haugh, 2010). Such transient behavior takes the form of accelerations from an otherwise low protrusion state or decelerations (pauses) from an otherwise persistent protrusion state. Positive feedback amplification via Rac/PAK signaling and negative feedback attenuation via Src-mediated inhibition of adhesion maturation are capable of mediating these respective behaviors. If both signaling mechanisms are in play as we would propose, the same cell could employ one or the other mechanism at different times and/or at different subcellular locations.
Simulation results show that in order to achieve protrusion under high ECM density or high myosin activity conditions, the magnitude of the Src-mediated inhibition of maturation must be of a certain magnitude relative to the inhibition of protrusion by stable adhesions. Because Src-mediated buffering of adhesion maturation does not prevent adhesion formation under low ECM/low myosin conditions, this hypothetical mode of regulation presents an attractive means for maintaining sensitivity to changes in ECM density or myosin activity across wide ranges of these variables (Welf and Haugh, 2010).
Our original hypothesis held that model bistability would be important for stochastic phenotype switching. Although such behavior is likely to occur in regions of parameter space that are close to the bistability envelope, we found that model bistability is not required for the model to produce switching behavior. Bistable regions of parameter space usually lie between those regions that give monostable low and monostable high protrusion, and in the vicinity of the interface between the two, the stochastic model readily produces transient departures from the stable state.
Open Challenges
A central issue in formulating increasingly useful models of cellular processes is how best to rectify the increasing molecular-level detail of the biology knowledge base with a desire to create holistic models encompassing a large set of regulatory interactions. In general, the granularity of a model should be determined by how well the constituent mechanisms are understood, balanced by the need to specify values of their corresponding rate parameters and tempered by the availability of quantitative data (Mogilner et al., 2006; Cirit and Haugh, 2011). In many biological systems, biochemical complexity is combined with the need to describe mechanical effects and account for spatial concentration and stress gradients. Particularly in systems where spatial considerations are clearly important, as in cell migration, inclusion of all known biochemical interactions is computationally intractable. Further, many important cellular phenomena, such as those mediating mechanotransduction, remain to be characterized mechanistically (Bershadsky et al., 2006). Although mechanical and biochemical models of cell migration have been independently proposed, and integration of biochemical and mechanical phenomena has been achieved recently in the context of leukocyte rolling and firm adhesion (Caputo and Hammer, 2009), these two fundamental modes of regulation have yet to be combined in a satisfactory way in a single model of cell migration.
In this chapter we have presented one approach for integrating the spatial and mechanical processes mediated by stable adhesion formation and myosin contractility into the biochemical framework that regulates cell protrusion. Our treatment of these processes represents only the most basic relationships between model variables, and these relationships should be refined as new data, especially those of a quantitative nature, become available. The recent development of new experimental approaches for perturbing and analyzing the spatial, temporal, and mechanical aspects of cell signaling will enable collection of such data (Grashoff et al., 2010; Toomre and Bewersdorf, 2010; Wu et al., 2009). Hence, as increasingly detailed descriptions of the underlying network are developed, it will be necessary to evaluate and compare their emergent properties, mapped to the behaviors encoded by the more coarse-grained or phenomenological treatments used to construct necessarily less-detailed, holistic models.
Computational Methods
Parameter nomenclature
Certain model parameters are dimensionless and phenomenological; these are classified by whether they characterize enhancement of species i formation (Ei), inhibition of species i formation (Ii), or augmentation of species i consumption rate (Ci). Other parameters have dimensions and include first-order rate constants with units of inverse time, characterizing assembly/activation or disassembly/deactivation of species i (ka,i or kd,i, respectively), and diffusion coefficients with units of area/time (Di). Dimensionless parameters Ki denote ratios of rate constants, characterizing the rate of assembly or activation relative to that of disassembly or deactivation for species i (Ki = ka,i/kd,i). Definitions of all model parameters are listed in Table 1.
Model equations
We constructed model equations considering conservation of molecular and adhesion-based species based on the conceptual model shown in Figure 2. We have explored two variations of the model, each corresponding to the scaffolding effect of a different phosphorylation site or sites on paxillin: serine 273 (Cirit et al., 2010) or tyrosines 31 and 118 (Welf and Haugh, 2010). The equations for each instance of the model were identical, except as indicated. The dimensionless densities of nascent adhesions (n), stable adhesions (s), and recruited myosin (m) are generally written as follows.
| (1) |
| (2) |
and
| (3) |
The value of the parameter maps in some way to the density and character of the ECM, and v is the dimensionless protrusion velocity. The algebraic function f(m,x31/118) describes the enhancement of adhesion maturation by myosin and its inhibition by paxillin phosphorylated on tyrosines 31 and 118, which directs Src recruitment; in the model considering serine 273 only, the dependence on the x31/118 variable is absent.
Previous theoretical studies have analyzed in detail how the kinetics of actin polymerization might affect local membrane protrusion (Gov, 2006; Zimmermann et al., 2010; Barnhart et al., 2011); in this work we employ a simple functional relationship between Rac activity (r) and membrane protrusion, such that the protrusion velocity increases in response to Rac signaling until a saturation limit is reached.
| (4) |
The function g(s) specifies the relationship between stable adhesion density and inhibition of protrusion.
Although various phenomenological forms of the f and g functions may be proposed, we adopted simple, linear forms as follows.
| (5) |
| (6) |
Again, the variable x31/118 in the f function is effectively fixed at zero in the βPix/no DOCK180 model (Cirit et al., 2010).
The equations for the signaling circuit variables are as follows. The variable xi (i = 273 or 31/118) represents the subset of n harboring phosphorylated paxillin (and, implicitly, GIT1/βPIX/PAK or CrkII/DOCK180 complexes), r is the density of active Rac (activated by βPIX or DOCK180), and p is the subset of x273 harboring Rac-activated PAK. For the case where we consider phosphorylation of serine 273 (Cirit et al., 2010), we write:
| (7) |
The small basal paxillin phosphorylation activity, p0, is included so that x273, r, and p can evolve in time when all initial values are zero. Likewise, the fraction of nascent adhesions harboring paxillin phosphorylated on tyrosine 31/118 (Welf and Haugh, 2010) is written
| (8) |
The equation for the activation of Rac is written
| (9) |
or
| (10) |
In spatially extended simulations, the conservation of active Rac also includes lateral diffusion. For the βPix/no DOCK180 model, an additional equation describes the activation of PAK on paxillin/GIT1/PAK complexes.
| (11) |
Specification of stochastic models
To specify the stochastic model, we convert dimensionless model variables to numbers of molecules via scaling factors, indicated with an asterisk, e.g. N = N*n, where N is the absolute number of nascent adhesions in the control volume and n is the corresponding dimensionless variable. Based on the scaling of the conservation equations listed in the previous section, the other scaling factors are related to N* as follows.
| (12) |
| (13) |
| (14) |
Because our model contains certain phenomenological rate laws, the stochastic formulation is not automatically specified as in the case of a mass action model. Our reaction propensity functions, in units of number of molecules per minute, are specified as follows.
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
Stochastic simulations were performed using the Next Reaction Method (Gibson and Bruck, 2000), a modification of the Gillespie algorithm (Gillespie, 1977), implemented in MATLAB (MathWorks, Natick, MA). These methods simulate trajectories of the chemical master equation describing discrete stochastic systems, such as those encountered in cells where small numbers of reacting species or rare reaction events dominate system dynamics.
Spatially extended simulations
Spatially extended stochastic simulations were performed using the Next Subvolume Method (Elf and Ehrenberg, 2004), whereby diffusion of species i between adjacent compartments is modeled as a “hopping” reaction with first-order rate constant Di/L2, where Di is the diffusivity of species i, and L is the node spacing between adjacent compartments. A compromise between numerical accuracy and computational expense is achieved by setting the node spacing L equal to the smallest of the dynamic length scales, , where τi is the mean lifetime of diffusible species i. In most of our spatially extended simulations (Cirit et al., 2010), we assumed that only active Rac is diffusible, with τr = 1/kd,r. Estimates of Dr and kd,r were obtained from the literature (Moissoglu et al., 2006), yielding L = Lr ≈ 2 μm. We assumed a one-dimensional geometry, corresponding to the contour of a leading edge, with periodic boundary conditions.
Acknowledgments
This work was supported by NSF grant CBET-0828936, and E.S.W. was supported by the Cell Migration Consortium under National Institutes of Health grant U54-GM064346.
References
- Anderson TW, Vaughan AN, Cramer LP. Retrograde flow and myosin II activity within the leading cell edge deliver F-actin to the lamella to seed the formation of graded polarity actomyosin II filament bundles in migrating fibroblasts. Mol Biol Cell. 2008;19:5006–5018. doi: 10.1091/mbc.E08-01-0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnhart EL, Lee KC, Keren K, Mogilner A, Theriot JA. An adhesion-dependent switch between mechanisms that determine motile cell shape. PLoS Biol. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bershadsky A, Kozlov M, Geiger B. Adhesion-mediated mechanosensitivity: a time to experiment, and a time to theorize. Curr Opin Cell Biol. 2006;18:472–481. doi: 10.1016/j.ceb.2006.08.012. [DOI] [PubMed] [Google Scholar]
- Besser A, Schwarz US. Hysteresis in the cell response to time-dependent substrate stiffness. Biophys J. 2010;99:L10–12. doi: 10.1016/j.bpj.2010.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caputo KE, Hammer DA. Adhesive dynamics simulation of G-protein-mediated chemokine-activated neutrophil adhesion. Biophys J. 2009;96:2989–3004. doi: 10.1016/j.bpj.2008.12.3930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- Choi CK, Vicente-Manzanares M, Zareno J, Whitmore LA, Mogilner A, Horwitz AR. Actin and alpha-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat Cell Biol. 2008;10:1039–1050. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cirit M, Haugh JM. Quantitative models of signal transduction networks: How detailed should they be? Communicative & Integrative Biology. 2011;4:353–356. doi: 10.4161/cib.4.3.15149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cirit M, Krajcovic M, Choi CK, Welf ES, Horwitz AlanF, Haugh JM. Stochastic model of integrin-mediated signaling and adhesion dynamics at the leading edges of migrating cells. PLoS Comput Biol. 2010;6:e1000688. doi: 10.1371/journal.pcbi.1000688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox EA, Sastry SK, Huttenlocher A. Integrin-mediated adhesion regulates cell polarity and membrane protrusion through the Rho family of GTPases. Mol Biol Cell. 2001;12:265–277. doi: 10.1091/mbc.12.2.265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deakin NO, Turner CE. Paxillin comes of age. J Cell Sci. 2008;121:2435–2444. doi: 10.1242/jcs.018044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elf J, Ehrenberg M. Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases. Syst Biol (Stevenage) 2004;1:230–236. doi: 10.1049/sb:20045021. [DOI] [PubMed] [Google Scholar]
- Gardel ML, Schneider IC, Aratyn-Schaus Y, Waterman CM. Mechanical integration of actin and adhesion dynamics in cell migration. Annu Rev Cell Dev Biol. 2010;26:315–333. doi: 10.1146/annurev.cellbio.011209.122036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson MA, Bruck J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J Phys Chem A. 2000;104:1876–1889. [Google Scholar]
- Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- Gov NS. Dynamics and morphology of microvilli driven by actin polymerization. Phys Rev Lett. 2006;97:018101. doi: 10.1103/PhysRevLett.97.018101. [DOI] [PubMed] [Google Scholar]
- Grashoff C, Hoffman BD, Brenner MD, Zhou R, Parsons M, Yang MT, McLean MA, Sligar SG, Chen CS, Ha T, et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–266. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiyokawa E, Matsuda M. Regulation of focal adhesion and cell migration by ANKRD28-DOCK180 interaction. Cell Adh Migr. 2009;3:281–284. doi: 10.4161/cam.3.3.8857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Bhimalapuram P, Dinner AR. Model for how retrograde actin flow regulates adhesion traction stresses. J Phys Condens Matter. 2010;22:194113. doi: 10.1088/0953-8984/22/19/194113. [DOI] [PubMed] [Google Scholar]
- López JM. Digital kinases: A cell model for sensing, integrating and making choices. Commun Integr Biol. 2010;3:146–150. doi: 10.4161/cib.3.2.10365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machacek M, Danuser G. Morphodynamic profiling of protrusion phenotypes. Biophys J. 2006;90:1439–1452. doi: 10.1529/biophysj.105.070383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A. Mathematics of cell motility: have we got its number? J Math Biol. 2009;58:105–134. doi: 10.1007/s00285-008-0182-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Wollman R, Marshall WF. Quantitative modeling in cell biology: what is it good for? Dev Cell. 2006;11:279–287. doi: 10.1016/j.devcel.2006.08.004. [DOI] [PubMed] [Google Scholar]
- Moissoglu K, Slepchenko BM, Meller N, Horwitz AlanF, Schwartz MA. In vivo dynamics of Rac-membrane interactions. Mol Biol Cell. 2006;17:2770–2779. doi: 10.1091/mbc.E06-01-0005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nayal A, Webb DJ, Brown CM, Schaefer EM, Vicente-Manzanares M, Horwitz AR. Paxillin phosphorylation at Ser273 localizes a GIT1-PIX-PAK complex and regulates adhesion and protrusion dynamics. J Cell Biol. 2006;173:587–589. doi: 10.1083/jcb.200509075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palecek SP, Loftus JC, Ginsberg MH, Lauffenburger DA, Horwitz AF. Integrin-ligand binding properties govern cell migration speed through cell-substratum adhesiveness. Nature. 1997;385:537–540. doi: 10.1038/385537a0. [DOI] [PubMed] [Google Scholar]
- Parsons JT, Horwitz AR, Schwartz MA. Cell adhesion: integrating cytoskeletal dynamics and cellular tension. Nat Rev Mol Cell Biol. 2010;11:633–643. doi: 10.1038/nrm2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabass B, Schwarz US. Modeling cytoskeletal flow over adhesion sites: competition between stochastic bond dynamics and intracellular relaxation. J Phys Condens Matter. 2010;22:194112. doi: 10.1088/0953-8984/22/19/194112. [DOI] [PubMed] [Google Scholar]
- Smith HW, Marra P, Marshall CJ. uPAR promotes formation of the p130Cas-Crk complex to activate Rac through DOCK180. J Cell Biol. 2008;182:777–790. doi: 10.1083/jcb.200712050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toomre D, Bewersdorf J. A new wave of cellular imaging. Annu Rev Cell Dev Biol. 2010;26:285–314. doi: 10.1146/annurev-cellbio-100109-104048. [DOI] [PubMed] [Google Scholar]
- Tsubouchi A, Sakakura J, Yagi R, Mazaki Y, Schaefer E, Yano H, Sabe H. Localized suppression of RhoA activity by Tyr31/118-phosphorylated paxillin in cell adhesion and migration. J Cell Biol. 2002;159:673–683. doi: 10.1083/jcb.200202117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsukada Y, Aoki K, Nakamura T, Sakumura Y, Matsuda M, Ishii S. Quantification of local morphodynamics and local GTPase activity by edge evolution tracking. PLoS Comput Biol. 2008;4:e1000223. doi: 10.1371/journal.pcbi.1000223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicente-Manzanares M, Newell-Litwa K, Bachir AI, Whitmore LA, Horwitz AR. Myosin IIA/IIB restrict adhesive and protrusive signaling to generate front-back polarity in migrating cells. J Cell Biol. 2011;193:381–396. doi: 10.1083/jcb.201012159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicente-Manzanares M, Zareno J, Whitmore L, Choi CK, Horwitz AlanF. Regulation of protrusion, adhesion dynamics, and polarity by myosins IIA and IIB in migrating cells. J Cell Biol. 2007;176:573–580. doi: 10.1083/jcb.200612043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welf ES, Haugh JM. Signaling pathways that control cell migration: models and analysis. Wiley Interdiscip Rev Syst Biol Med. 2011;3:231–240. doi: 10.1002/wsbm.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welf ES, Haugh JM. Stochastic dynamics of membrane protrusion mediated by the DOCK180/Rac pathway in migrating cells. Cell Mol Bioeng. 2010;3:30–39. doi: 10.1007/s12195-010-0100-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu YI, Frey D, Lungu OI, Jaehrig A, Schlichting I, Kuhlman B, Hahn KM. A genetically encoded photoactivatable Rac controls the motility of living cells. Nature. 2009;461:104–108. doi: 10.1038/nature08241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann J, Enculescu M, Falcke M. Leading-edge-gel coupling in lamellipodium motion. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82:051925. doi: 10.1103/PhysRevE.82.051925. [DOI] [PubMed] [Google Scholar]