Large-scale dissipative particle dynamics simulations of self-assembly amphiphilic systems

Abstract

We present large-scale simulation results on the self-assembly of amphiphilic systems in bulk solution and under soft confinement. Self-assembled unilamellar and multilamellar vesicles are formed from amphiphilic molecules in bulk solution. The system is simulated by placing amphiphilic molecules inside large unilamellar vesicles (LUVs) and the dynamic soft confinement-induced self-assembled vesicles are investigated. Moreover, the self-assembly of sickle hemoglobin (HbS) is simulated in a crowded and fluctuating intracellular space and our results demonstrate that the HbS self-assemble into polymer fibers causing the LUV shape to be distorted.

Self-assembly, which makes use of molecular rather than atomic units, offers a “bottom–up” approach to the development of complex materials at different length scales.^{1, 2} The ability to self-assemble into well-defined structures is inherent in natural biological macromolecules such as DNA and histone proteins but also in synthetic amphiphiles such as surfactants and block copolymers. Amphiphilic molecules, which contain hydrophilic and hydrophobic groups, exhibit a rich variety of different morphologies with shape- and size-dependent potential applications in many fields such as drug delivery and nanotechnology.^{3, 4} The self-assembly behaviors of amphiphilic molecules have been a topic of high importance over the past two decades. It is generally believed that confinement of amphiphilic molecules provides a powerful means to manipulate their self-assembled microstructures due to relatively high local concentration and restricted movement freedom of amphiphilies.⁵ Generally, the amphiphilic self-assembly in a confined space is performed in hard confinement, in which the shape of the confining geometry is fixed a priori and cannot be changed by the variation of either the internal self-assembled microstructures or external conditions.

In biological systems such as red blood cells (RBCs), the self-assembly takes place in a soft confined environment with boundaries which are not rigid but compliant. The self-assembled microstructures under the soft confinement should be different because of the flexibility of the confined boundaries and the fluctuation of the intracellular space. However, compared with the large amount of articles on the self assembly of amphiphilic molecules in bulk solution and under hard confinement, papers on amphiphilic self-assembly under soft confinement are not as many. In a recent study, Chi et al. simulated soft confinement-induced morphologies of amphiphilic molecules, in which they employed a “bad solvent” condition to describe the soft confinement effect.⁶ To the best of our knowledge, this is the only work related to the soft confinement-induced amphiphilic self-assembly using particle-based molecular simulations. However, the shape fluctuations and elastic properties of the cell membrane were neglected in their model. A membrane vesicle, which consists of fluid enclosed by an amphiphilic membrane, mimics essential characteristics of the RBC. Thus, it has gained popularity as a model system to study the cell dynamics and membrane biophysics in general.⁷ Membrane vesicles are highly adaptive structures having a rich variety of shapes. This feature makes them very interesting candidates to investigate the influence of geometrical confinement on both structure and dynamics.

In our previous simulations, we have successfully applied the dissipative particle dynamics (DPD) method to investigate the shape transformations of the self-assembled membrane vesicles.^{8, 9} In order to simulate the amphiphilic self-assembly under soft confinement, a giant vesicle containing a large number of solvent particles and amphiphilic molecules is required. Our new GPU-accelerated DPD _USERMESO package has enabled us to perform simulations for amphiphilic systems containing over 100 million particles,¹⁰ which is sufficiently large to allow the simulations of the phenomenon of interest. So, we address the questions: What will the new pattern images be if we scale the simulation to 100 times larger than the previous ones? What is the effect of the soft confinement on the self-assembly of the trapped amphiphilic molecules in a large membrane vesicle? An insight into the kinetic details of these processes and the events taking place inside the vesicle are helpful for understanding the underlying molecular principles governing the amphiphilic self-assembly. In this communication, the self-assembly behavior of amphiphilic molecules are studied both in bulk solution and under confinement.

Presently, membrane vesicles can be prepared from compounds such as surfactants, phospholipids and block copolymers. Their common feature is the presence of hydrophilic heads and hydrophobic tails in the molecules as well as the ability to self-assemble into bilayer membranes. If there is only one bilayer in the membrane, it is called unilamellar vesicle, including small unilamellar vesicle and large unilamellar vesicle (LUV); otherwise it is called multilamellar vesicle. As suggested by Voskuhl and Ravoo,¹¹ the smallest unilamellar vesicle contains about ten thousand amphiphilic molecules, whereas large unilamellar and multilamellar vesicles contain about a hundred thousand molecules and many millions of molecules, respectively. Indeed, we observed these three different types of vesicles when we increased the system size while keeping the concentration of amphiphilic molecules and the particle number density constant, see Fig. 1. If there are only several hundred coarse-grained amphiphilic molecules in a small simulation box, a small spherical micelle is observed (Fig. 1a). When we increase the simulation box, we find the small unilamellar vesicle (Fig. 1b). A further increase in the system size causes formation of the LUV (Fig. 1c). If the simulation system is sufficiently large, the multilamellar vesicle appears (Fig. 1d), which is a result of the fusion of small unilamellar vesicles. The formation of these morphologies can be understood in terms of the packing parameter P: for spherical micelles, we have the expectation that $0<P\le \frac{1}{3}$, while $\frac{1}{3}<P\le \frac{1}{2}$ for cylindrical micelles. Bilayers are preferred in the range for $\frac{1}{2}<P\le 1$. These morphologies also depend on two aggregation concentrations, namely, the critical micellar concentration and the critical vesicle concentration (CVC). In a small simulation box, the local concentration of amphiphilies, which is the number of amphiphilies divided by their occupied volume, may fall below the CVC, and hence the amphiphilic molecules form spherical micelles spontaneously in aqueous solution (see Fig. 1a). When we increase the simulation box, the local concentration of amphiphilies exceeds the CVC, and the amphiphilic molecules form spontaneous unilamellar vesicles (see Fig. 1b).

Fig. 1.

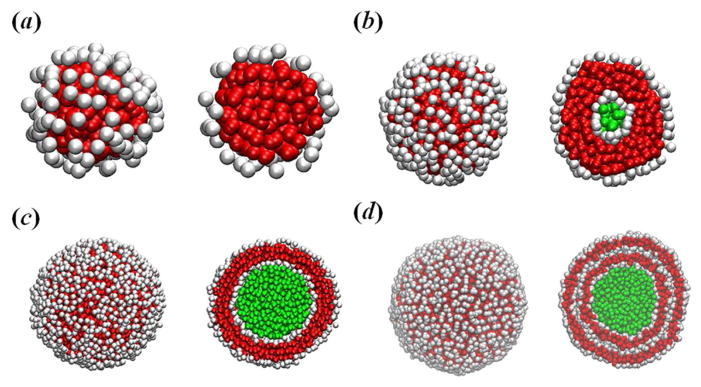
Self-assembled microstructures of amphiphilic molecules: (a) small spherical micelle, (b) small unilamellar vesicle, (c) large unilamellar vesicle, and (d) multilamellar vesicle. During the simulations, we find that only a few amphiphilic monomers coexisting with the small micelles and vesicles; instead, more small micelles/vesicles coexist with these aggregates. Solvent, hydrophilic and hydrophobic particles are rendered in green, white and red, respectively. Slices of these shapes are shown for clarity.

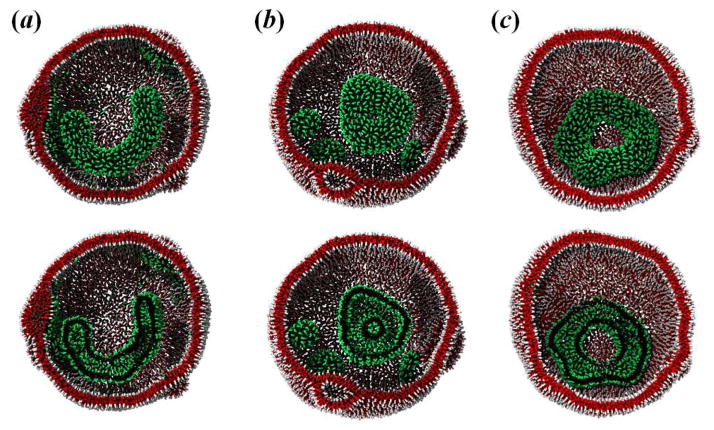
After a LUV is formed from amphiphilic molecules, we place another type of amphiphilic molecules inside the compliant LUV and simulate their self-assembly under soft confinement. A plethora of complex vesicle shapes, including U-like and toroidal vesicles, are obtained in DPD simulations, see Fig. 2. The simulation also provides a good method to understand the dynamic process of spontaneous micelle formation under different conditions. Figure S2 together with the video clip in the Supplementary Information provide a typical dynamic formation process of toroidal vesicle. It reveals that the amphiphilic molecules initially aggregate rapidly into spherical and cylindrical vesicles (Figs. S2a–S2b). Due to the confinement, the cylindrical vesicle then gradually buckle itself to conform with the curvature of the LUV membrane and subsequently evolves into a toroidal vesicle with one end-cap via the inter-association of the spherical vesicle (Figs. S2c–S2d). A pure closed ring-like vesicle is finally formed when the end-cap merges into the vesicle (Fig. S2e). In order to provide a more quantitative insight into the formation of toroidal vesicle, we calculated the conservative energy associated with the amphiphilic molecules during the time evolution, see Fig. S3. During the process of toroidal vesicle formation, the conservative energy diminishes by 1.5–2.3 k_BT. It is confirmed that the toroidal vesicle is formed through the spherical/cylindrical vesicles to minimize the hydrophobic interaction energy between the amphiphilies and solvents. In addition, we also observe the U-like vesicle under soft confinement at a lower a_HE (or a_TF), see Fig. 2a. The U-like vesicle structure formation may be influenced by prominent kinetic barriers: at a lower a_HE (or a_TF), there is not enough force with which to push the middle cylindrical structure to form toroids; instead, they are trapped at the U-like intermediate structure.

Fig. 2.

Amphiphilic self-assembly under soft confinement at a_HE (or a_TF) = (a) 15.0; (b) 50.0; and (c) 240.0. The self-assembled amphiphilic vesicle and LUV are shown as green/black and red/white colors, respectively. Slices of these shapes are shown for clarity.

Amphiphilic self-assembly is fundamental to the construction of biologic molecular assemblies in living organisms, and so is crucial to the function of cells as well as a number of human diseases including sickle cell anemia. The self-assembly of sickle hemoglobin (HbS), which is demonstrated to be the primary cause of the sickle cell disease, takes place within the RBC membrane. Thus, it is one type of soft confined self-assembly systems. In a previous study, we have studied the HbS self-assembly both in open-space and under hard confinement;¹² however, it could not accurately reflect the distortion of RBCs into sickle shapes. To illustrate the effect of soft confinement on HbS fibers residing in a crowded and fluctuating intracellular space, we simulate the HbS self-assembly in a compliant LUV at a_HHS = a_TTS = 240.0. From the DPD simulations, we find that HbS can self-assemble into elongated step-like fibers and network microstructures, and the trapped amphiphilic molecules can also deform the shape of the LUV, see Fig. 3. We then calculated the instantaneous length of polymer fibers to quantify the confinement effect on HbS self-assembly, see Fig. S4(Left). We find that the fiber length increases with time, and the growth rate in soft confinement is lower than that in hard confinement, indicating that the self-assembly process of amphiphilies under soft confinement is slower than that under hard confinement.

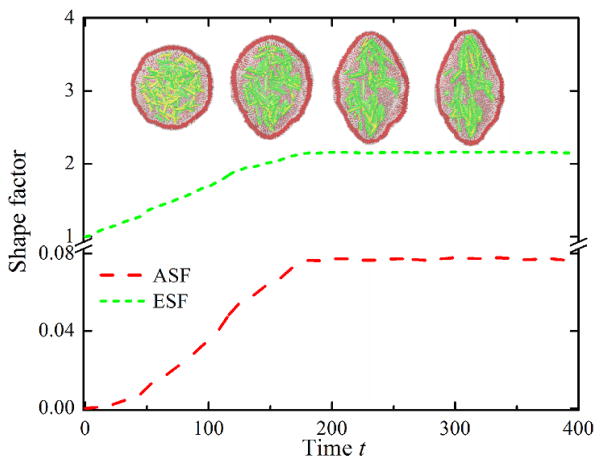
Fig. 3.

Instantaneous values of asphericity and elliptical shape factors of LUV with time. Sequential snapshots of self-assembled HbS fibers are also shown. The HbS fibers and LUV are rendered in green/yellow and red/white, respectively.

To quantify the shape deformation of the compliant LUV, we computed asphericity shape factor (ASF) and elliptical shape factor (ESF). Figure 3 shows the instantaneous ASF and ESF with time. Starting from a spherical shape, the two shape factors show gradually increases with time due to the initial aggregation, alignment and growth of polymer fibers, whereas they then smoothly approach saturation. A more quantitative insight into the distortion of the LUV membrane can be found from the dependence of ESF on ASF, see Fig. S4(Right). At the initial state, the LUV has a spherical shape with the corresponding values of ASF and ESF approximately equal to 1 and 0, respectively. These values gradually increase with time, indicating that the shape of the LUV membrane is deformed. Hence, in our simulations we find that the HbS molecules can indeed self-assemble into polymer fibers inside a compliant membrane. Thus, by combining a triangulated cytoskeletal network with particle-based bilayer membrane, which is similar to that of the two-component whole-cell model,¹³ it is possible to investigate the uncoupling phenomenon of the cytoskeleton from the lipid bilayer in sickle cell anemia.¹⁴ In this communication we have simulated a particle-based coarse-grained vesicle model and applied it in amphiphilic self-assembly. The model can be used to explore other typical soft matter issues such as molecular crystallization.¹⁵