Security Enhanced User Authentication Protocol for Wireless Sensor Networks Using Elliptic Curves Cryptography

Abstract

Wireless sensor networks (WSNs) consist of sensors, gateways and users. Sensors are widely distributed to monitor various conditions, such as temperature, sound, speed and pressure but they have limited computational ability and energy. To reduce the resource use of sensors and enhance the security of WSNs, various user authentication protocols have been proposed. In 2011, Yeh et al. first proposed a user authentication protocol based on elliptic curve cryptography (ECC) for WSNs. However, it turned out that Yeh et al.'s protocol does not provide mutual authentication, perfect forward secrecy, and key agreement between the user and sensor. Later in 2013, Shi et al. proposed a new user authentication protocol that improves both security and efficiency of Yeh et al.'s protocol. However, Shi et al.'s improvement introduces other security weaknesses. In this paper, we show that Shi et al.'s improved protocol is vulnerable to session key attack, stolen smart card attack, and sensor energy exhausting attack. In addition, we propose a new, security-enhanced user authentication protocol using ECC for WSNs.

1. Introduction

Wireless sensor networks (WSNs) provide a feasible real-time monitoring system. Wireless sensors can be easily deployed in various environments such as military surveillance, forest fire detection, health care and wildlife monitoring. WSNs basically consist of users, sensors and gateways whose communication security is a significant concern in real-world applications [1]. Users and gateways have sufficient resources to be used in the system, but sensors are different. Sensors have limited computational ability, low battery, low bandwidth, and a small amount of memory. Therefore, in WSNs, it is important to reduce the use of sensors to extend their lifespans [2–4].

Various user authentication protocols have been proposed for securing WSNs while minimizing the use of sensors. In 2004, Watro et al. proposed a user authentication protocol employing the RSA and Diffie-Hellman algorithms [5]. In 2006, Wong et al. proposed an efficient dynamic user authentication protocol using a hash function [6]. However, Tseng et al. demonstrated that Wong et al.'s authentication protocol is vulnerable to stolen-verifier attack, replay attack and forgery attack [7,8]. Later in 2009, Das proposed a two-factor user authentication protocol using smart cards. Das showed how to design an authentication protocol where only the user who is in possession of both the smart card and the password can pass the verification of the gateway [8]. However, several security-related flaws in Das's protocol have been disclosed by later studies as summarized below:

• He et al. demonstrated that Das's protocol is vulnerable to insider attacks and impersonation attacks, and that it does not allow users to change their passwords freely. He et al. proposed an improved two-factor protocol [9] which can resist insider and impersonation attacks.

• Khan and Alghathbar showed that Das's protocol fails to provide mutual authentication between the gateway and the sensor, and due to this failure, it is not secure against a gateway bypassing attack and a privileged-insider attack [10].

• Chen et al. also pointed out that Das's protocol does not achieve mutual authentication between the gateway and the sensor, and proposed a robust authentication protocol that provides the property of mutual authentication [11].

In 2011, Yeh et al. [2] revealed that Chen et al.'s protocol has difficulty in updating users' passwords and is vulnerable to an insider attack. As an improvement of Chen et al.'s protocol, Yeh et al. presented the first user authentication protocol that uses elliptic curve cryptography (ECC) in WSN environments. However, Han [12] showed that Yeh et al.'s protocol has still some security weaknesses: it does not provide perfect forward secrecy and fails to achieve mutual authentication and key agreement between the user and the sensor. To address these problems with Yeh et al.'s protocol, Shi et al. [3] have recently proposed a new smart-card-based user authentication protocol using ECC for WSNs. Shi et al.'s protocol performs more efficiently, both in terms of computation and communication costs, and provides better security than Yeh et al.'s protocol. However, we found that Shi et al.'s improvement is not secure enough yet and their protocol is susceptible to session key attacks, stolen smart card attacks, and sensor energy exhausting attacks. In addition to reporting the security weaknesses, we also show how to enhance the security of Shi et al.'s protocol with no significant increase in communication and computation costs. We analyze and verify the security of the proposed protocol using non-monotonic cryptographic logic (Rubin logic).

Throughout the paper, we make the following assumptions on the capabilities of the probabilistic polynomial-time adversary 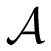in order to properly capture security requirements of two-factor authentication protocols using smart cards in wireless sensor networks.

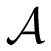• has the complete control of all message exchanges between the protocol participants: a user, a sensor and the gateway. That is, 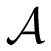can eavesdrop, insert, modify, intercept, and delete messages exchanged among the three parties at will.

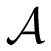• is able to (1) extract the sensitive information on the smart card of a user through a power analysis attack [13,14] or (2) find out the user's password possibly via shoulder-surfing or by employing a malicious card reader. However, it is assumed that is unable to compromise both the two factors: the information on the smart card and the password of the user; it is clear that there is no way to prevent from impersonating the user if both factors are compromised.

2. Overview of Elliptic Curves Cryptography

In 1985, Neal Koblitz and Victor S. Miller proposed the use of elliptic curves in cryptography. After various studies on ECC, it has been widely used since the early 21st century. ECC is a type of public-key cryptography and based on the algebraic structure of elliptic curves over finite fields. Elliptic curves are also used in several integer factorization algorithms. ECC provides the important benefit of a smaller key size, despite which it is able to maintain the same degree of security as other types of public-key cryptography, such as RSA, DH and DSA. Therefore, ECC is especially useful for wireless devices, which typically have limited CPU capacity, power and network connectivity. Table 1 shows the NIST guidelines on choosing key sizes in ECC and other public key cryptography [15].

Table 1.

ECC key sizes compared with other PKC schemes.

Security (bits)	ECC	RSA/DH/DSA	MIPS-Years to Attack	Protection Lifetime
80	160	1,024	1012	until 2010
112	224	2,048	1024	until 2030
128	256	3,072	1028	beyond 2031
192	384	7,680	1047	beyond 2031
256	512	15,360	1066	beyond 2031

ECC has three related mathematical problems: the Elliptic Curve Discrete Logarithm Problem (ECDLP), Elliptic Curve Computational Diffie-Hellman Problem (ECCDHP), and Elliptic Curve Decisional Diffie-Hellman Problem (ECDDHP). No polynomial time algorithm can solve the ECDLP, ECCDHP and ECDDHP with non-negligible probability.

Let p > 3 be a large prime and choose two field elements a, b ∈ F_p satisfying 4a³ + 27b² ≠ 0 mod p to define the equation of a non-supersingular elliptic curve E: y² = x³ + ax + b mod p over F_p. Choose a generator point P = (xP, yP) whose order is a large prime number q over E(F_p). In the same way, a subgroup G of the elliptic curve group E(F_p) with order q is constructed. Then, the three mathematical problems in ECC are defined at various study [16–18] as follows.

• ECDLP: Given a point element Q in G, find an integer x ∈ ${\mathbf{\text{Z}}}_q^{*}$ such that Q = xP, where xP indicates that the point P is added to itself x times by the elliptic curves operation.

• ECCDHP: For a, b ∈ ${\mathbf{\text{Z}}}_q^{*}$, given two point elements aP, bP in G, compute abP in G.

• ECDDHP: For a, b, c ∈ ${\mathbf{\text{Z}}}_q^{*}$, given three point elements aP, bP and cP in G, decide whether cP = abP.

3. Review of Shi et al.'s Protocol

In Shi et al.'s protocol [3], the gateway is a trusted node that holds two sufficiently large master keys, x and y. Before starting the system, the gateway and the sensors share a long-term secret key SK_GS = h(ID_Sn‖y). Shi et al.'s protocol consists of four phases; user registration phase, login phase, authentication phase, and password update phase. For convenience, the notations used throughout this paper are summarized in Table 2.

Table 2.

Notations.

Symbol	Description
p, q	Two large prime numbers
FP	A finite field
E	An elliptic curve defined on finite field FP with large order
G	The group of elliptic curve points on E
IDU	The identity of user U
IDSn	The identity of sensor Sn
pwU	The user U's password
GW	The gateway of WSN
x, y	The master keys of GW
h(·)	A secure one-way hash function
‖	A string concatenation operation
⊕	A bitwise XOR operation

3.1. Registration Phase

In this phase, the user U securely submits its identity ID_U and password pw_U to the gateway GW. Then, GW issues U a smart card containing the user authentication information, as shown in Figure 1.

Figure 1.

The registration phase of Shi et al.'s protocol.

3.2. Login and Authentication Phases

In the login and authentication phases, when U enters ID_U and pw_U into a smart card terminal, the smart card must validate the legitimacy of U. Then, U, S_n and GW authenticate with each other. This protocol uses 4 messages (M₁, M₂, M₃, M₄) for mutual authentication, as described in Figure 2. Lastly, U and S_n share the session key sk. After the authentication phase, U and S_n communicate with each other using the session key sk.

Figure 2.

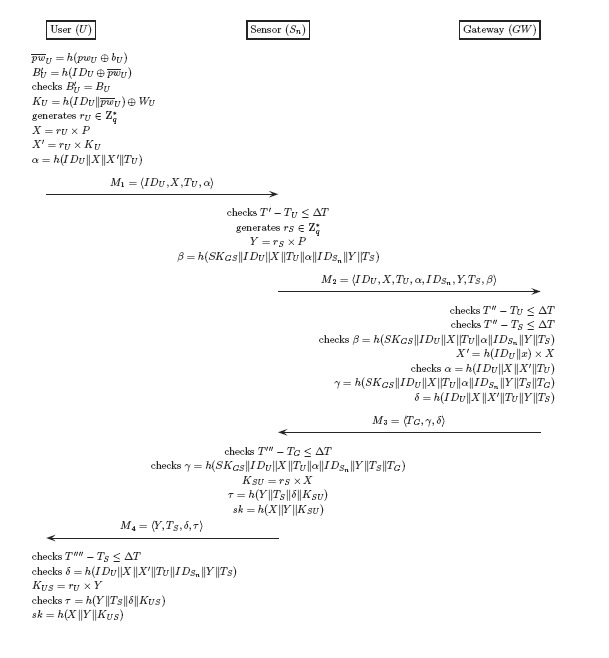
The login and authentication phases of Shi et al.'s protocol.

3.3. Password Update Phase

In the password update phase, U enters the identity ID_U, the old password pw_U, and the new password $p{w}_U^{\prime }$. Then, the smart card updates the password after first checking the correctness of the old password, as shown in Figure 3.

Figure 3.

The password update phase of Shi et al.'s protocol.

4. Security Weaknesses in Shi et al.'s Protocol

This section shows that Shi et al.'s protocol is vulnerable to a session key attack, a stolen smart card attack, and a sensor energy exhausting attack.

4.1. Session Key Attack

In Shi et al.'s protocol, the user U and the sensor S_n have to perform the login and authentication phases when they want to share a session key which will be used for protecting their subsequent communication. A problem occurs if U shares its session key with an attacker, not with the intended sensor S_n. In the protocol, the gateway GW and the user U check each other's legitimacy using the authenticators α and δ, respectively. However, α and δ do not include information about the sensor S_n with which U intends to establish a session key. The attacker exploits this design flaw in mounting a session key attack. The attack is depicted in Figure 4 and its description follows.

Figure 4.

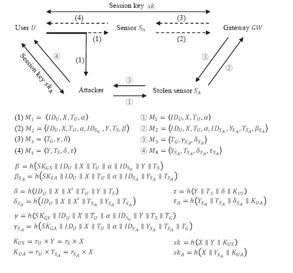
A session key attack on Shi et al.'s protocol.

When U inputs ID_U and pw_U, and sends M₁ to sensor S_n, the attacker intercepts M₁ and sends it to sensor S_a which was previously stolen by the attacker. Upon receiving M₁, the stolen sensor S_a will generate the message A₂ and send it to the gateway GW. However, the attacker replaces ID_Sn contained in A₂ with ID_a to make GW believe that ID_U wants to communicate with sensor S_a, not with S_n. After receiving A₂, the gateway GW generates A₃ without noticing any discrepancy and sends it to sensor S_a. Lastly, the attacker sends the user U the message A₄ generated by S_a using the message A₃ from GW. Because there is no information about the sensor S_n in A₄ and M₄, the user U undoubtedly shares the session key with the attacker while thinking that it has shared the key with the sensor S_n.

4.2. Stolen Smart Card Attack

Kocher et al. and Messerges et al. pointed out that the confidential information stored in smart cards could be extracted by physically monitoring its power consumption [13,14]. Therefore, it is fair to say that if a user loses his or her smart card, all information in the smart card may be revealed to the attacker.

In Shi et al.'s protocol, the smart card stores various information for user login and authentication. The smart card for the user ID_U includes b_U, B_U, W_U and h(·). Using these information and ID_U, an attacker can guess U's password pw_U. If ID_U is used in public communication, the attacker can obtain or steal it without difficulty. Figure 5 describes a stolen smart card attack against Shi et al.'s protocol.

Figure 5.

A stolen smart card attack on Shi et al.'s protocol.

The attacker can obtain information from the smart card using attacks such as simple power analysis (SPA) and differential power analysis (DPA). This information includes b_U, B_U, W_U and h(·). Recall that B_U = h(ID_U ⊕ h(pw_U ⊕ b_U)). Using B_U as a password verifier, the attacker can easily find out the password pw_U by mounting an offline password guessing attack (also known as an offline dictionary attack) [19–22] if the password pw_U is not long enough. After successfully mounting the password guessing attack, the attacker can login and authenticate with the sensor S_n and the gateway GW using the identity ID_U and the password pw_U.

4.3. Sensor Energy Exhausting Attack

The computational cost of a sensor is a critical consideration in the design of WSNs as it increases the consumption of the battery power of the sensor. Often it is economically advantageous to discard a sensor rather than recharge it. For this reason, the battery power of a sensor is usually important in wireless devices, with its lifetime determining the sensor lifetime. Previous work have suggested several types of energy exhausting attacks. Buttyan et al. [23] investigated the reliability of transport protocols for WSNs. Brownfield et al. [24] researched the battery depletion effect through the reduction of sleep cycles. Khouzani et al. [25,26] investigated malware attacks in battery-constrained wireless networks. As shown by the previous researches, WSNs need to eliminate unnecessary computational costs of sensors so that the effects of an energy exhausting attack on sensors can be minimized.

In Shi et al.'s protocol, the sensor performs various cryptographic operations such as one-way hash function evaluations, scalar-point multiplications, random number generations, and map-to-point hash function evaluations. Scalar-point multiplications are much more expensive than hash function evaluations. The computational costs of generating a random number and evaluating a map-to-point hash function are about half the cost of performing a scalar-point multiplication. A sensor consumes a large amount of energy to perform a scalar-point multiplication and very little to perform a hash function evaluation [27–29].

Figure 6 shows the possibility of a sensor energy exhaustion attack. The attacker can keep sending malicious messages, A₁, A₂, A₃, generated to consume the battery power of the sensor. The attacker can do so because the sensor only checks the freshness of the timestamp in M₁. For each of these fake messages, the sensor checks the freshness of the timestamp and proceeds to perform the subsequent cryptographic operations, thereby consuming large amounts of energy. Accordingly, it is necessary to modify the protocol so that the sensor can check if the message M₁ is from a legitimate user, not from an imposter.

Figure 6.

A sensor energy exhausting attack on Shi et al.'s protocol.

5. The Proposed Protocol

Like Shi et al.'s protocol, our proposed protocol is divided into three phases: the user registration phase, login and authentication phase, and password update phase. Before the protocol is ever executed, the gateway generates two master keys, x and y, and shares a long-term secret key SK_GS = h(ID_Sn ‖ y) with the sensor S_n. In describing the protocol, we use the same notations as in Table 2 unless stated otherwise.

5.1. Registration Phase

For a user U, this phase is performed only once when U registers itself with the gateway GW. Figure 7 illustrates how the phase works, and its description follows:

• (1)The user U chooses its identity ID_U and password pw_U freely, generates a random number b_U, and computes ${\overline{pw}}_U=h\left(p{w}_U\oplus b_U\right)$. U sends ID_U and ${\overline{pw}}_U$ to GW via a secure channel.
• (2)
  The gateway GW computes:

  $$\begin{array}{lll}{K}_U& =& h\left(I{D}_U\Vert x\right)\times P\\ A_U& =& {\overline{pw}}_U\oplus h\left(x\oplus y\right)\\ B_U& =& h\left(I{D}_U\Vert {\overline{pw}}_U\Vert h\left(x\oplus y\right)\right)\\ W_U& =& h\left(I{D}_U\Vert {\overline{pw}}_U\Vert \right)\oplus K_U\end{array}$$

  Then, GW issues U a smart card loaded with {A_U, B_U, W_U, h(·)}.
• (3)Lastly, U inputs the random number b_U into the smart card.

Figure 7.

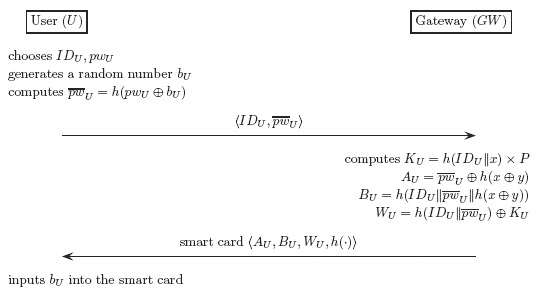
The registration phase.

5.2. Login and Authentication Phase

This phase is carried out whenever U wants to gain access to the WSN. During the phase, U establishes a session key with the sensor S_n while being authenticated by the gateway GW. The phase proceeds as follows (see also Figure 8):

• Step 1.
  U inserts its smart card into the card reader and inputs its identity ID_U and password pw_U. Then, the smart card computes:

  $$\begin{array}{cc}\hfill {\overline{pw}}_U& =h\left(p{w}_U\oplus b_U\right)\hfill \\ \hfill B_U^{\prime }& =h\left(I{D}_U\Vert {\overline{pw}}_U\Vert h\left(x\oplus y\right)\right)\hfill \end{array}$$

  and checks if B_U is equal to $B_U^{\prime }$. If not equal, the smart card aborts the protocol. Otherwise, it retrieves the current timestamp T_U, chooses a random number r_U ∈ ${\mathbb{Z}}_q^{*}$, and computes:

  $$\begin{array}{cc}\hfill K_U& =h\left(I{D}_U\Vert {\overline{pw}}_U\right)\oplus W_U\hfill \\ \hfill X& =r_U\times P\hfill \\ \hfill X^{\prime }& =r_U\times K_U\hfill \\ \hfill \omega & =h\left(I{D}_U\Vert h(I{D}_{S_n}\Vert h\left(x\oplus y\right)\Vert T_U\right)\hfill \\ \hfill \alpha & =h\left(I{D}_U\Vert I{D}_{S_n}\Vert X\Vert X\prime \Vert T_U\Vert \omega \right)\hfill \end{array}$$

  After the computations, the smart card sends the message M₁ = 〈ID_U, ID_Sn, X, T_U, α, ω〉 to the sensor S_n.
• Step 2.
  Upon receiving M₁ from U, the sensor S_n retrieves the current timestamp T′ and verifies the freshness of U's timestamp T_U by checking that:

  $$T^{\prime }-T_U\le \mathrm{\Delta }T$$

  where ΔT is the maximum allowed time difference between T_U and T′. If T_U is not fresh, S_n rejects U's request and aborts the protocol. Otherwise, S_n checks if ω is equal to the hash value h(ID_U‖h(IDs_n‖h(x ⊕ y)) ‖ T_U). If they are not equal, S_n aborts the protocol. Otherwise, S_n generates a random number r_S ∈ $Z_q^{*}$ retrieves the current timestamp T_S, and computes:

  $$\begin{array}{ll}Y\hfill & =r_S\times P\hfill \\ \beta \hfill & =h\left(S{K}_{GS}\Vert I{D}_U\Vert X\Vert T_U\Vert \alpha \Vert \omega \Vert I{D}_{S_n}\Vert Y\Vert T_S\right)\hfill \end{array}$$

  Then, S_n sends the message M₂ = 〈ID_U, X, T_U, α, ω, ID_Sn, Y, T_S, β〉 to the gateway GW.
• Step 3.
  After receiving M₂, GW retrieves the current timestamp T″ and verifies the freshness of the timestamp T_S by checking that T″ − T_S ≤ ΔT. If T_S is not fresh, GW aborts the protocol. Otherwise, GW computes X′ = h(ID_U‖x) × X and checks if α equals h(ID_U‖ID_Sn‖X‖X′‖T_U‖ω) and β equals h(SK_GS‖ID_U‖X‖T_U‖α‖ω‖ID_Sn‖Y‖T_S). If either of the checks fails, GW aborts the protocol. Otherwise, GW retrieves the current timestamp T_G and computes:

  $$\begin{array}{ll}\gamma \hfill & =h\left(S{K}_{GS}\Vert I{D}_U\Vert X\Vert T_U\Vert \alpha \Vert I{D}_{S_n}\Vert Y\Vert T_S\Vert T_G\right)\hfill \\ \delta \hfill & =h\left(I{D}_U\Vert X\Vert X^{\prime }\Vert T_U\Vert I{D}_{S_n}\Vert Y\Vert T_S\right)\hfill \end{array}$$

  Then, GW sends M₃ = 〈T_G, γ, δ〉 to the sensor S_n.
• Step 4.
  Having received M₃, S_n retrieves the current timestamp T‴ and checks if T‴ − T_G ≤ ΔT and γ = h(SK_GS‖ID_U‖X‖T_U‖α‖ID_Sn‖Y‖T_S‖T_G) Only if both the checks hold, S_n retrieves the new timestamp $T_S^{\prime }$ and computes:

  $$\begin{array}{cc}\hfill K_{SU}& =r_S\times X\hfill \\ \hfill \tau & =h(Y\Vert T_S^{\prime }\Vert \delta \Vert K_{SU})\hfill \\ \hfill sk& =h(X\Vert Y\Vert K_{SU})\hfill \end{array}$$

  Then, S_n sends M₄ = 〈Y, T_S, $T_S^{\prime }$, δ, τ〉 to the user U.
• Step 5.
  With M₄ in hand, U retrieves the current timestamp T⁗, computes K_US = r_U × Y, and checks if (1) T⁗− T′_S ≤ ΔT; (2) δ = h(ID_U‖X‖X′ ‖T_U‖ID_Sn‖Y‖T_S); and (3) $\tau =h(Y\Vert T_S^{\prime }\Vert \delta \Vert K_{US})$. If any of the checks fail, U aborts the protocol. Otherwise, U computes:

  $$sk=h\left(X\Vert Y\Vert K_{US}\right)$$

Figure 8.

The login and authentication phase.

5.3. Password Update Phase

Our protocol allows users to freely update their passwords. The password update phase works as follows (see also Figure 9):

1. The user U inserts its smart card into a smart card reader and enters the identity ID_U, the old password pw_U, and the new password pw′_U.

2. The smart card computes ${\overline{pw}}_U=h\left(p{w}_U\oplus b_U\right)$, $h\left(x\oplus y\right)=A_U\oplus {\overline{pw}}_U$, and $B_U^{\prime }=h\left(I{D}_U\Vert {\overline{pw}}_U\Vert h\left(x\oplus y\right)\right)$ and checks if B′ is equal to B. If they are not the same, the password update phase stops. Otherwise, the smart card computes:

   $$\begin{array}{cc}\hfill K_U& =W_U\oplus h(I{D}_U\Vert {\overline{pw}}_U)\hfill \\ \hfill {\overline{p{w}^{\prime }}}_U& =h(p{w^{\prime }}_U\oplus b_U)\hfill \\ \hfill {A^{\prime }}_U& ={\overline{p{w}^{\prime }}}_U\oplus h(x\oplus y)\hfill \\ \hfill {B^{\prime }}_U& =h(I{D}_U\Vert {\overline{p{w}^{\prime }}}_U\Vert h(x\oplus y))\hfill \\ \hfill {W^{\prime }}_U& =h(I{D}_U\Vert {\overline{p{w}^{\prime }}}_U)\oplus K_U\hfill \end{array}$$

   and replaces A_U, B_U and W_U with A′_U, B′_U and W′_U, respectively.

Figure 9.

The password update phase.

6. Performance Comparison

Table 3 compares our improved protocol with Yeh et al.'s protocol [2] and Shi et al.'s protocol [3] in terms of the computational costs required by the protocols. The efficiency comparison is based on theoretical analysis and experimental results [3,27–29].

Table 3.

Efficiency comparison.

Protocol	Computational Cost
	User	Sensor	Gateway
Yeh et al.'s protocol	2M +1R+1A+4H	2M +1R +1A+ 1P +1H	3M +1R+1P + 1H
Shi et al.'s protocol	3M +5H	2M +3H	1M +4H
Our protocol	3M +7H	2M +4H	1M +4H

Notations used in Table 3 are described as follows:

M	scalar-point multiplication
R	random point generation
A	point addition
P	map-to-point hash function evaluation
H	hash function evaluation

The computational costs of generating a random point and evaluating a map-to-point hash function are about half the cost of performing a scalar-point multiplication. Hash function evaluations and point addition operations are often ignored in cost estimates since they are much faster than scalar-point multiplications. If we ignore hash function evaluations, the computational costs described in Table 3 can be estimated as in Table 4.

Table 4.

Estimated efficiency comparison.

Protocol	Computational Cost
	User	Sensor	Gateway
Yeh et al.'s protocol	2.5M	3M	3M
Shi et al.'s protocol	3M	2M	1M
Our protocol	3M	2M	1M

As shown in Tables 3 and 4, our proposed protocol and Shi et al.'s protocol are more efficient than Yeh et al.'s protocol, in terms of the computational costs of the sensor and the gateway. In WSNs, it is important to minimize the energy consumption of the sensor node. In this sense, it is fair to say that our protocol and Shi et al.'s protocol are better suited for WSNs than Yeh et al.'s protocol. The performance of our proposed protocol is similar to that of Shi et al.'s protocol. But, as we demonstrated in Section 4, Shi et al.'s protocol is vulnerable to a session key attack, a stolen smart card attack, and a sensor energy exhausting attack. Consequently, we can say that our protocol enhances the security of Shi et al.'s protocol while maintaining the efficiency of the protocol.

7. Security Analysis and Verification

In this section, we first provide a heuristic security analysis for the proposed protocol and then formally verify the security analysis by using Rubin logic.

7.1. Heuristic Security Analysis

7.1.1. Stolen-Verifier Attack

In WSNs, an attacker may attempt to mount a stolen-verifier attack if the gateway stores a password verifier [30] and then, impersonate a legal user using the verifier stolen from the gateway. However, in our protocol, the gateway does not store a password verifier of any kind but stores only the master secret keys x and y which are used in computing:

$$\begin{array}{ll}S{K}_{GS}\hfill & =h(I{D}_{S_n}\Vert y)\hfill \\ X^{\prime }\hfill & =h\left(I{D}_U\Vert x\right)\times X\hfill \end{array}$$

7.1.2. Insider Attack

An insider attack occurs when the gateway manager or system administrator can access a user's secret (e.g., user password) and then impersonate the user. However, in our protocol, the user U does not send a plain password to the gateway, but sends only the password-derived hash value ${\overline{pw}}_U=h(p{w}_U\oplus b_U)$. Since b_U is a sufficiently high-entropy random number, the gateway cannot learn the password pw_U from the hash value ${\overline{pw}}_U$. In addition, the gateway does not manage any table for storing user passwords or their verifiers (e.g., an ID/password table) Therefore, an insider attack is not possible against our protocol.

7.1.3. Replay Attack

In our protocol, each of the protocol messages (M₁, M₂, M₃ and M₄) accompanies at least one of the authenticators (α, β, γ, δ, τ and ω) which are generated using a timestamp (T_U, T_S, T′_S or T_G) as part of the hash input. The protocol participants (U, S_n and GW) verify the authenticity of incoming messages by checking the freshness of the timestamps and the legitimacy of the authenticators. But, an attacker cannot compute any of the authenticators for a fresh timestamp without knowing an appropriate secret. Therefore, our proposed protocol is secure against replay attacks.

7.1.4. Man-in-the-Middle Attack

It is impossible for an attacker to mount a man-in-the-middle attack against our proposed protocol. In a typical man-in-the-middle attack, an attacker intercepts the messages being exchanged between the communicating parties and instead, sends arbitrary messages for its own benefit impersonating one of them to the other. But, our protocol allow the parties to authenticate all the protocol messages with the authenticators α, β, γ, δ, τ and ω, and therefore, is secure against man-in-the-middle attacks.

7.1.5. Gateway Impersonation Attack

An attacker cannot impersonate the gateway because it cannot forge the message:

$$M_3=\langle T_G,\gamma ,\delta \rangle$$

To generate γ or δ, one needs to know either SK_GS or h(ID_U‖x). However, h(ID_U‖x) is the secret shared only between the user and the gateway while SK_GS is the secret shared between the sensor and the gateway. Therefore, it is impossible for an attacker to mount a gateway impersonation attack.

7.1.6. User Impersonation Attack

It is impossible for an attacker to impersonate the user as it cannot forge the message:

$$M_1=\langle I{D}_U,I{D}_{S_n},X,T_U,\alpha ,\omega \rangle$$

The attacker should know X′ to compute α and should know h(x ⊕ y) to compute ω. But, the attacker knows neither X′ nor h(x ⊕ y) and therefore, cannot mount a user impersonation attack.

7.1.7. Sensor Impersonation Attack

An attacker cannot impersonate the sensor because it can forge the messages M₂ = 〈ID_U, X, T_U, α, ω, ID_Sn, Y, T_S, β〉 and M₄ = 〈Y, T_S,T′_S, δ, τ〉. The attacker cannot compute β without knowing SK_GS and cannot compute δ without knowing the secret h(ID_U‖x). But, the attacker knows neither SK_GS nor x and therefore, cannot mount a sensor impersonation attack.

7.1.8. Mutual Authentication

Mutual authentication is an important security property that an authentication protocol should achieve [31,32]. Our proposed protocol provides mutual authentication among the three parties: the user, the sensor and the gateway.

• The gateway authenticates the user using α in M₂.

• The gateway authenticates the sensor using β in M₂.

• The sensor authenticates the gateway using γ in M₃.

• The user authenticates the gateway using δ in M₄.

• The user and the sensor authenticate each other via δ from the gateway.

This means that our protocol achieves mutual authentication.

7.1.9. Perfect Forward Secrecy

Perfect forward secrecy means that a session key derived from a set of long-term keys will not be compromised even if one of the long-term keys is compromised in the future. The proposed protocol uses the session key sk = h(X‖Y‖r_S × X) for the sensor and sk = h(X‖Y‖r_U × Y) for the user. Even though h(ID_U‖x) and x are compromised, an attacker cannot know r_U or r_S. Under the assumption that the ECCDHP problem is hard, the attacker cannot compute r_S from r_S × X and r_U from r_U × Y. Therefore, our protocol provides perfect forward secrecy.

7.1.10. Key Agreement

The proposed protocol provides key agreement between the user and the sensor. To the session-key computation, the user contributes its random number r_U while the sensor contributes its random number r_S. It is straightforward to verify that K_SU and K_US are equal:

$$\begin{array}{ll}{K}_{SU}\hfill & =r_S\times X=r_S\times r_U\times P\hfill \\ K_{US}\hfill & =r_U\times Y=r_U\times r_S\times P\hfill \end{array}$$

Since K_SU = K_US, it is clear that the user and the sensor compute session keys of the same value:

$$\begin{array}{cc}sk& =h\left(X\Vert Y\Vert K_{US}\right)\\ & =h\left(X\Vert Y\Vert K_{SU}\right)\end{array}$$

7.1.11. Session Key Attack

In our protocol:

• α is combined with two identities ID_U and ID_Sn, which indicates that the user U wants to communicate with the sensor S_n,

• δ is also combined with ID_U and ID_Sn, which indicates that the gateway has authenticated both the user ID_U and the sensor ID_Sn.

But, no attacker can compute α and δ, and therefore, can share a session key with the user.

7.1.12. Stolen Smart Card Attack

In Shi et al.'s protocol, the attacker can obtain b_U and B_U from the smart card and thus can use B_U = h(ID_U ⊕ h(pw_U ⊕ b_U)) as the password verifier in its offline dictionary attack. However, in our protocol, B_U is computed as $B_U=h(I{D}_U\Vert {\overline{pw}}_U\Vert h(x\oplus y))$. Even if the attacker obtains b_U and B_U from the smart card, it cannot use B_U as a password verifier since it does not know the hash value h(x ⊕ y). Therefore, no attacker can mount an offline dictionary attack against our protocol.

7.1.13. Sensor Energy Exhausting Attack

In Shi et al.'s protocol, the sensor has to generate a random number and execute a scalar-point multiplication whenever it receives the message M₁ from the user. Random number generations and scalar-point multiplications are expensive and exhaust a large amount of the sensor's energy. This makes Shi et al.'s protocol vulnerable to a sensor energy exhausting attack. However, in our protocol, the sensor first checks the validity of ω = h(ID_U‖h(ID_Sn‖h(x ⊕ y))‖T_U) before generating a random number and performing a scalar-point multiplication. Checking the validity of ω only requires one hash function evaluation. Therefore, our proposed protocol is secure against a sensor energy exhausting attack.

Table 5 summarizes and compares the security of our protocol, Yeh et al.'s protocol, and Shi et al.'s protocol.

Table 5.

Security comparison.

Attack and Security Property	Yeh et al.'s Protocol	Shi et al.'s Protocol	Our Protocol
Stolen-verifier attack	Secure	Secure	Secure
Insider attack	Secure	Secure	Secure
Replay attack	Secure	Secure	Secure
Man-in-the-middle attack	Secure	Secure	Secure
Gateway impersonation attack	Secure	Secure	Secure
User impersonation attack	Secure	Secure	Secure
Sensor impersonation attack	Insecure	Secure	Secure
Mutual authentication	No	Yes	Yes
Perfect forward secrecy	No	Yes	Yes
Key agreement between user and sensor	No	Yes	Yes
Session key attack	Insecure	Insecure	Secure
Stolen smart card attack	Insecure	Insecure	Secure
Sensor energy exhausting attack	Insecure	Insecure	Secure

7.2. Rubin Logic Verification

We analyze the proposed protocol using Rubin logic which can be applicable in analyzing an authentication protocol. Rubin logic integrates protocol analysis with specification and uses the notions of global sets, local sets, and actions. As the protocol run is progressed, the possession and belief sets (specified by local sets) are modified for each principal by inference rules (specified by global sets) and actions [33,34]. As the possession and belief sets are modified, secret set and observers sets (specified by global sets) are modified as well.

Global Sets

The first step of the specification of any protocol using Rubin logic is to instantiate the global sets with values. Global sets are public to each principal in a protocol specification.

• Principal Set: This set contains the principals who participate in a protocol.

• Rule Set: This set contains inference rules for deriving new statements from existing assertions.

• Secret Set: This set contains all of the secrets that exist at any given time in the system.

• Observers Sets: For each secret, its set contains all the principals who could possibly know the secret by listening to network traffic or generating it themselves.

Local Sets

Local sets are private to each principal in a protocol specification [35]. For each principal, P_i, Rubin logic defines the following sets:

• Possession Set(P_i): This set contains all the data relevant to security that this principal knows or possesses. We denote this set by POSS(P_i) = (poss₁, poss₂, ⋯, poss_n).

• Belief Set(P_i): This set contains all the beliefs hold by a principal. For example, the keys it holds between itself and other principals, beliefs about jurisdiction, beliefs about freshness, and beliefs about the possessions of other principals. We denote this set by BEL(P_i) = (bel₁, bel₂, ⋯, bel_n).

• Behavior List(P_i): This item is a list rather than a set because the elements are ordered. BL(P_i) = Behavior List of P_i.

Actions

Rubin logic defines actions for dealing with the knowledge in a protocol [36]. The action lists that precede and follow message operations in a principal's behavior list determine a sequence of events performed by the principal during a protocol run. We use the following actions:

• Generate-nonce(N)

• Send(P_i, X)

• Receive(P_i, X)

• Update(X)

• Forget(X)

• Concat(X₁, X₂, ⋯,X_n)

• XOR(X₁, X₂, ⋯,X_n)

• Check(X₁, X₂, ⋯, X_n)

• Scalar-multiplication(X₁, X₂, ⋯, X_n)

• Hash(h(·); X₁, X₂, ⋯, X_n)

• Check-freshness(T)

Here, Concat(X₁, X₂, ⋯, X_n) is the action that concatenates the submessages X₁, X₂, ⋯, X_n.

7.2.1. Protocol Specification

Notations used for the protocol specification is the same as those in Table 2. Phases 1, 2 and 3 represent the registration phase, the login and authentication phase, and the password updated phase. The global and local sets for the protocol are specified as follows:

Global Sets

The global sets are specified as follows:

• Principal set: A principal is one of U, S_n and GW. U is the protocol initiator.

• Rule set:

  • –
    X contains Y: Y appears as a submessage of X.
  • –
    S ≔← f(S): S is replaced by the value f(S).
  • –
    X from E: X is received from E.
  • –
    LINK(N): LINK is used to link responses to challenges. When a principal generates a nonce, N, the formula LINK(N) is added to the belief set of the principal.

• Secret Set: {pw_U, b_U, x, y, h(x ⊕ y), SK_GS}

• Observers Sets:

  • –
    Observers(pw_U): {U}
  • –
    Observers(b_U): {U}
  • –
    Observers(x): {GW}
  • –
    Observers (y): {GW}
  • –
    Observers(h(x ⊕ y)): {S_n,GW}
  • –
    Observers(SK_GS): {S_n,GW}

Local Sets

The local sets are defined for each U, S_n and GW. Tables 67 and 8 show the specification of the local sets for U, S_n and GW, respectively.

Table 6.

Local sets specification for principal U.

Principal U
POSS(U) = {pwU, bU, {IDU}}	(U16) Update(IDU, IDSn, X, TU, α, ω)
BEL(U) = {#(pwU), #(bU)}	(U17) Receive(Sn, {Y, TS, δ, τ})
BL(U)	(U18) Check-freshness(T′S)
Phase 1	(U19) Check (δ, Hash(h(·); Contat(IDU, X, X′,TU, IDSn, Y, TS)))
(U1) ${\overline{\mathit{\text{pw}}}}_U\leftarrow \text{Hash}(h(\cdot );\text{XOR}(p{w}_U,b_U))$
(U2) Send (GW,{IDU, ${\overline{pw}}_U$})	(U20) KUS ← Scalar-multiplication(rU, Y)
(U3) Update(IDU, ${\overline{pw}}_U$)	(U21) Check(τ, Hash(h(·); Contat(Y, T′S, δ, KUS)))
(U4) Receive(GW, {AU, BU, WU, h(·)})	(U22) sk ← Hash(h(·); Contat(X, Y, KUS))
Phase 2	Phase 3
(U5) ${\overline{\mathit{\text{pw}}}}_U\leftarrow \text{Hash}(h(\cdot );\text{XOR}(p{w}_U,b_U))$	(U23) ${\overline{\mathit{\text{pw}}}}_U\leftarrow \text{Hash}(h(\cdot );\text{XOR}(p{w}_U,b_U))$
(U6) h(x⊕y) ← XOR( ${\overline{pw}}_U$, AU)	(U24) B′U ← Hash(h(·); Concat (IDU, ${\overline{pw}}_U$, h(x(⊕ y))
(U7) B′U ← Hash(h(·);Concat (IDU, ${\overline{pw}}_U$, h(x⊕y)))	(U25) Check(B′U, BU)
(U8) Check(B′U, BU)	(U26) KU ← XOR(Hash(h(·); Concat(IDU, ${\overline{pw}}_U$)), WU)
(U9) KU ← XOR(Hash(h(·); Concat(IDU, ${\overline{pw}}_U$)),WU)	(U27) h(x(⊕ y) ← XOR( ${\overline{pw}}_U$, AU)
(U10) Generate-nonce(rU)	(U28) ${\overline{pw\prime }}_U\leftarrow \text{Hash}(h(\cdot );\text{XOR}(pw{\prime }_U,A_U))$
(U11) X ← Scalar-multiplication(rU, P)	(U29) A′U ← XOR ( ${\overline{pw}}_U$, h(x ⊕ y))
(U12) X′ ← Scalar-multiplication(rU, KU)	(U30) B′U ← Hash(h(·); Concat(IDU, ${\overline{p{w}^{\prime }}}_U$, h(x(⊕ y)))
(U13) ω ← Hash(h(·); Concat(IDU, Hash(h(·);IDSn, h(x ⊕ y)), TU))	(U31) W′U ← XOR(Hash(h(·); Concat(IDU, ${\overline{p{w}^{\prime }}}_U$)), KU)
	(U32) AU ← A′U
(U14) α ← Hash(h(·); Concat(IDU, IDSn, X, X′, TU,ω))	(U33) BU ← B′U
(U15) Send(Sn, {IDU, IDSn, X, TU, α, ω})	(U34) WU ← W′U

Table 7.

Local sets specification for principal S_n.

Principal Sn
POSS(Sn) = {SKGS, h(x ⊕ y), {IDSn}}	(SN7)
BEL(Sn) = {#(SKGS), #(h(x ⊕ y))}	Send(GW, {IDU, X, TU, α, ω, IDSn, Y, TS, β})
BL(Sn)	(SN8) Update(IDU, X, TU, α, ω, IDSn, Y, TS, β)
Phase 2	(SN9) Receive(GW, {TG, γ, δ})
(SN1) Receive(U, {IDU, IDSn, X, TU, α, ω})	(SN10) Check-freshness(TG)
(SN2) Check-freshness(TU)	(SN11) Check
(SN3) Check	(γ,Hash(h(·); Concat(SKGS,IDU,X,TU,α,IDSn,Y,TS,TG)))
(ω, Hash(h(·);Concat(IDU,Hash(h(·);IDSn,h(x ⊕ y)),TU)))	(SN12) KSU ← Scalar-multiplication(rS, X)
(SN4) Generate-nonce(rS)	(SN13) τ ← Hash(h(·); Concat(Y, T′S, δ, KSU))
(SN5) Y ← Scalar-multiplication(rS, P)	(SN14) sk ← Hash(h(·); Contat(X, Y, KSU))
(SN6) β ← Hash	(SN15) Send(U, {Y, TS, T′S, δ, τ})
(h(·); Concat (SKGS, IDU, X, TU, α, ω, IDSn, Y, TS))	(SN16) Update(Y, TS,T′S,δ, τ)

Table 8.

Local sets specification for principal GW.

Principal GW
POSS(GW) = {x, y, h(x ⊕ y), SKGS}	Phase 2
BEL(GW) = {#(x), #(y), #(h(x ⊕ y)), #(SKGS)}	(GW9) Receive(Sn, {IDU, X, TU, α, ω, IDSn, Y, TS, β})
BL(GW)	(GW10) Check-freshness(TS)
Phase 1	(GW11) Check (β, Hash(h(·); Concat(SKGS, IDU, X, TU, α, ω, IDSn, Y, TS)))
(GW1) Received(U, {IDU, ${\overline{pw}}_U$)
(GW2) KU ← Scalar-multiplication(Hash(h(·); Concat(IDU, x)), P)	(GW12) X′ ← Scalar-multiplication(Hash(h(·); Concat(IDU, x)), X)
(GW3) AU ← XOR ( ${\overline{pw}}_U$, h(x ⊕ y))	(GW13)
(GW4) BU ← Hash(h(·); Concat(IDU, ${\overline{pw}}_U$, h(x ⊕ y)))	Check(α, Hash(h(·); Concat(IDU, IDSn, X, X′, TU, ω)))
(GW5)	(GW14) γ ←
WU ← XOR(Hash(h(·); Concat(IDU, ${\overline{pw}}_U$)), KU)	Hash(h(·); Concat(SKGS, IDU,X,TU,α,IDSn,Y,Ts,TG))
(GW6) Send(U, {AU, BU, WU, h(·)})	(GW15) δ ← Hash(h(·);Contat(IDU, X, X′, TU, IDSn, Y, TS))
(GW7) Update(AU, BU, WU, h(·))	(GW16) Send(Sn, {TG, γ, δ})
(GW8) Forget(IDU, ${\overline{pw}}_U$, AU, BU, KU, WU)	(GW17) Update(TG, γ, δ)

7.2.2. Analysis and Verification

In phase 1, U initiates the protocol, and then the actions in BL(U) are performed. Firstly, (U1)–(U3) actions in BL(U) are performed, which represent that U sends ID_U and ${\overline{pw}}_U$ to GW for registration. Next, (GW1)–(GW8) actions in BL(GW) are performed to generate A_U, B_U, K_U and W_U, and to send them to U. By (GW8), GW deletes ID_U, ${\overline{pw}}_U$, A_U, B_U, K_U and W_U from POSS(GW) and BEL(GW). Lastly, the (U4) action in BL(U) is executed, then phase 1 is finished. Due to the (GW8) forget action, the local sets of GW are not changed. However, the local sets of principal U are changed as described below.

• POSS(U) = {pw_U, b_U, ${\overline{pw}}_U$, {ID_U}, {A_U, B_U, W_U, h(·)} from GW}

• BEL(U) = {#(pw_U), #(b_U), #( ${\overline{pw}}_U$)}

Accordingly, the global sets are modified as follows:

• Secret set: {pw_U, b_U, ${\overline{pw}}_U$, x, y, SK_GS, h(x ⊕ y)}

• Observers sets:

  • –
    Observers ( ${\overline{pw}}_U$): {U}

In the (U5)–(U8) actions in BL(U) of phase 2, the smart card authenticates U, who inputs ID_U and pw_U, by checking whether B_U and $B_U^{\prime }$ are same or not. Next, the (U9)–(U15) actions are executed to generate the protocol values X, X′, h(x ⊕ y), ω, α and r_U. After the (U16) update action, the local sets of U are changed as follows:

• POSS(U) = {ID_Sn, pw_U, b_U, ${\overline{pw}}_U$, X, X′, h(x ⊕ y), T_U, α, ω, r_U, {ID_U}}

• BEL(U) = {#(pw_U), #(b_U), #(r_U), #( ${\overline{pw}}_U$), #(X′), #(h(x ⊕ y)), #(T_U), LINK(r_U)}

Then, the global sets are modified as follows:

• Secret set: {pw_U, b_U, ${\overline{pw}}_U$, x, y, X′, SK_GS, h(x ⊕ y)}

• Observers sets:

  • –
    Observers(X′): {U}
  • –
    Observers(h(x ⊕ y)): {U}

After the (U5)–(U16) actions are finished, S_n starts the actions in BL(S_n) with the incoming message M₁ from U. The (SN1)–(SN3) actions in BL(S_n) are performed to verify the correctness of message M₁. If the check succeeds, the (SN4)–(SN8) actions are performed to make the values Y, β and r_S, and to send the message M₂. The local sets of S_n are changed as follows.

• POSS(S_n) = {Y, T_S, r_S, β, SK_GS, h(x ⊕ y), {ID_Sn}, {ID_U, X, T_U, α, ω} from U}

• BEL(S_n) = {#(r_S), #(SK_GS), #(h(x ⊕ y)), #(T_S), LINK(r_S)}

In this case, the global sets remain unchanged and thus, the secret set is the same as above:

• Secret set: {pw_U, b_U, ${\overline{pw}}_U$, x, y, X′, SK_GS, h(x ⊕ y)}

After (SN1)–(SN8) actions of BL(S_n) are finished, (GW9)–(GW17) actions of BL(GW) are executed. (GW9)–(GW13) actions check the timestamp of S_n, and then verify the legitimacy of U and S_n. If they are correct, (GW14)–(GW17) actions of BL(S_n) are executed to make values(γ, δ) for authentication and send message. γ is used for authentication with S_n and δ is used for authentication with U.

After the (SN1)–(SN8) actions are done, the (GW9)–(GW13) actions in BL(GW) are performed to check the legitimacy of U and S_n. If the verification succeeds, the (GW14)–(GW17) actions are performed to generate γ and δ and to send the message M₃ to S_n. The local sets of GW are modified as shown below.

• POSS(GW) = {T_G, γ, δ,x, y, X′, SK_GS, h(x ⊕ y), {ID_U, X, T_U, α, ω, ID_Sn, Y, T_S, β} from S_n}

• BEL(GW) = {(#(x), #(y), #(X′), #(SK_GS), #(h(x ⊕ y)), #(T_G)}

The global sets are updated as follows:

• Secret set: {pw_U, b_U, ${\overline{pw}}_U$, x, y, X′, SK_GS, h(x ⊕ y)}

• Observers sets:

  • –
    Observers(X′) = {GW}

After the (GW9)–(GW17) actions are finished, the (SN9)-(SN11) actions in BL(S_n) are conducted to verify the legitimacy of GW and U via the authenticator γ. If the verification process is completed, the (SN12)–(SN16) actions are performed to generate τ and sk from r_S, K_SU, X and Y, and to send the message M₄ to U. The local sets of S_n is updated as follows:

• POSS(S_n) = {Y, $T_S^{\prime }$, K_SU, r_S, τ, sk, SK_GS, {ID_Sn},{T_G, γ, δ} from GW}

• BEL(S_n) = {#(K_SU), #(sk), #(SK_GS), #( $T_S^{\prime }$), LINK (r_S)}

Accordingly, the global sets are modified as follows:

• Secret set: {pw_U, b_U, ${\overline{pw}}_U$, x, y, K_SU, sk, X′, SK_GS, h(x ⊕ y)}

• Observers sets:

  • –
    Observers (K_SU) = {S_n}
  • –
    Observers(sk) = {S_n}

The (U17)–(U19) actions in BL(U) are to check the legitimacy of GW and S_n while the (U20)–(U22) actions are to generate the session key sk from r_U, K_US, X and Y. So, the conditions for the linkage rule are satisfied.

• POSS(U) = {K_US, sk, {ID_U}, {Y, $T_S^{\prime }$, δ, τ} from S_n}

• BEL(U) = {#(K_US), #(X′), #(sk), #(h(x ⊕ y)}

• Secret set: {pw_U, b_U, ${\overline{pw}}_U$, x, y, K_SU, K_US, sk, X′, SK_GS, (x ⊕ y)}

• Observers sets:

  • –
    Observers (K_US) = {U}
  • –
    Observers(sk) = {U}

In phase 3, U changes its password and updates A_U, B_U and W_U stored in the smart card. In this phase, the local sets of U and the global sets remain unchanged.

The following shows the final version of the global sets.

• Secret set: {pw_U, b_U, ${\overline{pw}}_U$, x, y, K_SU, K_US, sk, X′, SK_GS, h(x ⊕ y)}

• Observers sets:

  • –
    Observers (pw_U): {U}
  • –
    Observers (b_U): {U}
  • –
    Observers( ${\overline{pw}}_U$): {U}
  • –
    Observers(x): {GW}
  • –
    Observers(y): {GW}
  • –
    Observers (K_SU): {S_n}
  • –
    Observers (K_US): {U}
  • –
    Observers(sk): {U, S_n}
  • –
    Observers(X′): {U,GW}
  • –
    Observers(SK_GS): {S_n, GW}
  • –
    Observers(h(x ⊕ y)): {U, S_n, GW}

This result implies that:

• pw_U, b_U and ${\overline{pw}}_U$ are known only to the user U.

• x and y are known only to the gateway GW.

• The long-term key SK_GS shared between S_n and GW is not exposed.

• X′ is only known to U and GW.

• K_US and K_SU are only available to U and S_n.

• The session key sk is securely shared between U and S_n.

• h(x ⊕ y) is only known to the authorized principals: U, S_n and GW.

• U, S_n and GW are mutually authenticated during the protocol execution.

This verifies the security claims we made in the previous subsection.

8. Conclusions

In this paper, we have identified that Shi et al.'s ECC-based authentication protocol designed for wireless sensor networks (WSNs) is vulnerable to: a session key attack, a stolen smart card attack, and a sensor energy exhausting attack. We have also proposed a new authentication protocol that addresses the identified security weaknesses. Our proposed protocol is as efficient as Shi et al.'s protocol and is better suited for WSNs than Yeh et al.'s protocol, the predecessor of Shi et al.'s protocol. As for the security of the proposed protocol, we have provided a heuristic analysis and formally verified the analysis using Rubin logic.

Author Contributions

Younsung Choi, Donghoon Lee, Jiye Kim, Jaewook Jung, Junghyun Nam and Dongho Won have contributed to security analysis, design of the proposed scheme, and manuscript preparation.

Conflicts of Interest

The authors declare no conflict of interest.