VISCOELASTIC PROPERTIES OF NORMAL AND INFARCTED MYOCARDIUM MEASURED BY A MULTIFREQUENCY SHEAR WAVE METHOD: COMPARISON WITH PRESSURE-SEGMENT LENGTH METHOD

Abstract

Our aims were (i) to compare in vivo measurements of myocardial elasticity by shear wave dispersion ultrasound vibrometry (SDUV) with those by the conventional pressure-segment length method, and (ii) to quantify changes in myocardial viscoelasticity during systole and diastole after reperfused acute myocardial infarction. The shear elastic modulus (μ₁) and viscous coefficient (μ₂) of left ventricular myocardium were measured by SDUV in 10 pigs. Young’s elastic modulus was independently measured by the pressure-segment length method. Measurements made with the SDUV and pressure-segment length methods were strongly correlated. At reperfusion, μ₁ and μ₂ in end-diastole were increased. Less consistent changes were found during systole. In all animals, μ₁ increased linearly with left ventricular pressure developed during systole. Preliminary results suggest that m1 is preload dependent. This is the first study to validate in vivo measurements of myocardial elasticity by a shear wave method. In this animal model, the alterations in myocardial viscoelasticity after a myocardial infarction were most consistently detected during diastole.

INTRODUCTION

Physiologic (e.g., aging) and pathologic processes are associated with modifications in tissue elasticity, including myocardium. Several conditions such as ischemic heart disease, cardiomyopathies and heart failure with normal ejection fraction are associated with alterations in ventricular and myocardial stiffness (Burkhoff et al. 2005; Burlew and Weber 2002; Diamond and Forrester 1972; Kawaguchi et al. 2003; Zile et al. 2004). These alterations may contribute to diastolic dysfunction, elevated filling pressures and exercise intolerance in these patients. Thus, quantification of mechanical properties of the myocardial tissue may help with the assessment of the health of the tissue. Comprehensive echocardiographic evaluation of systolic and diastolic function provides objective evidence for functional abnormalities that corroborate with clinical presentation and patient symptoms. However, a significant number of patients have inconclusive results and are sent for invasive evaluation. Echocardiography (ECG) provides information on ventricular chamber stiffness from blood flow kinetics, but measurements suffer from the influence of confounding factors (Little et al. 1995; Nagueh et al. 2009; Oh et al. 2006).

Several shear wave techniques have recently been developed to evaluate tissue elasticity and viscoelasticity using magnetic resonance (Muthupillai et al. 1995; Rump et al. 2007; Vappou 2012) and ultrasound (Bercoff et al. 2004; Chen et al. 2009; Kanai 2005; Nightingale et al. 2003; Sarvazyan et al. 1998) imaging. These techniques share the same principle: Shear waves are induced by an external force, wave propagation is measured by motion tracking and shear elasticity (or viscoelasticity) is estimated from the speed of wave propagation using different models and approaches. Measurements on the heart have been reported using magnetic resonance elastography, acoustic radiation force imaging, supersonic shear wave imaging and shear wave dispersion ultrasound vibrometry (SDUV) (Couade et al. 2011; Hsu et al. 2007; Kanai 2005; Kolipaka et al. 2010; Nenadic et al. 2011; Nightingale et al. 2003, Pislaru et al. 2009; Urban et al. 2013), among other techniques. To our knowledge, shear wave measurements on the myocardium have not been validated in vivo. Shear elasticity is related to tensile elasticity (i.e., Young’s elastic modulus), which is the most common measure of tissue elasticity. Considering the evidence for changes in tissue stiffness with various developing pathologies and in different organs, it is hoped that measurements of myocardial shear elasticity may be of clinical value.

This study had two aims. The first was to compare myocardial elasticity estimated by SDUV against standard measures of myocardial elasticity and stiffness obtained with the conventional pressure-segment length method in a large animal model. The second aim was to characterize differences in viscoelastic properties of the myocardium during systole and diastole in normal and infarcted myocardium. We hypothesized that alterations in myocardial stiffness caused by acute ischemia and re-perfusion (Diamond and Forrester 1972; Pirzada et al. 1978) can be quantified in vivo by the shear wave method, SDUV. The effect of preload on viscoelastic estimates was also assessed.

METHODS

All procedures were designed in accordance with the National Institutes of Health guidelines. The protocol was approved by the Mayo Clinic Institutional Animal Care and Use Committee. Farm pigs (3–4 month old) were sedated (telazol 5 mg/kg, atropine 0.05 mg/kg, xylazine 2 mg/kg), anesthetized (continuous inhalation of isoflurane 1%–2%) and mechanically ventilated. A dual-sensor pressure catheter (Millar Instruments, Houston, TX, USA) was used to measure left ventricular (LV) and aortic pressure. After sternotomy, the heart was suspended in a pericardial cradle. Piezoelectric crystals (Sonometrics, London, ON, Canada) were inserted, 1–1.5 cm apart, from the epicardial side into the subendocardium of the anterior and inferolateral LV walls to measure segment lengths and LV chamber minor radius. Preload was increased by rapid intravenous saline infusion (0.5–1 L). ECG and pressure signals were digitized and continuously recorded.

Acute myocardial infarction (MI) was induced by ligature of the mid- to distal left anterior descending coronary artery for 1–3 h, followed by 1–2 h of reperfusion. Presence of severe ischemia was confirmed by segment lengthening (bulging) during systole and development of cyanosis. Reperfusion was achieved by removal of the ligature. At the end of the experiment, the transmural extent of infarction in the target area was quantified by triphenyltetrazolium chloride staining of the excised hearts, as previously described (Pislaru et al. 2001).

Shear wave dispersion ultrasound vibrometry

This technique is based on shear wave velocity dispersion (i.e., the variation of wave speed with frequency) and Lamb’s theory of wave propagation in plates (Lamb 1917) for estimating material viscoelastic properties (Kanai 2005; Nenadic et al. 2011). The details of the technique and some preliminary results in normal animals were previously reported (Pislaru et al. 2009; Urban et al. 2013). Shear elasticity (shear elastic modulus, μ₁, in kPa) and viscosity (viscous coefficient, μ₂, in Pa · s) can be estimated from a small region of interest (~1 cm). The viscoelastic properties of the myocardium were modeled as an elastic spring (μ₁) in parallel with a dashpot (μ₂) (i.e., Voigt model). Thus, μ₁ represents the storage modulus (frequency-independent), whereas μ₂ is a constant responsible in part for the frequency-dependent increase in wave speed. The method assumes local homogeneity, isotropy and incompressibility.

Figure 1 illustrates the experimental setup. Small sinusoidal vibrations (10–100 μm in amplitude) were applied on the surface of the heart using a mechanical actuator (V203, Ling Dynamic Systems, Hertfordshire, UK), driven with a signal generator (33120 A, Agilent, Santa Clara, CA, USA) and an amplifier (XLS 202, Crown Audio, Elkhart, IN, USA). The signal generator was used to vary the amplitude and frequency of excitation. The resulting shear wave motion propagating along the heart wall was tracked with a 5-MHz linear array transducer (L9-4/38) and Sonix RP scanner (Ultrasonix Medical, Vancouver, BC, Canada) using eight M-mode lines and frame rates between 2000 and 2500 Hz. The transducer was oriented approximately parallel to the long axis of the left ventricle. The transducer was attached to the surgical table, and measurements were performed on the same myocardial segment throughout the experiment. Care was taken to fine-tune the position of the rod to obtain robust motion data measurable by ultrasound, while minimizing the pressure applied on the heart and avoiding the obstruction of coronary arteries and major branches. Ultrasound data were acquired at fixed frequencies between 50 and 400 Hz, in 50 Hz increments, continuously for 2.5–3 s. For clarity, here we present wave velocity results between 100 and 350 Hz, which was generally the frequency range used for estimation of shear wave parameters, as previously discussed (Urban et al. 2013).

Fig. 1.

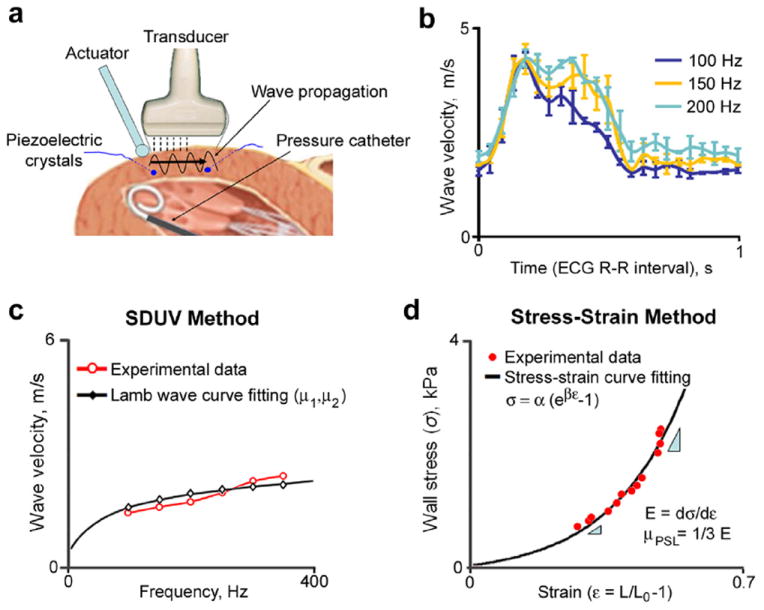
(a) Experimental setup. (b) Examples of phase velocities measured from one animal at three different frequencies. (c) Estimation of shear wave parameters (μ₁ and μ₂) from wave velocity dispersion and Lamb wave curve fitting. (d) Calculation of shear elastic modulus from stress-strain data (μ_PSL). ECG = electrocardiography, SDUV = shear wave dispersion ultrasound vibrometry.

Each measurement was repeated five times (up to 15 heart cycles acquired in total). Data acquisition was synchronized with the ECG signal. One complete set of measurements took 5–10 min to acquire, and constant tissue properties were assumed based on hemodynamics.

Wave propagation velocities were calculated offline every 20–50 ms. Median velocity through wall thickness was considered representative of full thickness. Because of the non-linear response of the actuator and the rigid setup, some data were discarded when deemed unreliable: linear regression coefficient r² < 0.70 for phase velocity estimation, no consistent results between consecutive heart beats, unreliable phase velocity estimation because of low amplitude of motion at higher frequencies (i.e., 350–400 Hz) or tracking errors in the near field of the transducer during heart dilation with volume loading. Data from occasional ectopic beats (mostly at reperfusion) were excluded. Wave velocities from several heart cycles in sinus rhythm were averaged, then plotted versus frequency and fitted to the Lamb wave dispersion equation to estimate μ₁ and μ₂ (Fig. 1c). The equation requires input of wall thickness, which was obtained from M-mode data. For each data set, the variation in μ₁ and μ₂ through the heart cycle was obtained. The end-diastolic and mean systolic (ejection phase) μ₁ and μ₂ were calculated. The net increase in μ₁ during systole was calculated by subtracting the end-diastolic value from the mean systolic value. Cardiac phases were identified from aortic and LV pressure tracings.

Pressure-segment length method

Standard measures of myocardial elasticity and stiffness were calculated from end-diastolic pressure-segment length and stress-strain relationships during volume loading (Mirsky 1976). The end-diastolic pressure-segment length data were fit to an exponential function, and stiffness coefficients (α, β) were calculated from the corresponding stress-strain relationship:

$$\sigma =\alpha \left[\exp \left(\beta \cdot \epsilon \right)-1\right],$$ (1)

where ε is strain, ε = (SL – SL₀)/SL₀, SL₀ is unstressed segment length, and σ is wall stress calculated from LV pressure (P), LV midwall radius (b) and wall thickness (h), as previously suggested (Yin 1981):

$$\sigma =\left(Pb/2h\right){\left(1-h/2b\right)}^2$$ (2)

The elastic modulus (Young’s modulus or tangent modulus) is the slope of the stress-strain relationship and describes the effective tensile elasticity (Fig. 1d):

$$E=d\sigma /d\epsilon$$ (3)

For isotropic linearly elastic materials, shear elasticity (μ) is related to tensile elasticity through Poisson’s ratio (ν):

$$E=2\mu \left(1+\nu \right)$$ (4)

Assuming tissue incompressibility (ν ≅ 0:5), this approximates to

$$\mu =E/3$$ (5)

This modulus obtained from pressure-segment length data (μ_PSL) was compared with shear elasticity estimated by SDUV (μ₁).

Regional systolic function was quantified by systolic shortening as the change in segment length from end-diastole to end-systole relative to end-diastolic length.

A note about nomenclature on elasticity: In medical literature, a stiffer tissue is commonly referred to as having a lower elasticity (distensibility or stretchiness) and a higher slope of stress-strain relationship (Burkhoff et al. 2005; Mirsky 1976). In engineering terms, this is called a higher modulus of elasticity. In this article, the term elasticity refers to the modulus or the slope of the stress-strain relationship measured in this study.

Statistical analysis

Data are presented as means ± standard deviations. Analysis was performed using SAS/STAT software (Version 4.3, SAS Institute, Cary, NC, USA). Data were tested for normal distribution, and transformations were used when appropriate (μ₂ and α coefficient). The strength of the relationship between μ₁ and μ_PSL was evaluated using Pearson’s correlation coefficient. Limits of agreement were analyzed using the Bland-Altman method. Differences in parameters between normal animals and those with MI were evaluated using unpaired t-tests, and those between baseline and reperfusion, using paired t-tests. Least-squares linear regression was used to evaluate the relationship between μ₁ and μ₂ with LV pressure. Statistical significance was considered at p < 0.05 (two-tailed).

RESULTS

Data from a total of 10 animals that completed the experiments were used in the final analysis. In 8 animals, the myocardial elastic modulus was independently measured by the pressure-segment length method. In 5 animals, measurements were performed before and after induction of a reperfused MI in the tested area. The effect of preload was assessed by comparing data at rest and peak volume loading in 8 animals; however, because of the rigid setup, reliable measurements at peak loading could be obtained in only 4 animals (1 normal, 3 with MI).

Global infarct size was <10% of the LVarea, and the transmural extent of infarction within the tested area was 62 ± 24%. Systolic shortening was 17.6 ± 5.0% at baseline and 1.2 ± 2.6% at reperfusion (p = 0.006). Hemodynamic parameters remained relatively constant during the experiment: heart rate (79 ± 8 beats/min vs. 88 ± 14 beats/min, baseline vs. reperfusion, respectively, p = 0.395), LV end-diastolic pressure (LVEDP, 11.4 ± 1.8 mm Hg vs. 13.6 ± 4.1 mm Hg, p = 0.269) and LV peak systolic pressure (77 ± 6 mm Hg vs. 80 6 ± mm Hg, p = 0.177).

Phase velocities

Wave velocities increased with frequency and were higher during systole (Fig. 2). At end-diastole, values ranged between 0.8 and 2.5 m/s in normal myocardium and were higher, on average, by ~60% at reperfusion. During systole, wave velocities ranged between 3.5 and 8 m/s in normal myocardium and changed, on average, only slightly at reperfusion (p = NS for most frequencies) (Fig. 2).

Fig. 2.

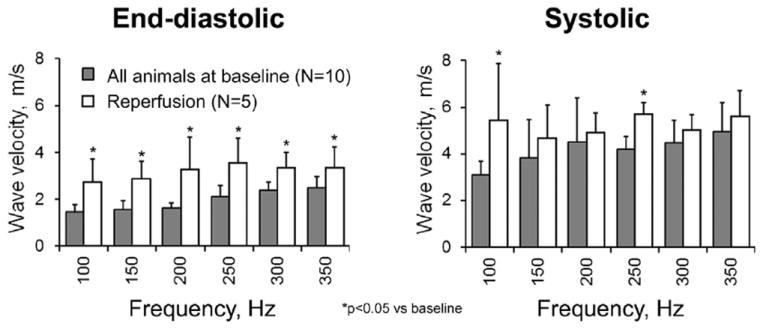
Wave velocities measured in normal and infarcted myocardium.

The repeatability of phase velocity measurement was high: The mean difference between five measurements was 0.11 ± 0.06 m/s (<6.5%) in the range 50–200 Hz and 0.24 ± 0.20 m/s (<9.5%) in the range 250–350 Hz.

Shear elasticity and viscosity

In Figure 3 are two examples of the variation in μ₁ and μ₂ in normal myocardium during the heart cycle. Figure 4 provides the average values from all animals. There was a consistent increase in μ₁ during systole versus diastole. The pattern of the change in μ₂ during systole was variable from animal to animal, particularly at baseline.

Fig. 3.

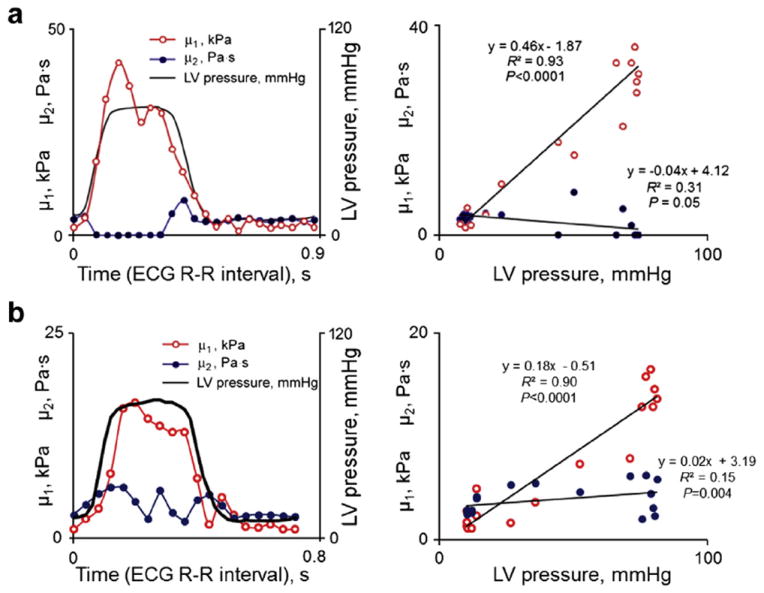
Two examples of the variation in shear elastic modulus (μ₁) and viscous coefficient (μ₂) through the cardiac cycle from two animals (a and b, left panels). μ₁ was consistently higher during systole than in diastole. In contrast, the variation in μ₂ during the cardiac cycle was more variable, with different patterns seen in different animals. (a and b, right panels) Corresponding correlations of μ₁ and μ₂ with left ventricular pressure. ECG = electrocardiography, LV = left ventricular.

Fig. 4.

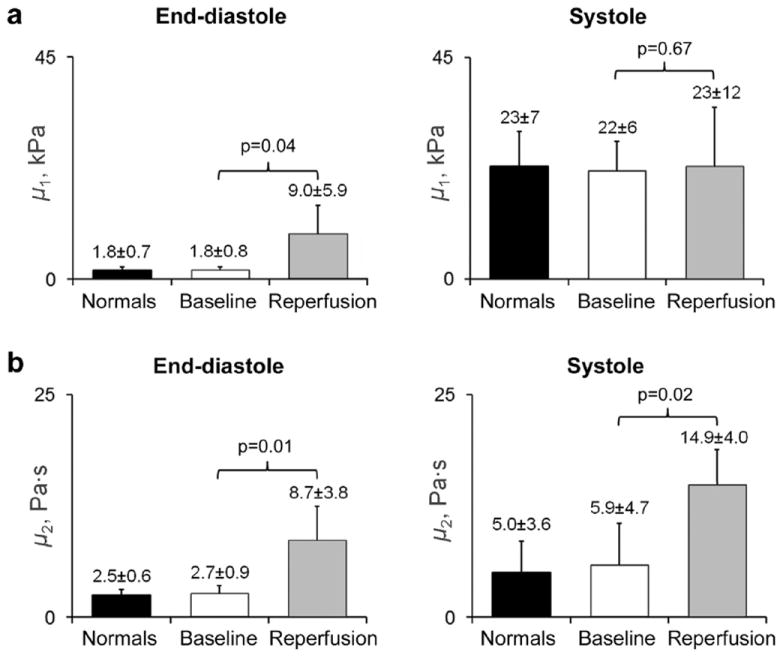
Average values of the shear elastic modulus, μ₁ (a), and viscous coefficient, μ₂ (b), in all animals. End-diastolic μ₁ and μ₂ and systolic μ₂ were higher at reperfusion than at baseline (normal myocardium). No differences were found for systolic μ₁.

At reperfusion, end-diastolic μ₁ increased significantly compared with baseline; however, changes in systolic μ₁ were less consistent (statistically non-significant). The systolic increment in μ₁ was borderline smaller at reperfusion (14 ± 8 kPa vs. 20 ± 6 kPa, respectively, p = 0.053). Conversely, μ₂ was higher at reperfusion during both diastole and systole (Fig. 4).

During the cardiac cycle, μ₁ correlated well with developed LV pressure in individual animals (Fig. 3b). The mean r² for all animals was 0.84 ± 0.10 at baseline and 0.87 ± 0.14 at reperfusion (p < 0.001 for all). The slope of this relationship was variable and did not reach statistical significance (range at baseline: 0.17–0.48, reperfusion: 0.03–0.41, p = 0.147). There was no consistent variation in μ₂ with LV pressure (normal animals: r² = 0.26 ± 0.54), except at reperfusion (r² = 0.88 ± 0.10, p < 0.05).

Comparison with independent method

There was a strong correlation between μ₁ and μ_PSL at end-diastole (r² = 0.895, p = 0.0003) (Fig. 5). The agreement between the two measurements was fair, with a mean difference ranging from −2.7 to +3.5 kPa (mean: −0.2 ± 1.9 kPa). The μ_PSL was higher at reperfusion than at baseline, at similar LVEDP levels.

Fig. 5.

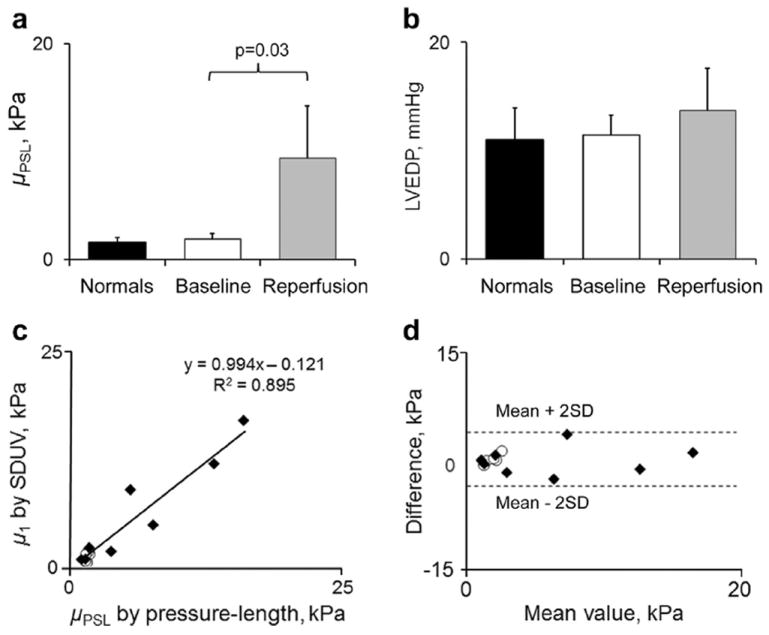
Pressure-segment length data. (a) Shear elastic modulus (μ_PSL) and (b) left ventricular end-diastolic pressure (LVEDP) in all animals. (c, d) Correlation and agreement between shear elastic modulus measured by shear wave dispersion ultrasound vibrometry (SDUV) and shear elastic modulus measured by the pressure-segment length method (Bland- Altman analysis). One data point represents one animal. Baseline values for animals with myocardial infarction (open symbols) are provided for comparison.

Analysis of individual end-diastolic stress-strain relationships confirmed the increase in passive myocardial stiffness at reperfusion (Fig. 6). In each animal, these relationships were steeper compared with baseline (higher β slope, p = 0.05) and shifted leftward, indicating altered tissue properties.

Fig. 6.

Stress-strain relationships at baseline/normal myocardium (black) and after reperfusion (red) and corresponding preload-independent coefficients of myocardial stiffness.

Effect of preload

Volume loading increased μ₁ and μ_PSL (Fig. 7a). For a 15 to 20 mm Hg rise in LVEDP, μ₁ increased by 0.5 kPa in the normal animal tested and by 5.8 ± 4.0 kPa in three animals with MIs. These results were confirmed by μ_PSL. Conversely, μ₂ did not change with loading in these animals.

Fig. 7.

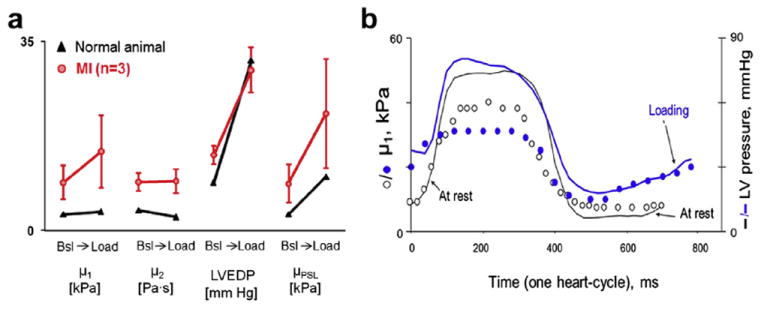
Effect of preload on shear wave parameters in four animals. (a) Compared with baseline (Bsl), shear elastic modulus (μ₁) increased at peak volume loading in three animals with myocardial infarction (MI) (red). This was confirmed by the independent method (μ_PSL). Very little change was seen in the normal animal (black), despite a similar change in left ventricular end-diastolic pressure (LVEDP). (b) Example of variation in μ₁ during the cardiac cycle in one animal with transmural infarct, at rest and at peak volume loading. At rest (open circles), μ₁ was 9.1 kPa at end-diastole. At peak volume loading (blue circles), μ₁ increased further during ventricular filling, concomitant with chamber pressure, reaching ~20 kPa at end-diastole. The corresponding μ_PSL values in this animal were 9.2 and 17.2 kPa, respectively.

A similar effect of loading was seen from analysis of single heartbeats. In Figure 7b is an example from an animal with a transmural MI. At rest, μ₁ was already high during mid- to late diastole (a period mostly influenced by loading and material properties). At peak volume loading, μ₁ increased further during ventricular filling, in parallel with LV pressure, suggesting an effect of preload on μ₁.

DISCUSSION

This is the first study to validate in vivo shear wave-based measurements of myocardial elasticity. We found that myocardial elasticity estimated in vivo by the shear wave method was comparable to elastic modulus measured by the invasive pressure-segment length method. The results also indicate that early after reperfusion for MI, infarcted myocardium has altered elastic and viscous properties, but these changes were most consistently apparent during diastole. However, like other classic measures of elasticity, shear elastic modulus measured by SDUV is preload dependent.

Sources of viscoelasticity

Myocardial elasticity and its changes with muscle contraction have been studied both in vitro and in vivo (Diamond and Forrester 1972; Little and Freeman 1987; Pirzada et al. 1978; Suga and Sugawa 1974). At end-diastole, the myocardium is relaxed, and passive characteristics are dominant. During systole, muscle stiffness increases as a result of activation of contractile apparatus (crossbridge formation) and changes in chamber pressure. Elasticity is responsible for energy storage (released as recoil), whereas viscosity contributes to energy loss caused by viscous friction. However, elasticity is the most sought after tissue property, because of the magnitude of changes occurring with disease and the consistency of findings and ease of measurement. Titin molecules, collagen fibers, microtubules and other intra-/extracellular components and external factors contribute to the overall viscoelasticity of the myocardial wall (Granzier and Irving 1995; Resar et al. 1993). Parameters measured here reflect their combined effect, and relative contributions cannot be separated.

Comparison of tissue elasticity measured by SDUV with that measured by the pressure-segment length method

In this study, myocardial elasticity was quantified using a shear wave method without measuring chamber pressure, which is an advantage for the non-invasive use of this type of technique. The stiffer the tissue, the faster is the speed of shear wave propagation. In this study, measurements compared well against the pressure-segment length method, supporting the fundamental soundness of the shear wave method. The correlation between the two techniques was strong, and the agreement was within acceptable limits. The results indicated that measurements of shear elasticity are able to track changes in tensile elasticity. It should be noted that a perfect correlation was not expected, particularly in the intact heart, as the two techniques are not strictly comparable and other factors can change this correlation (e.g., wall composition with respect to fiber direction, method for wall stress estimation, rheological model chosen to simulate mechanical properties of the tissue, assumptions made of tissue incompressibility, homogeneity). Most importantly, measurements correlated well, and the effect of acute intervention (MI) was clearly detected over a wide range of elasticity (>1-fold). The experimental error for wave velocity measurement was below the magnitude of changes occurring with the MI process, which increases confidence in the wave method.

Myocardial shear elasticity

The results from this study agree quantitatively with previous findings using other shear wave methods; however, new techniques require validation. With the same method, an end-systolic μ₁ of 24–30 kPa was estimated in ventricular septum of healthy volunteers (Kanai 2005). A μ₁ of 7.8–16.5 kPa (μ₂ of 5.9–8.3 Pa · s) was reported in excised bovine myocardium (Nenadic et al. 2011). Magnetic resonance elastography studies reported shear elastic moduli between 5 and 27 kPa during diastole and systole in normal patients (Rump et al. 2007). Other studies using supersonic shear wave imaging reported values between 2 and 30 kPa for diastole and systole, respectively, in an ovine model (Couade et al. 2011). Displacement or strain ratio was also employed as a means to detect localized (relative) stiffening of the myocardium (Luo et al. 2007; Pislaru et al. 2004). Shear wave speed can also be considered an indicator of tissue elasticity (Bouchard et al. 2009). Of note, only a few methods include a viscous term. Because wave speeds vary with frequency and are sensitive to boundary conditions (wall thickness), they need to be compared at similar frequencies and geometry.

In this study, infarcted reperfused myocardium was significantly stiffer (two to eight times) and more viscous (three to four times) than normal myocardium, consistent with previous observations using other (non-shear wave) techniques (Diamond and Forrester 1972; Hsu et al. 2007; Luo et al. 2007; Pirzada et al. 1978; Pislaru et al. 2004). Values of μ₁ > 4 kPa and μ₂ > 4 Pa·s fell outside the normal range for this animal model and physiologic levels of preload. Changes were confirmed by the independent method and load-independent indices of myocardial stiffness indicating genuine changes in tissue properties. However, like other classic measures of elasticity, μ₁ varied with preload.

Systolic elasticity

End-systolic elastance is a measure of myocardial contractility at chamber level (Burkhoff et al. 2005; Little and Freeman 1987; Suga and Sugawa 1974). Shear modulus estimated by other shear wave techniques was found to increase with contractility (Kolipaka et al. 2012; Pernot et al. 2011). Some discrepancies were also observed in vivo (Kolipaka et al. 2012). In the present study, in animals with MI, systolic μ₁ was either reduced, normal or increased compared with baseline. This result cannot reflect unchanged contractility, as these animals had persistent systolic dysfunction early after reperfusion due to a mixture of stunning and necrosis characteristic of this animal model. Potential explanations for these results could include the contribution of passive elasticity to systolic elasticity and alterations in loading and/or heart rate (though minimal) at reperfusion.

Chamber pressure can also modify myocardial elasticity. The present study extends previous reports on the direct relationship between myocardial elasticity and LV pressure in normal patients (Kolipaka et al. 2012; Rump et al. 2007) and also indicates that a similar relationship exists in animals with MIs. Thus, more complex interactions may be expected during systole.

Several factors may be responsible for the higher consistency of the results during diastole. The most obvious reason is that different factors operate during systole and diastole. Autonomic reflex responses and medication could also bring variations in cardiovascular conditions including contractility, heart rate, peripheral vascular resistance and afterload, which predominantly affect systolic properties. These responses should be amplified in the conscious state. Segment bulging during systole stretches the elastic elements and increases wall stiffness by a variable degree, depending on various factors and their complex interaction (e.g., blood pressure, tissue properties, chamber geometry, stroke volume). In addition, shear wave measurements are more accurate when tissue is stationary. Higher errors in faster moving tissue or stiff myocardium (systole) are also possible, as suggested by the high standard deviation for phase velocities during systole.

Shear viscosity

The multifrequency approach allowed estimation of viscous properties. Values for μ₂ were similar in magnitude to those reported for liver and skeletal muscle (Asbach et al. 2008; Bercoff et al. 2004; Chen et al. 2009), but smaller than those for ventricular septum in humans (Kanai 2005). With infarction, μ₂ increased several fold compared with that for normal myocardium and was highest during systole. It is unclear whether there is an impact of this property on cardiac function, as the effects previously described and attributed to viscosity were generally small (Nicolic et al. 1990; Rankin et al. 1977; Templeton and Nardizzi 1974). The different definitions and experimental conditions used make comparisons between studies more challenging. The incremental value of the viscous term remains to be proven. In this study, μ₂ was three orders of magnitude smaller than the elastic term, in both normal and infarcted myocardium. Nevertheless, at physiologic heart rates, the impact of tissue viscosity is expected to be low (negligible). At frequencies used by the shear wave methods (100–1000 Hz), neglecting the viscous term may overestimate the elasticity.

Effect of preload

Although preliminary, the results obtained with volume loading deserve attention. It was found that μ₁ increases with preload, particularly in animals with MI. The increase in μ₁ indicates non-linear material properties, which is expected from the exponential stress-strain relationship characteristic for the myocardium. A large increase suggests a progressively steeper slope of the stress-strain relationship. This is characteristic of diseased (stiff) myocardium and high preload levels. Conversely, a small change in μ₁ seen in the normal animal suggests an almost linear stress-strain relation and is consistent with a highly compliant tissue such as normal myocardium at low pre-load levels. Analysis of μ₁ during diastole from single heartbeats led to a similar conclusion on the effect of loading; however, single-beat methods are less recommended. Current results agree with recent findings from magnetic resonance elastography studies reporting similar magnitudes of changes in shear modulus with loading in four normal pigs (~2–4 kPa) (Kolipaka et al. 2011); however, no diseased animals were tested in that study. In contrast to the elastic term, μ₂ did not change with preload.

Clinical significance

Non-invasive measurements of myocardial elasticity (viscoelasticity) using transthoracic ultrasound and magnetic resonance imaging (Elgeti et al. 2010; Muthupillai et al. 1995; Rump et al. 2007; Vappou 2012) are now under development and will facilitate clinical implementation. Recent results in seven healthy volunteers indicate that shear wave measurements in the heart using transthoracic ultrasound imaging are possible (Song et al. 2013). However, the technique is not yet available for clinical testing using commercial ultrasound systems. An intracardiac application of shear wave measurements of the myocardium is also being explored (Hollender et al. 2012). The clinical impact of these measurements can be anticipated. LV/myocardial stiffening occurs in several cardiovascular conditions, such as heart failure with normal ejection fraction (Braumwald et al. 1992; Burlew and Weber 2002; Kawaguchi et al. 2003; Westermann et al. 2008; Zile et al. 2004). LV stiffening may contribute to elevated filling pressures and exercise limitation in these patients. These measurements may have the potential to facilitate earlier detection of changes with pathology and allow monitoring of the effect of medical therapies in individual patients.

Limitations

In this study, an invasive setup was used to validate a concept in controlled conditions, which was the goal of the study. The actuator was employed to produce tissue displacements of sufficient magnitude (10–100 μm) required for robust motion tracking using the techniques available to us at the time of the study. Using specific frequencies with an actuator also increased the signal-to-noise ratio for wave detection. The SonixRP was used in this study did not have enough power to generate focused ultrasound with sufficient intensity to move the cardiac tissue. Using an additional external transducer to create the radiation force would have been cumbersome. However, recent findings indicate that shear waves can also be induced transcutaneously using ultrasound radiation force, and shear wave propagation can be measured by the same transducer (Song et al. 2013). New scanners (Verasonics, Redmond, WA, USA) can produce higher tissue displacements (higher power output) allowing non-invasive and faster measurements. Regardless of the system used for induction of shear waves, the fundamental principle is the same. The strengths and limitations of the SDUV technique were discussed elsewhere (Chen et al. 2009; Kanai 2005; Nenadic et al. 2011; Urban et al. 2013).

There was no systematic interference on the linear array transducer while imaging the heart or when processing the shear wave data. The signal from the piezocrystals (1.2 MHz resonant frequency) was outside of the useful bandwidth of the transducer used (5 MHz center frequency, 65% fractional bandwidth). However, there was a small interference in the sonomicrometry signal during the shear wave data acquisition. For this reason, we used the data immediately after the shear wave data acquisition ended. Thus, measurements were not simultaneous but close enough (5 s apart) to assume constant tissue properties.

The absolute values obtained with an open-chest preparation do not necessarily translate to closed chest and intact pericardium. However, a major goal was to validate a new technique against a current gold standard that required invasive measurement of pressure and segment lengths. A small area of infarction was created to avoid changes in hemodynamics; however, altered loading conditions may occur in patients with extensive MI. Measurements were performed only in one segment (average through thickness) and along one direction (longitudinally), which reproduced a common scenario for measurements in patients. Nevertheless, stiffness varies with fiber direction, as confirmed by shear wave techniques (Couade et al. 2011).

The pressure-segment length method has its own limitations, which include its invasive nature, the assumptions made (local homogeneity, tensile deformation with no shearing deformation, negligible viscosity) and the errors associated with wall stress estimation.

The viscous coefficient was not validated because of the lack of an established gold standard. Changes with loading are reported in only four animals; however, the trends were clear and concur with previous studies using magnetic resonance elastography (Kolipaka et al. 2012) and exponential stress-strain theory for the myocardium.

CONCLUSIONS

In this large animal model, measurements of passive myocardial elasticity quantified by a multifrequency shear wave method were correlated with elastic modulus measured by the invasive pressure-segment length method. Shear wave estimates of myocardial shear elasticity and viscosity in reperfused acute myocardial infarction were highly abnormal compared with those for normal hearts; however, differences were most apparent during diastole. Shear wave estimates varied with left ventricular chamber pressure both during systole and diastole. The results are relevant for non-invasive quantification of myocardial elasticity.