Absolute quantification by droplet digital PCR versus analog real-time PCR

Abstract

Nanoliter-sized droplet technology paired with digital PCR (ddPCR) holds promise for highly precise, absolute nucleic acid quantification. Our comparison of microRNA quantification by ddPCR and real-time PCR revealed greater precision (coefficients of variation decreased by 37–86%) and improved day-to-day reproducibility (by a factor of seven) of ddPCR but with comparable sensitivity. When we applied ddPCR to serum microRNA biomarker analysis, this translated to superior diagnostic performance for identifying individuals with cancer.

Traditional digital PCR¹ is a method of absolute nucleic acid quantification based on the partitioning of individual analyte molecules into many replicate reactions at limiting dilution, resulting in one or zero molecules in most reactions. After endpoint PCR, the starting concentration of template is determined by Poisson statistical analysis of the number of positive (containing amplified target) and negative (no amplified target detected reactions. The digital PCR concept² has many potential advantages over real-time PCR, including the capability to obtain absolute quantification without external references and robustness to variations in PCR efficiency³. Recently, technology has become commercially available that permits reactions to be partitioned into nanoliter-sized, aqueous droplets in oil rather than multiwell plates. Rapid microfluidic analysis of thousands of droplets per sample^4,5 makes ddPCR practical for routine use. In addition, the practical dynamic range of the system is substantially improved by using highly uniform droplets, which (with Poisson correction for multiple target molecules per droplet) enable the precise calculation of concentrations even above conditions of limiting dilution^4,5.

Data regarding the empirical operating characteristics of ddPCR versus real-time PCR including technical precision, sensitivity, accuracy and day-to-day reproducibility are scant. A recent study had suggested comparable performance of the two methods but was limited to a single target in one background matrix and revealed contradictory performance in analyses of laboratory standards versus clinical specimens⁶. Here we report a systematic comparison of ddPCR and real-time PCR performance, using a range of synthetic targets, different background matrices, as well as low-target-abundance biological samples. We focused on the quantification of cDNAs corresponding to microRNAs (miRNAs), which are small regulatory RNA molecules with diverse cellular functions⁷. miRNAs also exist in highly stable extracellular forms in the vascular circulation^8,9 with potential hormonal function¹⁰ and can be useful as blood-based biomarkers for cancer⁸ and other diseases¹¹.

We used serial dilutions of synthetic oligoribonucleotides (Supplementary Fig. 1 and Supplementary Table 1) representing six different mature human miRNAs: miR-141, miR-375, miR-210 (circulating miRNA cancer biomarkers^8,12,13), miR-135b, miR-205 (tissue-based cancer biomarkers^14,15) and miR-16 as a broadly expressed control. To assess variation at different stages of the procedure (preparation of serial dilution, reverse transcription (RT) and PCR), we used a hierarchical experimental design of nested replicates (Supplementary Fig. 1). For each miRNA, we prepared a twofold dilution series and reverse-transcribed it in triplicate. We analyzed each RT reaction in triplicate by ddPCR and real-time PCR, using aliquots of the same PCR reaction mixture. We replicated this entire workflow in triplicate, with individual dilution series replicates prepared on different days. Furthermore, we prepared each dilution series using, in parallel, water and plasma RNA from a healthy donor in solution as diluents, to determine performance in the setting of pure template as well as in a complex background matrix.

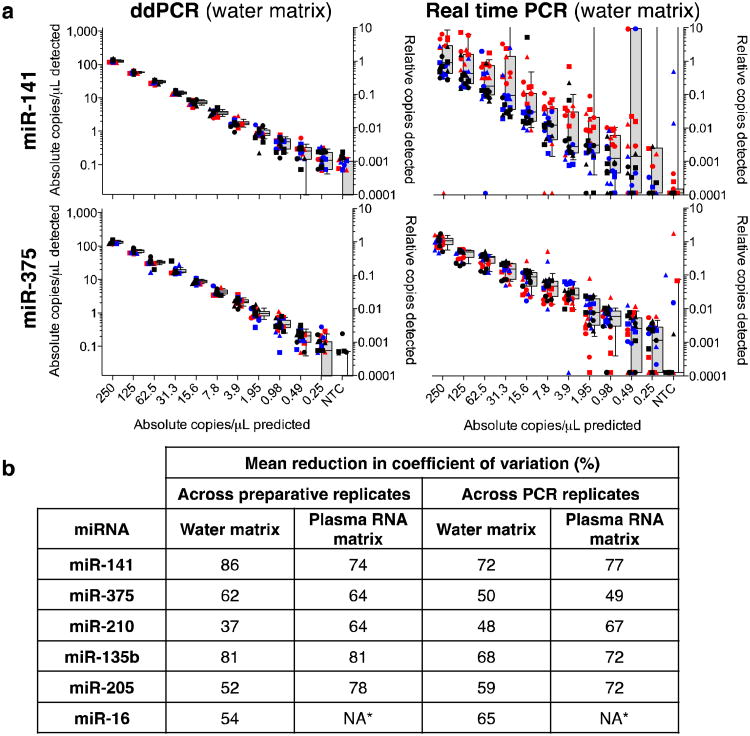
In the water matrix, ddPCR reduced mean coefficients of variation (CVs) 37–86% compared to real-time PCR with respect to overall variation (Fig. 1a,b) and 48–72% with respect to PCR-specific variation (Supplementary Table 2). ddPCR consistently displayed lower variation than real-time PCR for all miRNAs tested, in both matrices (Fig. 1a and Supplementary Fig. 2) and whether calculated across PCR replicates, RT replicates or serial dilution preparation replicates (Supplementary Figs. 3–6, and Supplementary Tables 2 and 3). However, ddPCR was not uniformly more sensitive compared to real-time PCR across the six microRNAs examined (Supplementary Tables 4 and 5). As an additional performance metric that cannot be examined using real-time PCR, we noted that absolute measurements by ddPCR corresponded to 49–114% of the theoretically input copies (Supplementary Table 6), indicating that absolute detection by ddPCR is remarkably efficient.

Figure 1.

Quantification of synthetic miRNA oligonucleotides by ddPCR and real-time PCR. (a) Comparative analysis of dilution series of indicated miRNAs in water. Each color represents one preparative (independent preparation of a dilution series) replicate and each shape represents individual RTs. (RT 1, circle; RT 2, square; and RT 3, triangle). Box and whisker plots (gray) show median (center line), 25^th and 75^th percentiles (box), and 10^th and 90^th percentiles (whiskers). NTC: No Template Control. (b) Reduction in CV, measured as (CV_{real-time PCR} – CV_ddPCR)/(CV_{real-time PCR}). *, endogenous abundance of miR-16 in plasma RNA was higher than the maximum concentration of synthetic oligonucleotide examined.

To compare the diagnostic sensitivity and specificity of ddPCR versus real-time PCR on clinical serum samples, we collected sera from 20 patients with advanced prostate cancer and from 20 age-matched, healthy male controls, and measured the abundance of miR-141, which has been shown to be elevated in the serum of patients with advanced prostate cancer^8,12. We analyzed aliquots of cDNA corresponding to the serum RNA samples using our ddPCR workflow and, in parallel, a current standard real-time PCR method widely used for serum miRNA biomarker analysis¹⁶, in triplicate on three different days (Fig. 2a and Supplementary Fig. 7). We also analyzed aliquots of the ddPCR master mix for each reaction in parallel by real-time PCR (Fig. 2a), in similar fashion to the previous experiments analyzing synthetic miRNAs. In the analysis of synthetic miR-141 standard curves run in parallel, ddPCR showed greater precision (Supplementary Fig. 8) but was not more sensitive (Supplementary Table 7), consistent with the results presented above (Fig. 1 and Supplementary Tables 2 and 4).

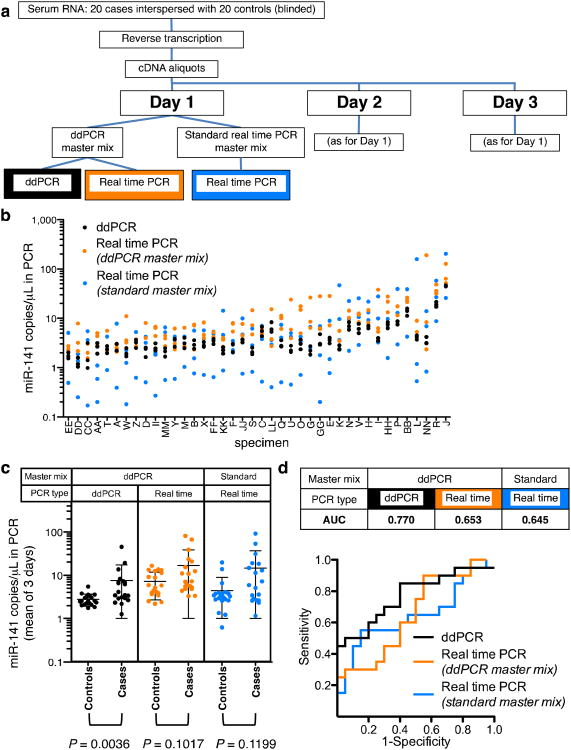
Figure 2.

Quantification of circulating miRNA biomarker in clinical serum samples by ddPCR and real-time PCR. (a) Workflow used to measure the abundance of a circulating miRNA biomarker in clinical samples. (b) Replicate analyses of serum-derived miR-141 over 3 d. Data represent metawell analysis of three ddPCR replicates per day or the means of three real-time PCR replicates per day (individuals are sorted on the x-axis by mean abundance of ddPCR values). See Supplementary Data for key to specimen identifiers. (c) Data from b presented as the means of results over 3 d for cases and controls. Over the dot plots, central lines indicate the mean; error bars, s.d. (n = 20) P values: Mann-Whitney test, two-tailed. (d) ROC curve analysis of data in c.

Absolute quantification by ddPCR reduced variation in measurement of miR-141 in clinical serum samples by an average factor of seven relative to standard real-time PCR (Fig. 2b, and Supplementary Tables 8 and 9). Although all three methods detected higher average miR-141 abundance in the serum RNA of cases (prostate cancer patients) than in controls, ddPCR better resolved cases from controls (Fig. 2c), and in a nonparametric analysis, the difference reached statistical significance (Mann-Whitney test, P = 0.0036), whereas statistical significance was not reached in a real-time PCR analysis of the ddPCR mixture (P = 0.1017) or standard real-time PCR in this sample set (P = 0.1199). Receiver operating characteristic (ROC) analysis revealed that ddPCR more accurately classified case versus control specimens (Fig. 2d), as reflected by an increased area under a ROC curve (AUC of 0.770 for ddPCR versus AUC of 0.653 for the ddPCR mixture analyzed by real-time PCR and AUC of 0.645 for standard real-time PCR).

We speculate that ddPCR may also be more resilient to differences in sample quality; by virtue of being an end-point approach, it is more tolerant to PCR inhibitors, which affect amplification efficiency. Furthermore, although our study focused on cDNAs reverse-transcribed from miRNAs, it fundamentally represents a characterization of the empirical operating characteristics of ddPCR versus real-time PCR and should be relevant to a broad variety of applications where high-performance quantification of nucleic acid targets is required.

Online Methods

General procedure for generation of miRNA standard curves

Six RNase-free, HPLC-purified 5′-phosphorylated miRNA oligoribonucleotides were synthesized (Integrated DNA Technologies) for the analytical portion of this study, corresponding to hsa-miR-16 (5′-phospho-UAGCAGCACGUAAAUAUUGGCG-OH-3′), hsa-miR-141 (5′-phospho-UAACACUGUCUGGUAAAGAUGG-OH-3′), hsa-miR-135b (5′-phospho-UAUGGCUUUUCAUUCCUAUGUGA-OH-3′), hsa-miR-205 (5′-phospho-UCCUUCAUUCCACCGGAGUCUG-OH-3′), hsa-miR-210 (5′-phospho-CUGUGCGUGUGACAGCGGCUGA-OH-3′) and hsa-miR-375 (5′-phospho-UUUGUUCGUUCGGCUCGCGUGA-OH-3′). Stock solutions of 10 μM synthetic oligonucleotide in RNase-free/DNase-free water were prepared according to the concentrations and sample purity quoted by the manufacturer (based on spectrophotometry analysis). To minimize uncertainty resulting from pipetting, all dilutions where the volumetric dilution factor exceeded 2× (see Supplementary Table 1, dilutions 1–4) were performed on an analytical balance, such that the predicted copies going into the standard curves could be accurately⁵ scaled using a gravimetric dilution factor. All further dilutions for the standard curve (Supplementary Table 1, dilutions 5–11) were performed volumetrically. Approximately 5–5,000 copies per 20 μl PCR reaction with nine intermediate twofold serial dilutions and additional no template controls (NTCs; zero copies) were examined. Dilution series for each of the synthetic miRNAs were made in either RNase/DNase-free H₂O or in healthy human donor plasma RNA solution to provide a constant background of endogenous miRNAs. Our modified procedure used for isolating miRNAs from plasma with miRNeasy kits (Qiagen) has been described previously¹⁶. To ensure a homogenous plasma RNA solution for use as diluent, multiple plasma RNA extraction batches collected using this protocol¹⁶ were pooled and mixed by gentle pipetting, then divided into 60-μl aliquots and stored at −80 °C until use. All experiments for this work were conducted at the Fred Hutchinson Cancer Research Center.

Procedure for reverse transcription–ddPCR and reverse transcription–real-time-PCR

RT of input miRNAs (Supplementary Table 1, dilutions 5–11) was conducted using reagents from the TaqMan miRNA Reverse Transcription Kit and 60× target-specific RT primers (both from Applied BioSystems, Inc.). The kit contains the following components that, together with the stem-loop primers and RNase/DNase-free H₂O, comprise what is forthwith referred to as ‘RT mix’ (numbers in parentheses are final volumes in a 10-μl RT reaction containing 8 μl RT mix): 10× RT buffer (1 μl), RNase inhibitor (0.12 μl), 100 mM each dNTP (0.1 μl), Multiscribe reverse transcriptase (0.66 μl), 60× RT primer (0.17 μl), RNase/DNase-free H₂O (5.95 μl). The volumetric ratio of RT mix to input miRNA solution was 4:1, and triplicate 10 μl RT reactions (Supplementary Fig. 1) for each point of the curves were taken from a corresponding well-mixed stock solution of a given concentration (34 μl total volume; 7 μl input miRNA). The reverse transcription thermal-cycling procedure for triplicate 10 μl RTs used holds at 16 °C for 30 min, then 42 °C for 30 min and 85 °C for 5 min (Tetrad2 Peltier Thermal Cycler; Bio-Rad). 7 μl of RT product for each concentration was thoroughly mixed by pipette resuspension with 133 μl solutions containing Master Mix (Bio-Rad, 70 μl of 2× mix), the target-specific TaqMan Real Time PCR primer probe set (Applied Biosystems, 2.33 μl of 60× solution) and RNase/DNase-free H₂O (60.67 μl). From this bulk solution, triplicate PCR reactions were carried out using both ddPCR (20 μl PCR reaction) and real-time PCR (5 μl PCR reaction), such that both ddPCR and real-time PCR reactions had identical concentrations of synthetic miRNA oligonucleotides. Real-time PCR experiments were performed on an Applied Biosystems Viia 7 instrument with the following thermal-cycling procedure; 95 °C for 10 min, followed by 40 cycles of 95 °C for 15 s and 60 °C for 1 min (1.6 °C/s ramp rate) as specified in the TaqMan MicroRNA Assay protocol provided by the manufacturer (Applied Biosystems).

To provide the best possible analysis of the raw real-time PCR data for comparison to ddPCR, real-time PCR data collected in this manner were analyzed with the Viia 7 instrument software v1.0 using three separate conventional approaches^3,17 and compared side by side to deduce which method gave the lowest variability (data not shown). When using the first method, we examined the effect of using a universal baseline and threshold to aid data consistency across the study. The baseline was set between 8 cycles and 20 cycles (to base this on the background signal found in early cycles of amplification) with a manual fluorescence threshold of 20,000 Relative Fluorescence Units (RFUs) with ROX (carboxy-x-rhodamine passive reference dye) normalization disabled (ddPCR master mix does not contain ROX dye). In the second method, the threshold was manually set by the operator to exclude spurious noise and intersect the exponential amplification portion of the fluorescence curve as centrally as possible. ROX normalization was disabled. The third method used the Viia 7 signal processing algorithm to automatically call baseline and threshold, with ROX normalization disabled. Method 3 was found to give the lowest variability between PCRs, and therefore this method was used for analysis of all data derived from real-time PCR analysis of ddPCR reaction mixtures. Note that data derived from the standard real-time PCR protocol (i.e., used to analyze clinical specimens) was analyzed using its corresponding data analysis procedure⁸, which was identical to method 3 above with the exception of inclusion of ROX normalization. Curves that did not show typical exponential amplification morphology were included in the presentation of the whole data (Fig. 1a and Supplementary Fig. 2) but were excluded from subsequent summary operating characteristic and statistical analysis (Supplementary Figs. 3–6 and Supplementary Tables 2–5) to provide the best possible estimate of real-time PCR performance. Undetermined cycle thresholds were arbitrarily set to 40 as a limiting estimate of the maximum possible abundance of target. Target abundance relative to the mean of highest concentration tested was determined by Pfaffl analysis of the cycle-threshold (Ct) data¹⁸, using the empirically determined PCR efficiency for each miRNA. In the case of the standard curves generated for the analysis of clinical specimens, results are presented as the mean of real-time PCR triplicates.

Limit of quantification (LOQ) was defined as the lowest concentration tested that remained above or equal to the lower limit of linear range of the assay (LLLR) and above or equal to the limit of detection (LOD). Linear range was determined by runs-testing¹⁹, removing successive dilution points until the P value was >0.05, indicating no significant deviation from linearity (Prism Version 5.0c software). LOD was defined as <x>_bi + ks_bi, where <x>_bi equals the mean of the no-template controls, s_bi is s.d. of no-template controls, and k = 2.479 (99% confidence interval)²⁰.

The ddPCR system, workflow, operating characteristics and analytical performance has been recently described in detail by some of the authors of this paper in two recent publications^4,5, but a brief summary of this technology follows. At the start of these studies, the instrument and reagents used were manufactured by Quantalife, Inc., which was subsequently acquired by Bio-Rad, Inc., which is the current manufacturer and distributor. Each 20 μl PCR reaction (see above) was loaded into an 8-channel, single-use consumable droplet generation cartridge. 60 μl of oil containing emulsion-stabilizing, biocompatible surfactant was loaded into adjacent oil wells, and the microfluidic chip was loaded into a beta-series prototype droplet generator (DG). The DG applies a vacuum to the outlet well creating a pressure difference across the cartridge that simultaneously partitions the sample present in each of the 8 wells into ∼20,000 monodisperse droplets of accurately known volume. This process occurs at a rate of ∼1,000 droplets/s per well. The resulting water-in-oil emulsions were pipette-transferred from the outlet well to a 96-well polypropylene plate (Eppendorf), sealed with foil and then amplified to endpoint using a Tetrad2 Peltier Thermal Cycler (Bio-Rad) and the cycling protocol: 95 °C for 10 min then 40 cycles of 95 °C for 15 s and 60 °C for 1 min (2.5 °C/s ramp rate) with a final 10 min hold at 98 °C. Plates containing amplified droplets were loaded into an early-access, beta-version of the commercially available QX100 droplet reader (Bio-Rad), which aspirates droplets from the 96-well plate, one well at a time, and streams them single-file (∼1,500 droplets/s) past a two-color FAM/VIC (FAM and VIC fluorescence dyes, Life Technologies Corp.) detector sampling at 100 kHz. Discrimination between droplets that did not contain target (negatives) and those that did (positives) was achieved by applying a global fluorescence amplitude threshold. For all of the miRNA assays, the global fluorescence threshold was set at 4,000 relative fluorescence units (RFUs) regardless of the assay efficiency. Concentration estimates (λ) were based on the fraction of droplets where amplification has occurred (p) modeled as a Poisson distribution (equation (1)).

$$\lambda =-ln(1-p)$$ (1)

Because each droplet is an independent PCR reaction vessel of equal and defined volume, the droplets of technical replicates (triplicate wells) can be pooled to create a ‘metawell’. To compute total ± 95% confidence intervals about concentration estimates of metawells (comprised of previously described^21,22 Poisson ± 95% CIs and ‘real world error’; concentration differences between wells) we applied the following meta-analysis techniques. Given k replicates with concentrations m₁, m₂, … m_k and Poisson variances v₁, v₂, … v_k, respectively, we define the weight (w) of replicate i as reciprocal of its variance as

$$w_i=\frac{1}{v_i}$$ (2)

Let m̅ be the weighted average of concentrations and consider the following random variable that measures fluctuation of concentrations around this weighted mean:

$$T={\sum }_{i=1}^k{w}_i{(m_i-\overline{m})}^2$$ (3)

This is the sum of squares of approximately standard normal random variables and can therefore be approximated as a chi-squared distribution. The mean of the distribution is the number of degrees of freedom (df = k – 1). If T is less than df, we say that there is no additional real-world variance. If T is more than df, then it suggests there is additional real-world variance r = T – df. As T is based on standard normal variables, we scale back r to r′ in original units after applying an appropriate correction factor:

$$r\prime =\frac{r}{\sum w_i-\frac{\sum w_i^2}{\sum w_i}}$$ (4)

We can add r′ to Poisson variance to give total variance for each replicate. We redefine the weight of each replicate as:

$$w_i=\frac{1}{v_i+r\prime }$$ (5)

from which we can compute the total uncertainty around the metawell as

$$v=\frac{1}{\sum w_i}.$$ (6)

The final estimate m̅ is recomputed as weighted average of concentrations with new weights. By setting r′ to 0, we will get estimate of v in presence of only Poisson error. This meta-analysis is a statistically rigorous method to test the existence of real-world error in a group of replicate droplet digital PCR wells (US Patent Application 20130017551). All of these data-analysis methods are implemented in the Quantasoft (1.1.1.0) data analysis package, installed with the droplet reader.

Procedure for the quantitation of miR-141 in clinical specimens

Human serum samples from individuals with metastatic prostate cancer and prostate-cancer–negative controls were collected after written informed consent was obtained. All participants signed a University of Washington Human Subjects Committee approved Informed Consent Form for a peripheral blood draw and the research was approved and supervised by the University of Washington and Fred Hutchinson Cancer Research Center Institutional Review Boards. Prostate-cancer–negative donors were recruited among individuals undergoing screening for prostate cancer and found to be negative by digital-rectal examination (DRE) and serum PSA analysis. Individuals with metastatic prostate cancer were recruited among previously diagnosed patients undergoing treatment at the University of Washington (Seattle). Procedures for sample collection, pretreatment and RNA extraction have been described previously¹⁶. The same protocol was adopted here without modification. In this study, a smaller cohort of clinical specimens corresponding to n = 20 advanced prostate cancer cases and n = 20 healthy controls was analyzed (previously, n = 25 each group). The patient specimens studied here were distinct from (not a subset of) those we studied previously⁸. Using the population-variance data from the previous study, we performed a power calculation and determined that n = 12 individuals per group would result in 81% power to detect a difference in means of fourfold (alpha = 0.05, two tails). We chose to analyze specimens from n = 20 individuals per group, as this was above the minimum predicted by the power calculation, feasible and simplified the technical work relative to the previous study. The experimenter was kept blinded to case status (i.e., cancer versus control).

For comparing the performance of ddPCR to real-time PCR in the clinical specimens, we used the standard real-time PCR method that we previously described¹⁶. Synthetic miR-141 standard curves used in this portion of the study were made using MS2 carrier RNA, which leads to improved circulating miRNA precision in real-time PCR analyses²³ and therefore was included to provide the best possible real-time PCR performance to compare with ddPCR. ddPCR showed superior precision (Supplementary Fig. 8), consistent with our results displayed in Figure 1a,b and comparable limits of quantification (Supplementary Table 7) for miR-141 in the analyses of these standard curves. Owing to limited serum RNA volume for the large number of replicates needed for this study, we diluted the initial serum RNA specimens by a factor of 1.5. To allow a direct comparison of performance between ddPCR (which uses Bio-Rad ddPCR Supermix for Probes, 186-3010) and standard circulating miRNA real-time PCR (which uses ABI Taqman Universal PCR MasterMix no UNG, 4326614), differences in the reagent volumes used between the Bio-Rad ddPCR and the standard circulating miRNA real-time PCR protocols needed to be accommodated to achieve the same concentration of cDNA in each comparable reaction across the methods (Supplementary Fig. 7). As a result of these necessary adjustments, the concentration of input cDNA analyzed per reaction for both ddPCR and real-time PCR methods was ultimately about tenfold lower than that used previously⁸. After reverse transcription, the cDNAs corresponding to the sets of standard curves (Supplementary Fig. 8) and the 40 clinical specimens (Fig. 2) were each split into six aliquots for subsequent PCR reactions (see below). Three of these six cDNA aliquots were added to ABI master mix for subsequent real-time PCR, and the remaining three were added to Bio-Rad mastermix to conduct ddPCR and real-time PCR (Fig. 2). The prepared 100 μl ddPCR master mix for each sample was divided into three 20 μl aliquots for analysis by ddPCR and three 5 μl aliquots for analysis by real-time PCR. The prepared 20 μl standard real-time PCR master mix for each sample was divided into 3 × 5 μl aliquots for analysis by real-time PCR (Fig. 2 and Supplementary Fig. 7). For the analysis of clinical specimens, ddPCR triplicates were combined into a single metawell before Poisson analysis and recovery correction by Caenorhabditis elegans recovery-yield miRNA spike-ins¹⁶. For real-time PCR, the concentration of analyte was calculated by Ct comparison to the standard curve, and results were presented as the mean of the PCR triplicates corrected by C. elegans spike-ins¹⁶. Statistical significance was determined by Mann-Whitney analysis (95% confidence intervals, two tails) and receiver operating characteristic (ROC) analysis was performed using Prism 5.0c software.

Supplementary Material

Supplementary Figure 1| Detailed schematic diagram of workflow to determine ddPCR operating characteristics relative to real time PCR. Standard curves were prepared by two -fold serial dilution (Supplementary Table 1) of synthetic miRNA stock oligonucleotides into either water or plasma RNA solution background matrices. Each dilution series contained a no -template control (matrix only) as a final point. Reverse transcription (RT) of each standard curve was performed in triplicate followed by triplicate analysis of each RT by both ddPCR and real time PCR. The gradient of shading in the plate row icons represents the standard curve concentration gradient. The same homogenous reaction mixture (cDNA + mastermix + primers/probe) was used for ddPCR and real time PCR, thus affording an analysis-platform-specific comparison of the two methods. For each of the six miRNAs studied here, the entire workflow including preparation of standard curves was repeated three times. Complete experimental details are given in Methods.

Supplementary Figure 2| miRNA quantification by ddPCR and real time PCR. The graphs show side-by-side results generated from ddPCR and real time PCR analysis of dilution series of representative synthetic miRNA oligonucleotides in water or plasma RNA matrices. For each miRNA, the results are organized by color, where each color represents one replicate (preparation) of the complete workflow outlined in Supplementary Figure 1 and shape represents PCR reactions de rived from individual RTs (RT1 = circle, RT2 = square, RT3 = triangle). This amounts to nine PCRs per color for each point of the standard curve (1 preparation × 3 RTs × 3 PCRs). ddPCR data is presented as absolute concentration measured (left -axis) and relative concentration normalized to the mean average of all data for dilution point 1 (right -axis). As absolute quantification is not possible by real time PCR, results are displayed as relative concentration normalized to the mean average of all data for dilution point 1 and transformed from cycle -threshold (Ct) space to linear space by Pfaffl -analysis utilizing the empirically determined PCR efficiency of each assay. Real time PCR reactions of undetermined Ct were assigned Ct = 40. Relative (normalized) r esults between ddPCR and real time PCR analysis are therefore directly comparable on the graphs. The statistical parameters used to generate the box and whisker plots (gray) for the combined data were median (center line), 25 ^th and 75^th percentiles (box), 10^th and 90^th percentiles (whiskers). Some clear outliers corresponding to failed replicate wells of real time PCR (e.g. miRNA-135b plasma RNA matrix) were excluded from subsequent computation of analytical figur es of merit given in Supplemental Figures 3-6 and Supplemental Tables 2-5. *Note: The obscured dilution response for miR -16 is because this miRNA is present endogenously in plasma RNA at levels above the maximum synthetic oligonucleotide input.

Supplementary Figure 3| ddPCR displays consistently lower variation than real time PCR. Coefficients of variation determined for both methods for each of the eleven oligonucleotide standard curve dilution points are displayed. Coefficient of variation measured at the level of PCR (across -PCR %CV) was determined by calculating the s.d. within each set of PCR triplicates (n = 9), dividing each of these by their respective mean values and then expressing the result as the overall mean of these individual %CV estimates. %CV measured at the level of reverse transcription (across-RT %CV) was determined by calculating the s.d. across all PCR data derived from a set of RT triplicates (n = 3), dividing this by the corresponding mean and then expressing the result as the mean of these individual %CV estimates. %CV measured at the level of preparation (across-preparation %CV) was determined by calculating the s.d. across all the PCR data derived from the three preparative replicates, dividing the result by the corresponding mean and expressing this value. The data clusters consistently above the line of identity, showing consistently higher %CV in the case of real time PCR. Note: %CV for real time PCR was calculated using linear-scale values (relative quantification) rather than Ct values in order to be directly comparable to ddPCR %CV as ddPCR data is ou tput on a linear scale. Therefore real time PCR %CV values displayed here are higher than if calculated using Ct values.

Supplementary Figure 4| ddPCR and real time PCR variation is dependent upon analyte concentration. Coefficient of variation at the level of PCR (across -PCR %CV) was determined by calculating the s.d. within each set of PCR triplicates (n = 9), dividing each of these by their respective mean values and then expressing the result as the overall mean and s.d. of these individual %CV estimates. %CV at the level of reverse transcription (across-RT %CV) was determined by calculating the s.d. across all PCR data derived from a set of RT triplicates (n = 3), dividing this by the corresponding mean and then expressing the result as the mean and s.d. of these individual %CV estimates. %CV at the level of prepar ation (across-preparation %CV) was determined by calculating the s.d. across all the PCR data derived from the three preparative replicates, dividing the result by the corresponding mean and expressing this value. Note: %CV for real time PCR was calculated using linear-scale values (relative quantification) rather than Ct values in order to be directly comparable to ddPCR %CV as ddPCR data is output on a linear scale. Therefore real time PCR %CV values displayed here are higher than if calculated using Ct v alues.

Supplementary Figure 5| ddPCR shows consistently lower variation relative to real time PCR measured across-PCR, across-RT or across-preparation replicates (water matrix). Mean %CV data from Supplementary Figure 2 presented in trendline format with ddPCR and real time PCR data plotted on opposing y -axes and a common x-axis. Note: %CV for real time PCR was calculated using linear-scale values (relative quantification) rather than Ct values in order to be di rectly comparable to ddPCR %CV as ddPCR data is output on a linear scale. Therefore real time PCR %CV values displayed here are higher than if calculated using Ct values.

Supplementary Figure 6| ddPCR shows consistently lower variation relative to real time PCR measured across-PCR, across-RT or across-preparation replicates (plasma RNA matrix). Mean %CV data from Supplementary Figure 2 presented in trendline format with ddPCR and real time PCR data plotted on opposing y-axes and a common x-axis. Note: %CV for real time PCR was calculated using linear-scale values (relative quantification) rather than Ct values in order to be di rectly comparable to ddPCR %CV as ddPCR data is output on a linear scale. Therefore real time PCR %CV values displayed here are higher than if calculated using Ct values.

Supplementary Figure 7| Schematic illustrating the quantitative details of the workflow used in Figure 2. RNA was reverse transcribed as for analysis by ddPCR or a standard real time PCR method. cDNAs were aliquotted and stored at −80°C. Individual cDNA aliquots were prepared for analysis using ddPCR master mix or standard real time PCR master mix on each of three separate days. Aliquots of the ddPCR master mix solution were also analyzed by real time PCR. Standard real time PCR master mix was analyzed only by real time PCR (these reagents are not compatible with ddPCR analysis). To enable appropriate quantitative comparison, the concentration of input RNA (as cDNA) for ddPCR and real time PCR was kept constant (i.e. cDNA concentration input into the PCR corresponded to 0.01 μL RNA solution per μL PCR reaction).

Supplementary Figure 8| Operating characteristics of ddPCR and real time PCR for measuring the circulating cancer biomarker miRNA, miR-141. Synthetic miRNA oligonucleotide standard curves were prepared, reverse -transcribed and analyzed as described in Methods and Supplementary Figures 2 and 7. Results are presented as the concentration determined by Poisson -metawell analysis of ddPCR triplicates or the mean concentration of three real time PCR replicates, respectively. Whiskers represent 10 -90^th distribution percentiles.

Supplementary Table 1| Dilution Protocol used to produce the standard curves for miRNAs (Figure 1, Supplemental Figures 2 and 8) and their predicted concentration in a PCR reaction assuming 100% RT efficiency and an accurate known concentration of the synthetic miRNA supplied by the vendor.

Supplementary Table 2| Coefficients of Variation (%CV) for ddPCR and real time PCR (water matrix). Coefficient of variation measured at the level of PCR (across -PCR %CV) was determined by calculating the s.d. within each set of PCR triplicates (n = 9), dividing each of these by their respective mean values and then expressing the result as the overall mean of the individual %CV estimates. %CV at the level of reverse transcription (across-RT %CV) was determined by calculating the s.d. across all PCR data derived from a set of RT triplicates (n = 3), dividing this by the corresponding mean and then expressing the result as the mean of these individual %CV estimates. %CV measured at the level of dilution series p reparation (across-preparation %CV) was determined by calculating the s.d. across all the PCR data derived from the three preparative replicates, dividing the result by the corresponding mean and expressing this value. Reduction in CV was calculated as the difference between the real time PCR CV (CV_realtime) and ddPCR CV (CV_ddPCR) divided by the real time PCR CV and expressed as a percentage: Reduction in CV = (CV _{real time} − CV_ddPCR)/(CV_{real time}). Note: %CV for real time PCR was calculated using linear-scale values (relative quantification) rather than Ct values in order to be directly comparable to ddPCR %CV as ddPCR data is output on a linear scale. Therefore real time PCR %CV values displayed here are higher than if calculated using Ct values.

Supplementary Table 3| Coefficients of Variation (%CV) for ddPCR and real time PCR (plasma RNA matrix). Coefficient of variation measured at the level of PCR (across -PCR %CV) was determined by calculating the s.d. within each set of PCR triplicates (n = 9), dividing each of these by their respective mean values and then expressing the result as the overall mean of the individual %CV estimates. %CV at the level of reverse transcription (across-RT %CV) was determined by calculating the s.d. across all PCR data derived from a set of RT triplicates (n = 3), dividing this by the corresponding mean and then expressing the result as the mean of these individual %CV estimates. %CV measured at the level of dilution series p reparation (across-preparation %CV) was determined by calculating the s.d. across all the PCR data derived from the three preparative replicates, dividing the result by the corresponding mean and expressing this value. Reduction in CV was calculated as the difference between the real time PCR CV (CV_{real time}) and ddPCR CV (CV_ddPCR) divided by the real time PCR CV and expressed as a percentage: Reduction in CV = (CV _{real time} – CV_ddPCR)/(CV_{real time}). Note: %CV for real time PCR was calculated using linear-scale values (relative quantification) rather than Ct values in order to be directly comparable to ddPCR %CV as ddPCR data is output on a linear scale. Therefore real time PCR %CV values displayed here are higher than if calculated using Ct values.

Supplementary Table 4| Operating characteristics based on ddPCR and real time PCR analysis of synthetic miRNA oligonucleotides (water matrix). Limit of quantification (LOQ) was defined as the lowest concentration tested that remained above or equal to the limit of detection (LOD)* and above or equal to the lower limit of linear range of the assay (LLLR)**. * LOD was defined as = <x>_bi + ks_bi, were <x>_bi = mean of the no-template controls, s_bi = standard deviation of no-template controls, k = 2.479 (99% confidence interval). LOD determinations here are likely to be biased in favor of real time PCR, as undetermined Cts are set uniformly to 40, artificially lowering s_bi estimates for real time PCR. ** LLLR was determined by runs-testing, removing successive lowest dilution points until the P-value was >0.05, indicating no significant deviation from linearity.

Supplementary Table 5| Operating characteristics based on analysis of synthetic miRNA oligonucleotides (plasma RNA matrix). Limit of quantification (LOQ) was defined as the lowest concentration tested that remained above or equal to the limit of detection (LOD)* and above or equal to the lower limit of linear range of the assay (LLLR)**. * LOD was defined as = <x>_bi + ks_bi, were <x>_bi = mean of the no-template controls, s_bi = standard deviation of no-template controls, k = 2.479 (99% confidence interval). LOD determinations here are likely to be biased in favor of real time PCR as undetermined Cts = 40, artificially lowering s_bi estimates for real time PCR. **LLLR was determined by runs-testing, removing successive lowest dilution points until the P-value was >0.05, indicating no significant deviation from linearity. * Note: operating characteristics for miR-16 could not be determined in plasma RNA matrix, as the endogenous abundance of miR -16 in plasma RNA is higher than the maximum concentration of synthet ic oligonucleotide examined.

Supplementary Table 6| Absolute ddPCR detection efficiency. The mean average of the number of copies detected across all ddPCR data for a given miRNA at the 250 -copy input dilution were divided by the predicted 250 input copies and expressed as a percentage.

Supplementary Table 7| Operating characteristics of ddPCR and real time PCR for miR -141 measurement. LOQ, LOD and LLLR were defined as for Supplemental Tables 2 and 3. *LOD determinations here are likely to be biased in favor of real time PCR as uniformly setting undetermined Cts = 40 would artificially lower s_bi estimates for real time PCR as previously described.

Supplementary Table 8| Day-to-day variability of miR-141 quantification from clinical samples (ddPCR master mix analyzed by ddPCR and real time PCR). Results are presented as copies of miR-141 per μL in PCR reaction. s.d.: standard deviation. %CV: Coefficient of variation calculated from replicates over 3 days (percentage). Fold-change of %CV was calculated as the ratio of %CV for real time PCR results to %CV for ddPCR results.

Supplementary Table 9| Day-to-day variability of miR-141 quantification from clinical samples (ddPCR vs. standard real time PCR). Results are presented as copies of miR-141 per μL in PCR reaction. s.d.: standard deviation. %CV: Coefficient of variation calculated from replicates over 3 days (percentage). Fold -change of %CV was calculated as the ratio of %CV for real time PCR results to %CV for ddPCR results.