Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2014 Jun 12;165(4):1399–1408. doi: 10.1104/pp.114.237115

Matching Patterns of Gene Expression to Mechanical Stiffness at Cell Resolution through Quantitative Tandem Epifluorescence and Nanoindentation1,[C],[W],[OPEN]

Pascale Milani 1,2, Vincent Mirabet 1,2, Coralie Cellier 1, Frédérique Rozier 1, Olivier Hamant 1, Pradeep Das 1,*, Arezki Boudaoud 1,*
PMCID: PMC4119026  PMID: 24924426

Stem cells from the central zone in Arabidopsis shoot meristems exhibit an enhanced stiffness.

Abstract

Cell differentiation has been associated with changes in mechanical stiffness in single-cell systems, yet it is unknown whether this association remains true in a multicellular context, particularly in developing tissues. In order to address such questions, we have developed a methodology, termed quantitative tandem epifluorescence and nanoindentation, wherein we sequentially determine cellular genetic identity with confocal microscopy and mechanical properties with atomic force microscopy. We have applied this approach to examine cellular stiffness at the shoot apices of Arabidopsis (Arabidopsis thaliana) plants carrying a fluorescent reporter for the CLAVATA3 (CLV3) gene, which encodes a secreted glycopeptide involved in the regulation of the centrally located stem cell zone in inflorescence and floral meristems. We found that these CLV3-expressing cells are characterized by an enhanced stiffness. Additionally, by tracking cells in young flowers before and after the onset of GREEN FLUORESCENT PROTEIN expression, we observed that an increase in stiffness coincides with this onset. This work illustrates how quantitative tandem epifluorescence and nanoindentation can reveal the spatial and temporal dynamics of both gene expression and cell mechanics at the shoot apex and, by extension, in the epidermis of any thick tissue.

Morphogenesis is a complex process that results from the coordinated actions of many genes and gene products across developing tissues and organs. Because shape is a function of the structural elements of cells, the molecular and genetic control of growth and morphogenesis must rely on the regulation of the mechanics of these elements. In this context, cell differentiation has been linked with mechanical stiffness in animal single-cell systems (Collinsworth et al., 2002; Balland et al., 2006; Engler et al., 2006; Darling et al., 2008), although the direct measurement of cell mechanics in growing animal tissues remains elusive (Blanchard and Adams, 2011; Davidson, 2011).

In plants, growth involves a delicate mechanical balance: it is powered by turgor pressure and contained by cell wall stiffness (Cosgrove, 1986). Several groups have recently achieved mechanical measurements made at a subcellular resolution in plants (Milani et al., 2011; Peaucelle et al., 2011; Fernandes et al., 2012; Radotić et al., 2012; Routier-Kierzkowska et al., 2012) using scaled-down indentation methods (Geitmann, 2006; Hayot et al., 2012; Milani et al., 2013; Routier-Kierzkowska and Smith, 2013), wherein one quantifies the force needed to push down on a sample to a prescribed depth. These studies have revealed spatiotemporal patterns of stiffness, notably in tissues (Milani et al., 2011; Peaucelle et al., 2011; Fernandes et al., 2012; Routier-Kierzkowska et al., 2012).

However, these measurements have not been associated directly with cell identity. This association would become feasible if mechanical measurements were combined with optical imaging of fluorescent reporters. Such a combination, termed nanoindentation coupled to inverted optical microscopy, has already been developed for single animal cells and for thin plant tissues, (Rotsch and Radmacher, 2000; Routier-Kierzkowska and Smith, 2014), but it cannot be extended to thick tissues because they are opaque, making it impossible to simultaneously observe the tissue surface optically with an inverted microscope and probe it mechanically. To circumvent this difficulty, we have developed a methodology involving the use of three microscopes to image the same sample: (1) an atomic force microscope (AFM), which is a nanoindentation system for obtaining stiffness maps of the surface of a sample; (2) an AFM-coupled upright epifluorescence macroscope to precisely identify the points to be probed; and (3) a confocal microscope to determine cell fate at cellular resolution, which may in turn be correlated with the stiffness maps. We call this methodology quantitative tandem epifluorescence and nanoindentation (qTEN), and we use it to probe the shoot apical meristem (SAM) of Arabidopsis (Arabidopsis thaliana), which is a good model system in which to investigate morphogenesis.

The SAM is located at the growing tip of the shoot and consists of distinct functional zones (Ha et al., 2010). One of these zones is the slow-dividing central zone (CZ), which can be defined by the expression of the CLAVATA3 (CLV3) signaling glycopeptide. Through cell division, cells exit the CZ into the surrounding peripheral zone (PZ). In the PZ, cells proliferate rapidly, and some become incorporated into organ primordia, thus yielding all aerial organs of the plant. Recent work on the SAM has revealed patterns of mechanical properties (Milani et al., 2011; Peaucelle et al., 2011; Kierzkowski et al., 2012; Braybrook and Peaucelle, 2013), but it is still unclear how these patterns are related to the activity of the SAM or to its functional zonation. Here, we analyze the dynamics of such a mechanical pattern in vivo and show that it is spatially and temporally related to stem cell fate.

RESULTS

Measurement of Mechanical Properties in a Cellular Domain Using an AFM Coupled to an Epifluorescence Macroscope

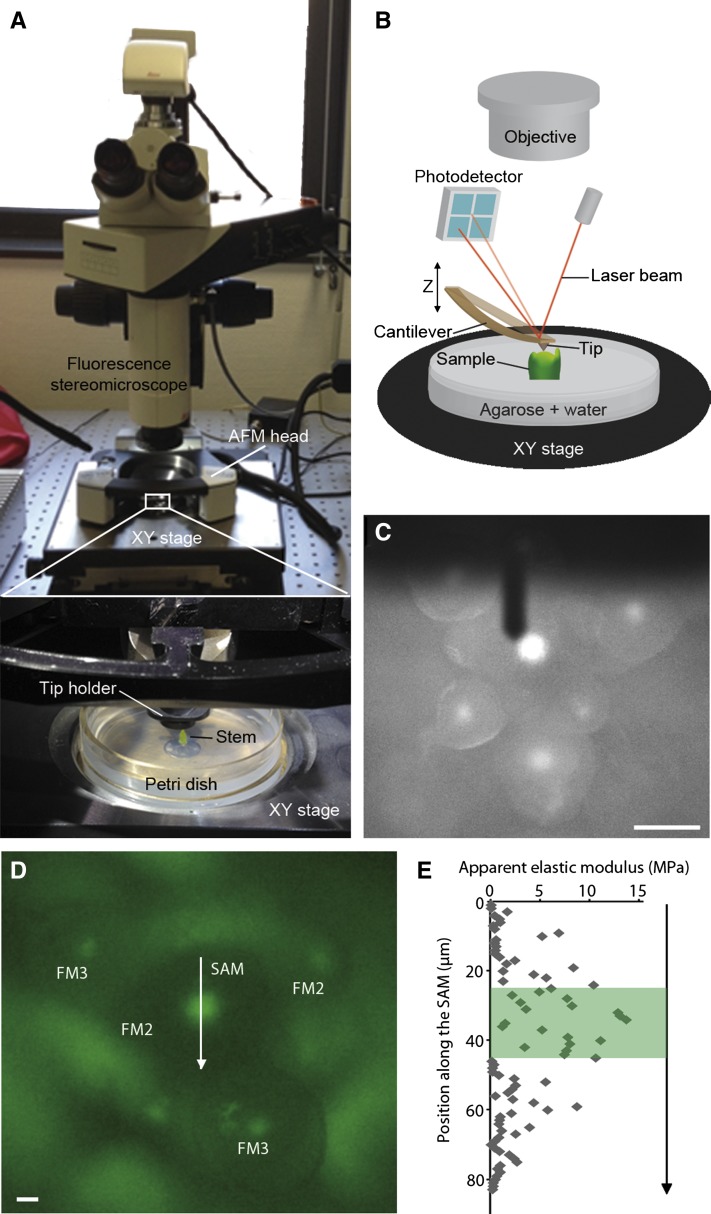
In order to simultaneously observe cell fate and measure stiffness at cellular resolution, we imaged living SAMs of plants carrying a pCLV3::GFPer reporter construct (Reddy and Meyerowitz, 2005) with both fluorescence and atomic force microscopy. We first confirmed that the observed temporal patterns of GFP expression match CLV3 RNA expression using fluorescent whole-mount in situ hybridization (Supplemental Fig. S1, A and B). We designed a customized coupling between an AFM and an upright epifluorescence macroscope in order to position both the mechanical probe and the lens specifically over the GFP domain of shoot apices (Fig. 1, A–C). We used a sharp pyramidal tip and a maximal force of approximately 10 nn, as described previously (Milani et al., 2011; Sampathkumar et al., 2014), to very locally measure the apparent elastic modulus (Ea) of the cell wall at a set of user-defined locations (e.g. regularly spaced along a line; Fig. 1D). We found that the expression of GFP correlated with a greater Ea (Fig. 1E), consistent with our earlier findings that the shoot summit is stiffer (Milani et al., 2011). Similar results were obtained on floral meristems of stage 3 flowers, which also express CLV3 (Supplemental Fig. S1, C and D). However, we were unable to associate mechanical properties with identity at a cellular resolution, because the relatively small indentation depths (50–100 nm) used in this protocol do not reveal cell outlines and because the macroscope does not provide cellular expression data. Therefore, we sought another approach, such that cell fate could be ascertained in individual cells and related to their stiffness maps.

Figure 1.

Figure 1.

Open in a new tab

Experimental setup for determining stiffness patterns. A and B, Photograph (A) and schematic (B) of the customized coupling of an AFM to an upright epifluorescence macroscope that was used to image specific regions within dissected shoot apices. C, Fluorescence image of a pCLV3::GFPer Arabidopsis inflorescence, as viewed with the macroscope. The cantilever of the AFM appears as a long, dark rectangular object above the sample. D, Closeup of a different pCLV3::GFPer inflorescence, with the SAM and stage 2 (FM2) and stage 3 (FM3) floral meristems indicated. E, Plot of the Ea, extracted from the AFM force-displacement curves, as a function of the position along the arrow shown in D, with the fluorescent region highlighted in green. Bars = 50 µm in C and 15 µm in D.

qTEN Enables the Identification of Genetic and Mechanical Properties at Cell Resolution

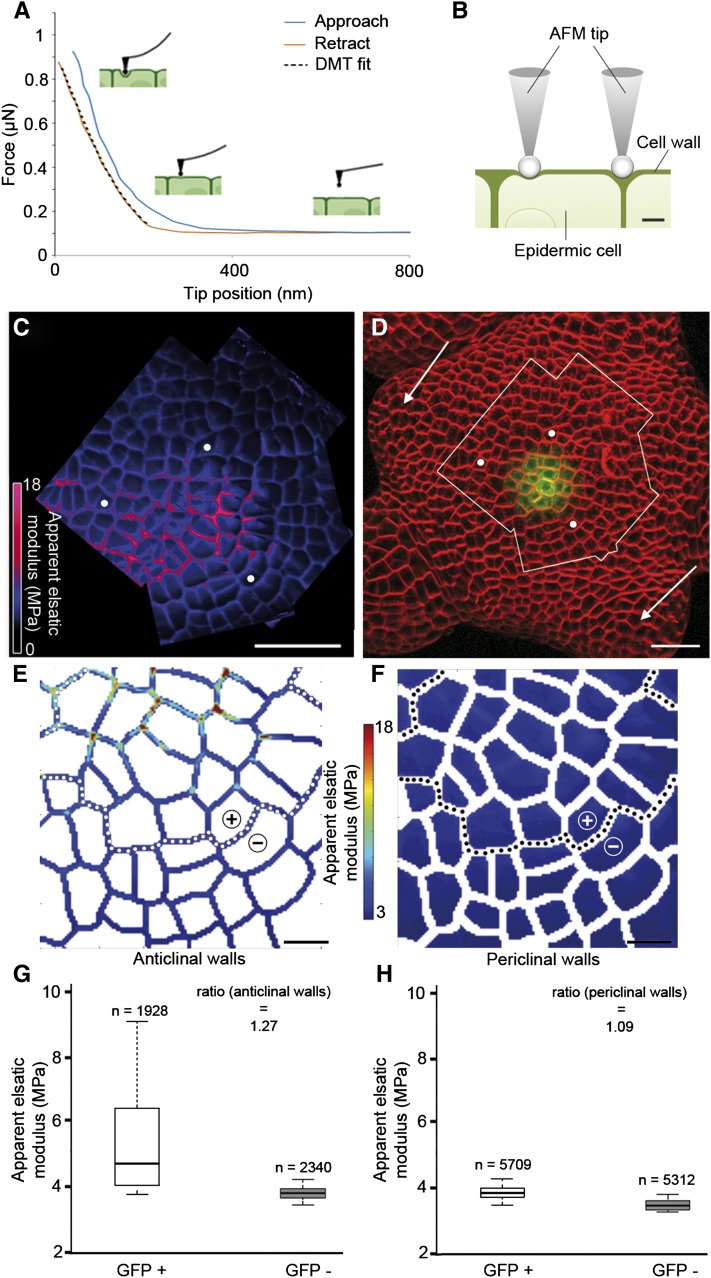
In order to further investigate the link between gene expression and stiffness patterns at cell resolution, we switched to another protocol coupling confocal and mechanical imaging, which we termed qTEN. We employed larger indentations (200–500 nm) that allowed cell geometry delineation, using a cantilever with a spherical tip (diameter of 800 nm) and a force of approximately 1 μn. The probe was oscillated at a low frequency while horizontally scanning the sample, and a force curve was generated each time the AFM probe made contact with the sample. The Ea was then extracted from each force curve using the Derjaguin-Muller-Toporov (DMT) model (Fig. 2A; see “Materials and Methods”), yielding two-dimensional stiffness maps, where each pixel (of size 0.2–0.4 µm) represents one force curve. To measure stiffness in the SAM, we first generated a series of smaller (local) stiffness maps, from which we assembled a global map (Fig. 2C; Supplemental Fig. S2). Such maps are typified by the presence of narrow bands of stiffer material corresponding to anticlinal cell walls (that are perpendicular to the surface) surrounding large areas of softer material that correspond to the periclinal cell walls (that are parallel to the surface). Such cellular patterns are similar to published measurements made on plasmolyzed apices, with a slightly larger 1-µm spherical tip (Peaucelle et al., 2011). A comparison with the confocal image of the same apex (Fig. 2D) shows that all cells that express GFP lie within a stiff region (Fig. 2, C and D, bounded by white dots; n = 3 SAMs). These observations are overall consistent with previous work showing enhanced stiffness at the very tip of the shoot (Milani et al., 2011; Peaucelle et al., 2011; Kierzkowski et al., 2012; Braybrook and Peaucelle, 2013). Additionally, we also observed that the anticlinal walls corresponding to recent cell divisions often appeared softer than other anticlinal walls.

Figure 2.

Figure 2.

Open in a new tab

Mechanical measurements and cellular quantification of stiffness. A, Typical force-tip position approach (blue) and retraction (red) curves obtained on a SAM with a spherical probe tip. The retraction curve (red) is fitted using the DMT model (black dotted line) to obtain the value of the Ea. B, Diagrammatic representation of the AFM tip indenting an epidermal cell in the SAM, either on an outer (periclinal) wall or on walls normal to the surface (anticlinal). When indentation depth is greater than wall thickness, periclinal walls are expected to bend more and to appear softer than anticlinal walls. C and D, Analysis of stiffness in the SAM from a pCLV3::GFPer plant. Shown is the global map of the Ea of a region of the SAM (C), delimited by the white outline in the surface projection of the confocal image (D), with the white dots serving as reference landmarks and the arrows indicating stage 1 and 2 primordia. The plant was stained with the FM4-64 dye to detect cell contours (in red), while GFP expression is shown in green. E and F, Quantification of stiffness maps. Maps of anticlinal (E) and periclinal (F) walls were reconstituted after segmentation of one of the AFM stiffness maps from the global map shown in C (Supplemental Fig. S2). The dotted lines separate the GFP+ (CLV3-expressing zone) and GFP− regions, which are indicated with + and −. G and H, Box plots for anticlinal (G) and periclinal (H) walls obtained by analysis of the stiffness maps in E and F, respectively. The boxes extend from the first quartile to the third quartile and the whiskers from 10% to 90% of all the data set. Pixels were separated into two groups, GFP+ and GFP−. The number of pixels analyzed in each group is indicated. The ratio of median Ea values of GFP+ and GFP− is shown. Bars = 20 µm in C and D and 5 µm in E and F.

Data Analysis Demonstrates a Correlation between Gene Expression and Cell Mechanics

To go beyond these qualitative assessments, we developed a pipeline to quantitatively analyze the data collected (see “Materials and Methods”). Briefly, we generated cell outlines from the stiffness maps and then used the confocal data to determine which cells expressed GFP. Every pixel in the AFM map was then annotated for two criteria: wall type (anticlinal or periclinal) and, when applicable, cell fate (presence or absence of GFP). Quantifications of these data were then carried out, and an estimate of the relative stiffness of the GFP+ and GFP− groups was calculated as the ratio of their median Ea values. The Wilcoxon test was used to assess the statistical significance of the observed differences. In this way, we analyzed one of the individual stiffness maps from the SAM. We found that the GFP+ group was stiffer than the GFP− group, both for anticlinal and periclinal walls (Fig. 2, E–G; n = 15,269 pixels from about 35 cells), with relative stiffness values of 128% and 109%, respectively (P < 0.001). Overall, these results show that genetic and mechanical identities in the Arabidopsis SAM can be accurately measured at cellular resolution.

In Flowers, Enhanced Stiffness Is Correlated with GFP Expression

In order to test whether stiffness is temporally correlated with GFP expression, we turned to floral meristems, where GFP appears transiently during flower development (Fletcher et al., 1999; Brand et al., 2000). Whereas no reporter expression is observed in young (stage 1; Smyth et al., 1990) flower buds that have just initiated on the flanks of the SAM (Fig. 2D), GFP becomes visible in a small group of cells from mid stage 2 onward, once the flower has separated from the SAM. Expression persists until stage 6, when this region is incorporated into the female reproductive organs, the carpels.

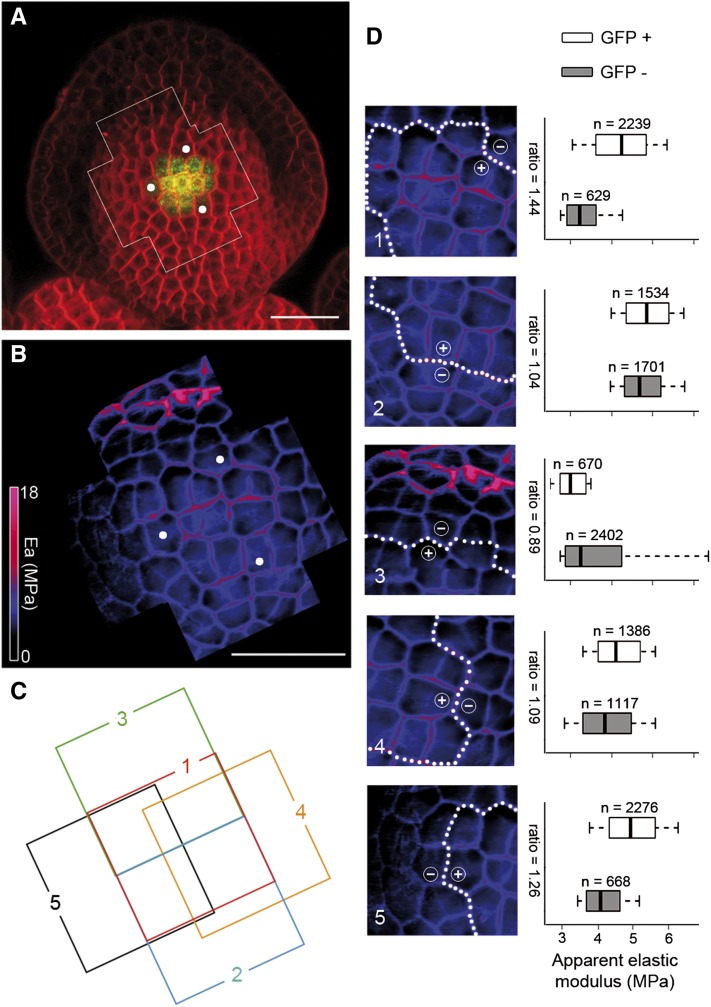
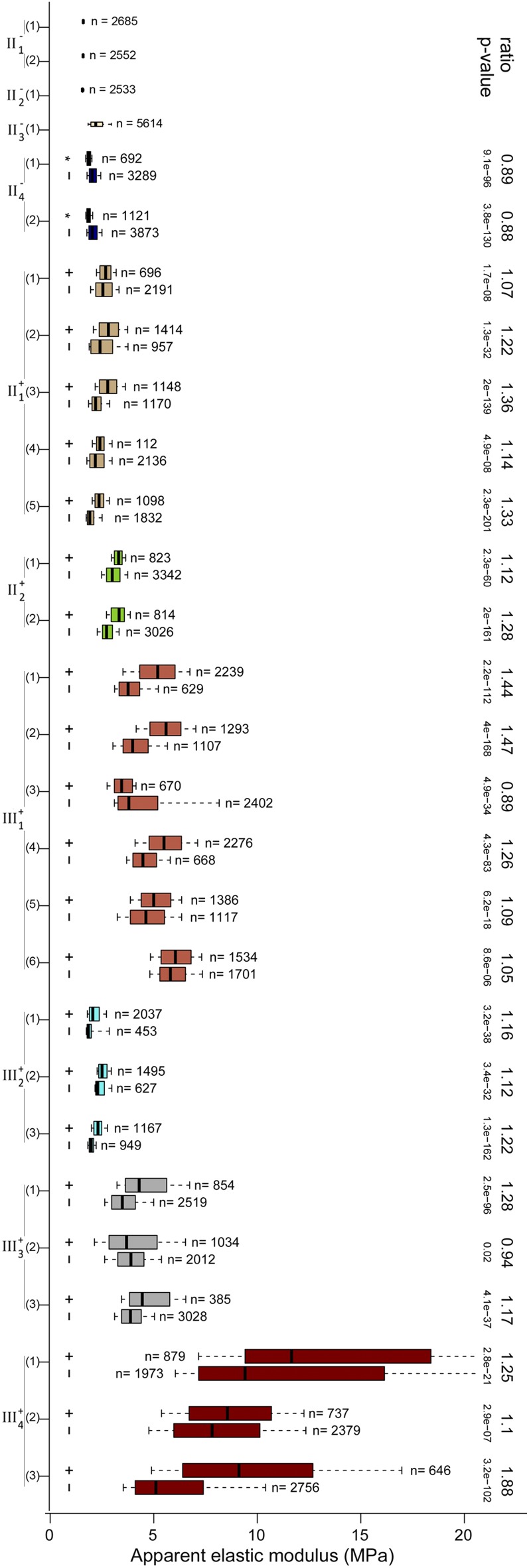
We next asked whether GFP+ cells in the flower also display the higher stiffness seen in SAM GFP-expressing cells (Fig. 3A). We first considered flowers at stage 3, which is characterized by the emergence of sepals. As in the SAM, we observed zonal differences of mechanical properties, which correlate with the presence or absence of GFP (Fig. 3, A and B [n = 6]; Supplemental Fig. S3). A pixel-level quantification of the individual stiffness maps (Fig. 3, C and D; Supplemental Fig. S4) showed that cells expressing GFP had a relative stiffness of 104% to 144% when compared with all other cells (Fig. 3D, stiffness maps 1/2 and 4/5; n = 14,622 pixels, P < 0.001), except for a few cells in the boundary between the floral dome and the sepals (Fig. 3D, map 3). Consistent with this, we found that all measured stage 2 flowers that expressed GFP also displayed a higher stiffness in the CZ (n = 3), whereas younger flowers with no CLV3 expression do not have such a stiffness pattern (n = 4). Thus, in the floral meristem, as in the SAM, CZ fate correlates with greater stiffness.

Figure 3.

Figure 3.

Open in a new tab

Cell fate correlates with a higher stiffness in the floral meristem. A, Surface projection from a confocal image of a stage 3 flower carrying the pCLV3::GFPer reporter, showing CLV3 expression (green) and cell outlines (red). B, Global map of the Ea of the framed region of the same stage 3 flower (A), with white dots serving as landmarks. C, Arrangement of the individual stiffness maps that constitute the global stiffness map of the flower shown in B, with each map numbered and positioned from front (map 1) to back (map 5; Supplemental Fig. S3). D, Pixel-level quantification of the individual maps (left column) and their corresponding box-plot representations (right column), summarizing the Ea distributions of GFP+ (CLV3-expressing zone) and GFP− anticlinal pixels. In each map, the white dotted line separates the GFP+ and GFP− regions, which are indicated by + and −, respectively. The numbers of analyzed pixels and median Ea ratios are indicated in the box plots, which are constructed as in Figure 2. Bars = 20 µm in A and B.

The Stiffness Pattern Is Temporally Correlated with Gene Expression

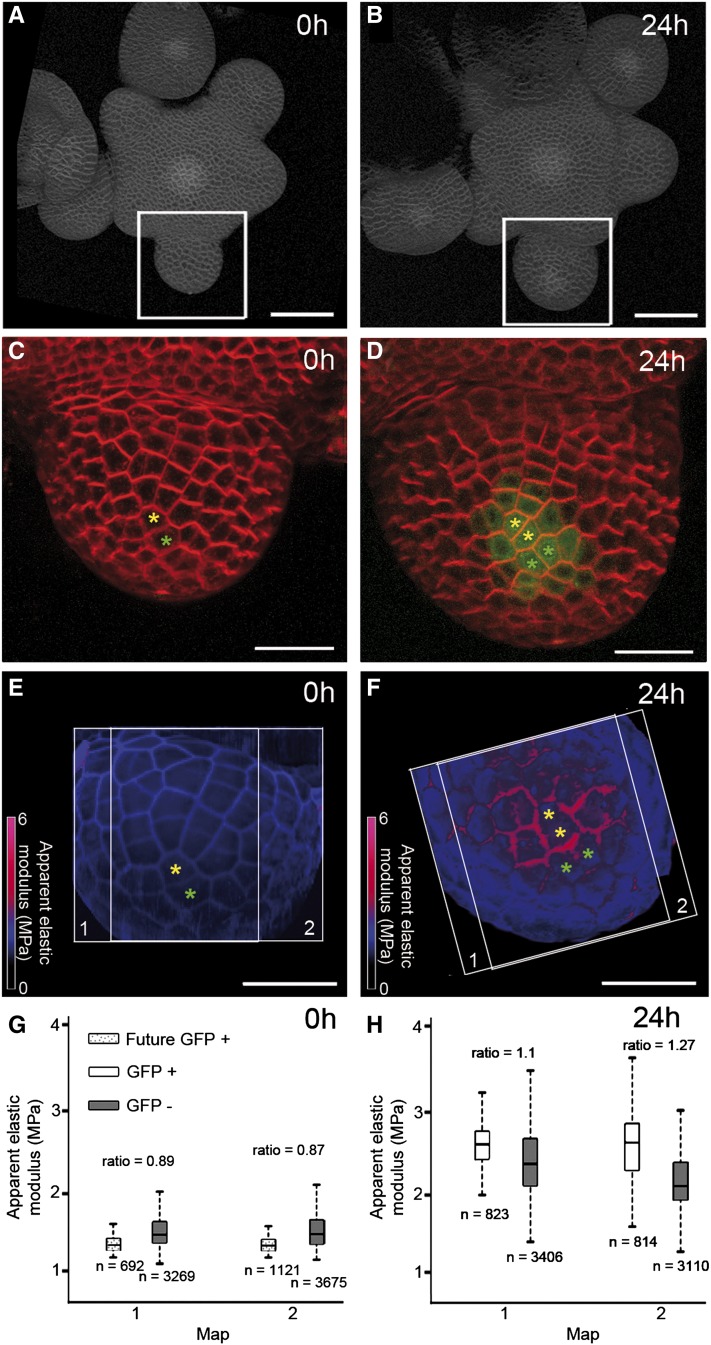
The absence of a stiffer region in stage 1 flowers suggests that the onset of CZ identity is temporally coincident with an increase in stiffness. To test this more directly, we performed time-lapse experiments on individual flowers (Fernandez et al., 2010), tracking them over 24 to 48 h with both optical and mechanical imaging. At the first time point, we imaged an early stage 2 flower with no detectable GFP expression (Fig. 4, A and C). Twenty-four hours later, the same flower displayed GFP expression in about 15 epidermal cells (Fig. 4, B and D). The stiffness maps showed no clear pattern in the first time point (Fig. 4E), consistent with all other stage 2 GFP− flowers, whereas a stiffer region was manifest after 24 h, in the CLV3-expressing region (Fig. 4F). The relatively short time interval also allowed us to trace cell lineages between the two time points. We then carried out a pixel-level quantification of the stiffness maps, additionally using cell lineages to identify the mother cells (at 0 h) of the cells that express GFP at 24 h. We found that at 24 h, the GFP+ cells had a relative stiffness of 110% to 127% (n = 8,005 pixels, P < 0.001), whereas at 0 h, their mother cells were less stiff than their neighbors (relative stiffness = 88%, n = 8,975 pixels, P < 0.001). Thus, the pattern of stiffness was established concomitantly with CZ fate, as indicated by CLV3 expression.

Figure 4.

Figure 4.

Open in a new tab

The stiffness pattern is established dynamically along with GFP expression. Analysis of stiffness in a single pCLV3::GFPer flower was imaged at 0 h (A, C, E, and G) and 24 h (B, D, F, and H). A and B, Projections of confocal images of the whole inflorescence observed, with white frames showing the stage 2 flower studied. C and D, Closeups of the stage 2 flower, with GFP expression visible at 24 h (D) but not at 0 h (C). Yellow and green asterisks indicate lineage for two cells within the emerging CZ. E and F, Global Ea maps of the same flower, with white frames delimiting the individual stiffness maps. G and H, Pixel-level quantification of the individual maps, summarizing the Ea distributions of anticlinal pixels from GFP−, GFP+, and 0-h mother cells of 24-h GFP+ cells. The numbers of analyzed pixels and median Ea ratios are indicated in the box plots, which are constructed as in previous figures. Bars = 50 µm in A and B and 20 µm in C to F.

DISCUSSION

We have developed a methodology to measure cell mechanics in specific domains and at cellular resolution. In the first step, we used confocal microscopy to obtain high-resolution images of a fluorescent marker in a whole tissue and to identify an appropriate region of interest. In the second step, we used an upright macroscope with epifluorescence to position the AFM cantilever over the desired region, where we then measured tissue mechanics using a cantilever with a micrometric spherical tip, which allowed us to detect cell contours. The order of these first two steps was unimportant in the experiments we performed, although we cannot exclude that laser exposition or nanoindentation might have had an impact either on the fluorescence level of other markers or on the stiffness in other tissues, respectively. In the third step, we associated optical and mechanical images based on cell contours in order to match cell identity and mechanics. Finally, we quantitated the results to identify any significant cellular trends in the measurements.

We applied the qTEN methodology to the CZ of the SAM and floral meristems, using pCLV3::GFP as a reporter of cell fate. In principle, qTEN can be applied to other reporters, such as pAHP6::GFP (Besnard et al., 2014), which is expressed in incipient floral and sepal primordia (Supplemental Fig. S5, A and B). More generally, qTEN could be used to address questions concerning epidermal cells in their organ context. For instance, we could associate optical images and AFM stiffness maps of Arabidopsis pavement cells in whole cotyledons to identify specific cells (Supplemental Fig. S5, C and D).

Using the qTEN methodology, we demonstrate that CLV3-expressing cells exhibit greater stiffness than their neighbors in the Arabidopsis SAM. These results are consistent with previous studies showing that stiffer regions were located roughly at the shoot summit (Milani et al., 2011; Peaucelle et al., 2011; Kierzkowski et al., 2012; Braybrook and Peaucelle, 2013). We now show that this enhanced stiffness is correlated with CLV3 expression. Alternatively, enhanced stiffness may also serve as an indicator of cell fate at the shoot apex.

Formally, there are alternative scenarios that might account for the apparent greater stiffness of the CZ in SAMs and in flowers. Our results exclude tissue shape as an explanation for this phenomenon, because young wild-type flowers do not exhibit tissue stiffness patterns, and we found no correlations between apparent elastic moduli and geometric features such as height, slope, or curvature (Supplemental Fig. S6). Other explanations for the phenomenon could be either a strain-stiffened CZ (Kierzkowski et al., 2012) or an enhanced turgor pressure in the CZ. While we do not rule out a partial role for these two factors, it is clear that cell walls contribute significantly to the tissue stiffness pattern that we detected. Indeed, we also measured wall stiffness very locally using a sharp tip and found the CZ to be stiffer than the PZ (Fig. 1E; Supplemental Fig. S1).

Although the biological mechanisms underlying this close correlation remain to be established, the functional importance of an enhanced stiffness could be multifold. Stiffer cell walls could reduce growth and proliferation rates, a known characteristic of the CZ of the wild-type SAM (Laufs et al., 1998; Reddy et al., 2004). This may also provide CZ cells with protection from fluctuating differentiating signals, as the slow growth dynamics of cells in the CZ may make them react only to persistent signals (Fuchs, 2009).

We observed a differential stiffness between the CZ and the PZ in all the flowers that display CLV3 expression. Similarly, cells in the boundary regions between the floral dome and the sepals also displayed an enhanced stiffness (Fig. 3D, map 3), which we would predict to be correlated with low proliferation rates, with slow growth, as well as with the expression of boundary genes (Breuil-Broyer et al., 2004). These results hint at a framework in which patterning genes would control growth and morphogenesis through cell wall stiffness. Indeed, stiffness has been observed to be inversely correlated with growth rates, suggesting that cell wall extensibility is also correlated with stiffness (Milani et al., 2013). However, we observed some variability in absolute stiffness, while the overall trend observed in the quantified floral data are that the average stiffness gradually increases as the flower develops (Fig. 5). This suggests that stiffness ratios across the tissue might be more important than absolute stiffness values for proper morphogenesis to occur. Indeed, the shape of a growing organism only depends on the ratios of growth rates: a proportional modulation of all growth rates would only slow down or accelerate morphogenesis, while an outgrowth requires a locally higher growth rate.

Figure 5.

Figure 5.

Open in a new tab

Distribution of Ea for all the flowers that were analyzed quantitatively. Box-plot representations of the Ea distribution for all maps and groups (GFP+ and GFP−) of each flower are shown. The boxes extend from the first quartile to the third quartile and the whiskers from 10% to 90% of each data set; the number of analyzed pixels is indicated. The ratio between median Ea of GFP+ and GFP− and the corresponding P values (Wilcoxon test; see “Materials and Methods”) are shown where appropriate; the Ea ratio of mother cells of GFP+ cells to mother cells of GFP− cells is also specified for flower II−4 (Fig. 4G). [See online article for color version of this figure.]

More generally, our methodology provides a fresh perspective in the study of the link between cellular identities and tissue growth, which is fundamental to all morphogenetic processes and which is beginning to be examined in detail by other groups (Green et al., 2010; Schiessl et al., 2012).

MATERIALS AND METHODS

Plant Growth and Microscopy

pCLV3::GFPer and wild-type Arabidopsis (Arabidopsis thaliana) plants (Landsberg erecta ecotype) were grown on soil under continuous light. pAHP6::GFP plants (Columbia-0 ecotype) were grown in short-day conditions (8 h of light/16 h of dark) for 4 to 5 weeks and then transferred to long-day conditions (16 h of light/8 h of dark). Immediately after bolting, and usually before any flowers were open, the stems were cut and placed in dissection boxes containing growth medium as described (Fernandez et al., 2010). Flower buds were removed from the inflorescence meristem until the desired stages were readily accessible for either atomic force or confocal microscopy (for local stiffness measurements or tissue/cell shape determination, respectively). Cotyledons were obtained as described previously (Sampathkumar et al., 2014). In most cases, confocal images were obtained before measurements on the AFM were taken. For the optical imaging of cell outlines, samples were stained with FM4-64 (approximately 1 μL of a 330 μg mL−1 stock) for about 10 min and then observed using either a Leica macroscope (MacroFluo) or a Zeiss LSM 510 or Zeiss LSM 700 system with a water-dipping 40× objective.

Fluorescent Whole-Mount RNA in Situ Hybridization

Whole-mount in situ hybridization was performed as described previously (Besnard et al., 2014), except that the revelation step was carried out with fluorescent signals using Tyramide Signal Amplification technology (Invitrogen). In this step, the samples were placed in the following solution for 30 min: 3 μL of Alexa in 100 μL of amplification buffer containing a 1:20,000 dilution of hydrogen peroxide. These were washed three times in 1× phosphate-buffered saline for 5 min each and then incubated in 0.1% (w/v) fluorescent brightener (Sigma) for 1 h. The samples were then mounted and imaged on an upright confocal microscope (Leica SP5) with a 40× water-immersion objective.

Atomic Force Microscopy

Atomic force microscopy indentation experiments were carried out with a Catalyst Bioscope (Bruker Nano) mounted under an optical epifluorescence macroscope (MacroFluo; Leica), enabling the use of a 2× Plano objective to observe the apex (Leica; Fig. 1A). To record surface topology and stiffness modulus maps, PeakForce QNM AFM mode (Bruker Nano/Veeco) was used (Nanoscope V controller and Nanoscope software version 8.1). All quantitative measurements were performed using special 0.8-µm-diameter spherical probes (SD-Sphere-NCH; Nanosensors). The spring constant of cantilevers was measured using the thermal tuning method (Hutter and Bechhoefer, 1993; Levy and Maaloum, 2009) and ranged from 35 to 45 n m−1. The deflection sensitivity of cantilevers was calibrated against a clean sapphire wafer. We also used cantilevers with pyramidal tips for more local measurements, as described previously (Milani et al. 2013). All measurements were made under water at room temperature, and the standard cantilever holder for operating in liquid environments was used. The 30-mm petri dishes containing the sample (5 mm of stem, stabilized in agarose in a petri dish) was placed on an XY stage in a specially designed sample holder. Then, the AFM head was mounted onto the stage and positioned so that the cantilever was in the vicinity of the GFP-expressing region.

Mechanical property mapping with PeakForce QNM hinges on the ability of the system to acquire and analyze the individual force curves from every tap of the cantilever and the attached probe on the sample that occurs during the imaging process. The requested applied force (PeakForce set point) during imaging was 1 µn, which corresponded to indentation depths generally in the range 200 to 500 nm above anticlinal walls. The topography and stiffness images were usually collected over rectangular areas of 30 to 50 µm per side and at a digital resolution of 128 × 128 pixels (for details, see Supplemental Fig. S4). A scanning rate of 0.3 Hz per line was used, corresponding to 38 Hz per pixel; the approach and retract velocities were equal and ranged from 30 to 80 µm s−1. Occasionally, due to the high scanning speed and to instabilities in the control loops of the AFM system, the force applied by the system on the sample differed significantly from the requested one. The difference between the PeakForce set point and the real applied force is indicated in a PeakForce Error map (Ferr), which we used to assess the quality of mechanical measurements. Control experiments where different forces were applied to our samples have shown that the stiffness maps obtained are very similar for a force range of 0.5 to 1.5 μn. Based on this, pixels (measures) for which the applied force was less than 0.5 µn or greater than 1.5 μn (or, alternatively, the absolute value of Ferr was greater than 0.5 µm) were automatically discarded from subsequent quantification. For the extraction of elastic moduli from the force-indentation retract curves, we used the DMT model, which applies to the (possibly) adhesive contact between two elastic, thick isotropic solids (Derjaguin et al., 1975):

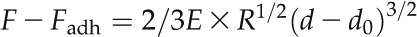graphic file with name pp_237115_E1.jpg

where F is the force on the cantilever relative, Fadh is the adhesion force between the two solids, R is the known tip end radius (0.4 µm), and d – d0 is the deformation undergone by the sample, relative to the contact height d0. The result of the fit yields the adhesion force, the contact height, and the reduced modulus E*. If the Poisson’s ratio (ν) is known, the Young’s modulus of the sample (E) is related to the sample modulus by E* = E/(1 − ν2) when the tip modulus is considered to be much bigger than that of the sample. As generally assumed for biological samples, we considered our sample as perfectly incompressible, taking the value 0.5 for the Poisson’s ratio. We sought to minimize the potential influence of turgor on moduli by focusing on anticlinal walls, reasoning that the greater depth of wall material below the probe increased the applicability of the DMT model. However, because of the potential anisotropy of cell walls, we report in this work only an apparent modulus (Ea).

Data Analysis

Stiffness maps provided by the AFM software were converted into two-dimensional matrices. In order to determine cell contours, maps were segmented manually using the signal corresponding to anticlinal walls, assuming three pixel widths for the anticlinal walls. The periclinal part of the image was simply the complementary of all pixels associated with anticlinal walls. Areas surrounded by pixels corresponding to anticlinal walls were defined as cells and given a label. Cells present in multiple stiffness maps of the same tissue were labeled identically in segmentations. Maps were filtered solely to remove regions where (1) the whole cell could not be enclosed by the segmentation and (2) the AFM indicated an absolute peak force error higher than 0.5 µn. These criteria led to the exclusion of between 3% and 28% of pixels, depending on the map.

Cell shapes in the L1 epidermal cell layer were extracted from the confocal optical stacks using the Merryproj software (Barbier de Reuille et al., 2005), which creates a two-dimensional projection of the tissue surface. Cells from the optical images and from the stiffness maps were associated manually based on their shape. Cells were subsequently defined as CLV3+ or CLV3− using pCLV3::GFPer expression. In series obtained from time-lapse imaging, cell lineages were defined manually based on cell shapes. This allowed us to label mother cells in young stage 2 flowers according to whether their daughters did or did not express CLV3+ or CLV3−.

Every pixel in a stiffness map corresponds to one data point. It is labeled with the following information: sample number, map number, anticlinal or periclinal, cells with which it is associated (one cell if periclinal, two or three cells if anticlinal), CLV3+ or CLV3− status of associated cells, and CLV3+ or CLV3− status of the daughters of associated cells (in time series). We defined the status of the pixel as CLV3+ if one of the cells to which it was associated was CLV3+; otherwise, it was labeled as CLV3−. Data sets were extracted based on the labels. Except for the SAM in Figure 1, we have only presented data corresponding to anticlinal walls, because our experimental setup was better suited to examining such walls (Peaucelle et al., 2011; Routier-Kierzkowska et al., 2012).

The quantitative representations of data sets use a box-and-whisker plot derived from the box-plot function from the R software (R Development Core Team, 2008). The box limits are the first and third quartiles of the values, and the median line represents the median value. In this modified version, whiskers extend from the first 10% of values to 90%. We assessed the statistical relevance of the difference between modules measured on CLV+ and CLV− anticlinal walls. We implicitly considered that each pixel corresponds to an independent measurement. As a Shapiro-Wilk test showed that data are not distributed according to normal distributions, we decided to resort to nonparametric tests. We used a Wilcoxon test on each stiffness map and obtained the corresponding P values. Both the Shapiro-Wilk and Wilcoxon tests were performed using the standard statistical package from the R distribution (R Development Core Team, 2008). All quantifications are shown in Figure 5, and the corresponding flowers appear in Supplemental Figure S4.

In order to test whether sample geometry had an influence on apparent elastic moduli, we determined slopes and mean curvature from the height maps, which were computed, respectively, from the norm of the gradient of the height and the Laplacian of the height (the Laplacian is a good approximation of the mean curvature when slopes are small, as here). For each stiffness map, we performed linear regressions between the Ea and the geometric variables: height and slope (Supplemental Fig. S6A) or mean curvature (Supplemental Fig. S6B). We computed the corresponding coefficients of determination, r2 (Supplemental Fig. S6C), and correlation coefficients (Supplemental Fig. S6D). We concluded that the Ea is not correlated with sample geometry.

Supplemental Data

The following materials are available in the online version of this article.

Supplementary Material

Supplemental Data
supp_165_4_1399__index.html (1.1KB, html)

Acknowledgments

We thank Françoise Argoul and Alain Arnéodo for introducing us to atomic force microscopy, Platim (UMS 3444 Biosciences Gerland-Lyon Sud) for help with confocal imaging, and Marina Oliva and Teva Vernoux for providing plants carrying the pAHP6::GFP construct.

Glossary

AFM

atomic force microscope

qTEN

quantitative tandem epifluorescence and nanoindentation

SAM

shoot apical meristem

CZ

central zone

PZ

peripheral zone

DMT

Derjaguin-Muller-Toporov

Ea

apparent elastic modulus

Footnotes

1

This work was supported by the Agence Nationale de la Recherche (grant no. ANR–10–BLAN–1516), by the European Research Council (PhyMorph starting grant no. 307387), and by the Institut National de la Recherche Agronomique (Chaire d’Excellence initiative award to P.D.).

[C]

Some figures in this article are displayed in color online but in black and white in the print edition.

[W]

The online version of this article contains Web-only data.

[OPEN]

Articles can be viewed online without a subscription.

References

  1. Balland M, Desprat N, Icard D, Féréol S, Asnacios A, Browaeys J, Hénon S, Gallet F. (2006) Power laws in microrheology experiments on living cells: comparative analysis and modeling. Phys Rev E Stat Nonlin Soft Matter Phys 74: 021911. [DOI] [PubMed] [Google Scholar]
  2. Barbier de Reuille P, Bohn-Courseau I, Godin C, Traas J. (2005) A protocol to analyse cellular dynamics during plant development. Plant J 44: 1045–1053 [DOI] [PubMed] [Google Scholar]
  3. Besnard F, Refahi Y, Morin V, Marteaux B, Brunoud G, Chambrier P, Rozier F, Mirabet V, Legrand J, Lainé S, et al. (2014) Cytokinin signalling inhibitory fields provide robustness to phyllotaxis. Nature 505: 417–421 [DOI] [PubMed] [Google Scholar]
  4. Blanchard GB, Adams RJ. (2011) Measuring the multi-scale integration of mechanical forces during morphogenesis. Curr Opin Genet Dev 21: 653–663 [DOI] [PubMed] [Google Scholar]
  5. Brand U, Fletcher JC, Hobe M, Meyerowitz EM, Simon R. (2000) Dependence of stem cell fate in Arabidopsis on a feedback loop regulated by CLV3 activity. Science 289: 617–619 [DOI] [PubMed] [Google Scholar]
  6. Braybrook SA, Peaucelle A. (2013) Mechano-chemical aspects of organ formation in Arabidopsis thaliana: the relationship between auxin and pectin. PLoS ONE 8: e57813. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Breuil-Broyer S, Morel P, de Almeida-Engler J, Coustham V, Negrutiu I, Trehin C. (2004) High-resolution boundary analysis during Arabidopsis thaliana flower development. Plant J 38: 182–192 [DOI] [PubMed] [Google Scholar]
  8. Collinsworth AM, Zhang S, Kraus WE, Truskey GA. (2002) Apparent elastic modulus and hysteresis of skeletal muscle cells throughout differentiation. Am J Physiol Cell Physiol 283: C1219–C1227 [DOI] [PubMed] [Google Scholar]
  9. Cosgrove D. (1986) Biophysical control of plant cell growth. Annu Rev Plant Physiol 37: 377–405 [DOI] [PubMed] [Google Scholar]
  10. Darling EM, Topel M, Zauscher S, Vail TP, Guilak F. (2008) Viscoelastic properties of human mesenchymally-derived stem cells and primary osteoblasts, chondrocytes, and adipocytes. J Biomech 41: 454–464 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Davidson LA. (2011) Embryo mechanics: balancing force production with elastic resistance during morphogenesis. Curr Top Dev Biol 95: 215–241 [DOI] [PubMed] [Google Scholar]
  12. Derjaguin BV, Muller VM, Toporov YP. (1975) Effect of contact deformations on the adhesion of particles. J Colloid Interface Sci 53: 314–326 [Google Scholar]
  13. Engler AJ, Sen S, Sweeney HL, Discher DE. (2006) Matrix elasticity directs stem cell lineage specification. Cell 126: 677–689 [DOI] [PubMed] [Google Scholar]
  14. Fernandes AN, Chen X, Scotchford CA, Walker J, Wells DM, Roberts CJ, Everitt NM. (2012) Mechanical properties of epidermal cells of whole living roots of Arabidopsis thaliana: an atomic force microscopy study. Phys Rev E Stat Nonlin Soft Matter Phys 85: 021916. [DOI] [PubMed] [Google Scholar]
  15. Fernandez R, Das P, Mirabet V, Moscardi E, Traas J, Verdeil JL, Malandain G, Godin C. (2010) Imaging plant growth in 4D: robust tissue reconstruction and lineaging at cell resolution. Nat Methods 7: 547–553 [DOI] [PubMed] [Google Scholar]
  16. Fletcher JC, Brand U, Running MP, Simon R, Meyerowitz EM. (1999) Signaling of cell fate decisions by CLAVATA3 in Arabidopsis shoot meristems. Science 283: 1911–1914 [DOI] [PubMed] [Google Scholar]
  17. Fuchs E. (2009) The tortoise and the hair: slow-cycling cells in the stem cell race. Cell 137: 811–819 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Geitmann A. (2006) Experimental approaches used to quantify physical parameters at cellular and subcellular levels. Am J Bot 93: 1380–1390 [DOI] [PubMed] [Google Scholar]
  19. Green AA, Kennaway JR, Hanna AI, Bangham JA, Coen E. (2010) Genetic control of organ shape and tissue polarity. PLoS Biol 8: e1000537. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ha CM, Jun JH, Fletcher JC. (2010) Shoot apical meristem form and function. Curr Top Dev Biol 91: 103–140 [DOI] [PubMed] [Google Scholar]
  21. Hayot CM, Forouzesh E, Goel A, Avramova Z, Turner JA. (2012) Viscoelastic properties of cell walls of single living plant cells determined by dynamic nanoindentation. J Exp Bot 63: 2525–2540 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hutter JL, Bechhoefer J. (1993) Calibration of atomic-force microscope tips. Rev Sci Instrum 64: 1868–1873 [Google Scholar]
  23. Kierzkowski D, Nakayama N, Routier-Kierzkowska AL, Weber A, Bayer E, Schorderet M, Reinhardt D, Kuhlemeier C, Smith RS. (2012) Elastic domains regulate growth and organogenesis in the plant shoot apical meristem. Science 335: 1096–1099 [DOI] [PubMed] [Google Scholar]
  24. Laufs P, Grandjean O, Jonak C, Kiêu K, Traas J. (1998) Cellular parameters of the shoot apical meristem in Arabidopsis. Plant Cell 10: 1375–1390 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Levy R, Maaloum M. (2009) Measuring the spring constant of atomic force microscope cantilevers: thermal fluctuations and other methods. Nanotechnology 13: 33–37 [Google Scholar]
  26. Milani P, Braybrook SA, Boudaoud A. (2013) Shrinking the hammer: micromechanical approaches to morphogenesis. J Exp Bot 64: 4651–4662 [DOI] [PubMed] [Google Scholar]
  27. Milani P, Gholamirad M, Traas J, Arnéodo A, Boudaoud A, Argoul F, Hamant O. (2011) In vivo analysis of local wall stiffness at the shoot apical meristem in Arabidopsis using atomic force microscopy. Plant J 67: 1116–1123 [DOI] [PubMed] [Google Scholar]
  28. Peaucelle A, Braybrook SA, Le Guillou L, Bron E, Kuhlemeier C, Höfte H. (2011) Pectin-induced changes in cell wall mechanics underlie organ initiation in Arabidopsis. Curr Biol 21: 1720–1726 [DOI] [PubMed] [Google Scholar]
  29. R Development Core Team (2008) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. http://www.R-project.org
  30. Radotić K, Roduit C, Simonović J, Hornitschek P, Fankhauser C, Mutavdžić D, Steinbach G, Dietler G, Kasas S. (2012) Atomic force microscopy stiffness tomography on living Arabidopsis thaliana cells reveals the mechanical properties of surface and deep cell-wall layers during growth. Biophys J 103: 386–394 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Reddy GV, Heisler MG, Ehrhardt DW, Meyerowitz EM. (2004) Real-time lineage analysis reveals oriented cell divisions associated with morphogenesis at the shoot apex of Arabidopsis thaliana. Development 131: 4225–4237 [DOI] [PubMed] [Google Scholar]
  32. Reddy GV, Meyerowitz EM. (2005) Stem-cell homeostasis and growth dynamics can be uncoupled in the Arabidopsis shoot apex. Science 310: 663–667 [DOI] [PubMed] [Google Scholar]
  33. Rotsch C, Radmacher M. (2000) Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys J 78: 520–535 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Routier-Kierzkowska AL, Smith RS. (2013) Measuring the mechanics of morphogenesis. Curr Opin Plant Biol 16: 25–32 [DOI] [PubMed] [Google Scholar]
  35. Routier-Kierzkowska AL, Smith RS. (2014) Mechanical measurements on living plant cells by micro-indentation with cellular force microscopy. Methods Mol Biol 1080: 135–146 [DOI] [PubMed] [Google Scholar]
  36. Routier-Kierzkowska AL, Weber A, Kochova P, Felekis D, Nelson BJ, Kuhlemeier C, Smith RS. (2012) Cellular force microscopy for in vivo measurements of plant tissue mechanics. Plant Physiol 158: 1514–1522 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Sampathkumar A, Krupinski P, Wightman R, Milani P, Berquand A, Boudaoud A, Hamant O, Jönsson H, Meyerowitz EM. (2014) Subcellular and supracellular mechanical stress prescribes cytoskeleton behavior in Arabidopsis cotyledon pavement cells. eLife 3: e01967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Schiessl K, Kausika S, Southam P, Bush M, Sablowski R. (2012) JAGGED controls growth anisotropy and coordination between cell size and cell cycle during plant organogenesis. Curr Biol 22: 1739–1746 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Smyth DR, Bowman JL, Meyerowitz EM. (1990) Early flower development in Arabidopsis. Plant Cell 2: 755–767 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Data
supp_165_4_1399__index.html (1.1KB, html)
supp_pp.114.237115_237115MilanSupplement.doc (5.8MB, doc)

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES