Abstract
Ion-mediated electrostatic interactions play an important role in RNA folding stability. For a RNA in a solution with higher Mg2+ ion concentration, more counterions in the solution can bind to the RNA, causing a strong many-body coupling between the bound ions. The many-body effect can change the effective potential of mean force between the tightly bound ions. This effect tends to dampen ion binding and lower RNA folding stability. Neglecting the many-body effect leads to a systematic error (over-estimation) of RNA folding stability at high Mg2+ ion concentrations. Using the tightly bound ion model combined with a conformational ensemble model, we investigate the influence of the many-body effect on the ion-dependent RNA folding stability. Comparisons with the experimental data indicate that including the many-body effect led to much improved predictions for RNA folding stability at high Mg2+ ion concentrations. The results suggest that the many-body effect can be important for RNA folding in high concentrations of multivalent ions. Further investigation showed that the many-body effect can influence the spatial distribution of the tightly bound ions and the effect is more pronounced for compact RNA structures and structures prone to the formation of local clustering of ions.
INTRODUCTION
RNA folding plays a crucial role in cellular functions.1,2 The equilibrium pathway of RNA folding can generally be characterized into three states: (a) the unfolded state (U), an extended state with no stable secondary or tertiary interactions, (b) the intermediate state (I), a state with stable secondary structures and no stable tertiary interactions and (c) the folded state (N), and a state with stable tertiary interactions.3–6 For a RNA pseudoknot, the intermediate state is a hairpin formed by one of the native helix stems.7–9 The folding stability is defined as the free energy difference between the folded state and the unfolded state. The prediction of the folding stability is highly challenging (partly) due to the difficulty for modeling the unfolded state. For the pseudoknots in the present theoretical study, for the purpose of direct comparison with the experimental data, we focus on the tertiary folding stability of RNA, which is defined as the free energy difference between the tertiary structure and the secondary state.3,9–12 For RNAs that fold through hierarchical pathways (fully unfolded → intermediate secondary structure → folded tertiary structure), the ion-dependence of the free energy difference between the folded state and the intermediate state provides important insights into the ion-mediated tertiary folding stability.
The ionic solution condition and RNA conformational ensemble are two important factors that affect RNA folding stability. The highly negative charges on RNA backbone tend to unfold the RNA due to the repulsive force between the nucleotides while the surrounding cations tend to facilitate the folding through neutralizing RNA backbone charges. Therefore, RNA folding is sensitive to the property of the surrounding ions, such as the ion type, size, valence, and concentration.4,13–28 Furthermore, RNA molecules can be highly dynamic. For a RNA in the unfolded and the intermediate states, RNA can sample an ensemble of conformations.9,11,29–32 Different conformations result in the different distributions of the surrounding ions and hence the different ion-RNA interactions. Therefore, to compute the ion-dependence of RNA folding stability, we need to consider the ion-RNA interactions for each discrete conformation in the conformational ensemble.33,34
Molecular dynamics simulation (MD)35–42 and coarse grained conformational sampling43,44 are the two main methods for RNA 3D conformational modeling. Using the whole space sampling method, Cao and Chen developed a virtual bond-based RNA conformational model (Vfold model) for the calculation of the free energies of loops, secondary structures, and pseudoknots with different loop and helix lengths.43 Experimental tests suggest that the Vfold model may be quite reliable.45–47 Combining the coarse grained description of RNA structure and the molecular dynamics simulation, Ding et al. developed the discrete molecular dynamics (DMD) simulation method to sample RNA conformations.35 The DMD-predicted 3D structures are very close to the experimental structures.35 Based on the Stochastic Dynamics (SD) simulation with a multi-scale modeling method, Chu et al. studied the ion-dependence of the folding stability for simple helix junctions and the predicted results are in good agreement with the experimental findings.36 Using coarse-grained Go-like models,48 Hyeon et al. investigated the structural transitions for three pseudoknots and the predicted melting temperatures agree well with the experimental data.31 By employing a series of experimental methods and replica exchange molecular dynamics (REMD) simulation,38 Stoddard et al. investigated the detailed mechanism of ligand-free interactions in S-adenosylmethionine binding riboswitch at the local and global levels. The findings also support that MD simulations can provide efficient sampling for RNA conformations. Combining conformational sampling and the generalized Born method, Tjong et al. successfully predicted the salt effects on the electrostatic energies in protein-protein interactions.49,50 Furthermore, the MD simulations have been employed to calculate ion distributions around a RNA.23 Such detailed ion distribution, which may not be achievable by a coarse-grained model, have provided highly needed information for understanding ion-mediated RNA stabilization.
One of the most important issues in theoretical prediction of RNA folding stability is the evaluation of the electrostatic interactions between the different components in the solution, such as ion-RNA, ion-ion, RNA-RNA interactions. In ion-RNA interaction, the (multivalent) Mg2+ ions can reach a high concentration in the close vicinity of the RNA. The bound ions become coupled through the long-range Coulomb force. A result of the coupling (correlation) is that the electric potential acting on an ion is not only a function of its own coordinates but also a function of the simultaneous configuration of the other ions. The ion correlation effect is stronger for higher valent ions at higher concentrations. One of the consequences of the ion correlation is the coupling between the different ion binding events to the different nucleotides, namely, ion binding to a nucleotide is not only dependent on the RNA structure and the ion concentration but also on the ion binding events at other locations.
To account for the ion correlation and fluctuation effects, we developed the Tightly Ion Binding (TBI) model.51 The essence of the model is to treat the strongly correlated ions separately by enumerating their many-ion distributions. The model is different from the mean field-based models which treat ions as uncoupled particles. The complete sampling of full continuous ion distributions around the RNA is computationally intractable. In the TBI model, we describe multi-ion distributions using discrete ion binding modes. Specifically, each ion binding mode is described as a way to partition the ions onto the different nucleotides.51,52 For each ion binding mode, the total energy is evaluated as the sum of the effective pairwise interactions between the different pairs of the bound ions. It is important to note that such an effective pairwise interaction (potential of mean force) can be strongly influenced by the presence of ions bound to the nearby nucleotides.53 As a result, the effective pairwise interaction is determined not only by the coordinates of the ion pair under consideration but also by the distribution of the other ions. This is a many-body effect.
The original TBI model accounts for the correlated ion distribution by enumerating all the possible discrete ion binding modes. However, the model does not consider the influence of the other (nearby) ions on the pairwise potential of mean force. For a high divalent ion concentration such as [Mg2+]> 5 mM, computational models show a systematic error of over-estimating Mg2+ ion binding and folding stability.11,51,54,55 In the present study, we develop a modified TBI model by accounting for the many-body effect.
The many-body effect has been observed in other systems such as charged colloids. Wu et al. applied a van der Waals-type theory to investigate the many-body effect on the phase behavior of charged colloids56 and found that, when colloidal triplets are close to each other, the many-body force can be strong. Depending on the separation of the charged particles, the three-body force can be repulsive or attractive. Berk et al. use the local ion concentration-dependent effective dielectric constant57 to simulate the multi-ion correlation effect. The effective ion-ion interaction potential successfully reproduced the solution osmotic properties and the ion coordination up to concentrations of 2.8 M aqueous NaCl.57 These studies suggest that the many-body effect may indeed play an important role.
In addition to considering the many-body effect, we also develop a theoretical framework for predicting ion-dependent RNA pseudoknot tertiary folding stability through conformational sampling. Applications of the theory to three representative examples (T2, BWYV pseudoknots and yeast tRNAPhe) show that the new model reported here leads to much improved theory-experiment agreements.
METHODS
Structural model
The tertiary folding free energy is defined as the free energy difference between the folded (N) and the intermediate (I) states. For the folded state (pseudoknot), we use the structure from the Protein Data Base (PDB): The beet western yellow virus pseudoknot (BWYV, PDB code: 437D)58 and T2 gene 32 mRNA pseudoknot (T2, PDB code: 2TPK).59 For the intermediate state (hairpin), we use an ensemble of conformations generated by molecular dynamic simulations (MD). The initial 3D hairpin structures in the simulations are the ones adopted from the native pseudoknots (see Figs. 1(a) and 1(b)).11,60 To test the sensitivity to the choices of the initial structures in the simulation, we also select the different initial structures.
FIG. 1.
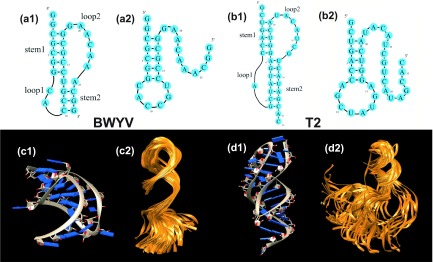
The 2D (a1, a2, b1, b2) and 3D (c1, c2, d1, d2) structures of the folded (pseudoknot: a1, b1, c1, d1) and the intermediate (hairpin: a2, b2, c2, d2) states of two pseudoknot-forming RNAs: BWYV (a1, a2, c1, c2) and T2 RNA (b1, b2, d1, d2). The PDB codes of the 3D structures are 437D for the BWYV pseudoknot (c1)58 and 2TPK for the T2 pseudoknot (d1),59 respectively. (c2) and (d2) show the conformational ensembles of the intermediate states. Each conformational ensemble contains 100 conformations extracted from a MD trajectory.
An intermediate state such as a hairpin can access a large ensemble of three-dimensional conformations10 and the different conformations have the different ion-RNA interactions. To generate the conformations for the intermediate (hairpin) state, We perform MD simulations starting from the initial hairpin structure. The initial hairpin structure is embedded in the TIP3 box with the water shell, using the Solvate plug-in in VMD.61 The MD simulations are carried out using the NAMD 2.8 package.62 The temperature is kept at the experimental condition (298 K for BWYV and 310 K for T2) and the Sodium concentration is kept at 1 M. For each RNA, we perform 5 independent simulations (trajectories) and the total time of each simulation is 18 ns. The coordinates of all the atoms are written to the NAMD dcd file every 5 ps. We obtain 3600 conformations (snapshots) for each trajectory. We then use the uniform Monte Carlo sampling method to randomly select 100 out of the 3600 structures (see Figs. 1(c) and 1(d)). For each selected conformation, we run electrostatic calculation (TBI) for the given ionic condition. For a given ion concentration, the mean free energy of the system is computed as the arithmetic average of the five datasets.
The tightly bound ion model
Through the enumeration of the discrete multi-ion distributions, the TBI model accounts for the correlated ion binding modes and the fluctuation of ion distribution.3,51,54,63–65 The model classifies the ions into two types according to their correlation strengths: The tightly bound ions (strongly correlated) and the diffusive ions (weakly correlated). The tightly bound ions are distributed in the close vicinity of RNA surface while the diffusive ions are distributed in the bulk solution. The region around the RNA is correspondingly divided into the tightly bound and the diffusive regions. For an N-nt RNA, the tightly bound region can be divided into N cells, where each cell is around a phosphate. For the tightly bound ions, by partitioning the tightly bound ions among the N cells, we enumerate the discrete ion configurations. For the diffusive ions, we use the mean-field theory (nonlinear Poisson-Boltzmann equation, NLPB or PB).23,66,67
For each ion binding mode M, we calculate the partition function of the system by sampling the coordinates of the tightly bound ions within their respective cells,
| (1) |
where is the partition function for the uniform ion solution (without the polyelectrolytes). NZ is the total number of the z-valent counterions and V is the volume of the solution. Nb and are the number and the volume integral for the tightly bound ions, respectively. ΔGb is the mean Coulomb interaction energy between all the discrete charge-charge pairs (including the phosphate groups and the tightly bound ions) in the tightly bound region; ΔGd is the free energy for the electrostatic interactions between the diffusive ions and between the diffusive ions and the discrete charges in the tightly bound region, and the entropic free energy of the diffusive ions. is the (Born) self-polarization energy for the discrete charges in the tightly bound region.8,10
Averaging over all the possible ion distributions of the tightly bound ions gives the electrostatic free energy of the system,
| (2) |
Conformational ensemble
In general, an intermediate state (such as a hairpin) of a RNA can adopt a large ensemble of three-dimensional conformations due to the flexibility of the loop and the tails.10 Our ensemble-based approach to the intermediate state is quite different from the previous approaches which replaced the ensemble of conformation with a rigid helix.3,7,68 The previous simplified method ignores the complex details of RNA 3D structure and the method may not be valid for complex RNA structures because the free energy for an ensemble of conformations can be different from that of a rigid structure.
We first test the sensitivity of the electrostatic free energy to the structure model of the intermediate state (hairpin). Previous studies used a rigid RNA helix to represent the average effect of the conformational ensemble for the intermediate state.7,68 The method is based on the hypothesis that in the intermediate state, the average electrostatic property of a nucleotide in the intermediate state is mainly determined by the helical elements in the secondary structure,7,68 therefore, the total free free energy can be approximated as the number of nucleotides multiplied by the free energy per nucleotide computed for the helix system. Such an approximation gave good predicted results for low [Mg2+]. However, the validity of the approximation has not been tested for more general ion solutions.
To test the sensitivity of the folding stability to the variation of the intermediate structure model, we compute the folding stability of he yeast tRNAPhe (PDB code: 1TRA).69 We choose two different helices (11-bp and 25-bp) for the evaluation of the free energy per nucleotide. As shown in Fig. S4 of the supplementary material,76 we find that for low [Mg2+] (< 0.4 mM), the different structure models give nearly the same results. For higher [Mg2+], however, the estimated folding stability based on the 25-bp model is lower than that from the 11-bp model. The result suggests that for higher [Mg2+] the previous simplified approach may not be accurate and the prediction of the folding stability is sensitive to the intermediate structure model.
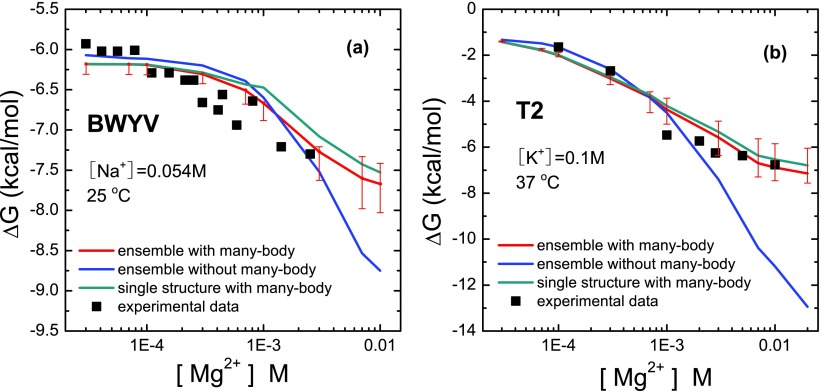
We then examine the effect of the conformational ensemble on the calculation of the RNA folding free energy, we compare the results based on the single structure (the lowest energy structure of the selected 500 conformations) and the ensemble of conformations for the intermediate state (hairpin). For the RNAs that we tested (BWYV and T2 pseudoknot-forming RNAs), the lowest energy structure-based calculations slightly underestimate the folding stability than the ensemble-based results (see Fig. 4). The result suggests the importance of accounting for the effect of the flexible conformations.
FIG. 4.
A test to show the potential significance of the many-body effect: the calculated [Mg2+]-dependence of the folding free energies for BWYV11 (a) and T260 (b). Each plot contains four datasets in order to show the impact of the many-body effect and the effect of the conformational ensemble (for the intermediate state). The comparisons with experimental data suggest the importance of the many-body effect at high [Mg2+]. We show the dispersion for the ensemble-based results with the many-body effect. The dispersion is for the different sets of the conformational ensembles.
To further test the sensitivity of the predicted tertiary folding free energy to the conformational sampling scheme, we perform two tests. In the first test, we randomly select two different conformational ensembles, a 100-conformation ensemble and a 300-conformation ensemble from a trajectory of the T2 pseudoknot (see Fig. S5a of the supplementary material76). We find that the two ensembles give nearly the same folding free energy as the original one (see Fig. S5a of the supplementary material76). All the conformations are randomly selected through uniform Monte Carlo sampling from the snapshots of an 18-ns MD trajectory. The result (Fig. S5a of the supplementary material76) suggests that the free energy predictions may be stable against the variations of the sampling scheme. In the second test, we run simulations starting from the different initial structures with RMSD over 8 Å (see Figs. S5b and S6 of the supplementary material76). We find that the different initial (hairpin) structures will slightly affect RNA folding stability.
Many-body effect
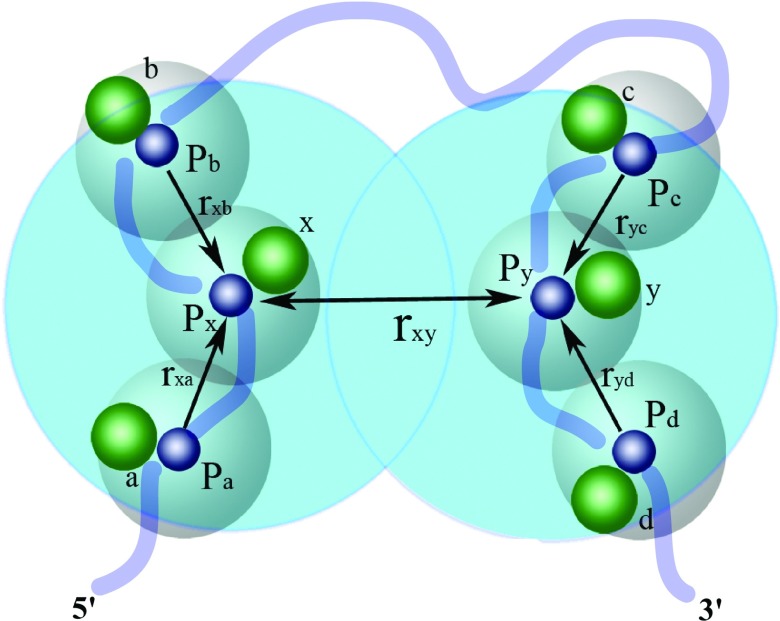
We investigate the influence of the many-body effect on the effective interaction energy (potential of mean force) between ion pairs. As shown in Fig. 2, we consider two Mg2+ ions x and y, each can sample positions in their respective tightly bound cells (denoted in Fig. 2 as the steel-blue region around a phosphate). We examine the influence of the other tightly bound Mg2+ ions, such as ions a and b around ion x and ions c and d around ion y, on the potential of mean force between x and y. Each ion can move around about the phosphate in the respective tightly bound cell, so the mean distance between the ions can be roughly described by the distance between the respective phosphates. For a given ion (e.g., x in Fig. 2), we consider the effect of all the ions within a distance Rmin. Our extensive tests (Fig. S1 in the supplementary material76) point to an estimated Rmin value at 17 Å. The value of Rmin is close to twice the diameter of a hydrated Mg2+ ion, whose radius is about 4.5 Å. As shown below, the estimated value for Rmin is consistent with the results for charged colloid systems. A previous study indicated that the many-body effect for a charged colloid system becomes significant when the inter-particle separation is within about 1.5 times the diameter of the colloid particles. Our value of Rmin is roughly in the same range as . The previous study for the colloid systems focused on the three-body effect. The fact that our estimated Rmin is larger than suggests that the many-body effect in the ion-RNA system may go beyond the three-body effect.
FIG. 2.
A schematic figure for the many-body effect: the (small) blue and (large) green spheres represent the phosphates and the bound (hydrated) Mg2+ ions, respectively. The steel-blue shaded region around each phosphate denotes the tightly bound cell around a nucleotide.51 The large sky-blue regions denote the many-body region within which the many-body effect is strong. The blue chain represents the RNA conformation.
The total free energy of the system ΔGtot can be partitioned into the pairwise term without the many-body effect ΔG(0) and the many-body correction ΔG(corr),
| (3) |
where ΔG(0) can be calculated from the original TBI model51 and ΔG(corr) can be calculated as a sum of the three-body, four-body, ..., and higher order correlation energies.70,71 For instance, the three-body correlation energy for any ion triad ijk is given by
| (4) |
where ΔGijk is the full free energy by sampling all the possible three-ion configurations, (ab = ij, ik or jk) is the pairwise free energy (potential of mean force) calculated by ignoring the presence of the third ion. In our calculation, to sample the bound ion positions, we discretize the tightly bound region with grids and enumerate all the possible coordinates of the three ions (on the grids). For each ion configuration, we evaluate the Coulombic energy for the charged system. Averaging over all the possible three-ion configurations gives the three-body free energy ΔGijk. The model treats ions as hard spheres and accounts for the volume exclusion of the ions in the enumeration of ion configurations. Therefore, the calculation takes into account both the steric correlation and the Coulomb correlation.
We tested the three-body correlation energy for the BWYV RNA; See Fig. 1-(a1) and (c1) for the two-dimensional and three-dimensional structures of the BWYV pseudoknot. Without the many-body effect, the original TBI model significantly overestimates the BWYV folding stability for [Mg2+] higher than 5 mM. Including the three-body correlation, however, is not sufficient to account for the difference between the theoretical prediction and the experimental data. The result suggests that we need to include higher order correlation terms. Explicit calculations for the four-body and higher order terms require prohibitively long computer time. Therefore, we will use a heuristic method to estimate the many-body effect.
The intensity of the many-body effect is related to the local concentration (density) of the ions. The higher local concentration leads to a stronger many-body correlation effect. For a given RNA system, the number of the bound Mg2+ ions is dependent on the RNA structure as well as the ion concentration. We propose the following form for ΔG(corr),
| (5) |
Here Dmin is equal to the diameter of the ions (Dmin = 9 Å for Mg2+) and is the minimum distance between two ions. rion is the distance between the tightly bound Mg2+ ions , such as rxa and rxb in Fig. 2. ⟨rion⟩ is the average distance. For example, in the many-body region for Mg2+ ion in Fig. 2, the ⟨rion⟩ is computed as . Thus, our model contains only one fitted parameter α. For a given bound ion around a phosphate (e.g., ion x around phosphate Px or ion y around phosphate Py), we define its “many-body region” using the criteria rion ⩽ Rmin = 17 Å. For a given ion x, its the many-body region is the spherical volume about x with radius Rmin. All the ions such as ions a and b around x in Fig. 2 that are within the many-body region should be considered for the many-body effect. The actual value of ⟨rion⟩ for a given ion binding mode is determined from the average over the inter-ion distances for all the ions within the many-body region. The weighting factor α is a coefficient. For the RNA systems that we have tested, we found α ≃ 1 gives robust results for the different RNAs in the different solution conditions. Thus, the modified pairwise interaction energy between two tightly bound cells, such as the tightly bound cells around phosphates Px and Py in Fig. 2, can be computed as
| (6) |
where, is the free energy (potential of mean force) between the tightly bound cells x and y without considering the many-body effect. is given by the original TBI model. and are the mean inter-ion distance for ions in the many-body regions around Px and Py, respectively.
Ion-dependent RNA tertiary folding free energy
We focus on the tertiary folding free energy, defined as the free energy difference between the intermediate state (I) and the folded state (F). For the folded state, for the PDB 3D structures of the RNA, we calculate the electrostatic free energy ΔGel(F) using the above modified TBI model, which accounts for the many-body effect.
For each conformation i in the conformational ensemble of the intermediate state, we compute the electrostatic free energy using the modified TBI model. The Boltzmann average over all the possible conformation for state I gives the free energy of the state ΔGel(I),
| (7) |
The total RNA tertiary folding free energy ΔGtot is approximately the sum of the electrostatic contribution ΔGel and the non-electrostatic contribution ΔGnel,3,63,72
| (8) |
Assuming the non-electrostatic contribution ΔGnel is independent of the ionic concentration, we can estimate ΔGnel from the experimental result for a reference ion concentration such as 1M NaCl,
where is the total folding free energy as determined by experiment at the experimental ionic condition. ΔGel(Na+) is the electrostatic free energy at the same condition of the experiment. ΔGel(Na+) can be determined from the TBI model.
RESULTS AND DISCUSSION
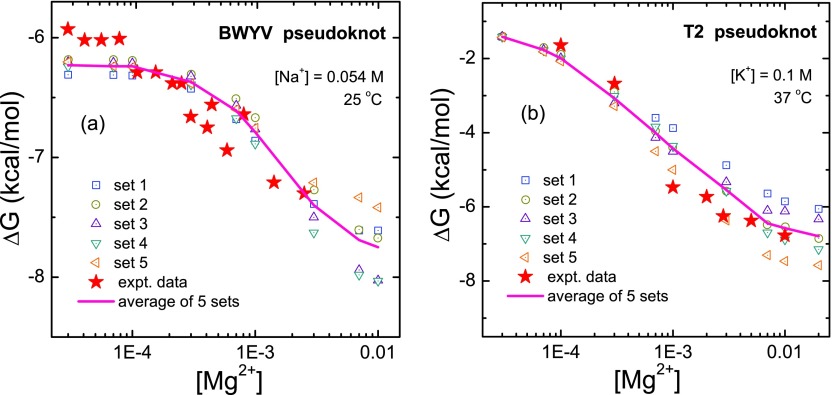
As shown in Fig. 3, for the two RNAs (BWYV and T2) that we studied, the different ensembles of the intermediate structures lead to slightly different tertiary folding stabilities. The average folding free energies (the pink solid line in Fig. 3) are in good agreement with the experiment data. This suggest that our approach for intermediate state conformations may be reliable.
FIG. 3.
Theory-experiment comparisons of the folding free energy for (a) the BWYV and (b) the T2 pseudoknots. In the theoretical predictions, we use the same temperature and ionic solution condition as the experiment. Here the folding free energy is defined as the free energy difference between the folded state (pseudoknot) and the folding intermediate (hairpin). The red filled stars denote the experimental data for BWYV11 and T2,60 respectively. For each case, we select five sets of hairpin conformational ensembles, each with 3600 conformations generated from MD simulations. The conformations are randomly selected from the conformations generated from MD trajectories. For each set of the conformational ensemble, the ensemble-averaged result for the folding free energy is marked with an open symbol. In each figure, the pink solid line shows the average value of the five sets of the results. The x-axis denotes the ion concentration in units of M.
Many-body effect on folding stability
To understand how the many-body effect influences the RNA folding stability, we compare the results predicted by the original and the modified TBI model. As shown in Figs. 4(a) and 4(b), the many-body effect does not affect the low-[Mg2+] behavior for the two pseudoknots. For higher [Mg2+] (>1mM), however, the many-body effect can be important. Without the many-body effect, the folding stability is significantly overestimated. The many-body effect leads to notable improvements in the predictions. For a solution with high [Mg2+], the impact of the many-body effect is pronounced. In our calculation, at [Mg2+] = 10 mM, the many-body effect can cause the tertiary folding free energy to change by 4 kcal/mol and 1 kcal/mol for the T2 and BWYV pseudoknots, respectively. It is important to note that there exist many other factors, such as the detailed force field and ion-specific hydration effect in ion-RNA interaction, that could also influence the predicted ion-dependence of the folding stability, The improved results here suggest that the many-body effect may be one of the factors that could influence the predicted ion-dependent folding stability.
The improved prediction for the ion-dependence of the folding free energy at high [Mg2+] can also be found for the yeast tRNAPhe system. As shown in Fig. S4 of the supplementary material,76 the many-body effect leads to a better prediction for the folding stability at high [Mg2+]. As pointed out by Soto et al.,11 the nonlinear Poisson-Boltzmann model (PB) causes a systemic error in the prediction of the folding stability7,11,68 especially under the high [Mg2+] condition. This could be caused by neglecting ion-ion correlation, ion dehydration and other effects.11 One of the differences between PB and our TBI model is the ion correlation. The improved predictions by the TBI model (see, for example, Fig. 4S of the supplementary material76) suggests that ion-ion correlation may be a factor worth considering in the Mg2+-mediated RNA folding.3,51,54,63–65,72
Physically, depending on the distribution of the Mg2+ ions, the many-body effect could increase or decrease the electrostatic free energy for a given RNA. For a pair of ions such as x and y in Fig. 2, if the surrounding ions such as a and b for x and c and d for y are located between x and y, the surrounding ions tend to push x and y away from each other and to lower the potential of mean force (between x and y). In contrast, if the surrounding ions flank the two sides of the (x, y) pair, the surrounding ions tend to push x and y closer, causing an increase in the potential of mean force. This would lead to an increase in the electrostatic energy and a decrease in ion binding. For the low energy modes, we found that the former scenario is less likely to occur because the average distance of two tightly bound ions (x and y in Fig. 2) is generally not large enough to allow the insertion of (hydrated) ions between x and y. Instead, we found that the later scenario occurs more frequently, in which case the many-body effect tends to increase the electrostatic energy. Since the effect is stronger for the folded state than for the unfolded state (see below), the net result of the many-body effect is to lower the folding stability. This analysis is consistent with the conclusions drawn from the previous theory-experiment comparisons, which showed that ignoring the many-body effect could cause a systematic over-estimation of the folding stability at high [Mg2+].
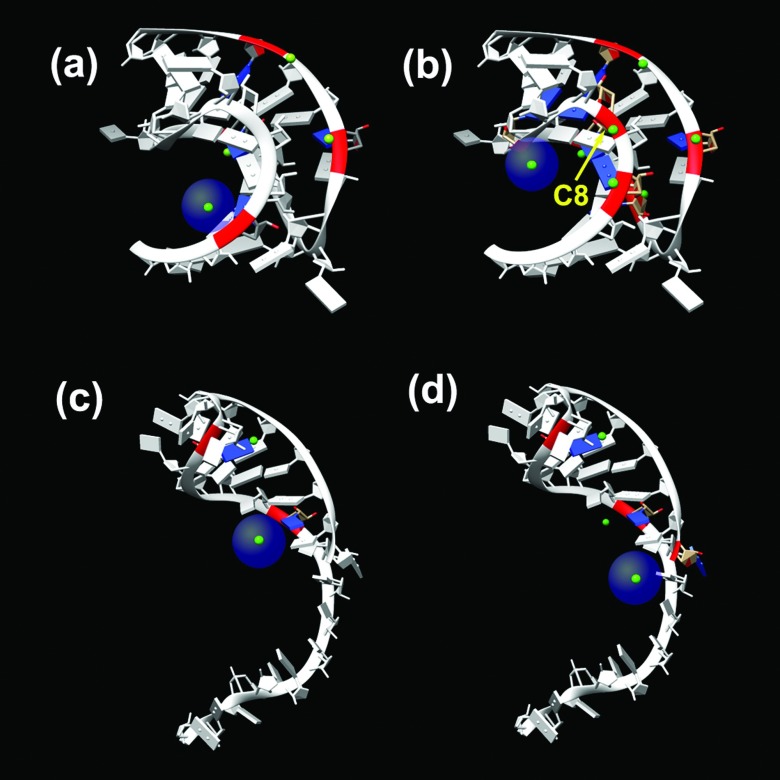
In a low [Mg2+] solution ([Mg2+] < 1mM), the concentration of the tightly bound Mg2+ ions is quite low for both the folded and the unfolded states and the many-body effect on the folding stability can be neglected. At higher [Mg2+], however, the concentration of the tightly bound ions is increased. Because the native structure (pseudoknot for T2 and BWYV RNA) is more compact and hence has a higher charge density than the (partially) unfolded structure (hairpin for T2 and BWYV), the native state attracts more tightly bound ions and hence a stronger many-body effect than the unfolded structure. For example, for the BWYV RNA (Fig. 5) in a solution with 0.054 mM Na+ and 0.02 M Mg2+ at 25 °C, the TBI model predicts that the number of bound Mg2+ ions in the lowest energy binding mode is reduced from 7 (without the many body effect) to 4 (with the many body effect) for the pseudoknot as compared to a reduction from 3 to 2 for the hairpin.
FIG. 5.
The lowest energy ion binding mode for BWYV RNA in 0.02 M Mg2+ and 0.054 M Na+ at T = 25 °C. The half-transparent spheres denote the (hydrated) Mg2+ ions. (a) and (c) The predicted ion distribution from the current modified TBI model with the many-body effect for (a) the native pseudoknot and (c) the hairpin structure. For comparison, (b) and (d) show the (lowest energy) ion binding mode for the pseudoknot and hairpin structures with the original TBI model without the many-body effect.
Furthermore, because the native structure is more compact and has a larger number of bound ions, the average distance between the tightly bound ions of compact native (pseudoknot) structure is shorter than that of the less compact (partially) unfolded (hairpin) structure. For example, for the BWYV native pseudoknot, in the lowest energy ion binding mode, the nucleotide C8 has a bound Mg2+ ion (Fig. 5(b)). The distances between the C8 phosphate and other ion binding sites (phosphate) are all less than 17 Å. For the corresponding unfolded (hairpin) structure, the average distance between the bound Mg2+ ions is approximately 20 Å (>17Å). As a result, the many-body effect is stronger for the compact native structure than for the unfolded hairpin structure. Through reducing the number of bound ions, the net result of the many-body effect is to lower the folding stability of the compact native structure. Furthermore, the effect is stronger for higher ion concentrations, causing a more pronounced many-body effect as shown in Fig. 4.
Many-body effect on the bound ions distribution
The TBI model63,64 gives the mean fraction of the tightly bound ions for a given nucleotide i by the following equation:
| (9) |
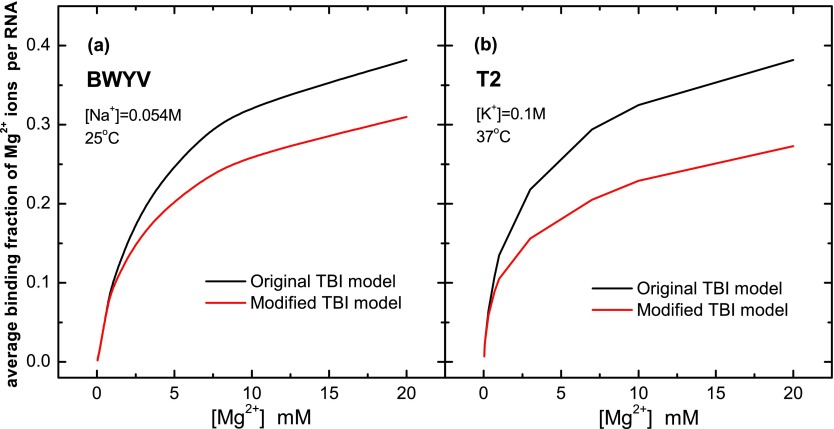
where is the number of bound ions on the ith nucleotide in ion binding mode M, ZM is the partition function for mode M, Z is the total partition function for all the modes (Eq. (1)). Fig. 6 shows the comparison between the predictions from the original (without the many-body effect) and the modified (with the many-body effect) TBI models for the average Mg2+ ion binding fraction. We found that the many-body effect can indeed reduce ion binding.
FIG. 6.
Comparison of the average Mg2+ ion binding fraction with and without the many-body effect for BWYV and T2 RNAs, respectively.
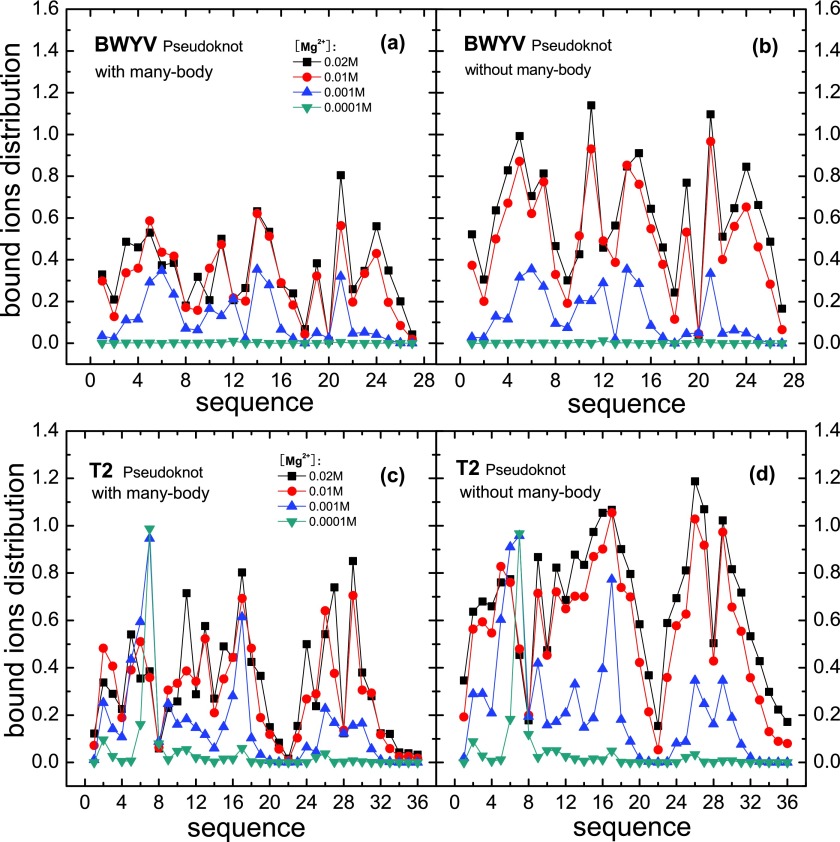
Furthermore, we go beyond the number of bound ions by calculating distribution of the bound ions using Eq. (9). The calculation revealed several features regarding ion distributions (see Figs. 7 and S2 of the supplementary material76). For both BWYV and T2 RNAs, at low [Mg2+], the number of bound ions is relatively small and the many-body effect is weak, so the distributions of the tightly bound ions with (Figs. 7(a) and 7(c)) and without (Figs. 7(b) and 7(d)) the many-body effect are nearly identical. At high [Mg2+]([Mg2+] > 5 mM), the larger number of bound ions and the stronger many-body effect cause a considerable change in the tightly bound ion distribution. First, except for the several most probable binding sites, the binding fractions for most binding sites (phosphates) are significantly reduced by the many-body effect. For example, at the relatively high ion concentration [Mg2+] = 0.02 M, [Na+] = 0.054 M and 25 °C, as shown in Fig. 5, the many-body effect causes the number of bound ions in the lowest free energy binding mode to be reduced by three and the bound ions become less densely populated. Second, some peak locations (most probable binding sites) on the tightly bound ion distribution curve are slightly shifted. The many-body effect from the nearby Mg2+ ions causes an effective restriction on the sampling space of the ions. The nearby ions could also push around and eventually displace a tightly bound ions, causing the change in the ion distribution.
FIG. 7.
The average Mg2+ ion distributions for BWYV (a,b) and T2 (c,d) with (a,c) and without (b,d) the many-body effect. Solution condition: [Na+] = 0.054 M and T = 25 °C for BWYV; [K+] = 0.1 M and T = 37 °C for T2.
RNA structure and the many-body effect
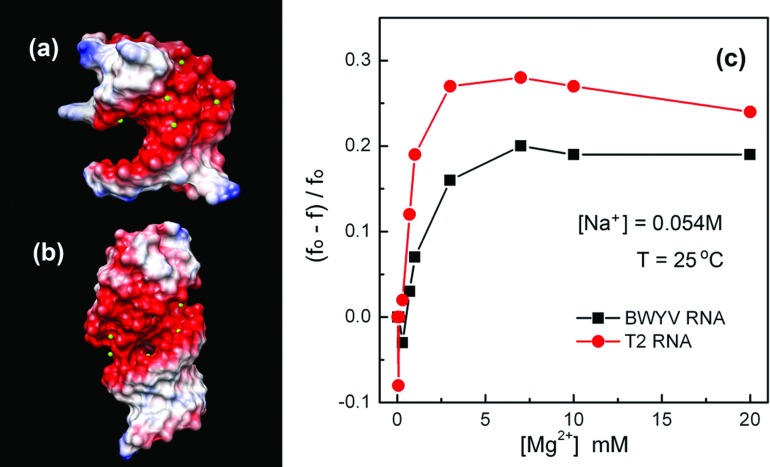
The free energy changes caused by the many-body effect are structure-dependent. To understand the influence of the RNA structure on the many-body effect, we compare the ion effects between BWYV and T2 pseudoknots at [Na+] = 0.054 M and T = 25 °C. At [Mg2+] = 0.02 M, the many-body effect causes the number of the bound Mg2+ ions at the lowest energy mode to be reduced by six and three for the T2 and BWYV RNAs, respectively. For other [Mg2+] ⩾ 1 mM, we found that the many-body effect is consistently stronger for T2 than for BWYV (see Fig. 8).
FIG. 8.
The electric potential distribution for BWYV (a) and T2 (b). The area rendered red color is the negative electric potential area. The colored surface images for the two RNAs are produced by UCSF Chimera (version 1.8).75 Figure (c) shows the many-body effect-induced changes in the average binding fraction of the divalent ions. The y-axis in (c) is the relative change of the Mg2+ ion binding fraction induced by the many-body effect. f and f0 are the binding fraction with and without the many-body effect.
The many-body effect arises from the electrostatic interactions among the vicinal tightly bound Mg2+ ions. Thus the magnitude of the many-body effect is directly related to the local density (concentration) of the tightly bound ions. At the same ionic condition, the density of bound ions depends on the structure of RNA. For example, without the many-body effect, the numbers of bound Mg2+ ions for the lowest energy mode are 11 and 7 for T2 and BWYV, respectively. For the different structures, the bound ions can be partitioned among the RNA nucleotides in different ways. In general, ions have high probability to bind to the region of high RNA charge density such as the major grooves of the helices and the pocket structures formed by tertiary motifs. The number of bound ions and the distribution of the tightly bound ions are dependent on the structure. For example, a more compact structure would attract more ions and consequently, the closer clustering of the tightly bound ions causes a stronger many-body effect. To compare the T2 with BWYV pseudoknots, we found that the average distance and the shortest distance between the tightly bound Mg2+ ions in the lowest energy mode are 12.5 Å and 9 Å for T2 13.4 Å and 11.6 Å for BWYV, respectively. The tightly bound Mg2+ ions on T2 are more densely populated than the tightly bound ions on BWYV. This may be the reason why the many-body effect for T2 is stronger than for BWYV.
The influence of monovalent cations on the many-body effect
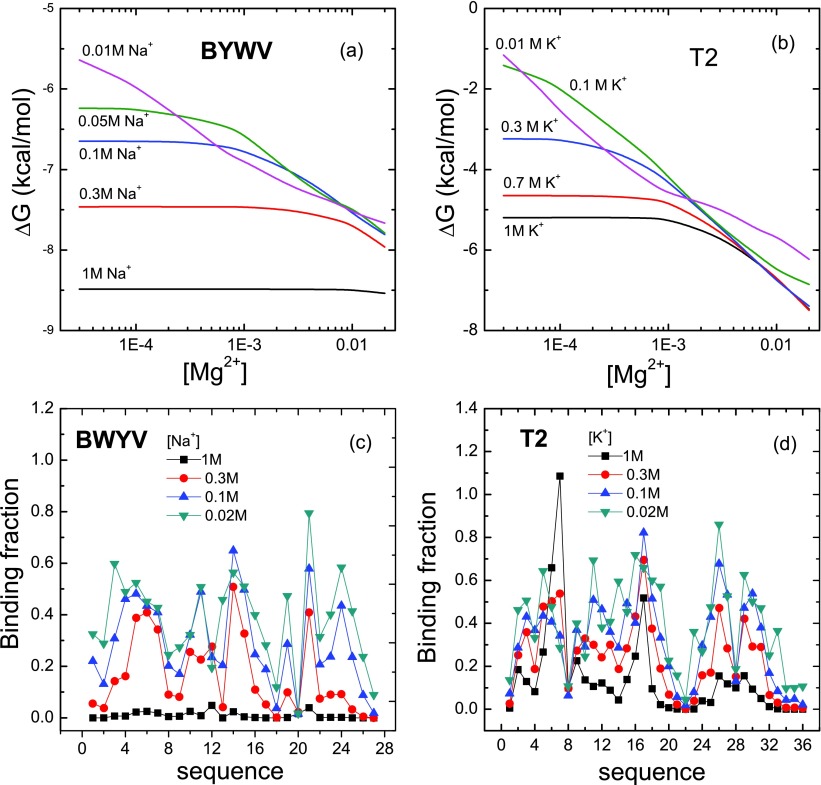
In a monovalent/divalent ion mixture solution, for a low monovalent ion concentration, divalent ion binding is dominant. The larger number of bound divalent ions can lead to a stronger many-body effect which tends to decrease the RNA folding stability (Fig. 9). A high concentration of the monovalent ion would dampen the effect of Mg2+ binding and cause a decreased number of bound Mg2+ ions (see Fig. 9). Thus, for a given [Mg2+], the many-body effect is more pronounced for a lower monovalent ion concentration.
FIG. 9.
The [Mg2+]-dependent folding free energy of BWYV (a) and T2 (b) RNA pseudoknots under various monovalent ion concentrations. The x-axis denotes the ion concentration in units of M. (c) and (d) The average distributions of the bound ions for the native structures under four different monovalent ion concentrations. In order to be consistent with the experimental condition, we assume T = 25 °C for BWYV and T = 37 °C for T2.
To investigate how the many-body effect impacts the interplay between the monovalent and divalent ions, we applied both the original TBI model (without the many-body effect) and the modified TBI model (with the many-body effect) to compute the binding fraction of the two types of ions. As shown in Table I, we found that the many-body effect weakens Mg2+ ion binding and effectively enhances monovalent ion binding. Furthermore, Table I shows that the binding fraction of Na+ is (20% in Table I) higher than K+. This is because a (hydrated) Na+ (3.5 Å in radius) is less bulky than a (hydrated) K+ ion (4.5 Å in radius) and can approach the RNA with a closer distance with a stronger ion-RNA attraction. Accordingly, the binding fraction of Mg2+ is (10% in Table I) smaller for a Mg2+/Na+ mixture than for a Mg2+/K+ solution of the same ion concentration.
Table I.
The table shows the average binding fractions of divalent and monovalent ions for the T2 RNA in a divalent/monovalent mixture solution. We found that the binding fraction of Na+ is about 20% higher than that of K+ and the ion binding fraction of the divalent ions in the Mg2+/K+ mixed solution is 10% less than in the Mg2+/Na+ mixed solution.
| 0.02M Mg2+/0.1 M K+ | 0.02M Mg2+/0.1 M Na+ | |||
|---|---|---|---|---|
| Divalent ion | Monovalent ion | Divalent ion | Monovalent ion | |
| With the many-body effect | 0.27 | 0.28 | 0.24 | 0.34 |
| Without the many-body effect | 0.38 | 0.13 | 0.35 | 0.17 |
CONCLUSION
To summarize, we have developed a conformational ensemble-based TBI model for the ion-dependent free energy of RNA intermediates. The ensemble-based model gives improved predictions than the models based on the rigid helix representation of the folding intermediates. Applying the model to BWYV and T2 RNAs, we have shown that the many-body effect of the ions can influence the effective interaction energy (potential of mean force) between the tightly bound ions through Coulomb repulsion and volume exclusion. This effect is more important for (a) multivalent ions such Mg2+ than monovalent ions such as Na+ and (b) higher ion concentrations, in which case there are a larger number of bound ions on RNA. Our other main conclusions are:
-
1.
Previous studies without considering the many-body effect tend to systematically over-estimate the RNA folding stability at higher Mg2+ concentration. Comparisons with the experimental data (for BWYV and T2) show that the inclusion of the many-body effect leads to much improved predictions for the folding stability at higher Mg2+ concentration. This test supports the conclusion that the many-body effect may be important for ion effect in RNA folding at high Mg2+ concentration (e.g., [Mg2+] ⩾ 5 mM).
-
2.
The many-body effect could influence the ion binding in two ways. First, it tends to lower the overall number of bound ions. Second, the repulsion from other ions could cause a minor shift in the distribution of the bound ions.
-
3.
The results of the many-body effect are dependent on the RNA structure. In general, more compact structures can cause more densely populated tightly bound ions and a stronger many-body effect.
-
4.
Although the many-body effect for monovalent ions is weak, the concentration of monovalent ions can modulate the binding of the multivalent ions and the resultant many-body effect (of the multivalent ions). A higher concentration of the monovalent ion can dampen the divalent ion binding and weaken the overall many-body effect.
Despite the useful conclusions listed above, the current model has several limitations. For example, it is limited by the crude estimation for the many-body effect-induced changes of the potential of mean force. Further development should be based on a more rigorous theory for the many-body correlations either through an analytical theory for many-body Coulomb correlation or through accurate numerical computation based on the configurational sampling for the many-ion system. Moreover, experimental test/validation for the predicted ion distributions (Figs. 7 and 9) would be highly needed.73,74 Nevertheless, the combination of the conformational sampling and the computation of the electrostatic free energy based on the current modified Tightly Bound Ion model may offer a useful starting point for further studies of problem.
ACKNOWLEDGMENTS
This research is supported by NIH Grant No. GM063732 and NSF Grant No. MCB0920411. Most of computations involved in this research are performed on the HPC resources at the University of Missouri Bioinformatics Consortium (UMBC).
REFERENCES
- 1.Adams P. L., Stahley M. R., Kosek A. B., Wang J., and Strobel S. A., Nature 430, 45–50 (2004). 10.1038/nature02642 [DOI] [PubMed] [Google Scholar]
- 2.Schroeder R., Barta A., and Semrad K., Nat. Rev. Mol. Cell Biol. 5, 908–919 (2004). 10.1038/nrm1497 [DOI] [PubMed] [Google Scholar]
- 3.Tan Z. J. and Chen S. J., Met. Ions Life Sci. 9, 101–124 (2011). [PMC free article] [PubMed] [Google Scholar]
- 4.Draper D. E., Grilley D., and Soto A. M., Annu. Rev. Biophys. Biomol. Struct. 34, 221–243 (2005). 10.1146/annurev.biophys.34.040204.144511 [DOI] [PubMed] [Google Scholar]
- 5.Fang X. W., Pan T., and Sosnick T. R., Biochemistry 38, 16840–16846 (1999). 10.1021/bi991700n [DOI] [PubMed] [Google Scholar]
- 6.Giedroc D. P., Theimer C. A., and Nixon P. L., J. Mol. Biol. 298, 167–185 (2000). 10.1006/jmbi.2000.3668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Misra V. K., Shiman R., and Draper D. E., Biopolymers 69, 118–136 (2003). 10.1002/bip.10353 [DOI] [PubMed] [Google Scholar]
- 8.Woodson S. A., Curr. Opin. Chem. Biol. 9, 104–109 (2005). 10.1016/j.cbpa.2005.02.004 [DOI] [PubMed] [Google Scholar]
- 9.Grilley D., Soto A. M., and Draper D. E., Proc. Natl. Acad. Sci. U.S.A. 103, 14003–14008 (2006). 10.1073/pnas.0606409103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grilley D., Misra V., Caliskan G., and Draper D. E., Biochemistry 46, 10266–10278 (2007). 10.1021/bi062284r [DOI] [PubMed] [Google Scholar]
- 11.Soto A. M., Misra V., and Draper D. E., Biochemistry 46, 2973–2983 (2007). 10.1021/bi0616753 [DOI] [PubMed] [Google Scholar]
- 12.Tinoco I. Jr. and Bustamante C., J. Mol. Biol. 293, 271–281 (1999). 10.1006/jmbi.1999.3001 [DOI] [PubMed] [Google Scholar]
- 13.Ha B. Y. and Thirumalai D., Macromolecules 36, 9658–9666 (2003). 10.1021/ma021226k [DOI] [Google Scholar]
- 14.Draper D. E., RNA 10, 335–343 (2004). 10.1261/rna.5205404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Leipply D., Lambert D., and Draper D. E., Meth. Enzymol. 469, 433–463 (2009). 10.1016/S0076-6879(09)69021-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen A. A., Marucho M., Baker N. A., and Pappu R. V., Meth. Enzymol. 469, 411–432 (2009). 10.1016/S0076-6879(09)69020-0 [DOI] [PubMed] [Google Scholar]
- 17.Moghaddam S., Caliskan G., Chauhan S., Hyeon C., Briber R. M., Thirumalai D., and Woodson S. A., J. Mol. Biol. 393, 753–764 (2009). 10.1016/j.jmb.2009.08.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li P. T. X. and Tinoco I., J. Mol. Biol. 386, 1343–1356 (2009). 10.1016/j.jmb.2009.01.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stepenson W., Asare-Okai P. N., Chen A. A., Keller S., Santiago R., Tenenbaum S. A., Garcia A. E., Fabris D., and Li P. T. X., J. Am. Chem. Soc. 35, 5606–5611 (2013). 10.1021/ja310820h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li P. T. X. and Tinoco I., Annu. Rev. Biochem. 77, 77–100 (2008). 10.1146/annurev.biochem.77.061206.174353 [DOI] [PubMed] [Google Scholar]
- 21.Qiu X. Y., Parsegian V. A., and Rau D. C., Proc. Natl. Acad. Sci. U.S.A. 107, 21482–21486 (2010). 10.1073/pnas.1003374107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bowman J. C., Lenz T. K., Hud N. V., and Williams L. D., Curr. Opin. Chem. Biol. 22, 262–272 (2012). 10.1016/j.sbi.2012.04.006 [DOI] [PubMed] [Google Scholar]
- 23.Kirmizialtin S., Pabit S. A., Meisburger S. P., Pollack L., and Elber R., Biophys. J. 102, 819–828 (2012). 10.1016/j.bpj.2012.01.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chen H., Meisburger S. P., Pabit S. A., Sutton J. L., Webb W. W., and Pollack L., Proc. Natl. Acad. Sci. U.S.A. 109, 799–804 (2012). 10.1073/pnas.1119057109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Andresen K., Das R., Park H. Y., Kwok L. W., Lamb J. S., Smith H., Herschlag D., Finkelstein K. D., and Pollack L., Phys. Rev. Lett. 93, 248103 (2004). 10.1103/PhysRevLett.93.248103 [DOI] [PubMed] [Google Scholar]
- 26.Qiu X., Giannini J., Howell S. C., Xia Q., Ke F., and Andresen K., Biophys. J. 105, 984–992 (2013). 10.1016/j.bpj.2013.07.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Harris R. C., Boschitsch A. H., and Fenley M. O., J. Chem. Phys. 140, 075102 (2014). 10.1063/1.4864460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lipfert J., Sim A. Y. L., Herschlag D., and Doniach S., RNA 16, 708–719 (2010). 10.1261/rna.1985110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Staple D. W. and Butcher S. E., PLoS Biol. 3, e213 (2005). 10.1371/journal.pbio.0030213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen S. J., Annu. Rev. Biophys. 37, 197–214 (2008). 10.1146/annurev.biophys.37.032807.125957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cho S. S., Pincus D. L., and Thirumalai D., Proc. Natl. Acad. Sci. U.S.A. 106, 17349–17354 (2009). 10.1073/pnas.0906625106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Boehr D. D., Nussinov R., and Wright P. E., Nat. Chem. Biol. 5, 789–796 (2009). 10.1038/nchembio.232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Philips A., Milanowska K., Lach G., Boniecki M., Rother K., and Bujnicki J. M., Bioinformatics 28, 198–205 (2012). 10.1093/bioinformatics/btr636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.He Z., Zhu Y., and Chen S. J., Phys. Chem. Chem. Phys. 16, 6367–6375 (2014). 10.1039/c3cp53655f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ding F., Sharma S., Chalasani P., Demidov V. V., Broude N. E., and Dokholyan N. V., RNA 14, 1164–1173 (2008). 10.1261/rna.894608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chu V. B., Lipfert J., Bai Y., Pande V. S., Doniach S., and Herschlag D., RNA 15, 2195–2205 (2009). 10.1261/rna.1747509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Baird N. J., Gong H., Zaheer S. S., Freed K. F., Pan T., and Sosnick T. R., J. Mol. Biol. 397, 1298–1306 (2010). 10.1016/j.jmb.2010.02.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stoddard C. D., Montange R. K., Hennelly S. P., Rambo R. P., Sanbonmatsu K. Y., and Batey R. T., Structure 18, 787–797 (2010). 10.1016/j.str.2010.04.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hayes R. L., Noel J. K., Mohanty U., Whitford P. C., Hennelly S. P., Onuchic J. N., and Sanbonmatsu K. Y., J. Am. Chem. Soc. 134, 12043–12053 (2012). 10.1021/ja301454u [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Borkar A. N., De Simone A., Montalvao R. W., and Vendruscolo M., J. Chem. Phys. 138, 215103 (2013). 10.1063/1.4804301 [DOI] [PubMed] [Google Scholar]
- 41.Stephenson W., Asare-Okai P. N., Chen A. A., Keller S., Santiago R., Tenenbaum S. A., Garcia A. E., Fabris D., and Li P. T., J. Am. Chem. Soc. 135, 5602–5611 (2013). 10.1021/ja310820h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cisneros G. A., Karttunen M., Ren P., and Sagui C., Chem. Rev. 114, 779–814 (2014). 10.1021/cr300461d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cao S. and Chen S. J., Nucleic Acids Res. 34, 2634–2652 (2006). 10.1093/nar/gkl346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Xia Z., Gardner D. P., Gutel R. R., and Ren P. Y., J. Phys. Chem. B 114, 13497–13506 (2010). 10.1021/jp104926t [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cao S. and Chen S. J., Phys. Biol. 5, 016002 (2008). 10.1088/1478-3975/5/1/016002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cao S. and Chen S. J., RNA 17, 2130–2143 (2011). 10.1261/rna.026658.111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cao S. and Chen S. J., Nucleic Acids Res. 40, 4681–4690 (2012). 10.1093/nar/gks052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hyeon C. and Thirumalai D., Proc. Natl. Acad. Sci. U.S.A. 102, 6789–6794 (2005). 10.1073/pnas.0408314102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tjong H. and Zhou H. X., J. Phys. Chem. B 111, 3055–3061 (2007). 10.1021/jp066284c [DOI] [PubMed] [Google Scholar]
- 50.Tjong H. and Zhou H. X., J. Chem. Phys. 126, 195102 (2007). 10.1063/1.2735322 [DOI] [PubMed] [Google Scholar]
- 51.Tan Z. J. and Chen S. J., J. Chem. Phys. 122, 044903 (2005). 10.1063/1.1842059 [DOI] [Google Scholar]
- 52.Borukhov I., Bruinsma R., Gelbart W., and Liu A., Phys. Rev. Lett. 86, 2182–2185 (2001). 10.1103/PhysRevLett.86.2182 [DOI] [PubMed] [Google Scholar]
- 53.Zimmermann M. T., Leelananda S. P., Gniewek P., Feng Y., Jernigan R. L., and Kloczkowski A., J. Struct. Funct. Genomics 12, 137–147 (2011). 10.1007/s10969-011-9113-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tan Z. J. and Chen S. J., Biophys. J. 101, 176–187 (2011). 10.1016/j.bpj.2011.05.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.He Z. J. and Chen S. J., J. Chem. Theory Comput. 8, 2095–2102 (2012). 10.1021/ct300227a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Wu J. Z., Blanch H. W., Bratko D., and Prausnitz J. M., J. Chem. Phys. 113, 3360–3365 (2000). 10.1063/1.1287173 [DOI] [Google Scholar]
- 57.Hess B., Holm C., and Vegt N., Phys. Rev. Lett. 96, 147801 (2006). 10.1103/PhysRevLett.96.147801 [DOI] [PubMed] [Google Scholar]
- 58.Su L., Chen L. Q., Egli M., Berger J. M., and Rich A., Nat. Struct. Biol. 6, 285–292 (1999). 10.1038/6722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Holland J. A., Hansen M. R., Du Z. H., and Hofman D. W., RNA 5, 257–271 (1999). 10.1017/S1355838299981360 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nixon P. L. and Giedroc D. P., Biochemistry 37, 16116–16129 (1998). 10.1021/bi981726z [DOI] [PubMed] [Google Scholar]
- 61.Humphrey W., Dalke A., and Schulten K., J. Mol. Graphics 14, 33–38 (1996). 10.1016/0263-7855(96)00018-5 [DOI] [PubMed] [Google Scholar]
- 62.Phillips J. C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R. D., Kale L., and Schulten K., J. Comput. Chem. 26, 1781–1802 (2005). 10.1002/jcc.20289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tan Z. J. and Chen S. J., Biophys. J. 92, 3615–3632 (2007). 10.1529/biophysj.106.100388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Tan Z. J. and Chen S. J., Biophys. J. 99, 1565–1576 (2010). 10.1016/j.bpj.2010.06.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Tan Z. J. and Chen S. J., Biophys. J. 94, 3137–3149 (2008). 10.1529/biophysj.107.122366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Onufriev A., Ann. Rep. Comput. Chem. 4, 125–137 (2008). 10.1016/S1574-1400(08)00007-8 [DOI] [Google Scholar]
- 67.Baker N. A., Bashford D., and Case D. A., in New Algorithms for Macromolecular Simulation, edited by Leimkuhler B., Chipot C., Elber R., Laaksonen A., Mark A., Schlick T., Schutte C., and Skeel R. (Springer-Verlag Berlin and Heidelberg GmbH & Co. K; 2006). [Google Scholar]
- 68.Misra V. K. and Draper D. E., J. Mol. Biol. 317, 507–521 (2002). 10.1006/jmbi.2002.5422 [DOI] [PubMed] [Google Scholar]
- 69.Westhof E. and Sundaralingam M., Biochemistry 25, 4868–4878 (1986). 10.1021/bi00365a022 [DOI] [PubMed] [Google Scholar]
- 70.Hankins D., Moskowitz J. W., and Stillinger F. H., J. Chem. Phys. 53, 4544 (1970). 10.1063/1.1673986 [DOI] [Google Scholar]
- 71.Chen W. and Gordon M. S., J. Phys. Chem. 100, 14316–14328 (1996). 10.1021/jp960694r [DOI] [Google Scholar]
- 72.Tan Z. J. and Chen S. J., Biophys. J. 90, 1175–1190 (2006). 10.1529/biophysj.105.070904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Meisburger S. P., Sutton J. L., Chen H., Pabit S. A., Kirmizialtin S., Elber R., and Pollack L., Biopolymers 99, 1032–1045 (2013). 10.1002/bip.22265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Greenfeld M. and Herschlag D., Methods Enzymol. 469, 375–389 (2009). 10.1016/S0076-6879(09)69018-2 [DOI] [PubMed] [Google Scholar]
- 75.Pettersen E. F., Goddard T. D., Huang C. C., Couch G. S., Greenblatt D. M., Meng E. C., and Ferrin T. E., J. Comput. Chem. 25, 1605–1612 (2004). 10.1002/jcc.20084 [DOI] [PubMed] [Google Scholar]
- 76. See supplementary material at http://dx.doi.org/10.1063/1.4890656E-JCPSA6-141-062428 for additional tests and illustrations.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4890656E-JCPSA6-141-062428 for additional tests and illustrations.