The Importance of the Hook Region of the Cochlea for Bone-Conduction Hearing

Abstract

For the most part, the coiled shape of the cochlea has been shown to have only minor importance for air-conducted hearing. It is hypothesized, however, that this coiled shape may play a more significant role for the bone-conducted (BC) route of hearing, through inertial forces exerted by the middle ear and cochlear fluid, and that this can be tested by comparing the results of applying BC stimuli in a variety of different directions. A three-dimensional finite element model of a human middle ear coupled to the inner ear was formulated. BC excitations were simulated by applying rigid-body vibrations normal to the surface of the basilar membrane (BM) at 0.8 (d¹), 5.8 (d²), 15.6 (d³), and 33.1 (d⁴) mm from the base of the cochlea, such that relative motions of the fluid within the cochlea produced excitations of the BM. The vibrational direction normal to the BM surface at the base of the cochlea (d¹) produced the highest BM velocity response across all tested frequencies—higher than an excitation direction normal to the BM surface at the nonbasal locations (d²–d⁴), even when the stimulus frequency matched the best frequency for each location. The basal part of the human cochlea features a well-developed hook region, colocated with the cochlear vestibule, that features the largest difference in fluid volume between the scala vestibuli (SV) and scala tympani (ST) found in the cochlea. The proximity of the hook region to the oval and round windows, combined with it having the biggest fluid-volume difference between the SV and ST, is thought to result in a maximization of the pressure difference between the SV and ST for BC stimuli normal to the BM in this region, and consequently a maximization of the resulting BM velocity.

Introduction

The cochlea is the auditory portion of the inner ear, consisting of fluid-filled chambers, the basilar membrane (BM), and the organ of Corti, which is the sensory component. The name cochlea, however, is derived from its peculiar shape. The cochlea is a spiral-shaped cavity in the bony labyrinth, which in humans makes 2.5 turns around its axis, the modiolus. The curvature of the cochlear spiral changes smoothly from the tightly curved turn at the apex to the less curved turn near the base. Due to this smooth change in curvature, the BM within the cochlear fluid chambers also exhibits smooth changes in its curvature. At the base of the cochlea, however, the curvature of the cochlear spiral and the BM changes more radically, resulting in a normal direction to the BM surface that is significantly different from those at the more-apical regions. This basal region, in which a radical change in curvature occurs, is called the hook region.

The effect of the smooth curvature of the cochlea on hearing thresholds has been studied in comparison with models representing the cochlea as a straight box shape. Viergever (1) and Steele and Zais (2) concluded, through mathematical models solving Laplace’s equation, that there should be an insignificant difference in the BM velocity between a coiled BM and a straight BM in the cochlea. Contrary to their conclusions, however, others have predicted that the coiled shape should, in fact, have a significant effect on hearing, given that 1), the shear gain of the cochlear partition (defined as the ratio of shearing displacements of the tectorial membrane and the top of the organ of Corti in response to BM deflection) increases at the apex (3); and 2), the ratio of the radii of curvature from the outermost turn to the innermost turn of the cochlear spiral correlates strongly with low-frequency hearing limits (4,5). However, these studies are limited in that 1), the effect of the coiled shape on hearing was examined only for the air-conduction (AC) pathway, with the bone-conduction (BC) pathway left unconsidered; and 2), the more significant change in curvature taking place in the hook region was not considered. Recently, Steele et al. (6) modeled the full three-dimensional (3-D) behavior of the viscous fluid in the hook region of the human cochlea. Although they were able to show the evanescent wave as well as the fast wave in the scalae fluid ducts of the hook region, the effect of the hook region on BC hearing was not considered. In short, despite several studies concerning the hook region, only AC hearing, and not BC hearing, had been examined.

In BC hearing, the inertia of the middle ear (ME) ossicles and cochlear fluid are believed to play a significant role (7). Specifically, when the skull is shaken by BC inputs such as from loud sounds impinging on the head, from a tuning fork, or from a BC transducer, these inputs are thought to primarily produce an inertial input to the cochlea. Bárány (8) and Békésy (9) investigated the relationship between the shaking direction of the skull and BC hearing through various measurements. Békésy posited that the human ME structure is optimized so as to minimize the hearing of one’s own voice through bone conduction. He showed several characteristics of the ME ossicles that might minimize the transmission of ME inertial motions into the cochlea. For example, he showed that the skull predominantly vibrates in the vertical direction during the phonation of the vowel oo (as in pool), and additionally claimed that the oval shape of the stapes footplate is for the purpose of reducing the input energy into the cochlea due to such vertically oriented skull vibrations. Thus, one could expect that changing the direction of vibration could alter the rotational axes of the ME ossicles or stapes footplate, and that this could in turn affect one’s sensitivity of BC hearing. Our working hypothesis is that BC vibrations presented along a direction normal to the BM surface in the hook region produce larger vibrations of the BM in comparison to BC vibrations presented in other directions. Here, it should be noted that the hook region in this study indicates the entire region over which the vestibule meets the scala vestibuli (SV), which is also where the curvature of the BM is significantly different from the more apical regions.

To test this hypothesis, we developed a 3-D finite element (FE) coiled-cochlea model of the human auditory periphery. Specifically, to investigate the effects of input direction on BC hearing, the geometry for the FE model was obtained from microcomputed tomography (μCT) images of a human-cadaver temporal bone, such that the geometry, including that of the hook region, is more anatomically realistic than that of previous models (10,11). The current model was validated by comparing model responses (e.g., the ME pressure-gain function, cochlear impedance, BM velocity, and best-frequency (BF) map) with published data (see the Supporting Material).

BC excitations were simulated by shaking the fixed bony structures of the model, such that the ME structure and cochlear fluid could experience relative vibrations depending on their coupling to the vibrating bone and their inertia. To investigate the effects of stimulation direction on BM vibration, a total of seven different shaking directions were tested and compared, consisting of 1), the x, y, and z directions of the Cartesian coordinate axes, which were respectively defined as the lateral, superior, and anterior directions of the skull; and 2), the d¹, d², d³, and d⁴ directions that were defined as vectors orthogonal to the BM surface at four different locations along the BM, spanning from the base to the apex. The results indicate that vibrations orthogonal to the BM at the d¹ position in the hook region dominate the response.

Methods

Although the ME model used in this study is identical to what Homma et al. (12) and Kim et al. (10) used previously, the cochlear model is identical to the one used in another previous study (13), but without the inclusion of a superior semicircular canal dehiscence. The superior semicircular canal dehiscence was the main focus of the previous publication. The geometries of the cochlear components, including the semicircular canals, were derived from μCT scanned images of a human temporal bone. Therefore, for the current model the cochlear geometry is spiral-shaped instead of having the simplified box shape. The FE model mesh was created using HYPERMESH (Altair Engineering, Troy, MI), an FE pre/postprocessing program, and the model simulations were performed using ACTRAN (Free Field Technologies, Belgium), a vibroacoustic FE solver, which is well suited for frequency domain and vibroacoustic coupling calculations. Fig. 1 shows the current FE model of the human auditory periphery, consisting of the ME and cochlea, and including the semicircular canals. A detailed description of the ME structure can be found in Homma et al. (12).

Figure 1.

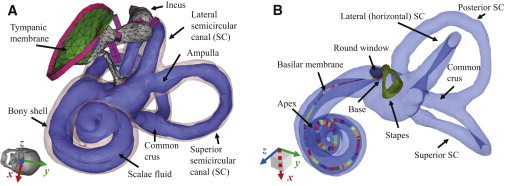
An FE model of the human auditory periphery. (A) ME structures, the bony shell of the cochlea (light pink), and the scalae fluid (light purple), including the semicircular canals. (B) The stapes, RW, and BM. The SV is connected to the ST through the helicotrema, which is a hole located at the end of the BM at the apex. The various colors along the BM are used solely to distinguish neighboring sections, with each section having its own Young’s modulus and set of local coordinates. The global x, y, and z directions correspond to the lateral, superior, and anterior directions of the skull, as shown by the tilted skull image of panel A. To see this figure in color, go online.

Due to the spiral cochlear geometry, the mechanical properties of some components (i.e., the BM, stapes annular ligament, and round window (RW)) were tuned to make the model results consistent with published experimental data (see the Supporting Material) such as a map of the BF locations along the BM (14), as well as ME transfer functions (15–18).

Material properties

Material properties for the FE model were reported previously (10), except for the RW, stapes annular ligament, and BM, because the properties of those components were altered from the previous model due to the modified geometry. The density of the RW membrane was set to 1200 kg/m³, its Young’s modulus was set to 0.05 MPa, and its loss factor was set to a frequency-independent value of 0.8. The density of the stapes annular ligament was also set to 1200 kg/m³, but its Young’s modulus was set to 0.7 MPa, and its loss factor was set to vary linearly with the log-scaled frequency, such that its value was 0.017 at 0.1 kHz, 0.17 at 1 kHz, and 1.7 at 10 kHz. In this study, the BM was divided into 35 sections of equal length. To model the stiffness change along the length of the BM, the Young’s modulus of the BM was gradually decreased from the base to the apex (i.e., from 6.5 to 5.5 MPa in the longitudinal direction, and 0.2 to 0.1 GPa in the transverse direction, with a loss factor of 0.3). The density of the BM was assumed to be 1000 kg/m³, because the density of soft tissue is usually assumed to match that of water, and its orthotropic material properties were determined by tuning the Young’s moduli to make the BF-to-place cochlear map reasonably consistent with experimental data (14). The orthotropic ratio (E_x/E_y, where E_x and E_y are the Young’s moduli for the local longitudinal and transverse directions relative to the BM, respectively) was nearly 0.03 throughout. The detailed process for tuning the model has been described previously (10). It should be noted that the fluid in both the SV and ST is assumed to be almost incompressible, because the speed of sound in fluid is a high but finite (i.e., not infinite) value of 1500 m/s.

The model geometry and FE mesh

The BM width changed linearly from 170 μm at the base to 500 μm at the apex, and the thickness changed from 7 μm at the base to 0.9 μm at the apex. The BM was meshed using 18,400 six-noded pentahedral shell elements, and the RW was meshed using 400 four-noded tetrahedral elements. The SV and ST cochlear fluid chambers were meshed using 518,600 four-noded linear tetrahedral elements.

With the inclusion of the semicircular canals in the current model, their ∼120 mm³ of additional fluid volume brought the total fluid volume to 280 mm³. The fluid in the cochlea was all assumed to be perilymph, so the scala media containing the endolymph fluid has been collapsed into the cochlear partition, whose properties are dominated by the pectinate zone of the BM. In addition, the present model formulation is for passive mechanics and does not consider the active cochlear amplification mechanisms (19–22).

Simulations using AC or BC excitation

AC excitation was simulated by assigning a uniformly distributed dynamic unit pressure over the tympanic membrane surface on the ear canal side. Fixed-displacement boundary conditions were applied to boundaries of the structure, such as the ends of the ligaments and tendons, the edge of the tympanic annulus, and the bony shell of the cochlea. On the other hand, among the inertial and compressional inputs to the cochlea thought to be important for BC hearing (23), only the inertial component is considered here. The inertial BC excitations were simulated by assigning sinusoidal displacement vectors of equal magnitude and direction at the boundaries of the model. These boundaries include the wall of the cochlea and the ends of the ME supporting structures such as the incus ligament, tensor tympani muscle, anterior ligament, lateral ligament, stapedius tendon, and tympanic annulus. Assigning directional vibrations to these boundary conditions effectively produces rigid body vibrations of the bony parts of the temporal bone. It should be noted that in reality, the strain of the bone may not be negligible at high frequencies, such that the outer bony shell may not move in-phase with one another. However, in this simulation, because the bone was assumed to have a high Young’s modulus, the outer bony shells do show in-phase movement within the simulated frequency range. The directions of excitation corresponded to the x, y, and z axes defined in Fig. 1, which represent the lateral, superior, and medial directions of the skull, respectively; and to vectors normal to the BM surface at four locations between the cochlear base and apex, i.e., d¹–d⁴, as defined in Fig. 2. The magnitude of the applied displacement vector, D_b, was 0.01 μm for each of these directional vibrations. Although this magnitude was selected arbitrarily, it was large enough to reveal the inertial effects of the ME ossicles and fluid in the cochlea. Because this is a linear model, the cochlear responses were not affected by the choice of input magnitude, since the output variables were normalized by the relevant input variable, such as the input velocity or input volume velocity into the cochlea.

Figure 2.

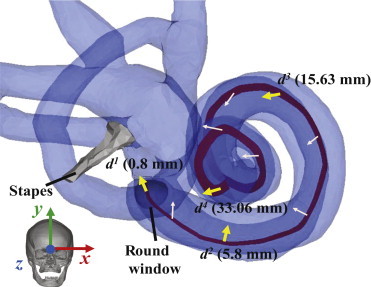
Directional vectors of simulated BC stimuli, denoted by x, y, z, d¹, d², d³, and d⁴. As in Fig. 1, the x, y, and z directions correspond to the lateral, superior, and anterior directions of the skull (see inset image), respectively. The thick yellow arrows, for d¹, d², d³, and d⁴, represent stimuli normal to the BM at distances 0.8, 5.8, 15.63, and 33.06 mm from the base, respectively. The thin light-pink arrows represent normal directions to the BM at intermediate positions. To see this figure in color, go online.

The d¹, d², d³, and d⁴ directions shown in Fig. 2 constitute directions normal to the BM surface at distances from the base of the cochlea of, respectively, 0.80, 5.80, 15.63, and 33.06 mm. Although d¹–d⁴ were all defined to be normal to the local BM surface, the coiled and angled shape of the BM is such that the orthogonal vector components of these four directions were different enough from one another so as to stimulate different 3-D motions of the BM. These BC simulations with different excitation directions were performed both with and without the ME ossicles, to distinguish the inertial contributions of the ME ossicles from those of the cochlear fluid by itself. Removing the ME ossicles was implemented by deleting all of the ME components except for the stapes and stapes annular ligament, and then essentially removing any remaining inertial contribution from the stapes by decreasing its density by two orders of magnitude.

Decomposition analysis for pressures in the scalae fluid, and BM velocity

The SV and ST fluid pressures along the BM length, P_SV(χ) and P_ST(χ), respectively, were calculated for model elements directly adjacent to the BM surface, on the longitudinal centerline of the BM. P_SV(χ) and P_ST(χ), and the volume velocities of the oval window (U_OW) and round window (U_RW), were decomposed into symmetric components, P_S(χ) and U_S, and antisymmetric components, P_A(χ) and U_A, according to the following equations (10):

$$\begin{array}{c}{P}_{\text{S}}\left(\chi \right)=\frac{1}{\sqrt{2}}\left[P_{\text{SV}}\left(\chi \right)+P_{\text{ST}}\left(\chi \right)\right],U_{\text{S}}=\frac{1}{\sqrt{2}}\left[U_{\text{OW}}+U_{\text{RW}}\right],\\ P_{\text{A}}\left(\chi \right)=\frac{1}{\sqrt{2}}\left[P_{\text{SV}}\left(\chi \right)-P_{\text{ST}}\left(\chi \right)\right],and{U}_{\text{A}}=\frac{1}{\sqrt{2}}\left[U_{\text{OW}}-U_{\text{RW}}\right].\end{array}$$ (1)

The BM velocity along the BM length, V_BM(χ), was calculated in the direction normal to the BM surface at each of the locations, χ.

Validation of the FE model, and cochlear responses to AC and BC excitation

The responses of the current model (e.g., the ME pressure-gain function, cochlear impedance, BM velocity, and BF map) were compared against published data (see the Supporting Material). In addition, the cochlear responses to AC and BC excitation were calculated to verify their consistency with the previous model’s (10) cochlear responses (not shown). The detailed processes of model validation are described in the Supporting Material.

Results

Directional effects of BC excitation

Varying the vibratory direction for a fixed input frequency

The BC excitations were simulated in the x, y, z, d¹, d², d³, and d⁴ directions (see Fig. 2). The resulting relative BM velocities for these excitation directions are respectively denoted as V^x, V^y, V^z, V^d1, V^d2, V^d3, and V^d4; and each of these was normalized by the BM velocity for the d¹ directional excitation (V^d1) to reveal any differences due to the direction of the BC excitation. Note that in taking these ratios, both velocities are, in fact, relative BM velocities of the form ΔV_BM = V_BM – V_B, where V_BM is the BM velocity and V_B is the velocity of the bone, even though we drop the preceding Δ and the subscript BM from the notation for convenience and refer to them simply as velocity ratios (e.g., V^d1 is defined as V_BM^d1 – V_B^d1, where V_B^d1 is the BC velocity in the d¹ direction used to stimulate the model). If the velocity ratios between each case and the d¹ directional excitation (V/V^d1) are below 0 dB for every simulated frequency, then the BM-velocity magnitudes for the d¹ directional excitation (V^d1) are higher than those for the other directional excitations (V^d2, V^d3, and V^d4). Figs. 3 and 4 present these normalized BM velocities, of the form V/V^d1, up to the BF positions at 0.5 kHz (24 mm; A), 1 kHz (20 mm; B), and 7 kHz (8 mm; C), both without (Fig. 3) and with (Fig. 4) the ossicular inertia of the middle ear. As can be seen in Figs. 3 and 4, the magnitude of every normalized result lies below 0 dB, except for the case of V^x/V^d1 with the middle ear at 1 kHz, which means that the magnitude of the BM velocity due to the d¹ directional excitation is almost always higher than those due to the other directional excitations. Interestingly, although the V^y/V^d1 ratios were decreased by ∼2 dB after adding the ME ossicles, the ratios for the other directions were all increased due to the added ME inertia. However, because each velocity in the plotted ratios is affected differently by the presence or absence of the ME inertia, according to the excitation direction, it is difficult to determine the specific effects of the ME inertia for a given excitation direction based on the ratios shown in Figs. 3 and 4 alone. For this reason, see Fig. 7, which plots velocity ratios for each excitation direction between the case without the ME and the case with the ME, thus allowing the effects of the ME for each excitation direction to be seen directly.

Figure 3.

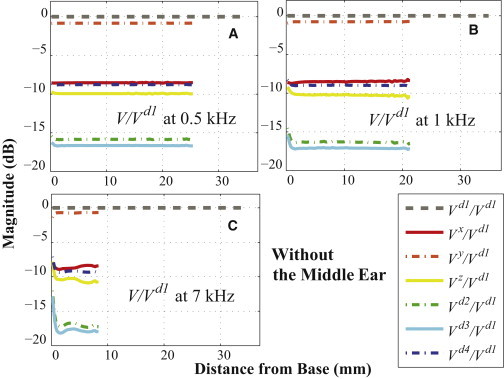
(A–C) Ratios of the BM velocities, V/V^d1, for BC excitations at (A) 0.5 kHz, (B) 1 kHz, and (C) 7 kHz. Every V represents a relative BM velocity, ΔV_BM = V_BM– V_B, for a given excitation direction. For this figure, the ME structure was not included. To see this figure in color, go online.

Figure 4.

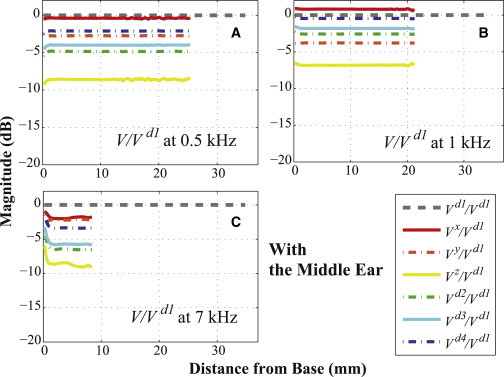
The same as Fig. 3, except the ME structure was included. To see this figure in color, go online.

Figure 7.

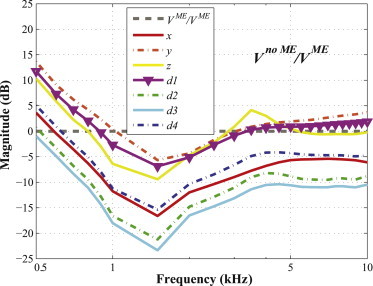
Ratios of the relative BM velocity in each vibrational direction (i.e., x, y, z, d¹, d², d³, and d⁴), between cases without the ME (V^{no ME}) and with the ME (V^ME). To see this figure in color, go online.

Varying the input frequency for a fixed vibratory direction

Figs. 5 and 6 are based on the same kind of BM velocity distribution results shown in Figs. 3 and 4, plotted up to the BF position and normalized by the velocity of the d¹ directional excitation (V/V^d1), except each panel now corresponds to just one excitation direction and contains curves for a total of 24 different stimulus frequencies (spaced every 0.1 kHz from 0.5 to 1 kHz, and every 0.5 kHz from 1 to 10 kHz), without the ME structure (Fig. 5) and with the ME structure (Fig. 6). Because every line is shown up to the BF position corresponding to the input frequency, the lines feature different lengths along the horizontal axis of the figures. The frequency is indicated by the coloring of the lines, with blue-violet representing 0.5 kHz, and red-brown representing 10 kHz.

Figure 5.

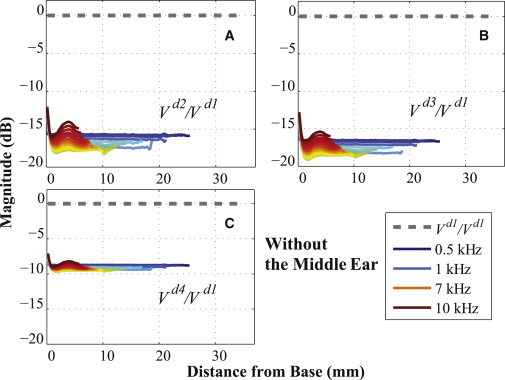
Ratios of BM velocities for different excitation directions, (A) V^d2/V^d1, (B) V^d3/V^d1, and (C) V^d4/V^d1, for 24 frequencies from 0.5 to 10 kHz (spaced every 0.1 kHz from 0.5 to 1 kHz, and every 0.5 kHz from 1 to 10 kHz). As in Figs. 3 and 4, every V represents a relative BM velocity, ΔV_BM = V_BM– V_B, for a given excitation direction. In the legend, only four frequencies (0.5, 1, 7, and 10 kHz) among all the simulated frequencies are marked. For this figure, the ME structure was not included. To see this figure in color, go online.

Figure 6.

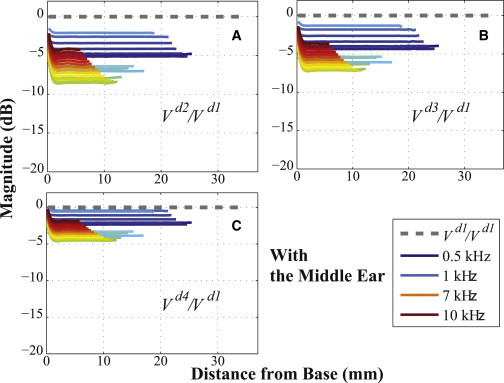
The same as Fig. 5, but with the ME structure included. To see this figure in color, go online.

In summary, in Figs. 3–6, all of the simulated velocity ratios (relative to V^d1) are <0 dB, except for V^x with the ME structure at 1 kHz, showing that the d¹ velocity almost always produces the largest simulated BM magnitude.

Fig. 7 shows the relative BM velocity without the ME mass (V^{no ME}) normalized by the relative BM velocity with the ME mass (V^ME), for each vibrational direction (x, y, z, d¹, d², d³, and d⁴). The lines for all directions in Fig. 7 reach their lowest values near 1.5 kHz, and most values of the ratios lie below 0 dB, which indicates that the velocities tend to be smaller in the absence of the ME ossicles contributing their inertia. Exceptions to this, in which the velocities become larger without the presence of the ME ossicles, include the values for the y, z, and d¹ directions below 1 kHz and above 5 kHz, and the values for the x and d⁴ directions below 0.6 kHz.

Discussion

Directional effects

Effects of the d¹ directional excitation of the hook region

Figs. 3 and 4 show the BM velocity distributions along the length of the BM for six different directions of BC stimulation (x, y, z, d², d³, and d⁴) and for three different input frequencies (0.5, 1, and 7 kHz), with each result normalized by the BM velocity due to the d¹ directional BC excitation. All of the calculated BM velocity ratios have a magnitude of <0 dB, with the sole exception of the x-directional BC excitation with the ME structure at 1 kHz (see Fig. 4 B), which means that the BM velocity due to the d¹-directional BC stimulation (V^d1) has a larger magnitude than the BM responses for all the other directional BC inputs. Furthermore, Figs. 5 and 6 show that V^d1 has the largest magnitude among all the simulated frequencies from 0.5 to 10 kHz, for the given BC excitations in the d², d³, and d⁴ directions. Even compared to when the direction of the BC input is normal to the BF location on the BM corresponding to the input frequency, the d¹ direction still ends up having a more significant effect on the BM response. For example, consider a 3 kHz input frequency, whose BF position on the BM is ∼15 mm from the base (see Fig. S4 in the Supporting Material). In this study, the d³ direction is normal to the BM at 15.63 mm from the base, which is close to the BF position for a 3 kHz input frequency; but even though the d³ direction is normal to this BF position, Figs. 5 B and 6 B show that the d¹-directional excitation for 3 kHz still generates a higher BM velocity than the d³-directional excitation.

Based on this observation, it can be said that the inertial effects of BC excitation can differ depending on the direction of the excitation. It appears that the vibratory direction normal to the BM in the hook region of the cochlea affects the BM velocity most significantly, thus providing computational evidence to support our hypothesis that the normal directional vibration to the BM surface at the cochlear base would produce the maximum BM velocity. The precise mechanism for this is not well understood. However, one anatomical observation is that the difference in the cross-sectional areas of the SV and ST happens to be largest in the vicinity of the hook region at the base of the cochlea. We hypothesize that this large difference in cross-sectional areas between the SV and ST in the hook region can cause a more significant antisymmetric pressure component to emerge in the SV and ST across the BM when the direction of the BC excitation is normal to the BM surface in this region. Fig. 8 shows the ratios of the antisymmetric component of the scalae fluid pressure of the six directions (x, y, z, d², d³, and d⁴) relative to the d¹ direction, P_A/P_A^d1, which are calculated at the BF position for each input frequency. Fig. 8 indicates that BC excitation in the d¹ direction almost always produces the largest P_A magnitude, because the ratios are all <1 except for the x direction between 0.8 kHz and 1.3 kHz. Future calculations that involve systematic changes to the cochlear geometry in the vestibule region are needed to come to conclusions about this hypothesis. The exceptional case, the x-directional vibration, will be discussed in the next section.

Figure 8.

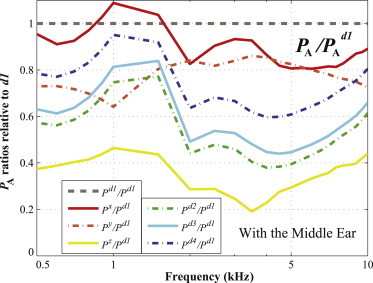
Ratios of the antisymmetric scalae fluid pressure components, P_A/P_A^d1, for all six directions (i.e., x, y, z, d², d³, and d⁴), calculated at the BF position for each input frequency. To see this figure in color, go online.

Effects of the directional excitation of the ME

Fig. 7 shows that the values of V^y at 1 kHz are the same with or without the ME (i.e., the ratio is ∼0 dB), whereas at the same frequency V^z with the ME is ∼6 dB larger than without the ME and V^x with the ME is ∼12 dB larger than without the ME. This unusually high contribution of the ME inertia to the BM velocity under x-directional stimulation can be said to contribute to the exceptional case of the response due to the x direction exceeding that due to the d¹ direction at 1 kHz, as shown in Fig. 4 B. Based on these observations, it could be expected that the ME ossicles would contribute to BC hearing by differing amounts depending on the excitation direction. In addition, comparing the results of Figs. 3 and 4 supports the idea that the direction of excitation affects how much the ME ossicles contribute to BC hearing. For example, when there are no ME ossicles (Fig. 3), V^d3 shows the lowest values relative to V^d1 among all six results. However, when the ME ossicles are added (Fig. 4), V^d3 rises to third or fourth place among the six different results. Due to the direction-dependent effects of the ME ossicles, the relative ordering of the BM-velocity magnitudes among different directional results can change depending on whether the ME is present or not. Bárány (8) already predicted such direction-dependent effects of the middle ear. Stenfelt et al. (24) found that different directions of vibration (orthogonal to one another) caused differences in magnitude of at most 5 and 12 dB for the stapes footplate and umbo velocities, respectively. Fig. 9, A and B, plot the stapes footplate and umbo velocities resulting from each directional excitation. The stapes footplate velocities are presented as ΔV_STAPES / V_B, where ΔV_STAPES = V_STAPES – V_B, V_STAPES is the stapes footplate velocity, and V_B is the bone velocity; and the umbo velocities are presented in an analogous way, as ΔV_UMBO / V_B. The magnitudes of the velocity vectors for the stapes footplate and umbo were calculated as projections onto the normal direction of the stapes footplate and umbo, respectively. In Fig. 9 A, although the differences in the stapes footplate velocity between two orthogonal directions, x and y, are within 5 dB, the z-directional results show a difference of ∼5–10 dB. Similarly, in Fig. 9 B, the z-directional results show a difference of ∼10–20 dB or more when compared with the y-directional results. Additionally, the different levels of the stapes footplate and umbo velocities in Fig. 9 provide further evidence of the existence of direction-dependent effects of the ME in response to BC stimuli. In this simulation, because the stapes footplate contacts the fluid in the SV, the stapes footplate and umbo velocities are affected by the fluid inertia as well as the ME inertia. Therefore, care must be taken when attempting to draw conclusions about which direction drives the maximum ME inertia. However, based on the higher stapes footplate and umbo velocities in Fig. 9, A and B, it appears that the d¹ direction can produce significant effects in the ME inertia as well as in the cochlear fluid inertia.

Figure 9.

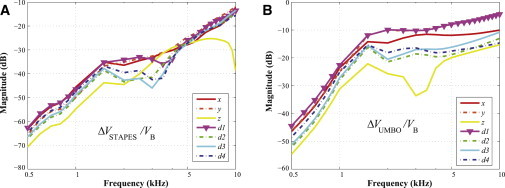
(A) Stapes footplate and (B) umbo velocities in response to BC excitation for each vibrational direction (i.e., x, y, z, d¹, d², d³, and d⁴). The stapes footplate velocity is presented as ΔV_STAPES / V_B, where ΔV_STAPES = V_STAPES– V_B, V_STAPES is the stapes footplate velocity, and V_B is the bone velocity; and the umbo velocity, ΔV_UMBO / V_B, is presented in an analogous way. The magnitudes of the velocity vectors for the stapes footplate and umbo were calculated as projections onto the normal direction of the stapes footplate and umbo, respectively. To see this figure in color, go online.

The relative effects of excitation direction on cochlear fluid inertia versus ME inertia

In comparing cases without and with the ME, three points should be discussed. First of all, the addition of the ME mass generally served to increase the BM velocity, which corresponds in Fig. 7 to the ratios of the absolute BM velocities being below 0 dB. Specifically, in the 1–2 kHz range, the effects of the ME mass on the BM velocity were the most significant (up to 24 dB). The 1–2 kHz range is well known to be where the resonance frequency of the ME exists for BC excitation (25,26). Therefore, the Carhart’s notch phenomenon (25), which involves a dip in the BC audiogram around 2 kHz as a result of otosclerosis, could be explained by the loss of ME inertial motion due to ossification of the stapes annular ligament.

The second point has to do with the case in which the ME ossicles are not included, such that the effects of the inertia of the cochlear fluid are all that is shown. The y direction (i.e., the superior direction relative to the skull) happens to have the smallest angle difference with respect to the d¹ direction (33°, versus 60°–80° for the other directions, which are d², d³, d⁴, x, and z), and as a consequence of this, the antisymmetric pressure component (and resulting BM velocity ratio) ends up being higher for the y direction than for the other directions, except d¹. Therefore, V^y/V^d1 is the closest to V^d1/V^d1 in Fig. 3. This similar behavior between the d¹ and y directions, as compared to the other directions, is easiest to observe when the ME ossicles are not present, because the inclusion of the ME affects V^d1 somewhat differently than V^y (Fig. 7).

Finally, in Fig. 7, the closer a line is to the flat reference line, the less significant the added ME inertia is to the BM velocity. The results for the d¹ and y directions tend to be the closest to this reference line, so the BM velocities for these directions are therefore affected less by the presence of the ME than is the case for the other directions. This can be explained by the relatively large effects of the cochlear fluid inertia for excitations in the d¹ or y directions (Fig. 3), such that the addition of the effects due to ME inertia has a relatively small influence on the total for these directions. One could consider, on the other hand, that proximity to the reference line in Fig. 7 could have more to do with a relatively smaller effect from the ME inertia rather than a relatively larger effect from the cochlear fluid. However, in Fig. 9 A, the stapes footplate velocities for the d¹ and y directions are either the highest or within only a few dB of being the highest, which suggests that the effects of the ME inertia are relatively large for those directions. On the other hand, for the z direction, the relatively low stapes velocity values in Fig. 9 A suggest that the proximity to the reference line in Fig. 7 has more to do with the ME inertia having a relatively small effect in that direction.

Conclusion

FE model simulations of the human auditory periphery, consisting of both the ME and the cochlea, were performed to gain insight into the mechanics of BC hearing. The geometry of the ME and the coiled cochlea, including the semicircular canals, was obtained via μCT imaging. The model results for both AC and BC stimuli are consistent with previous modeling studies (10) in that regardless of excitation type or direction, the antisymmetric fluid pressure is highly correlated with the BM velocity (see the Supporting Material). Detailed analyses using this model indicate that the directional BC vibrations normal to the BM in the basal hook region of the cochlea affect the BM responses most significantly when compared to other directions of BC excitation. It is hypothesized that, due to the asymmetric cross-sectional areas of the SV and ST in the hook region, the directional BC vibrations normal to the BM in that region end up producing the largest antisymmetric scalae fluid pressure components, which in turn initiate the maximum BM velocity.