Chloride-driven Electromechanical Phase Lags at Acoustic Frequencies Are Generated by SLC26a5, the Outer Hair Cell Motor Protein

Abstract

Outer hair cells (OHC) possess voltage-dependent membrane bound molecular motors, identified as the solute carrier protein SLC26a5, that drive somatic motility at acoustic frequencies. The electromotility (eM) of OHCs provides for cochlear amplification, a process that enhances auditory sensitivity by up to three orders of magnitude. In this study, using whole cell voltage clamp and mechanical measurement techniques, we identify disparities between voltage sensing and eM that result from stretched exponential electromechanical behavior of SLC26a5, also known as prestin, for its fast responsiveness. This stretched exponential behavior, which we accurately recapitulate with a new kinetic model, the meno presto model of prestin, influences the protein’s responsiveness to chloride binding and provides for delays in eM relative to membrane voltage driving force. The model predicts that in the frequency domain, these delays would result in eM phase lags that we confirm by measuring OHC eM at acoustic frequencies. These lags may contribute to canceling viscous drag, a requirement for many models of cochlear amplification.

The outer hair cell (OHC) is one of two receptor cell types in the organ of Corti, but unlike the inner hair cell it displays electromotile behavior distinct from any other form of cellular motility (1–4). OHC electromotility (eM) arises from the concerted action of millions of molecular motors embedded in the lateral membrane of the cell. They respond directly to membrane voltage and evidence reciprocal activity; namely, they are piezoelectric-like (5–7). Indeed, there is clear evidence that surface area changes accompany state transitions in the motor [see (8)]. The identification of these motors as members of the anion transporter family SLC26 (9), of which prestin is the 5th member (a5), underscores an interesting molecular evolution designed to boost the performance of auditory sensitivity and selectivity. This enhancement is known as cochlear amplification (10).

A class of cochlear models requires an electromechanical phase disparity for effective cochlear amplification (11–13), OHC eM lagging receptor potentials. Traditionally, these models assign the mechanism to processes other than the OHC itself. The phase lag provides for the properly timed injection of mechanical force into the cochlear partition to counter viscous detriment. Most molecular models of prestin behavior envision tightly coupled interactions between membrane voltage and eM, arising from sensor charge movements obeying Boltzmann statistics (14–20). Thus, Boltzmann characteristics of sensor charge and eM, namely Q_max /eM_max and Q V_h / eM V_h, are commonly believed to tightly correspond. However, we recently showed significant uncoupling of these characteristics depending on rate and polarity of voltage stimulation and on intracellular chloride level (21). We showed that a slow intermediate transition placed between prestin’s chloride binding transition and the voltage dependent transition responsible for eM could qualitatively account for the data, and we surmised that a molecularly based phase lag should arise. In this study we test this hypothesis by measuring eM at acoustic frequencies and find that indeed substantial frequency dependent phase lags are produced between membrane voltage and eM, showing chloride dependence. An enhanced stretched-exponential kinetic model, termed the meno presto model of prestin, nicely fits the data, whereas a model lacking the intermediate transitions fails.

Methods

Whole cell recordings were made from single isolated OHCs from the organ of Corti. Hartley albino guinea pigs were overdosed with isofluorane, the temporal bones excised and the top turns of the cochleae dissected free. Enzyme treatment (1 mg/ml Dispase I, 10 min) preceded gentle trituration, and isolated OHCs were placed in a glass-bottom recording chamber. Either a Nikon E600-FN microscope with 40× water immersion lens or an inverted Nikon Eclipse TI-2000 microscope with 40× lens was used to observe cells during voltage clamp. Experiments were performed at room temperature.

Solutions

Chloride levels were set to surround the 10 mM intracellular level in intact OHCs (22). Valid measures of membrane capacitance required an ionic blocking solution to remove ionic currents. The base high Cl solution contained (in mM): NaCl 100, TEA-Cl 20, CsCl 20, CoCl₂ 2, MgCl₂ 1, CaCl₂ 1, and Hepes 10. Lower chloride concentrations (10, 1, and 0.1 mM) were achieved by substituting chloride with gluconate. Base intracellular solutions contains (in mM): CsCl 140, MgCl2 2, Hepes 10, and EGTA 10. To unequivocally set intracellular chloride levels in the subplasmalemmal space of the OHC, both intracellular and extracellular chloride concentrations were set equal. All chemicals used were purchased from Sigma (Sigma-Aldrich, St. Louis, MO).

Cell capacitance and mechanical response

An Axon (Molecular Devices, Sunnyvale, CA) 200B amplifier was used for whole cell recording. Coupled voltage ramps (depolarizing followed immediately by hyperpolarizing ramp) of 100 and 500 ms were delivered to the cells from a holding potential of 0 mV. No averaging was done.

Nonlinear capacitance was measured using a continuous high resolution (2.56 ms sampling) two-sine stimulus protocol (10 to 20 mV peak at a primary frequency of 390.6 and harmonic of 781.2 Hz) superimposed onto the voltage ramps (23,24). It is mandatory that ionic conductances be blocked to insure accurate results, and imperative that system calibration be performed, as specified in our software design, jClamp (Scisoft, Ridgefield, CT). Capacitance data were fit to the first derivative of a two-state Boltzmann function (15) as follows:

$$C_m=Q_{max}\frac{ze}{kT}\frac{b}{{\left(1+b\right)}^2}+C_{lin},b=\exp \left(\frac{-ze\left(V_m-V_h\right)}{kT}\right)$$

providing Q_max, the maximum nonlinear charge moved; V_h, the voltage at peak capacitance or equivalently, at half maximum charge transfer; z, the valence; and C_lin, the linear membrane capacitance.

Simultaneous eM measurements were made either with fast video recording or photo diode. A Prosilica GE680 camera (Allied Vision Technologies, Exton, PA) was used for video measures, and details can be found in a previous publication (21). For photodiode measures, the image of the OHC apical region was projected onto a photodiode to measure cell movement, in a similar fashion to the method of Clark et al. (25). Two aligned, same optical axis, microscope cameras (Logitech webcam C650, Newark CA) were used: one to image the cell during patch recording and the other to ensure proper image placement. The inner camera (Fig. 1 A, 1) sensor area (white bordered quadrangles), upon which a 1.1 × 2.67 mm photodiode (SD076-11-31-211, Advanced Photonics, Ann Arbor, MI) was mounted (yellow boxed area), monitored only the OHC apex, whereas the other camera (Fig. 1 A, 2) sensor region (which actually viewed the whole cell) was used for patch electrode placement and monitoring image rotation and x-y shifts utilizing a dove prism and gimbaled mirror, respectively. Video capture was made with the wide field camera to determine actual cell displacement magnitude. With either the Prosilica camera or the photo diode approach, the edge of the cuticular plate was used to track OHC length change, the patch electrode providing a fixed point at the basal end of the cell. For photodiode measures, calibration was additionally made by movements of the OHC image via gimbaled mirror tilt (see Fig. 5). Sigmoidal fits (four parameters) provided estimates of V_h, maximal movement, and slope factor, b. Shift of motility against NLC (NonLinear Capacitance) is calculated by subtracting NLC V_h from eM V_h.

Figure 1.

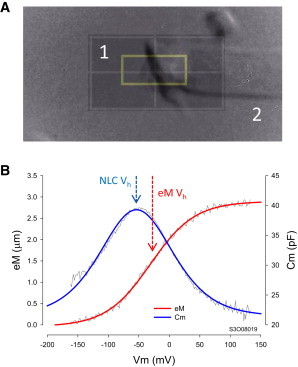
Electromechanical measures of prestin activity. (A) Image of OHC apical region was projected onto a photodiode to measure cell movement. (B) Simultaneous measures of OHC NLC and eM, measured via photodiode. No averaging. Note that NLC V_h and eM V_h differ (arrows) with that of eM shifted rightward. Chloride level was 1 mM. To see this figure in color, go online.

Figure 5.

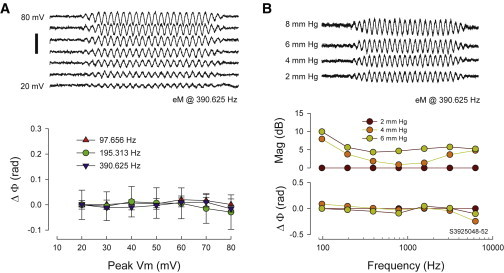
Effects of Vm magnitude and turgor pressure on eM phase. (A) Command magnitude was varied from 20 to 80 mV peak at 98, 195, and 391 Hz. Example traces are in top panel; average (+/−se) phase (re: 20 mV response) is plotted in bottom panel. No differences in phase were found. (B) Turgor pressure was varied from 0 to 8 mm Hg via the patch pipette. Though magnitude increased with pressure, phase remains unaffected. Example traces are in top panel (low frequency responses to left of eM response were calibration movements of the image). Note that smart averaging (see Methods) was performed for each trace, hence the different noise levels. An example of frequency dependence is in bottom panel. No changes were observed. Average results for three cells at 390 Hz (mean +/− se @ 4, 6, and 8 re: 2 mm Hg condition) are -0.063 +/− 0.02, -0.055 +/− 0.04, and -0.019 +/− 0.06, respectively. All phase analysis was via FFT. Scale bar: 3 um. Chloride is 140 mM. To see this figure in color, go online.

AC analysis of membrane currents (I_m) and eM were made by stimulating cells with voltage bursts at harmonic frequencies from 12.207 to 6250 Hz, with a 10 μs sample clock. Voltage bursts were ramped on and off to avoid transients. Magnitude and phase of responses were computed by FFT (fast Fourier transform) in jClamp. Fits in Matlab were made using least squares simultaneously on the transformed real and imaginary components of all spectral components of both eM and I_m. The effects of turgor pressure and magnitude of voltage stimulation on eM phase were also investigated. Turgor pressure was modified by applying pressure to the patch pipette using an ALA’s High Speed Pressure Clamp, HSPC-1 (Westbury, NY).

Model assessment

A kinetic model, termed the meno presto model of prestin, was used to fit the eM data. The meno presto model (Fig. 3) was assessed using Matlab Simulink in conjunction with jClamp. It is an extension of the simple model in Song and Santos-Sacchi (2013) that now introduces stretched exponential behavior in the intermediate transition between chloride binding and voltage dependency.

$${\mathsf{X}}_{\mathsf{O}}\underset{{\mathrm{k}}_2}{\overset{{\mathrm{k}}_1}{\rightleftharpoons }}{\mathsf{X}}_{\mathsf{C}}\begin{array}{c}\underset{{\text{β}}_1}{\overset{{\text{α}}_1}{\rightleftharpoons }}{\mathsf{X}}_1\underset{{\text{β}}_1}{\overset{{\text{α}}_1}{\rightleftharpoons }}\\ \cdot \cdot \cdot \\ \underset{{\text{β}}_n}{\overset{{\text{α}}_n}{\rightleftharpoons }}{\mathsf{X}}_{\mathsf{n}}\underset{{\text{β}}_n}{\overset{{\text{α}}_n}{\rightleftharpoons }}\end{array}{\mathsf{X}}_{\mathsf{d}}\underset{\text{β}}{\overset{\text{α}}{\rightleftharpoons }}\mathsf{C}$$

X_o state is unbound by anion. X_c state is bound by anion but intrinsic voltage sensor charge is not responsive to membrane electric field. A slow, multi-exponential conformational transition to X_d state via X_n states enables voltage sensing within the electric field. Depolarization moves positive sensor charge outward, simultaneously resulting in compact state C, which corresponds to cell contraction. The differential equations are as follows:

$$\frac{d{X}_o}{dt}=X_c\cdot k_2-X_o\cdot \left[C{l}^{-}\right]k_1$$

$$\frac{d{X}_c}{dt}=X_o\cdot \left[C{l}^{-}\right]k_1+\sum _{n=1}^{27}{X}_n\cdot {\beta }_n-X_c\cdot k_2-\sum _{n=1}^{27}{X}_c\cdot {\alpha }_n$$

$$\frac{d{X}_n}{dt}=X_c\cdot {\alpha }_n+X_d\cdot {\beta }_n-X_n\cdot {\alpha }_n-X_n\cdot {\beta }_n$$

$$\frac{d{X}_d}{dt}=C\cdot \beta +\sum _{n=1}^{27}{X}_n\cdot {\alpha }_n-X_d\cdot \alpha -\sum _{n=1}^{27}{X}_d\cdot {\beta }_n$$

$$\frac{dC}{dt}=X_d\cdot \alpha -C\cdot \beta$$

where α_n = A^∗(exp(-(n-1)))^w, β_n = α_n, w = 0.6, A=2.5e4 for n = 0.25, k₁ = 1.5e5, k₂ = k₁^∗k_d, k_d =.012, z = 0.7, nPres = 25e6, α = 1.3e6 ^∗ exp((z^∗F^∗V_m/(2^∗R^∗T))), β = 7.7e4 ^∗ exp((-z^∗F^∗V_m/(2^∗R^∗T))). Equivalence of α_n and β_n transition rates assures detailed balance of the reaction scheme (26). Parameters were varied until a good approximation of the data was obtained. We used 27 intermediate transitions to get as many exponential components such that a range of frequencies could be fit by the model. A single exponential intermediate transition will only influence one small frequency range, as we showed in our PNAS paper (21). Basically the prestin model is frequency sensitive, showing effects across our measured frequency range.

Figure 3.

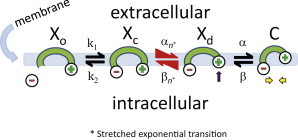
Stretched kinetic model of prestin activity within the plasma membrane. Xo state is unbound by anion. Xc state is bound by anion but intrinsic voltage sensor charge is not responsive to membrane electric field. Slow, multi-exponential conformational transition to Xd state via Xn state enables voltage sensing of electric field. Depolarization moves positive sensor charge outward, simultaneously resulting in compact state C, which corresponds to cell contraction. Equivalence of α_n and β_n transition rates assures detailed balance of the reaction scheme. To see this figure in color, go online.

jClamp provides an automation link to Matlab that allows voltage stimuli to be delivered to and current responses to be obtained from Simulink models. Solutions were obtained with the ode45 (Dormand-Prince) solver at a fixed absolute tolerance of 10⁻⁶. The meno presto model was interfaced to jClamp via a model of the patch clamp amplifier and OHC. The linear component of the patch-cell model was composed of R_s (pipette resistance) in series with a parallel combination of R_m (membrane resistance) and C_lin (linear capacitance). For the AC data fits, an additional uncompensated stray pipette capacitance modeled as a series combination of resistance (R_p) and capacitance (C_p) was included (24). Given the above meno presto model parameters, fits of AC data were made with patch clamp parameters of R_s = 6.1 MΩ, R_m = 275 MΩ, C_lin = 23 pF, R_p = 15 MΩ, C_p = 0.4 pF for the 140 mM chloride condition, and R_s = 6.6 MΩ, R_m = 265 MΩ, C_lin = 26.5 pF, R_p = 10 MΩ, and C_p = 0.4 pF for the 1 mM chloride condition. The exact same voltage stimuli and exact same analysis of model data were performed as with the biophysical data. For comparison purposes, a model emulating a fast two-state Boltzmann, with the intermediate transitions removed and k₁ rate constant set to 1.5e10, was evaluated, as well. Mechanical contraction data of the model, namely eM, was taken as the accumulated residence in the C state (see Fig. 3).

Results

Under whole cell voltage clamp, OHCs change length when membrane voltage is altered. Fig. 1 B shows an example of an OHC mechanical response (eM) measured with photodiode during a voltage ramp. Simultaneously, a bell-shaped nonlinear capacitance (NLC) is measured, an estimate of prestin’s voltage sensor charge movement. Note that the arrows depicting NLC V_h and eM V_h are separated, with eM shifted rightward along the voltage axis. This disparity underscores an uncoupling between voltage sensor and eM.

The magnitude of this V_h disparity is dependent both on the polarity of the voltage ramp that is used to obtain C_m-V_m functions and on intracellular chloride level. Hyperpolarizing ramps (Fig. 2 A) produce a maximal disparity appreciably less than depolarizing ramps (Fig. 2 B), each polarity, however, showing larger disparities as chloride levels are reduced. Plots show means and se (5 to 15 cells per point) of the average responses to 100 and 500 ms ramps. At the 0.1 mM chloride level, eM V_h was 32.9 +/− 6.9 mV and NLC V_h was 16.9 +/− 4.8 mV for hyperpolarizing ramps, whereas for depolarizing ramps eM V_h was 67.8 +/− 6.6 mV and NLC V_h was 23.8 +/− 3.9 mV (n = 5). In individual cells with faster ramps, we have observed such disparities greater than 60 mV. Similarly, disparities in Q estimates and eM measures are found as chloride levels are lowered (Fig. 2 C and D). Whereas estimates of Q from NLC are highly chloride dependent, showing a K_1/2 of 0.3 mM from Hill fits, eM changes very little across chloride levels. These data indicate an uncoupling between sensor charge movement determined from NLC and OHC mechanical activity. In simple two-state models of electromotility, no disparities are expected.

Figure 2.

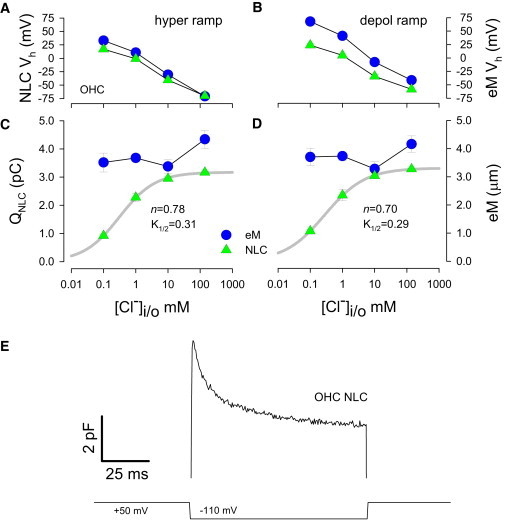
Chloride dependence of Boltzmann characteristics of eM and NLC as a function of depolarizing and hyperpolarizing ramps. (A) NLC Vh disparities arise as chloride levels are decreased, with effects being larger on eM, and larger disparities being observed with depolarizing ramps (B). (C) Q_max, determined from NLC fits, decreases as chloride levels are lowered. Hill coefficient (n) and K_1/2 are shown. Contrarily, eM magnitude is little affected. Similar results are obtained with depolarizing ramps (D). Plots are of average (+/−se) results from combined responses to 100 ms and 500 ms ramps, (n = 5 to 15). (E) Stretched exponential changes in OHC NLC occur during a constant voltage step from + 50 mV to -110 mV. 4 μsec clock, C_m inspection resolution 0.512 ms. To see this figure in color, go online.

Thus, we believe that this uncoupling results from an additional slow molecular transition in prestin that derives from a more complicated molecular scheme (21); this slow process is readily evidenced as a stretched exponential component of OHC C_m when membrane voltage is stepped. Fig. 2 E illustrates the resulting complex behavior in C_m during a fixed step from +50 mV to -100 mV, showing an initial rapid rise in C_m followed by a multi-exponential decay with tau components ranging from millisecond to seconds (27). Unfortunately, our recently developed model (21), which introduces an intermediate transition between chloride binding and voltage-dependent mechanical activity, cannot account for the observations shown in Fig. 2 because it provides only a single exponential transition. To more accurately account for our experimental findings, we expanded on this model to give stretched exponential behavior. A cartoon of the new meno presto model is shown in Fig. 3 and is described in detail in the Methods section. As can be seen in Fig. 4, the model results show marked similarities to the biophysical data, with V_h disparities showing chloride dependence and depolarizing ramps producing larger disparities (Fig. 4 A and B). K_1/2 values for NLC-derived Q are quantitatively similar to those in OHCs (Fig. 4 C and D), and importantly, stretched exponential behavior of C_m arises during step voltages (Fig. 4 E). To reiterate, these results are not observed with our previous single exponential model (21). Thus, we believe that an intermediate transition with stretched exponential kinetics is required to recapitulate the biophysical data.

Figure 4.

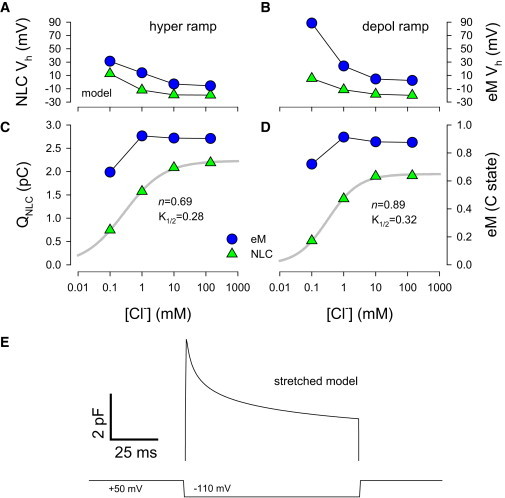
Stretched kinetic model recapitulates Boltzmann characteristics of eM and NLC. (A) In the model, NLC V_h disparities arise as chloride levels are decreased, with effects being larger on eM, and larger disparities being observed with depolarizing ramps (B). (C) Q_max, determined from NLC fits, decreases as chloride levels are lowered. Hill coefficient (n) and K_1/2 are shown. Contrarily, eM magnitude is little affected. Similar results are obtained with depolarizing ramps (D). (E) Stretched exponential changes in model NLC occur during a constant voltage step from + 50 mV to -110 mV. 4 μsec clock, C_m inspection resolution 0.512 ms. To see this figure in color, go online.

To appreciate the impact of prestin’s complex behavior on audition, we measured the magnitude and phase of OHC eM at acoustic frequencies. We stimulated cells with a nominal 50 mV peak AC voltage command under whole cell voltage clamp. Such magnitudes allowed us to generate eM magnitudes easily measurable via photodiode with fairly low number of averages to ensure maintenance of patch recording and limit cell damage. Because we were especially interested in phase behavior of the OHC eM, we ensured that phase behavior was not stimulus magnitude dependent (Fig. 5 A). We also determined that phase behavior was not dependent on steady-state turgor pressure, because this may vary among cells (Fig. 5 B). Though turgor pressure did not affect phase, magnitude of eM increased with pressure. Thus, cell magnitudes are reported as relative to lowest frequency response. Fig. 6 shows the average (+/− se; n = 5 to 8) magnitude and phase of both measured membrane current (I_m, blue symbols) and eM (red symbols) for two groups of cells under (A) 140 mM chloride and (B) 1 mM chloride conditions. The correspondingly colored solid lines are fits with the meno presto model, quantitatively falling within the standard errors for each condition at every frequency. Model parameters are reported in the Methods section. The thick solid green lines depict the membrane voltage magnitudes and phases. The striking observation is that there is a frequency dependent phase lag between V_m and eM, for both low and high chloride conditions, with the lag being significantly larger at several frequencies in the low chloride condition (asterisks in Fig. 7). Furthermore, the eM magnitude roll-off is greater than that of V_m, showing some chloride level dependence. For comparison, the V_m and eM magnitude and phase of a simple fast kinetic model (see Methods) is plotted (eM, red square symbols; V_m, dark green dashed line) and demonstrates neither phase lags nor magnitude disparities between the two. Indeed, the phase and magnitude of biophysical data cannot be fit by such simple models. We conclude that a slow, stretched exponential behavior of prestin generates the disparities between membrane voltage/sensor charge movement and electromotility.

Figure 6.

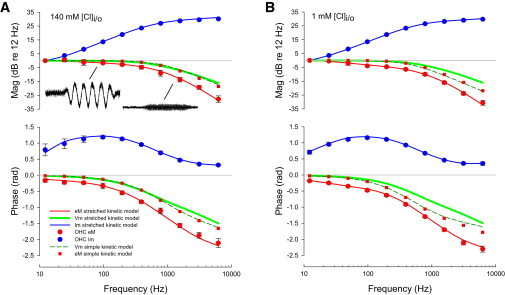
Chloride effects on magnitude and phase of simultaneously measured membrane current and eM. High frequency mechanical responses were measured with a photodiode under whole cell voltage clamp. eM waveforms shown are averaged responses to sinusoidal voltage bursts of 98 (1.9 μm pk-pk response) and 1563 Hz. Frequency response was measured up to 6.25 kHz and subsequently analyzed by FFT. Smart averaging in jClamp (see Methods) assured that a minimum number of averages was performed to establish a given signal-to-noise ratio, thereby limiting cell stimulation. Because of robust mechanical response, repeated stimulation can cause loss of cell recording. In these examples, the 98 Hz response was averaged eight times, and the 1563 Hz response was averaged 64 times. (A) 140 mM condition. Fundamental magnitude and phase of OHC I_m (blue) and eM (red) are plotted. Standard errors are given and mostly fall within symbol size. Solid red and blue lines are model fits (see Methods). The solid green line is the membrane voltage of the patch clamp–kinetic model. Note frequency dependent phase lag between membrane voltage and eM, and faster roll of eM magnitude than membrane voltage. For comparison, a fast simple kinetic model without intermediate transitions is plotted. V_m and eM of that simple model show neither phase nor magnitude differences, as expected for a simple 2-state model of prestin activity. (B) 1 mM chloride condition. Notable differences from (A) include a greater magnitude roll-off in eM vs. V_m and a greater frequency dependent phase lag. The simple model again shows no differences between V_m and eM magnitude and phase. To see this figure in color, go online.

Figure 7.

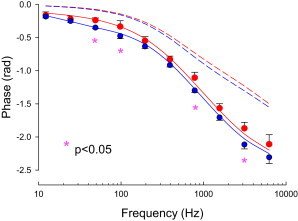
Expanded, overlapped plot of phase from high and low chloride conditions. Red symbols are from OHCs with 140 mM Cl intracellular pipette solutions, and blue symbols with 1 mM Cl solutions. Asterisks denote significantly different phases (p < 0.05, t-test, 2-tailed). Red dashed line is estimated membrane voltage phase under high chloride condition, and the blue dashed line under the 1 mM Cl condition. Regardless of chloride condition, the stretched exponential behavior of prestin results in phase lags in eM versus membrane voltage. Data from Fig. 6. To see this figure in color, go online.

Discussion

Our data show marked uncoupling of OHC eM, voltage sensor charge movement and membrane voltage. The ensuing disparities in those measures are chloride dependent, with lower chloride levels producing greater uncoupling. In the frequency domain, these disparities display as a differential roll-off in magnitude and a phase lag between membrane voltage and electromotility. The meno presto kinetic model that we developed fits the data quantitatively, and illustrates how molecular delays introduced by multi-exponential transitions can influence OHC electro-mechanics. A simple model without a stretched-exponential intermediate transition cannot account for our data.

Chloride and the OHC

Prestin is a member of the SLC26 solute carrier family and as such is expected to bear archetypal interactions with anions. Indeed, early experiments on OHC NLC pointed in this direction. In the mid-1990s, the anion salicylate was shown to interfere with NLC and eM, working intracellularly with a Hill coefficient of 1 (28,29). Additionally, the anionic, lipophilic molecule tetraphenylborate (TPB^-), unlike its cationic counterpart tetraphenylphosphonium (TPP⁺), modulates NLC (30). Thus it was not totally unexpected that normally residing intracellular anions, including chloride and bicarbonate, were found to influence prestin activity (31). We have amassed evidence that chloride ions modulate prestin in an allosteric-like manner, where intrinsic residue charge provides for voltage sensing (21,32–37). In some ways, the meno presto model, which fashions chloride as an enabler of voltage sensitivity, possesses qualities of an allosteric process whereby binding of a ligand to a remote site (or in response to other biophysical forces) induces a conformation state change that promotes the primary function of the protein (38,39), in our case electromotility. Though the occurrence of anion transport in prestin is a controversial issue (33,40–43), we believe that the slow intermediate transition that we have identified is related to prestin’s ancestral transporter legacy.

Coupling between charge movement and electromotility

Our data show an apparent dissociation between voltage sensor charge movement and electromotility. For example, V_h of the two during depolarizing ramps under 0.1 mM chloride conditions can differ by greater than 60 mV, and NLC Q_max is reduced by one-third with little effect on eM. The reason for the disparity is the existence of an intermediate transition between chloride binding and mechanical response. The delays afforded by the stretched exponential transition may appear to separate sense and effect, but do not indicate that the two are unrelated. An analogy between voltage-dependent ion channels can be made where the current onset after a step voltage is delayed (44). The greater the number of intermediate states before pore opening, the greater is the delay in current onset. In our case, we observe the mechanical response delayed relative to sensing; however, according to our meno presto kinetic model the delay need not be imposed between charge movements per se and eM (C state occupancy). In fact, in a linked reaction scheme, all transitions (including voltage-independent ones) influence each other (45–47). Thus, what appears to be an event before voltage sensing (chloride binding and an exponential evolution into voltage dependence) does in fact alter the balance of transition rates between states X_d and C, thereby altering V_h during fast ramps. Indeed, the hysteresis and charge immobilization that we initially observed in the Q-V_m response of OHCs (23) and in prestin expressing cells (48) must arise from a process that is not expected of simple fast two-state Boltzmanns, such as previous models of prestin (14–20). Consequently, because of the real complexity of prestin kinetics phase lags between V_m and eM will ensue.

Phase behavior of OHC electromotility

The phase of OHC eM has been studied previously. In 1992, in an effort to confirm voltage vs. current dependence of eM, we measured magnitude and phase in a similar manner to our experiments here (49). We concluded that the phase of eM followed predicted V_m under whole cell voltage clamp. This complemented our previous work showing eM voltage dependence (4). However, whereas there was apparent correspondence between V_m and eM phase, perusal of the phase data in our previous manuscript clearly indicates a significant phase lag in all cells studied. In fact, we had corrected for some phase discrepancies by introducing delays in the fits, and in low frequency data by shifting V_m and eM to overlap (see Fig. 5 A in (49)). Our current work indicates that those delays were actually correcting for the kinetic behavior of prestin. Indeed, our present eM phase data can be approximated by a delay that is inversely proportional to frequency. In this study, unlike our previous work, we did not use series resistance compensation, which can introduce lags in measured phase. Frank et al. (50) measured magnitude and phase of OHC eM using an extracellular microchamber technique, which although allowing for extended frequency perturbation, provides for neither direct membrane voltage control nor measures of membrane current (51). They provided corrected zero lag phase plots that were flat out to tens of kilohertz. Still, to fully account for the frequency response they needed to model the response with an electrical and mechanical component, showing second-order resonant effects to fit their data. Though the microchamber effectively produces a simple capacitive divider for the linear-membrane capacitance, any effects on a frequency-dependent, voltage-dependent and polarity dependent capacitance such as that resulting from OHC sensor charge movement is presently unresolved. Thus, they may have been inadvertently correcting for prestin-based phase characteristics. It will be interesting to see how simulations of the meno presto model compare with their data when inserted into a microchamber model. Regardless, the ability to simultaneously fit both actual I_m magnitude and phase, and eM magnitude and phase, as we have done in this study (and cannot be done with the microchamber approach), is important for accurately modeling eM data. We are confident that the correspondence of our meno presto model responses to the measured frequency response of eM, to the measured stretched exponential behavior of NLC, and to the measured chloride dependence of NLC and eM indicate a successful understanding of prestin behavior on OHC electromechanical behavior.

Our identification of substantial eM phase lag leads us to concur with early modelers on its role in cochlear amplification. A preponderance of cochlea models find that a phase lag between receptor potential and eM is required for effective cancellation of viscous drag expected from the cochlea environment (11–13). Indeed, the dependence of phase on prestin’s stretched exponential behavior that we find must also be significant, because it augments the phase lag toward the 90 degree requirement of cochlear modelers. We have previously shown that altering perilymphatic chloride levels, which effectively alters intracellular chloride concentration via the lateral membrane chloride conductance, G_metL (36), can reversibly modify cochlear amplification (22). Because we have shown here that the magnitude of eM is little affected by chloride level, we conclude that phase characteristics provided by the evolution of chloride-bound prestin into a voltage-enabled state predominantly underlie the OHC’s role in contributing to hearing sensitivity and selectivity by cochlear amplification. Furthermore, contrary to all cochlear models, we place a significant component of the phase lag not on cochlear partition super structures, but within the OHC motor itself. Finally, we note that implications of our in vitro observations for in vivo performance, where additional loads may impinge on the OHC requires further exploration. In fact, any biophysical study of hair cells in isolated or explant conditions in the absence of in vivo structures, such as those evaluating electro-mechanics or stereociliary transduction mechanisms, require cochlear modeling to assess physiological impact.