Probing the Conformation of FhaC with Small-Angle Neutron Scattering and Molecular Modeling

Abstract

Probing the solution structure of membrane proteins represents a formidable challenge, particularly when using small-angle scattering. Detergent molecules often present residual scattering contributions even at their match point in small-angle neutron scattering (SANS) measurements. Here, we studied the conformation of FhaC, the outer-membrane, β-barrel transporter of the Bordetella pertussis filamentous hemagglutinin adhesin. SANS measurements were performed on homogeneous solutions of FhaC solubilized in n-octyl-d17-βD-glucoside and on a variant devoid of the α helix H1, which critically obstructs the FhaC pore, in two solvent conditions corresponding to the match points of the protein and the detergent, respectively. Protein-bound detergent amounted to 142 ± 10 mol/mol as determined by analytical ultracentrifugation. By using molecular modeling and starting from three distinct conformations of FhaC and its variant embedded in lipid bilayers, we generated ensembles of protein-detergent arrangement models with 120–160 detergent molecules. The scattered curves were back-calculated for each model and compared with experimental data. Good fits were obtained for relatively compact, connected detergent belts, which occasionally displayed small detergent-free patches on the outer surface of the β barrel. The combination of SANS and modeling clearly enabled us to infer the solution structure of FhaC, with H1 inside the pore as in the crystal structure. We believe that our strategy of combining explicit atomic detergent modeling with SANS measurements has significant potential for structural studies of other detergent-solubilized membrane proteins.

Introduction

Membrane proteins perform a wide range of functions within cells, are involved in a number of genetic diseases, and have considerable therapeutic importance since 60% of drug targets are membrane receptors or ion channels. Membrane proteins are also essential for the virulence of pathogens. However, their biochemical and structural characterization remains limited compared with that of soluble proteins. For example, membrane proteins account for ∼30% of the genomic sequences but represent <1% of protein structures solved at the atomic scale.

This is due to the technical challenges associated with the properties of these macromolecules embedded in lipid membranes, including production in sufficient amounts, solubilization by detergents, purification in a functional form, and crystallization. Detergents are amphiphilic molecules bearing a hydrophilic head and hydrophobic tail. Above their critical micelle concentrations (CMCs), detergents not only occur as monomers but also assemble into micelles and cover the hydrophobic surfaces of membrane proteins, thus allowing their solubilization. Detergent monomers and micelles (which may contain dissolved lipids) coexist in solution with protein-detergent complexes (PDCs; which may also contain lipids and/or cofactors). Thus, membrane protein samples are always complex, multicomponent systems.

Small-angle neutron scattering (SANS) is a unique technique for investigating the structure of complex systems in solution (1,2). It can be used in combination with contrast variation, i.e., by varying the deuterium content of the protein and/or detergent components and/or the solvent using H₂O/D₂O mixtures to mask the signal from one type of component (e.g., the detergent). Structural information about the protein within the PDC can therefore be obtained with minimal contributions from the detergent (for a recent review, see Breyton et al. (3)). Mathematical approaches have been developed over the last two decades to interpret the information from small-angle x-ray scattering (SAXS) or SANS scattering curves (4,5), allowing comparisons between crystal and solution structures as well as ab initio, low-resolution modeling. However, only a few studies have applied these techniques to membrane proteins, despite the considerable interest in investigating the conformational changes associated with their function. This is due in particular to the intrinsic chemical heterogeneity (aliphatic chains versus hydrophilic heads) of most detergent molecules. As a consequence, their contribution, in general, cannot be completely removed at all scattering angles, even under conditions in which the detergent molecules are globally masked. Therefore, there is a clear need for tools to model detergent organization around membrane proteins for a proper interpretation of SANS data, allowing the discrimination of moderate conformational changes.

TpsB transporters are components of two-partner secretion (TPS) systems in Gram-negative bacteria. They secrete large, mostly β-helical proteins, collectively called TpsA proteins, that generally serve as virulence factors (6). TpsB transporters function as monomers and without accessory factors. The structure of FhaC, the outer-membrane transporter that secretes the Bordetella pertussis filamentous hemagglutinin adhesin (FHA) (7), has served as a model for the Omp85 superfamily of protein transporters. The FhaC structure shows a β barrel with an N-terminal extension consisting of an α helix and two periplasmic POTRA domains, each organized around a mixed, three-stranded β sheet and one or two α helices (Fig. 1 A). The β barrel consists of 16 antiparallel β strands connected by short turns at the periplasmic side and long loops at the cell surface. The channel within the barrel is occluded by the extracellular loop L6, which folds into the barrel, and by the N-terminal α helix, H1, which spans the channel interior. H1 is joined to the first POTRA domain by a 22-residue-long linker that is not resolved in the x-ray structure, indicating that it is disordered.

Figure 1.

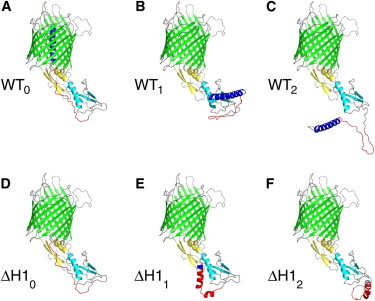
The six models of WT FhaC and the FhaC-ΔH1 variant used in the study. Color coding: blue, H1 (residues 1–30); cyan, POTRA1 (residues 53–134); yellow, POTRA2 (residues 135–208); green, β-barrel strands; gray, loops. The linker region, which was not resolved in the crystal structure, was modeled and is colored red (residues 31–52). (A) WT FhaC, displayed in cartoon representation. (B and C) Alternative conformations with H1 outside the β barrel. (D–F) Models of FhaC-ΔH1. (D) As in (A), but with H1 deleted from the structure file. (E and F) Alternative conformations of FhaC-ΔH1. All figures were created with PyMol (PyMOL Molecular Graphics System, version 1.6.0; Schrödinger, LLC). To see this figure in color, go online.

The crystal structure does not permit us to understand how FhaC mediates the secretion of its partner protein, because the residual opening of the β barrel pore is much too narrow for the translocation of a protein, even in an extended conformation: plain removal of H1 would create a roughly 8-Å-wide pore. Upon reconstitution of FhaC into planar lipid bilayers and application of a transmembrane potential, 8- to 10-Å-wide channels were revealed (7,8). Thus, the FhaC channel appears to be dynamic: in solution, it might open by extrusion of the α helix H1 and/or loop L6, thus creating a protein translocation pathway. L6, which is conserved among TpsB proteins, as well as in the Omp85 superfamily (9), was demonstrated to be a key element for the function of FhaC (7). In addition, earlier work indicated that it might change conformation when its cargo, FHA, is coproduced (10). H1 is also a conserved element in the TpsB family (9). Its deletion had little effect on FhaC secretion activity, although it increased the permeability of the outer membrane to antibiotics (7,8). This indicated that H1 might have a channel-plugging function in the closed conformation and move out of the pore in the course of secretion (the open conformation). Therefore, it is likely that both loop L6 and helix H1 undergo topological rearrangements that play crucial functional roles in the mechanism of secretion.

Our aim in this work was to probe the conformation of FhaC in solution by SANS before FHA binding. At the contrast match point (CMP) of the detergent, we expected to visualize the position of H1 inside or outside the β barrel. We analyzed full-length FhaC and a modified version of the protein harboring a deletion of H1, FhaC-ΔH1, to help decipher the significance of differences between the measured scattering curves. SANS measurements were performed on homogeneous solutions of detergent-solubilized protein in two solvent conditions corresponding to the match points of the protein and the detergent, respectively. The selected detergent, n-octyl-d17-βD-glucoside (d17-OG), has a residual signal even at its match point. We developed a strategy to model individual detergent molecules bound to the surface of the protein explicitly, and thereby compare their contributions to the back-calculated scattering curves from the protein-detergent models in an accurate manner. The combination of SANS and modeling clearly enabled us to infer the location of the H1 helix inside the β barrel of FhaC in solution. The results also provided insight into the structure of the detergent micelle around the protein. We believe that our strategy of combining explicit atomic detergent modeling with SANS measurements will prove to be generally useful for structural studies of detergent-solubilized membrane proteins.

Materials and Methods

Detergent samples

d17-OG was purchased from Anatrace (ref. No. O311T). Two samples of d17-OG at 30 mg/mL in H₂O or D₂O were prepared by weighted dissolution using a METTLER AE240 balance (precision 2 10⁻⁶ g) and mixed or diluted to obtain other concentrations and/or % D₂O.

Production and purification of the proteins

Protocols developed for x-ray studies (7) were adapted to obtain homogeneous solutions of FhaC and FhaC-ΔH1 in perfectly defined solvents containing d17-OG at controlled concentrations. Briefly, the two proteins (8) were overexpressed in Escherichia coli, extracted with OG, and purified with cation exchange chromatography in OG (7). Then, each protein was loaded in parallel onto two HisTrap affinity columns and eluted with 1% d17-OG, 0.5 M imidazole pH 6 in either H₂O (H₂O buffer) or D₂O (D₂O buffer). The eluted proteins, at concentrations between 3 and 10 mg/mL, were then dialyzed in their respective elution buffers and eventually diluted in their dialysis buffers.

Analytical ultracentrifugation

Sedimentation velocity experiments were recorded on an analytical ultracentrifuge XLI (acquisition program v4.5; Beckman Coulter, Palo Alto, CA) with a rotor speed of 42,000 rpm, at 20°C, using a rotor Anti-50, and double-sector cells with an optical path length of 3 mm equipped with sapphire windows, with the solvent compartments filled with the sample buffer without detergent. Acquisitions were made using absorbance and interference optics. Analyses in terms of the distribution c(s) of sedimentation coefficients s, and of noninteracting species were done with the program SEDFIT (v 8.9) from P. Schuck (National Institutes of Health; available free of charge at http://www.analyticalultracentrifugation.com/). The parameters of the c(s) analysis were typically 200 particles, with a confidence level of 0.68 for the regularization procedure, and the option “buffer mismatch” for the interference data. d17-OG was investigated using interference optics at 30, 20, and 10 mg/mL in H₂O and D₂O, and the analysis was performed as described previously (11). The samples of FhaC and FhaC-ΔH1 were used following dialysis at concentrations of ≈3 mg/mL and ≈1.5 mg/mL in D₂O and H₂O buffers, respectively. The solvent density and viscosity of 1.010 g/mL and 1.07 mPa.s for the buffer and of 1.110 g/mL and 1.30 mPa.s for the D₂O buffer were measured at 20°C on a density meter (DMA 5000) and a viscosity meter (AMVn; Anton-Paar, Graz, Austria). Partial specific volumes of 0.728 mL/g, molar masses of 62.10 and 59.83 kDa, and extinction coefficients of 1.36 and 1.423 mL g⁻¹ cm⁻¹ for FhaC and FhaC-ΔH1, respectively, were calculated with the program SEDNTERP created by D. Hayes et al. (USA; available free at http://bitcwiki.sr.unh.edu/). We used the refractive index increment ∂n/∂c = 0.187 mL/g, which is typical of membrane proteins (12), and a molar mass in the deuterated solvent increased by a factor of 1.013, as determined from the chemical structure. Details of the analysis, including estimates of the amount of bound detergent from the combination of the absorbance and interference signals, are provided elsewhere (13,14).

SANS experiments and data analysis

All detergent and protein samples were measured in Hellma 100-QS quartz cells (path length = 1 mm) on the small-angle diffractometer D22 at the Institut Laue-Langevin (Grenoble, France). Transmissions T of all samples were recorded systematically. In addition, water (H₂O), boron, and empty-cell references were recorded for detector efficiency, electronic background, and empty-cell subtraction procedures.

Scattering data from the d17-OG detergent were measured for 10 min at concentrations C between 10 and 30 mg/mL in 0%, 25%, 50%, 75%, and 100% D₂O solutions using two instrumental configurations (2 m/2 m and 8 m/8 m collimator/detector distances) with a fixed neutron wavelength λ = 6 Å. One-dimensional (1D) scattering intensities I(Q) were obtained using Institut Laue-Langevin in-house software (15), with the scattering vector $Q=\left(4\pi /\lambda \right)\sin \left(\theta \right)$, 2θ being the scattering angle. The intensities in the forward scattering direction, I(0), and the radii of gyration, R_G, were extracted by the Guinier approximation (16) using the program PRIMUS (17). The CMC was determined from a linear fit of the concentration series at a given contrast, and the CMP was extracted by plotting $\sqrt{I\left(0\right)/\left[\left(C-cmc\right)T\right]}$, with C being the overall concentration, from the data sets with the highest concentration (i.e., 30 mg/mL), as a function of contrast.

The PDCs (wild-type (WT) FhaC at 3 and 13 mg/mL, and FhaC-ΔH1 at 3 mg/mL) were measured at two different contrasts in buffers with 42% and 90% D₂O (CMP of FhaC and d17-OG, respectively), and d17-OG at 24 mg/mL in buffer with 90% D₂O, in the same experimental setup used for the detergent contrast series. Exposure times were ∼60 min per sample. The SANS intensities were back-calculated from the atomic PDCs using the program CRYSON (18,19) in default setup for 42% and 90% D₂O and scored in a least χ² fit against the respective experimental SANS data sets.

Creation of detergent topology and structure library

An initial detergent topology was created using the Automated Topology Builder (20) with a PM3 optimized geometry. The topology was translated into a residue building block for use with the Gromacs suite of programs (21) and manually modified to reflect bonded and nonbonded parameters of likewise functional groups from the Gromos 43a2 force field (22). One to five additional exclusions involving polar hydrogen atoms in the sugar ring were introduced. The structure was energy minimized in vacuo using 1000 steps of steepest descent, employing angular removal of mass motion at every step. A molecular-dynamics (MD) simulation of 1 ns was performed using a time step of 2 fs. A Coulomb and van der Waals cutoff distance of 8 nm was set, resulting in an effective complete evaluation of forces. The system was coupled to a temperature bath of 310 K (23). Bonds were constrained to their equilibrium values with LinCS (24). Configurations were saved every 1 ps (500 steps), and thus a library of 1001 detergent structures was obtained.

Modeling of the FhaC linker between H1 and POTRA1

The crystal structure of FhaC (PDB 2qdz) shows disorder for residues 31–52, corresponding to a 22-residue linker region between H1 and the first POTRA domain. With H1 inside the barrel, the linker has to span a distance of ∼5 nm, which leaves no possibility to form secondary structure elements. We modeled the atomic coordinates of residues 31–52 using the Jackal package (25), refining only the inserted region. The resulting structure is depicted in Fig. 1 A, with the linker colored red. Additional residues that were modeled at the same time were residues 1 and 2, and the extracellular loop L5 formed by residues 384–397. Individual missing atoms were reconstructed as well, without modifying the backbone conformation. The final structure is referred to as WT₀ in the text.

Modeling of FhaC with H1 outside

We investigated the possible orientations of H1 with respect to POTRA1 by submitting the sequence of FhaC, residues 1–133 (H1+linker+POTRA1), to the I-TASSER structure prediction server (26). The resulting five best models were fitted back onto the crystal structure using the POTRA1 domain as reference. Two of the models could be discarded because the fit resulted in steric clashes due to overlapping domains, and a third model corresponded to our previous modeling of the linker region, with a slightly different orientation. The two remaining models were retained. Both models were incorporated into the crystal structure using the Jackal package, replacing residues 1–62 by the model and fitting on POTRA1 (72 residues from 63 onward). In addition, all loop regions were refined. The resulting models (depicted in Fig. 1, B and C, and referred to as WT₁ and WT₂, respectively, in the text) were prepared for detergent modeling according to the procedure described below.

Modeling of ΔH1 constructs

We investigated the possible orientation of the linker in FhaC-ΔH1 by submitting the sequence of residues 27–133 to I-TASSER and fitted the resulting five best models onto the crystal structure. All five models predicted the linker region to be α helical. One model again led to overlapping domains and three others resembled one another. Thus, two distinctly different models remained for further analysis. No elaborate fitting was required to build complete models, as the start of the POTRA1 domain in both cases overlapped with the end of the modeled structure. In the preparation of the protein in a lipid bilayer, position restraints were removed from the linker atoms (see below). Fig. 1, D–F, depict the three FhaC-ΔH1 structures used in the analysis, which are subsequently referred to as ΔH1₀, ΔH1₁, and ΔH1₂. ΔH1₀ corresponds to WT₀ without H1.

Preparation of FhaC in a lipid bilayer

Each of the six FhaC structures was placed in a lipid bilayer of dipalmitoylphosphatidylcholine (DPPC) molecules according to a procedure similar to that described by Lensink et al. (27) and Kandt et al. (28). Briefly, an equilibrated bilayer of DPPC lipids was expanded in the xy plane (with the z axis being the normal to the bilayer plane) and FhaC/FhaC-ΔH1 was placed in the resulting vacuum at the center. Its position along the z axis was such that the water-to-membrane transfer energy was minimized (29,30). In subsequent iterations, the system was restored to the reference area per lipid by shrinking the x and y coordinates by 2% and deleting all overlapping lipid molecules. The shrinking factor was increased to 5% after eight iterations. Each iteration was accompanied by 100 steps of steepest-descent energy minimization, applying strong position restraining (10⁵ kJ/nm²) on the protein atoms. After ∼30 iterations, the system was found to be restored to its original size. The system box was then extended by 1.2 nm in the z axis and solvated with ∼26,000 water molecules, avoiding solvation of the hydrophobic membrane core by applying a van der Waals radius of 6 Å to the lipid tail atoms. The system was neutralized by adding chloride ions (31) and then subjected to 1000 steps of steepest-descent energy minimization, followed by 100 ps of MD using weak position restraints (10³ kJ/nm²) on the nonhydrogen protein atoms to relax the lipids surrounding the protein. The final frame was used as the starting point for the next step.

Modeling of detergent around FhaC

An initial structure of FhaC with detergent was obtained by replacing a fixed number of DPPC lipid molecules by detergent molecules, using the program DOPE (M.F.L.; to be published elsewhere, available upon request). In short, this was done by iteratively replacing a lipid from the input file by a molecule from the detergent library structures by aligning the detergent’s molecular structure principal axes to the system axes. Subsequently, the overlap with other molecules in the system was checked and a replacement was accepted if no contacts shorter than 2 Å were detected. If such contacts occurred, the library molecule was rotated in increments of 60° about its z axis and contacts were again evaluated. If no solution was found, the next molecule from the library was tried until a solution was found and the total number of molecules to be replaced had been reached. We varied the number of detergent molecules from 120 to 160, in increments of 5. For every such combination (FhaC plus n detergent molecules), 20 different detergent configurations were generated. To increase the variance between them, a different random number seed was used for every configuration. From each of the resulting 180 configurations, the solvent was removed (only FhaC and detergent remaining) and the system was subjected to a short energy minimization, followed by an MD simulation in vacuo, and in both cases the protein dynamics were removed from the equations of motion. In essence, this means that the protein coordinates were kept fixed in space while the detergent belt would associate around it. It was found that after ∼100 ps of simulation the association was completed, and each system was run for 200 ps to ensure this was done. All end configurations were processed to produce an all-atom system, with deuterium atoms placed on the detergent tails, and nonassociated detergent clusters were removed from the system.

In an alternative approach, we modeled 200 detergent molecules around FhaC using the approach described above, and then reduced the detergent belt by iteratively removing individual detergent molecules until 140 of them remained associated with FhaC. To determine which detergent molecule to remove, we calculated for each detergent molecule the closest distance to any protein atom. The detergent molecule that had the highest value of these, i.e., of which the closest atom was located the farthest away from the protein, was removed. One hundred different detergent configurations were generated using this approach.

Results

Sample design

We chose to investigate the conformation of FhaC solubilized in OG, as this detergent was used for the determination of the high-resolution structure by x-rays. The purification protocol was suitable to provide protein samples at an appropriate concentration for SANS (3–13 mg/mL), with a controlled concentration of detergent micelles and a controlled D₂O content, allowing contrast variation.

To determine the position of the helix inside or outside the barrel in solution, we used full-length FhaC and a variant deleted of the helix H1 (FhaC-ΔH1). Our rationale was that a detectable difference in SANS between FhaC and FhaC-ΔH1 would be indicative of an extended, open conformation in solution, whereas a closed, compact conformation should yield similar results for both proteins. In addition, analysis of FhaC-ΔH1 was expected to provide indications about the position of the linker in the open conformation. A model of WT FhaC with H1 and the linker fully extended was thus generated, and a large change in the calculated radius of gyration (program CRYSON (18,19)) between FhaC in this open conformation and FhaC closed as in the crystal structure was predicted (37 vs. 29 Å) (not shown).

The hydrogenated form of the detergent has a calculated CMP of 19% D₂O, which would provide only a low contrast for the protein (CMP 42% D₂O). The completely deuterated OG, which is commercially available, has a CMP of ∼120% D₂O, which cannot be experimentally matched. The tail-deuterated d17-OG has a theoretical CMP of 90% D₂O, in which hydrogenated proteins have a significant contrast (3). FhaC and FhaC-ΔH1 were thus purified in this detergent, in solvents containing H₂O and 100% D₂O.

Quality control and estimation of bound detergent by analytical ultracentrifugation

The analyses of d17-OG in pure H₂O and D₂O (Fig. S1 and Table S1 in the Supporting Material) yielded a CMC of 9.1 ± 0.4 mg/mL (29.5 mM), an aggregation number of 74 ± 10, and a refractive index increment of 0.135 ± 0.005 mL/g, which are similar to those given in the literature (http://www.affymetrix.com/) (32). The homogeneity of FhaC and FhaC-ΔH1 in d17-OG was excellent, as assessed by analytical ultracentrifugation (AUC). Fig. 2 shows the analysis of the sedimentation velocity profiles for the two proteins in D₂O buffer. Samples in H₂O buffer at 3 and 1.5 mg/mL (not shown) behaved similarly considering the differences in solvent density and viscosity. There are only two detectable contributions. The detergent micelles are detected at 1.6 ± 0.1 and 0.85 ± 0.05 S in H₂O and D₂O buffers (s_20w = 2.1 ± 0.1 S) only with interference optics, at concentrations in the 0–1.7 mg/mL range, close to the expected value of 0.9 mg/mL (total concentration C of 10 mg/mL minus CMC). The sedimentation coefficients of the FhaC and FhaC-ΔH1 complexes are indistinguishable: s = 4.76 ± 0.12 S and 2.79 ± 0.08 S in H₂O and D₂O buffers, respectively. The average number of detergent molecules bound to the protein was also determined from the combination of the absorbance and interference signals to be 142 ± 10 mol/mol, which combined with s-values corresponds to a frictional ratio of 1.33 ± 0.03, close to the usual value of 1.25 for a globular compact assembly. Analysis of the sedimentation profiles in terms of noninteracting particles (small monomer or solvent species, detergent micelle, and FhaC complex) give independent estimates of the sedimentation and diffusion coefficients, and thus of the buoyant mass of the complex. The derived average number of bound detergent is 90 ± 20 mol/mol, and, given the s-values, would correspond to a frictional ratio of 1.27 ± 0.04. The difference between these values may be due to uncertainties in the extinction coefficients in the first or second method, or (more likely) to a slight overestimation of the diffusion coefficients.

Figure 2.

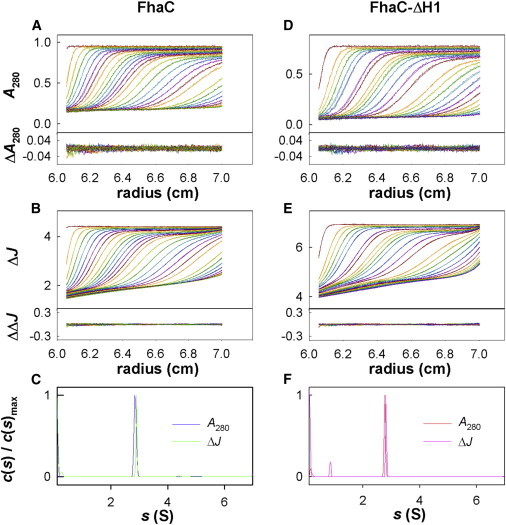
Sedimentation velocity of FhaC at 3.3 mg/mL and FhaC-ΔH1 at 3.0 mg/mL in 1% d17-OG, 0.5 M imidazole pH 6, 100% D₂O. (A, B, D, and E) Superposition of experimental and fitted sedimentation velocity profiles and their differences (top and bottom subpanels), at 280 nm (A and D), and using interference optics (B and E). (C and F) Sedimentation coefficient distributions c(s) normalized to the main protein peak value. To see this figure in color, go online.

SANS analyses

d17-OG scattering curves at 30 mg/mL were recorded as a function of contrast (Fig. S2 A). The CMC was determined to be 8 ± 1 mg/mL from the d17-OG concentration series (Fig. S2 B). Using this value, we determined the aggregation number from the 30 mg/mL data in H₂O to be 85, and the detergent CMP to be 90% D₂O (Fig. S2 C). The scattering curve of d17-OG at 24 mg/mL at its CMP, in the buffer used for FhaC with 90% D₂O, is presented in Fig. 3. Due to the chemical heterogeneity of d17-OG (tail versus head), there is a significant residual signal at the match point.

Figure 3.

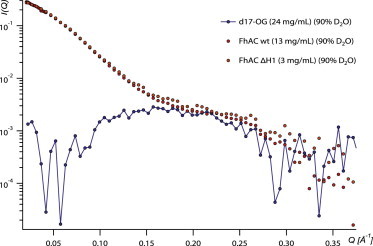
SANS curves of d17-OG at the CMP of d17-OG in the FhaC buffer with 90% D₂O. d17-OG in the protein sample is at 10 mg/mL. To see this figure in color, go online.

The scattering curves of two proteins (FhaC at 3 and 13 mg/mL, and FhaC-ΔH1 at 3 mg/mL) were then measured at 42% and 90% D₂O. At 42% D₂O, the detergent dominates the signal, with the protein being matched; at 90% D₂O (Fig. 3), the protein dominates the signal, with the detergent being matched. All four data sets are of excellent quality in terms of signal/noise ratios and no signs of aggregation were detected, confirming the homogeneity found for all samples in the AUC experiments. To interpret the data with some precision in terms of protein structure, and given that the detergent is not homogeneously masked at its match point, we chose to model atomic detergent molecules explicitly. Note that during sample preparation, we avoided concentration steps using ultrafiltration and used dialysis against solvents with the same detergent and D₂O concentrations to strictly control them. Therefore, there was no need to model detergent micelles, because their contribution was removed by subtraction of the solvent scattering.

Modeling the PDCs

The computational treatment of the template structures (as displayed in Fig. 1), with the number of detergent molecules varying in steps of 5 between 120 and 160, and 20 configurations for each combination of protein and detergent, led to 6 ×180 models of detergent arrangement around FhaC/FhaC-ΔH1. We found the arrangement of detergent to be nonhomogeneous, but nonetheless centered around the β barrel. In addition, detergent could bind to solvent-exposed regions of the protein close to the lipid bilayer, such as POTRA2 or the extracellular loops. Whereas those cases generally resulted in good fits, we found that the structures with detergent bound to POTRA1 (and to H1 in templates WT₁ and WT₂) made for bad χ² fits when we back-calculated the theoretical SANS curves (see below).

In an alternative approach (applied only to WT₀), we modeled 140 detergent molecules more compactly onto the FhaC surface by deleting the most distant 60 molecules from an initial amount of 200 detergent molecules (see Figs. 5 B and 6 C). In general, all of these 100 reduced-detergent-belt models displayed fewer and smaller detergent-free patches (if any) on the β-barrel FhaC surface with respect to the first modeling approach.

Figure 5.

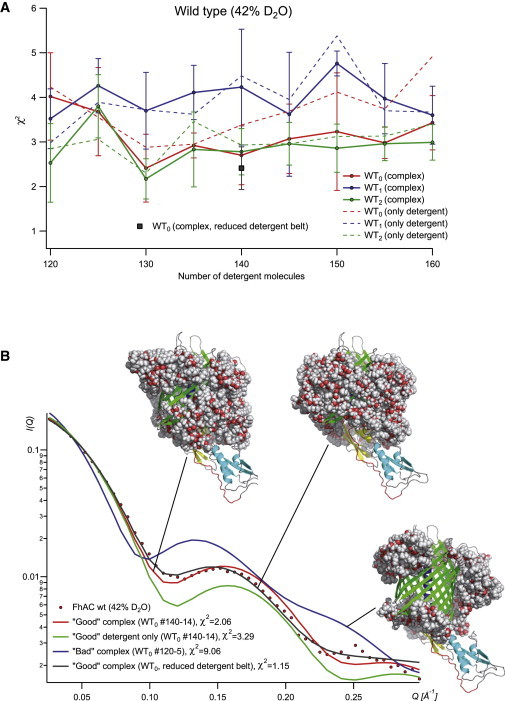
Modeling detergent-WT complexes at 42% D₂O. (A) χ² versus detergent number. (B) Superposition of experimental and modeled I(Q) from two WT₀ models. To see this figure in color, go online.

Figure 6.

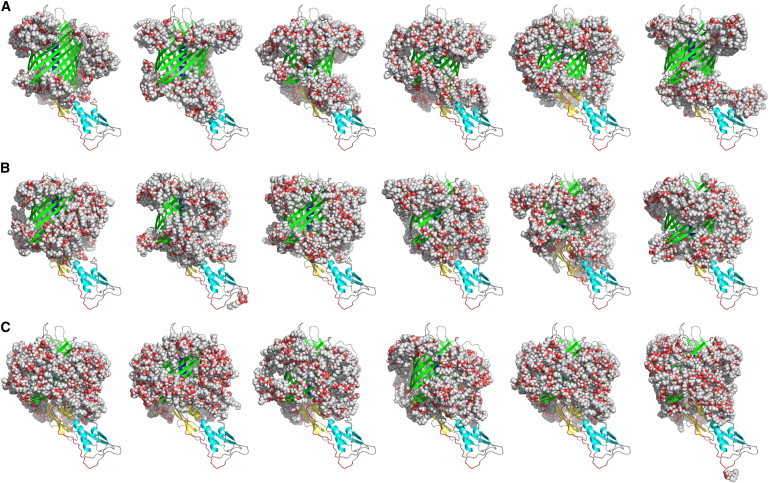
(A–C) WT FhaC-detergent models (WT₀) corresponding to bad (A), good (B), and good compact (C) fits. Color coding as in Fig. 1; detergent molecules shown in sphere representation. To see this figure in color, go online.

SANS analysis of WT FhaC models at 90% D₂O

The scattering curves were back-calculated for all models and compared with the experimental curves using the program CRYSON. The quality of the fit was evaluated by χ². Details regarding the individual models are provided in Tables S2 and S4. Fig. 4 A gives an overview of the χ² average values for the five best (out of 20) fitting models (complex), calculated for each detergent number (25 best of 100 for the reduced-detergent-belt models). It also shows the χ² values calculated without detergent (only protein). Even though at 90% D₂O the detergent contribution was matched on average, we still observed a marked decrease of χ² when detergent was explicitly modeled. Improvement of the fit by detergent modeling appears clearly in Fig. 4 B, which shows the superposition of the experimental and fitted scattering curves obtained with and without detergent. Among the three WT FhaC conformations, the one with the H1 helix inside the β barrel, i.e., WT₀, corresponding to the crystal structure, fits the SANS data best. Within each configuration series, the average χ²-values do not vary a lot as a function of the number of detergent molecules present. This indicates that the 90% D₂O SANS data sets are not very discriminative regarding the shape of the detergent belt, as expected at the detergent match point. A small but significant improvement is observed for the compacted (reduced-detergent-belt) models with respect to their noncompacted counterparts. The remaining minor variations of the χ²-values can probably be attributed to residual detergent heterogeneities and/or to effects of the modeled hydration shell by CRYSON, which varies as a function of the detergent shape.

Figure 4.

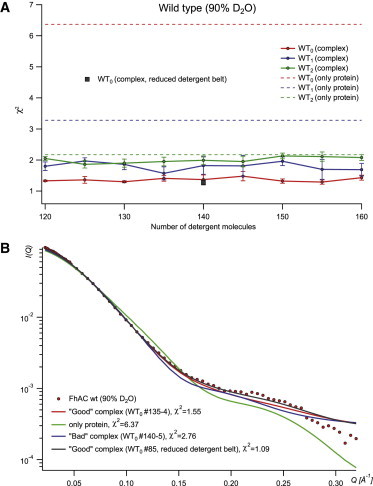
Modeling detergent-WT complexes at 90% D₂O. (A) χ² versus detergent number. (B) superposition of experimental and modeled I(Q) curves from good and bad WT₀ models. To see this figure in color, go online.

SANS analysis of WT FhaC models at 42% D₂O

Good χ²-values of the models against the SANS data at 42% D₂O (detergent visible, protein matched; Tables S2 and S4; Fig. 5 A) are found for individual models in the entire 120–160 detergent molecules range, indicating that the volume of detergent bound to FhaC fits within that range, in good agreement with the AUC results (140 molecules). Fig. 5 A was built considering the five best (out of 20) χ² values per FhaC conformation and detergent quantity (25 best out of 100 for the compacted reduced-detergent-belt models). Among the 20 individual models generated for a given, fixed number of detergent molecules, the χ²-values vary more widely than do their average values for different numbers of detergent molecules. Accordingly, the superposition of fitted and experimental scattering curves allows a clear distinction between appropriate and inappropriate models (Fig. 5 B). Compacted reduced-detergent-belt models displayed on average better fits with the SANS data, with the best χ² values being close to one. Moreover, the considerable variation of the fit values between different individual detergent models can be used to determine general structural features at low resolution of the detergent belt around FhaC. Fig. 6, A–C, show several bad detergent models (χ² > 8), several good detergent models (χ² < 2.5), and several good compact (reduced-detergent-belt) models, respectively (χ² < 2.3; higher-resolution images are provided in the Supporting Material). A comparison of the general features of the detergent models in Fig. 6 reveals that good fits are only obtained for relatively compact, connected detergent belts, whereas models that fit the SANS data very poorly are rather disconnected detergent topologies, with large, central parts of the transmembrane β-barrel wall being detergent free, and detergent molecules accumulating at the top and bottom of the barrel. Several, slightly different, good detergent topologies fit the SANS data equally well (Fig. 6, B and C).

SANS analysis of the FhaC-ΔH1 models

The SANS curves for the 20 models of FhaC-ΔH1 generated at each of the nine different quantities of detergent and for each of the three protein conformations (ΔH1₀, ΔH1₁, and ΔH1₂; presented in Fig. 1) were back-calculated. A detailed analysis of the χ² fits over all models is included in Table S3. For the 90% D₂O data sets (protein visible), the average values of the best five χ² fits (for each of the detergent numbers and protein conformations) and a comparison with the χ² values from the corresponding protein-only models are shown with selected superposition of experimental and fitted scattering curves in Fig. S3, A and B. Explicit incorporation of detergent in the models (complex) improves the fits significantly with respect to the protein-alone models. However, very good fits can be found for all three protein conformations, and thus our SANS data do not allow us to discriminate among these three conformations in solution. The results are more discriminating for the 42% D₂O SANS data sets (detergent visible, protein invisible): the ΔH1₁ models represent the detergent belt better than do the ΔH1₀ and ΔH1₂ series (Fig. S4 A). Most of the 20 models generated with the three distinct conformations fit the experimental data sets poorly, and very few structures yield satisfactory fits against the experiment SANS data. Examples of representative good and bad structures in Figs. S4 B and S5 show that the detergent location around the barrel generally improves the fit, unlike its positioning on the POTRAs. For the truncated FhaC-ΔH1 variant, removing the protein moiety from the models, even if it is globally matched, significantly decreases the quality of the fit.

Discussion

The study of membrane proteins represents a formidable challenge for most biophysical techniques in solution, and in particular small-angle scattering, due to the presence of detergent molecules in the sample. Their contribution is relatively strong in the case of x-rays (SAXS) and needs to be taken into account in explicit protein-detergent models where the protein and detergent parts contribute simultaneously, in a weighted manner, to the scattering curve (33). In contrast to SAXS, neutron scattering (SANS) using contrast variation has the advantage of providing independent structural data about either the protein or the detergent within a complex. For instance, SANS is able to mask the scattering contribution from detergent molecules on average (i.e., the I(Q = 0) intensity is zero) and to focus on the protein topology in situ (34). However, in general, the chemical heterogeneity between detergent head and tail moieties yields residual scattering contributions for Q > 0 that contribute to the scattering intensity and affect low-resolution modeling of the protein (35,36). Only some specific surfactants (37) or mixtures of deuterated and hydrogenated detergents (38) can be homogeneously masked (for a review, see Breyton et al. (3)). In this work, we demonstrated that explicit modeling of a PDC combined with SANS and contrast variation can yield excellent results. We were able to probe fine structural details of the protein in the presence of detergent, such as the position of the N-terminal α helix in FhaC, and discard several potential conformations. We observed a significant improvement of the fit when the detergent was explicitly incorporated into the models. Moreover, by obtaining a valid atomic model of the protein (that could be validated against the SANS data), we were able to study the structural properties of an explicit detergent belt and determine its general features. We believe that our approach can be applied to several membrane protein systems in solution, which are otherwise (e.g., by crystallography) very difficult to approach. It allows one to study the structural features of both the protein conformation and the shape of the detergent bound in a complex in situ by simply adjusting the H₂O/D₂O levels to the respective CMPs. However, we would like to stress that three key factors are very important for a successful application of our approach: 1), excellent sample quality (in particular, regarding the monodispersity of the PDCs, which ideally should be checked by AUC before SANS analyses); 2), a sufficient contrast between the protein and detergent parts, which in practice requires the use of either deuterated proteins or deuterated detergents; and 3), a sufficiently wide sampling of the modeled detergent belt.

When applied to membrane proteins, SAXS and SANS methods therefore need to deal with the detergent belt. It has been theorized that the detergent around membrane proteins organizes in a homogeneous, belt-like manner. Theoretical contributions originating from ellipsoidal detergent shapes were calculated in a SAXS study of Photosystem I-detergent complexes (39). It turned out to be impossible to match the SAXS data to the crystal structure embedded in a disk of detergent, which was interpreted as the protein being partially unfolded in solution. A SANS study of Light-Harvesting Complex II in detergent suggested also that the detergent does not homogeneously surround the hydrophobic periphery of the protein (40). A more recent study combined SAXS analyses of Aquaporin-0 with modeling of the detergent organization as an elliptical toroid (33). Although a good correspondence of the theoretical scattering curve with the experimental one was observed, the authors recognized the fact that the detergent corona is unlikely to adopt a static elliptical conformation, as the ellipsoid can be interpreted as resulting from a dynamic detergent behavior, the average of which is measured by SAXS. They recently extended their method by adopting both coarse-grained and atomistic modeling studies, allowing the deformation of an assumedly elliptical detergent toroid (41) and resulting in slightly improved χ² fits. In an elegant approach, detergent molecules were guided toward an elliptical detergent organization through nonequilibrium MD simulations with explicit water. Although the procedure gives promising results and will mark an important step in the study of the detergent belt in small-angle scattering experiments, only a single conformation is generated, and simulations in explicit solvent are relatively expensive.

In this study, we did not assume an elliptical organization; rather, we used molecular modeling to generate an ensemble of FhaC-detergent arrangements from their mutual association based on physicochemical interaction parameters. We did ask where the detergent would partition in such a system, and since the detergent was needed to solubilize FhaC in the first place, the obvious answer is, near or around the hydrophobic β barrel. Several tools exist to place a membrane protein in a lipid bilayer for the purpose of MD simulations (28,42), and we decided to adopt an approach in which FhaC is initially placed in a lipid bilayer, a sufficient number of lipid molecules are replaced by detergent, and, after removal of water, a simulation is run in vacuo to let the detergent molecules associate with FhaC. The procedure is then repeated 20 times to generate an ensemble of FhaC-detergent conformations. The association of detergent with FhaC is illustrated in Movie S1.

This approach does require some CPU-intensive steps. The initial placement in the lipid bilayer uses iterative energy minimization steps and a short MD simulation is run to relax lipids around the protein; the lipid-detergent replacement routines apply a number of mathematical operations to rotate and translate the detergent molecules, fit them to lipids, and evaluate any atomic overlap; and the final conformation is used for a short MD simulation in vacuo. Nevertheless, the total CPU time is limited to ∼2 hr per configuration on present-day laptop and desktop machines. The total simulation time required for the six protein conformations, nine different detergent quantities, and 20 different configurations amounts to ∼90 days of CPU time, a duration that is quite manageable for even small computing clusters. Previous simulations of OmpA and GpA in detergent (43–46) required an equilibration time of 20–50 ns for the association of detergent with protein. These simulations generally show that the detergent covers at least 80% of the hydrophobic surface, also in a nonhomogeneous manner. If we consider our vacuum simulations, we have a total simulation time of 9 × 20 × 200 ps = 36 ns per protein variant. This is comparable in terms of CPU time, but offers 180 different detergent arrangements.

The trade-off between speed and accuracy is obvious: although a large number of protein-detergent arrangements can be produced relatively quickly, a significant fraction of these arrangements are unrealistic. Here, unrealistic arrangements either correspond to detergent binding at the level of the POTRA domains or show large uncovered regions on the hydrophobic β barrel. However, the χ²-values of the back-calculated curves are decidedly discriminative. This is an important aspect of our approach, as it allows the elimination of bad protein structures as well as bad detergent belts.

In an attempt to reach a more homogeneous distribution, and having confirmed the conformation of WT FhaC in solution as WT₀, we also simulated the association of excess detergent (200 molecules) to FhaC. In subsequent iterative steps, we then removed the detergent molecules located the farthest away from the β barrel until the required number of associated detergent molecules (140) was reached. We produced 100 such configurations. In general, this procedure results in small but significant improvements of the χ² fits (see Figs. 4 and 5). The procedure is computationally somewhat more expensive, since the iterative replacement procedure converges more slowly to a solution for the larger detergent amounts. However, we consider this approach to be superior, since for more complicated systems, such as those showing moderate to large conformational changes, it will provide better sampling than simply increasing the number of different configurations. Such cases of limited sampling are readily identified by the χ² fits.

We would like to emphasize that what is measured experimentally is not a particular generated conformation, but rather the average signal of a large number of conformations, originating from the many proteins in the sample and from dynamic variations within each sample. The variation in protein-detergent conformations and their theoretical scattering curves led us to include only the five best-fitted models for further consideration. It is not unexpected that the best fits show the detergent to cover the larger surface area, but, interestingly, many of the good models display small detergent-free patches on the outer surface of the β barrel, i.e., the barrel is not completely covered with detergent molecules. Such patches are still observed in our reduced-detergent-belt approach, but they are fewer in number and smaller, and the ensemble of structures shows a good coverage of the β barrel. As to the shape of the detergent belt (40), our SANS data are compatible with a slightly nonhomogeneous distribution of detergent around the hydrophobic β barrel of the protein. Given that SANS provides an average intensity over all particle conformations present at a given moment in solution, it is conceivable that there are indeed several different, interconverting detergent arrangements possible around FhaC in solution, and that these are sampled by our modeling approach. The fact that several slightly different detergent belt structures are in excellent agreement with our SANS data (Fig. 6 C) illustrates the accuracy and uniqueness of such a low-resolution approach. Within these limits, a possible interpretation of our data is that a detergent belt is a dynamic entity consisting of an ensemble of slightly different, interchanging conformations.

The results clearly show the feasibility of our approach, as we could confirm that WT FhaC in solution adopts a structure similar to the crystallographic structure and rule out two alternative conformations (WT₁ and WT₂). The approach developed here may apply to membrane proteins of known or unknown structures. It can be used in combination with both SANS and SAXS studies. (In the case of SAXS, the free micelles need to be separated from the complex by using size exclusion chromatography directly on the beamline (33)). The association of detergent is flexible and can use any template structure or detergent molecule (after development of adequate force-field parameters). Subsequent comparison of the theoretical and experimental scattering curves allows the identification of good and bad models, in terms of both protein structure and detergent organization, when measured at the match point of either one. It can thus also be applied to models originating from ab initio modeling tools, such as I-TASSER (26), to help validate or discard them. This flexibility makes it a powerful tool for studying membrane proteins, including their conformational span.

Regarding the protein under study in this work, the crystal structure of full-length FhaC is in excellent agreement with the SANS data in solution. The conformation with the helix inside the pore could be discriminated from two alternative conformations, with the helix outside the barrel. This result does not solve the question about the conformational changes that occur to open the FhaC channel and to allow the passage of the cargo protein FHA. Open and closed conformations might be in equilibrium, but the open conformations are likely to be poorly populated in a detergent environment. It is possible that an open structure exists or is more populated in a lipid environment when compared with the detergent-solubilized state. The membrane environment was shown to be required for the native conformation of the KvAP voltage-dependant channel (47). Similarly, the kinetics of the photocycle of bacteriorhodopsin depends on its hydrophobic environment (48). The large conformational changes associated with the function of the reticulum Ca²⁺-ATPase are allowed by small rearrangements of the lipid bilayer and of the protein in its transmembrane part (49). In the case of FhaC, 8- to 10-Å-wide channels were revealed by means of electrophysiology techniques with the protein inserted into a bilayer.

Conclusions

Despite the ever-growing interest in membrane protein structure and dynamics, it remains notoriously difficult to study them. Solubilization requires the use of amphiphilic molecules (detergent) to act as a buffer between the solvent and the transmembrane domain, but little is known about the arrangement of detergent around the protein. We have successfully applied a combination of SANS and molecular modeling to probe the conformational space of the membrane protein FhaC. Since a residual contribution remained at the CMP of the detergent, we used molecular modeling to generate an ensemble of detergent arrangements around the WT protein and putative alternative conformations. Thus, we were able to confirm that WT FhaC in solution adopts a conformation similar to the x-ray structure, while ruling out alternative conformations at the same time. This study provides valuable insight into the organization of the detergent belt. Modeling studies may employ various detergent molecules and can be combined with both SANS and SAXS studies. The general applicability of this approach makes it an extremely powerful and significant tool that may allow more detailed studies of membrane protein structure and dynamics.

Supporting Material

Movie S1. Illustrative Movie of the Association of 140 Detergent Molecules with the Membrane Protein FhaC

FhaC was initially placed in a lipid bilayer and then selected lipids were replaced by d17-OG detergent molecules. A subsequent molecular-dynamics simulation in vacuo, in which protein coordinates were removed from the equations of motion, relaxed the detergent into a momentaneous, nonhomogeneous organization around the protein.

Supporting Citations

References (50,51) appear in the Supporting Material.