A Modular View of the Diversity of Cell-Density-Encoding Schemes in Bacterial Quorum-Sensing Systems

Abstract

Certain environmental parameters are accessible to cells only indirectly and require an encoding step for cells to retrieve the relevant information. A prominent example is the phenomenon of quorum sensing by microorganisms, where information about cell density is encoded by means of secreted signaling molecules. The mapping of cell density to signal molecule concentration and the corresponding network modules involved have been at least partially characterized in many bacteria, and vary markedly between different systems. In this study, we investigate theoretically how differences in signal transport, signal modification, and site of signal detection shape the encoding function and affect the sensitivity and the noise characteristics of the cell-density-encoding process. We find that different modules are capable of implementing both fairly basic as well as more complex encoding schemes, whose qualitative characteristics vary with cell density and are linked to network architecture, providing the basis for a hierarchical classification scheme. We exploit the tight relationship between encoding behavior and network architecture to constrain the network topology of partially characterized natural systems, and verify one such prediction by showing experimentally that Vibrio harveyi is capable of importing Autoinducer 2. The framework developed in this research can serve not only to guide reverse engineering of natural systems but also to stimulate the design of synthetic systems and generally facilitate a better understanding of the complexities arising in the quorum-sensing process because of variations in the physical organization of the encoder network module.

Introduction

Cells constantly monitor their surroundings to detect and adapt to salient changes in environmental conditions. Many environmental cues are directly accessible to cells because they activate a signal transduction pathway. However, certain parameters, such as cell density, cannot be sensed directly. To be able to infer information about cell density, an additional step is required: cells must first “encode” this information in the form of a directly perceptible signal. They do this by secreting signaling molecules that accumulate in the external medium in a manner that reflects the population density of the emitting cells. The signal compounds are subsequently detected by cellular signal transduction systems that “decode” the information and shape an appropriate “quorum response” (Fig. 1 A). Quorum sensing is widely used by cells to regulate gene expression in response to cell density (1–3). It has been studied most extensively in bacteria but is also present in eukaryotic microorganisms (4,5). It plays an important role in microbial physiology and ecology and has important repercussions for human, animal, and plant health (6). In addition, quorum-sensing circuitry has become an integral component of many synthetic systems. Since the earliest experiments in synthetic biology, it has been engineered into diverse cellular backgrounds, including metazoans (7), starting with relatively simple, synthetic toy systems (8,9) and extending to more sophisticated applications in advanced biosensors (10–12), synthetic ecology (13), and systems engineering of multicellular behaviors (14), in recent years.

Figure 1.

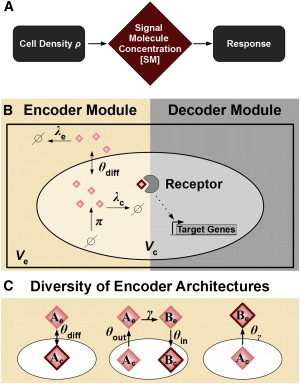
Cell-density-encoding schemes in bacterial quorum-sensing systems. (A) Cells encode information about the cell density into the SM concentration and decode it to control a target response. (B) The quorum-sensing network can be divided into an encoder module (EM, left) and a decoder module (DM, right). The EM produces SMs (diamonds) at rate π inside the cell (volume V_c), which are exchanged (θ_diff) with the environment (volume V_e) and are degraded both intra- and extracellular (λ_c, λ_e). The concentration of the SM detected by the receptor (diamond surrounded by a bold red line) determines the encoding behavior of the system. The DM transduces the signal from the receptor to regulate target gene expression. (C) Different encoding schemes. Left: abstract representation of EM shown in (B): intracellular encoding with diffusive SMs (A_c, A_e). Subscripts c and e denote cellular and extracellular concentrations, respectively. Middle: molecules A are actively exported (θ_out) and modified (γ) into molecules B, which are again imported (θ_in). [B_c] is detected by the receptor. Right: molecules A are modified during export (θ_γ) into molecules B. The extracellular concentration [B_e] is detected by the receptor. To see this figure in color, go online.

In accordance with the two-step nature of quorum sensing, one may partition the underlying quorum-sensing network into two functional modules: an “encoder module” (EM) and a “decoder module” (DM) (Fig. 1 B). In this study, we define the EM to comprise all network components that are required to convert information about cell density ρ into a corresponding concentration of signaling molecules [SM], e.g., the signal synthase, signal modification enzymes, and signal transporters. The quorum-sensing receptor perceives the signaling molecules (SMs) and provides the interface between the EM and the DM. On the one hand, the specificity of the receptor for a particular SM and the location of the receptor are crucial elements of the encoding process, as they determine which concentration is detected by the cell. For example, when cells detect intracellular (extracellular) concentrations, they employ an intracellular (extracellular) encoding scheme. On the other hand, properties of the receptor that determine how the concentration of SMs is transduced into a cellular response, such as the affinity of the receptor, can be considered to be part of the DM. The DM consists of the signal transduction and gene regulatory components of the network that are required to control target gene expression in accordance with the level of the signal. In some quorum-sensing systems, the encoding and decoding processes appear to be largely decoupled; e.g., for ComX in Bacillus subtilis or AI-2 in Vibrio harveyi there is no feedback on any known component of the EM (15,16). Other systems make use of feedback on encoder components, e.g., in the LuxIR system of V. fischeri SM production is up-regulated upon activation of the pathway (17). One may therefore classify the former as feedforward and the latter as feedback encoding systems.

This modular view of quorum-sensing systems, although never formally introduced in this way before, has already been quite successfully applied in the past to selectively characterize the decoder module by focusing on the signal transduction process. To this end, the DM is typically isolated (and decoupled) from the EM that is experimentally achieved by studying mutant systems, e.g., systems where the signal synthase has been knocked out. The DM can then be probed by stimulation with varying levels of externally supplied SMs by measuring the activity of the pathway. The systematic analysis of such input-output relationships has begun to reveal intricate relationships between network architecture and response behavior, in both natural (18–21) and synthetic systems (17,22). Thus, quorum-sensing systems have been shown to be capable of implementing a rather diverse spectrum of cellular response behaviors that is comparable with those of other sensory systems, and permits graded, threshold, and bistable responses (22–24).

On the other hand, much less is known about the role of the encoder module in shaping the quorum-sensing process. Quantitative determination of the concentration profile of the SMs as a function of the cell density, i.e., [SM](ρ), provides insight into the encoding behavior of a quorum-sensing system. Available measurements by means of quantitative bioassays or mass spectrometry suggest that the density encoding implemented by natural EMs comprises quite a diverse set of linear and nonlinear encoding relationships that include linear, saturating, hypersensitive, and even inverted regimes, where the concentration of the SM falls as cell density increases (25–27). From a systems perspective, the EM could be studied with the same rigor as the DM by focusing on its function instead of that of the decoder. This could be achieved for instance, by using similar strategies, such as decoupling the EM and DM of feedback systems, by studying, e.g., receptor mutants to assess the properties of the open loop, i.e., the feedforward, encoder module. In addition, one naturally expects a tight relationship between system behavior and system structure. Just as the architecture of the decoder network determines the dose-response behavior of the system to SM stimulation, the architecture of the encoder network is expected to leave its imprint on the cell-density-encoding profile [SM](ρ) and shape the overall cell density encoding process. Such relationships have not yet been systematically investigated, despite the fact that nature has come up with quite a rich repertoire of encoder architectures. For example, some cells produce SMs that can freely diffuse across the cell membrane, whereas others use transport proteins that pump SMs into or out of the cell (28,29). SMs may also be subject to modification, either intracellularly, extracellularly, or during transport through the cell membrane (30,31). Furthermore, cells make use of either extra- or intracellular encoding, as signals may activate either transmembrane receptors or cytoplasmic receptors (32,33). Fig. 1 C schematically illustrates the architectural diversity of the EM.

In this paper, we develop a theoretical model to systematically study the encoding profile, and its sensitivity and noise properties, in relation to the underlying network architecture of the encoder module. The model suggests that feedforward encoders show a wide variety of linear and nonlinear encoder functions that are shaped by the presence in the encoder network of certain core architectural elements. These elements can be combined to yield more complex encoding behaviors in systems with signal modification, allowing us to build a hierarchical classification scheme. We take advantage of this knowledge to derive predictions regarding the physical network architecture of partially characterized feedforward encoders, based on published experimental data on encoder functions, and demonstrate the utility of our approach by experimentally verifying one such prediction, namely that V. harveyi cells are indeed capable of AI-2 uptake.

Materials and Methods

Models of feedforward encoder network architectures

To model the encoding process we follow the approach developed in a previous study (34) and consider a homogenous cell population with cell density (or cell volume fraction) ρ = V_c/V_e. We assume that SMs A are produced at a constant rate π inside the cell (Fig. 1 B). SMs are secreted from the cell to the environment, where they are diluted by the factor ρ (and concentrated accordingly upon reimport if applicable). There are different possibilities of how SMs are transported out of and into the cell, and we consider diffusion with rate θ_diff as well as unidirectional transport by protein pumps (θ_in and θ_out), which we generally assume to be operating in the linear concentration regime. The SMs A may be modified to become SMs B either inside the cell, in the extracellular environment or while being transported out of or into the cell. We assume that modification also operates in the linear concentration regime with modification rates γ or θ_γ for transport independent and transport coupled modification, respectively. Molecules B may be transported into and out of the cell using the same spectrum of transport mechanisms as molecules A at their individual rates. All SMs are subject to first-order degradation with individual degradation rates λ_z, with (z = A_c, A_e, B_c, B_e), where the cellular and extracellular concentrations of the respective SMs A and B are denoted by the subscripts c and e, respectively. We then comprehensively model different encoding schemes by a set of linear ordinary differential equations (ODEs). For example, the EM architecture in Fig. 1 C shown on the left is modeled by the following:

$$\begin{array}{l}\frac{d\left[A_c\right]}{dt}=\pi -{\theta }_{A,diff}\left(\left[A_c\right]-\left[A_e\right]\right)-{\lambda }_{A_c}\left[A_c\right]\\ \frac{d\left[A_e\right]}{dt}=\rho {\theta }_{A,diff}\left(\left[A_c\right]-\left[A_e\right]\right)-{\lambda }_{A_e}\left[A_e\right]\end{array}$$ (1)

where the brackets denote the respective SM concentrations. The complete set of systems equations for all different architectures considered in this work can be found in the Supporting Material. Each EM is characterized by a different set of ODEs with a parameter set P = {P_i}, where i runs from 1 to N with N being the total number of parameters. For example, for the encoding system described by Eq. 1, P = {P₁ = π, P₂ = θ_A,diff, P₃ = λ_Ae, P₄ = λ_Ac}. We consider the steady-state concentration of signaling molecules [SM] (=[A_c], [A_e], [B_c] or [B_e]) that is detected by the receptor as the relevant output of the EM. [SM] (ρ) was computed algebraically for each architecture (see Supporting Material).

Characterization of the encoding process

Sensitivity of the encoding process

To characterize the phenotypic encoder properties of an EM, we determine the sensitivity ε of the encoding process by computing the elasticity coefficient as a function of cell density from the following [SM] profile:

$$\epsilon \left(\rho \right)=\frac{\partial \log \left[SM\right]\left(\rho \right)}{\partial \log \left(\rho \right)}.$$ (2)

We use a literature-derived discrete set of [SM] measurements at different cell densities ρ_i to estimate the sensitivity of natural encoding systems. At each data point i, we calculate the difference quotient to the left and to the right (between data points i and i - 1 (i.e., left) and i and i + 1 (i.e., right)): Δ[SM]_i,j/Δρ_i,j (j = left, right) to obtain ${\tilde{\epsilon }}_{i,j}=\left({\rho }_i/{\left[SM\right]}_i\right)\left(\text{Δ}{\left[SM\right]}_{i,j}/\text{Δ}{\rho }_{i,j}\right)$ and average to determine ${\epsilon }_i=\left({\tilde{\epsilon }}_{i,left}+{\tilde{\epsilon }}_{i,right}\right)/2$ the sensitivity at data point i.

Noise of the encoding process

At a given cell density, fluctuations in SM concentrations give rise to encoding noise. Noise may arise from the variability in the values of the parameters P of an EM, which is denoted as extrinsic noise. For simplicity, we assume that P is normally distributed with probability p(P) around some mean μ = {μ_i} and standard deviation σ = {σ_i}. In addition, even for fixed parameter values, noise may arise because of stochastic fluctuations in the number n of detected SMs, which is denoted as intrinsic noise. For an intracellular encoding system, n is the number of SMs within the cell with volume V_c. For an extracellular encoding system, n is the number of SMs that are sufficiently “close” to the membrane bound receptors, i.e., the number of particles contained in a cell proximate volume V_p that is assumed to be of the same size as V_c (i.e., V_p ∼ V_c). V_p is part of the environmental compartment V_e.

To numerically estimate the encoding noise, we thus implemented each EM model into the software package COPASI (35). To compute the noise at a cell density ρ = V_c/V_e we adjusted V_e and chose 50 random sets of parameter values according to p(P). For each set we conducted a stochastic simulation more than 1000 time steps by using the Gibson-Bruck algorithm (36). To obtain the total relative encoding noise η, we determined the overall variance in n and normalized it to the mean number of particles.

One may also estimate the noise analytically from a heuristic noise model inspired by an earlier study (37) by considering the relative noise being composed out of intrinsic ${\sigma }_{\mathrm{int}}^2=\overline{\langle n^2\rangle -{\langle n\rangle }^2}$ and extrinsic ${\sigma }_{ext}^2=\overline{{\langle n\rangle }^2}-{\left(\overline{\langle n\rangle }\right)}^2$ contributions as follows:

$${\eta }^2=\frac{{\sigma }_{\mathrm{int}}^2+{\sigma }_{ext}^2}{{\left(\overline{\langle n\rangle }\right)}^2}.$$ (3)

The overline represents averaging over the parameter noise and the brackets averaging over intrinsic fluctuations. We found that the total relative noise from our stochastic simulations is very well approximated by (see Supporting Material for details):

$${\eta }^2\approx \frac{1}{{\langle n\left(\mathit{\mu }\right)\rangle }^2}\left(\langle n\left(\mathit{\mu }\right)\rangle +{\frac{1}{2}\sum _{i=1}^N{\sigma }_{\text{i}}^2\frac{{\partial }^2\langle n\left(\mathit{P}\right)\rangle }{\partial P_i^2}|}_{\mathit{P}=\mathit{\mu }}+\sum _{i=1}^N{\sigma }_{\text{i}}^2{\left({\frac{\partial \langle n\left(\mathit{P}\right)\rangle }{\partial P_i}|}_{\mathit{P}=\mathit{\mu }}\right)}^2\right).$$ (4)

In this equation, 〈n(P)〉 is the mean particle number under steady-state conditions for an EM with parameters P. 〈n(P)〉 is derived from the steady-state concentration of the corresponding (linear) ODE-model by multiplying with V_c or V_p, respectively. All parameter values used can be found in the Supporting Material.

Bacterial strains and growth conditions

Genotypes of strains and plasmids used in this study are listed in Tables S1 and S2 in the Supporting Material. Primer sequences are available on request. Escherichia coli and Vibrio harveyi strains were routinely grown in AB (37) or LB (Lysogeny broth) medium at 37°C (E. coli) and 30°C (V. harveyi), respectively. Solid media contained 1.5% (w/v) agar. Media were supplemented with antibiotics (ampicillin sodium salt: 100 μg/ml; kanamycin sulfate: 50 μg/ml), meso-diaminopimelic acid (DAP) (300 μM), or AI-2 (20 μM) where indicated.

Strain construction

Molecular methods followed standard protocols (38) or were carried out according to the instructions supplied by manufacturers. Plasmid DNA and genomic DNA were isolated with the HiYield Plasmid Mini-Kit (Sued-Laborbedarf, Gauting, Germany) and the DNeasy Blood and Tissue Kit (Qiagen, Hilden, Germany), respectively. DNA fragments were purified from agarose gels using the Hi-Yield PCR Clean-up & Gel Extraction Kit (Sued-Laborbedarf). Q5 High-Fidelity DNA polymerase (New England Biolabs, Frankfurt Germany) was used according to supplier’s instructions. Restriction enzymes and other DNA modification enzymes were purchased from New England Biolabs. Replicative plasmids were transferred into E. coli strains by transformation using chemically competent cells (39) and into V. harveyi by conjugation as described earlier (40). The in-frame deletion mutant of V. harveyi was constructed according to a previous study (40).

β-Galactosidase activity assay

Overnight cultures of V. harveyi were diluted to an OD₆₀₀ of 0.1 in fresh autoinducer bioassay (AB) medium containing kanamycin. Cultures were grown at 30°C for 6 h to an OD₆₀₀ of 0.7 to 0.9, and subsequently harvested. β-Galactosidase activity was determined from at least three different experiments and was calculated and expressed as described by Miller (41).

Results

A set of 116 networks captures the full architectural diversity of feedforward encoding modules

To investigate how different encoding architectures affect the encoding properties, we conducted a comprehensive systematic analysis of the effects of the physical organization of the encoder network on encoding behavior. The basic processes that determine the encoding abilities of a feedforward encoding system can be abstracted in the following way (Fig. 2): SMs or their precursors A are always produced intracellularly (A_c) and are then either secreted directly into the environment (A_e) or are modified to yield molecules B (B_c or B_e). Transport modules may employ active export, active import, or passive diffusion. Molecules A may be modified to produce molecules B intracellularly, extracellularly, during import or export, or not at all. All SMs are subject to degradation. Finally, the receptor might sense either molecules A or B, either intracellularly (X_c = A_c, B_c) or extracellularly (X_e =A_e, B_e). The molecular species represent the nodes of the encoding module, where the directed links describe the processes of structural or state conversion of these species resulting from transport and/or signal modification. By combining fundamental transport, modification, and receptor modules in all possible ways, one can build 116 different encoder architectures in total (see the Supporting Material for details). Architectures without modification of SMs contain only unmodified molecules A, and are thus only able to form two-node networks consisting of molecules A_c and A_e. Architectures in which intracellular SMs A are modified either intracellularly or during export can form two- or three-node networks consisting of A_c, B_c, and B_e. The most complex architectures arise when the SMs A are modified either extracellularly or during import. These architectures are able to form three- or four-node networks consisting of all species A_c, A_e, B_c and B_e (Fig. S1 A in the Supporting Material).

Figure 2.

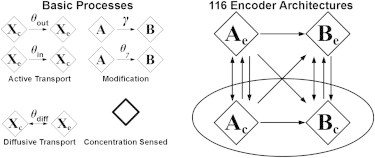
Diversity of encoder architectures. By combining different basic processes (transport, modification, receptor location, and specificity) in all possible ways, one can build 116 different feedforward encoder architectures, which are summarized schematically by a network diagram that comprises all architectures considered. The different molecular species (X = A, B) represent the nodes of the encoding module. The arrows describe the processes of structural or state conversion of these species.

Sensitivity and noise characteristics of the encoding process can vary with cell density in many different ways

Each encoding network generates a well-defined encoding function that relates the steady-state concentration of signaling molecules [SM] to the cell density ρ. To characterize the encoding process we focus on the sensitivity and noise characteristics of the encoder function [SM] (ρ). A common measure for the sensitivity of the output [SM] to changes in the input parameter ρ is the dimensionless elasticity coefficient ε, which measures the relative change in [SM] caused by a relative change in ρ. For example, ε(ρ) = 1 means that the concentration increases linearly with cell density, whereas ε(ρ) = 0 means that the concentration remains constant. We also analyze the noise properties of the encoding process by estimating the relative noise in the SM concentration η(ρ) as a function of cell density by considering contributions from both extrinsic-parameter noise and intrinsic noise because of small number fluctuations (42). Figs. 3 A and 4 A provide an overview of the typical “basic” and “complex” encoding behaviors that are found for the different encoder architectures, which are discussed in detail in the next sections. We find that even linear feedforward encoder modules are capable of implementing a surprisingly rich repertoire of linear, in addition to various nonlinear encoding functions, which include regimes of ultra-sensitive and inverted cell-density encoding. In general, the sensitivity and the noise of the encoding process will vary with cell density. Moreover, although the quantitative encoding behavior of each encoder system is clearly determined by its systems parameters (the parametric steady-state solution for each system is given in the Supporting Material), its qualitative behavior is firmly linked to network architecture and independent of precise parameter values, as will be shown in a subsequent section.

Figure 3.

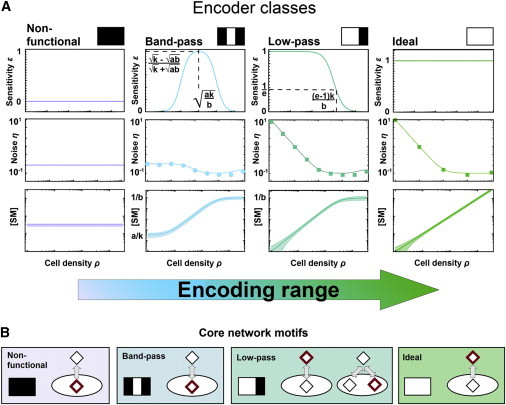
Encoder characteristics and definition of basic encoder classes. (A) Every EM has a characteristic sensitivity, noise, and [SM] profile. Noise can be determined from stochastic simulations (dots) and approximated analytically (lines). The shaded area in the [SM] profile denotes the magnitude of the noise. These profiles define four basic encoder classes schematically represented by icons derived from their sensitivity profiles and are ordered from left to right according to increasing encoding range. (B) Prototype networks (“core motifs”) define the encoding behavior. White ovals denote cells. Red diamonds mark the site where SMs are detected; double arrows denote bidirectional SM flow, directed arrows denote unidirectional SM export. A key feature of the low-pass architecture shown on the right is that it detects modified SMs. This is visualized by including an additional diamond. To see this figure in color, go online.

Figure 4.

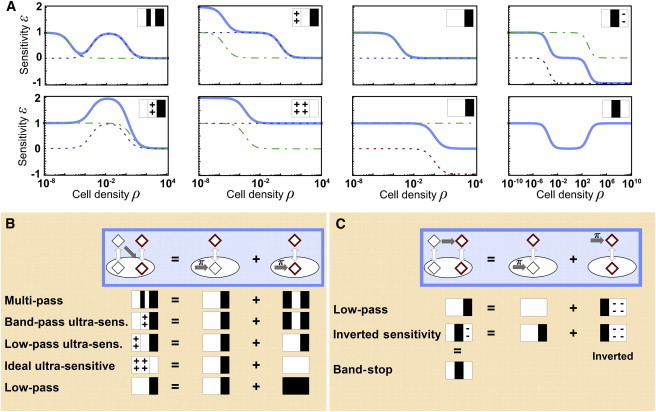
Decomposition of complex encoding architectures. (A) Sensitivity profiles (blue, solid line) generated by four-node networks showing ultrasensitive (ε > 1) and inverted sensitivity (ε < 0) regimes. The dashed and dashed-dotted, green, blue, and red lines show the basic profiles from which the complex encoding behavior can be derived. (B) and (C) Origins of encoding complexity: decomposition of complex networks into basic networks (top). Networks with modification (dark gray arrow) during import (B) can be decomposed into pairs of two-node networks with intracellular SM production (gray arrow marked with π). Networks with extracellular modification (C) can be decomposed into one two-node network with intracellular and one with extracellular SM production. Complex networks sense the modified SMs (red diamonds) either intracellular or extracellular. In the first two-node network the extracellular SM concentration determines the behavior, the second network senses the same concentration as the complex four-node network. Bottom: the overall sensitivity characteristics (novel icons, “+” and “-“ denoting ultra- and negative sensitivity, respectively) follow from a superposition of the underlying basic encoder profiles (icons as defined in Fig. 3). To see this figure in color, go online.

Sensitivity and noise characteristics are shared among networks belonging to the same encoder class

The majority of all EMs, namely 80 architectures (i.e., all two-, all three-, and four-node networks sensing unmodified molecules), generate one of four basic encoder profiles shown in Fig. 3 A (Fig. S1 B in the Supporting Material for details). These are arranged in the order of increasing encoding range from left to right in Fig. 3 A. At one extreme, architectures generate “ideal” cell-density encoder profiles (Fig. 3 A, right), in the sense that [SM] always tracks the cell density linearly, i.e., ε(ρ) = 1, over the entire input range. At the other extreme the [SM] is completely insensitive to changes in the cell density, i.e., ε(ρ) = 0 for any cell density and hence these architectures may be classified as “nonfunctional” (Fig. 3 A, left). Networks may also be capable of sensitively reflecting cell density over a limited density range only. For example, for some architectures, ε differs significantly from 0 only in a band of intermediate cell densities, or sensitive encoding is limited to the low end of the density regime. These latter encoders are thus referred to as “band-pass” and “low-pass” encoders, respectively. The noise profiles for the different encoders are shown in the middle row of Fig. 3 A. The lines plot the results of the analytical noise computation obtained from Eq. 4. and the dots depict the results of stochastic simulations. Importantly we find that networks that share the same qualitative encoder profile and sensitivity characteristics also show the same qualitative noise characteristics η. For example, whereas the nonfunctional and band-pass architectures always maintain some basal level of SMs even at very low-cell densities, in low-pass and ideal architectures [SM] is more and more diluted and vanishes as the cell density approaches zero. Therefore, in the two latter classes, the intrinsic noise, i.e., the stochastic fluctuation of [SM], diverges at very low-cell densities. In the nonfunctional and band-pass classes the noise level remains relatively low over the whole input range.

Each basic encoder class is linked to a core network motif in the EM

We next analyzed the relationship between encoding behavior and network structure by counting how many networks within each category share a given feature (Fig. S1 C). The spatial organization (e.g., the location of receptors and modification enzymes) and the directionality of SM flow (e.g., SM reimport) are the most important features that determine the encoding behavior. For the subset of topologically “simpler” EMs, one can define core network motifs for each encoder class (Fig. 3 B). For example, obviously all networks that sense intracellularly but are devoid of signal import are trivially nonfunctional. Likewise, an ideal encoder results when the extracellular concentration is sensed in the absence of SM import. With increasing cell density the number of SM-producing cells increases, while none of the cells consumes the extracellular SMs. Therefore, the extracellular SM concentration always increases linearly with cell density. Extracellular receptors combined with SM import result in a low-pass characteristic. Here the number of producer cells increases with increasing cell density. However, all cells also consume the SMs, and therefore the concentration of SMs saturates toward high-cell densities. This causes a drop in the sensitivity toward zero. Finally the combination of intracellular receptors and import of SMs can either result in band-pass or low-pass encoder characteristics, depending on whether short-circuiting is possible, i.e., producing and sensing the same molecules intracellularly. The intracellular concentration of intracellularly produced SMs approaches a basal level at low-cell densities, implying loss of encoding sensitivity, which is a characteristic feature of a band-pass encoder. This short-circuit is avoided if SMs are modified during or after export and the modified SMs are sensed intracellular. In this case the sensitivity remains high at low-cell densities (no basal SM level) and the encoder shows low-pass behavior. The four core motifs dominate the qualitative system behavior independent of parameters and generate a set of well-defined basic encoder profiles that are robust to parameter perturbations and even tolerate certain architectural changes.

EMs with signal modification have modular architectures and generate complex encoding functions that derive from superpositions of encoder motifs

EMs that modify the SMs A, then sense and respond to the modified SMs B (i.e., 36 different four-node architectures) can generate encoder functions that give rise to the complex elasticity profiles shown in Fig. 4 A. These include multipass encoding, i.e., high encoder sensitivity under different input regimes, ultrasensitive encoding, i.e., cell density regimes with a nonlinear increase in SM concentration, and inverted sensitivity encoding, i.e., encoders whose response characteristics can, under certain cell density regimes, give rise to situations in which SM concentration decreases (!) with increasing cell density, resulting in a negative elasticity. Furthermore, inverted sensitivity encoders may also allow for band-stop behavior. Such systems cannot transmit information about cell density under some intermediate cell density regime, while maintaining sensitive regimes at both low and at high-cell densities, albeit with different signs. If the decoding process responds to changes in SM concentration—regardless of their sign—a band-stop behavior will result. Ultrasensitive encoders can be further subdivided into band-pass ultrasensitive encoders, i.e., the ultrasensitive regime occurs at intermediate cell densities, low-pass ultrasensitive encoders, i.e., the ultrasensitive regime occurs at low-cell densities and sensitivity progressively drops to zero as cell density increases, and ideal ultrasensitive encoders, i.e., systems that maintain a sensitivity that is always ≥ 1.

Interestingly, we find that these 36 more complex networks can be decomposed into subnetworks, which can be further reduced to core motifs to rationalize their complex encoding behavior. In Fig. 4 B and C we show the rules for the decomposition of four-node networks—with signal modification occurring either during import (Fig. 4 B) or in the extracellular environment (Fig. 4 C)—into 2 two-node networks for the unmodified SMs A and their modified forms B. In both cases, the SM concentration of the complete system is the product of the SM concentrations of the two subnetworks A and B, with the “concentration” of the second subnetwork being dimensionless. Therefore, the sensitivity of the whole system is the sum of the subnetwork sensitivities (cf. Eq. 2; see the Supporting Material for details). With one notable exception, the assignment of a unique encoder class to a given network is again independent of parameters and is solely defined by the architecture. The only instance of parameter-dependent encoding is found in networks that are composed of a low-pass and a band-pass encoder. Here the architecture restricts the encoder function to only two options (namely, multipass and band-pass ultrasensitive), whereas the final outcome is determined by the network parameters. Moreover, the noise characteristics of the more complex networks are also dominated by those of the two subnetworks, although the relationship is more complicated than a simple superposition. It is possible to show that intrinsic noise is approximately multiplicative between the two subnetworks whereas the extrinsic noise contributions add up. The total noise of the complex system is then well approximated by taking the sum of the joint intrinsic and extrinsic noise according to Eq. 3 (see the Supporting Material).

A hierarchical classification scheme for feedforward encoder modules

Based on our analysis we can now build a biophysical taxonomy for the different encoder architectures (Fig. 5), which is determined from the signaling sensitivity and noise characteristics (for a complete list of encoder architectures see Table S3 in the Supporting Material). The vast majority of potential encoder network architectures is capable of sensitive cell-density encoding, at least over some input regime, and can therefore in principle function as quorum-sensing architectures. Only a minority of networks is nonfunctional, i.e., insensitive to changes in the cell density. Moreover, there exists a hierarchy of “simple” and more “complex” ways in which cell density information can be encoded in the concentration profile of a SM. This taxonomic scheme remains unchanged even if saturating SM transport is used in the model. Although the encoding behavior changes slightly in this case, the overall qualitative behavior remains unchanged. On the first level, EMs split up into three basic encoder classes (band-pass, low-pass, and ideal), whereas the more complex encoder classes on the second level are composed of two out of the three basic plus nonfunctional or inverted encoder functions. The complexity of the encoder functions is mirrored by the complexity of the networks: architecturally simpler networks generate basic encoder functions. The simpler networks can be combined to build more complex networks that are capable of more complex and often surprising encoding behavior. The Venn diagram in Fig. 5 illustrates the relationship between basic and derivative encoders and the distribution of the 116 signal-generating networks across the different encoder classes. The composite systems are shown as overlaps of the four basic classes plus the inverted subnetwork, which does not exist on its own but only as part of a decomposed network.

Figure 5.

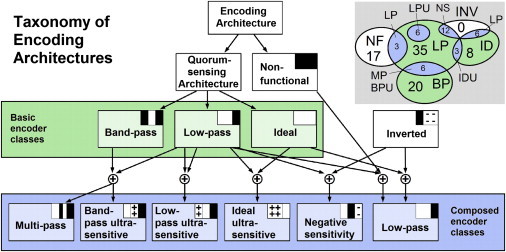
Taxonomic scheme for classifying encoding architectures into distinct encoder classes based on their sensitivity profiles. The connections illustrate the hierarchical relationship between functional and nonfunctional quorum-sensing systems, basic and derived encoder classes. The Venn diagram orders all 116 encoding architectures into nine distinct encoder classes denoted as BP (band-pass), LP (low-pass), ID (ideal), NF (nonfunctional), MP (multipass), BPU (band-pass ultrasensitive), LPU (low-pass ultrasensitive), IDU (ideal ultrasensitive), NS (negative sensitivity), and INV (inverted).

Experimental verification of inferred aspects of encoder network architecture: The AI-2 encoder module of Vibrio harveyi includes an AI-2 importer

Although quorum-sensing systems have been studied quite extensively, aspects of the network topology of the encoder module remain unresolved even in systems from well-studied model organisms. One example is the AI-2 signaling system of V. harveyi. Several members of the genus Vibrio contain parallel quorum-sensing systems. In the case of V. harveyi, the quorum system consists of the AI-2-responsive LuxPQ, the CAI-1-responsive CqsS, and the acylhomoserine lactone (AHL)-responsive LuxN membrane-bound receptors. Information from all three receptors is channeled into the same phosphorelay cascade, resulting in a differentiated response of the two transcriptional regulators LuxR and AphA (reviewed in (43,44)). AI-2 is a widespread signaling molecule in both Gram-negative and Gram-positive bacteria. Nevertheless for most bacteria, the AI-2 transport mechanism has not been elucidated yet. Because AI-2 exhibits low affinity toward lipids, a transport system is likely to be required (45). Thus far, the AI-2 encoder network has been best characterized for E. coli. Here, AI-2 is taken up and processed via the Lsr transport system (46). External AI-2 binds to the periplasmic binding protein LsrB and is imported by the Lsr ABC transporter (LsrACD). Once in the cytoplasm, AI-2 is phosphorylated by LsrK (with ATP as phosphate donor), and this modified form subsequently binds to the transcriptional regulator LsrR, thereby derepressing lsr expression (47). AI-2 signaling in V. harveyi differs strikingly from this pattern. It uses extracellular encoding by feeding into a signaling cascade, and it lacks a comparable lsr uptake system for AI-2. It is therefore not known whether or not V. harveyi is able to internalize AI-2 molecules once they have been secreted (Fig. 6 A). Furthermore, instead of the elaborate feedback encoding scheme used by E. coli (27), there are no feedbacks known that act on components of the encoder network in V. harveyi (16). Note again that feedbacks that operate within the decoder network, such as feedback on receptors, for example, will not affect the encoding module. This suggests that V. harveyi may use a feedforward encoding scheme, which could allow one to deduce information about network topology from the experimentally determined concentration profile of the SM in the wild-type. Fig. 6 B shows the sensitivity profile for the AI-2 precursor (S)-4,5-dihydroxy-2,3-pentanedione (DPD) in V. harveyi that was derived from the analysis of quantitative liquid chromatography-tandem mass spectrometry measurements conducted by Gooding et al. (26). The V. harveyi system shows a linear encoding regime, in which the SM concentration first linearly increases with cell density (ε = 1) and subsequently the SM concentration saturates toward high-cell densities (ε decreases). Hence the elasticity profile qualitatively matches that typical of a low-pass encoder. Assuming that AI-2 signaling in V. harveyi can be described by our parsimonious modeling framework, the observed low-pass profile is inconsistent with the common belief in the field that AI-2 cannot enter the cell, in which case one would have expected an ideal profile. Instead, the observed encoding behavior is indicative of an underlying low-pass encoder core motif, whose characteristic architectural features involve the import of the SMs. This therefore suggests the presence of an AI-2 importer in V. harveyi.

Figure 6.

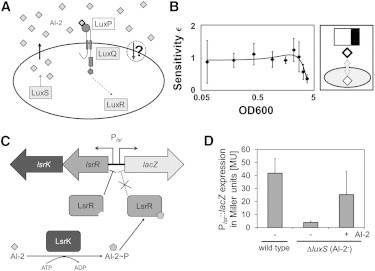
AI-2 import in V. harveyi. (A) Whether V. harveyi is able to internalize AI-2 molecules or not (circled arrow marked with question mark) can be predicted from its encoder profile. A low-pass profile implies the capacity for import, an ideal profile suggests that such a capacity is lacking. (B) The form of the AI-2 encoder sensitivity profile for V. harveyi derived from data in a previous study (26) is qualitatively compatible with the behavior of a low-pass encoder. This implies the presence of an uptake mechanism for AI-2 molecules in V. harveyi. (C) Schematic representation of the heterologous lsrKR-based P_lsr::lacZ reporter system in V. harveyi. (D) Histograms showing β−galactosidase activity (as a measure of P_lsr::lacZ expression) of AI-2-producing V. harveyi wild-type cells, the nonproducing mutant (ΔluxS) and the nonproducing mutant after external addition of AI-2 (20 μM).

To investigate whether V. harveyi actually has an alternative uptake system for AI-2, an appropriate reporter strain was constructed. The V. harveyi reporter strain contains a vector encoding the kinase LsrK and the repressor LsrR from E. coli, as well as a lsr promoter-lacZ fusion (P_lsr-lacZ) (Fig. 6 C). The resulting vector pBBR1-MCS2-lsrKRP_lsr::lacZ was introduced into a wild-type V. harveyi strain and an AI-2 nonproducing mutant (ΔluxS). Exponentially growing V. harveyi naturally produces and secretes up to 20 μM AI-2 (26). Accordingly, wild-type cells containing the reporter plasmid expressed lacZ demonstrated by a β-galactosidase activity of 42 MU (Fig. 6 D). In contrast, lacZ was not induced in the AI-2^- mutant (4 MU). Strikingly, the addition of 20 μM AI-2 to the medium induced the expression of P_lsr-lacZ (25 MU; Fig. 6 D), demonstrating the uptake of AI-2 by V. harveyi via a thus far unknown mechanism. This matches the prediction derived from our model of encoder module architecture in this species, and demonstrates the utility of our theoretical framework for deducing network structure from experimentally accessible components of a system’s response.

Discussion and Conclusions

Quorum sensing might be considered as an “active” sensing process, since the inferred environmental parameter “cell density” cannot be “passively” detected by the cellular sensing machinery but must first be mapped onto a biochemical or biophysical parameter by a molecular encoding process. This “encoding” process has, however, been less well studied than the “decoding” of quorum-sensing signals. In this study we have focused on the development of a comprehensive theoretical classification scheme for feedforward encoder architectures. The rather high frequency (> 85%) with which one can obtain encoder networks capable of sensitive cell density encoding at least under some cell density regimes by “randomly connecting” different basic functions, such as receptors, transporters, and signal-modifying enzymes, suggests that multiple evolutionary trajectories could have given rise to functionally distinct quorum-sensing systems independently. But perhaps this finding should also warn us that not every network that has the capacity to mediate quorum sensing has necessarily been selected to carry out this function (48). Different architectures result in basic and more complex cell-density-encoding schemes that go beyond the “more cells—more signal” relationship. Although encoding relationships have not been systematically investigated by experimentalists, the data available indicates that the encoding relationships found in nature are likewise quite diverse. The biological function of these differences is essentially unknown, but it is intriguing to speculate that different systems may have evolved to create distinct “brands” of quorum sensing.

Classification of encoding architectures

Our model suggests that there is a tight relationship between network architecture and encoding behavior, which can be traced down to the presence of basic “core motifs.” This modular decomposition of the network provides the foundation for the development of an alternative classification scheme for encoder architectures. Importantly, although our analysis was focused on feedforward encoding systems, such as AI-2 in V. harveyi and ComX in B. subtilis, our taxonomic classification is also relevant for studying feedback encoder systems, such as the prominent acylhomoserine lactone (AHL) systems found in Gram-negative bacteria that operate with feedback on the signal synthase (17). By disrupting the coupling between decoder and encoder modules (e.g., by studying receptor mutants), the encoder function of these systems could be studied experimentally in the open-loop regime (which is captured by the model). Given sufficient insight into the topology of an encoder network, one may make predictions regarding its encoding behavior. For example, AHLs with short acyl-chains are apparently freely diffusive, thereby ensuring import of the SM (28). Hence, the open-loop behavior of many AHL systems is expected to implement a band-pass or low-pass encoding function, depending on whether they sense the intracellular (such as the Lux system in V. fischeri) or the extracellular SM concentration (such as the Ain system in V. fischeri), respectively. In contrast, Gram-positive bacteria often use signaling peptides, which generally cannot diffuse freely across lipid membranes, and are often modified after production of pre-peptides (49). One expects these systems to show low-pass or ideal encoding behavior, depending on whether they sense intracellular or extracellular, respectively. Furthermore, the posttranslational modification of the SMs potentially gives rise to more complex encoder characteristics, depending on where the modification takes place. Examples include the Phr systems in B. subtilis, where modification may either occur tightly linked to transport or in the extracellular environment (50). The latter alternative theoretically allows for an inverted sensitivity regime at high-cell densities according to our model. Such inverse encoding relationships might be relevant for terminating signaling, e.g., in biofilms.

Feedback encoder systems

The role of feedback encoding, although common in nature, is not well understood. Starting from an understanding of the open-loop encoder one may be able to parse out the contributions to the shaping of the encoder function that result from feedback and from the effects of the physical network architecture by comparing the encoding behavior of the open with that of the closed-loop in the wild-type system. Of course, the model can also be expanded to include feedback regulation. In analogy to theoretical studies that focus on architectural features of the DM and therefore treat the EM in a rather implicit way (17,24), one could adopt the reverse approach to implicitly model the effect of the DM in the model of the EM. For example, one can add up-regulation of SM production that depends in a Michaelis-Menten–like fashion on the relevant SM concentration. Although this feedback would obviously not change the nonfunctional encoder, it will increase the sensitivity of the quorum-sensing architectures in that part of the input regime where the feedback sets in (Fig. S3 in Supporting Material). This would, for example, enable members of the basic encoder classes to express ultrasensitive regimes (i.e., ε(ρ) > 1). However, the sensitivities in the limits of high- and low-cell densities (ρ → 0 and ρ → ∞) remain unchanged in all classes. Feedback on SM production is especially well known in LuxIR-type systems (17). These systems share the architectural features of a band-pass encoder, which is the only functional encoder in our model with a sensitivity smaller than one (ε(ρ) < 1) over the whole input range. Therefore it might make sense for these systems to increase the sensitivity of the encoding process by applying positive feedback on their SM production.

Reverse engineering of quorum-sensing encoder modules

Motivated by the vision of developing new therapeutics based on the manipulation of quorum sensing (51), the molecular identification of quorum-sensing network components that may affect the decoding but also the encoding process is an important task in the search for potential drug targets. However, it is clear that, for many quorum-sensing systems, not all network components have been identified. Generally speaking, the reverse engineering of a molecular system remains quite challenging. Although our theory cannot make predictions that pinpoint any particular molecule that might act in the encoder module, it may still serve as a useful tool for guiding network reconstruction by constraining the topology of the physical network. Along these lines, we have successfully used our model to make a prediction regarding the network topology of the AI-2 signaling system in V. harveyi. Surprisingly we found that V. harveyi is capable of importing AI-2. Elucidating the nature of the transport mechanism and studying the functional consequences of this unexpected import are important points for future investigations. Another example for a partially reconstructed encoder network is the ComX system in B. subtilis, in which an isoprenylated peptide SM activates a two-component system. As in the case of AI-2 in V. harveyi, the transport mechanism for ComX has not been experimentally determined. It may be excreted by passive diffusion because of its hydrophobic modification, or it might be transported by the modification enzyme ComQ or alternatively transported by an unknown transporter(s) (52). As with the AI-2 system in V. harveyi, the B. subtilis ComX signaling system is apparently based on a feedforward encoding module, as there is no feedback on any known component of the encoder network (15). The sensitivity of extracellular SM concentration profiles for the ComX pheromone in B. subtilis, obtained from bioassays published by Bacon Schneider et al. (25), suggests the presence of linear encoding over the entire input regime (although we cannot strictly exclude the possibility that saturating levels of ComX were not observed experimentally because of a finite cell-density input range). According to our model, this encoding behavior is suggestive of an ideal encoder core motif. The most likely explanation for the observed encoding behavior is therefore that ComX transport across the cytoplasmic membrane occurs via an active export system (or at least if ComX reimport exists it will be negligible under these conditions). For many quorum-sensing systems, such as the ComX and AI-2 examples, the mode of transport of SM in and out of the cells is still unclear, and our approach could therefore be of use to a broader community.

Outlook and conclusions

Dedicated experimental studies aimed at elucidating the encoding process are still scarce. By comparison with the quite impressive efforts that have gone into the development of experimental set-ups for quantitatively studying the decoding process, the approaches available for elucidating the encoding process might still be considered rather primitive. Most measurements rely on bioassays obtained from growing cultures, where the molecular concentrations may differ from the steady-state values (27,50,53–55), WHICH report on the average encoding behavior only and which almost exclusively measure the extracellular concentration only. Developing assays that are capable of quantitatively reporting on the intracellular concentrations of SMs to allow us to probe encoding systems using intracellular receptors, or measuring fluctuations in signal concentrations under steady-state conditions represent important experimental challenges for the future. Measurements of noise levels might be particularly interesting, as noise has become a powerful source of information that facilitates an understanding of the decoding system (17,19,56). Our model likewise suggests that noise might be an important factor in understanding the limitations of the encoding process. Moreover, high-quality quantitative data on encoder profiles are also expected to enable us to go beyond the topological toward a quantitative network reconstruction. This may in turn permit realistic estimations of parameters and may then require an expansion of our basic model to include more mechanistic details and/or relax certain model assumptions.

In conclusion, the classification of encoder modules and their encoding characteristics developed here provides a basis for a deeper understanding of the differences among the diverse signaling architectures used in quorum sensing, as it can help to elucidate their potentials and limitations. Thus it opens up new opportunities for the reverse engineering of natural, and the forward engineering of synthetic quorum-sensing systems. However, to obtain a complete picture of quorum-sensing systems, knowledge of both network modules—the decoder and the encoder—must eventually be productively combined.