Abstract
Fluorescently labeled proteins that are found both in the cytoplasm and at the plasma membrane, such as peripheral membrane proteins, create stratified fluorescent layers that present a challenging environment for brightness studies with fluorescence fluctuation spectroscopy. The geometry of each layer along with fluorescence and brightness contributions from adjacent layers generates a convoluted raw brightness that conceals the underlying brightness of each individual layer. Because the brightness at a layer establishes the oligomeric state of the fluorescently labeled protein at said layer, we developed a method that connects the experimental raw brightness with the physical brightness at each layered compartment. The technique determines the oligomerization in each compartment from an axial intensity scan through the sample, followed by a fluorescence fluctuation spectroscopy measurement at each layer. We experimentally verify the technique with H-Ras-EGFP as a model system and determine its oligomeric state at both the plasma membrane and in the cytoplasm. Furthermore, we study the oligomerization of the Gag matrix domain of Human T-lymphotropic virus Type 1. The matrix domain targets the Gag polyprotein to the plasma membrane where, subsequently, viral assembly occurs. We determine the oligomerization of matrix in the cytoplasm and observe the onset of protein-protein interactions at the membrane. These observations shed light on the early assembly steps of the retrovirus.
Introduction
Peripheral or extrinsic membrane proteins associate temporarily with the membrane to perform a variety of cellular processes including signal transduction, cytoskeletal membrane interactions, membrane trafficking, and enzymatic activities like phospholipid metabolism and catabolism. Membrane association and dissociation of peripheral membrane proteins provide a mechanism for triggered conformational changes that serve to regulate protein-protein interactions and biological activity (1–5). This work introduces a method based on fluorescence fluctuation spectroscopy (FFS) to study the oligomeric state of peripheral membrane proteins that reside in the cytoplasm and at the plasma membrane. FFS techniques like fluorescence correlation spectroscopy (6–8) and brightness analysis of fluctuations (9–11) have been successfully used to study protein behavior both at the membrane and in the cytoplasm of living cells (12–19). Here, we focus on the use of brightness analysis for studying the interactions of peripheral membrane proteins that reside concurrently in the cytoplasm and at the plasma membrane.
Because peripheral membrane proteins associate reversibly with the membrane, they often exist in two pools: a membrane-bound form and a free soluble form in the cytoplasm. This leads to three distinct layers in a cell adherent to a coverslip (see Fig. 1 A). The first layer consists of the basal or bottom plasma membrane in contact with the glass. The second layer is the cytoplasmic compartment, followed by the apical or top membrane as the last layer. The axial extent of the optical excitation is much larger than the thickness of the membrane, which ensures coexcitation of proteins in the membrane-bound and cytoplasmic pools. The fluorescence fluctuation contributions from both sources need to be disentangled to reliably identify the brightness and oligomeric state of proteins at the membrane and in the cytoplasm.
Figure 1.
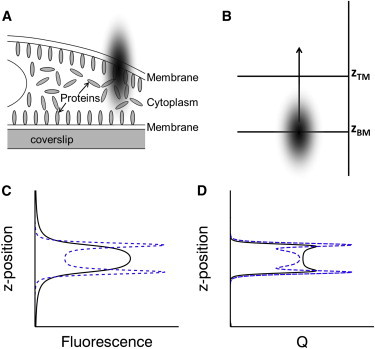
Concept of z-scan FFS. (A) Three distinct cell layers: the bottom membrane, cytoplasm, and top membrane. The axial length of optical excitation (solid oval) leads to coexcitation of layers. (B) The slab model defines the geometry by specifying the location of the bottom and top membrane by zBM and zTM, respectively. The cytoplasmic layer extends from zBM to zTM. The two-photon excitation spot is scanned along the z axis. (C) Sketch of the average intensity for a cell expressing cytoplasmic EGFP (solid line) and a membrane bound-EGFP fusion protein (dotted line). (D) Q-parameter versus z position for the same parameters as panel C. To see this figure in color, go online.
Z-scan FFS provides a method for untangling the fluorescence contributions of a multilayered protein system, and allows the brightness of the sample at each layer to be established. The technique was previously introduced to properly account for fluorescence fluctuations in thin cytoplasmic sections (20) and is based off earlier work on z-scan fluorescence correlation spectroscopy by Benda et al. (21). This study extends the theory of z-scan FFS to multiple strata, converts the theoretical concepts into a measurement strategy, and applies z-scan FFS to peripheral membrane proteins. We investigate the protein H-Ras as a model system and determine its oligomeric state at the plasma membrane and in the cytosol.
The Gag polyprotein plays a pivotal role in the assembly and release of retroviruses (22). Recent studies indicated fundamental differences between the early assembly events of two retroviruses, human T-cell leukemia virus type 1 (HTLV-1) and human immunodeficiency virus type 1 (HIV-1) (23,24). Although HIV-1 Gag requires the onset of cytoplasmic Gag-Gag interactions to promote translocation to the inner leaflet of the plasma membrane (25–27), HTLV-1 Gag appears to engage the plasma membrane as a monomer (24). Because the matrix (MA) domain of Gag is the primary driver of Gag association with the inner leaflet of the plasma membrane (28–32), this study investigates the peripheral membrane protein MA by z-scan FFS to shed light on the ability of HTLV-1 Gag to bind to the membrane as a monomer and to identify its oligomeric state at the membrane.
Materials and Methods
Experimental setup
Experiments were performed on a modified two-photon microscope, as previously described in Chen et al. (13). Detailed information about the experimental setup, the sample preparation, plasmid construction, and brightness analysis is found in the Supporting Material.
Z-scan calibration
A z-scan calibration procedure was carried out to determine specific parameters of the modified squared Gaussian-Lorentzian point-spread function (PSF) as described by Macdonald et al. (20). A series of eight z-scans were performed on a cell expressing EGFP starting at the nucleus and moving to thinner sections of the cell. A collective fit of the z-scan intensity profiles using the PSF defined by Eq. 9 resulted in z0 = 0.95 ± 0.1 μm and y = 1.95 ± 0.14 for a radial beam waist of w0 = 0.47 μm. These values are consistent with previously reported parameters (20) and will remain fixed for the remainder of the experiment.
Z-scan FFS procedure
In a three-layer protein system, an intensity trace is measured along the z axis of the cell. A fit of the z-dependent intensity data provides the location for the point FFS measurements: the bottom membrane layer zBM, the top membrane layer zTM, and the midpoint of the cytoplasmic layer zmid = (zBM + zTM)/2. Point FFS measurements are then performed by focusing the excitation PSF at zBM, zTM, and zmid. Movement of the cell or focus drift during the FFS measurements would compromise the result. We performed an intensity z-scan directly before and after the FFS measurement as a control. Changes in the intensity profile between the first and second z-scans indicate the presence of motion. We only accepted FFS data for brightness analysis when the intensity profiles agreed.
Data analysis
The z-scan photon counts sampled at 20 kHz were rebinned by a factor of 80 by software, which corresponds to a z-scan sampling time of Tz = 4 ms. The z-scan speed vz = 4.82 μm/s results in a step size Δz = vzTz = 19.3 nm between binned photon counts kz. Fluorescence intensity was determined by 〈F(z)〉 = kz/Tz. Least-squares fitting of an experimental z-scan intensity profile 〈F(z)〉 to Eq. 6 was accomplished by a Levenberg-Marquardt algorithm, where the PSF parameters z0 and y were fixed to the experimentally determined values and the standard deviation of the binned photon counts was estimated from the unbinned counts. The fit determined the position of the bottom and top membrane (zBM, zTM) as well as the maximum fluorescence intensities of the bottom membrane, the top membrane, and the cytoplasm (FBM,max, FTM,max, and Fcyto,max).
Results
Z-scan FFS of a single layer
Scanning the two-photon excitation spot uniformly along the z axis of a cell (Fig. 1 B) results in a z dependence of the fluorescence signal (Fig. 1 C). For a cell expressing an homogeneously distributed cytoplasmic protein like EGFP, the first two moments of the fluorescence intensity have been described previously by Macdonald et al. (20),
| (1) |
The fluorescence intensity 〈F(z)〉 and variance 〈ΔF2(z)〉 of the fluorescence depend on the cytoplasmic brightness λ and concentration 〈c〉 of the fluorescently labeled protein. The z dependence is introduced by the generalized volume function
which depends on the PSF raised to the rth power and the sample shape factor S(z). The shape factor for a cytoplasmic protein is given by a slab geometry starting at the bottom plasma membrane (BM) and ending at the top plasma membrane (TM). If we mark the location of both membranes by zBM and zTM (Fig. 1 B), the shape factor of the cytoplasmic protein is described by a Boxcar function starting at zBM and ending at zTM,
| (2) |
The fluorescence intensity profile 〈F(z)〉 for the slab geometry is depicted by the solid line in Fig. 1 C and reaches its peak at midheight (zmid = zBM + zTM/2) of the slab, because the volume overlap between the PSF and the sample is maximized.
The fluorescence brightness λ is determined from Mandel’s Q-parameter (33,34),
| (3) |
By inserting Eq. 1 we show that Q is the product of the brightness and a z-dependent gamma factor γ2(z) = V2(z)/V1(z), as described previously, Q(z) = γ2(z) ⋅ λ (20). The z-dependent Q-parameter for the slab geometry is illustrated by the solid line in Fig. 1 D. This is an extension of conventional FFS, where the sample volume is considered to be infinite. Conventional FFS is characterized by a z-independent Q-parameter, Q = γ2,∞ ⋅ λ, where γ2,∞ specifies the conventional gamma-factor.
Z-scan FFS of multiple layers
The above equations have been successfully applied to a single geometric layer to determine the brightness of proteins in thin cytoplasmic sections and to identify their stoichiometry (20). In this article, we expand z-scan FFS to describe geometries comprised of several layers. A simple example of such a system is realized by a protein that resides both in the cytoplasm and at the plasma membrane. We expect that the presence of the protein at the plasma membrane gives rise to two additional peaks in the intensity profile (dotted line, Fig. 1 C) and the Q-parameter profile (dotted line, Fig. 1 D), reflecting the contributions from fluorescent proteins at the bottom and top plasma membranes.
To treat membrane-bound proteins and other complex layered geometries requires a generalization of the theory beyond that given in the previous section. Because the first and second moments of the fluorescence intensity from multiple independent sources are additive, for a multilayered sample the contributions from each layer are added up to give the total average fluorescence intensity and its variance as
| (4) |
The ith layer is described by its brightness λi, concentration 〈ci〉, and shape factor 〈Si(z)〉, which make up the fluorescence intensity 〈Fi(z)〉 and variance 〈Fi2(z)〉 of the layer as described in Eq. 1.
We are specifically interested in modeling proteins found concurrently at the plasma membrane and in the cytoplasm. This situation is best described by a three-layer system, consisting of a bottom membrane (BM) located at ZBM, a cytoplasmic layer (Cyto), and a top membrane (TM) located at ZTM. Because a membrane is much thinner than the linear dimension of the PSF, its geometric shape factor is well approximated by a delta-function. We refer to membranes as delta layers to contrast their geometry with that of the slab model used for the cytoplasm. Thus, the geometry is described by SBM(z) = δ(z – zBM) for the bottom membrane layer, STM(z) = δ(z – zTM) for the top membrane layer, and SCyto(z; zBM, zTM) for the cytoplasmic layer.
The fluorescence intensity and fluctuations of a delta layer are still described by Eq. 1, but with a reinterpretation of some parameters. The volume concentration 〈c〉 is replaced by the surface concentration 〈σ〉 at the membrane and the generalized volume function Vr(z) now represents an area function (20). These changes are a consequence of the delta-function and provide a rigorous interpretation of z-scan intensity parameters.
The z-dependence of the fluorescence intensity of the three-layer system is given by
| (5) |
For fitting purposes, it is more convenient to express Eq. 5 as
| (6) |
where Fi,max represents the peak amplitude of the fluorescence profile 〈Fi(z)〉 from the ith layer and is the scaled volume function
The Q-parameter for the three-layer model is directly computed from Eq. 4 by inserting the appropriate shape factor into the generalized volume function Vr,i(z),
| (7) |
Each layer is specified by its Q-factor, Qi(z) = γ2,i(z) ⋅ λi, and fractional intensity, fi(z) = 〈Fi(z)〉/〈F(z)〉. The total Q-factor is given by summing the Q-factor of each layer weighted by its fractional intensity fi(z).
It is convenient to report the brightness of each layer λi as a normalized value by comparing it to the brightness λEGFP of EGFP, bi = λi/λEGFP. A normalized brightness bi = 1 indicates a monomeric protein, whereas bi = 2 indicates a dimer in the ith layer. For measurements of stoichiometry, it is helpful to convert the Q-factor into a z-dependent normalized brightness by dividing Q(z) by the brightness of EGFP and the conventional gamma factor γ2,∞,
| (8) |
where we introduced the gamma factor ratio μi = γ2,i/γ2,∞. We stress that bBM, bTM, and bCyto are the proper brightness values of the three layers. However, these values are not directly experimentally accessible. The experimental brightness at each z position is a complex composite containing the brightness from each layer. Because requires further processing to extract the oligomeric state of proteins at each layer, we refer to it as “raw brightness” throughout the rest of the article.
Experimental intensity profiles of multiple layers
Applying the above theory to experimental data requires one more crucial ingredient, the PSF, because it connects the shape factor with the generalized volume function Vr(z). The experimental PSF is commonly approximated by either the three-dimensional Gaussian function or the squared Gaussian-Lorentzian function. However, neither of these functions sufficiently approximates the axial profile of our PSF. We chose to model experimental z-scan data with the modified squared Gaussian-Lorentzian function (20)
| (9) |
The radial and axial beam waist are characterized by w0 and z0, whereas y adjusts the axial decay of the PSF. The z0 and y parameters of the PSF were determined experimentally, as described in Materials and Methods.
The plasma membrane protein EGFP-H-Ras expressed in U2OS cells served as a multilayer test system. The z-dependent intensity trace shows a distinct double peak (see Fig. 2 A, solid line), suggesting that the protein is predominantly located at the cell membrane. We initially fit the experimental intensity profile with a two-layer model by setting 〈FCyto(z)〉 in Eq. 5 to 0. The result of this fitting was unsatisfactory, because systematic deviations between data and model were observed (reduced χ-squared of 2.8). We suspected that the misfit was caused by the presence of cytoplasmic EGFP-H-Ras. We removed the constraint 〈FCyto(z)〉 = 0 and successfully refit the EGFP-H-Ras intensity profile with the general three-layer model. The fit (Fig. 2 A, shaded line) shows no systematic deviations and has a reduced χ-squared of 1.4. In fitting the data, information was obtained about the z-dependent intensity for the cytoplasmic component (dotted-dashed line), the z-dependent intensities from the membrane components (dotted lines), and cell height h = zTM – zBM. Because the cytoplasmic contribution to the signal was small, EGFP-H-Ras is a useful model system for a predominantly membrane-bound protein distribution.
Figure 2.
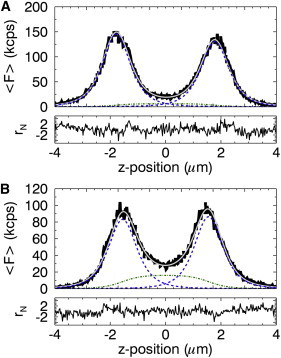
The z-dependent fluorescent intensity profile in kilo counts/s. (A) The profile (solid line) from EGFP-H-Ras and its fit (shaded line) to Eq. 6 (reduced χ2 = 1.4). (Dotted-dashed line) Contribution from the cytoplasmic (slab) layer; (dotted lines) contribution from the membrane (delta) layers. (B) The intensity profile (solid line) from the combined fluorescence of EGFP-H-Ras and mCherry and its fit (shaded line) to Eq. 6 (reduced χ2 = 1.3). The increase in the cytoplasmic intensity (dotted-dashed line) stems from the addition of the mCherry signal. To see this figure in color, go online.
Finally, we varied the ratio of cytoplasmic to membrane-bound protein by coexpressing mCherry and EGFP-H-Ras in U2OS cells. The mCherry protein populated the cytoplasmic pool, whereas EGFP-H-Ras contributed mainly to the membrane-bound component. Expressing two differently colored fluorescent proteins provided a convenient method to quickly select transfected cells expressing each protein at the desired intensity ratio. Although the fluorescence was split into a green and a red detection channel, we combined the photon counts of both channels in software to mimic the fluorescence signal of a single-colored fluorescent protein found in the cytoplasm and at the membrane. The z-scan intensity profile (solid line) of the combined signal from a coexpressing cell is shown in Fig. 2 B together with a successful fit (shaded line) of the data by Eq. 6 with a reduced χ-squared of 1.3. Although the additional presence of mCherry made the cytoplasmic intensity more prominent than in Fig. 2 A, each membrane layer along with the cytoplasmic layer was still cleanly resolved by the fit. Thus, the three-layer model successfully described the z-dependent intensity profiles for proteins with membrane-bound and cytoplasmic populations.
Brightness measurements in multilayer protein geometries
Before taking brightness measurements, it is illustrative to consider the influence of the three-layer geometry on the raw brightness by studying the z-dependence of Eq. 8 for a few select cases. For a purely cytoplasmic monomeric protein, such as EGFP, Eq. 8 reduces to
with bCyto = 1. The corresponding raw brightness curve (see Fig. 3 A, shaded line) for a thick (5-μm) cytoplasmic layer approaches 1 as the focus of the beam reaches the center of the sample where μcyto = 1, because the entire PSF is embedded in the sample. These are the conditions where conventional FFS, which ignores sample geometry, is valid.
Figure 3.
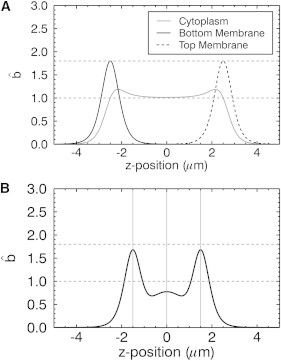
Modeling of raw brightness as a function of z position. (A) The raw brightness is calculated assuming a cell with a height of 5 μm. (Shaded line) for EGFP in a cell. (Solid and dashed lines) for a monomeric membrane protein labeled with EGFP located at either the bottom or top plasma membrane. (B) The raw brightness is calculated assuming a cell with a height of 3 μm and a monomeric protein distributed between the cytoplasm and the plasma membrane with an intensity ratio of FBM,max: FCyto,max: FTM,max of 3:1:3. The raw brightness in the cytoplasm and also at the plasma membrane is suppressed as compared to panel A due to the coexcitation of fluorescent proteins across adjacent sample layers.
Next, consider a monomeric protein only found at the bottom plasma membrane, which simplifies Eq. 8 to
with bBM = 1. The brightness curve (Fig. 3 A, solid line) has a single peak with a maximum at the position of the bottom membrane. We notice that the raw brightness at the bottom membrane exceeds 1. This increase is caused by the sample geometry, which is reflected in the gamma factor ratio μBM (zBM) = γ2,BM (zBM)/γ2,∞. In fact, one may think of the gamma factor ratio μi(z) as the bias factor in brightness due to sample geometry. The bias factor of a delta layer is μBM (zBM) ≈ 1.8 for our PSF. Thus, conventional FFS analysis of a protein at the membrane overestimates brightness by ∼1.8 due to the thin geometry. The raw brightness curve for a monomeric protein at the top membrane (Fig. 3 A, dashed line) is identical to that of the bottom membrane except for a shift in the z-position, reflecting the different location of the membrane.
The general case involves proteins occupying the cytoplasm and the membranes. The resulting raw brightness curve is, according to Eq. 8, the superposition of the raw brightness curve from each layer (Fig. 3 A) weighted by its fractional intensity fi(z). The dependence of the raw brightness on the fractional intensity, the geometric bias factor, and the brightness of each layer, leads to a convoluted signal that is not straightforward to interpret. We illustrate this point in Fig. 3 B by plotting Eq. 8 for a slab with a thickness of 3 μm with monomeric EGFP (bBM = bCyto = bTM = 1) distributed among the bottom membrane, the cytoplasm, and the top membrane with an intensity ratio FBM,max/FCyto,max/FTM,max of 3:1:3. We see that the raw brightness peaks at the membranes are reduced as compared to the value of 1.8 expected for a monomeric protein at the membrane, as discussed earlier. The raw brightness at the center of the cytoplasmic slab is less than the expected value of 1. Thus, quantitative analysis of the raw brightness curve is essential to link to the actual brightness of each layer.
Measuring the complete raw brightness curve and fitting it to Eq. 8 is very time-consuming, because an FFS measurement at a single z-position takes tens of seconds. A closer look at Eq. 8 reveals that measuring at three different locations (zBM, zTM, and zmid) is sufficient to calculate the brightness of each layer (bBM, bCyto, and bTM). The additional information needed for Eq. 8 is obtained by a fit of the intensity profile 〈F(z)〉, which provides the fluorescence signal 〈Fi(z)〉 from each layer as well as the location (zBM, zTM) of the membrane layers. This information serves to calculate the gamma factor ratios and fractional intensities that appear in Eq. 8. For the three raw brightness values , we chose to measure at the bottom membrane, at the top membrane, and at midheight in the cytoplasm. The experimental values , , and together with the fit of the intensity profile 〈F(z)〉 and Eq. 8 supply three equations
| (10) |
where the matrix elements are given by αi(z) = μi(z)fi(z). Inverting the above equation determines the parameters bBM, bCyto, and bTM.
To test multilayer brightness analysis at the plasma membrane, cells expressing the membrane protein EGFP-H-Ras were used as an experimental trial system. An intensity z-scan was followed by point FFS measurements at the top plasma membrane (zTM), the bottom plasma membrane (zBM), and in the cytoplasm (zmid). The brightness values measured at the top and bottom membrane exceeded 1, and brightness measured in the cytoplasm scattered between 0.3 and 1 (see Fig. 4 A). By analyzing the raw brightness as described above, we identify the brightness from each layer (Fig. 4 B). The analysis reveals that in U2OS cells, EGFP-H-Ras is monomeric both at the membrane and in the cytoplasm for all measurements.
Figure 4.
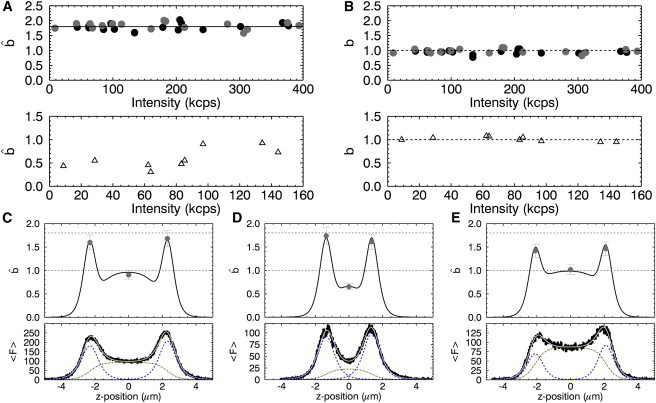
Z-scan brightness analysis in U2OS cells expressing EGFP-H-Ras. (A) (Top panel) Raw brightness measured at the top (shaded circles) and bottom (solid circles) membrane versus the fluorescence intensity (mean and standard deviation (SD) of 1.72 ± 0.13). (Bottom panel) Raw brightness from the midpoint in the cytoplasm (open triangles) (mean and SD of 0.59 ± 0.22). (B) (Top panel) True EGFP-H-Ras brightness bmembrane at the top (shaded circles) and bottom (solid circles) membrane (mean and SD of 1.00 ± 0.06); (bottom panel) true brightness bcyto (open triangles) in the cytoplasm (mean and SD of 1.01 ± 0.06). (C and D) EGFP-H-Ras z-scan plots for two cells with different thicknesses. (Bottom panels) Intensity traces in kilo counts/s (solid line) and fit (shaded line) along with the fitted profiles from each layer. (Top panels) Measured raw brightness (shaded circles) at zBM, zmid, and zTM. The raw brightness curves (solid line) are generated for the lower-panel intensity curves assuming monomeric proteins at both membranes and in the cytoplasm. (E) Z-scan FFS experiment of a cell expressing EGFP-H-Ras and EGFP. The graphs and labeling are identical to panel C. To see this figure in color, go online.
We provide a detailed analysis of two separate z-scan FFS experiments performed on cells expressing EGFP-H-Ras to illustrate the dependence of on geometry. The bottom panel of Fig. 4 C shows the intensity profile of a cell with a wider separation of the membranes than the cell in Fig. 4 D. After fitting the intensity profile of both cells, the raw brightness curves were calculated assuming a brightness of 1 at the membrane and in the cytoplasm. Thus, the raw brightness curves shown in the top panels of Fig. 4, C and D, represent the case of monomeric EGFP-H-Ras, and the measured brightness values (shaded dots) at the membranes and in the center of the cytoplasmic slab are in good agreement with the raw brightness curve. The raw brightness at the membrane in Fig. 4, C and D, is close to the value of 1.8. The slight reduction in brightness reflects the coexcitation of cytoplasmic protein that leads to a drop in the fractional intensity at the membrane. Because the intensity contributions from the cytoplasm are small, the decrease in the fractional intensity at the membrane is minor and the raw brightness predominantly reflects the brightness of a purely membrane-bound protein enhanced by the geometric bias factor of 1.8 (see Fig. 3 A).
The raw brightness in the cytoplasm, on the other hand, is significantly affected by the thickness of the cell at the position of the z scan. Although a thick slab (Fig. 4 C) leads to very little suppression of due to contributions of the membrane signal, a thinner slab (Fig. 4 D) leads to a significant reduction in . This coexcitation dependence on brightness is largely responsible for the scatter in the measured raw brightness values of Fig. 4 A.
The coexcitation dependence also affects the brightness at the membrane when a large relative pool of protein exists in the cytoplasm. Because cytoplasmic protein levels for EGFP-H-Ras alone were relatively low, we demonstrated this effect by increasing the pool of cytoplasmic fluorescent proteins through coexpression of EGFP and EGFP-H-Ras. Fig. 4 E shows the z-scan FFS analysis of a cell expressing both proteins in which the fluorescence of the cytoplasmic pool (Fig. 4 E, bottom panel) is much larger than for EGFP-H-Ras alone. This leads to a significant reduction of the raw brightness at the membrane position from the value of 1.8 (Fig. 4 E, top panel), because the larger cytoplasmic fluorescence introduces a pronounced drop in the fractional intensity of the membrane signal.
Matrix domain of HTLV-1 Gag
Although assembly of the retrovirus requires the full-length Gag protein, the process is complex and involves hundreds-to-thousands of Gag copies that pack together into individual Gag puncta. We chose to simplify the problem by investigating the MA domain of Gag inasmuch as MA is the primary driver of Gag association with the inner leaflet of the plasma membrane, but it lacks the ability to multimerize into large complexes (30,32). We first assessed the potential of MA-EGFP to bind to the plasma membrane. Z-scans were performed on U2OS cells transiently expressing either HTLV-1 MA-EGFP or HIV-1 MA-EGFP. Visual inspection of the z-scan intensity trace from each protein (see Fig. 5 A) identified distinct differences in behavior. HIV-1 MA-EGFP (shaded line) appears to be a cytoplasmic protein, whereas HTLV-1 MA-EGFP (solid line) has a significant membrane-bound component, as indicated by the double peak in the intensity profile.
Figure 5.
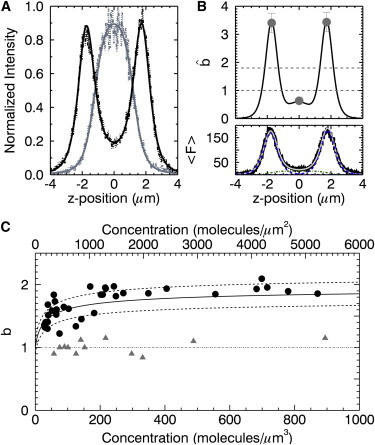
MA domain of retroviral Gag proteins. (A) Normalized intensity of HIV-1 MA-EGFP (light dotted line) and fit (shaded line) to cytoplasmic slab model and of HTLV-1 MA-EGFP (dark dotted line) and fit (solid line) to Eq. 6. (B) Brightness and intensity data from a cell expressing HTLV-1 MA-EGFP. The raw brightness (shaded circles) taken at the bottom membrane, cytoplasm, and top membrane (top panel) together with a modeled brightness curve generated for the intensity trace (bottom panel) assuming a monomeric protein in the cytosol and a dimeric protein at the plasma membrane. (C) Brightness from a population of cells expressing HTLV-1 MA-EGFP. The brightness at the membrane (solid circles) as a function of areal protein density (μm−2) shows a concentration-dependent monomer to dimer transition. Dimer binding curve (solid line) with a dissociation coefficient of ∼300 μm−2 and ±10% error bounds (dotted lines) for brightness at the membrane. The brightness in the cytoplasm (shaded triangles) as a function of volume protein density (μm−3) is monomeric at all measured concentrations. To see this figure in color, go online.
A fit of the data to the three-layer model confirmed that the HIV-1 MA-EGFP trace has no detectable protein component at the membrane, whereas HTLV-1 MA-EGFP has the majority of its intensity coming from the membrane, suggesting a strong plasma membrane component. Repeating z-scan measurements on cells expressing the protein at various concentrations confirmed these observations (data not shown). HIV-1 MA-EGFP is only found in the cytoplasm, whereas HTLV-1 MA-EGFP has a significant membrane-bound component. Although we often observed differences in the intensity peaks at the top and bottom membrane, there was no systematic trend favoring one membrane over the other. The differential binding of MA to the plasma membrane for these two retroviruses agrees with a previous study (24).
Raw brightness measurements were taken for HIV-1 MA-EGFP in the cytoplasm and z-scan FFS analysis, as previously described for a single layer, and were used to determine the cytoplasmic brightness (20). HIV-1 MA-EGFP displayed monomeric brightness at all concentrations (data not shown). This is consistent with the literature, which suggests that the HIV-1 MA protein does not exhibit appreciable homo-interactions at physiological concentrations (35,36). For HTLV-1 MA-EGFP, we measured raw brightness values at both plasma membranes and at the midsection in the cytoplasm (Fig. 5 B). The top panel of Fig. 5 B shows the raw brightness (shaded dots) as well as a theoretical raw brightness curve determined from the z-intensity trace (bottom panel). We note that at the membrane exceeds 1, whereas in the cytoplasm is typically <1, which reflects the multilayer nature of the sample. For this specific HTLV-1 MA-EGFP measurement, the raw membrane brightness exceeded 3, which suggested the presence of protein-protein interaction at the membrane. After applying Eq. 10 to the raw brightness values, we determined that the true brightness values are bBM = 1.97 ± 0.21, bTM = 1.97 ± 0.21, and bcyto = 1.06 ± 0.12.
To further study the behavior of HTLV-1 MA-EGFP at the plasma membrane, we performed z-scan FFS measurements on a population of cells with varying HTLV-1 MA-EGFP concentrations. We applied the matrix analysis of Eq. 10 to the experimental data to isolate the membrane brightness (bBM, bTM) and cytoplasmic brightness (bCyto) of the tagged HTLV-1 MA protein (Fig. 5 C). The cytoplasmic brightness bCyto is concentration-independent, bcyto 1.01 ± 0.12. The brightness of HTLV-1 MA-EGFP at the plasma membrane, on the other hand, exhibits a concentration-dependent increase from ∼1 at low concentration to a value of 2 at high concentration. Thus, the data reveal that HTLV-1 MA-EGFP undergoes a monomer-to-dimer transition with the solid line representing a binding curve with a dimerization dissociation coefficient of ∼300 molecules/μm2.
Discussion
Our results demonstrate that properly identifying the brightness of fluorescently-labeled proteins found both at the plasma membrane and in the cytoplasm is challenging. A few earlier studies have noted that fluorescence from neighboring layers qualitatively affects the measured brightness (37–39). In addition, brightness bias at the membrane due to delta-layer geometry was mentioned, but could not be experimentally identified (40). This study demonstrates that there are primarily three factors that confound quantitative interpretation of brightness measurements: the geometry of the layer, the intensity contribution from adjacent layers, and the brightness of adjacent layers. We briefly discuss each of these factors.
The first factor is the geometric effect, which for a stratified layer boils down to the thickness of each layer. When applying conventional FFS, a layer that is thinner than the axial length of the excitation PSF will lead to an increase in the raw brightness as originally reported by Macdonald et al. (20). In the extreme case of a delta layer, as is used to describe the plasma membrane, the raw brightness is increased by ∼1.8 for our excitation PSF.
The second factor accounts for the presence of background fluorescence from neighboring layers. The fluorescence signal of a layer is diluted by this background signal, which lowers the fractional intensity and thereby the raw brightness.
The third factor accounts for differences in brightness at neighboring layers. To illustrate its effect, we used Eq. 8 to calculate the raw brightness at the bottom membrane as a function of the fractional intensity fBM(zBM) for a cell with both membrane-bound and free cytoplasmic protein populations (see Fig. 1 A). In Fig. 6, we systematically changed the actual brightness at the membrane from a monomer to a trimer, while keeping the cytoplasmic protein as a monomer in all cases. The raw brightness decreases as a function of fractional intensity for all cases, but the slope differs significantly. In general, a larger brightness difference between the cytoplasmic and membrane-bound protein leads to a steeper drop in raw brightness with fractional intensity. This issue is significant because membrane binding frequently promotes oligomerization of the protein at the membrane whereas the cytoplasmic fraction remains in monomer form. Thus, the fluorescence background from the cytoplasm and the brightness difference between the membrane-bound and cytoplasmic fractions lead to a reduced measured brightness at the membrane, which hampers the proper identification of the oligomeric state.
Figure 6.
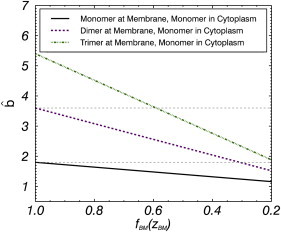
The modeled raw brightness at the bottom membrane is given as a function of the fractional intensity fBM(zBM) for a cell with both membrane-bound and cytoplasmic protein populations. was modeled for monomeric, dimeric, and trimeric protein at the membrane, while keeping the cytoplasmic protein a monomer in all cases. The raw brightness decreases as a function of fractional intensity in all cases but decreases more rapidly as the brightness difference between the cytoplasm and membrane increases. To see this figure in color, go online.
Although this work used a Gaussian-Lorentzian PSF model for fitting the data, it is important to emphasize that the z-scan method is not tied to any particular PSF model. The only requirement is an accurate parameterization of the experimental PSF. Extension of the z-scan method to one-photon excitation only requires a proper parameterization of the one-photon PSF. To be more precise, one-photon excitation uses the observation volume O(ρ, ζ) instead of the PSF to account for the effect of the pinhole on the collected fluorescence emission. This observation volume can be modeled by multiplying the excitation PSF by a collection profile function (41). Once a proper parameterization of O(ρ, ζ) has been obtained, z-scan analysis with one-photon excitation can be performed by replacing the PSF of Eq. 9 with O(ρ, ζ).
If a protein resides exclusively at the plasma membrane, then the problem reduces to a single layer, provided the top and bottom membrane are sufficiently far apart to avoid coexcitation. In this case, the brightness of a protein at the plasma membrane can be measured directly (38,39,42). Relating the measured brightness with the oligomeric state of the protein relies on a calibration experiment with a monomeric membrane protein to identify the monomeric brightness value. H-Ras appears to be an acceptable monomeric brightness standard for U2OS cells, but we observed both monomeric and higher brightness states for EGFP-H-Ras in MDCK cells (data not shown). It was recently reported that H-Ras was found in both monomeric and cluster form at a ratio of 70:30 for each respective species (43) in BHK cells. Thus, identifying a brightness standard for membrane measurements appears challenging, because the cell line and cell environment can potentially alter the oligomerization and clustering of the protein.
To avoid these potential complications, we suggest a straightforward alternative to establish the monomeric brightness at the membrane. A routine measurement of the fluorescent protein in the cytoplasm or nucleoplasm determines the true monomeric brightness λmonomer. We account for the delta-layer geometry of the membrane by multiplying λmonomer by the geometric bias factor μM(zM) for a membrane, which is calculated as described earlier. The product
represents the calibration brightness for a monomer at the membrane. This calibration procedure works as long as the brightness near the membrane and in the cytoplasm are the same. A constant brightness is an essential property of any fluorescent protein suited for quantitative brightness experiments and needs to be established independently for each new fluorescent label (44). For example, EGFP has a stable brightness that remains unchanged when tagged to another protein, as well as, when measured in the nucleus, cytoplasm and in vitro (12,44). As expected and shown by our data, the brightness of EGFP at the plasma membrane and in the cytosol is the same as long as geometry is accounted for. Thus, the above calibration procedure should prove useful for any fluorescent protein suited for quantitative brightness experiments.
Fluorescence from neighboring layers also affects the raw brightness in the cytoplasm, although this issue has not received much attention yet. A 2011 study observed unphysically low brightness values in the cytoplasm when studying HIV-1 and HTLV-1 Gag interactions in cytoplasm (23), which were traced back to the presence of fluorescence from a membrane-bound fraction of labeled Gag proteins. Here we observed the same phenomenon for H-Ras (Fig. 4 A) and HTLV-1 MA (Fig. 5 B). However, unlike the earlier study we used quantitative z-scan FFS to identify the correct brightness in the cytoplasm and at the membrane. Studying the MA domains of both HIV-1 Gag and HTLV-1 Gag revealed a purely cytosolic distribution of HIV-1 MA-EGFP, while HTLV-1 MA-EGFP was distributed between the cytoplasm and the plasma membrane, which agrees with recent observations (24) and implies fundamental differences between the early steps in HIV-1 and HTLV-1 assembly.
Our study further provides evidence that cytoplasmic HTLV-1 MA-EGFP binds the plasma membrane as a monomer, because HTLV-1 MA-EGFP was entirely monomeric in the cytoplasm and only exhibited a concentration-dependent monomer to dimer transition at the plasma membrane. This observation is supported by immunoprecipitation and immunoblotting studies that identified the presence of stable MA dimers at the plasma membrane (45). Because we measure both cytoplasmic and membrane-bound pools of HTLV-1 MA-EGFP, our brightness data provide evidence that links the monomeric MA in the cytoplasm with the observed dimers at the membrane through the presence of MA-MA interactions that occur in the membrane-bound form. Of course, dimerization is only the first step toward assembly of the complete viral-like particle. Observing additional steps requires future experiments with the full-length Gag protein to account for the additional interactions outside the MA domain that play a role in the formation of high-order Gag complexes (46). The advances in brightness experiments presented here not only provide the foundation for future work with the full-length HTLV-1 Gag protein, but also should prove useful for studies of any protein that is distributed across stratified layers within the cell.
Acknowledgments
This research was supported by National Institutes of Health (grant No. R01GM064589) and the National Science Foundation (grant No. PHY-0346782). E.M.S. was supported by the National Institute of Allergy and Infection Diseases of National Institutes of Health grant No. 5T32A1083196 (Minnesota Training Program in Virology) and the University of Minnesota Graduate School Doctoral Dissertation Fellowship.
Supporting Material
References
- 1.Johnson J.E., Cornell R.B. Amphitropic proteins: regulation by reversible membrane interactions. Mol. Membr. Biol. 1999;16:217–235. doi: 10.1080/096876899294544. [DOI] [PubMed] [Google Scholar]
- 2.Cho W., Stahelin R.V. Membrane-protein interactions in cell signaling and membrane trafficking. Annu. Rev. Biophys. Biomol. Struct. 2005;34:119–151. doi: 10.1146/annurev.biophys.33.110502.133337. [DOI] [PubMed] [Google Scholar]
- 3.Smotrys J.E., Linder M.E. Palmitoylation of intracellular signaling proteins: regulation and function. Annu. Rev. Biochem. 2004;73:559–587. doi: 10.1146/annurev.biochem.73.011303.073954. [DOI] [PubMed] [Google Scholar]
- 4.Glomset J.A. Protein-lipid interactions on the surfaces of cell membranes. Curr. Opin. Struct. Biol. 1999;9:425–427. doi: 10.1016/s0959-440x(99)80058-x. [DOI] [PubMed] [Google Scholar]
- 5.Goñi F.M. Non-permanent proteins in membranes: when proteins come as visitors. Mol. Membr. Biol. 2002;19:237–245. doi: 10.1080/0968768021000035078. [DOI] [PubMed] [Google Scholar]
- 6.Elson E.L., Magde D. Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 1974;13:1–27. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 7.Magde D., Elson E.L., Webb W.W. Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers. 1974;13:29–61. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 8.Rigler R., Mets Ü., Kask P. Fluorescence correlation spectroscopy with high count rate and low background: analysis of translational diffusion. Eur. Biophys. J. 1993;22:169–175. [Google Scholar]
- 9.Qian H., Elson E.L. On the analysis of high order moments of fluorescence fluctuations. Biophys. J. 1990;57:375–380. doi: 10.1016/S0006-3495(90)82539-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen Y., Müller J.D., Gratton E. The photon counting histogram in fluorescence fluctuation spectroscopy. Biophys. J. 1999;77:553–567. doi: 10.1016/S0006-3495(99)76912-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Müller J.D. Cumulant analysis in fluorescence fluctuation spectroscopy. Biophys. J. 2004;86:3981–3992. doi: 10.1529/biophysj.103.037887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen Y., Müller J.D., Gratton E. Molecular brightness characterization of EGFP in vivo by fluorescence fluctuation spectroscopy. Biophys. J. 2002;82:133–144. doi: 10.1016/S0006-3495(02)75380-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen Y., Wei L.-N., Müller J.D. Probing protein oligomerization in living cells with fluorescence fluctuation spectroscopy. Proc. Natl. Acad. Sci. USA. 2003;100:15492–15497. doi: 10.1073/pnas.2533045100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen Y., Wei L.-N., Müller J.D. Unraveling protein-protein interactions in living cells with fluorescence fluctuation brightness analysis. Biophys. J. 2005;88:4366–4377. doi: 10.1529/biophysj.105.059170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ries J., Chiantia S., Schwille P. Accurate determination of membrane dynamics with line-scan FCS. Biophys. J. 2009;96:1999–2008. doi: 10.1016/j.bpj.2008.12.3888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ruan Q., Cheng M.A., Mantulin W.W. Spatial-temporal studies of membrane dynamics: scanning fluorescence correlation spectroscopy (SFCS) Biophys. J. 2004;87:1260–1267. doi: 10.1529/biophysj.103.036483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Humpolícková J., Gielen E., Engelborghs Y. Probing diffusion laws within cellular membranes by Z-scan fluorescence correlation spectroscopy. Biophys. J. 2006;91:L23–L25. doi: 10.1529/biophysj.106.089474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Berland K.M., So P.T., Gratton E. Two-photon fluorescence correlation spectroscopy: method and application to the intracellular environment. Biophys. J. 1995;68:694–701. doi: 10.1016/S0006-3495(95)80230-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schwille P., Haupts U., Webb W.W. Molecular dynamics in living cells observed by fluorescence correlation spectroscopy with one- and two-photon excitation. Biophys. J. 1999;77:2251–2265. doi: 10.1016/S0006-3495(99)77065-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Macdonald P.J., Chen Y., Mueller J.D. Brightness analysis by Z-scan fluorescence fluctuation spectroscopy for the study of protein interactions within living cells. Biophys. J. 2010;99:979–988. doi: 10.1016/j.bpj.2010.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Benda A., Beneš M., Hof M. How to determine diffusion coefficients in planar phospholipid systems by confocal fluorescence correlation spectroscopy. Langmuir. 2003;19:4120–4126. [Google Scholar]
- 22.Wills J.W., Craven R.C. Form, function, and use of retroviral gag proteins. AIDS. 1991;5:639–654. doi: 10.1097/00002030-199106000-00002. [DOI] [PubMed] [Google Scholar]
- 23.Fogarty K.H., Chen Y., Mueller J.D. Characterization of cytoplasmic Gag-Gag interactions by dual-color z-scan fluorescence fluctuation spectroscopy. Biophys. J. 2011;100:1587–1595. doi: 10.1016/j.bpj.2011.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fogarty K.H., Berk S., Mueller J.D. Interrelationship between cytoplasmic retroviral Gag concentration and Gag-membrane association. J. Mol. Biol. 2014;426:1611–1624. doi: 10.1016/j.jmb.2013.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lindwasser O.W., Resh M.D. Multimerization of human immunodeficiency virus type 1 Gag promotes its localization to barges, raft-like membrane microdomains. J. Virol. 2001;75:7913–7924. doi: 10.1128/JVI.75.17.7913-7924.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sandefur S., Varthakavi V., Spearman P. The I domain is required for efficient plasma membrane binding of human immunodeficiency virus type 1 Pr55Gag. J. Virol. 1998;72:2723–2732. doi: 10.1128/jvi.72.4.2723-2732.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Perez-Caballero D., Hatziioannou T., Bieniasz P.D. Human immunodeficiency virus type 1 matrix inhibits and confers cooperativity on gag precursor-membrane interactions. J. Virol. 2004;78:9560–9563. doi: 10.1128/JVI.78.17.9560-9563.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hamard-Peron E., Muriaux D. Retroviral matrix and lipids, the intimate interaction. Retrovirology. 2011;8:15. doi: 10.1186/1742-4690-8-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ono A., Demirov D., Freed E.O. Relationship between human immunodeficiency virus type 1 Gag multimerization and membrane binding. J. Virol. 2000;74:5142–5150. doi: 10.1128/jvi.74.11.5142-5150.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ono A., Ablan S.D., Freed E.O. Phosphatidylinositol (4,5) bisphosphate regulates HIV-1 Gag targeting to the plasma membrane. Proc. Natl. Acad. Sci. USA. 2004;101:14889–14894. doi: 10.1073/pnas.0405596101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Saad J.S., Miller J., Summers M.F. Structural basis for targeting HIV-1 Gag proteins to the plasma membrane for virus assembly. Proc. Natl. Acad. Sci. USA. 2006;103:11364–11369. doi: 10.1073/pnas.0602818103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bryant M., Ratner L. Myristoylation-dependent replication and assembly of human immunodeficiency virus 1. Proc. Natl. Acad. Sci. USA. 1990;87:523–527. doi: 10.1073/pnas.87.2.523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mandel L. Sub-Poissonian photon statistics in resonance fluorescence. Opt. Lett. 1979;4:205–207. doi: 10.1364/ol.4.000205. [DOI] [PubMed] [Google Scholar]
- 34.Sanchez-Andres A., Chen Y., Müller J.D. Molecular brightness determined from a generalized form of Mandel’s Q-parameter. Biophys. J. 2005;89:3531–3547. doi: 10.1529/biophysj.105.067082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Burniston M.T., Cimarelli A., Luban J. Human immunodeficiency virus type 1 Gag polyprotein multimerization requires the nucleocapsid domain and RNA and is promoted by the capsid-dimer interface and the basic region of matrix protein. J. Virol. 1999;73:8527–8540. doi: 10.1128/jvi.73.10.8527-8540.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dalton A.K., Ako-Adjei D., Vogt V.M. Electrostatic interactions drive membrane association of the human immunodeficiency virus type 1 Gag MA domain. J. Virol. 2007;81:6434–6445. doi: 10.1128/JVI.02757-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ruan Q., Chen Y., Mantulin W.W. Cellular characterization of adenylate kinase and its isoform: two-photon excitation fluorescence imaging and fluorescence correlation spectroscopy. Biophys. J. 2002;83:3177–3187. doi: 10.1016/S0006-3495(02)75320-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Saffarian S., Li Y., Pike L.J. Oligomerization of the EGF receptor investigated by live cell fluorescence intensity distribution analysis. Biophys. J. 2007;93:1021–1031. doi: 10.1529/biophysj.107.105494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Malengo G., Andolfo A., Caiolfa V.R. Fluorescence correlation spectroscopy and photon counting histogram on membrane proteins: functional dynamics of the glycosylphosphatidylinositol-anchored urokinase plasminogen activator receptor. J. Biomed. Opt. 2008;13:031215. doi: 10.1117/1.2940570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Godin A.G., Costantino S., Wiseman P.W. Revealing protein oligomerization and densities in situ using spatial intensity distribution analysis. Proc. Natl. Acad. Sci. USA. 2011;108:7010–7015. doi: 10.1073/pnas.1018658108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hess S.T., Webb W.W. Focal volume optics and experimental artifacts in confocal fluorescence correlation spectroscopy. Biophys. J. 2002;83:2300–2317. doi: 10.1016/S0006-3495(02)73990-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vetri V., Ossato G., Gratton E. Fluctuation methods to study protein aggregation in live cells: concanavalin A oligomers formation. Biophys. J. 2011;100:774–783. doi: 10.1016/j.bpj.2010.11.089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Plowman S.J., Muncke C., Hancock J.F. H-ras, K-ras, and inner plasma membrane raft proteins operate in nanoclusters with differential dependence on the actin cytoskeleton. Proc. Natl. Acad. Sci. USA. 2005;102:15500–15505. doi: 10.1073/pnas.0504114102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen Y., Johnson J., Mueller J.D. Observing protein interactions and their stoichiometry in living cells by brightness analysis of fluorescence fluctuation experiments. Methods Enzymol. 2010;472:345–363. doi: 10.1016/S0076-6879(10)72026-7. [DOI] [PubMed] [Google Scholar]
- 45.Mazurov D., Heidecker G., Derse D. HTLV-1 Gag protein associates with CD82 tetraspanin microdomains at the plasma membrane. Virology. 2006;346:194–204. doi: 10.1016/j.virol.2005.10.033. [DOI] [PubMed] [Google Scholar]
- 46.Ako-Adjei D., Johnson M.C., Vogt V.M. The retroviral capsid domain dictates virion size, morphology, and coassembly of Gag into virus-like particles. J. Virol. 2005;79:13463–13472. doi: 10.1128/JVI.79.21.13463-13472.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen Y., Müller J.D., Gratton E. Probing ligand protein binding equilibria with fluorescence fluctuation spectroscopy. Biophys. J. 2000;79:1074–1084. doi: 10.1016/S0006-3495(00)76361-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


