Modeling intracellular signaling underlying striatal function in health and disease

Abstract

Striatum, which is the input nucleus of the basal ganglia, integrates cortical and thalamic glutamatergic inputs with dopaminergic afferents from the substantia nigra pars compacta. The combination of dopamine and glutamate strongly modulates molecular and cellular properties of striatal neurons and the strength of corticostriatal synapses. These actions are performed via intracellular signaling networks, containing several intertwined feedback loops. Understanding the role of dopamine and other neuromodulators requires the development of quantitative dynamical models for describing the intracellular signaling, in order to provide precise unambiguous descriptions and quantitative predictions. Building such models requires integration of data from multiple data sources containing information regarding the molecular interactions, the strength of these interactions, and the subcellular localization of the molecules. Due to the uncertainty, variability, and sparseness of these data, parameter estimation techniques are critical for inferring or constraining the unknown parameters, and sensitivity analysis evaluates which parameters are most critical for a given observed macroscopic behavior. Here, we briefly review the modeling approaches and tools that have been used to investigate biochemical signaling in the striatum, along with some of the models built around striatum. We also suggest a future direction for the development of such models from the, now becoming abundant, high-throughput data.

Introduction

The basal ganglia, a group of phylogenetically conserved structures in vertebrates, are critical for the motivational and habitual control of motor and cognitive behaviors (Liljeholm & O’Doherty, 2012; Redgrave et al., 2010) both in health and disease. Several serious diseases, such as Parkinson’s (Redgrave et al., 2010), Huntington’s (Macdonald et al., 1993), schizophrenia (Simpson, Kellendonk, & Kandel, 2010), addiction to psychostimulants (Philibin, Hernandez, Self, & Bibb, 2011) and pharmacologically induced dyskinesia (e.g. LID) (Santini, Valjent, & Fisone, 2008), are caused by degeneration or dysfunction in various basal ganglia structures. Despite the prevalence and severity of diseases affecting the basal ganglia,the development of drugs for these and other central nervous system disorders suffer from the highest attrition rates in the pharmaceutical industry (Geerts, 2011; Nutt & Goodwin, 2011). This is due to our lack of mechanistic understanding about the underlying system. The ultimate causes of these disorders are poorly understood, and most drugs are chosen based on symptom relief rather than on identified disease mechanisms. In order to design effective pharmacological interventions, the complexity of the nervous systemrequires an integrated understanding at the molecular, cellular and neuronal networklevels.

The striatum, the basal ganglia input stage, integrates cortical and thalamic inputs in functionally segregated pathways and loops (Alexander, Crutcher, & DeLong, 1990). The output of the striatum innervates the globuspallidus and substantianigra pars reticulata, which control both the thalamus and additional targets in the brainstem (Grillner, Hellgren, Ménard, Saitoh, & Wikström, 2005), see Figure 1. The function of the basal ganglia circuitry is complicated by feedback loops between and within these structures. Further compounding this complexity is the non-linear dynamic nature of cellular properties and synaptic connections. Dopaminergic afferents from the midbrain play a crucial role in modulating signaling through the basal ganglia, in particular through modification of molecular and cellular properties of striatal neurons as well as connection strength between neurons. The importance of dopamine is further highlighted by the number of pharmaceuticals which target dopamine receptors to treat basal ganglia disorders (Philibin et al., 2011; Redgrave et al., 2010; Simpson et al., 2010).

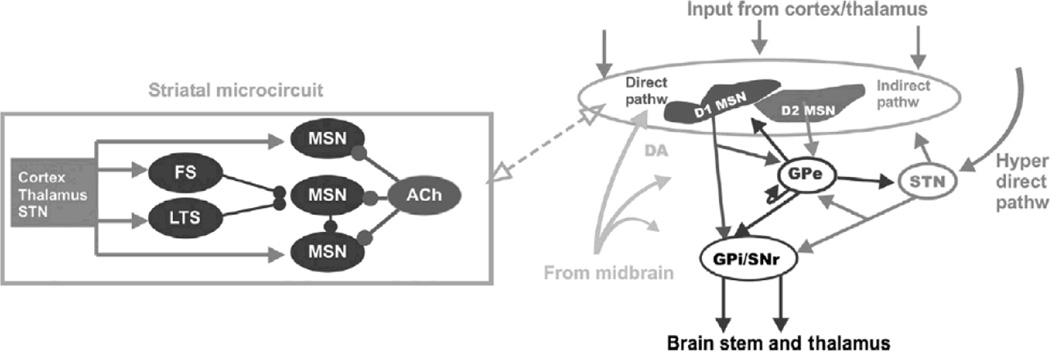
Figure 1.

An overview of the basal ganglia. Left: A schematic representation of the striatal micro-circuitry. The main neuron type in the striatum is the medium spiny neuron (MSN), constituting ~95% of striatal neurons. MSNs are the projection neurons from the striatum and receive convergent excitatory glutamatergic input mainly from cortex and thalamus, inhibitory GABAergic input from neighboring MSNs and striatal fast-spiking (FS) and low-threshold spiking (LTS) neurons, cholinergic input from cholinergic interneurons (ACh), and dopaminergic input from substantianigra pars compacta in the midbrain (SNc). Right: an illustration of the basal ganglia macro-circuitry, showing the glutamatergic and dopaminergic afferent inputs to striatum, as well as the projections via the direct, indirect and hyperdirect pathways. Approximately half of the MSNs belong to the direct pathway; they carry dopamine type 1 receptors and project to GPi/SNr. The other MSNs express dopamine type 2 receptors and project to GPe (globus pallidus externa) before reaching basal ganglia output structures. These output structure neurons control the activity levels of (motor) programs in the brain stem and thalamus.

There is a large body of experimental data gathered over the years concerning information processing in the basal ganglia in health and disease. The size and complexity of this data make it difficult to synthesize a coherent picture. Development of quantitative models is needed for integrating the knowledge obtained from diverse experimental approaches. Such models further provide a compact and standardized means to represent current knowledge and constitute a tool for guiding experiments and generating predictions that can be tested experimentally. Such models further provide a compact and standardized means to represent current knowledge and constitute a tool for guiding experiments and generating predictions that can be tested experimentally. These models comprise not just a collection of nodes and edges within each scale but also the dynamics of these interactions which are an integral part of the information flow. Since most pharmaceuticals target transmembrane receptors and downstream signalling molecules, and due to the importance of dopamine in basal ganglia disorders, quantitative models of dopaminergic system along with the signalling pathways affected by dopamine have the potential for greatly enhancing our understanding of underlying mechanisms of pathological conditions.

In the next section, we explain the procedures for developing quantitative models of intracellular signaling, with a focus on data sources, model building, parameter estimation and sensitivity analysis. Then we review many of the published models addressing different aspects of the information flow in the striatum at the molecular level in normal and pathological conditions. These include models for synaptic plasticity in the principal neurons of striatum, known as medium spiny neurons (MSN),as well as the life cycle of dopamine in the striatum.

Modeling biochemical reaction cascades

Building the network from multiple sources of information

Several types of information are required to build a quantitative mathematical model of intracellular signaling. First, proteins and other molecules that process and transmit information must be identified. Second, the pairwise interactions between these molecules must be determined. Third, the dynamics of these interactions must be accounted for. The specific proteins and their interactions represent the nodes and edges, respectively, of a chemical reaction network. The kinetics of these interactions transforms a static network into a dynamical one, in which the reaction rates define the behavior of the system. Most of the data that are used to define the interactions between signaling molecules comes from literature surveys of papers employing classical experimental studies addressing only a few interacting molecules at a time. These experiments could be pull-down assays where the physical interaction between two proteins is determined. There have also been several efforts to determine protein-protein interactions using high-throughput amenable techniques such as yeast two-hybrid (Rual et al., 2005; Stelzl et al., 2005). A major challenge still remaining is to interpret these available high throughput data to develop hypotheses on a systems level because the interactions detected in such screenings may lack functional mapping, i.e., the actual effect of the interaction in vivo. However, the importance of high throughput data generation is increasingly being acknowledged in formulating biological hypothesis (Ge, Walhout, & Vidal, 2003; Hernández Patiño, Jaime-Muñoz, & Resendis-Antonio, 2012).

Similarly, information regarding strength and rate of molecule interactions, i.e. kinetics and affinity of reactions, is mainly obtained from surveying papers addressing the interaction dynamics of two or three molecular species. There are no high throughput techniques for generating this data yet. Classically, such kinetic experiments target a specific protein in order to identify its role in the system of interest (Bibb et al., 1999; Hemmings, Greengard, Tung, & Cohen, 1984). Notably, there are large amounts of experimental data of this type for certain molecules, and very little such data for most of the other molecules. Thus, this data source is far from sufficient to identify all model parameters and also have some other limitations (see below). The process of model building can further be supplemented by specific in vitro experiments, particularly to identify the range of critical parameters.

An important part of the available interaction information has been organized into a few signaling pathways databases which have proven to be valuable. Databases like Reactome (Croft, 2013)and KEGG (Kanehisa, Goto, Kawashima, Okuno, & Hattori, 2004) contain static interaction information, and can assist the building of neuron specific reaction networks. On the other hand, model databases like BioModels (C. Li et al., 2010), ModelDB (Hines, Morse, Migliore, Carnevale, & Gordon, 2013)and DOQCS (Sivakumaran, Hariharaputran, Mishra, & Bhalla, 2003) contain published quantitative signaling models which are amenable to be reused, especially those that have been validated for signaling in neurons.

Modeling techniques and tools

Once the structure of the signaling network has been identified, as described in the preceding section, this information is translated into a mathematical form suitable for rendering a quantitative dynamical description. Depending on the biological system being studied, the nature of the question, the assumptions made and the available computational power, different simulation techniques can be used. In models of striatal signaling two types of modeling strategies have been used, ordinary differential equations (ODE) and stochastic-reaction modeling. In both cases the rate of change of each of the system’s species results from the contribution of individual reactions which produce and consume the species. Each of these reaction rates are expressed following the law of mass-action, which states that the rate is proportional to the product of a kinetic constant and some power of the reactant concentrations. Whether the concentration change is implemented as deterministic or stochastic in a given time step is the main difference between these two modelling strategies. This in turn depends on a critical assumption regarding the number of molecules in the system.

In the deterministic implementation, the rate equations are modelled as a system of ordinary differential equations with one ODE per species which render the same solution for repeated simulations with a given initial condition. For most relevant cases this system of ODEs does not have analytical solutions so that numerical integration utilizing one among several existing solvers is required to run simulations of the system dynamics. The ODE-based simulation is underlined by a fundamental assumption: the number of species’ particles is high enough to ignore the stochasticity of the reaction events. However, when modeling cellular processes occurring in a very small volume like the dendritic spine, this assumption may not hold true for many molecular species.

In a system with very few number of particles, the effect of the stochasticity of the reaction events becomes more pronounced and the evolution of the system differs from what an ODE-based description render not just because fluctuations around the mean are not considered but, more critically, because the mean dynamics can be qualitatively different (Bhalla, 2004a; Vilar, Kueh, Barkai, & Leibler, 2002). This common situation then requires a stochastic simulation which, however, is more computationally demanding. In this approach, the rate constants and the reactant concentrations do not unequivocally determine the rate of change in each time step, but define a probability for the reaction to occur which may be realized or not depending on the outcome of a random sampling (Gillespie, Hellander, & Petzold, 2013).

Another relevant issue is the simulation of spatial heterogeneities which result either from reactions occurring far faster than the diffusion of reactants and products or due to biological design, as in the case of compartmentalized signaling. This situation is the norm in intracellular signalling and it is commonly addressed in simulations by meshing the space of interest into sub-volumes which are considered homogeneous (or well-stirred) and exchange mass according to a first order process (Hepburn, Chen, Wils, & De Schutter, 2012; Oliveira et al., 2010). It is worth mentioning that while the definition of sub-volumes corresponding to functionally relevant compartments (e.g. a dendritic spine, cell membrane, PSD, etc.)is done at the level of the model building, as it entails biological knowledge (Oliveira et al., 2010), the meshing to account for diffusion is rather a physical problem constrained by the diffusion properties (Drawert, Engblom, & Hellander, 2012; Santamaria, Antunes, & Schutter, 2012). Thus, both ODEs (Bhalla, 2011)and stochastic simulation approaches (Oliveira et al., 2010) have been used to simulate the reaction within each sub-volume and the mass exchange between sub-volumes.

There are more accurate stochastic and deterministic methods where no meshing is performed and heterogeneities are considered all over the space at far higher resolutions. On the stochastic side there is single particle tracking (Leier & Marquez-Lago, 2011) and on the deterministic one there are partial differential equations. These are quite computationally demanding.

Parameter estimation and sensitivity analysis

One persistent concern in these types of models is the estimation of all rate constants and total amounts of conserved moieties. A conserved moiety can be a molecule that can exist in several forms, such as phosphorylated or non-phosphorylated forms, but the summed quantity of all forms is conserved. Biochemical estimates of these parameters obtained in test tube experiments with isolated components are valuable (Ajay & Bhalla, 2004). However, this kind of data typically provides affinities, and rarely provides estimates of the forward and backward reaction rates. Furthermore, the experimental conditions in a test tube do not match those inside the cell. In addition, most models are built under a considerable number of simplifying assumptions about the modular nature of real systems and the possibility to lump reaction steps or additional factors involved. Therefore, many intracellular signaling models are to different extents of a phenomenological character (Brown & Sethna, 2003). The models correspond to “grey” boxes where, despite their apparent straightforward interpretability, a variety of processes have been lumped together in each model reaction. This certainly obscures the use of parameters estimated from biochemical experiments with purified components in intracellular signaling models. A complementary approach of estimating parameters is to fit the model to sets of data obtained in experiments that can better represent the modeled system (Gutenkunst et al., 2007), such as cell cultures, tissue slices or whole organisms. This process of matching outputs from a more complex model to experimental data to find parameter estimates is sometimes referred to as calibration and the broader term reverse engineering appears frequently as well.

Within the field of modelling intracellular signaling in striatum and in fact in other systems (Chen et al., 2009), most calibration methods are built on trial and error experience, where parameters are fitted by hand until the model output corresponds to what is seen in experiments. There is a lot to learn from the field of systems biology, where automatic parameter estimation is an increasingly used procedure (Ashyraliyev, Fomekong-Nanfack, Kaandorp, & Blom, 2009; Lillacci & Khammash, 2010). Here different local and global optimization techniques are used to minimize an objective function, corresponding to the difference between the model output and the experimental results. In the context of parameter estimation one can also note that, given the experimental data and the model, it is not always possible to find unique values for all parameters. The relationship between the experimental data and the model can be such that the system is non-identifiable (Ashyraliyev et al., 2009; Raue et al., 2009).

A question related to parameter estimation is that of robustness. It has been argued that biological signaling cascades with similar functions can work in very different contexts, such as different cells, animals or environments, and therefore have to be robust against changes in, for example, rate constants and other parameters (Morohashi et al., 2002; von Dassow, Meir, Munro, & Odell, 2000). This implies that changes in these parameters do not have a large effect on the system output. Within the modeling field described here, tests for parameter robustness has mostly been performed by changing parameters one-at-a-time, and then recording the output. If the output after perturbations in a certain parameter is similar to what it was before, the model is considered to be robust against perturbations to this parameter. Here, one can note that the system cannot be robust against everything, as a signaling cascade has to be sensitive to some signals.

Considerable system insights can also be retrieved by analysing how the model output depends on the model parameters by the means of local or global sensitivity analysis (Saltelli, Tarantola, Campolongo, & Ratto, 2004). The local sensitivity of the system output o_i, with respect to the parameter input p_i is measured by the first order partial derivative, $\frac{\partial o_i(p_j)}{\partial p_1},$ or derivations thereof, (Saltelli et al., 2004) and describes how the model output depends on different parameters in the neighborhood of a specific point in parameter space. For biological systems, with a large uncertainty in the parameters, it might be more interesting to perform a global sensitivity analysis, where the aim is to investigate a larger part of the parameter space. Global methods are most often based on analyses of random parameter samples, and performed by statistical methods, for example by decomposing the variance of the output into different parts that can be attributed to a single input parameter or combinations thereof (Homma & Saltelli, 1996; Sobol′, 2001).Within the systems biology field, sensitivity has started to become an important part of the modelling process (Zi, 2011), but also within the field of neuroscience some studies have been performed (Qi, Miller, & Voit, 2008).

A modeling example

Here, we illustrate a modelling procedure by a simple model example describing calcium dependent activation of calmodulin (CaM), calcineurin, and calcium/calmodulin-dependent protein kinase II (CaMKII). Calmodulin is a calcium binding protein which is involved in various signalling processes and is strongly implicated in synaptic plasticity (Xia & Storm, 2005). Calmodulin contains four calcium binding domains and each of them binds to one calcium ion (Weinstein & Mehler, 1994). The binding of calcium with calmodulin is a cooperative process (Stemmer & Klee, 1994). Calcium bound calmodulin activates protein phosphatase 2B (PP2B), also known as calcineurin (CaN) (King & Huangs, 1983). This protein is also highly implicated in the molecular processes related to learning. As we see in the next section, this protein has a role in striatal signaling. Calcium/Calmodulin dependent protein kinase II (CaMKII) is a kinase which is activated by the binding of calcium/calmodulin. CaMKII molecules exist as a dodecamer (Rosenberg, Deindl, Sung, Nairn, & Kuriyan, 2005), with two juxtaposed hexamers. If two of its neighboring subunits in a hexamerare active by calcium/calmodulin then one unit can phosphorylate the other one at Thr-286 (Bradshaw, Kubota, Meyer, & Schulman, 2003). The phosphorylated unit can remain active even in the absence of calcium/calmodulin (Yang, 1999). A reaction scheme for the model of activation of calmodulin and subsequent activation of PP2B and CaMKII is shown in Figure 2.

Figure 2.

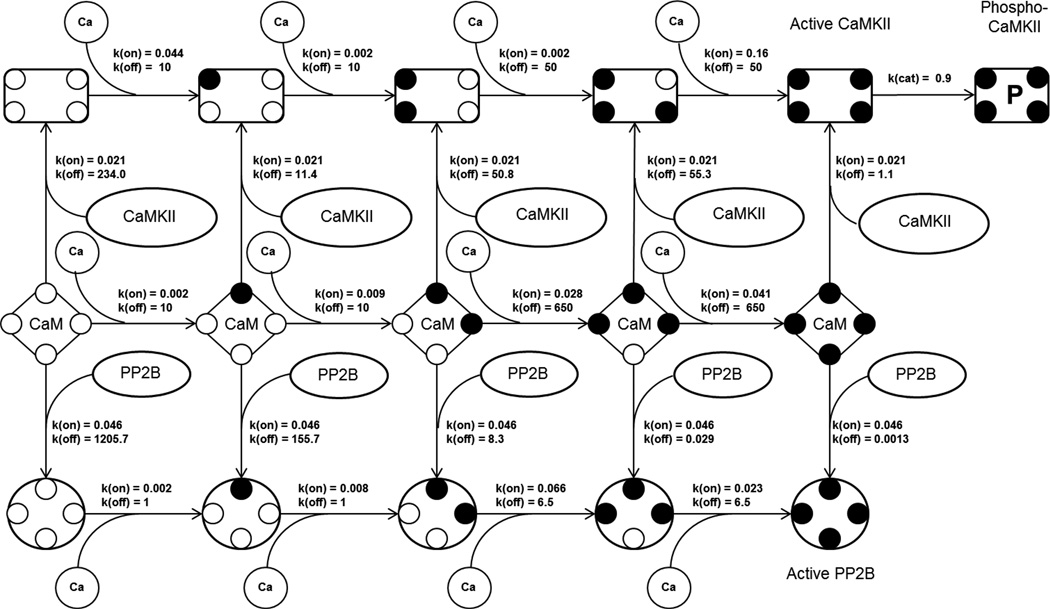
Reaction scheme for the model example along with the reaction rate constants where k(on) is the forward rate constant, k(off) is the reverse rate constant and k(cat) is the catalytic rate constant. All the reactions having a k(on) and a k(off) are reversible reactions. This represents the calcium binding to the calmodulin (CaM) as a four step process. The species at each step can bind to its target, either CaMKII or PP2B.The first, second and third row in the diagram represents the calcium binding to CaM-CaMKII complex, CaM, and CaM-PP2B complex respectively. The CaM-CaMKII complex (rectangle with 4 smaller circles, first row) or CaM-PP2B complex (circle with 4 smaller circles, third row) can bind to calcium until all the four calcium binding sites of calmodulin are occupied. Active CaMKII can be phosphorylated to phospho-CaMKII. The unit for k(on) is nM⁻¹s⁻¹, k(off) is s⁻¹ and k(cat) is s⁻¹.

The model has been implemented using a deterministic approach with Simbiology toolbox in Matlab. The activation of calmodulin by calcium is modeled as a four step reaction. In order to obtain the dissociation constants for each of these calcium calmodulin binding steps we have used the Adair-Klotz equation (Klotz, 2004, equation 8). According to this there should be one dissociation-constant for each step. So, there should be four constants for this particular binding reaction. The steady-state data is taken from Stemmer et. al. (Stemmer & Klee, 1994). The estimated dissociation constant, Kd, and the dissociation rate constants, k(off), obtained from additional experimental measurement (Martin, Andersson Teleman, Bayley, Drakenberg, & Forsen, 1985) are then used to calculated the forward rate constants of the reactions, k(on), using the relation, Kd = k(off)/k(on). At each calcium-binding step a calcium-calmodulin complex can bind to calmodulin-target-proteins, namely PP2B and CaMKII, Figure 2. The parameters for these binding steps are estimated by fitting the model against experimental data for CaMKII, and PP2B activation (Bradshaw et al., 2003; Martin et al., 1985; O’Donnell, Yu, Fowler, & Shea, 2011; Quintana, Wang, Forbes, & Waxham, 2005; Shifman, Choi, Mihalas, Mayo, & Kennedy, 2006). The fitting of the model to these measurements are shown in Figure 3. It could be noted that there are a number of cyclic reactions in the model, e.g., a complex containing calcium, calmodulin and PP2B can be formed via two routes. Either it can be formed by the association of a calcium-bound-calmodulin with a PP2B or calcium binding to a calmodulin-PP2B complex. Thermodynamically, the net free energy change for both these paths should be the same. This thermodynamic constraint is taken into consideration while estimating the reaction parameters. The input to the final model is a calcium transient which is modelled as a double-exponential by fitting the intracellular calcium measurement using fluorescence (Sabatini, Oertner, & Svoboda, 2002), Figure 3 (F), with a maximum amplitude of 700 nM. The phosphorylation of CaMKII is calculated with an approach similar to the one used by Li et al (L. Li, Stefan, & Le Novère, 2012) where the possible concentration of active CaMKII to be phosphorylated is calculated by taking the average number of times two active CaMKII appear as a neighbour in a hexamer for 1000 random samples.

Figure 3.

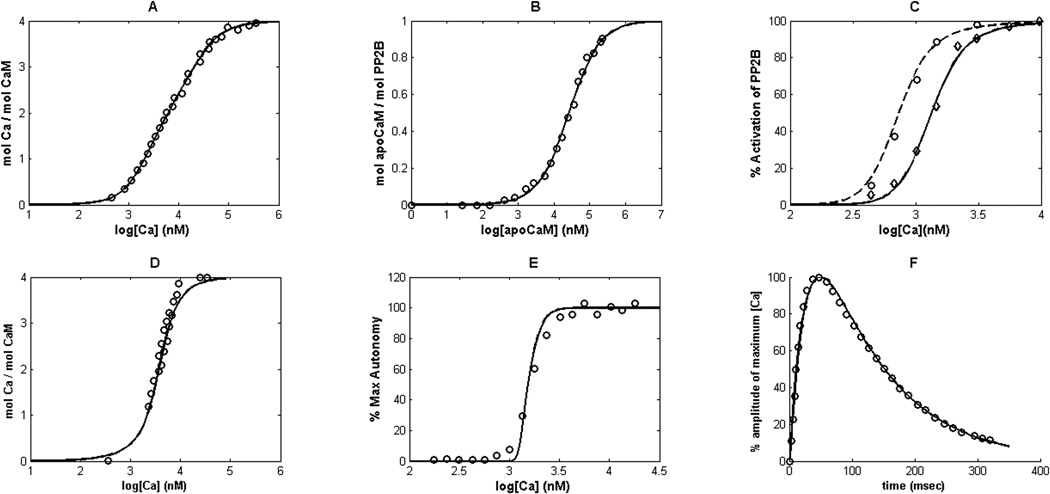
Model fitting to the experimental measurements.(A)Number of moles of calcium(Ca) bound to each mole calmodulin (CaM)versus calcium concentration, the line(—) represents the model and the empty circles(○) represents the data from (Stemmer & Klee, 1994). (B) Number of moles of apo-calmodulin (apoCaM, calmodulin without calcium bound to it) bound to each mole PP2B versus the concentration of apoCaM, the line(—) represents the model and the empty circles(○) represents the data from (O’Donnell et al., 2011). (C) % activation of PP2B versus calcium concentration at various concentrations of CaM:30nM(experiment ◊, model —), and 300nM(experiment ○, model – –), (Stemmer & Klee, 1994). (D) Number of moles calcium bound to per mole CaM against calcium concentration in presence of CaMKII, the line(—) represents the model and the empty circles(○) represents the data from (Shifman et al., 2006). (E) % of phosphorylated CaMKII (autonomy in CaMKII activity)versus calcium concentration, the line(—) represents the model and the empty circles(○) represents the data from (Bradshaw et al., 2003). (F) Intracellular calcium concentration in terms of percentage change of calcium fluorescence for a single synaptic activation as measured by Sabatini et.al.(Sabatini et al., 2002). This calcium transient is used as the model input as shown in Figure 4.

Next, we investigate how this simple model behaves for different frequencies of calcium inputs, two of them are shown in Figure 4(B). The output which we are interested in is the difference in the activity of CaMKII and PP2B. This variable is of physiological relevance as described in the next section. The model is being simulated for 10 sec with 10 calcium transients for frequencies ranging from 1 to 25 Hz. The initial concentrations of CaM, PP2B, and CaMKII are 5µM, 1µM, and 5µM, respectively. The activation of PP2B follows qualitatively the calcium transient and eventually saturates at higher frequencies. In contrast, the CaMKII needs higher amount of calcium calmodulin (CaCaM) to get activated because its affinity towards CaCaM is lower (higher Kd) than the affinity of PP2B towards CaCaM. Therefore, CaMKII requires higher effective calcium as in Figure 4(B, ii) to be significantly activated. To quantify the activity of CaMKII and PP2B we used the area under the curve (AUC) for the trajectory of the species. It means that the difference in the activity of CaMKII and PP2B corresponds to the difference in their AUC. The results for calcium inputs with different frequencies are shown in Figure 4(C). For lower frequencies the activity of PP2B dominates over the activity of CaMKII. As the frequency of the input, and thereby the effective calcium concentration, increases this leads to the activation of CaMKII and in turn its autophosphorylation. Due to the increased autophosphorylation, the decay in the CaMKII activity, after the calcium spike ends, is slow. Since, the initial concentration of CaMKII is higher than that of PP2B and there is an increased phosphorylation, its activity dominates for higher frequencies in our model. This frequency dependent differential activity level has been studied previously, as well (L. Li et al., 2012). This shows how even a small model can enhance our mechanistic understanding about the dynamic behavior of a signaling module.

Figure 4.

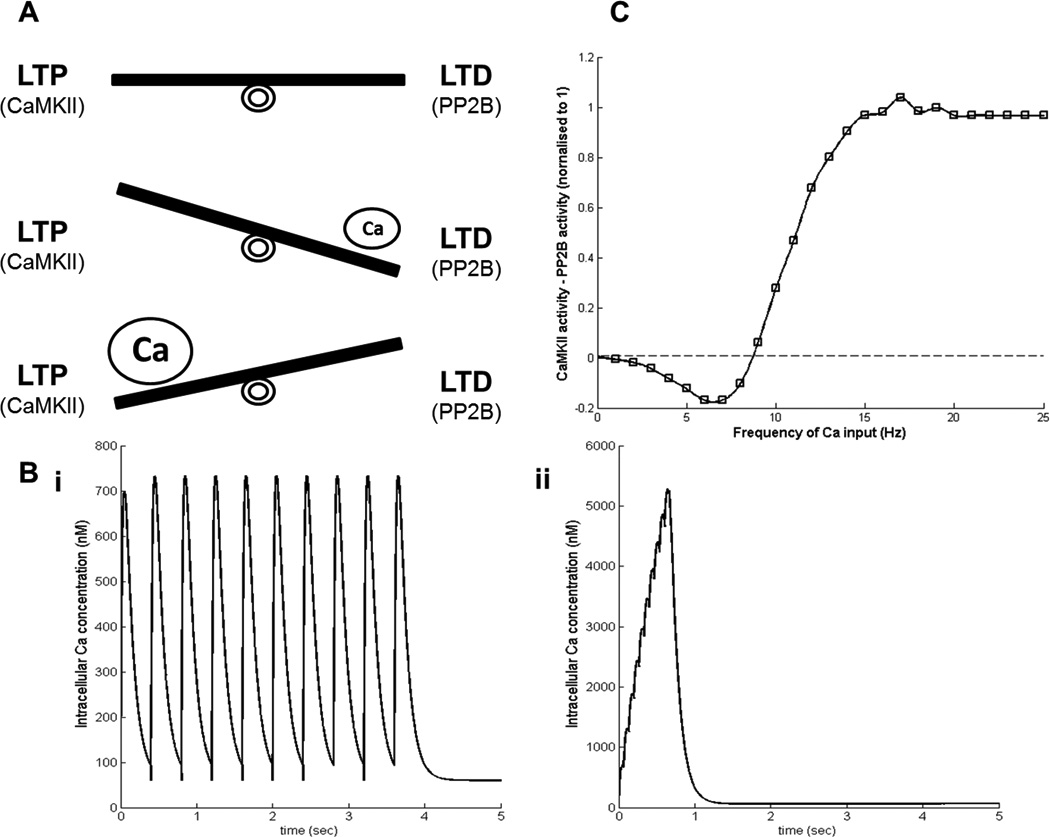
(A) Schematic representation of balance between LTP (higher activity of CaMKII) and LTD (higher activity of PP2B). For lower calcium(Ca) LTD dominates and for higher Ca LTP dominates. (B) Shapes of inputs with 10 calcium transients, (i) is a 2.5 Hz input and (ii) is a 15 Hz input (note the differences in the scale). (C) Normalized difference between the activity of CaMKII and PP2B produced by the model for different frequencies of Ca inputs (10Catransients). The results are for a simulation time of 10 sec.

Subcellular models representing striatal signaling

The glutamatergic projections from prefrontal cortex and dopaminergic projections from the midbrain innervate many of the neuronal types in the striatum in particular, the two GABAergic projection neurons (medium spiny neurons, MSN) which together comprise about 95% of the striatal neurons. They are distinguished by the differential expression of dopamine D1 and D2 receptors (D1R and D2R), and there is a small population co-expressing both receptors (Bertran-Gonzalez et al., 2008; Bertran-Gonzalez, Hervé, Girault, & Valjent, 2010). The convergence of corticostriatal glutamate and dopamine from the midbrain on these striatal neurons triggers synaptic plasticity processes that underlie reinforcement learning and pathological conditions such as psychostimulant addiction. The phasic changes in striatal dopamine signal encompass different time scales in these two situations. A transient (subsecond) but high amplitude dopamine signal results from a reward in reinforcement learning trials (Schultz, 2007) while an hour long elevation in striatal dopamine level occurs upon administration of psychostimulants (Volkow, Wang, Fowler, Tomasi, & Telang, 2011). This prolonged dopamine increase is likely to produce abnormal synaptic plasticity, whereas the lack of dopamine in Parkinson’s disease leads to a different abnormality in synaptic plasticity. Therefore, understanding the intracellular signaling pathways activated by convergent glutamate and dopamine is crucial to understanding aberrant synaptic plasticity associated with these disorders.

Postsynaptic signaling models

DARPP32 is a phosphoprotein, abundantly expressed in MSNs, which integrates the dopaminergic and glutamatergic inputs. It acts as one of the major points of interaction between the two inputs (Figure 5). The physiological effects of the inputs depend on the level of phosphorylation at different residues of this molecule (Per Svenningsson et al., 2004). This has been the focus of many modeling studies because of its involvement in pathological conditions (Håkansson, Lindskog, Pozzi, Usiello, & Fisone, 2004; Santini et al., 2008). One of the earliest efforts to model the DARPP32 dynamics, by Kötter,captured some interesting aspects of the glutamatergic and dopaminergic signal integration but it was challenged by the scarcity of detailed data about the other proteins involved (Kötter, 1994).

Figure 5.

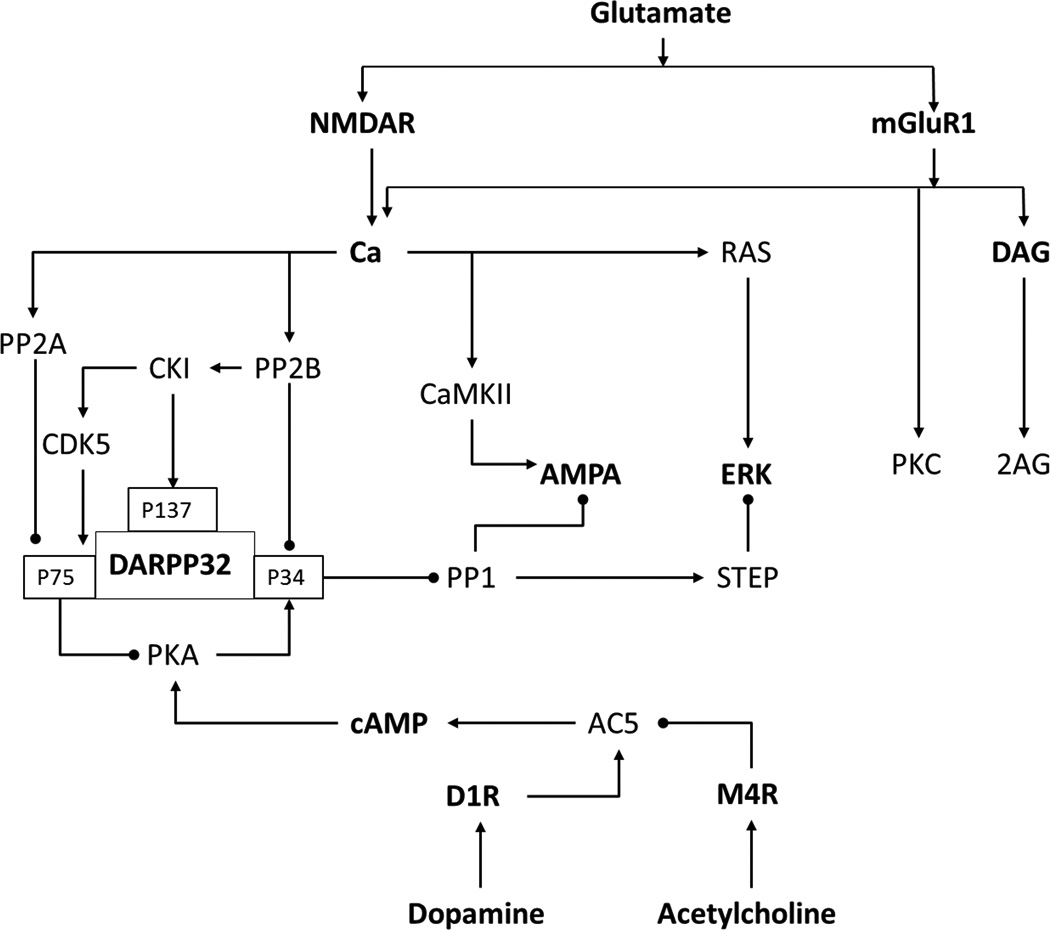
Signaling pathways involved in striatal signaling of D1R MSN.

The first two sufficiently detailed intracellular signaling models for striatum were single compartment mass action models which independently addressed the integration by DARPP32 of dopamine and glutamate triggered signaling cascades in medium spiny neurons carrying D1R dopamine receptors (Fernandez, Schiappa, Girault, & Le Novere, 2006; Lindskog, Kim, Wikström, Blackwell, & Kotaleski, 2006). DARPP32 when phosphorylated by PKA at Thr34 is turned into a nanomolar inhibitor of the phosphatase PP1. As this phosphatase acts on many of the proteins phosphorylated by protein kinase A (PKA), DARPP32 is expected to act as a booster of D1R mediated activation of PKA by dopamine. Besides the phosphorylation at threonine (Thr) 34, there are at least three other residues phosphorylated by different kinases. The modification of Thr75 by Cdk5 turns DARPP32 into a micromolar inhibitor of PKA. On the other hand, the Ca²⁺ entering the cell by the glutamatergic activation of NMDAR receptors activate the phosphatases PP2B and PP2A, which are known to dephosphorylate DARPP32. These opposing changes on DARPP32 Thr34 phosphorylation levels were thought to be the regulator of the kinase-phosphatase ratio. Prolonged treatment with Ca²⁺ and dopamine, separately, has opposite effect on Thr34. D1Rstimulation increases the phosphorylation of Thr34 whereas increased Ca²⁺, induced by glutamate receptor agonists, decreases the phosphorylation of Thr34.

One of the early models on this system (Lindskog et al., 2006) was built to understand the response evoked by transient dopamine and Ca²⁺ inputs. In this model it is assumed that Thr34 and Thr75 are the two important phosphorylation sites on DARPP32majorly affected by the inputs. A conclusion drawn by this model is that the transient inputs produce different downstream effects compared to the prolonged inputs. The model investigated how a combined input of dopamine and Ca²⁺, which represents a combined activation of nigrostriatal and corticostriatal afferents, could produce a larger activation of PKA and inhibition of PP1 as compared to separate activation of these afferents.

The understanding of DARPP32 regulation was further enhanced by a model with an increased number of DARPP32-phosphorylation sites (Fernandez et al., 2006). In this model an additional, well characterized, phosphorylation site, at Serine (Ser) 137,was also considered along with the other two previously mentioned sites (Figure 5). Ser137 is phosphorylated by casein kinase 1(CK1) and dephosphorylated by protein phosphatase-2C (PP2C). Phosphorylation at this site decreases the rate of dephosphorylation at Thr34 by PP2B. The activity of CK1 itself is regulated by autophosphorylation and dephosphorylation by PP2B. An autophosphorylated state of the kinase is inactive. Activation of PP2B removes this inhibitory phosphorylation and renders kinase activity to it. This incoherent type feed-forward loop has a significant effect on the sharpness and the duration of the response evoked by dopamine at Thr34. They went further and studied the effect of Ser137 mutation on the function of DARPP32 as a signal integrator and concluded that the function was impaired.

A pathway which affects DARPP32 phosphorylation state at Thr75 is the Cdk5 pathway (Figure 5). This was stressed in one of the later models (Nakano, Doi, Yoshimoto, & Doya, 2010). Cdk5 is activated by CK1 which in turn is activated by Ca²⁺. Cdk5 then phosphorylates Thr75 of DARPP32 which is dephosphorylated by PP2A. PP2A can also be activated by calcium. A weak calcium input leads to a dominant CK1-Cdk5 arm of the signaling cascade which is surpassed by the PP2A arm in response to strong calcium.

A more recent model for the dopamine D1R and ionotropic glutamate receptor induced cascade looks into considerable details of downstream interactions (Gutierrez Arenas, Ericksson, & Hellgren Kotaleski, 2013) (Figure 5). It presents a hypothesis of physical segregation between different pathways, namely the Ca²⁺ dependent ERK phosphorylation and the dopamine dependent GluR1 phosphorylation. The model tries to explain how the two different arms of the signaling network interact with each other via the striatal enriched tyrosine phosphatase (STEP).This model is an example of how integrating relatively large amounts of data could bring new insights about the plausible properties of a reaction compartment, physical segregation in this case. It also takes into account the phosphorylation state of different proteins, like ERK and GluR1, in the psychostimulant paradigm and elaborates on the effects of knocking down key signaling molecules, like DARPP32. Crosstalk between the two signaling modules is one important aspect and how different crosstalk schemes can affect the measured outputs is illustrated. Even though the complexity of this model is high, still there is room for improvement to explain in more detail the multitude of physiological behaviors manifested by these complex signaling networks.

While modeling a small volume, like a dendritic spine, it should be noted that the actual number of molecules present may be too low to safely assume the well mixed assumption of chemical kinetics (Bhalla, 2004b). In this case the stochastic nature of chemical reactions and diffusion of different signaling molecules should be taken into account (Bhalla, 2004a). By taking into account the stochastic and diffusive effects for the signaling molecules, it has been possible to model the effects of subcellular localization on the efficiency of information transmission between signaling proteins connected through a second messenger, e.g., the colocalization of PKA with adenylyl cyclase in dendritic spines leads to a higher Thr34 phosphorylation (Oliveira, Kim, & Blackwell, 2012).

The signaling pathways aforementioned are involved in long term synaptic plasticity in the striatum and over the years it has become clear that synaptic plasticity such as LTP (long-term potentiation) or LTD (long-term depression) not only underlies learning and memory in the healthy brain but also the aberrations in a diseased brain (Picconi et al., 2005). Disturbances in synaptic plasticity can explain onset of drug addiction, progression of neurodegenerative disease symptoms as well as side effects following their prolonged treatment (Kasanetz et al., 2010; Picconi et al., 2003). DARPP32 is involved in these plasticity events but the induction of LTP and LTD also depends on the differential activation of a variety of signaling molecules other than DARPP32. This induction requires certain criteria to be satisfied, e.g., NMDAR calcium current seems to be important for LTP induction whereas release of endocannabinoids may be important for LTD induction (Malenka & Bear, 2004) (Figure 6). Endocannabinoids are small lipid soluble molecules released into the synaptic cleft by the postsynaptic site. They activate the presynaptic cannabinoid receptors which in turn reduces the neurotransmission (Lovinger & Mathur, 2012). Several other neurotransmitters, like acetylcholine and GABA, also affect synaptic plasticity (Bonsi et al., 2008; Paille et al., 2013). Similar to that observed in the hippocampus, the selection between LTD and LT Psometimes depends on the frequency and time duration of the input signal (Charpier, Mahon, & Deniau, 1999; Ronesi & Lovinger, 2005).

Figure 6.

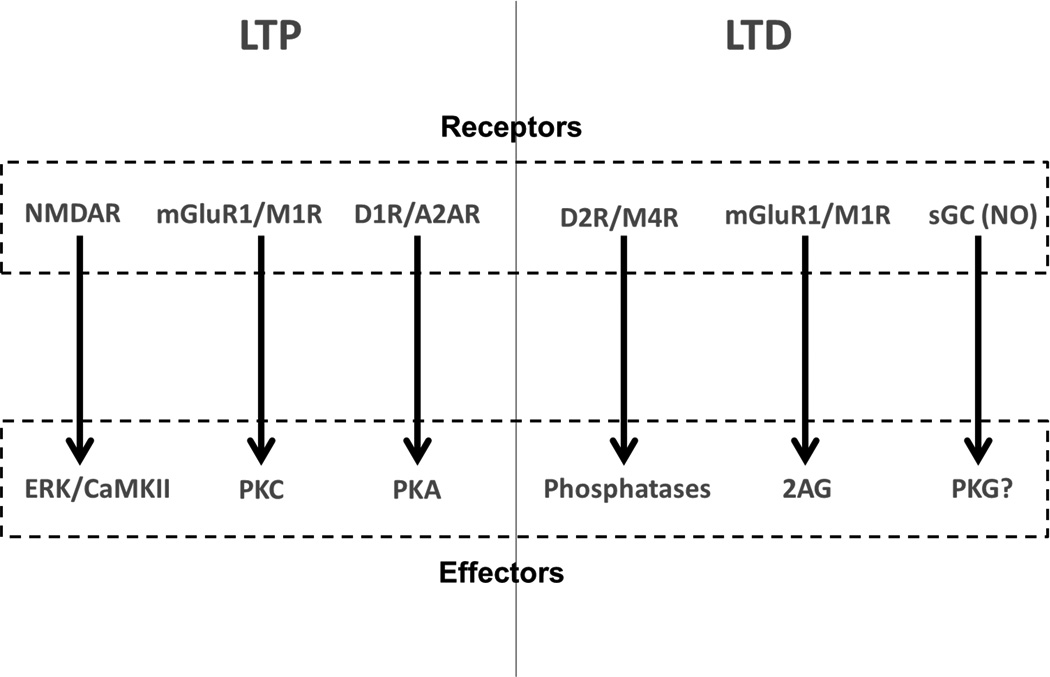
Receptors and downstream effectors involved in synaptic plasticity. The effectors represented here are markers for LTD and LTP (Calabresi, Picconi, Tozzi, & Di Filippo, 2007; Gerfen & Surmeier, 2011; Lovinger, 2010; Tritsch & Sabatini, 2012).

One of the recent striatal models tries to explain the selection between LTP and LTD based on the temporal patterns of the synaptic input (Kim, Hawes, Gillani, Wallace, & Blackwell, 2013). The LTP and LTD markers used in this model are protein kinase C (PKC) and encannabinoids, respectively. Both of these molecules require activation of metabotropic glutamate receptor type I (mGluR) and calcium. The inputs to the model are mGluR agonist and calcium. The simulation results highlight that an extended 20 Hz input signal induces LTD in corticostriatal synapses while a theta burst protocol induces LTP due to differential level of effector activation. Specifically, theta burst protocol resulted in an increase in the ratio of protein kinase C to endocannabinoid production while the 20 Hz stimulation had the reverse effect. These themes of competing pathways and balance between effectors, e.g. kinases and phosphatases, have been looked at with interest in a number of studies where one pathway leads to LTP and the other leads to LTD. A balance between CaMKII and PP2B has been used as a factor involved in the selection between LTP and LTD in various studies of (L. Li et al., 2012; Stefan et al., 2008). The balance between CaMKII and PP2B controls the phosphorylation state ofionotropic glutamate receptors (Hayashi, 2000; Nakano et al., 2010). At a low calcium elevation, such as produced by a weak stimulation, the PP2B activity dominates, leading to a reduction in the number of synaptic ionotropic glutamate receptors, mainly the GluR1 subunit of the AMPA type receptor. At a higher calcium level, such as produced by strong stimulation, CaMKII activity takes over (L. Li et al., 2012), producing an increase in these receptors. This phenomenon has been highlighted as important for the striatal system as well (Nakano et al., 2010), where the AMPA type receptor concentration in the post synaptic membrane was considered as a marker for synaptic plasticity. Our example model, Figure 4(A), also schematically describes this balance.

For our example model, the balance between phosphatase and kinaseis expressed as the difference between the activity of PP2B and CaMKII (Figure 4(B)). The balance between PP2B and CaMKII is of relevance not only in the hippocampus but also to striatal signaling, because PP2B decreases the inhibition of phosphatase PP1 by dephosphorylating the T34 residue on DARPP32 (Hemmings et al., 1984; P Svenningsson et al., 2000). This in turn increases the dephosphorylation of GluR1 subunits, which are phosphorylated by CaMKII (Snyder et al., 2000). In addition, there is a PP2B mediated, but PP1 independent effect, on GluR1dephosphorylation (Snyder et al., 2003). In summary, there seems to be an opposing effect of PP2B and CaMKII on AMPA receptor subunit phosphorylation state in the striatum, which would control the synaptic plasticity direction depending upon the calcium concentration as has been observed in the hippocampus (Castellani, Quinlan, Bersani, Cooper, & Shouval, 2005). This balance can be seen by the same number of calcium inputs but with different frequencies to the model (Figure 4(C)). For lower frequencies the PP2B activity is higher because of its high affinity with calcium/calmodulin and vice versa for CaMKII, as explained above.

Here, we have reviewed different aspects of existing post synaptic signaling network models in MSNs thought to be involved in synaptic plasticity. These models provide us with a better mechanistic understanding of the functioning of this complex system, and can, hopefully, serve as tools to understand the aberrations in pathological conditions.

Modeling dopamine metabolism and energy demand in midbrain dopaminergic neurons

It is not only the post synaptic signaling events in MSNs which have been formalized using modeling approaches. Signaling in the presynaptic dopamine neurons has also been modeled because of its implications in pathological conditions such as Parkinson disease which results from the death of midbrain dopaminergic neurons. The innervation of the striatum by the axonal arbor of these neurons is so dense that most of the cell volume is located there (Matsuda et al., 2009). There has been an intense debate on the cause of demise of these neurons and several lines of evidence point to oxidative stress as one potential factor. To explore possible factors contributing to dopaminergic cell death, two different groups have modeled physiological aspects of midbrain dopaminergic neurons.

The synthesis, release, uptake and degradation of dopamine have been modeled using the biochemical system theory (Qi et al., 2008). In this framework, the rate of change of the system species is represented as a power law of its concentrations. This is an approximation to mechanistic steady state formalisms like Michaelis-Menten or Hill equations (Voit & Savageau, 1987; Voit, 2013). Interestingly, while the model parameters were set to match metabolite amounts according to “experts”, the model reproduced with relatively high accuracy experimental results obtained with mutants and knock outs of several enzymes in the system. Assisted by sensitivity analysis the authors suggested the possible therapeutic intervention of several enzymes for increasing dopamine level in Parkinsonian patients. For example, while the inhibition of monoamine oxidase (MAO) does increase the dopamine level by reducing its degradation, it also increased the level of reactive metabolites that could contribute to the demise of dopaminergic neurons characteristic of Parkinson disease. This sensitivity-based analysis suggested that the enhancement of the vesicular transporter of dopamine (VMAT2) or addressing multiple targets were better strategies. The analysis also illustrates a low sensitivity of the output to most of parameters in the model, which was interpreted as the model being robust to moderate perturbations (Qi et al., 2008; Qi, Miller, & Voit, 2012).

Another study addressed the energy demand of electrical conduction along the uniquely extensive and non-myelinated axon of these neurons (Pissadaki & Bolam, 2013). The authors developed a multi-compartment single neuron model based on previous models for these neurons (Canavier & Landry, 2006) but with a more detailed representation of the axonal arbor and including intracellular Ca⁺² buffers. With this model they estimated the amount of ions that moved down the electrochemical gradient upon an action potential. These ions are pumped back to re-establish resting conditions with an energy cost that was estimated from the stoichiometry of ions per ATP by the Na⁺-K⁺ and Ca²⁺ pumps. The authors predicted that these neurons are subjected to extraordinary energy demands which growth exponentially with the complexity of the axonal arbor. These demands would stress the cell with the higher amount of reactive oxygen species generated by mitochondrial respiration. The dependency on axonal complexity would explain why the disease appears in larger animals like humans but not in smaller animals. While the conclusions of this work are connected to intracellular energy generation pathways, they are not modeled explicitly and the core of the argument rests on the cellular model.

The way forward: multi-scale modeling and data integration

The basal ganglia are both experimentally and computationally studied on several levels, from subcellular, cellular and synaptic properties to involvement in behavior in health and disease. The macroscopic properties of the neurons and synapse, e.g. membrane excitability and synaptic strength, can be controlled by molecular events, like dopamine receptor activation (Nicola, Surmeier, & Malenka, 2000; Szalisznyó & Müller, 2009). In order to integrate data from these different levels and sources in a manner that supports a quantitative understanding, modeling spanning the subcellular - microcircuit - systems level is necessary.

To reach a thorough quantitative understanding how phenomena on e.g. the subcellular level affect the cellular/network levels, one needs eventually to combine "classic" computational neuroscience with modeling of subcellular processes (which rather can be classified as systems biology). Such multi-scale approaches are necessary to trace the casual chain of events in neural systems (Kotaleski & Blackwell, 2010). There have been attempts to integrate the different levels of abstraction (Bhalla, 2011; Mattioni & Le Novère, 2013). However, such integration between the scales, if done at runtime, is computationally demanding.

To integrate neural levels in practice implies that models built by different research groups on different scales or representing different brain structures need to be possible to combine and build further on to eventually construct simulations on how different scales interact. Historically, however, models of individual neurons/networks or subcellular systems have been developed in single labs, possibly using a standard simulator or using custom code in a high level language. How should we go about integrating models of several brain areas or description levels of a certain brain systems? One approach of integrating scales would be to rework all the models in a single simulation environment. However, this is enormously wasteful of previous coding effort and debugging, and is fraught with potential for misrepresenting the model and obtaining the wrong behavior. In addition, in a multi-scale approach, it is unlikely that a single simulation environment will work for all scales of analysis. One solution is to reuse the code bases for all the individual contributions and tie them together with a ‘middleware’ which deals transparently with inter-language problems, simulation timing issues, and other technical issues which should not have to be solved at every step. Fortunately such middleware exist. MUSIC, the Multi-Simulation Coordinator (Djurfeldt et al., 2010), is a software which allows parallel neuronal simulators to communicate on-line in a super-computer. This allows large-scale simulations to be built in a modular way, and allows for the composition of models written for different simulation software such as Neuron, MOOSE, and Nest. It could provide one of the technologies when moving towards multi-scale and multi-physics simulations (Brandi et al., 2011).

In addition to runtime model integration discussed above, computational predictions obtained at different scales can be used as constraints during the model building process, e.g., the molecular structures of the proteins involved can put constraints on reaction schemes for a biochemical signaling network. This could be illustrated with following example. If it is known that protein A and protein B interact and protein C disrupts this interaction, two types of inhibitory interactions may occur: (a) a competitive inhibition, which consists of two separate binary complexes, namely AB and AC, or (b) a non-competitive inhibition model which also contains a ternary complex ABC. With protein structural information in hand, a computational protein-protein docking exercise (Dominguez, Boelens, & Bonvin, 2003) can help to resolve which type of inhibition occurs. As mentioned earlier, one of the most important steps in building signaling models is to identify the interactions between different molecules. Despite all efforts, like high throughput pull down techniques, it is difficult to capture all the protein-protein interactions due to their transient nature (Beltrao, Kiel, & Serrano, 2007). Here the protein structural details come in handy (Aloy & Russell, 2006). Apart from providing the details of how to model a reaction qualitatively, computational methods can also help us with estimation of quantitative parameters of an interaction, such as association rate constants (Kiel, Aydin, & Serrano, 2008). If the affinity constant is known for an interacting homologous protein pair then a range of affinity constants can be estimated using structural information and programs like FoldX (Beltrao et al., 2007; Guerois, Nielsen, & Serrano, 2002; J. W. H. Schymkowitz et al., 2005; J. Schymkowitz et al., 2005).

It is not just the protein interaction or structural data which could be used for model building at the subcellular level, but high throughput data could also assist this process. In the last decade, proteomics has contributed considerably to the field of neuroscience in delineating the machineries involved in synaptic dynamics and nervous system disorders (Grant, Marshall, Page, Cumiskey, & Armstrong, 2005; Husi & Grant, 2001; Micheva, Busse, Weiler, O’Rourke, & Smith, 2010). Efforts have also been made to develop new techniques and resources to generate gene expression data (Doyle et al., 2008; Heiman et al., 2008) and organize them into databases like, GENSAT and Allen Brain Atlas (Gong et al., 2003; Lein et al., 2007). Not surprisingly, transcriptome for the striatal medium spiny neurons (MSN) also exists (Heiman et al., 2008; Lobo, Karsten, Gray, Geschwind, & Yang, 2006). This information can help us greatly to extend the already existing models in the field. For example, the transcriptome data show that a number of signal transduction proteins currently not included in any models and molecules like CalDAGGEFs, EPAC are known to be involved in the MAPK/ERK activation, etc. These components could be included into the existing models to get a better understanding of the system. We therefore feel that multi-scale modeling together with high throughput data integration should be an important way forward.